Marcus kinetics control singlet and triplet oxygen evolving from superoxide

Abstract

Oxygen redox chemistry is central to life¹ and many human-made technologies, such as in energy storage^2,3,4. The large energy gain from oxygen redox reactions is often connected with the occurrence of harmful reactive oxygen species^3,5,6. Key species are superoxide and the highly reactive singlet oxygen^3,4,5,6,7, which may evolve from superoxide. However, the factors determining the formation of singlet oxygen, rather than the relatively unreactive triplet oxygen, are unknown. Here we report that the release of triplet or singlet oxygen is governed by individual Marcus normal and inverted region behaviour. We found that as the driving force for the reaction increases, the initially dominant evolution of triplet oxygen slows down, and singlet oxygen evolution becomes predominant with higher maximum kinetics. This behaviour also applies to the widely observed superoxide disproportionation, in which one superoxide is oxidized by another, in both non-aqueous and aqueous systems, with Lewis and Brønsted acidity controlling the driving forces. Singlet oxygen yields governed by these conditions are relevant, for example, in batteries or cellular organelles in which superoxide forms. Our findings suggest ways to understand and control spin states and kinetics in oxygen redox chemistry, with implications for fields, including life sciences, pure chemistry and energy storage.

Main

More than half a century after the discovery that singlet oxygen forms from superoxide⁸, what governs the evolution of singlet or triplet oxygen under many conditions relevant to life and human-made oxygen redox systems remains unknown. Oxygen redox chemistry is crucial to life¹ and encompasses some of the most fundamental and widespread chemical reactions, including those in batteries^2,3,4,9, fuel cells and electrocatalysis¹⁰, and organic chemistry¹¹. The oxidation states that are accessed in these reactions range from 0 (dioxygen) to –2 (oxide), with intermediate redox states of –½ and –1, pertaining to superoxide (O₂⁻) and peroxide (O₂²⁻) or the oxide radical (O^•–). Superoxide is pivotal in oxygen reduction and evolution reactions because it is the closest oxidation state to dioxygen. Dioxygen appears either in its ground state as triplet oxygen (³O₂ or ³Σ_g^–) or as singlet oxygen (¹O₂ or ¹Δ_g) in its first electronically excited state. Whereas ³O₂ is relatively unreactive, ¹O₂ is highly reactive with most organic matter^11,12. This is readily evidenced in metal-ion batteries^6,7 and metal-O₂ batteries^3,4, in which ¹O₂ is the primary source of degradation, causing decomposition of organic electrolytes and conductive carbon additives, which ultimately degrades the overall device function. Moreover, ¹O₂ and (su)peroxide are well-known reactive oxygen species in biological systems and are involved in several processes from signalling to cell damage^1,5.

Superoxide liberates oxygen under a broad range of oxidizing conditions. A prevalent process is disproportionation due to the instability of superoxides in most of the environments^3,9,13. This reaction occurs in both protic (aqueous)^14,15 and aprotic environments with relatively strong Lewis acids such as Li⁺ and Na⁺ (refs. ^6,9,13,16). During disproportionation (2O₂⁻ → O₂ + O₂²⁻), one superoxide molecule is reduced to peroxide, whereas the other is oxidized to form either ³O₂ or ¹O₂. Examples can be found in both cellular respiration^1,5 and batteries^{13,16,17,18,19,20}. Relative ³O₂ and ¹O₂ yields and kinetics of superoxide disproportionation, and superoxide oxidation more generally, are therefore fundamental to these systems, but underlying mechanisms are still unknown.

Here we examined ¹O₂ evolution from the oxidation of superoxide through both chemical reaction and disproportionation over a wide range of driving forces. On the basis of this, we observe distinct Marcus normal and inverted region behaviour for ³O₂ and ¹O₂ evolution, which explains ¹O₂ formation over a broad range of scenarios in which superoxide oxidation occurs, for example, in biological systems and energy storage.

Excited species through electron transfer

Superoxide oxidation may form both ³O₂ and ¹O₂ according to Wigner–Witmer spin conservation rules²¹. This applies to disproportionation, in which two doublet superoxides can produce triplet or singlet products¹⁷, and to oxidation by a redox mediator (RM^ox) to form one excited (¹O₂) and one ground state molecule (the reduced mediator, RM^red) (ref. ²²).

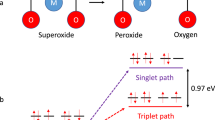
We previously investigated the mediated oxidation of superoxide through the reaction KO₂ + RM^ox → O₂ + RM^red + K⁺ in the search for possible ¹O₂ evolution¹⁸. The potential ${E}_{{\text{RM}}^{\text{ox}/\text{red}}}^{\circ }$ was limited to moderate values because of the stability of the ether electrolyte used. We measured ³O₂ and ¹O₂ yields using mass spectrometry and a chemical trap, respectively, and tracked the reaction kinetics using ultraviolet–visible (UV–Vis) spectroscopy. The data shown in Extended Data Fig. 1 supported two main conclusions: first, ¹O₂ was observed with RMs with ${E}_{{\text{RM}}^{\text{ox}/\text{red}}}^{\circ }\gtrsim {E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\text{KO}}_{2}}^{\circ }+1\,{\rm{V}}$, which could be in accordance with the frequently quoted threshold^{3,23,24,25,26} for ¹O₂ evolution based on the energy difference of 0.97 eV between ³O₂ and ¹O₂; and second, the kinetics of superoxide oxidation over the measured range of driving forces exhibited Marcus normal and inverted region behaviour. This behaviour is characterized by a parabolic relationship between the logarithm of the kinetic constant k and the driving force (free energy change) $-\Delta {G}^{\circ }=\left({E}_{{\text{RM}}^{\text{ox}/\text{red}}}^{\circ }-{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\text{KO}}_{2}}^{\circ }\right)F$:

$$k={Z}_{{\rm{el}}}\cdot {{\rm{e}}}^{\frac{-(\Delta {G}^{\circ }+\lambda {)}^{2}}{4RT\lambda }}$$

(1)

where Z_el is the collision factor, λ is the reorganization energy and F is the Faraday constant^22,27,28. The kinetic constant k reaches a peak when –ΔG° = λ and electron transfer becomes barrierless. The inverted region results from growing barriers at even higher driving forces. The data suggested that superoxide oxidation kinetics follow a single parabola and that some ¹O₂ is generated for –ΔG° ≳ 0.97 eV. However, what controls the extent to which ¹O₂ or ³O₂ evolve is yet unknown.

¹O₂ evolution should be a distinct elementary step both thermodynamically and kinetically. We, therefore, propose that the observed parabola in Extended Data Fig. 1 describes oxidation to ³O₂, and a second parabola should appear at sufficiently large driving forces, representing oxidation to ¹O₂ (Fig. 1a). The intersection of these two parabolas would indicate the transition from ³O₂ to ¹O₂. This follows classical work by Marcus on the electrogeneration of electronically excited species^22,27. However, this hypothesis has not yet been experimentally evaluated for ¹O₂ generation.

Fig. 1: Marcus theory suggests separate kinetics of superoxide oxidation to ³O₂ and ¹O₂.

a, Hypothesis for how the driving force could govern ³O₂ and ¹O₂ formation kinetics from superoxide oxidation. The left parabola results from previously measured rate constants for mediated superoxide oxidation with driving forces up to –ΔG° ≈ 1.2 eV as shown in Extended Data Fig. 1. However, a single kinetic parabola could not conclusively explain why ¹O₂ formed for –ΔG° ≳ 1 eV. Based on the considerations in b, individual kinetic parabolas (k₃ and k₁) for the reactions yielding ³O₂ and ¹O₂ can be constructed with the full line showing their sum. The maxima are shifted by ${\Delta G}_{1\leftarrow 3}^{\circ }\approx 0.97{\rm{eV}}$ (see text), and equal prefactors and reorganization energies are assumed. The blue- and red-shaded area shows the transition from k₃/(k₁₊₃) = 0.99 to k₁/(k₁₊₃) = 0.99. b, Potential energy surfaces for mediated superoxide oxidation for different driving forces. Black, blue and red parabolas denote reactants (KO₂ + RM^ox) and ³O₂ or ¹O₂ in the products (³O₂ + RM^red or ¹O₂ + RM^red), respectively. The cases shown are for barrierless reactions to ³O₂ (i) and ¹O₂ (iii) and equal barriers (ii). The subscripts 3 and 1 denote triplet and singlet states, respectively.

Source Data

Based on equation (1), a kinetic expression with separate terms for ³O₂ and ¹O₂ evolution can be given as

$${k}_{1+3}={k}_{3}+{k}_{1}={Z}_{{\rm{el}},3}\cdot {{\rm{e}}}^{\frac{-{(\Delta {G}^{\circ }+{\lambda }_{3})}^{2}}{4RT{\lambda }_{3}}}+{Z}_{{\rm{el}},1}\cdot {{\rm{e}}}^{\frac{-{(\Delta {G}^{\circ }+{\Delta G}_{1\leftarrow 3}^{\circ }+{\lambda }_{1})}^{2}}{4RT{\lambda }_{1}}}.$$

(2)

The subscripts 3 and 1 on k, Z_el and λ denote values for ³O₂ and ¹O₂, respectively. The blue- and red-dashed parabolas in Fig. 1a represent the terms for ³O₂ and ¹O₂, whereas the solid line shows their sum. The k₃ parabola results from the transition from the black to the blue potential energy surfaces in Fig. 1b, which are shown for –ΔG° ≈ λ₃ for case (i). The vibrational ground states of ³O₂ and ¹O₂ differ by ${\Delta H}_{1\leftarrow 3}^{\circ }=\Delta {H}^{\circ }\left(\genfrac{}{}{0ex}{}{1}{}\,{\Delta }_{\text{g}}\leftarrow \genfrac{}{}{0ex}{}{3}{}\,{\Sigma }_{\text{g}}^{-}\right)=0.97\,{\rm{eV}}$, where ΔH is the enthalpy change¹². Assuming, for now, a vanishing entropy change ΔS as typically done in electrochemiluminescence literature²⁸, ${\Delta G}_{1\leftarrow 3}^{\circ }=\Delta {G}^{\circ }\left(\genfrac{}{}{0ex}{}{1}{}\,{\Delta }_{\text{g}}\leftarrow \genfrac{}{}{0ex}{}{3}{}\,{\Sigma }_{\text{g}}^{-}\right)\approx {\Delta H}_{1\leftarrow 3}^{\circ }$, by which the singlet potential energy surface shifts vertically (Fig. 1b, red). For sufficiently large driving forces, the barriers ΔG^‡ and kinetics for crossing to ³O₂ and ¹O₂ become equal (Fig. 1, case (ii)) or even barrierless to ¹O₂ (case (iii)). Hence, individual kinetic parabolas for superoxide oxidation to ³O₂ and ¹O₂ can be constructed. The hypothetical parabola for ¹O₂ evolution can be drawn if we further assume, for now, equal collision factors Z_el,1 = Z_el,1 and equal reorganization energies λ₁ = λ₃ as fitted to the data in Extended Data Fig. 1. The theory developed initially for homogeneous electron transfer can still be used for semiconductors or insulators, as noted by Marcus²². Therefore, the considerations in Fig. 1 apply to the oxidation of solid superoxides and superoxide solutions.

Kinetics over extended driving forces

To test the hypothesis of individual kinetic parabolas for ³O₂ and ¹O₂ evolution, we selected acetonitrile (MeCN) as the solvent. Acetonitrile is highly stable against oxidation and, therefore, allows for large driving forces (Extended Data Fig. 2a) to be tested. We used a wide range of mediators (Extended Data Fig. 2b) with redox potentials that exceed the expected maximum of the ¹O₂ parabola. Figure 2a shows the measured kinetics as a function of driving force relative to ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\text{KO}}_{2}}^{\circ }$ (Methods). The measured kinetics can be adequately fitted to equation (2). The blue- and red-dashed parabolas represent the terms for ³O₂ and ¹O₂ evolution, whereas the solid line shows their sum. Evidence for these parabolas corresponding to ³O₂ and ¹O₂ is provided by measured yields (Fig. 2b,c). The ³O₂ yields were measured by mass spectrometry and quantified as the molar ratio ³O₂/RM^ox. ¹O₂ formation was measured by its specific 1,270 nm near-infrared (NIR) radiation (Methods). Absolute quantification of ¹O₂ is difficult, and values were, therefore, normalized to the maximum observed.

Fig. 2: Free energy dependence of superoxide oxidation kinetics to ³O₂ and ¹O₂ and their yields.

a, We measured the kinetic constants k for mediated KO₂ oxidation in MeCN electrolyte with mediators covering a large range of redox potentials. Plot of ln(k) compared with the mediator potential (${E}_{{\text{RM}}^{\text{ox}/\text{red}}}^{\circ }$, top axis) and driving force (–ΔG°, bottom axis). $-\Delta {G}^{\circ }=\left({E}_{{\text{RM}}^{\text{ox}/\text{red}}}^{\circ }-{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\text{KO}}_{2}}^{\circ }\right)\,F$, where ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\text{KO}}_{2}}^{\circ }=2.48\,{\rm{V}}$ on the K/K⁺ scale. The mediators are shown in Extended Data Fig. 2. The full line best fits equation (2); the broken line parabolas represent the first and second terms in equation (2). The fitted values are Z_el,3 = 1.10 × 10^–2 cm s^–1, Z_el,1 = 7.00 × 10^–2 cm s^–1, λ₃ = λ₁ = 0.95 eV, ${\Delta G}_{1\leftarrow 3}^{\circ }=0.84\,{\rm{eV}}$ and R² = 0.998. Based on these fits, the standard potential ${E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{\text{KO}}_{2}}^{\circ }$ and associated driving force ${\Delta G}_{1\leftarrow 3}^{\circ }$ are marked. They are linked by ${E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{\text{KO}}_{2}}^{\circ }\,=\,{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\text{KO}}_{2}}^{\circ }+{\Delta G}_{1\leftarrow 3}^{\circ }/F$. The blue- and red-shaded area indicates the transition from k₃/(k₁₊₃) = 0.99 to k₁/(k₁₊₃) = 0.99. b, ³O₂ yield per mole of RM^ox (bars) during KO₂ oxidation as measured by mass spectrometry. The dashed line and the circular markers show simulated ³O₂ yields considering ¹O₂ quenching by solvent and redox mediator (Methods and Extended Data Fig. 3). The dashed line used the trend line for the mediator quenching rate constant k_Q, whereas the markers use the individually measured values (Extended Data Fig. 3c). c, Normalized 1,270 nm NIR emission (bars) during KO₂ oxidation. The dashed line and the circular markers show the simulated NIR emission considering ¹O₂ formation with the kinetics k₁ (the right parabola in a) and ¹O₂ quenching by solvent and redox mediator (Methods and Extended Data Fig. 3). Data are presented as mean ± s.d. (n ≥ 3).

Source Data

Observable yields of ³O₂/RM^ox and NIR intensities do not simply resemble the relative kinetics of ³O₂ and ¹O₂ formation as obtained in Fig. 2a. Instead, the formed ¹O₂ undergoes multiple decay pathways, of which some yield ³O₂ and only a small fraction emits the NIR radiation¹². To rationalize the measured values, we simulated them based on formation rates and ¹O₂ decay processes (Methods and Extended Data Fig. 3): (1) ³O₂ and ¹O₂ formation rates as given by the parabolas in Fig. 2a; (2) physical and reactive ¹O₂ quenching by the solvent; (3) physical and reactive ¹O₂ quenching by the mediators; and (4) ³O₂ losses resulting from reactive quenching of ¹O₂ with solvent or mediator. Simulation results are shown as dashed lines and markers in Fig. 2b,c and resemble the measured data. Deviations result from simplifications of the model, such as not accounting for specific reactivities of the chemically diverse mediators (Methods). Overall, a proper fit of the kinetics to the double parabola in equation (2) (Fig. 2a), the deficiencies in ³O₂ yields and the growing NIR signal beyond the predicted onset potential (Fig. 2b,c) all support the proposed hypothesis that individual Marcus parabolas govern ³O₂ and ¹O₂ formation from superoxide.

The adequate fit supports several important conclusions: (1) The prefactors Z_el,1 ≈ 6.3 × Z_el,3 result in substantially higher maximum kinetics for ¹O₂ evolution. (2) Driving forces for maximum kinetics are solvent-dependent, as shown by the comparison between values in ether solvent (Fig. 1a; λ₃ = 0.61 eV) and acetonitrile (Fig. 2a; λ₃ = 0.95 eV). This aligns with the prediction²⁷ of Marcus and work by Miller²⁹. The crossing point of the two parabolas is not at a constant driving force, which benefits ¹O₂ for solvents with lower λ (Extended Data Fig. 4a). (3) ${E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{\rm{superoxide}}}^{\circ }$ should not be considered the threshold above which ¹O₂ rather than ³O₂ forms^18,24,26 as suggested from the electrochemiluminescence literature (Methods) but as a possible onset of ¹O₂. Reaching ${E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{\rm{superoxide}}}^{\circ }$ per se tells little about the relative ³O₂ and ¹O₂ formation kinetics because of the solvent-dependent reorganization energy (Extended Data Fig. 4). Instead, driving forces –ΔG° > λ₃ are required to slow ³O₂ formation to benefit ¹O₂. (4) In the electrochemiluminescence literature, the entropy change is unknown and typically neglected²⁸. Having data that show the peaks for ³O₂ and ¹O₂ permits us to determine ${\Delta G}_{1\leftarrow 3}^{\circ }=0.84\,{\rm{eV}}$ and with ${\Delta H}_{1\leftarrow 3}^{\circ }=\,{\Delta G}_{1\leftarrow 3}^{\circ }+T{\Delta S}_{1\leftarrow 3}^{\circ }$ we obtain $T{\Delta S}_{1\leftarrow 3}^{\circ }=-\,0.13\,{\rm{eV}}$. Consequently, ${E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{\rm{superoxide}}}^{\circ }={E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}}^{\circ }+0.84\,{\rm{V}}$ can now be given more precisely, rather than with the typically used difference of 0.97 V.

Figure 2a establishes a working curve for an extensive range of ΔG°, facilitating an understanding of the behaviour of various important systems. Lewis-acid- and Brønsted-acid-driven superoxide disproportionation are two widely relevant cases, examined in the following sections. More examples of superoxide oxidation, in which an explanation of whether, or not, ¹O₂ forms has been unknown, but which can now be explained, are examined in Extended Data Fig. 4 and the Methods. These examples include superoxide in contact with CO₂ and organic peroxides, with relevance for energy storage and biological systems^1,4,30.

Disproportionation in non-aqueous systems

¹O₂ is known to cause degradation in non-aqueous alkali metal-O₂ batteries^{3,13,16,17,18,19}. The Li–O₂ battery, for example, operates by reversibly forming lithium peroxide at the positive electrode, O₂ + 2e^– + 2Li⁺ ⇄ Li₂O₂. Initially formed LiO₂ disproportionates, which always results in some ¹O₂ according to 2LiO₂ → Li₂O₂ + x³O₂ + (1 − x)¹O₂ (refs. ^{13,16,17,18,19}). Weak Lewis acids such as tetrabutylammonium (TBA⁺), or other similar cations from ionic liquid electrolytes, are often present in these cells. Despite not driving disproportionation themselves, weak Lewis acids were found to raise the ¹O₂ fraction from about 2% in pure Li⁺ electrolyte to around 20% for 1/1 Li⁺/TBA⁺ electrolyte¹⁶. However, to date, it has been unclear why pure Li⁺ generates ¹O₂ at all and why weak Lewis acids should increase the ¹O₂ fraction.

Figure 3a shows the thermodynamics of the relevant redox couples as a function of the Li⁺ and TBA⁺ salt fractions in glyme electrolyte. Figure 3b shows the NIR emission intensities on adding KO₂ as a superoxide source into these electrolytes. The thermodynamics are explored in further detail in the Methods and Extended Data Fig. 5 and are summarized here. Li₂O₂ is insoluble, and the potential ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{Li}}}_{2}{{\rm{O}}}_{2}({\rm{s}})}$, therefore, fixed (Fig. 3a, black line). However, superoxide is appreciably soluble in non-aqueous electrolytes^31,32,33: species include ${({{\rm{Li}}}^{+}{{{\rm{O}}}_{2}}^{-})}_{n\ge 1,({\rm{sln}})}$ clusters or ion pairs, where (sln) denotes solvate species. Solid LiO_2(s) has the lowest Gibbs free energy, and increasingly solvated species are increasingly less stable^32,33,34. The ³O₂/superoxide potentials are, therefore, within the upper limit of ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{Li}}{{\rm{O}}}_{2}({\rm{s}})}$ and the lower limit of ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}}$ (Fig. 3a, light-blue gradient-coloured box). When TBA⁺ is present, the lower limit extends to ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{TBA}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}}$.

Fig. 3: Driving forces, kinetics and ¹O₂ formation during Lewis-acid-induced superoxide disproportionation.

a, Thermodynamics of relevant redox couples for Li⁺-induced superoxide disproportionation as a function of the fractions of Li⁺ and TBA⁺ salt. The gradient boxes and short arrows indicate increasing superoxide solvation with potentials between values relevant for solid LiO_2(s) (dark colour), solvated ${({{\rm{Li}}}^{+}{{{\rm{O}}}_{2}}^{-})}_{n\ge 1,({\rm{sln}})}$ clusters, and solvated ${({{\rm{Li}}}^{+}{{{\rm{O}}}_{2}}^{-})}_{({\rm{sln}})}$ (faded colour). LiO₂ is in all relevant electrolytes at least somewhat soluble as ${({{\rm{Li}}}^{+}{{{\rm{O}}}_{2}}^{-})}_{n\ge 1,({\rm{sln}})}$ clusters. The nature of superoxide shifts from ${({{\rm{Li}}}^{+}{{{\rm{O}}}_{2}}^{-})}_{n\ge 1,({\rm{sln}})}$ towards ${({{\rm{TBA}}}^{+}{{{\rm{O}}}_{2}}^{-})}_{({\rm{sln}})}$ as the cation changes from pure Li⁺ towards pure TBA⁺. The inclined lines indicate the associated shift of the potentials. ${E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{\rm{superoxide}}}={E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}}+0.84\,{\rm{V}}$. The driving force $\Delta G=-\,({E}_{{\rm{superoxide}}/{\text{Li}}_{2}{\text{O}}_{2}}-{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}})F$ grows with the shift of the O₂/superoxide and superoxide/Li₂O_2(s) potentials. Note that the O₂ reduction potential changes nonlinearly with the Li⁺:TBA⁺ ratio³². b, Normalized 1,270 nm NIR emission as a function of Li⁺ mole fraction, which determines the driving force. The markers show superoxide disproportionation kinetics as measured by pressure evolution. The dotted line is a guide to the eye. Glyme served as the electrolyte solvent. Data are presented as mean ± s.d. (n ≥ 3).

Source Data

The superoxide/Li₂O_2(s) couple acts as the oxidant during superoxide disproportionation. ${E}_{{\rm{superoxide}}/{{\rm{Li}}}_{2}{{\rm{O}}}_{2(\text{s})}}$ exceeds ${E}_{{{}^{1}{\rm{O}}}_{2}/{\rm{superoxide}}}$ already in pure Li⁺ electrolyte, in which the superoxide species are solvated, and therefore explains why an onset of ¹O₂ is observed. ¹O₂ is detected in pure Li⁺ electrolyte using more sensitive chemical trapping¹⁶. Addition of TBA⁺ favours more solvated species, which also explains why TBA⁺ increases the fraction of ¹O₂. In line with this, Fig. 3b shows steeply increasing ¹O₂ evolution as the TBA⁺ mole fraction increases, along with faster kinetics.

Proton-induced disproportionation

We next investigated how pH-related changes in driving force affect the ¹O₂ formation from proton-induced superoxide disproportionation. This is particularly relevant for living organisms, in which superoxide is found in organelles with pH levels ranging between 4.7 and 8 (ref. ³⁵), as well as in aqueous electrocatalysis¹⁰. Figure 4a shows the Pourbaix diagram with the potentials of relevant redox couples as a function of pH. Again, the driving force for disproportionation is the difference between the ³O₂/superoxide and superoxide/peroxide couple, marked with the vertical arrows. It grows from about 0.5 eV at pH 14 to about 1.5 eV below pH 4.8 (Fig. 4b). The oxidant potential exceeds ${E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{{\rm{O}}}_{2}^{-}}^{\circ }$ at pH about 10.5, in which an onset of ¹O₂ formation can be expected.

Fig. 4: Driving forces and NIR emission during proton-induced superoxide disproportionation.

a, Pourbaix diagram showing the pH-dependent stability range of aqueous electrolyte and the standard potentials ${E}^{\circ }$ of the indicated redox couples on the normal hydrogen electrode (NHE) scale¹⁵. The kinks in the curves arise from the pK_a values of H₂O₂ (pK_a = 11.7) and HO₂ (pK_a = 4.8). For simplicity, O₂^–/H₂O₂ is written while the pH-dependent (de)protonated species are meant. ${E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{{{\rm{O}}}_{2}}^{-}}^{\circ }={E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{O}}}_{2}^{-}}^{\circ }+0.84\,{\rm{V}}.$ b, The pH-dependent driving force for superoxide disproportionation is $-\Delta {G}^{\circ }=({E}_{{{\rm{O}}}_{2}^{-}/{\text{H}}_{2}{\text{O}}_{2}}^{\circ }-{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{O}}}_{2}^{-}}^{\circ })F$ as indicated by the vertical arrows in a. c, ¹O₂-specific NIR emission at 1,270 nm as a function of pH. Each marker represents a single measurement. The dotted line is a guide to the eye. PBS, phosphate-buffered saline.

Source Data

Figure 4c shows the ¹O₂-specific NIR signal at 1,270 nm on proton-induced superoxide disproportionation over a pH range from about 1 to 10.8. We exposed KO₂ to various buffer solutions under vigorous stirring and recorded the NIR signal (Methods). A strongly increasing NIR signal with decreasing pH is in accord with the increasing driving force. A pH of around 11 giving low but non-negligible ¹O₂ yields is consistent with reliable theoretical¹⁷ and experimental works¹⁴ on the reaction ${{\rm{HO}}}_{2}+{{\rm{O}}}_{2}^{-}\to {{\rm{O}}}_{2}+{{\rm{O}}}_{2}^{-}$, which found ¹O₂ evolution only about 0.3 eV endoergic and around 0.2% ¹O₂ production on exposing KO₂ to H₂O₂ as the proton source.

Conclusions

We found that the driving force for superoxide oxidation to ³O₂ and ¹O₂ is the common descriptor that determines the spin state, following individual Marcus normal and inverted region behaviour. ¹O₂ can become significant only because the kinetics for ³O₂ evolution slows down in its inverted region. The results help clarify previously inconclusive findings about ¹O₂ formation from superoxide, including through interaction with chemical oxidants, and proton and Lewis-acid-driven disproportionation. For disproportionation, the results explain the increasing ¹O₂ formation with stronger Brønsted and weaker Lewis acidity, respectively, because of their impact on driving forces. Increasing ¹O₂ yield with lower pH aligns with higher driving forces as the pH decreases. This corresponds with higher and lower pH in respiratory (mitochondria) and degenerative organelles (lysosomes)³⁵, respectively, in which ¹O₂ must be avoided or may even be beneficial. This connection between pH and ¹O₂ formation may well have been a so far unrecognized evolutionary driver for the pH found in organelles. In human-made redox systems, in which ¹O₂ is, in most cases, detrimental and damaging, strategies to suppress ¹O₂ should aim at reducing the driving forces for superoxide oxidation, increasing the reorganization energy, or avoiding situations in which superoxide disproportionates. We discuss the wider relevance for oxygen redox systems in life sciences and energy, and for the electrogeneration of excited species more generally in the Methods. The findings offer insights into understanding and controlling spin states and kinetics in oxygen redox chemistry, with implications for fields such as the life sciences and energy storage.

Methods

Materials

All chemicals were from Sigma Aldrich unless indicated differently. Potassium superoxide (KO₂), potassium perchlorate (KClO₄, ≥99.99%), lithium bis(trifluoromethanesulfonyl)imide (LiTFSI, 99.99%) and tetrabutylammonium bis(trifluoromethanesulfonyl)imide (TBATFSI, ≥99.0%) were dried under reduced pressure for 24 h at 100 °C. Decamethylferrocene (DMFc), tris[4-(diethylamino)phenyl]amine (TDPA), N,N,N′,N′-tetramethyl-p-phenylenediamine (TMPD), ferrocene (Fc), ferrocenium tetrafluoroborate (FcBF₄), 9,10-diphenylanthracene (DPA), 1,4-bis(diphenylamino)benzene (DPAB), thianthrene (ThA), 1,4-dimethoxyanthracene (DMeOA, Acros Organics), 1,4-di-tert-butyl-2,5-dimethoxybenzene (tMeOB, BLDpharm) and 5,10-dihydro-5,10-dimethylphenazine (DMPZ, TCI chemicals) were used as received. N-methyl phenothiazine (MPT), 1,4-diazabicyclo[2.2.2]octane (DABCO) were sublimated. 18-Crown-6 and tetrafluorobenzoquinone (F₄BQ) were recrystallized from ethanol. Tetraethylene glycol dimethyl ether (TEGDME, ≥99%) was dried over lithium, distilled under vacuum and further stored over activated 3 Å molecular sieves. Acetonitrile (MeCN, 99.8% anhydrous) was stored over activated molecular sieves. Both solvents had a water content below 5 ppm as determined by Karl–Fischer titration (Mettler Toledo). All non-aqueous experiments were performed in an Ar-filled glovebox (Vigor) or hermetically sealed setups without air exposure. The structures of the mediators and their redox potentials are shown in Extended Data Fig. 2.

Electrochemistry and mediator oxidation

Electrochemistry experiments were performed using a BioLogic potentiostat (SP-300 and MPG-2). Cyclic voltammetry was performed with a glassy carbon disk as the working electrode and a glassy carbon rod as the counter electrode in a one-compartment glass cell. Partially delithiated Li_(1–x)FePO₄ (LFP, MTI), separated by a Vycor glass frit, was used as the reference electrode. DMFc/DMFc⁺ was used as the internal standard and converted using ${E}_{{\rm{DMFc}}/{{\rm{DMFc}}}^{+}}^{\circ }={E}_{{\rm{Li}}/{{\rm{Li}}}^{+}}^{\circ }+3.16\,{\rm{V}}={E}_{{\rm{K}}/{{\rm{K}}}^{+}}^{\circ }$$+3.02\,{\rm{V}}.$ DMeOA, tMeOB, DPA and ThA were electrochemically oxidized in an H-cell. The oxidation compartment contained a Pt working electrode, the reference electrode and 5 ml MeCN containing 2 mM RM and 10 mM KClO₄. The reduction compartment contained Ni foam as a counterelectrode with 5 ml of 100 mM 1,4-benzoquinone (sublimed) in MeCN. A K⁺ selective ion-exchange membrane separated the two compartments. RMs were oxidized galvanostatically to 80% of their total capacity. DMFc, TDPA, TMPD, DMPZ, MPT and DPAB were oxidized using 1 equiv. NOBF₄ in MeCN. After 3 h stirring, they were precipitated with cold diethyl ether, filtered and dried under a vacuum at 30 °C for 12 h. F₄BQ is the oxidized form itself.

Measurements of kinetics

Kinetics of mediated superoxide oxidation were measured using UV–Vis spectroscopy using an Avantes AvaSpec-HSC spectrometer with AVALIGHT-DH-S-BAL light source and fibre optics to perform measurements inside the glove box. Pure KO₂ powder was pressed into about 0.5 mm thick pellets using a 7 mm die set and a hand press (PIKE). In a 10-mm quartz cuvette (Hellma), a KO₂ pellet was placed in a polytetrafluoroethylene frame for alignment, followed by a magnetic stirring bar and then the cuvette was sealed with a gas-tight injection lid. RM^ox solution containing 10 mM KClO₄ was then injected using a gas-tight syringe (Hamilton). Consumption of RM^ox was followed except for F₄BQ, in which formation of RM^red was followed (Extended Data Fig. 7). Data and error bars are presented as mean ± s.d. (n ≥ 3). Error bars appear asymmetric on an ln(k) scale. Repetitions mean that each time a new portion of RM^ox was produced by electrochemically oxidizing a portion of RM^red or by dissolving the chemically produced oxidized form. Differences in the magnitude of the error bars among mediators arise from their large chemical diversity and specific reactivities. For example, Fc⁺ and reduced quinones react with O₂, or high-voltage RM^ox shows limited long-term stability in the electrolyte. For the latter, it was checked that degradation was at least several times slower than the oxidation of KO₂.

Kinetics of Li⁺-induced superoxide disproportionation in TEGDME were measured by placing KO₂ powder in a closed reaction vessel equipped with a pressure sensor (Omega, PAA35X) and injecting the Li⁺ electrolyte using a syringe through a septum (Extended Data Fig. 8).

³O₂ yields and 1,270 nm emission measurements

³O₂ yields on mediated superoxide oxidation were measured using mass spectrometry, as detailed previously³⁰. The RM^ox solutions were injected using a gas-tight syringe, and the measurement continued until the O₂ signal ceased. We used the ¹O₂-specific NIR emission at 1,270 nm from the decay of ¹O₂ to ³O₂ to determine ¹O₂ yields and lifetimes as detailed previously³⁰. The signal was recorded from the detector using an oscilloscope (Pico Technology) and at a gain of 820 V (control voltage). Extended Data Fig. 6 shows examples of the recorded signal during mediated oxidation, as well as Li⁺- and H⁺-induced disproportionation.

From oxidation rates to ³O₂ yields and NIR emission intensities

We use the yields of ³O₂/RM^ox and the normalized NIR intensities in Fig. 2b,c to prove that the two kinetic parabolas correspond to ³O₂ and ¹O₂ evolution. To rationalize their assignment, we use a minimal model to calculate expected ³O₂/RM^ox and NIR emission intensities based on formation rates and ¹O₂ decay processes. We considered the following processes: (1) ³O₂ and ¹O₂ formation rates (k₃ and k₁) as given by the two kinetic parabolas in Fig. 2a; (2) physical and reactive ¹O₂ quenching by the solvent; (3) physical and reactive ¹O₂ quenching by the reduced mediators RM^red. Note that the same processes with RM^ox are typically negligible in comparison because of the electron demand of these processes³⁶; and (4) ³O₂ losses (³O₂/RM^ox < 1) resulting from reactive quenching of ¹O₂ with solvent or mediator.

Losses in ³O₂/RM^ox in Fig. 2b result from incomplete physical quenching of ¹O₂ to ³O₂ due to reactions of ¹O₂ with electrolyte or RM. Hence, we start by considering the decay routes. There are multiple decay routes, as shown in Extended Data Fig. 3f, and only a small fraction of the total ¹O₂ can be detected by the NIR emission at 1,270 nm (refs. ^12,37). First, interactions of ¹O₂ with solvent will result in electronic-to-vibrational (e–v) deactivation and reactions with the solvent. The first-order ¹O₂ decay rate constant k_D = k_d,r + k_d is composed of a reactive fraction k_d,r and a non-reactive fraction k_d. Second, electron-rich species, such as reduced mediators, exert charge transfer quenching; however, they may also react with the electrophilic ¹O₂ along pathways depending on the particular chemistry³⁶. The rate constant k_Q = k_q,r + k_q is equally composed of a reactive fraction k_q,r and a non-reactive fraction k_q. Third, radiative decay of ¹O₂ to ³O₂ with the emission of a 1,270 nm photon.

We measured the rate constants k_D and k_Q using the luminescence lifetime. An O₂-saturated solution containing Rose Bengal (absorbance of about 0.1 in a 1 cm fluorescence cuvette) was illuminated using a pulsed Coherent OBIS 561 nm laser. The lifetime (τ) and the decay constant (k = 1/τ) of ¹O₂ were measured using the NIR detector. τ was obtained by fitting the decay profile with exp(–t/τ) (Extended Data Fig. 3a). τ in the absence of a quencher relates to the solvent quenching rate constant k_D. k_Q is obtained by plotting 1/τ against the RM^ox concentration ${c}_{{{\rm{RM}}}^{{\rm{ox}}}}$ (Extended Data Fig. 3b,c). Similar to previously reported quenchers¹², k_Q decreases with ${E}_{{\text{RM}}^{\text{ox}/\text{red}}}^{\circ }$ following a trendline with a slope of about –10^3.5 V⁻¹. The logarithmic dependence of the non-radiative fraction k_q is explicable by the required partial charge transfer from the e^–-rich quencher to the ¹O₂, which makes quenchers with lower redox potentials more efficient¹². We consider that the reactive fraction k_q,r depends similarly on redox potential, given that the addition reactions equally require charge transfer from the substrate to ¹O₂ (refs. ^12,36). The scattering of k_Q around the trendline arises from the large chemical diversity of the used mediators. We used both the trendline and the individual values of k_Q for the prediction of NIR intensities in Fig. 2c. As for the fraction of reactive deactivation, k_d,r/k_D and k_q,r/k_Q, these can be determined from ³O₂ consumption¹², which we do below when simulating values of ³O₂/RM^ox.

The surface area A of the KO₂ powder, needed for the calculations, was determined by analysing optical images (Extended Data Fig. 3d). KO₂ powder was dispersed in TEGDME, sonicated, a drop was placed between a microscope slide and a cover slip and sealed air-tight. Images were acquired with transmitted light on a Nikon Ti2E-01 inverted microscope using a Plan Apo λ 40×/0.95 DIC (Differential Interference Contrast) air PFS (Perfect Focus System) objective lens, resulting in a pixel size of 0.183 μm. The images were analysed using the ilastik pixel classification and object classification workflows (https://www.ilastik.org/), resulting in a histogram of particle sizes (Extended Data Fig. 3e). The surface area was calculated by assuming spherical particles, yielding A = 0.23 ± 0.04 m² g^–1.

As quantification of absolute ¹O₂ yields from NIR emission is not straightforward, we normalized the values. The NIR intensity at time t after bringing KO₂ in contact with RM^ox will be proportional to the ¹O₂ concentration, ${I}_{1,270{\rm{nm}}}(t)\propto {c}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)$. The ¹O₂ formation rate by mediated KO₂ oxidation is ${\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)=A\cdot {k}_{1}\cdot {c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)$, with k₁ being the rate constant as given in Fig. 2a. A is constant because the experiments were performed with a large excess of KO₂ over RM^ox. ${c}_{{{\rm{RM}}}^{{\rm{ox}}}}$ and ${c}_{{{\rm{RM}}}^{{\rm{red}}}}$ are given by ${c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)={c}_{{{\rm{RM}}}^{{\rm{ox}}}}(0)\cdot {{\rm{e}}}^{-{k}_{{\rm{tot}}}\cdot A\cdot t}$ and ${c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)={c}_{{{\rm{RM}}}^{{\rm{ox}}}}(0)-{c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)+$${c}_{{{\rm{RM}}}^{{\rm{red}}}}(0)-{\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2},{\rm{q}},{\rm{r}}}(t)\cdot t$, where k_tot = k₁ + k₃. The term ${\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2},{\rm{q}},{\rm{r}}}(t)$ is the rate at which ¹O₂ reacts with RM^red as detailed below. ¹O₂ formation and decay will balance³⁷, which results in the presence of solvent and mediator quenching in ${c}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)={\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)/({k}_{{\rm{d}}}+{k}_{{\rm{Q}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t))$. k_Q is either the measured value for the particular mediator or the trendline in Extended Data Fig. 3c. Finally, analogous to the experiment where we integrate the NIR signal until it ceases, we arrive at the expected NIR emission:

$${I}_{1270{\rm{nm}},{\rm{cum}}}\propto {\int }_{0}^{\infty }\,\frac{A\cdot {k}_{1}\cdot {c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)}{{k}_{{\rm{D}}}+{k}_{{\rm{Q}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)}{\rm{d}}t.$$

(3)

To simulate losses of ³O₂ (³O₂/RM^ox < 1 in Fig. 2b), we used the rate of reactive ¹O₂ decay ${\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2},{\rm{r}}}(t)=({k}_{{\rm{d}},{\rm{r}}}+{k}_{{\rm{q}},{\rm{r}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t))\cdot {c}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)$ to define f_r as the reactive fraction of the total ¹O₂ decay rate

$${f}_{{\rm{r}}}=\frac{{k}_{{\rm{d}},{\rm{r}}}+{k}_{{\rm{q}},{\rm{r}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)}{{k}_{{\rm{D}}}+{k}_{{\rm{Q}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)}.$$

(4)

${\nu }_{{}^{1}{\rm{O}}_{2},{\rm{r}}}(t)$ equals the total mediated ¹O₂ formation rate times f_r: ${\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2},{\rm{r}}}(t)={f}_{{\rm{r}}}\cdot A\cdot {k}_{1}\cdot {c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)$. As some of the RM^red reacts, its loss is accounted for using ${\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2},{\rm{q}},{\rm{r}}}(t)={k}_{{\rm{q}},{\rm{r}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)\cdot {c}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)={f}_{{\rm{q}},{\rm{r}}}\,\cdot A\cdot {k}_{1}\cdot {c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)$, where ${f}_{{\rm{q}},{\rm{r}}}=\,{k}_{{\rm{q}},{\rm{r}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)/({k}_{{\rm{D}}}+{k}_{{\rm{Q}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t))$. Calculations of f_r, f_q,r and ${c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)$ were iterated until convergence was achieved. Finally, ³O₂ yields are

$${{}^{3}{\rm{O}}}_{2}/{{\rm{RM}}}^{{\rm{ox}}}=1-{\int }_{0}^{\infty }{f}_{{\rm{r}}}\cdot A\cdot {k}_{1}\cdot {c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t){\rm{d}}t/{\int }_{0}^{\infty }A\cdot {k}_{{\rm{tot}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t){\rm{d}}t.$$

(5)

The fractions of reactive deactivation, k_d,r/k_D and k_q,r/k_Q were obtained by fitting the measured values of ³O₂/RM^ox in Fig. 2b with the simulated ones from equation (5). The simulated ³O₂/RM^ox are plotted as the dashed line in Fig. 2b.

Deviations between simulated and measured values may result from the simplicity of the model. The main simplification is as follows: (1) k_Q was measured in homogeneous solutions of RM^red and the model calculates bulk concentrations ${c}_{{{\rm{RM}}}^{{\rm{ox}}}}$ and ${c}_{{{\rm{RM}}}^{{\rm{red}}}}$, but during the heterogenous KO₂ oxidation, bulk and surface concentrations of RM^ox and RM^red differ. (2) We fitted a common fraction of mediator reactivity (k_q,r/k_Q) for all mediators, causing k_q,r and k_Q to decrease exponentially with growing ${E}_{{\text{RM}}^{\text{ox}/\text{red}}}^{\circ }$. As a trend, this is justified given that both reaction and charge transferquenching require e^– transfer, but individual reactivity will vary because of the large chemical diversity of mediators³⁶. (3) We did not account for quenching by O₂ and ${{\rm{O}}}_{2}^{-}$. (4) Some RMs show further reactivities, which can cause ³O₂ loss: Fc⁺ reacts with O₂ (ref. ³⁸), TDPA gets in contact with O₂ spontaneously oxidized to TDPA⁺ and TDPA²⁺ (ref. ¹⁸), and reduced quinones bind to O₂ (ref. ³⁹).

Proton-induced disproportionation

Six types of buffers were used for proton-induced superoxide disproportionation. Britton–Robinson (BR) buffers were prepared with 0.1 M acetic acid, 0.1 M boric acid and 0.1 M phosphoric acid. NaOH (1 M) and HCl (1 M) were used to adjust the pH. Phosphate-buffered saline (PBS) solution and aqueous PBS powder solution (for pH 7.4) were added and the pH was adjusted using 1 M NaOH or 1 M HCl. Citrate buffers were prepared using citric acid and trisodium citrate dihydrate. To adjust the pH, we varied the concentrations of citric acid and trisodium citrate dihydrate. Acidic buffers of KCl and HCl (pH 1 and 2) were prepared by mixing 0.2 M KCl with 0.2 M HCl and adjusting the volume. Neutral to basic buffers of KH₂PO₄/NaOH (pH 7.1 and 10.8) were prepared by mixing 0.1 M KH₂PO₄ with 0.1 M NaOH and adjusting the volume accordingly. To trap the hydrogen peroxide (H₂O₂) produced, to eliminate the possibility of forming ¹O₂ by peroxoacids⁴⁰, titanium(IV)oxysulfate solution (TiOSO₄, 15 wt% in dilute sulfuric acid), 1 M NaOH was used to adjust the pH of TiOSO₄ solutions to pH 1.2 and 1.55.

Figure 4c shows ¹O₂ yields still increasing when the pH is below 4.8, the pK_a of O₂⁻. KO₂ hydrolysis increases the pH in aqueous media according to KO₂ + H₂O → HO₂ + K⁺ + OH^–. Buffer capacities were selected so that the amount of KO₂ did not significantly affect the resulting pH after the reaction. However, despite the buffers, the local pH at the reaction site will be higher than the average. The importance of buffering for a local pH close to the average is evident in control experiments without a buffer. Even at a pH of 1.5, we could not detect ¹O₂ in an unbuffered H₂SO₄ solution, whereas we could in the buffered one (Extended Data Fig. 6e). Therefore, the ¹O₂ yields in Fig. 4c result from a higher local pH.

Driving forces on superoxide oxidation

Superoxide experiences a broad range of oxidizing conditions to liberate oxygen, but explanations for why and to what extent certain oxidizing redox couples evolve ¹O₂ have been unknown. Extended Data Fig. 4 shows the driving forces for superoxide oxidation with various redox couples. The driving forces are shown in comparison with the Marcus kinetic parabola in ether and acetonitrile solvent from Figs. 1 and 2. Li⁺- and H⁺-induced disproportionation are shown in Figs. 3 and 4. The other examples we discuss in Extended Data Fig. 4 arise from superoxide in contact with CO₂ or organic peroxides, with relevance for energy storage and biology^1,30,41.

Considering CO₂ first, we have previously shown that CO₂ in contact with O₂⁻ yields ¹O₂, but the energetics were unknown³⁰. CO₂ in contact with O₂⁻ is known to form peroxomonocarbonates and peroxodicarbonates by repeated uptake of CO₂ by O₂⁻. Intermediate peroxocarbonate species may be reduced by O₂⁻, which releases O₂ (refs. ^41,42,43,44). However, the O₂ spin state has previously not been considered. Extended Data Fig. 4c shows likely redox couples of oxidized/reduced peroxocarbonate species, but their redox potentials are not established experimentally. A previous study has shown, using density functional theory (DFT), that depending on the cation present and the solvent, the particular peroxocarbonate redox couples that oxidize O₂⁻ to O₂ differ⁴, but likely involve CO₄^•–/CO₄^2–, LiCO₄^•/LiCO₄^–, Li₂C₂O₆/Li₂C₂O₆^– or Li₃C₂O₆/Li₃C₂O₆^–. The calculations have shown reaction energies relative to the O₂⁻/³O₂ between about 1 and 1.4 eV. These driving forces, hence, explain ¹O₂ formation from CO₂ in contact with O₂⁻ (Extended Data Fig. 4b).

¹O₂ formation has been examined for exposure of superoxide to organic peroxides, given their occurrence in biological systems⁴⁵. No reaction was observed with alkyl peroxides, whereas acyl peroxides yielded ¹O₂ (refs. ^45,46); however, this has not been connected with driving forces for superoxide oxidation. Nucleophilic attack of O₂⁻ on acyl peroxides forms an acyl radical and carboxylate (Extended Data Fig. 4d). The potential for the acyl radical/carboxylate redox couple has been reported between 1.5 V and 1.7 V compared with SHE (ref. ²³) (1.95–2.05 V compared with O₂/O₂⁻), which explains ¹O₂ formation according to Extended Data Fig. 4a. Alkyl peroxides (ROOR) such as di-tert-butyl, dicumyl and di-n-butyl peroxide have been reported not to form ¹O₂ (ref. ⁴⁵). This can be understood by ROOR only breaking down to RO^– and RO^• at low potentials (–1.31 V to –1.15 V compared with SHE, that is, –0.86 V to –0.70 V compared with O₂/O₂⁻) (ref. ⁴⁷). The RO^•/RO^– couple (–0.06 V to 0.04 V compared with SHE, that is, 0.39–0.49 V compared with O₂/O₂⁻) could, if formed, oxidize O₂⁻, but not to ¹O₂.

Proton-induced disproportionation that yields low but non-negligible ¹O₂ yields at a high pH of about 11 is consistent with reliable theoretical and experimental works. Using a high-level ab initio method, a previous study¹⁷ found that the reaction HO₂ + O₂⁻ → O₂ + HO₂ can proceed by both the singlet and triplet pathways, with the singlet pathway being only about 0.3 eV endoergic. Equivalent experiments exposing KO₂ to H₂O₂ in toluene found about 0.2% ¹O₂ production, as measured using a chemical trap¹⁴. In this experiment, H₂O₂ was the proton source to first form HO₂ (H₂O₂ + O₂⁻ → HO₂⁻ + HO₂). The conditions in these theoretical and experimental studies correspond to a pH of about 11 (pK_a = 11.7 for H₂O₂), in which the reaction to ¹O₂ is only weakly driven. Conversely, ¹O₂ was not detected with alkyl hydroperoxides ROOH as the proton source (pK_a ≈ 12.6) (ref. ^45,48), a result that insufficient driving forces can now explain.

Relation between ${{\boldsymbol{E}}}_{{\genfrac{}{}{0ex}{}{1}{}{\bf{O}}}_{2}/{{\bf{O}}}_{{\bf{2}}}^{-}}^{\circ }$ and the ¹O₂ fraction

The electrochemiluminescence literature refers to energy-sufficient processes to form the electronically excited species^23,28,49. For example, consider the generic redox couples R/R^•– and M^•+/M (note that these could be, for example, ³O₂/O₂⁻ and RM^ox/RM^red). The process R^•– + M^•+ → ¹R^* + M is considered energy-sufficient to form the excited species ¹R^*, if $({E}_{{{\rm{M}}}^{\cdot +}/{\rm{M}}}^{\circ }-{E}_{{\rm{R}}/{{\rm{R}}}^{\cdot -}}^{\circ })F\ge \,-\Delta {H}^{\circ }(\,\genfrac{}{}{0ex}{}{1}{}\,{{\rm{R}}}^{* }\leftarrow {\rm{R}})$. This condition is fulfilled if the potential of the oxidizing redox couple exceeds the redox potential of the excited species: ${E}_{{{\rm{M}}}^{\cdot +}/{\rm{M}}}^{\circ }\ge {E}_{\genfrac{}{}{0ex}{}{1}{}{{\rm{R}}}^{* }/{{\rm{R}}}^{\cdot -}}^{\circ }={E}_{{{\rm{R}}/{\rm{R}}}^{\cdot -}}^{\circ }+\Delta {H}^{\circ }(\,\genfrac{}{}{0ex}{}{1}{}\,{{\rm{R}}}^{* }\leftarrow {\rm{R}})/F$. The connotation of energy-sufficient processes led to the interpretation that ${E}_{\genfrac{}{}{0ex}{}{1}{}{{\rm{R}}}^{* }/{{\rm{R}}}^{\cdot -}}^{\circ }$ or ${E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{{\rm{O}}}_{2}^{-}}^{\circ }$ establishes a threshold above which the excited species rather than ground state species forms^18,24,26. Extended Data Fig. 4a shows that reaching this threshold potential (or the driving force for which this is exceeded) gives no indication about the extent to which ¹O₂ rather than ³O₂ forms. An onset of ¹O₂ may be expected at ${\Delta G}_{1\leftarrow 3}^{\circ }$, but its formation will become significant only for driving forces –ΔG° > λ₃, for which ³O₂ formation slows down to benefit ¹O₂ formation.

Thermodynamics in mixed alkali metal/TBA⁺ electrolytes

Superoxide disproportionation in Li⁺ and Na⁺ containing glyme electrolytes was found to always yield some ¹O₂ according to 2MO₂ → M₂O₂ + x³O₂ + (1 − x)¹O₂ (refs. ^13,16,18,19). Li⁺ yielded small fractions (about 2%) at large kinetics, and Na⁺ yielded larger fractions (around 12%) at slow kinetics¹⁶. Often, electrolytes for non-aqueous metal-O₂ batteries contain weakly Lewis acidic cations, such as tetrabutylammonium (TBA⁺) or other cations from ionic liquid electrolytes. In mixed Li⁺/TBA⁺ and Na⁺/TBA⁺ (1/1) electrolytes, the ¹O₂ yields increased to about 20 and 18%, respectively. The reasons for this behaviour must, hence, lie in (1) already sufficient driving forces for ¹O₂ formation in pure Li⁺ and Na⁺ electrolytes; and (2) increasing driving forces on adding TBA⁺.

M₂O₂ (M = Li⁺, Na⁺) are insoluble^50,51 and the potential ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{M}}}_{2}{{\rm{O}}}_{2}({\rm{s}})}^{\circ }\,=$ ${\Delta }_{{\rm{f}}}{G}^{\circ }({{\rm{M}}}_{2}{{\rm{O}}}_{2(\text{s})})/F=2.96\,{\rm{V}}$ compared with M⁺/M, therefore, fixed to the value obtained using the formation energy –Δ_fG° of solid Li₂O_2(s). Given that the superoxide/M₂O_2(s) couple acts as the oxidant during superoxide disproportionation, the driving force is given by $-\Delta G=({E}_{{\rm{superoxide}}/{{\rm{M}}}_{2}{{\rm{O}}}_{2(\text{s})}}-{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}})F$. Note that here superoxide does not denote a particular species, but it could be anything, including solid MO_2(s), solvated ${({{\rm{M}}}^{+}{{\rm{O}}}_{2}^{-})}_{n\ge 1,({\rm{sln}})}$ clusters and ion pairs, or the weakly coordinated ${({{\rm{TBA}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}$. ${E}_{{\rm{superoxide}}/{\text{M}}_{2}{\text{O}}_{2(\text{s})}}$ cannot be directly measured but can be inferred from ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{M}}}_{2}{{\rm{O}}}_{2(\text{s})}}$ and ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}}$. Using ΔG = –zFE, where z is the number of transferred electrons, it can be derived that ${E}_{{\rm{superoxide}}/{{\rm{M}}}_{2}{{\rm{O}}}_{2(\text{s})}}=2{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{M}}}_{2}{{\rm{O}}}_{2(\text{s})}}-{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}}$. For the stable solid compounds (Li₂O₂, Na₂O₂, NaO₂, K₂O₂ and KO₂), tabulated formation energies Δ_fG° can be found and the ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{M}}}_{2}{{\rm{O}}}_{2}({\rm{s}})}^{\circ }$ and ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{M}}{{\rm{O}}}_{2}({\rm{s}})}^{\circ }$ be calculated as shown in Extended Data Fig. 5a. On the basis of this, KO₂ is not expected to disproportionate to K₂O₂ and the K⁺-case, hence, not be further considered.

${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}}$ require further consideration given the electrolyte-dependent solubilities of superoxide. Theoretical work shows that solvated ${({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{n\ge 1,({\rm{sln}})}$ species are less stable in terms of Gibbs free energy than the bulk solid LiO_2(s), but as the cluster size n grows, the structure approaches bulk MO_2(s) and free energy approaches a constant value^16,50,51. Aggregation into ${({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{n > 1,({\rm{sln}})}$ clusters stabilizes the solvated species relative to separated ${({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}$ species^16,34. The Gibbs free energy grows, therefore, in the order of increasing solvation: LiO_2(s) < (Li⁺O₂^–)_n>1,(sln) < (Li⁺O₂^–)_(sln). Accordingly, the potentials in pure M⁺ electrolyte are in the order and within the limits ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{LiO}}}_{2(\text{s})}} > {E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{n > 1({\rm{sln}})}} > {E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}}$. If TBA⁺ is present, the even weaker association in ${({{\rm{TBA}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}$ extends the lower potential limit to ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{TBA}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}}$. The values for these potential limits, as shown in Fig. 3a, Extended Data Fig. 5c,d, were estimated from cyclic voltammograms with the salt shifting from pure M⁺ to pure TBA⁺ (Extended Data Fig. 5b). The largely solvation-independent DMFc/DMFc⁺ redox couple was used as internal standard. Δ_fG° of solid LiO_2(s) is not available, but ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{Li}}{{\rm{O}}}_{2}({\rm{s}})}$ may be estimated from cyclic voltammograms in poorly solvating electrolytes, in which large ${({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{n,({\rm{sln}})}$ clusters approach the thermodynamics of LiO_2(s). The shift in the onset of O₂ reduction in Li⁺ compared with TBA⁺ electrolyte at slow scan rates was taken as the difference between ${E}_{{{}^{3}{\rm{O}}}_{2}/{{\rm{LiO}}}_{2(\text{s})}}$ and ${E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{TBA}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}}.{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}}$ as the lower limit of potentials in pure Li⁺ electrolyte was estimated from the potential shift between pure Li⁺ and pure TBA⁺ electrolytes with the highly solvating solvent 1-methylimidazole. These were taken from ref. ³² and show a shift of 33 mV.

Extended Data Fig. 5d shows the analogous thermodynamics for Na⁺/TBA⁺ mixtures as shown in Fig. 3 for Li⁺/TBA⁺. Considerations as above for the relative stabilities of the Li superoxides apply analogously to the relative stability of Na superoxide clusters compared with the NaO_2(s) bulk. Theoretical work has similarly shown the stabilization by forming ${({{\rm{Na}}}^{+}{{{\rm{O}}}_{2}}^{-})}_{n > 1,({\rm{sln}})}$ clusters^52,53. Extended Data Fig. 5e shows the NIR emission on adding KO₂ into glyme electrolyte containing various Na⁺/TBA⁺ ratios. The data show that, even in a pure Na⁺ electrolyte, the driving force is sufficient for ¹O₂ formation and that added TBA⁺ increases the driving force and formation.

More generally, the electrolyte properties (solvent(s), salts(s) and their concentrations) will affect the reorganization energy and hence the maxima and crossing point of the two kinetic parabolas. The classical approach to accounting for this is the equation given by Marcus⁵⁴, which connects the reorganization energy with the effective dielectric properties of the electrolyte and the separation of the redox centres. A lower dielectric constant and smaller separation will result in a larger reorganization energy. A refined equation by Marcus⁵⁵ further takes into account the ionic environment. These considerations apply well, for example, to aqueous anionic redox couples and the series of alkali metal cations from Li⁺ to Cs⁺ as spectator cations, in which λ decreases⁵⁶. However, caution is required with non-aqueous, low dielectric constant media, in which strong ion pairing occurs. Some works suggest an inverse trend for λ among the alkali metals^19,57. Ion pairing and even clustering is particularly severe for (su)peroxide as the redox anions as discussed above. Superoxide forms in non-aqueous Li⁺ and Na⁺ electrolytes clusters^32,33 and the peroxides are practically insoluble⁵¹. The order and extent to which the reorganization energy changes for superoxide oxidation in non-aqueous media among the alkali cations may, therefore, not be predicted straightforwardly and would merit further investigation. As we observe ¹O₂ at low driving force for the Na⁺ electrolyte, the reorganization energy appears sufficiently low therein.

Wider relevance for life sciences and energy

Our study contributes to understanding how the pH affects the link between the four important reactive oxygen species (ROS) superoxide, peroxide, ³O₂ and ¹O₂. Disproportionation is notably the pathway to maintain a low superoxide concentration. However, detoxification from superoxide produces the harmful ¹O₂. Superoxide occurs in cells in several organelles with different pH levels between 4.7 and 8, but the superoxide-degrading enzyme superoxide dismutase occurs only in neutral to basic organelles³⁵. In pathological situations, the pH balance is known to be affected (typically towards lower pH) and therefore signalling, redox regulation and defence^58,59. Our study contributes to the understanding of how the redox chemistry of superoxide, pH and ¹O₂ formation are linked. We noted that in non-aqueous media, superoxide in contact with CO₂ forms ¹O₂. Given the ubiquity of CO₂ in organelles containing superoxide, further investigations into the aqueous chemistry of CO₂ and superoxide are warranted.

For energy applications, further relevance and future research directions emerge: (1) For suppressing ¹O₂, generally, the driving force should be decreased, and the reorganization energy for the superoxide oxidation reaction should be increased. The classical equation by Marcus⁵⁴, which connects the reorganization energy with the effective dielectric properties of the electrolyte and the separation of the redox centres, applies well to aqueous anionic redox couples⁵⁶. For non-aqueous, low dielectric constant media, in which strong ion pairing occurs, particularly so with superoxide, the change in reorganization energy among different cations and electrolytes may not be predicted straightforwardly and would merit further investigation. (2) Oxygen evolution catalysis from water: metal-superoxo species have been identified as preceding the O₂ evolution on, for example, the extensively studied Ni(Fe)OOH or CoOOH catalysts¹⁰. The metal M^n–1/n redox couple is considered to oxidize the superoxo moiety to O₂ (refs. ^10,60). Some of the most active M^n–1/n metal redox couples are typically a few 100 mV above the ¹O₂/superoxide potential shown in Fig. 4a and provide, in principle, enough driving force for ¹O₂ evolution. For example, at pH 14 ${E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{{{\rm{O}}}_{2}}^{-}}^{\circ }=1.32\,{\rm{V}}$, ${E}_{{{\rm{Co}}}^{{\rm{II}}/{\rm{III}}}}^{\circ }\approx 1.25\,{\rm{V}}$, ${E}_{{{\rm{Co}}}^{{\rm{III}}/{\rm{IV}}}}^{\circ }\approx 1.5\,{\rm{V}}$, ${E}_{{{\rm{Ni}}}^{{\rm{II}}/{\rm{III}}}}^{\circ }\approx 1.52\,{\rm{V}}$ and ${E}_{{{\rm{Ni}}}^{{\rm{III}}/{\rm{IV}}}}^{\circ }\approx 1.6\,{\rm{V}}$ on the RHE scale (refs. ^10,60). Further investigations specifically on ¹O₂ evolution in oxygen evolution catalysis are therefore warranted. (3) Both Li-stoichiometric⁶ and Li-rich transition metal (TM, for example, Ni, Mn and Co) oxide^2,7,61,62 intercalation materials used for positive electrodes in Li- or Na-ion batteries are known to undergo parasitic lattice oxygen loss at high states of charge. Both the intercalation material and the electrolyte degrade, hampering long-term cyclability. However, non-matching patterns of O₂ and CO₂/CO release from electrolyte decomposition (all containing lattice O as shown by isotopic labelling^7,62) and enhanced lattice O loss with surface carbonates present⁷ remain unexplained and highlight the need for a deeper understanding of the prevailing ROS and decomposition pathways. For LiNiO₂, ¹O₂ evolution has been suggested to result from the disproportionation of oxide radicals⁶. More generally, ¹O₂ may evolve from superoxo species (at the lattice surface, in (su)peroxocarbonates^4,30) at the available driving forces. The oxidants could be a combination of (su)peroxides (for example, coordinated by TMs or carbonates) that get stabilized by further reduction and TM redox, such as Co^III/IV or Ni^III/IV. Further investigations into the involvement of ¹O₂ evolution in TM oxide outgassing and surface reactions are therefore warranted.

The results expand the current knowledge on the electrogeneration of excited species more generally and pose open questions about the origin. Specifically, the process is more effective than typically assumed, given that ${\Delta G}_{1\leftarrow 3}^{\circ } < {\Delta H}_{1\leftarrow 3}^{\circ }$ and that Z_el,1 ≫ Z_el,3. Electrogeneration of excited ROS has significance ranging from biological systems to energy storage. Reactive excited species in life are very broadly associated with pathogenic events^1,63. Recombination reactions in redox flow batteries are recognized to cause self-discharge, but this has so far not been recognized to potentially form extremely energetic excited species. Soluble parasitic oxidized and reduced species at the cathode and anode of Li- and Na-ion batteries may recombine to form energetic excited species.