GCL_FCS30: a global coastline dataset with 30-m resolution and a fine classification system from 2010 to 2020

Abstract

The coastline reflects coastal environmental processes and dynamic changes, serving as a fundamental parameter for coast. Although several global coastline datasets have been developed, they mainly focus on coastal morphology, the typology of coastlines are still lacking. We produced a Global CoastLine Dataset (GCL_FCS30) with a detailed classification system. The coastline extraction employed a combined algorithm incorporating the Modified Normalized Difference Water Index and an adaptive threshold segmentation method. The coastline classification was performed a hybrid transect classifier that integrates a random forest algorithm with stable training samples derived from multi-source geophysical data. The GCL_FCS30 offers significant advantages in capturing artificial coastlines, reflecting strong alignment with location validation data. The GCL_FCS30 classification was found to achieve an overall accuracy and Kappa coefficient over 85% and 0.75. Each coastline category accurately covered the majority of the area represented in third-party data and exhibited a high degree of spatial relevance. Therefore, the GCL_FCS30 is the first global coastline category dataset covering the high latitudes in a continuous and smooth line vector format.

Background & Summary

The coastal zone is highly vulnerable and sensitive to external disturbances as a complex Coupled Human-Environment System. It faces various environmental and ecological problems such as increasing erosion, drastic expansion toward sea, sea level rise, and intensive human activities^1,2. Besides, some natural coastlines such as rocky reefs, sandy beaches, mudflats, and mangroves have been replaced with seawalls, break walls, wharves, piers, pontoons, and other structures³. Sustainable management of the coastal zone requires a thorough understanding of coastline dynamics. Providing a long-term coastline distribution and category dataset on a global scale is essential for advancing our understanding of coastal problems.

In recent years, the increasing availability of high-resolution earth observation data has made it feasible to obtain reliable, global scale coastline data^4,5. Especially with the breakthroughs in cloud computing, a series of coastline monitoring datasets and tools, such as Global shoreline vector (GSV), Global Multiple Scale Shorelines Dataset (GMSSD) and Coastsat toolkit^6,7,8, have been generated. However, most of them mainly focused on the observing and monitoring of coastline morphology and lacked in coastline classification. Existing classification studies tend to concentrate on a specific type of coastline like beaches, muddy and human infrastructure^9,10,11, often with short temporal extent and point vector formats. For instance, Sayre et al.¹² developed a global coastal dataset with Coastal and Marine Ecological Classification Standard (CMECS) labels at a 1 km resolution, offering a comprehensive and standardized geospatial layer of coastal ecological settings worldwide. However, this dataset lacks long-term categorical information and adopts a more ecological perspective in coastline classification. Moreover, global coastlines are highly diverse, encompassing various landforms and human infrastructure including beaches, estuaries, ports, artificial islands, and coastal wetlands, each of which responds differently to marine forces and environmental change and supports distinct land uses¹³. Therefore, developing a long-term, high-resolution global coastline product that provides detailed positions and classifications is essential.

Coastlines are immensely diverse, encompassing both natural surface covers (e.g., beaches, silts, and mangroves) and anthropogenic features (e.g., piers, harbours, and pipelines). The diverse types of coastlines and the complexity of their environments place significant demands on the spatio-temporal representation of coastline extraction and classification models. These models must accurately capture variations across different types of coastlines and adapt to changes over time to ensure reliable and comprehensive shoreline mapping^14,15,16. Therefore, the availability of high-confidence global training samples is the prerequisite and key to solve these problems. In the few studies where training data are publicly available, most primarily depict coastline, such as the Sentinel-2 Water Edges Dataset (SWED)⁸, or are generated from unknown locations and resolutions based on Google Earth images, as seen in Li et al.¹⁷ Although Hulskamp et al.¹⁰ developed training samples for five coastal geomorphological types at both pixel and transect levels, their focus was primarily on identifying muddy coastlines, and the sample lacks temporal representativeness. The Coast Train Data offers information on coastal environments, such as salt marshes, deltas, and estuaries, but is limited in spatial coverage, primarily focusing on the coastlines of U.S. Pacific, Atlantic, Gulf of Mexico and Great Lakes^18,19. Therefore, obtaining high-confidence coastline classification training data is the major difficulty for coastline mapping.

Here, we created a Global CoastLine dataset (GCL_FCS30) with a fine classification system and 30-m resolution using long-term Landsat imagery on the Google Earth Engine (GEE) platform, covering the period from 2010 to 2020. This dataset features a detailed classification system with six coastline categories: sandy, biogenic, rocky, muddy, estuary, and artificial coastlines. Additionally, a method for generating training samples from geophysical datasets was developed to enhance global coastline classification. The GCL_FCS30 dataset will be the first open-access global coastline dataset with high-accurate distribution and classification, which can provide strong support for efforts aimed at understanding the long-term global change effects of various coastline categories. The GCL_FCS30 will also help to understand the coastal systems and the future of coastal communities characterized with high population growth, coastal urbanization, climate change and sea level rise, and inform coastal management and efforts in achieving coastal sustainable development goals.

Methods

Data used in this study

Landsat surface reflectance data

This study utilized the Landsat Collection 2, which includes images acquired from the Thematic Mapper (TM), Thematic Mapper Plus (ETM+) and Operational Land Imager (OLI), to clearly capture the distributions and categories of coastlines. The dataset offers global coverage with a 30-meter spatial resolution and long-term data^20,21. The study area covers 3610 tiles (paths/rows) of the Landsat Worldwide Reference System (WRS-2). All Landsat Top-of-Atmosphere (TOA) reflectance images with less than 80% cloud cover from 2010 to 2020 were provided by the Google Earth Engine (GEE) Python API package. TOA images are calibrated to allow standardized comparison between images captured by different sensors on different dates, making them particularly suitable for long-term feature monitoring⁷. To minimize the effects of tides, we selected images taken from April to October across the years. “Low-quality” pixels, such as shadows, snow, clouds, and saturated pixels, were masked using the CFmask algorithm, which achieved an overall accuracy of 96.4% in identifying “poor-quality” pixels^22,23. In cases where image quality was poor, data from 1-2 additional years were used as supplements. For areas with extended periods of missing data, especially in high latitude regions, images from Google Earth or Sentinel-2 were utilized to fill the gaps. To average the impact of short-term changes (e.g., waves, vegetation seasonality, tides, and transient clouds), a by-year composite of the Landsat TOA reflectance imagery was created for each tile²⁴. This approach ensures more stable and reliable data for analysing coastline dynamics.

Global transect system

To address the dual land and sea nature of coastlines, a global transect system was established to support the classification. These transects were positioned perpendicular to the global coastline extracted for the intermediate year of this study, with a length of 1000 meters and a spacing of 100 meters²⁵. This systematic approach ensured consistent and comprehensive analysis of coastal features, facilitating accurate classification and mapping of diverse coastline types. The transects provided a structured framework for examining the interface between land and sea, thereby enhancing the precision and reliability of the classification process⁹.

Global coastal geospatial datasets

Following Sayre et al.²⁶, seven freely available global coastal datasets for elevation, mangroves, land cover and temperature were used in this study to enhance diverse physical geospatial characteristics (Table 1). These datasets are crucial for effectively identifying corresponding coastal categories. These coastal datasets were extracted along the transects and converted to relevant indicators for coastline classification. We combined long-term (GMF30) and high-resolution (HGMF) datasets, both of which demonstrated strong performance. To minimize the impact of classification errors in each mangrove product, we conducted a cross-consistency analysis. Only pixels that were consistently identified as mangrove across all datasets were retained.

Table 1 Overview of global coastal geospatial datasets used in this study.

Validation data for global coastline product. An accurate assessment of the quality of a global coastline dataset is dependent on the sample size of coastline validation points and the confidence in interpreting each validation point. In this study, a stratified random sampling algorithm was employed to determine the sample size of validation points²⁷. The calculation formulas for the total sample size and for specific coastline subcategories are outlined as follows:

$$n=\frac{{(\sum {W}_{i}{S}_{i})}^{2}}{{E}^{2}+\sum \frac{{W}_{i}{S}_{i}}{N}}$$

(1)

$${n}_{i}=n\frac{{W}_{i}{S}_{i}}{\sum {W}_{i}{S}_{i}}$$

(2)

$${S}_{i}=\sqrt{{p}_{i}(1-{p}_{i})}$$

(3)

where ${\rm{N}}$ is the total sample size required, ${{\rm{n}}}_{{\rm{i}}}$ is the sample size for the specific coastline category; ${\rm{E}}$ is the standard error of the estimated overall accuracy; ${\rm{N}}$ is the total number of coastline points; ${{\rm{S}}}_{{\rm{i}}}$ is the standard deviation of category ${\rm{i}}$; ${{\rm{W}}}_{{\rm{i}}}$ is the weight distribution of category ${\rm{i}}$; ${{\rm{p}}}_{{\rm{i}}}$ is the producer’s accuracy.

In this study, the target standard error for the overall accuracy was set to 0.01. Based on experience with similar coastline mapping efforts²⁸, errors of commission are more common for muddy, sandy, and artificial coastlines, while biogenic and rocky coastlines are more accurate. Consequently, we conjectured that the producer’s accuracy of the artificial, biogenic, sandy, muddy, rocky coastlines would be 0.85, 0.95, 0.85, 0.80 and 0.90²⁹. After statistics, the total sample size required was determined as 964, which can ensure the desired precision in estimating the overall accuracy is achieved, considering the variability and accuracy differences among different coastline categories. The sample sizes for artificial, biogenic, sandy, muddy and rocky coastlines were 80, 70, 210, 80 and 524, respectively.

High-resolution imagery from Google Earth was utilized to visually interpret the coastline status and establish validation points. Each validation point underwent independent interpretation by five experts to mitigate subjectivity, and only points demonstrating high agreement among the experts were considered for validation. The distribution of coastline validation points in this study is shown in Fig. 1.

Fig. 1

Spatial distribution of the validation points for global coastline product in 2015.

Methods used in this study

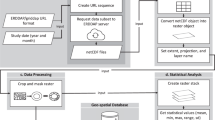
Figure 2 illustrates a flowchart of the method used for mapping global coastlines using time-series Landsat imagery. The process consists of three major components: pre-processing, coastline extraction, and classification. The pre-processing step of the Landsat imagery includes radiometric calibration, atmospheric correction, cloud masking and mean value compositing. A threshold segmentation method based on exponential time series was developed to accurately extract the coastlines from the imagery. A hybrid transect classifier, developed using globally distributed and temporally stable training samples, was used to categorize the extracted coastlines. Details of each procedure are explained in the following sections.

Fig. 2

Framework for global coastline mapping and classification.

Extraction of coastlines using remote sensing images

A coastline extraction algorithm combining the Modified Normalized Difference Water Index (MNDWI), Maximum between-class variance (OTSU) adaptive threshold segmentation method and Canny edge detector was developed in this study based on the GEE cloud platform³⁰. The mean high water line (MHWL) was adopted as the coastline in this study, as it is commonly used as a reference in cartography and long-term research. Additionally, since the error caused by the influence of tides is often less than 1 pixel³¹, tidal correction is not applied to the extraction results.

MNDWI construction

The MNDWI was utilized to preliminarily distinguish water and non-water pixels. This index leverages the significant difference in reflection and absorption characteristics between water and non-water surfaces in the green and mid-infrared wavelengths, which makes the water with positive values and the non-water with negative or zero values in image. Compared to the Normalized Difference Water Index (NDWI), MNDWI enhances the characteristics of open water and effectively suppresses or even eliminates noise from land, vegetation, and soil, making it superior for coastline extraction³². The calculation formula of MNDWI is as follows:

$${\bf{MNDWI}}=\frac{{{{\boldsymbol{\rho }}}_{{\bf{green}}}-{\boldsymbol{\rho }}}_{{\bf{SWIR}}{\bf{1}}}}{{{{\boldsymbol{\rho }}}_{{\bf{green}}}+{\boldsymbol{\rho }}}_{{\bf{SWIR}}{\bf{1}}}}$$

(4)

where ${{\rm{\rho }}}_{{\rm{SWIR}}1}$ and ${{\rm{\rho }}}_{{\rm{green}}}$ are the reflectance values of SWIR1 (Shortwave Infrared 1) and green bands in Landsat imagery, respectively. They correspond to the B5 and B2 of Landsat TM/ETM + images, respectively, and the B6 and B3 of Landsat OLI images, respectively.

Sea-land segmentation

The Maximum Between-Class Variance Method (OSTU) is used for sea-land segmentation in combination with MNDWI. It is a method for determining the optimal segmentation threshold using a gray level histogram³³. It represents the pixel values of an image as ${\rm{L}}$ gray levels and counts the number of pixels at each gray level, categorizing pixel values between $[1,{\rm{k}}]$ as foreground pixels and pixel values between $[{\rm{k}}+1,{\rm{L}}]$ as background pixels. By iterating ${\rm{k}}$ from 1 to ${\rm{L}}$, the between-class variance between foreground pixels and background pixels was calculated as follows:

$$\left\{\begin{array}{c}{\rm{u}}={{\rm{w}}}_{1}\ast {{\rm{u}}}_{1}+{{\rm{w}}}_{2}\ast {{\rm{u}}}_{2}\\ {\rm{s}}={{\rm{w}}}_{1}{({{\rm{u}}}_{1}-{\rm{u}})}^{2}+{{\rm{w}}}_{2}{({{\rm{u}}}_{2}-{\rm{u}})}^{2}\end{array}\right.$$

(5)

where ${\rm{u}}$ is the total average gray level of the image, ${{\rm{u}}}_{1}$ is the average gray level of foreground pixels, ${{\rm{w}}}_{1}$ is the ratio of foreground pixels to total image pixels, ${{\rm{u}}}_{2}$ is the average gray level of background pixels, ${{\rm{w}}}_{2}$ is the ratio of background pixels to total image pixels, and ${\rm{s}}$ is the between-class variance. After the iteration, the value of k that maximizes ${\rm{s}}$ is selected as the optimal segmentation threshold.

Edge detection

The Canny edge detector was used to get accurate coastlines based on sea-land segmentation. It is a multi-level edge detection algorithm that incorporates noise smoothing and is based on three key criteria: low error rate, optimal edge localization, and a single response to a single edge³⁴. The basic steps of the algorithm are as follows:

• a) Gaussian filter denoising process. The Gaussian filter denoising process involves using a convolution kernel to compute the weighted average of each pixel in an image based on its distance from the centre of the kernel. This approach increases the weight of pixels closer to the computed pixel while decreasing the weight of pixels further away. By doing so, the method effectively suppresses image noise and enhances edge localization accuracy.

• b) Image gradient computation. The Sobel operator is utilized to calculate the horizontal and vertical image gradients. The calculation formulas are as follows:

  $${{\rm{G}}}_{{\rm{x}}}=\left[-\mathrm{1\; 0\; 1}-\mathrm{2\; 0\; 2}-\mathrm{1\; 0\; 1}\right]$$

  (6)
  $${{\rm{G}}}_{{\rm{y}}}=\left[-1-2-\mathrm{1\; 0\; 0\; 0\; 1\; 2\; 1}\right]$$

  (7)

  where ${{\rm{G}}}_{{\rm{x}}}$ is the horizontal image gradient, and ${{\rm{G}}}_{{\rm{y}}}$ is the vertical image gradient.

  Based on the image gradient, the image gradient magnitude ${\rm{G}}$ and direction ${\rm{\theta }}$ are further calculated:

  $${\rm{G}}=\sqrt{{{\rm{G}}}_{{\rm{x}}}^{2}+{{\rm{G}}}_{{\rm{y}}}^{2}}$$

  (8)
  $${\rm{\theta }}={\tan }^{-1}\frac{{{\rm{G}}}_{{\rm{y}}}}{{{\rm{G}}}_{{\rm{x}}}}$$

  (9)

• c) Non-maximum value suppression. Non-maximum suppression compares the gradient magnitude of each pixel with its neighbouring pixels along the gradient direction. It is retained if the centre pixel has the highest gradient magnitude; otherwise, its value is set to zero. This process suppresses non-maximum values and preserves only the points with the largest local gradients, resulting in more refined edges.

• d) Dual thresholding to determine potential edges. Based on the results of the previous steps, dual thresholding is used to determine potential edges. The gradient magnitude of each pixel is compared against two predefined thresholds to identify the true boundary points.

Classification of coastlines using remote sensing images

A hybrid transect classifier, developed using globally stable training samples and a random forest algorithm, was used to group the extracted coastlines into sandy, biogenic, rocky, muddy, and artificial categories. This classifier achieved an overall accuracy of 87.5%. The estuary coastline was classified by visual inspection in combination with the Global Surface Water (GSW) dataset and Google Earth images⁶.

Coastline classification system

As shown in Table 2, the coastline was classified into two primary categories (artificial coastline and natural coastline) in GCL_FCS30D. The natural coastline was further subdivided into five secondary categories: sandy coastline, biogenic coastline, rocky coastline, muddy coastline and estuary coastline.

Table 2 Coastline classification system used in this study.

Deriving training samples for classifier from the coastal geophysical product

As the key for high-precision coastline mapping and classification, a globally distributed stable coastline training sample set (denoted as GCL_TrainSample) containing 5 clearly distinguishable coastline categories was generated in this study. It contains 1950 training data transects which were labeled with a coastline category through coastal geospatial datasets and visual inspection based on the methodology of Hulskamp et al.¹⁰, representing diverse coastal environments across the six continents (excluding Antarctica) (Fig. 3).

Fig. 3

The spatial distribution of the globally distributed coastline training samples (GCL_TrainSample) with five coastline categories in 2015.

The method for generating samples developed in this study utilizes geospatial data (elevation, mangroves, land covers and temperature) to facilitate the spatiotemporal migration of coastline samples (Fig. 4), even amidst constraints in sample sizes and temporal coverage³⁵. This method was categorized into three parts to distinguish different coastline samples.

• a) Generation of coastline samples. The sample transects were randomly generated along the extracted coastlines in this study, and the attributes of the geospatial datasets (Table 3) were extracted at each sample transect for initial classification, covering three time-steps: 2010, 2015, and 2020. The complex coastal geographic features and land cover may influence the integrity of the coastline samples. To improve this, a transect automated sampling technique was utilized based on the random points, which determines the feature of transects by appraising the proportion of geographic features within the transect. A transect is retained if the associated geospatial feature occupies more than 90% of the area^36,37.

  Table 3 Datasets used to evaluate the accuracy of coastline position.

• b) Filtering of potential coastline samples. A decision tree based on geospatial features and land cover was utilized for initial classification and generation. Thresholds for most coastline categories were derived through Kernel Density Estimation (KDE) analysis of sample data provided by Hulskamp et al.¹⁰. Specifically, a high and variable bed level calculated from elevation data is usually associated with a rocky coast. High temperatures and high rainfall are typically indicative of a muddy coast. Tidal flats are generally related to sandy or muddy coasts. The transect cross mangrove forests or coral reefs represent a biogenic coast, and cross the artificial surface represents an artificial coast. Following the initial classification, the temporal representativeness of sample transects was refined by comparing attributes across the different years to support long-term coastline classification. If the properties of any sample transects changed significantly during this period, they were removed from the sample pool. Only temporally stable coastline samples were retained after refinement.

• c) Confirmation of coastline samples. After sample refinement and initial classification, a visual inspection was performed on these temporally stable coastline samples to finalize the GCL_TrainSample dataset using high-resolution Google Earth images.

Fig. 4

The process of coastline sample generation based on geospatial datasets.

Compositing multispectral features

A set of 24 features from images were used as inputs for the classifier. These features included the pixel intensity in five multispectral bands (R, G, B, NIR, SWIR1), seven commonly used spectral indices (LTideI, NDWI, MNDWI, NDVI, EVI, RVI, NDBI), and the variance of each multispectral band and spectral index⁷. Vegetation indices such as the Normalized Difference Vegetation Index (NDVI), Enhanced Vegetation Index (EVI) and Ratio Vegetation Index (RVI) were utilized to better capture variability associated with biogenic coastlines. These indices help to distinguish vegetative cover and health, providing crucial insights into the characteristics of biogenic coastal environments (Fig. 5a). Additionally, the Normalized Difference Built-up Index (NDBI) was employed to identify and characterize artificial surfaces effectively, enhancing the detection of man-made structures along the coastline (Fig. 5c).

Fig. 5

Distribution of four index variables, based on 1950 labeled sample points. The vertical axis shows the density, and the horizontal axis represents the distribution of indices: (a) NDVI; (b) LTideI; (c) NDBI; (d) MNDWI. The solid lines show the kernel density estimation for the five coastal categories: artificial, biogenic, sandy, muddy and rocky coastlines.

Since the coastlines are simultaneously influenced by tidal and phenological variability, the maximum compositing of the LTideI (low Tide index) and MNDWI was used as a feature to capture the tides³⁵ (Fig. 5b,d). The LTideI is an index optimized from the NDVI, which fully utilizes the spectral characteristics of tides — high NIR reflectance and low red reflectance. It provides a more accurate and reliable method for distinguishing these areas from open water. In addition to these indices, the variance of each multispectral band and spectral index was also utilized to increase the separability between natural coastlines and anthropogenic coastlines, such as coastal aquaculture ponds. It enhanced the distinction by capturing subtle variations and differences in reflectance properties. The calculation formulas of these indices are as follows:

$${LTideI}=\frac{{\rho }_{{NIR}}-max({\rho }_{{blue}},{\rho }_{{green}},{\rho }_{{red}},{\rho }_{{SWIR}2})}{{\rho }_{{NIR}}+max({\rho }_{{blue}},{\rho }_{{green}},{\rho }_{{red}},{\rho }_{{SWIR}2})+L}\times (1+L)$$

(10)

$${NDWI}=\frac{{{\rho }_{{green}}-\rho }_{{NIR}}}{{{\rho }_{{green}}+\rho }_{{NIR}}}$$

(11)

$${NDVI}=\frac{{\rho }_{{NIR}}-{\rho }_{{red}}}{{\rho }_{{NIR}}+{\rho }_{{red}}}$$

(12)

$${NDBI}=\frac{{\rho }_{{SWIR}1}-{\rho }_{{NIR}}}{{\rho }_{{SWIR}1}+{\rho }_{{NIR}}}$$

(13)

$${EVI}=2.5\frac{{\rho }_{{NIR}}-{\rho }_{{red}}}{{\rho }_{{NIR}}+{6\rho }_{{red}}-7.5{\rho }_{{blue}}+1}$$

(14)

$${RVI}=\frac{{\rho }_{{NIR}}}{{\rho }_{{red}}}$$

(15)

where ${{\rm{\rho }}}_{{\rm{SWIR}}1}$, ${{\rm{\rho }}}_{{\rm{SWIR}}2}$, ${{\rm{\rho }}}_{{\rm{NIR}}}$, ${{\rm{\rho }}}_{{\rm{blue}}}$, ${{\rm{\rho }}}_{{\rm{green}}}$ and ${{\rm{\rho }}}_{{\rm{red}}}$ are the reflectance values of SWIR2 (Shortwave Infrared 2), SWIR1 (Shortwave Infrared 1), NIR (Near Infrared), red, green and blue bands in Landsat imagery, respectively. The adjustable term ${\rm{L}}$, which is used to improve the LTideI index’s robustness, was selected as 0.1³⁸.

Compositing geospatial features

In parallel to multispectral features, we also composited the physical geospatial features using coastal geospatial datasets. The elevation data was processed to derive maximum bed level and variance along the profile to identify rocky coastlines. Mangroves and coastal wetlands datasets were utilized to ascertain the presence of biogenic coastlines. Land cover data provided crucial information for classifying coastlines, particularly artificial coastlines. Surface water data supplemented visual interpretations of estuary coastlines. Due to its coarse resolution, temperature data underwent interpolation using a nearest neighbor technique. Climatological variables such as maximum temperature of the warmest month and minimum temperature of the coldest month were extracted from this dataset to further identify muddy coastlines^39,40.

Hybrid coastal transect classifier

The multispectral features from satellite images and the physical geospatial characteristics from coastal geospatial datasets were utilized to train a hybrid transect classifier. Specifically, an optimized random forest ensemble classifier was developed and its performance was assessed on the test set using overall accuracy and F1-score. This non-parametric machine learning classifier demonstrate greater tolerance to errors when compared with specific parametric classifiers. Based on the cross-validation, we set the number of decision trees to 100 and keep the other parameters as defaults. The 70% of the GCL_TrainSample data were used for training, while the remaining 30% were reserved for validation. The transect training dataset included 390 transects for each coastline categories. To account for variability induced by potential biases in the training-test split, this partitioning was performed randomly 100 times. Additionally, subsets of the training dataset of varying sizes were employed to investigate the impact of the training data size (Fig. 6a).

Fig. 6

(a) Learning curve of the hybrid coastal transect classifier. The vertical axis shows the accuracy (F1-score), and the horizontal axis represents the number of training transects. (b) Importance of features (mean decrease in impurity method) used in classifier, and the bars represent the average of the importance of each feature from multispectral satellite imagery (blue) and coastal geospatial datasets (orange). The black line indicates the standard deviation of the importance of each feature. Note: Max_elevation (maximum elevation in transect), Elevation var (variance height in transect), Min temp (minimum temperature).

The hybrid coastal transect classifier achieved an overall accuracy of 89.5%, with a 95% confidence interval of ±2.5%. For all continents, the overall accuracy rates exceeded 85% (Fig. 7). The mean decrease in the impurity method was employed to ascertain the importance of relative features (Fig. 6b). Among the 24 multispectral and 10 geospatial features, remote sensing indices and their variances significantly enhanced the classifier’s performance.

Fig. 7

The overall accuracy and F1-score of the hybrid coastal transect classifier in six continents.

Post-processing of coastline category assignment

After classification using the hybrid coastal transect classifier, the coastline categories were stored within the transect system. Various GIS methods were then employed to classify coastlines into categories. The proximity analysis (Fig. 8a) was used to identify the transect centroid within a 200 m buffer where the category changes. The identified transect centroids were then used to split the coastlines (Fig. 8b). Next, the occurrence probability of each coastline category within the internal transects of the split coastlines was counted. Finally, the category with the highest occurrence probability was assigned as the category for the split coastline (Fig. 8c).

Fig. 8

Schematic representation of coastline category assignment. (a) Proximity check identifies the transect centroid within the buffer where the category has changed. (b) Split the coastline using these transect centroids. (c) Count the coastline categories corresponding to transects inside the split coastline and assign the category with the highest occurrence probability as the category of this coastline.

Accuracy assessment

Accuracy assessment of coastline position

The Offset, Mean Offset and Root Mean Square Error (RMSE) of coastline location along with the global validation points selected from Google Earth (Fig. 1) and the points randomly generated on the third-party coastline datasets were used to evaluate the accuracy of the coastline extraction. The Mean Offset indicates the distance between the extracted coastline and the validation point, while the RMSE represents the standard deviation of this offset. The calculation formulas of them are as follows:

$${Offset}={E}_{n}$$

(16)

$${MeanOffset}=\frac{{E}_{1}+{E}_{2}+{E}_{3}+\cdots +{E}_{m}}{m}$$

(17)

$${RMSE}=\sqrt{\frac{{E}_{1}^{2}+{E}_{2}^{2}+{E}_{3}^{2}+\cdots +{E}_{m}^{2}}{m}}$$

(18)

where ${\rm{m}}$ is the number of validation points, and ${\rm{E}}$ is the euclidean distance from the validation point to the extracted coastline.

Three global coastline datasets were utilized as third-party validation data to assess the position of GCL_FCS30 in this study (Table 3). They are all widely used coastline position datasets that lack category information. The 2015 Global Multiple Scale Shorelines Dataset (GMSSD_2015) was obtained through human-computer interaction and Google Earth images, providing global vector shoreline data with meter-level resolution⁴¹. The Global Self-consistent, Hierarchical, High-resolution Geography Database (GSHHG) is a high-resolution geography dataset in WGS84 geographic coordinates, amalgamated from the World Vector Shorelines (WVS) and CIA World Data Bank II (WDBII) databases⁴². We also used coastline data from OpenStreetMap developed by the OSMCoastline program.

The relationship between line element uncertainty (U) and image resolution (r) obtained from remote sensing images is described in formula (16)³¹. Therefore, based on the resolution of Landsat imagery (30 m), the theoretical maximum allowable error for coastline extraction is 28.28 meters. The accuracy of the extracted coastline is considered to meet the standard when the Mean Offset and RMSE of the extracted coastline in this study are less than the theoretical maximum allowable error.

$$U=\frac{2\sqrt{2}}{3}r$$

(19)

Accuracy assessment of coastline classification

The error matrix and the product validation points selected from Google Earth were utilized to evaluate the accuracy of our coastline classification. This method has been widely recognized as the most effective means of assessing the accuracy of coastline classification^27,43. It describes the confusion between various categories and generates four accuracy metrics: producer’s accuracy (P.A.), user’s accuracy (U.A.), overall accuracy (O.A.), and kappa coefficient (Kappa). The overall success of classification was assessed by calculating the overall accuracy, while the level of agreement between the classification results and sample labels was evaluated by calculating the Kappa.

This study utilized four global coastline categories and coastal ecosystem datasets as third-party validation data (Table 4). The percentage of matching category regions and the consistency of specific coastline spatial distribution were used to comparison with third-party validation data. The International Union for Conservation of Nature (IUCN) Global Ecosystem Typology is a framework developed to classify and categorize ecosystems globally, providing a standardized and comprehensive approach to ecosystem understanding and management based on ecological characteristics and functions. It includes various shoreline types such as rocky, muddy, sandy, and anthropogenic shorelines, supported by high-quality datasets to ensure accuracy and reliability in ecosystem assessments and management strategies²⁸. However, it was designed to reflect the approximate distribution of the various coastline categories and was not intended to capture precise distributional information. The MuddyZonesFleming is delineated based on the framework established in “Muddy Coasts of the World: Processes, Deposits and Function”, which outlines the geographic distribution of muddy coasts as described by Flemming⁴⁰. Additionally, coastal locations classified by Hulskamp et al.¹⁰ were employed to evaluate the accuracy of sandy, muddy, and rocky coastlines in this study. The global 30 m impervious-surface dynamic dataset (GISD30) was used to evaluate the accuracy of artificial coastlines.

Table 4 Datasets used to evaluate the accuracy of coastline classification.

Data Records

The developed global 30 m coastline dataset with fine classification covering the period from 2010 to 2020 is freely available on the Zenodo platform (https://doi.org/10.5281/zenodo.13943679)⁴⁴. It is structured under the EPSG:4326 (WGS_1984) spatial reference system and provided in shapefile format. The dataset includes both length and category attributes. For the category attribute, coastlines are classified as follows: (0) artificial, (1) biogenic, (2) sandy, (3) muddy, (4) rocky, and (5) estuary. This dataset can be examined and visualized using ArcGIS, QGIS, or their alternatives.

We developed global 30-m coastline maps (GCL_FCS30) with six categories for 2010, 2015, and 2020 using Landsat imagery time series, a threshold segmentation method, and a hybrid coastal transect classifier based on random forest classification models. Figure 9 illustrates the global 30 m coastline map for the nominal year 2015, showing that the distribution of natural coastlines exhibits a clear relationship with latitude and climate²⁵. Sandy coastlines are more prevalent in subtropical and lower mid-latitudes. Rocky coastlines are widespread, concentrated primarily in bays, fjords (such as those along the California coast and in Norway), oceanic islands formed by volcanic activity (like Hawaii and the Galápagos Islands), and cold-water regions at mid-to-high latitudes. Muddy and biogenic coastlines are predominantly found in tropical humid regions characterized by high temperatures and rainfall, consistent with findings by Hulskamp et al.¹⁰ Muddy coastlines reflect the significant suspended sediment load carried by rivers draining the Himalayas, Southeast Asia, and the Amazon River basin. Biogenic coastlines cover major protected or conserved coastal areas worldwide, such as the Sundarbans, Everglades National Park, Lorentz National Park, and the Great Barrier Reef. In contrast to natural coastlines, the distribution of artificial coastlines is primarily influenced by global trade and rapid urbanization. GCL_FCS30 reveals distinct clusters of artificial coastlines, prominently observed in East Asia, Southeast Asia, the Middle East, Western Europe, and North America. The primary land uses on artificial coastlines include port extensions, residential areas, commercial districts, and industrial zones⁴⁵.

Fig. 9

The GCL_FCS30 coastline map in 2015 containing 6 fine coastline categories, excluding large inland lakes, the Greenlandic and Antarctic coastline. (a) The global coastline map; (b) Artificial coastline in East Asia; (c) Biogenic coastline in South Asia; (d) Muddy coastline in Australia; (e) Sandy coastline in Africa; (f) Rocky coastline in South America; (g) Estuary coastline in North America.

Technical Validation

Accuracy assessment using global validation data

The results of the extraction accuracy assessment based on the validation points are shown in Table 5. This assessment spans three distinct periods, and the Mean Offset and RMSE were consistently below 28.8 meters and were well within acceptable error limits. This means that the GCL_FCS30 coastline product has robust extraction accuracy and meets rigorous standards for precision in spatial data applications. In addition, the assessment results over different periods exhibited a high degree of temporal consistency, indicates the stability of the extraction methodology over time. Overall, the extraction method employed in this study fully ensures data integrity and usability.

Table 5 Accuracy assessment of coastline extraction using validation data.

The classification accuracy in three periods using error matrix based on global validation dataset is depicted in Table 6. The accuracy of GCL_FCS30 remained stable and satisfactory, with overall accuracy (O.A.) and Kappa coefficient of 85.79% and 0.78, respectively, in 2010, 83.82% and 0.75, respectively, in 2015, and 85.78% and 0.78, respectively, in 2020. Among the six categories, rocky coastline achieved the highest average F1 score (89.01%), followed by biogenic (83.55%), artificial (83.04%), and muddy (82.39%) coastlines. The sandy coastline achieved the lowest average F1 score (75%).

Table 6 The classification accuracy based on global validation points for 3 periods.

In terms of P.A. and U.A. (Table 6), the biogenic, muddy and rocky coastlines demonstrated higher accuracy than other categories, primarily due to their incorporation of rich prior knowledge. The category of muddy coastline poses the greatest challenge to accurately identifying biogenic coastline. While 87% of the transects classified as biogenic coastlines were correctly identified, 11% were mistakenly classified as muddy, with an additional 2% erroneously categorized as sandy. This confusion likely arises from their closely aligned geospatial characteristics¹⁰. The sandy and rocky coastlines exhibited a significant mutual influence on each other in classification, as their reflectance signatures in satellite imagery are challenging to differentiate due to their similar physical geospatial features⁹. While 84% of the transects classified as rocky coastline were correctly identified, 12% were mistakenly classified as sandy. Overall, the GCL_FCS30 product shows good temporal stability in terms of P.A. and U.A., reaching mean values of 82.41% and 84.34%, respectively. It achieved a higher U.A. (81.25%–87.50%) compared to P.A. (70.51%–93.42%), indicating a higher omission error and a lower commission error. By validation, the GCL_FCS30 accurately delineates the spatial distributions of various coastline categories, aligning closely with the actual global coastline patterns.

Inter-comparison with third-party products in coastline extraction

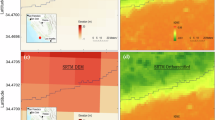
The extraction accuracy of GCL_FCS30 was also evaluated with three other global coastline datasets (GSHHG, GMSSD and OpenStreetMap) as listed in Table 3. As shown in Table 7, approximately 40,000 sample points randomly generated from the three third-party coastline datasets were used to verify the accuracy of coastline extraction³⁸. The results indicate that over 60% of sample points had offsets of less than one pixel, and over 80% had offsets of less than two pixels. The remaining points with offsets larger than two pixels were primarily located on artificial (harbors, aquaculture ponds, and artificial islands) and estuary coastlines. The mean offset and RMSE of all reference datasets consistently hovered around one pixel, indicating that the coastline positions derived from GCL_FCS30 met the required accuracy standards.

Table 7 Accuracy assessment of coastline extraction using third-party validation datasets.

In addition to the quantitative assessment, four typical region enlargements, covering various artificial and estuary coastlines, were selected to directly illustrate the performance of coastline extraction (Fig. 10). The GCL_FCS30 had a better advantage in spatial details compared to the GMSSD_2015 and GSHHG_2015 products over these local enlargements. For example, the harbor and wharf reclamation (Fig. 10a,b), the artificial island (Fig. 10c), and the estuary coastline (Fig. 10d) were more accurately captured in the GCL_FCS30. Overall, the GCL_FCS30 offers a more precise and detailed depiction of the artificial structure, complex coastal features and transitions. In contrast, the coarse coastline product (GSHHG) usually lacks these details, resulting in a loss of critical information on the artificial features and structures.

Fig. 10

Visual comparison between our coastline maps and third-party datasets (GMSSD_2015 and GSHHG_2015) in 2015. Background imagery is a true colour composite of Landsat imagery.

Inter-comparison with existing specific category products

As detailed in Table 8, the accuracy of each specific category was assessed based on the percentage of correctly matched categories. To mitigate the influence of difference in coastline category definitions¹⁰, the combination of muddy and biogenic coastlines in GCL_FCS30 was compared with the corresponding coastline categories in other datasets for matching assessment. The GCL_FCS30 demonstrated excellent agreement with other datasets over 80% of the area. Among the categories, the combined muddy and biogenic coastlines exhibited the highest matching level, achieving 96.7% with MuddyZonesFleming and 92.6% with the Hulskamp et al.¹⁰ dataset. This high agreement (96.7%) indicates that the product can capture muddy and biogenic regions in the world well previously reported in literature. Conversely, sandy and rocky coastlines showed lower matching rates, with 83.9% and 84.5%, respectively, when compared to the IUCN Global Ecosystem Typology, and 88.25% and 86.39%, respectively, relative to the Hulskamp et al. dataset. Notably, the GCL_FCS30, which features smooth and continuous coastline lines, aligns seamlessly across both analysis grid cells and satellite scene boundaries along the global coastline.

Table 8 Accuracy assessment of coastline classification using third-party datasets.

In addition, to avoid the influence of spatial errors in matching regions, the spatial distributions of specific coastline categories in the GCL_FCS30 were compared with data from Hulskamp et al. As illustrated in Fig. 11, the correlation (R²) between the coastline distributions in GCL_FCS30 and those from Hulskamp et al.¹⁰ was approximately 0.9 for all categories. Artificial coastlines showed particularly high agreement, with R²values of 0.96 for latitude and 0.93 for longitude, indicating a strong alignment between the two datasets. However, while there was also substantial agreement for rocky coastlines, the correlation was somewhat lower, with R²values of 0.86 for latitude and 0.81 for longitude. This lower correlation can be attributed to the fact that the data from Hulskamp et al. primarily cover ice-free coastlines and lack comprehensive coverage of coastlines in high-latitude regions. These high-latitude areas are predominantly characterized by rocky coastlines, which are underrepresented in the Hulskamp et al. dataset, leading to discrepancies in rocky coastline distribution.

Fig. 11

The comparison of pixel number of coastline spatial distribution between GCL_FCS30 and Hulskamp et al.¹⁰ includes sandy coastlines (a,b), muddy and biogenic coastlines (c,d), rocky coastlines (e,f), and artificial coastlines (g,h) along latitude and longitude, respectively. Specifically, muddy and biogenic coastlines were compared with muddy and vegetated coastlines, while artificial coastlines were compared with all other coastlines. In the figure, the black dashed line represents the 1:1 line, and the red solid line denotes the fitted line.

Usage Notes

Advantages of the GCL_FCS30 coastline product

Previous coastline products have traditionally emphasized coastline erosion and sedimentation, requiring frequent updates in coastline extraction^46,47. In contrast, the GCL_FCS30 primarily focuses on the composition of coastlines and their surroundings, specifically emphasizing on human activities. Compared to the transect format coastline categories dataset from Hulskamp et al.¹⁰, the GCL_FCS30 offers long-term category information and presents coastal category data in a line format, facilitating regional change studies at specific coastal locations in a spatially consistent manner.

In addition, the GCL_FCS30 also demonstrates significant strengths in its classification process, including the classification system, sample point generation, and feature selection. These aspects are critical for ensuring the global representativeness, stability, and consistency of the product. Coastline classification offers a systematic and standardized method to describe and identify coastal environments, serving as a fundamental dataset and scientific foundation. It has found extensive application in geomorphology to characterize the diverse coastal landforms and their contextual emergence. However, no single classification system has comprehensively covered all aspects in scope or coverage^48,49.

The coastline classification system in this study was developed based on the IUCN Global Ecosystem Typology, a novel framework that integrates all of Earth’s ecosystems into a unified theoretical context²⁸. To adapt to the demands of global observation using remote sensing technology, this study consolidates supralittoral coastal biome into a biogenic coastline category. This category encompasses vegetation cover, biodiversity, and the spatial distribution of biological communities. As shown in Table 9, compared to previous global coastline mapping studies, the classification system in GCL_FCS30 provides more detailed coastal information, particularly concerning human activities and coastal biodiversity. Different from previous regional coastline studies, artificial coastlines in GCL_FCS30 were not subdivided into secondary levels, offering the advantage of scalability to accommodate global perspectives seamlessly. In summary, the classification system in this study ensures consistency and comparability across different regions, facilitating comprehensive analyses and broader applications in global studies of coastal environments.

Table 9 The comparisons in coastline classification system between GCL_FCS30, global muddy coasts in Hulskamp et al.¹⁰ and mainland China coastline in Hou et al.³¹.

Global coastline extraction and classification present significant challenges due to the extensive data preprocessing requirements, high-performance computing demands, and the complexity of acquiring globally distributed and temporally stable training samples⁵⁰. The sample generation stands as the most significant obstacle in achieving accurate and reliable results across different geographical regions and periods. Therefore, this study presents a coastline stable sample generation method, optimizing the acquisition of coastline samples for coastline classification. It is based on a method for sample generation that involves a small amount of visual interpretation, integrating with coastal knowledge and rule-based thresholding³⁵. It is not labor-intensive and provides accurate coastline samples using minimal pre-existing ones. As shown in Fig. 12, the samples generated by this method demonstrate good spatiotemporal coherence. The potential of this method lies in reducing the spatiotemporal heterogeneity of coastline tidal effects by combining with coastal geographic characteristics.

Fig. 12

Generated coastline samples in 5 categories. (a) Artificial coastline, (b) Biogenic coastline, (c) Sandy coastline, (d) Muddy coastline, (e) Rocky coastline. Background imagery is a true color composite of Landsat imagery.

Due to the complex composition and surroundings of coastlines, the simple use of multispectral data does not provide sufficient information to discriminate highly mixed and spectrally similar types accurately. Moreover, multisource Earth observation data show significant potential for enhancing the classification accuracy of surface elements such as crops, aquatic lands, and forests^51,52,53. In this study, hybrid features combining multispectral satellite imagery with global coastal geophysical datasets were employed for coastline classification. This method mitigates issues related to data gaps and varying data availability scenarios⁵⁴, while also providing complementary information for the precise classification of specialized categories of coastlines. Additionally, the ancillary datasets significantly improve the overall performance of coastline classification. As shown in Fig. 6a and Fig. 13a, the inclusion of geophysical features enhanced the classifier’s performance by 15% compared to using information from multispectral satellite imagery alone. However, it is important to note that multispectral features still provide the vast majority of information, as evidenced by their higher importance scores compared to most geophysical features (Figs 6b, 13b).

Fig. 13

(a) Learning curve of the classifier using the multispectral satellite imagery alone, the vertical axis shows the accuracy (F1-score), and the horizontal axis represents the number of training transects. (b) Importance of features (mean decrease in impurity method) used in this classifier. The bars represent the average of the importance of each feature from multispectral satellite imagery (blue). The black line indicates the standard deviation of the importance of each feature.

Potential application of the GCL_FCS30 coastline product

The GCL_FCS30 coastline product from 2010 to 2020 provides detailed spatial information for patterns and trends in global coastal changes. Compared to previous global coastline databases, the advantage of the GCL_FCS30 lie in longer and more consistent time resolution, improved classification accuracy due to the incorporation of geophysical information, and the finer classification system. These improvements enable GCL_FCS30 to support a variety of applications, such as developing global policy frameworks on coastal land reclamation trends, identifying drivers of natural coastline loss and recovery, mapping biogenic coastline values, and setting and monitoring conservation and rehabilitation targets^55,56. Besides, the coastline categories play a crucial role in determining coastal vulnerability to environmental forcing and climate change, it is essential for differentiating various hazards and identifying the necessary approaches needed to evaluate impacts across different coastal areas^57,58. It can be a valuable input in climate change studies on coasts globally, including sandy beach erosion and coastal flooding^{13,59,60,61,62}.

Uncertainty and limitations of the GCL_FCS30 coastline product

This study explored potential solutions for coastline monitoring from a data perspective and unavoidably with some limitations. A limitation of this study is the lack of in-situ measurements of coastal positions for creating training data and evaluating results, which could enhance the precision and confidence in the labels. The problem of imperfect labels is unresolved, as conducting in-situ measurements is impractical for a study with a global scope. Instead, this study employed a sample generation method that combines geospatial data and visual interpretation. While this approach may introduce some uncertainty and make performance assessment challenging, it is a widely accepted practice in studies involving image analysis and machine learning with remote sensing imagery⁵⁶, and is perhaps the most practical solution for creating large, geographically distributed training and testing datasets.

The uneven spatial and temporal coverage of Landsat is another major limitation, particularly in high-latitude regions and areas with frequent cloud cover^63,64. Thus, future attempts would extend the temporal coverage of the GCL_FCS30 by incorporating data from multiple sources that complement Landsat satellites, such as Sentinel-2 satellites and Sentinel-1 satellites^13,59,60. In addition, although globally distributed training samples and a hybrid coastal transect classifier have been utilized to enhance the mapping accuracy of coastlines, the challenges of omission and commission errors persist due to the complex spatial and spectral characteristics of specific coastline categories. Some categories exhibited producer accuracy rates lower than 80%, indicating the need for continued refinement and improvement in classification methodologies to address these complexities.

The extraction method used in this study is influenced by environmental complexity and its sensitivity to threshold selection. Dense coastal vegetation can be difficult to distinguish from land or water using MNDWI, leading to inaccuracies in coastline extraction³⁰. While the OTSU adaptive thresholding method is effective for global thresholding, it may not perform optimally in heterogeneous coastal regions. The method may lack the robustness required to account for threshold variations in areas with diverse water colors, sediment types, and vegetation. Additionally, the accuracy of post-processing is highly sensitive to the choice of buffer size. The selected buffer distance can introduce uncertainty, as it may not accurately capture the true scale of coastal transitions. A larger or smaller buffer may yield different results, especially in areas where coastal categories change abruptly or extend over larger distances. In regions with abrupt transitions (e.g., from rocky shorelines to sandy beaches), a larger buffer could encompass both categories, resulting in a blending of features and leading to ambiguity in classification.