Dataset on guided waves from long-term structural health monitoring under uncontrolled and dynamic conditions

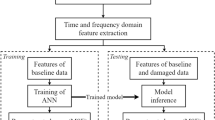
Abstract

Few studies address guided wave structural health monitoring under controlled and dynamic environments, largely due to the lack of a public benchmark dataset. To address this gap, this paper presents a public dataset from a long-term outdoor structural monitoring experiment conducted at the University of Utah, Salt Lake City. The monitoring, spanning over 4.5 years, collected approximately 6.4 million guided waves under both regular environmental variations (e.g., daily temperature changes ranging from 260.95 K (−12.2 °C) to 325.65 K (52.5 °C)) and irregular variations (e.g., rain and snow). The measured guided waves in the public dataset are also affected by sensor drift and installation shifts consistently over time. Additionally, thirteen types of damage were introduced to the monitored structure to support damage detection and severity evaluation under these conditions. The dataset includes measurement times, temperature, humidity, air pressure, brightness, and weather information to aid in damage detection. The provided public dataset aims to assist researchers in developing more practical methods for structural health monitoring in uncontrolled and dynamic environments.

Background & Summary

Guided wave-based structural health monitoring (SHM) is extensively used in modern society to support the operation of mechanical structures such as airplanes¹, wind turbines², ships³, rail⁴, as well as civil infrastructure like pipelines^5,6, bridges⁷, and dams⁸. This widespread application is attributed to the numerous advantages of guided waves, including their high propagation speed, which enables fast detection⁹, their ability to travel long distances with minimal attenuation, allowing large-area scanning with relatively fewer transducers¹⁰, and their high sensitivity to structural stiffness changes due to their high frequency^9,11,12,13. Additionally, the transducers used are inexpensive, lightweight, and easy to integrate into structures¹⁴. Numerous methods have been developed to exploit guided waves for structural evaluation, ranging from signal processing techniques to statistical and machine learning approaches^{11,15,16,17,18}.

However, evaluating and comparing the performance of these proposed structural health monitoring methods is challenging since they rely on specific guided wave datasets collected from different structures with varying geometries and materials, measured using diverse equipment, transducer technologies, actuators, and data acquisition systems^12,13,19. In other words, the structural health monitoring community currently lacks publicly available benchmark datasets that provide well-documented and accessible measurements for evaluating existing guided wave-based SHM methods, comparing new approaches, and developing novel evaluation techniques. Such datasets would also benefit guided wave beginners and researchers with innovative ideas but without access to expensive measurement equipment^12,13,19.

Recognizing the significant demand for publicly available benchmark datasets, Moll et al. have developed the Open Guided Waves (OGW) online platform to support advancements in guided wave-based structural health monitoring (SHM)¹². This platform comprises five benchmark datasets. The first dataset was collected using quasi-isotropic carbon-fiber-reinforced polymer (CFRP) plates with well-defined geometry and embedded piezoelectric transducers. To establish the baseline condition, ultrasound and X-ray tests were conducted. Material properties such as stiffness tensor and sample density were measured, validated, and compared against theoretical predictions. The OGW dataset includes two sets of measurements: 3D acoustic wave field measurements and SHM measurements under controlled conditions (23 °C and 50% relative humidity). A reversible defect model involving an aluminium disk attached to the CFRP plate with tacky tape was employed. For the 3D acoustic wave field measurements, a single piezoelectric transducer was centrally positioned to conduct full-wave field measurements using a 3D scanning laser Doppler vibrometer, analyzing guided wave propagation across various frequencies. Subsequent SHM measurements were conducted on the “SHM plate”, which was equipped with 12 piezoelectric transducers configured in a pitch-catch arrangement. The data acquisition process involved six phases: initially recording 20 baseline measurements of the intact structure, followed by placing the model defect at 11 different positions on the plate. Analysis indicated high-quality differential signals and demonstrated the feasibility of damage localization using this guided wave public benchmark dataset¹².

Subsequently, Moll et al. introduced another guided wave dataset (the second public benchmark dataset) within the Open Guided Waves platform¹³. This dataset utilized the same carbon fiber composite plates from their previous experiment¹², but an additional omega stringer was installed on the plate to represent real aircraft components. The data was collected under consistent laboratory-controlled conditions, with the SHM plate placed in a climate chamber maintained at a constant temperature of 23 °C and 50% relative humidity. Extensive measurements were conducted to investigate two primary aspects: (I) the effect of the omega stringer on guided wave propagation, and (II) the impact of elliptical reference damages of varying sizes, positioned at three different locations, on guided waves. As in the first public dataset¹², a reversible damage model was used, involving a metallic disc affixed to the composite structures with tacky tape. Thirteen reversible reference damages of varying sizes were placed at the three specified locations. Measurements were taken using two types of signals for guided wave excitation: narrowband excitation (5-cycle tonebursts at varying carrier frequencies) and broadband excitation (chirp waveforms). Narrowband excitation involved Hann-windowed sine waves with five cycles, centered at frequencies ranging from 40 kHz to 260 kHz in 20 kHz increments. Broadband excitation used a linear up-chirp lasting 0.125 ms, with frequencies ranging from 20 kHz to 500 kHz. Wave field measurements were captured using a 3D laser Doppler vibrometer under both narrowband and broadband excitations. This public benchmark dataset is valuable for evaluating the effectiveness of guided-wave-based systems in detecting damage of varying severity at different locations, with severity indicated by damage size. The dataset’s validation was carried out through damage severity assessments based on tomographic image reconstructions, demonstrating that larger damages corresponded to higher peak intensities in the reconstructed images¹³.

Pawel et al. expanded upon the public benchmark dataset generated from real damage using the same carbon fiber composite plate setup¹⁹, including an additional omega stringer, as detailed in the experiment by Moll et al.¹³. This dataset was also acquired under constant laboratory-controlled conditions (at 23 °C and 50% relative humidity). Unlike the first and the second public dataset^12,13, which focused solely on guided waves generated from reversible reference damages, this dataset offers three scenarios with data from actual damages: (1) wavefield measurements without damage, (2) wavefield measurements with a local stringer debond, and (3) wavefield measurements with a large stringer debond. These defects resulted from impacts applied to the backside of the plate. The comprehensive ultrasonic guided wavefield scans were achieved by a laser Doppler vibrometer (SLDV) positioned opposite to the piezoelectric transducer and omega stringer. Two types of signals were employed for guided wave excitation: chirp signals spanning a frequency range of 20–500 kHz, and tone-burst signals characterized by sine waves modulated with a Hann window, comprising 5 cycles at carrier frequencies of 16.5 kHz, 50 kHz, 100 kHz, 200 kHz, and 300 kHz. Validation of the public dataset was performed using simple signal processing methods such as weighted root mean square (WRMS). However, WRMS alone did not effectively highlight the damaged areas; only minor changes in energy distribution were discernible. Another post-processing technique utilized was local wavenumber mapping combined with the one-frequency approach was also used in the public data. This technique enabled the identification of discontinuities in wavenumbers caused by local variations in thickness. Nevertheless, without specific guidance, some damages might have been overlooked. Overall, this public benchmark dataset serves as a benchmark for evaluating methods to detect real debond damage on CFRP plates using guided waves¹⁹.

To complement the public benchmark dataset more closely related to practical applications on the Open Guided Waves platform^12,13,19, Marzani et al. collected guided waves propagating through a composite panel of a full-scale aeronautical structure, which was equipped with 160 piezoelectric transducers. This composite panel forms the bottom part of a wingbox, which, along with the leading edge, trailing edge, and wingtip, constitutes an outer wing demonstrator approximately 4.5 meters long and 1.2 to 2.3 meters wide. Electromechanical impedance and guided wave measurements were taken at four different stages: initially on the pristine panel (before loading), after the panel was assembled into the wing box and mounted on a metal frame in a cantilever configuration (before fatigue testing), after undergoing a 90,000-cycle aeronautical fatigue test (before impact testing), and finally after an impact test using an air gun to induce delaminations (after impacts). The structural health monitoring system was designed to (1) perform electromechanical impedance measurements at each transducer to assess their reliability and bonding strength, and (2) conduct active guided wave screening for damage detection in the composite panel. This dataset, with its large number of piezoelectric transducers, allows for the evaluation of signal processing methods by varying the number and positioning of the transducers, investigating the impact of damaged sensors, and testing sensor position optimization procedures. Additionally, it provides valuable insights into SHM system installation challenges, which may be less significant in laboratory settings but become critical in complex real-world scenarios. Overall, this database can be used for benchmarking guided wave algorithms in real-scale structural contexts, covering loading, fatigue, damage detection, characterization, and sizing⁹.

The public benchmark datasets mentioned above were collected under stable, lab-controlled conditions. However, environmental variables, such as temperature, humidity, wind speed, and other environmental and operational conditions, can significantly distort guided waves, often more than structural damage such as cracks, delaminations, or corrosion^20,21,22,23. For example, temperature variations are particularly influential for ultrasonic guided waves based structural health monitoring, as they can cause more pronounced signal changes than typical defects due to thermal expansion and temperature-induced changes in wave velocity. To account for these temperature effects and separate them from defect-induced scattering, several temperature compensation methods have been proposed in the literature^{10,24,25,26,27}. However, the geometry and materials to which these methods have been applied vary widely, complicating overall performance assessment. To address this issue, Moll et al. extended the Open Guided Waves repository by providing benchmark datasets obtained from a carbon fiber reinforced plastic (CFRP) plate²⁸, which was fully characterized in previous research¹². This study used the same reversible damage model as before—an aluminum disc mounted on the specimen’s surface with tacky tape^12,13. Guided wave-based structural health monitoring was carried out under controlled temperature experiments conducted in a climate chamber, ranging from 20 °C to 60 °C with 50% relative humidity, in increments of 0.5 °C. At each temperature level, all specified frequencies of guided waves were recorded. Two temperature cycles were measured for the intact structure and one for each simulated damage position. The technical validation of these datasets includes representative results using state-of-the-art signal processing techniques, such as Optimal Baseline Selection (OBS), Baseline Signal Stretch (BSS), Independent Component Analysis (ICA), Singular Value Decomposition (SVD). A quantitative analysis of temperature-dependent phase velocity variation illustrated changes in the antisymmetric wave mode at 40 kHz with temperature variations, showing a linear delay in time-of-flight changes with temperature. Overall, this public dataset enables performance analysis of existing temperature correction algorithms, the development of new temperature compensation methods, and damage detection methods under varying temperature conditons²⁸.

However, the aforementioned public datasets were collected in controlled laboratory environments^{9,12,13,19,28} and they are not suitable for evaluating the effectiveness of the proposed methods in uncontrolled structural health monitoring under outdoor conditions. In outdoor settings, the monitored structures are exposed to uncontrolled and dynamic environments, where temperature, humidity, brightness, and other environmental factors fluctuate together^17,20. Unlike the controlled experiments where temperature changes were stable²⁸, outdoor conditions introduce complex interactions among multiple environmental factors that distort the guided waves. These variations lead to unexpected changes in guided waves, making damage detection more challenging^22,23. Furthermore, aside from regular environment variations, such as daily environmental changes in temperature and humidity, the structures may also encounter irregular variations such as rain, snow, and extreme temperature conditions, which cause more significant distortions in guided waves compared to regular environmental and damage variations^16,29. These irregular environmental and operational variations can pose challenges for accurate damage detection and may even compromise the effectiveness of the entire monitoring process^16,17,30,31. Researchers need first to identify and account for these variations before proceeding with damage detection³⁰. In addition, structural health monitoring is typically conducted over long periods, during which sensor performance, bonding layers, and data acquisition systems may degrade due to environmental variations, such as fluctuating temperatures in pipelines. For example, Attarian et al. found that bonding adhesives deteriorate over time when subjected to cyclic thermal loading^32,33. This degradation can cause sensor drift and increase the residuals between current and baseline measurements, even if the environmental conditions during both measurements are similar, thereby complicating the detection of actual damage^34,35,36,37. In addition, after repairing or replacing a damaged or degraded sensor, the new setup may not be identical to the previous one due to intentional or unintentional variations in sensor quality, coupling layer type, or sensor positioning^9,34,36,37. These variations, known as installation shifts, can lead to significant differences in the guided waves recorded before and after sensor or other data acquisition system component replacements.

To address the need for public benchmark data for evaluating the effectiveness of damage detection methods in practical environmental and operational conditions, this work presents a public benchmark dataset³⁸ gathered from a long-term outdoor guided wave structural health monitoring experiment conducted under uncontrolled and dynamic conditions (as shown in the figshare data repository³⁸. The dataset was collected in outdoor environments at the University of Utah, Salt Lake City, between March 2018 and October 2022, amassing approximately 6.4 million guided wave data points under various environmental conditions³⁸. The dataset also includes corresponding measurements of surrounding environmental factors such as temperature, humidity, brightness, air pressure, and weather information during the guided wave collection process. A total of 13 different types of damage were introduced, ranging from minor to severe, including metal mass attachments, small dents, and through-hole damage. Detailed descriptions of the data acquisition equipment, collection processes, and damage generation methods are provided in this paper. Challenges in long-term structural health monitoring under uncontrolled and dynamic environmental conditions—including regular and irregular environmental variations, sensor drift, installation drift, and variations in damage severity—are demonstrated using correlation coefficients between adjacent guided waves and optimal correlation coefficients between guided waves and their baseline guided waves, based on the public benchmark dataset. The results show that certain regular and irregular environmental variations, sensor drift, and installation drift can distort guided waves more significantly than structural damage itself³⁸. Overall, this public dataset makes four key contributions to the structural health monitoring community:

• 1. Public Dataset for Real-World SHM Evaluation: We provide the first publicly available benchmark dataset specifically created to assess the effectiveness of guided wave-based methods for long-term structural health monitoring in uncontrolled and dynamic outdoor environments.

• 2. Identification of Key Challenges: The dataset highlights four primary challenges in the public dataset: regular (e.g., daily changes in temperature and humidity) and irregular environmental conditions (e.g., rain and snow), sensor drift, installation drift, and damage severity variation. These challenges will motivate researchers to develop more practical and robust damage detection techniques suitable for real-world outdoor monitoring.

• 3. Comprehensive Damage Types: We introduce 13 types of damage with gradually increasing severity, ranging from small dents to large through-hole damage. This enables the dataset to be used for evaluating the effectiveness of guided wave-based methods in assessing damage severity under uncontrolled, dynamic outdoor conditions.

• 4. Large-Scale Measurement Collection: The dataset includes measurements taken approximately every 170 seconds, with each measurement consisting of 8 guided waves (transmitted by 2 actuators and received by 4 sensors). The extensive data from various sensors facilitates research into data fusion. Over 4.5 years, the dataset contains about 6.4 million measurements, providing a rich benchmark for testing guided wave compression techniques and evaluating the efficiency of damage detection methods using fewer measurements.

Methods

The monitored structure, data acquisition system, experimental setup, and damage generation process will be detailed in the section.

We developed a structural health monitoring system at the University of Utah in Salt Lake City to implement and investigate long-term monitoring under uncontrolled and dynamic conditions. The monitored structure was initially an intact aluminum plate of 53 cm × 53 cm x 3 mm. This plate was placed on the first layer of the shelf, as illustrated in part (a) of Fig. 1. Eight circular lead-zirconate-titanate (PZT) transducers were installed on the plate and covered in epoxy for protection. Each sensor consists of a 7 mm diameter by 0.2 mm thick piezoelectric SM412 ceramic disc produced by StemInc, with a 300 kHz radial mode resonance. Ultrasonic guided wave signals were transmitted and collected by PZT transducers, which convert voltage to mechanical vibration or vice versa. Th locations of the transmitters and receivers (in centimeters) are shown in part (b) of Fig. 1. However, we used only 6 out of the 8 PZT sensors to transmit and receive guided signals. Sensors 1–4 were designated as guided wave receivers, while sensors 5 and 6 served as transmitters, as shown in Fig. 1. This setup allowed us to collect 8 guided waves per measurement, corresponding to paths 5-1, 5-2, 5-3, 5-4, 6-1, 6-2, 6-3, and 6-4. In each path designation, the first number indicates the transmitter, and the second number indicates the receiver. For example, a guided wave from path 5-1 means that the wave was excited by sensor 5 and received by sensor 1. The monitored plate was placed on the first layer of a shelf, as shown in part (a) of Fig. 2. To generate and receive guided waves, we transmitted a 1 ms linear chirp with a center frequency ranging from 5 kHz to 350 kHz using sensors 5 and 6. Each response was recorded at a sampling rate of 1 MHz. Measurements were taken approximately every 8.6 seconds, with only the first 10,000 samples (10 ms) recorded for each guided wave, as shown in part (a) of Fig. 3. The 8.6-second interval between measurements ensured that the ultrasonic signal from the previous excitation had dissipated before capturing the current response^39,40.

Fig. 1

The actual positions of the lead zirconate titanate (PZT) transmitters (sensors 5 and 6) and receivers (sensors 1, 2, 3,and 4) are displayed in the left figure, while the precise coordinates (X: cm, Y: cm) are provided in the right figure.

Fig. 2

(a) shows the monitored structure, an aluminium plate, positioned on the first layer of a shelf. The data acquisition system was housed in a foam box on the second layer of the shelf. (b) and (c) display the locations of the temperature, brightness, air pressure, and humidity sensors, which were mounted on the exterior of the foam box.

Fig. 3

Subplot (a) illustrates the original guided wave, consisting of 10,000 samples and lasting 10 ms. Subplot (b) shows the same guided wave from subplot (a) but retains only the first 2,000 samples. Subplot (c) displays the guided wave from subplot (b) after undergoing pulse compression using the excitation signal. This guided wave was collected from path 5-4 at 20:18:06 on April 24, 2021, at a measurement temperature of 289.72 K (16.57 °C).

Along with collecting guided wave data, the environmental information acquisition system recorded four environmental values for each measurement: temperature, humidity, air pressure, and brightness. These parameters were recorded by sensors connected to a separate data acquisition board housed in a foam box. The environmental sensors were mounted on a foam box on the second layer of the same shelf, within 50 cm of the aluminium panel but not in direct contact^39,40, as illustrated in parts (b) and (c) of Fig. 2. Details of the sensors and data acquisition system are provided in Table 1.

Table 1 Information of environmental sensors and DAQ system.

Long-term monitoring under uncontrolled and dynamic conditions

The monitored structure (an aluminium plate), along with the sensors and data acquisition systems, were placed in a small room with four walls but no roof at the University of Utah, Salt Lake City, as illustrated in part (a) of Fig. 2. This setup exposed the monitored structure and the structural health monitoring system to the outdoor environment under natural and dynamic conditions. The monitored structure and guided wave sensors endured various harsh environmental conditions, as depicted in Fig. 4. For example, rain left the plate wet, as shown in part (a), while ice would melt into surface moisture and refreeze with temperature fluctuations, as illustrated in part (b). Snow accumulation on the plate is shown in part (c) of Fig. 4. In contrast, the environmental sensors—such as temperature, humidity, brightness, and air pressure sensors—mounted on the second layer were not directly exposed to these conditions. However, these sensors were not completely shielded and occasionally experienced brief periods of direct sunlight during certain times of the year. This exposure led to rapid temperature increases, which significantly altered the guided waves, as evidenced by changes in the correlation coefficients of adjacent guided waves with temperature, shown in part (b) of Fig. 6.

Fig. 4

During long-term monitoring, the monitored plate and the structural health monitoring system were exposed to various weather conditions, including rain, icing, and snow, as shown in (a–c), respectively.

The long-term guided wave structural health monitoring experiment commenced in March 2018 and concluded in October 2022. Measurements were taken approximately every 9 seconds, resulting in over 10,000 measurements per day. By the end of the experiment, we had accumulated around 128 million measurements under various weather conditions, including rain, snow, direct sunlight, freezing, cloudy, and icing conditions. This extensive dataset provides researchers with a valuable benchmark dataset to evaluate the performance of structural health monitoring methods under long-term, uncontrolled, and dynamic conditions.

Damage generation and damage type information

Starting on April 17th, 2021, we introduced 13 types of damage to the monitored structure. The first type involved gluing a cubic aluminum mass on the plate on April 17th, 2021, which was removed on May 1st, 2021. Beginning on May 17th, 2021, we started generating irreversible damage to the structure. Initially, a minor dent was created at the center of the plate, and this dent was gradually enlarged from May 17th, 2021, to July 31st, 2022. Subsequently, starting on July 31st, 2022, a through hole was introduced at the center of the plate and was gradually enlarged until October 8th, 2022. Detailed information about the damage can be found in Table 2, and the damage positions and shapes are illustrated in Fig. 5. In total, 13 types of damage were generated, labelled from “D1” to “D13”, with the severity of the damage increasing progressively. This dataset can serve as a benchmark for evaluating the performance of guided wave-based structural health monitoring method in identifying damage and assessing damage severity.

Table 2 Description about the 13 types of damage on the aluminum plate.

Fig. 5

Six types of damage were created sequentially on the center of the same aluminum plate from April 17, 2021 to September 19, 2021.

Data Records

The dataset is available at the repository titled “Dataset on Guided Waves from Long-Term Structural Health Monitoring under Uncontrolled and Dynamic Conditions”³⁸ on figshare. In the repository, approximately five years of monitoring data are stored in 56 “.pickle” files. Each file is named in the format “measurements year_month.pickle”, where the numbers in the filename represent the year and month of the measurements it contains. For example, measurements from April 2018 are stored in “measurements 2018_04.pickle”. Each “.pickle” file is a dictionary with 10 keys, as shown in Table 3. The key “guided wave” contains 8 channels of ultrasonic guided waves. In the “measurements 2018_04.pickle” file, for example, the “guided wave” matrix has dimensions of 14,997 × 8 × 2000, representing 14,997 measurements with each measurement including 8 channels of guided waves from paths 5-1, 5-2, 5-3, 5-4, 6-1, 6-2, 6-3, and 6-4. Each guided wave comprises 2000 samples and lasts 2 ms. The keys “datatime”, “temperature”, “humidity”, “brightness”, and “air pressure” record the measurement time and the corresponding environmental conditions (temperature, humidity, brightness, and air pressure) at the time of guided wave measurement. The key “damage tag” provides damage information for each measurement, with a value of 0 indicating no damage and values from 1 to 13 denoting damage types from “D1” to “D13”, as shown in Table 2. Additionally, the key “weather tag” records the weather conditions from public weather website⁴¹ during each measurement, ranging from 0 to 5, with 0 representing “fair weather” and 1 to 5 corresponding to “precipitation”, “light rain”, “rain”, “snow”, and “mixed weather”, respectively. Note that the 15-mile distance between the meteorological station and the experiment location may introduce some imprecision in the weather records. The key information (“guided wave”, “datatime”, “temperature”, “humidity”, “brightness”, “air pressure”, “damage tag”, and “weather tag”) for each measurement file is explained under the “data inf” key within each file. To assist users in loading and interpreting these “.pickle” files, we have included a Python script (https://github.com/SmartDATA-Lab/Long_Term_Guided_Waves) in Code Availability section.

Table 3 Description about Public Dataset File.

It should be noted that the published data are downsampled and trimmed versions of the original data due to storage constraints. The published benchmark dataset is approximately 100 GB in size, whereas the original data amounts to around 9 TB, making it nearly impossible for most lab computers to load all at once for analysis and computation. To create the public benchmark dataset, we employed a two-step process to reduce its size. First, although guided wave measurements were originally collected every 8.6 seconds, the public dataset includes measurements taken approximately every 176 seconds. In other words, we store one measurement in the public dataset evenly from every 20 original measurements. This 20-fold downsampling has been shown to have minimal impact on the similarity between successive guided waves and on optimal baseline selection-based damage detection, as demonstrated in our previous work⁴². Second, we trimmed each guided wave measurement. The original data comprised 10,000 samples, but the latter 8,000 samples were relatively smaller in magnitude and filled with interference noise, as illustrated in part (a) of Fig. 3. Therefore, we retained only the first 2,000 samples of each guided wave, as shown in part (b) of Fig. 3. The remaining 2,000 guided wave samples have been validated effectively in our previous work on unsupervised anomaly detection^16,17,43.

Technical Validation

The study leverages correlation coefficients between adjacent guided waves, as well as optimal correlation coefficients with baseline guided waves, to validate structural health challenges present in the public dataset—challenges that are also common in practical structural health monitoring under uncontrolled and highly dynamic conditions. This technical validation helps researchers recognize the characteristics and challenges of guided waves obtained from real-world dynamic environments, aiding in the development of effective methods for practical structural health monitoring.

• 1. Challenge 1: Both regular and irregular environmental variations alter guided waves, with irregular variations like rain and snow sometimes causing greater impact than through-hole damage.

• 2. Challenge 2: Sensor drift over time can create differences in guided waves even under similar environmental conditions, complicating baseline comparisons and data-driven-based damage detection.

• 3. Challenge 3: Installation shifts, occurring during repairs or updates to the monitoring system, can lead to differences in guided waves, affecting baseline comparisons and data-driven-based damage detection.

• 4. Challenge 4: Certain types of damage may not significantly alter guided waves, making detection difficult.

Validation (Challenge) 1: Distortion of guided waves due to environmental variations

In the long-term uncontrolled structural health monitoring, the temperature varied from 260.95 K (−12.2 °C) to 325.65 K (52.5 °C), while humidity ranged from 0.5% to 146.3%. Theoretically, the maximum humidity value is 100%, and values exceeding 100%, such as 146.2%, occurred during precipitation events and resulted from improper calibration. Brightness was measured in lux, with values ranging from 0.0003 to 3615537.4. Air pressure varied from 867.2 hPa to 1335.3 hPa. Environmental variations can be classified into regular and irregular categories based on their frequency of occurrence. Regular environmental variations, such as daily changes in temperature and humidity, are consistent and prevalent throughout long-term monitoring. In contrast, irregular environmental variations, such as rain and snow, occur less frequently. Typically, regular environmental variations change gradually, while irregular variations fluctuate rapidly and dramatically. For instance, daily temperature changes are usually less than 2 °C per hour and relatively stable. However, during irregular environmental conditions, like rain or direct sunlight, temperature changes can be much more rapid and drastic, sometimes exceeding 10 °C per hour, as shown in part (b) of Fig. 6. The impact of both regular and irregular environmental variations on guided wave distortion is illustrated by changes in the (Pearson) correlation coefficient between adjacent guided waves, as shown in Fig. 6 and Fig. 7 and between guided waves and their optimal baseline (referred to as optimal correlation coefficients), as depicted in Fig. 9.

Fig. 6

The first two subplots in parts (a,b) show the correlation coefficients between two adjacent guided waves collected from paths 5-1 and 5-2. The corresponding time and humidity are depicted in the third and fourth subplots.

Fig. 7

This figure presents results similar to those in Fig. 6, but using guided waves from paths 5-1 and 5-2 collected at different times.

Distortion of guided waves due to regular environment variations

In long-term uncontrolled structural health monitoring, regular environmental variations, such as daily changes in temperature and humidity, are the dominant patterns. In parts (a) and (b) of Fig. 6 and Fig. 7, the first two subplots display the (Pearson) correlation coefficients between adjacent guided waves collected from paths 5-1 and 5-2, respectively. The calculation of correlation coefficients between adjacent guided waves is detailed in Eq. 1. The corresponding temperature and humidity during the guided wave measurements are shown in the third and fourth subplots. Daily periodic changes in temperature and humidity are typically observed, and during these times, the correlation coefficients between adjacent guided waves are very close to 1. This indicates that adjacent guided waves are highly similar during regular environmental variations.

$${r}_{i}=\frac{{({{\boldsymbol{x}}}_{i}-{\bar{x}}_{i})}^{T}({{\boldsymbol{x}}}_{i+1}-{\bar{x}}_{i+1})}{||{{\boldsymbol{x}}}_{{\boldsymbol{i}}}-{\bar{x}}_{i}||||{{\boldsymbol{x}}}_{i+1}-{\bar{x}}_{i+1}||}$$

(1)

where ||·|| denotes the Euclidean norm. In this equation, ${{\boldsymbol{x}}}_{{\boldsymbol{i}}}$ and ${\bar{x}}_{i}$ represent the i-th guided wave and mean of the $i$-th guided wave, respectively, while ${{\boldsymbol{x}}}_{{\boldsymbol{i}}+{\boldsymbol{1}}}$ and ${\bar{x}}_{i+1}$ represent the i+1-th guided wave and its mean.

We also compute the optimal correlation coefficient for each guided wave, which measures the correlation between the guided wave and its optimal baseline. The correlation coefficient ${r}_{i}^{{B}_{k}}$ between the $i$-th guided wave and the $k$-th baseline guided wave is given by Eq. 2.

$${r}_{i}^{{B}_{k}}=\frac{{({{\boldsymbol{x}}}_{{\boldsymbol{i}}}-{\bar{x}}_{i})}^{T}({{\boldsymbol{x}}}_{{\boldsymbol{k}}}^{{\boldsymbol{B}}}-{\bar{x}}_{k}^{B})}{||{{\boldsymbol{x}}}_{{\boldsymbol{i}}}-{\bar{x}}_{i}||||{{\boldsymbol{x}}}_{k}^{B}-{\bar{x}}_{k}^{B}||}$$

(2)

where ${{\boldsymbol{x}}}_{{\boldsymbol{k}}}^{{\boldsymbol{B}}}$ and ${\bar{x}}_{k}^{B}$ denote the $k$-th baseline guided wave and its mean, respectively. The optimal correlation coefficient ${r}_{i}^{{opt}}$ for the $i$-th guided wave is determined by selecting the correlation coefficient from the baseline that has the highest correlation with the $i$-th guided wave, as shown in Eq. 3.

$${r}_{i}^{opt}=\mathop{max\,}\limits_{k\in \,K}{r}_{i}^{{B}_{k}}$$

(3)

When calculating the optimal correlation coefficients for each guided wave in the long-term monitoring dataset, baseline guided wave data are sourced from measurements taken in July 2019. It is important to note that the guided waves were collected from 8 different channels. It should be noted that, to compute these optimal correlation coefficients, baseline guided waves from the same channel are used for comparison. For instance, when calculating the optimal correlation coefficients for guided waves from path 5-1, only baseline guided waves from path 5-1 are used, while guided waves from other channels, such as path 5-2, are not included in the calculation, as shown in Algorithm 1.

Algorithm 1

Calculate Optimal Correlation Coefficients (OptValues) for Guided Waves from 8 Transmission Paths.

The optimal correlation coefficients for guided waves from paths 5-1, 5-2, 6-1, and 6-2 are shown in the first four subplots of Fig. 9. It is observed that the optimal correlation coefficients for guided waves collected in July 2019 are close to 1, while those for waves collected at other times, such as June and August 2019, are lower. The relationship between optimal correlation coefficients and environmental variations (temperature and humidity) is illustrated in the fifth and sixth subplots of Fig. 9. Guided waves collected from environments significantly different from those of the baseline guided waves (collected during July 2019) show lower optimal correlation coefficients. This indicates that regular environmental variations over time can affect the similarity of guided waves to baseline waves. Therefore, to ensure effective baseline-based or data-driven damage detection, the baseline guided waves (or training data) need to be updated or expanded to account for changes in regular environmental variations for recent guided wave measurements (test data).

Distortion of guided waves due to irregular environment variations

Irregular environmental variations are infrequent in long-term uncontrolled monitoring and involve abrupt and rapid changes in conditions. Figures 6 and 7 illustrate four types of such irregular variations: rain, snow, direct sunlight, and freezing temperatures. During these irregular conditions, the correlation coefficients between adjacent guided waves decrease significantly, indicating a substantial reduction in similarity between adjacent waves. Figure 8 also provides guided waves collected under rain, freezing temperatures, direct sunlight, and damage conditions. For comparison, guided waves collected under fair weather, shown in Fig. 3, are included as background signals in Fig. 8. It is observed that the amplitude of guided waves collected during rain is lower than that collected during fair weather (see the first subplot of Fig. 8), while guided waves collected in freezing temperatures have almost no amplitude (see the second subplot). In contrast, guided waves collected under direct sunlight and through-hole damage have magnitudes similar to those collected during fair weather but exhibit noticeable phase shifts, as illustrated in the third and fourth subplots of Fig. 8.

Fig. 8

The blue curve in each of the four subplots represents guided waves collected from path 5-4 under different conditions: rain, freezing temperatures, direct sunlight, and through-hole damage, as indicated in the title of each subplot. The measurement time and temperature are labelled in the legend of each subplot. The background guided wave, marked with gray color, shown for comparison, was collected under fair weather conditions, as depicted in Fig. 3.

Moments marked in black in Fig. 6 and Fig. 7 represent recorded precipitation events, including rain and snow, from a public weather website⁴¹, such as the time around March 24, 2018, and April 6, 2018. Besides these recorded precipitation moments, there are also suspicious precipitation moments when humidity peaks and the decline of correlation coefficients of adjacent guided waves occurred simultaneously, such as around April 2, 2018. This discrepancy is due to the 15-mile distance between the meteorological station and the experiment location, which may cause some imprecision in the weather records, potentially missing some rain and snow events. During summer, we observe a decline in correlation coefficients of nearby guided waves during temperature peaks, as shown in part (b) of Fig. 6. These temperature peaks are caused by direct sunlight on the monitored plate. The monitored plate, temperature, and brightness sensors are not entirely shielded by the surrounding walls, leading to brief periods of direct sunlight on the plate and temperature sensor in the summer. Such direct sunlight causes a rapid increase in the temperature of the monitored structure, resulting in guided waves collected during these moments differing from those collected under other conditions. Another notable irregular environmental variation is freezing temperatures, occurring when the ambient temperature approaches or falls below 273.15 K (0 °C). During freezing conditions, the correlation coefficients of nearby guided waves decline noticeably. However, this change in similarity is not permanent. For example, between January 20th, 2019, and February 1st, 2019, when the temperature was below 273.15 K (0 °C), the correlation coefficients of nearby guided waves dropped significantly. Once the temperature rose above 273.15 K (0 °C), these correlation coefficients returned to 1, shown in part (b) of Fig. 7.

It is also important to recognize that irregular environmental variations affect guided waves collected from different sensors differently. For example, between February 2nd and February 15th, the decline in correlation coefficients for guided waves from path 5-2 was more pronounced compared to those from path 5-1, as shown in part (b) of Fig. 7. This difference may be attributed to the uneven distribution of irregular environmental conditions, such as rain and snow, across the monitoring area, or to variations in sensor and coupling layer quality, which respond differently to these conditions. Overall, irregular environmental variations can significantly distort guided waves and potentially lead to false alarms if not accurately identified

Validation (Challenge) 2: Distortion of guided waves due to sensor drift

The reliability of the monitoring system is critical for the successful implementation of structural health monitoring (SHM) systems^34,36,44,45. However, over time, sensors, coupling layers, and data acquisition systems may degrade, causing guided wave signals collected later to differ from earlier ones, even under identical environmental conditions. This phenomenon, commonly referred to as sensor drift, presents a significant challenge in long-term SHM applications. It has been widely observed in sensors such as PZT transducer³⁵, accelerometers, strain gauges⁴⁴, vibration sensors⁴⁵, and sensors measuring acceleration, strain, and displacement^36,37. Drift typically manifests as a slow, often linear, or exponential decline in accuracy, which can go undetected if not continuously monitored. When sensor accuracy falls below acceptable thresholds, it may result in false positives—prompting unnecessary on-site inspections—or worse, false negatives, where real damage goes undetected³⁶. Therefore, the development of robust and autonomous techniques for detecting, identifying, and compensating for sensor faults is essential for maintaining the long-term effectiveness and reliability of SHM systems^34,36,44.

Figure 9 demonstrates sensor drift by presenting the optimal correlation coefficients for guided waves from paths 5-1, 5-2, 6-1, and 6-2, marked as “Sensor Drift.” The baseline guided waves were collected in July 2019, and the optimal correlation coefficient for each path (e.g., 5-1) is calculated by comparing the guided waves from the corresponding baselines collected from the same path, using Algorithm 1. As seen in Fig. 9, the optimal correlation coefficients peak around July each year. However, while the coefficients for July 2019 approach 1, those for July in subsequent years, like 2020 and 2021, do not, even under similar environmental conditions. This decline is more noticeable for guided waves collected more later, indicating sensor drift. Additionally, sensor drift severity varies across sensors; for example, guided waves from path 6-1 in July 2020 and 2021 show optimal correlation coefficients closer to 1 compared to paths 5-1, 5-2, and 6-2. Sensor drift is a common issue in long-term monitoring, potentially leading to false alarms if not properly addressed through updated baseline datasets, training data, or drift compensation methods. Our public dataset provides a benchmark for evaluating the effectiveness of methods designed to detect damage in the presence of sensor drift, detect sensor drift, or compensate guided waves for sensor drift.

Fig. 9

The first four subplots display the optimal correlation coefficients for guided waves collected from paths 5-1, 5-2,6-1, and 6-2, respectively. The baseline guided waves were collected in July 2019. The corresponding temperature and humidity measurements are shown in the fifth and sixth subplots.

Validation (Challenge) 3: Distortion of guided waves due to installation shift

Another challenge is the occurrence of installation shifts during long-term structural health monitoring. Sensors, coupling layers, and data acquisition systems often require repair or updates over time. During the reinstallation of these components, installation shifts may occur. In other words, replaced sensors, coupling layers, or data acquisition and sampling systems may differ from the original ones. Additionally, their positions, such as those of PZT and environmental sensors, may not be exactly the same as before. Consequently, these installation shifts can result in collected guided waves differing from previous ones, even if the environmental and operational conditions remain unchanged⁹.

In our long-term monitoring system, we updated the brightness and air pressure sensors in November 2018. During this process, the system was shut down on November 20, 2018, at 07:26 AM and restarted on November 21, 2018, at 10:49 PM, as indicated in Fig. 9. During the reinstallation, the environmental setup and sensor positions were unintentionally altered, causing guided waves collected after the update to differ significantly from those collected earlier. This is marked as “installation shift” in Fig. 9, where the optimal correlation coefficients for 2018 are close to zero—even for guided waves collected in July 2018, which had similar environmental conditions to the baseline measurements from July 2019. To address this challenge, researchers and engineers should ensure that the same equipment and sensors are used and positioned consistently during system updates. Additionally, methods for detecting installation shifts under complex and dynamic conditions should be developed, along with compensation techniques to update baselines or training data, mitigating the effects of such shifts. Furthermore, for baseline comparison-based methods or historical health data-based damage detection techniques, such as anomaly detection using machine learning, a new reference phase may be necessary due to boundary condition changes introduced by installation shifts, to ensure effective performance.

Validation (Challenge) 4: Distortion of guided waves due to damage severity variation

Figures 10–16 show the optimal correlation coefficients for guided waves collected from the same monitored structure with various types of damage. Each subplot displays 10 days of test data, with five days before and after the introduction of new damage, highlighted in gray. The baseline guided waves for each dataset were collected during the 10 days preceding the test data. For example, in part (a) of Fig. 10, the test guided waves span from April 13th to April 22nd, 2021, covering five days of healthy conditions and five days with damage “D1”. The baseline guided waves were collected from April 4th to April 13th, 2021. Conversely, part (b) of Fig. 10 illustrates test guided waves from May 13th to May 22nd, 2021, including five days of healthy conditions and five days with damage “D2,” with the baseline collected from May 4th to May 13th, 2021. Each figure’s first four subplots show the optimal correlation coefficients for paths 5-1, 5-2, 5-3, 5-4, 6-1, 6-2, 6-3, and 6-4, using baseline guided waves from the corresponding sensor paths.

Fig. 10

The first four subplots in Part (a,b) illustrate the optimal correlation coefficients for measurements from paths 5-1, 5-2, 5-3, 5-4, 6-1, 6-2, 6-3, and 6-4. The corresponding measured temperature and humidity are shown in the fifth and sixth subplots. The shadow regions in part (a) and part (b) indicates that the measurements collected from healthy structure to the structure with damage D1, and to damage D2, respectively.

Fig. 11

These subplots illustrate the same contents as those in Fig. 10. The shadow regions in parts (a,b) indicate measurements collected from the structure with damage D2 to the structure with damage D3, and the structure with damage D3 to the structure with damage D4, respectively.

Fig. 12

These subplots illustrate the same contents as those in Fig. 10. The shadow regions in parts (a,b) indicate measurements collected from the structure with damage D4 to the structure with damage D5, and the structure with damage D5 to the structure with damage D6, respectively.

Fig. 13

These subplots illustrate the same contents as those in Fig. 10. The shadow regions in parts (a,b) indicate measurements collected from the structure with damage D6 to the structure with damage D7, and the structure with damage D7 to the structure with damage D8, respectively.

Fig. 14

These subplots illustrate the same contents as those in Fig. 10. The shadow regions in parts (a,b) indicate measurements collected from the structure with damage D8 to the structure with damage D9, and the structure with damage D9 to the structure with damage D10, respectively.

Fig. 15

These subplots illustrate the same contents as those in Fig. 10. The shadow regions in parts (a,b) indicate measurements collected from the structure with damage D10 to the structure with damage D11, and the structure with damage D11 to the structure with damage type D12, respectively.

Fig. 16

These subplots illustrate the same contents as those in Fig. 10. The shadow regions indicate measurements collected from the structure with damage D12 to the structure with damage D13.

For damage D-1, a notable drop in optimal correlation coefficients was observed for guided waves from paths 6-1, 6-2, 6-3, and 6-4, but not from paths 5-1, 5-2, 5-3, and 5-4. This decline could be due to rain around April 15th, which also caused a coefficient drop, as seen in part (a) of Fig. 10. No significant decline was noted when detecting damage “D2” from healthy conditions or damage “D3” from damage “D2”, possibly because the dents were too minor to significantly impact the guided waves, as illustrated in part (b) of Fig. 10 and part (a) of Fig. 11. In contrast, for damage “D4” and “D5”, a slight decline in optimal correlation coefficients was observed, suggesting that these dents were deep enough to significantly affect the guided waves, as shown in part (b) of Fig. 11 and part (a) of Fig. 12. Larger dents from damage “D6” and damage “D7” resulted in a more noticeable decline, as shown in part (b) of Fig. 12 and part (a) of Fig. 13. However, the overall decline in coefficients for damage “D3” to “D7” was minor.

When through-hole damage (from “D8” to “D13”) was introduced, a more significant decline in optimal correlation coefficients was observed, indicating that these damages had a more substantial impact on the monitored structure, as depicted in Figs. 13–16. However, irregular environmental variations, such as rain, caused an even more pronounced decline in coefficients compared to through-hole damages, as shown in Figs. 15 and 16. Therefore, accurate detection of environmental variations is crucial to minimize false alarms.

Validation (Challenge) 5: Damage localization with this public dataset

Theoretically, the public benchmark dataset can be used to evaluate methods for damage localization under complex and dynamic conditions, as each measurement collects 8 ultrasonic guided waves from 4 different receivers and 2 different transmitters. By analyzing the arrival time differences of signals induced by damage, the damage location can be determined^11,12. However, isolating damage-induced signals in this dataset is challenging due to multiple guided wave reflections from the edge of the monitored structure for two main reasons. First, the excitation signal duration is relatively long, lasting 1 ms, whereas the monitored structure is relatively small, measuring only 53 cm × 53 cm × 3 mm. Given that the guided wave speed is approximately 3 to 6 km/s⁴⁶, the time for guided waves to travel from one point to another on the plate is less than 0.2 ms, which is shorter than the duration of the chirp excitation signal (1 ms). Second, the positions of the guided wave receivers were very close to the plate’s edge. Consequently, before the end of the excitation signal, receivers will have already picked up multiple reflections from the plate’s edge. As illustrated in parts (a) and (b) of Fig. 3, determining the first arrival of guided waves, which is typically used to separate damage-induced signals for damage localization, is challenging. We also applied pulse compression to the guided waves using the excitation signal, a common method to locate the first arrival time by finding the peak value of the correlation coefficient between the excitation signal and the guided wave samples⁴⁷. The first arrival time for guided waves collected from path 5-4 should be less than 0.1 ms. However, the peak value for pulse-compressed guided waves from path 5-4 occurs around 0.2 ms, as shown in part (c) of Fig. 3. This delay in the peak value may be caused by reflected guided waves. In summary, while the public dataset can theoretically be used for damage localization, the challenges in separating the first arrival of guided waves from damage-induced waves require further investigation.