Introduction

Solar power collectors and drying technologies are two common uses for porous enclosure. In some application, researchers should consider two- temperature model. Alsabery et al.1 demonstrated nanoparticletransportation in a tilted porous cavity. They indicated that convective flow is significantly influenced by the permeable layer augmentation. Lu et al.2 investigated about nanofluid radiative three dimensional flow containing gyrotactic microorganism with anisotropic slip. They considered the effect of activation energy. Zaimi et al.3 illustrated nanofluid boundary layer movement on a porous plate. Sheikholeslami and Shehzad4 showed the two temperature model for nanoparticle migration inside a permeable medium. They revealed that Nu increases with decrease of porosity. Khan et al.5 reported the nanofluid mixed convection over an oscillating vertical plate. They utilized Laplace transform method to solve the governing equations.

Sheikholeslami and Shehzad6 investigated the role of radiation on nanoparticle treatment. They found that Nu decreases with reduce of radiation parameter. Haq et al.7 used carbon nanotubes to improve convective heat transfer over plate with slip flow. Carbon Nanotubes has been dispersed in to engine oil by Haq et al.8 is examined of magnetic forces. Tripathi et al.9 illustrated viscous dissipation and Hall effects on nanofluid rotating flow. Selimefendigil and Oztop10 depicted impact of inclination on hydrothermal behavior. They found that titled angle can be used as control parameter.

Promvonge et al.11 applied new way in a duct to improve the thermal characteristics. Sheikholeslami12 described the impact of electric filed on nanofluid free convection. He proved that Nusselt number enhances by adding electric field. Aman et al.13 illustrated the nanofluid thermal improvement in migration of CNTs nanoparticles. Sheikholeslami and Seyednezhad14 illustrated nanofluid Electrohydrodynamic flow in a permeable enclosure. Different applications of Fe3O4-water nanofluid were categorized by Sheikholeslami and Rokni15. Akbar et al.16 showed the role of Hartmann flow on nanoparticles migration in a duct. Najib et al.17 demonstrated the impact of chemical factor on flow style. They found that the Nu augments with augment of curvature. Various articles were been available about nanoparticle migration through porous media18,19,20,21.

Current publication is about nanoparticle migration in a porous enclosure with two temperature model via CVFEM considering magnetic force. Results illustrate the roles of significant parameters on contours.

Explanation of Geometry

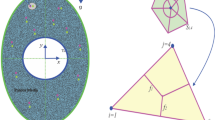
Figure 1 illustrates the details of current geometry. The hot wall can formulate by:

$${r}_{out}={r}_{in}+A\,\cos \,(N\,(\zeta -{\zeta }_{0}))$$
(1)

rout, rin, A, N are outer and inner radius, amplitude, number of undulation. The porous enclosure is full of nanofluid and influenced by magnetic force.

Figure 1
figure 1

(a) Geometry and the boundary conditions with (b). A sample triangular element and its corresponding control volume.

Full size image

CVFEM and Explanation

Formulation

According to existence of magnetic force and two temperature model for porous medium the basic formulas are:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$
(2)
$$-\frac{\partial P}{\partial x}+{\sigma }_{nf}{B}_{0}^{2}[v\,(\sin \,\gamma )(\cos \,\gamma )-u{(\sin \gamma )}^{2}]-\frac{{\mu }_{nf}}{K}u=0$$
(3)
$$\begin{array}{rcl}\frac{{\mu }_{nf}}{K}v & = & -\frac{\partial P}{\partial y}+(T-{T}_{c})g{\rho }_{nf}{\beta }_{nf}\\ & & +{\sigma }_{nf}{B}_{0}^{2}[u(\cos \,\gamma \,)(\sin \,\gamma )-v{(\cos \gamma )}^{2}]\end{array}$$
(4)
$$\frac{1}{\varepsilon }(u\frac{\partial {T}_{nf}}{\partial x}+v\frac{\partial {T}_{nf}}{\partial y})=\frac{{h}_{nfs}}{(\varepsilon ){(\rho {C}_{p})}_{nf}}(-{T}_{nf}+{T}_{s})+\frac{{k}_{nf}}{{(\rho {C}_{p})}_{nf}}(\frac{{\partial }^{2}{T}_{nf}}{\partial {y}^{2}}+\frac{{\partial }^{2}{T}_{nf}}{\partial {x}^{2}})$$
(5)
$$\frac{{k}_{s}}{{(\rho {C}_{p})}_{s}}(\frac{{\partial }^{2}{T}_{s}}{\partial {x}^{2}}+\frac{{\partial }^{2}{T}_{s}}{\partial {y}^{2}})+\frac{{h}_{nfs}}{(1-\varepsilon ){(\rho {C}_{p})}_{s}}({T}_{nf}-{T}_{s})=0$$
(6)

(ρCp)nf, (ρβ)nf, ρnf, σnf and knf, μnf can define as22:

$${(\rho {C}_{p})}_{nf}=\varphi {(\rho {C}_{p})}_{p}+(1-\varphi ){(\rho {C}_{p})}_{f}$$
(7)
$${(\rho \beta )}_{nf}=(1-\varphi ){(\rho \beta )}_{f}+\varphi {(\rho \beta )}_{p}$$
(8)
$${\rho }_{nf}={\rho }_{f}(1-\varphi )+{\rho }_{p}\varphi $$
(9)
$$\frac{{\sigma }_{nf}}{{\sigma }_{f}}=\frac{(MM-1)3\varphi }{(MM+2)+\varphi (1-MM)}+1,\,MM=\frac{{\sigma }_{p}}{{\sigma }_{f}}$$
(10)
$$\begin{array}{rcl}\frac{{k}_{nf}}{{k}_{f}} & = & 1-3\frac{(1-\frac{{k}_{p}}{{k}_{f}})\varphi }{(1-\frac{{k}_{p}}{{k}_{f}})\varphi +(\frac{{k}_{p}}{{k}_{f}}+2)}+\sqrt{\frac{{\kappa }_{b}T}{{\rho }_{p}{d}_{p}}}{c}_{p,f}(5\times {10}^{4})g^{\prime} ({d}_{p},\,T,\,\varphi ){\rho }_{f}\varphi \\ g^{\prime} ({d}_{p},\,T,\,\varphi ) & = & ({a}_{2}Ln({d}_{p})+{a}_{1}+{a}_{3}Ln(\varphi )+{a}_{5}Ln{({d}_{p})}^{2}+{a}_{4}Ln({d}_{p})Ln(\varphi ))Ln(T)\\ & & +({a}_{9}Ln({d}_{p})Ln(\varphi )+{a}_{10}Ln{({d}_{p})}^{2}+{a}_{7}Ln({d}_{p})+{a}_{6}+{a}_{8}Ln(\varphi ))\end{array}$$
(11)
$${\mu }_{nf}=\frac{{\mu }_{f}}{{(1-\varphi )}^{2.5}}+\frac{{\mu }_{f}}{{k}_{f}}({k}_{Brownian}/\Pr )$$
(12)

where ϕ is nanofluid volume fraction. Required characteristics and parameters are illustrated in Tables 1 and 222.

Table 1 The coefficient values of CuO−Water nanofluid.
Full size table
Table 2 Thermo physical properties of water and nanoparticles.
Full size table

Considering following definitions:

$$\begin{array}{rcl}v & = & -\frac{\partial \psi }{\partial x},(X,\,Y)=(x,\,y)/L,\,u=\frac{\partial \psi }{\partial y},\\ {\theta }_{nf} & = & ({T}_{nf}-{T}_{c})/({T}_{h}-{T}_{c}),{\rm{\Psi }}=\psi /{\alpha }_{nf},\,{\theta }_{s}=({T}_{s}-{T}_{c})/({T}_{h}-{T}_{c}),\end{array}$$
(13)

Final equations are:

$$\begin{array}{rcl}\frac{{\partial }^{2}{\rm{\Psi }}}{\partial {X}^{2}}+\frac{{\partial }^{2}{\rm{\Psi }}}{\partial {Y}^{2}} & = & -\,\frac{{A}_{6}}{{A}_{5}}Ha[\frac{{\partial }^{2}{\rm{\Psi }}}{\partial {Y}^{2}}({\sin }^{2}\gamma )+\frac{{\partial }^{2}{\rm{\Psi }}}{\partial {X}^{2}}({\cos }^{2}\gamma )+2\frac{{\partial }^{2}{\rm{\Psi }}}{\partial X\,\partial Y}(\sin \,\gamma )(\cos \,\gamma )]\\ & & -\frac{{A}_{3}\,{A}_{2}}{{A}_{4}\,{A}_{5}}\frac{\partial {\theta }_{nf}}{\partial X}Ra\end{array}$$
(14)
$$\varepsilon (\frac{{\partial }^{2}{\theta }_{nf}}{\partial {Y}^{2}}+\frac{{\partial }^{2}{\theta }_{nf}}{\partial {X}^{2}})+Nhs({\theta }_{s}-{\theta }_{nf})=-\,\frac{\partial {\theta }_{nf}}{\partial Y}\frac{\partial {\rm{\Psi }}}{\partial X}+\frac{\partial {\rm{\Psi }}}{\partial Y}\frac{\partial {\theta }_{nf}}{\partial X}$$
(15)
$$\varepsilon (\frac{{\partial }^{2}{\theta }_{s}}{\partial {Y}^{2}}+\frac{{\partial }^{2}{\theta }_{s}}{\partial {X}^{2}})+Nhs\,{\delta }_{s}({\theta }_{nf}-{\theta }_{s})=0$$
(16)

where:

$$\begin{array}{rcl}{A}_{1} & = & \frac{{\rho }_{nf}}{{\rho }_{f}},\,Ra={(\rho \beta )}_{f}\frac{Kg\,L\,{\rm{\Delta }}T}{{\alpha }_{f}{\mu }_{f}\,},\,{A}_{5}=\frac{{\mu }_{nf}}{{\mu }_{f}},\\ {A}_{2} & = & \frac{{(\rho {C}_{P})}_{nf}}{{(\rho {C}_{P})}_{f}},{\delta }_{s}={k}_{nf}/[{k}_{s}(1-\varepsilon )]{A}_{4}=\frac{{k}_{nf}}{{k}_{f}},\\ {A}_{3} & = & \frac{{(\rho \beta )}_{nf}}{{(\rho \beta )}_{f}},\,Ha=\frac{{\sigma }_{f}K\,{B}_{0}^{2}}{{\mu }_{f}},\\ Nhs & = & {h}_{nfs}{L}^{2}/{k}_{nf},\,{A}_{6}=\frac{{\sigma }_{nf}}{{\sigma }_{f}},\end{array}$$
(17)

Boundary conditions are:

$$\begin{array}{c}{\theta }_{nf}={\theta }_{s}=0.0\,\,{\rm{on}}\,{\rm{outer}}\,{\rm{wall}}\\ {\rm{\Psi }}=0.0\,\,\,\,{\rm{on}}\,{\rm{all}}\,{\rm{walls}}\\ {\theta }_{nf}={\theta }_{s}=1.0\,\,{\rm{on}}\,{\rm{inner}}\,{\rm{wall}}\end{array}$$
(18)

Nuloc and Nuave are:

$$N{u}_{loc}=(\frac{{k}_{nf}}{{k}_{f}})\frac{\partial {\theta }_{nf}}{\partial r}$$
(19)
$$N{u}_{ave}=\frac{1}{2\pi }{\int }_{0}^{2\pi }N{u}_{loc}\,dr$$
(20)

CVFEM

The innovative in which triangular element is used and upwind method is applied for advection term is CVFEM (Fig. 1(b)). Gauss-Seidel is the name of the method which is used for final step as mentioned in ref.23.

Mesh Independent Test and Validation

Obviously, the final outputs should not alter by changing mesh size. So, this test should be done for various cases as illustrated Table 3. Also, we should be sure about accuracy of written code by applying this code for previous published problem. Table 4 and Fig. 2 illustrates nice accuracy24,25,26.

Table 3 Comparison of the average Nusselt number Nuave for different grid resolution at Ra = 1000, Ha = 20, ε = 0.9, Nhs = 1000 and ϕ = 0.04.
Full size table
Table 4 Nuavefor various Gr and Ha at Pr = 0.733.
Full size table
Figure 2
figure 2

Comparison of the present solution with previous work (Kim et al.24) for different Rayleigh numbers when Ra = 105, Pr = 0.7; (b) comparison of the temperature on axial midline between the present results and numerical results obtained by Khanafer et al.25 for Gr = 104, ϕ = 0.1 and Pr = 6.2 (Cu−Water).

Full size image

Results and Discussion

In current article, migration of nanoparticle in a porous medium which is described by new porous model is presented. Numerical method is applied to display the roles of the porosity (ε = 0.3 to 0.9), Rayleigh number (Ra = 100,500 and 103), Hartmann number (Ha = 0 to 20) and Nhs (Nhs = 10 to 1000).

Influences of Nhs, Ra, ε and Ha on isotherms for solid (θs), streamlines (Ψ) and nanofluid (θnf) were depicted in Figs 3, 4, 5, 6, 7 and 8. When buoyancy force is weak, conduction mode is significant and the impacts of other variables are negligible. In this case, (θnf) contours are similar to (θs) contours. As Ra increase, thermal plume can be seen close to the vertical centerline and (θnf) contours become more complex but (θs) contours have no changes. Velocity of nanofluid decrease with augment of magnetic forces and the (θnf) contours are stratified with enhance of Ha. (Ψmax) enhances with augment of Nhs due to stronger convective flow. As ε enhances, the pores volume through the enclosure augments. Therefore, convective flow becomes stronger. Besides, the impact of ε on isotherms is as same as Nhs.

Figure 3
figure 3

Streamlines (Ψ), isotherms for the nanofluid (θnf) and the solid (θs) at Ra = 100, Ha = 0, ϕ = 0.04.

Full size image
Figure 4
figure 4

Streamlines (Ψ), isotherms for the nanofluid (θnf) and the solid (θs) at Ra = 100, Ha = 20, ϕ = 0.04.

Full size image
Figure 5
figure 5

Streamlines (Ψ), isotherms for the nanofluid (θnf) and the solid (θs) at Ra = 500, Ha = 0, ϕ = 0.04.

Full size image
Figure 6
figure 6

Streamlines (Ψ), isotherms for the nanofluid (θnf) and the solid (θs) at Ra = 500, Ha = 20, ϕ = 0.04.

Full size image
Figure 7
figure 7

Streamlines (Ψ), isotherms for the nanofluid (θnf) and the solid (θs) at Ra = 1000, Ha = 0, ϕ = 0.04.

Full size image
Figure 8
figure 8

Streamlines (Ψ), isotherms for the nanofluid (θnf) and the solid (θs) at Ra = 1000, Ha = 20, ϕ = 0.04.

Full size image

Figures 9 and 10 depict the impact of Nhs, ε, Ha and Ra, on Nuave. Nuave can calculate as:

$$\begin{array}{rcl}N{u}_{ave} & = & 1.64+1.3R{a}^{\ast }-0.16H{a}^{\ast }-0.12\varepsilon -1.24Nh{s}^{\ast }\\ & & -0.3R{a}^{\ast }H{a}^{\ast }-0.34R{a}^{\ast }\,\varepsilon -0.55R{a}^{\ast }Nh{s}^{\ast }+0.19H{a}^{\ast }\varepsilon +0.28H{a}^{\ast }Nh{s}^{\ast }\\ & & +\,0.34\varepsilon Nh{s}^{\ast }\\ & & -0.08{(R{a}^{\ast })}^{2}+0.74{(Nh{s}^{\ast })}^{2}-0.036{(H{a}^{\ast })}^{2}-0.2{(\varepsilon )}^{2}\end{array}$$
(21)

Coefficient of determination is 0.98 for this correlation. Also, in this formula we have: Ha* = 0.1Ha, Nhs* = 0.001Nhs, Ra* = 0.001Ra. Nuave is a reducing function of Nhs because temperature gradient decreases with augment of this factor. Decreasing porosity makes Nu to enhance which is similar of Ha impact. Nuave decreases with reduce of Rayleigh number.

Figure 9
figure 9

Contour plots for effects of Ra, Ha, ε, Nhs on average Nusselt number.

Full size image
Figure 10
figure 10

3D plots for effects of Ra, Ha, ε, Nhs on average Nusselt number.

Full size image

Conclusions

In current research, migration of CuO nanoparticles is simulated via Non-equilibrium. Innovative method is applied to show the impacts of porosity, buoyancy, magnetic forces and the Nhs. Results show that Nuave reduces with augment of Ha, ε, Nhs. Convective flow enhances with increase of Nhs and ε while it reduces with enhance of magnetic force. When Ra = 1000, ε = 0.3, increasing Nhs leads to 17.06 percent decrement of Nuave in absence of magnetic field. Impact of Nhs is negligible in existence of Lorenz force. Also Nuave decreases about 53% with augment of Hartmann number.