Introduction

One of the most prominent aspects of computational biology is network biology in which network science plays an essential role in discovering biological occurrences. Networks are reconstructed from different biological phenomena and deduced from mathematical and topological aspects. Protein-protein interaction (PPI), metabolic, and regulatory networks are examples of biological networks that have frequently been employed in recent years. However, nature comes with a lot of complexity. Inside a cell, there is a broad spectrum of entities contributing to create different cascading interactions that define the cell life and function. Considering these complexities in the modeling will gain comprehensive and valuable insights on biological events.

Currently, thanks to progress in high-throughput sequencing technologies and large projects such as TCGA1, there is a booming amount of omics data that could be used for wide-ranging analyses. Curated databases contain information for regulatory interactions between biomolecules and their targets, single nucleotide polymorphisms (SNPs), biological pathways, and gene expression profiles of various phenotypes. Moreover, tools and applications, developed by scientific societies, are increasingly accessible, resulted in an easier exploration of biological happenings2. However, these data are heterogeneous, inconsistent, and provider technologies may come with a bias3. To overcome these problems, data integration would be an asset. Recently, integrative systems biology has become a popular area in which more than just a single type of biologic data is incorporated4,5,6,7. Bearing these considerations in mind, the results will be more truthful and reliable. In an excellent review article written by Koyel et al.8, they described different approaches in integrative biological networks. Also, Peng et al.9 proposed a new multi-omics approach for bladder cancer-related genes discovery.

Systematically, multi-omics datasets could be regarded as multilayer networks. Based on scientific definitions10,11, a multilayer network contains multiple layers (different layers for different types of interactions) and considering the topology of layers, various kinds of multilayer networks are characterized. As Hmimida et al.12 mentioned, multilayer networks exploration can be executed in three ways. First, Layer Aggregation, in which all layers are aggregated to make a single network and traditional single layer (monoplex) analysis could be applied to explore it. Second, Ensemble (Consensus) approaches, in which each layer is individually evaluated; then, the results are combined to create the final consequence. Third, methods extended for multilayer networks (briefly called extended approaches), in which the analysis process is simultaneously conducted on all layers. Didier et al.13 compared these three approaches in terms of community detection and found that the extended modularity function has superiority over the other two methods.

The extension of topological attributes from monolayer to multilayer is a critical and challenging topic in this area12,14,15,16. Hmimida et al.12 have defined metrics (such as degree, shortest-path, neighbor set) for multiplex networks using an entropy-like aggregate function. Domenico et al.16 proposed reducibility methods for multilayer networks to eliminate redundant interactions and layers. In this context, community detection for multilayer networks is considered one of the most challenging topics. Given the topological perspective, a community is a cluster of densely connected nodes, which are far from other clusters. Communities may be either local or global and may have overlap with each other. Recently, various extended multilayer community detection algorithms have been proposed to seek modules in layers simultaneously17,18,19,20,21. A specific type of community detection method is based on seed-centric approach, in which communities are localized around predefined (manual or computational) seed nodes12,22.

Extended approaches for multilayer networks were recently used in biological and medical sciences. Berenstein et al.23 have taken benefit from these methods for the application of drug repositioning in neglected diseases. Furthermore, Rai et al.24 found a similar structure in the PPI network of seven types of cancers using spectral graph theory and the multilayer framework. Although these kinds of integrative methods were used recently in some contexts of biology, there is still a gap in their usage in prognosis and diagnosis of human disorders such as cancer even with the high availability of omics datasets. Also, because of the complexity of this kind of research with high dimensional data, previous multilayer-based works have relied mostly on the usage of two types of data and missed complementary interactions such as regulatory links in transcriptional and post-transcriptional phases.

Here, we utilize an extended approach to find functional communities in colon adenocarcinoma (COAD). To model such a multifaceted system in a realistic and comprehensive way, three levels of abstraction are declared. First, at the transcriptional level, gene correlations can be defined to represent the co-expression patterns among the genes. Second, at the post-transcriptional level, biomolecules such as RNAs and proteins have regulatory interrelations. Regulatory interactions indicate direct or indirect control of gene expression. Third, physical interactions show bindings of molecules such as proteins or RNAs to other molecules (such as protein-protein and RNA-protein bindings). In this arrangement, it is possible that a regulatory interaction may also be a physical binding interaction. Accordingly, we construct a three-layer network with co-expression, regulatory and physical interaction layers. One of the novelties addressed in this study is utilizing the most diverse types of interactions including co-expression, signaling, kinase-substrate, metabolic enzyme-coupled, nucleoproteins, protein complexes, RNA-RNA, and regulatory in a multi-layer framework to get a holistic view of the genes involved in carcinogenesis. The analysis program in this research contains the following steps to achieve potential biomarkers derived from raw datasets. We employ a local seed-centric community detection algorithm to explore modules in the multilayer network. In this process, to select seed items computationally, we propose an innovative multilayer heterogeneous random walker to score nodes. The top-ranked nodes are applied as seeds, and local communities around these seed nodes are computed as modules of interest. Out of the identified modules, those with a high overlap with COAD, based on validated databases, are selected as candidate modules for further steps. For every module, differential expression (DE) analysis is performed to extract differentially expressed genes (DEGs). We conduct the survival analysis for DEGs in the final step, to find genes that their differential expression influences the survival of patients with COAD. Modules containing a large amount of these genes are selected as final modules, and the functional enrichment was carried out on them. Finally, we discussed the upstream regulators of candidate genes to specify their role in the differential expression of target candidates and the related biological pathways. This kind of novel evaluation led us to identify a list of new potential targets in colorectal cancer25.

Materials and methods

Data collection and preprocessing

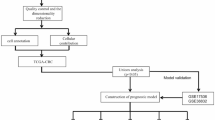
In the process of data collection, the information needed to build a multilayer network was gathered from multiple sources. As presented in the research workflow (Fig. 1), in this step, three types of data were used: gene expression profiles, regulatory relationships, and physically binding interactions. First, to build the co-expression network (layer 1), RNAseq data for COAD were exploited from the TCGA data portal26. In the preprocessing of expression data, we performed sample and gene filtering and then used the FPKM-UQ (Fragments Per Kilobase of transcript per Million mapped reads upper quartile) normalized data to generate the network. In the gene filtering step, genes with the following conditions were excluded: (1) missing values in any samples, (2) the expression count value of zero in more than 80% of all samples27, (3) genes that possessed the expression rates with zero standard deviation across all samples, and (4) genes with average CPM (count per million) lower than 1.

Figure 1
figure 1

The Workflow of the research.

Full size image

Second, for the generation of regulatory layer, we utilized the experimentally curated regulatory interactions using the NPInter (non-coding RNA interactions with biomolecules)28, the RegNetwork29 (Regulatory Network Repository of Transcription Factor and microRNA Mediated Gene Regulations), and the TRRUST (database of TF-target regulatory information)30 databases. Third, the network of physical interaction layer was assembled using the interactome data, as previously published31. These data comprise different interactions including (1) regulatory interaction of transcription factors, (2) yeast two-hybrid (Y2H) binary interactions, (3) metabolic enzyme-coupled interactions, (4) signaling interactions, (5) protein complexes, (6) kinase-substrate interactions, and (7) low-throughput manually curated interactions in the literature. In addition to the co-expression layer, in other layers (regulatory and physical interaction), genes possessing the average expression value of zero in transcriptomic data were also removed. Our reason is that genes with no expression will never be translated into proteins, and they have no regulatory function or physical binding interactions.

Multilayer network construction

Herein, we used FPKM-UQ normalized data and established the co-expression network using the WGCNA27 package in the R. In this layer; we selected those correlations having the values higher than 0.75 (considering scale-freeness of the network). Since the gene-set is made of both coding and non-coding RNAs and contains regulators and their targets, in the WGCNA “adjacency” function, we set the network type to “unsigned,” and correlations were calculated using the Pearson Correlation Coefficient (PCC) measure. The output is a weighted and undirected network in which the edge weights address correlations between the genes. We built other layers of the multilayer network (regulatory and physical binding layers) using interactions deduced by the experimentally curated databases. The regulatory network is directed, while the physical interaction network is undirected; however, both of them are unweighted networks. Figure 2A depicts such a heterogeneous multilayer network.

Figure 2
figure 2

(A) A sample heterogeneous multilayer network of the transcriptome to interactome. (B) A typical random walk with the random jump.

Full size image

Personalized seed selection

In most of the seed-centric community detection approaches, the seeds are either selected manually (such as predefined nodes) or based on their specific properties (such as being a hub). Here, to select seeds in a sophisticated way, nodes were ranked using a random walk with a random jump procedure. To attain this objective, we customized the random walker to walk in all three layers considering the heterogeneity. Since the network topology (node set, edge set, directedness, and edge weighting) is different in each layer (Fig. 2A), we proposed a walker algorithm (algorithm 1) to resolve this kind of ambiguity.

Algorithm 1
figure a

Proposed heterogeneous multilayer random walker.

Full size image

The walker must be able to move in all three layers with the ability to change layers and nodes. Figure 2B shows a sample walk with node and layer exchange. In this procedure, moving to a neighbor follows the probability function \({P}_{l}(i,j)\) defined in Eq. (1) for unweighted and Eq. (2) for weighted networks.

As defined by Kivelä et al.10, given a set of nodes \({\mathcal{V}}\) and a set of layers \({\mathcal{L}}=\{{L}_{1},\,{L}_{2},\,\ldots ,\,{L}_{s}\}\), \({V}_{{\mathcal{L}}}\subseteq {\mathcal{V}}\times {\mathcal L} \) specifies nodes and \({E}_{{\mathcal{L}}}\,\subseteq \,{V}_{{\mathcal{L}}}\times {V}_{{\mathcal{L}}}\) denotes the edge list (including inter-layer and intra-layer edges) in a multilayer framework. We indicated the multilayer network graph with notation \({G}_{{\mathcal{L}}}=({V}_{ {\mathcal L} },\,{E}_{{\mathcal{L}}},\,{\mathcal{V}},\,{\mathcal{L}})\). In this context, the probability of proceeding to a next neighbor in unweighted networks (regulatory and physical interaction layers) is defined as:

$${P}_{l}(i,j)=\frac{1}{{\sum }_{k{\epsilon }{m}_{l}}{A}_{l}(i,k)},\,{A}_{l}(i,j)=\{\begin{array}{cc}1 & if\,there\,is\,an\,edge\,from\,node\,i\,to\,j\\ 0 & else\end{array}$$
(1)

where \({P}_{l}(i,j)\) is the probability of proceeding from node i to any other neighbor (out-neighbors) j in layer l, \({m}_{l}\) indicates the neighbors (or out-neighbors if the network is directed) of node i in layer l, and \({A}_{l}\) demonstrates the adjacency matrix of the layer l. However, in the co-expression layer, we set the walk probabilities as:

$${P}_{l}(i,j)=\frac{{A}_{l}(i,j)}{{\sum }_{k{\epsilon }{m}_{l}}{A}_{l}(i,k)},\,{A}_{l}(i,j)=\{\begin{array}{cc}{Corr}_{l}(i,j) & if\,there\,is\,an\,edge\,from\,node\,i\,to\,j\\ 0 & else\end{array}$$
(2)

where \(Corr(i,j)\) implies the co-expression correlation between nodes (genes) i and j. Also, the walker must be able to go from a node to its counterparts in other layers. For instance, when the walker is at node x inside layer \(\,{L}_{1}\), for any layer \({L}_{r}\in {\mathcal{L}},\,r\ne 1\), if \({L}_{r}\)contains node x, the walker can jump to node x in \({L}_{r}\), or stay in \({L}_{1}\) itself. In each step, the walker should choose to go to one of its counterparts in other layers (line 7 in algorithm 1) or move to one of its neighbors in the same layer (lines 13 in algorithm 1). We set the probability of moving to a neighbor in the same layer as same as moving to its counterpart in a different layer to enable the walker to score nodes based on shared properties of nodes in all layers in an unbiased manner. Moreover, to avoid tangle in traps, we set the walker to jump with a predefined probability \({\rm{\beta }}\)or continue to walk with a probability of \(1-{\rm{\beta }}\) (line 10 in algorithm 1). To be fair in the selection of jump destination and ascribe it to the biological gene expression, we set the personalized random jump probability as:

$$pr(i)=\frac{\exp (i)}{{\sum }_{k=1}^{N}\exp (k)}$$
(3)

where \(pr(i)\) specifies the probability to jump to node i, \(\exp (i)\) indicates the average expression of gene i across the samples of patients with cancer and N is the total number of genes (nodes) in the multilayer framework.

Local seed-centric module detection

We used a local community detection approach to detect the functional composite modules around the seed nodes in our multilayer network. The idea underlying this approach is to find items that contribute to the development of carcinogenesis. Items are scattered in layers, and their nature might be a gene, RNA, or protein; however, we consider the equivalent gene names in the final module. Since currently there is not an applicable community detection algorithm about large heterogeneous multilayer networks compatible with our network; in this phase, we considered layers in an unweighted and undirected manner. We utilized ML-LCD local community detection method22 to discover modules for every seed node. It is a modularity expansion-based community detection method, which has better performance in large multilayer networks. Given a seed node \({v}_{0}\in {\mathcal{V}}\), ML-LCD algorithm attempts to find a subgraph \({G}_{{\mathcal{L}}}^{{v}_{0}}\subseteq \,{G}_{{\mathcal{L}}}\) that consisted of the seed node v0 and maximizes the local community function (LC) in Eq. (4). For simplifications, the letter C is used to denote local community subgraph. In this regard, \({E}^{C}\,\subseteq \,{E}_{{\mathcal{L}}}\) demonstrates the edge set of the subgraph.

$${G}_{{\mathcal{L}}}^{{v}_{0}}=\begin{array}{c}argmax\,LC(C)\\ C=(V,E,{\mathcal{V}},{\mathcal{L}})\subseteq {G}_{{\mathcal{L}}}\wedge {v}_{0}\in V\end{array}$$
(4)

where:

$$LC(C)=\frac{L{C}^{int}(C)}{L{C}^{ext}(C)}$$
(5)

In Eq. (5), \(L{C}^{int}(C)/L{C}^{ext}(C)\) indicates the density of links inside C, over the density of links between nodes inside and outside of the C. To formulate local community function LC, terms Shell Nodes and Boundary Nodes should be defined. In this regard, to specialize the edges inside the community C in a layer \({L}_{i}\), symbol \({E}_{i}^{C}=\{(u,\,v)|\exists ((u,\,{L}_{i}),\,(v,\,{L}_{i}))\in {E}^{C}\}\) will be used. For a local community being constructed, the shell nodes refer to nodes outside of the community that is a neighbor of nodes inside the community (displayed by symbol S), and these within-community neighbors of shell nodes are also called boundary nodes (depicted by symbol B):

$$S=\{v\in {\mathcal{V}}\backslash C|\exists ((u,{L}_{i}),(v,{L}_{j}))\in {E}_{{\mathcal{L}}}\wedge u\in C\}$$
$$B=\{v\in C|\exists ((u,{L}_{i}),(v,{L}_{j}))\in {E}_{{\mathcal{L}}}\wedge v\in S\}$$

Furthermore, \({E}^{B}=\{(u,v)|\exists ((u,\,{L}_{i}),\,(v,{L}_{j}))\in {E}_{{\mathcal{L}}}\wedge u\in B\wedge v\in S\}\) indicates the set of edges outgoing from the C, and for any layer \({L}_{i}\), \({E}_{i}^{B}=\{(u,v)|\exists ((u,\,{L}_{i}),\,(v,{L}_{i}))\in {E}^{B}\}\) is the portion of \({E}^{B}\) corresponding to edges of layer \({L}_{i}\). As reported by22, \(L{C}^{int}(C)\) and \(L{C}^{ext}(C)\) are defined as:

$$L{C}^{int}(C)=\frac{1}{|C|}\sum _{v\,\in C}\sum _{{L}_{i}\,\in \,{\mathcal{L}}}{\omega }_{i}|{E}_{i}^{C}(v)|$$
(6)
$$L{C}^{ext}(C)=\frac{1}{|B|}\sum _{v\,\in B}\sum _{{L}_{i}\,\in \,{\mathcal{L}}}{\omega }_{i}|{E}_{i}^{B}(v)|$$
(7)

where \({\omega }_{i}\) (for every \({L}_{i}\) ∈ \({\mathcal{L}}\)) is non-negative coefficient, with \(\,\sum _{{L}_{i}\,\in \,{\mathcal{L}}}{\omega }_{{L}_{i}}=1\), demonstrating layer weights.

Module validation and biomarker extraction

Communities detected by the mentioned approach should be validated by a biological viewpoint. Our goal was to seek modules (communities) that their genes were involved in the malignant tumor of the colon. We chose modules possessing considerable counts of genes associated with COAD according to the DisGeNet32 and containing a significant number of DEGs. For these disease-related modules, functional enrichment analysis is a strategy to check the role of module genes in pathways and processes. To enrich the discovered modules, we employed two popular tools, the Enrichr33,34 and ToppFun enrichment portal of the ToppGene35, and studied the presence of modules genes in tumor-associated pathways and biological processes. We selected the KEGG36 and Reactome37 as reference pathway databases.

For the genes inside the discovered modules, that were not previously reported as COAD-associated genes in the DisGeNet database, differential gene expression analysis was performed. Herein, we focused on genes that their expression pattern statistically differs in the malignant tumor. We did DE analysis using the Limma38 and the edgeR39 R packages based on workflow presented in40 and selected genes with larger fold changes (\(|\log (FC)| > 1\)) and smaller p-value (adj. p-value < 0.01).

To observe the effects of the expression level of discovered DEGs on the survival of patients, the survival analysis was carried out. This examination was applied to compare the lifespan of people when the expression of a gene differs from the normal. Kaplan-Meier (KM)41 curve is a worthy choice when the data are censored, and there is not complete information on subjects. It estimates the lifespan of a group of people having a low gene expression rate in comparison to another group with a high expression rate. The SurvExpress42 utility was used for the log-rank test and Kaplan-Meier survival analysis. In this phase, we chose those genes that a change in their expression rates influences the survival rate of patients with COAD and considered them as potential biomarkers. Although the impact of variations on the expression of upstream regulators is not the only reason for changes in the expression of downstream genes, it provides some explanations for these alterations. Finally, to validate changes in the transcription levels of biomarkers, in the regulatory layer, we performed a regulation follow-up on upstream items of biomarkers.

Results

Data preparation and network generation

The obtained dataset from the TCGA includes total RNAseq expression data for 60483 coding/non-coding RNAs in 424 samples that consisted of samples collected from healthy subjects and patients with colon cancer. Thus, we selected the paired samples that comprised of 49 samples obtained from healthy individuals and their cancer counterparts (49 normal specimens and 49 cancerous samples). Then, we carried out gene filtering as described in the “Materials and Methods” section. The cleaned data include the expression count value for 14515 genes in 98 samples. The 49-paired samples were used in the differential gene expression analysis. However, only the expression data of 49 cancerous samples were applied for the co-expression network construction. The generated co-expression layer comprises 5993 nodes and 75121 edges. On the other side, the regulatory and physical interaction layers were directly generated from source datasets. The physical interaction layer has 12751 nodes and 135712 edges, and the regulatory layer encompasses 17640 nodes with 133180 edges.

Personalized seed selection

We ranked nodes in the network using the proposed heterogeneous multilayer random walker. The walker was set to jump with a probability of \({\rm{\beta }}\) = 0.2 or continue to walk with a probability of 0.8. We ran the walker for three million moves and ranked nodes based on scores (Min. = 0.0, 1st Qu. = 0.0015, Median = 0.0032, Mean = 0.00612, 3rd Qu. = 0.00610, Max = 1.0). Although the goal of this project was far from the gene prioritization, to test the accuracy of our personalized seed selection algorithm against a random selection of genes, we examined the result of the walker in terms of precision and recall (Fig. 3). Precision (Eq. 8) measures the percentages of retrieved items that are relevant. However, recall (Eq. 9) evaluates the percentage of relevant items that have been retrieved. Results show that the proposed ranking system performs much better than the random assortment (diagonals of the chart). The complete result of random walker scores is provided in Supplementary File S1. We designated nodes with score larger than 0.5 (rw_score > 0.5) as seed nodes. As reported by the DisGeNET database, 11 out of 12 chosen seed nodes are involved in COAD, as previously mentioned, indicating that our computationally explored centroid seeds are biologically meaningful.

$$precision=\frac{|\{relevant\,items\}{\cap }^{}\{retrieved\,items\}|}{|\{retrieved\,items\}|}$$
(8)
$$recall=\frac{|\{relevant\,items\}{\cap }^{}\{retrieved\,items\}|}{|\{relevant\,items\}|}$$
(9)
Figure 3
figure 3

(A) Evaluation of walker in terms of precision and recall for COAD. (B) Distribution of nodes score.

Full size image

Module detection

For the selected seed nodes, we calculated local communities using the ML-LCD method. Since there is not any precedence on the three layers, we set layer weight \({\omega }_{{L}_{i}}=1/3\) for all layers equally. We selected modules whose genes (at least 25%) are known as predisposing genes in the development of COAD according to the reports by curated databases. Out of 12 modules found in this step, seven were related to colon cancer with an overlap more than the specified threshold (Table 1). The detailed information of 12 modules and their genes are available in Supplementary File S2.

Table 1 Explored modules around seed nodes with an overlap percentage higher than 0.25 in COAD.
Full size table

Also, we checked random walk scores of module items separately to observe if there is a relationship between the module score and the percentage of its overlap with COAD. In all validated modules (seven modules), the minimum, maximum, median, and average scores were calculated (Table 2). It was observed that the average module score was highly associated with the involvement of module in COAD. For example, for the module with the seed gene USF1 (called module USF1), the average score of module items was the highest (avg. score = 0.05692) and it was the most related module to cancer (overlap = 61%). It emphasizes that COAD-related modules contain nodes with a high random walk score (hub nodes in the multilayer framework).

Table 2 Module relevance to COAD in terms of Random walk scores.
Full size table

DEG analysis and module evaluation

To assess each detected module, we applied differential gene expression analysis, with limitations adj. p-value < 0.01 and \(|\log (FC)| > 1\). As presented in Table 3, the module E2F1 has the highest value of differentially expressed genes (100 DEGs from 117 genes). We started with DEGs that their expression rate was changed in the transition from healthy to cancer state, and continued to survival analysis. Among the identified DEGs that were not reported in databases, 10 genes had different expression patterns (modules with seed genes E2F1 and USF1), resulting in a different survival rate with log-rank test p-value < 0.05 (Table 3, Fig. 4). The genes CDC6, RRM2, ORC1, NCAPG, MAD2L1, MCM6, CCNF, CDCA2, ECT2, and DEPDC1B, are the output candidate genes identified in explored modules, which are differentially expressed between normal and cancer states, and their differential expression levels have noteworthy effects on the lifespan of patients. Since we looked for novel unreported genes, we ignored modules with low coverage of DEGs and survival biomarkers and proceed with two significant modules, the module E2F1 (high DEG and survival rate) and the module USF1 (high overlap) for functional enrichment analysis.

Table 3 Module comparison and evaluation.
Full size table
Figure 4
figure 4

Kaplan-Mier curves (from SurvExpress tools) for candidate biomarkers RRM2, ORC1, NCAPG, MAD2L1, MCM6, and CDCA2 selected with log-rank test p-Value < 0.05.

Full size image

In another parallel process, we performed another tryout to validate our approach in finding differentially expressed genes inside detected modules. For this purpose, the proportional test was used to check the accuracy of our method in distinguishing genes that their expression varies between healthy samples and patients with COAD. In other words, this test was designed to answer the question of whether the proposed approach would be sufficiently precise in discovering DEGs inside the identified modules. For this aim, the “One-sample proportions test with continuity correction” method was applied. This was executed through the prop.test function in the R. The prop.test can be used for examination of the null hypothesis if the proportions (probabilities of success) in several groups are the same, or they have certain equal values. Pearson’s chi-square test statistic 16.87184 with degree freedom of 1 and a p-value of 3.99906e-05 demonstrates relatively high precision in the detection of DEGs in our proposed module detection approach.

Functional enrichment

The module E2F1 has the highest number of differentially expressed genes that have survival impact; however, it has a low coverage with respect to the predefined COAD genes. On the side, the module USF1 covers more percentage of COAD-related genes but contains fewer DEGs and effects on the survival rate. To study these two modules deeply, we utilized the human Functional Linkage Network (FLN), in which each node is a protein, and there is an edge between two nodes if there is evidence that nodes have a degree of the functional similarity. In this network, edges are weighted and predicted based on PPI interactions, gene expression profiles, literature mining, experimental techniques, and computational approaches43,44. A common methodology for predicting function based on FLNs applies a simple local threshold rule (mentioned as ‘guilt-by-association’)45. For the genes inside modules that were not specified as COAD related genes in databases, to explore their role in neoplastic cellular processes, we used functional linkage similarities of those genes with previously annotated genes. In the full FLN network, edge weights demonstrate the functional similarity between proteins. We extracted the subnetworks of the two modules from the human FLN network provided that the edge weights were higher than the average of the whole network. The E2F1 FLN (Fig. 5A) is a dense subnetwork with an average path length of 1.18 and a density of 0.41. Out of 156 genes inside the module, 148 genes have functional similarities above the average values with respect to other module members. We surveyed the direct neighbors (containing 12111 nodes) of the module E2F1 (module boundary); of them, 1496 were specified as cancer-related genes (coverage = 0.78). The module USF1 (Fig. 5B) has a high intersection with the COAD; however, its boundary neighbors also have a tight coverage with cancer-related genes (coverage = 0.84). It is a dense subnetwork with a density of 0.59 and a network diameter of 1.4. Among genes belonging to the module USF1, 153 genes were in its FLN subnetwork, demonstrating the biological and chemical similarities between them. The functional linkage subnetworks are biological evidence on the modularity and resemblance of their genes and suggest a strong possibility to constitute a module and act together in biological pathways.

Figure 5
figure 5

FLN subnetworks for modules with seed nodes (A) E2F1 and (B) USF1. Nodes’ sizes are based on their degree.

Full size image

Additionally, to evaluate the relevance of selected modules to the development of carcinogenesis, we performed functional enrichment analysis. Results showed a significant correlation between discovered modules and pathways involved in the malignant tumors of the colon. Therefore, we set a threshold of 0.05 for enrichment adj. p-value. The extracted significant pathways for modules USF1 and E2F1 are listed in Tables 4 and 5, respectively. The detailed results for functional enrichment of the two modules are accessible in Supplementary File S3. It was found that both modules were involved in pathways such as Adipogenesis, Cell Cycle, Chromosomal and microsatellite instability in colorectal cancer, and TGF-beta Signaling Pathway that they play crucial roles in colorectal cancer. However, the module E2F1 seems to be involved in a specific way. Its genes have roles in key pathways involved in colon cancer such as Wnt Signaling Pathway, Apoptosis, Tumor suppressor activity of SMARCB1, G1 to S cell cycle control, TGF-beta Signaling Pathway, H19 action Rb-E2F1 signaling, and CDK-Beta-catenin activity, Regulation of Wnt/B-catenin Signaling by Small Molecule Compounds and lncRNA involvement in canonical Wnt signaling and colorectal cancer. Moreover, Gene Ontology (GO) that is associated with E2F1 modules includes biological processes such as mitotic cell cycle, cell division, chromosome organization, G1/S transition of the mitotic cell cycle, DNA metabolic process, and DNA repair which are linked to cell proliferation (Supplementary File S3).

Table 4 Significant pathways for the module USF1.
Full size table
Table 5 Significant pathways for the module E2F1.
Full size table

Method evaluation

In order to evaluate the framework of this study against other community detection methods, we defined a two-step comparative analysis.

First, to assess our results in contrast with other multilayer methods, two well-known frameworks, Gene4x46 and mPageRank19, were selected and measures of central tendency were used to examine the distribution of each method overlap with disease-related genes (Table 6). We applied the mPageRank on the two layers of co-expression and PPI, by choosing random seeds from COAD-specific genes, as defined in the original article. However, the Gene4x is not a seed-centric approach, and from its multiple output modules, we selected top-ranked ones with considerable size for the valuation task. Here, due to the unavailability of differential expression data for the Gene4x method, evaluation has continued with the finding of the similarity of modules to gene sets involved in colorectal cancer. The results of this evaluation reveal the accuracy of our method in finding relevant communities.

Table 6 The overlap of communities resulted from multi-network methods with DisGeNet.
Full size table

Second, to test the performance of the prepared framework with other single-layer methods, another validation on detected modules was accomplished using DEG-based criteria defined by Cantini et al.46. We selected two single-layer community detection algorithms, Loavin47 and Label-propagation48, which were applicable to large networks. In comparing the proposed multi-layer framework with the module identification methods in single-layer networks, our aim is to investigate whether adding more layers to the proposed method has led to the identification of better modules. The two methods were executed on the co-expression layer and their output modules having an acceptable size were selected to be assessed. Here, we examined the fold change and p-value of differentially expressed genes inside modules. Data distribution for the logarithm of fold change values, student’s t-test p-value and standard deviation of fold change values for the modules are depicted in Fig. 6. The comparison results denote that the approach presented here outperforms the other two methods in terms of unfolding homogenous modules containing genes with a higher change in their expression with low p-values.

Figure 6
figure 6

Comparison of single-layer methods, Loavin and Label-propagation, with our approach using DEG-based criteria defined by Cantini et al.46. (A) |mean i∈C (log2 (fold change)i)|; (B) sdi∈C (log2 (fold change)i); (C) Student’s t-test p-value. The framework employed here unfolds homogenous communities (low standard deviation of expression change) containing genes with higher changes in their expression and less p-value.

Full size image

Discussion

In the previous sections, we investigated the relevance of the modules with COAD in terms of functional linkage networks and pathway analyses, and results suggest that the two modules were highly correlated with the disease causality. Therefore, we discussed the candidate biomarkers of the two modules extracted from the survival analysis: CDC6, RRM2, ORC1, NCAPG, MAD2L1, MCM6, CCNF, CDCA2, ECT2, and DEPDC1B.

ORC1 is a protein-coding gene, which is overexpressed in colon cancer. ORC1 is involved in some critical pathways: Cell Cycle, DNA Replication, E2F transcription factor network, G1 to S cell cycle control, and Retinoblastoma (RB) in cancer. Gene ontology annotations that are related to this gene include chromatin binding. MCM2 and MCM6 are the upstream transcription factors regulating the ORC1 protein factor and are upregulated in the case of cancer; therefore, it could provide some explanations for the upregulation of ORC1 (Fig. 7). ORC1 is an important paralog of CDC6. The CDC6 protein is essential for the initiation of DNA replication, which is a crucial phase during the cell division. This protein acts as a regulator at the early steps of DNA replication. It could be localized within the cell nucleus during cell cycle G1 but translocated to the cytoplasm at the initiation of S phase. Among its related pathways, namely Cell cycle_Role of APC in cell cycle regulation and CDK-mediated phosphorylation and removal of CDC6 are more characterized compared with others. Gene ontology annotations that are associated with this gene comprise nucleotide and kinase binding. Among its regulators, MCM3, E2F2, MCM2, E2F1, E2F7, FOXM1, ARID3A and MCM7 are all overexpressed in cancer. Correspondingly, MYC and AR are the other regulators, down-regulated when the cells are transformed into cancer cells.

Figure 7
figure 7

Three-layer overview of genes, namely ORC1, MCM2, and MCM6. (A) Regulatory layer. MCM2 and MCM6 (from MCM complex family) both regulate the transcription of the gene ORC1. (B) Co-expression layer. All three genes have expression correlations (negative and positive). (C) Physical binding layer.

Full size image

CCNF (cyclin F) is another protein-coding gene, which encodes a member of the cyclin family. Cyclins are regulators of cell cycle transitions through their capability to bind and activate cyclin-dependent protein kinases. It is introduced as a key gene in carcinogenic pathways associated with colorectal adenoma-to-cancer progression49. In the same way, MAD2L1 (Mitotic Arrest Deficient 2 like 1) is a component of the mitotic spindle assembly checkpoint that prevents the onset of anaphase until all chromosomes are suitably aligned at the metaphase plate. Among its associated pathways, Mitotic Metaphase and Anaphase and Cell cycle_Role of APC in cell cycle regulation are well-defined and investigated. In a study conducted by Abal et al.50, they mentioned that APC inactivation is associated with abnormal mitosis and concomitant BUB1B/MAD2L1 up-regulation. However, the overexpression of these two genes was correlated with tumor metastasis and poor prognosis of patients with breast cancer51. Its expression is amplified in colon cancer as well.

The CDCA2 gene encodes a subunit of protein phosphatase 1, which is associated with cell cycle and has relatively higher expression in cancer conditions. POU2F2 is a regulator of CDCA2, which is down-regulated in colon cancer, and it is a negative regulator of CDCA2. Conversely, POU5F1 is another controller of CDCA2, which is overexpressed in cancer and a positive regulator.

Among the proposed gene list, ECT2 (Epithelial Cell Transforming 2) is another biomarker previously mentioned that it is involved in breast cancer52. Its expression is increased in tumor tissues of patients and involved in the following pathways RET signaling and G-protein signaling_RhoA regulation. Annotations that are associated with this gene include protein homodimerization activity and GTPase activator activity. Its role in colorectal cancer is discussed earlier by Chen et al.53 and Luo et al.54.

Condensin complex is responsible for the condensation and stabilization of chromosomes during mitosis and meiosis. NCAPG (Non-SMC Condensin I Complex Subunit G) encodes a subunit of Condensin complex, and phosphorylation of the encoded protein activates the complex. Mitotic Prometaphase and Cell cycle Chromosome condensation in prometaphase are biological pathways in which NCAPG plays a role in them. RRM2 (Ribonucleotide Reductase Regulatory Subunit M2) is another DEG that it has a crucial impact on the survival rate of patients with cancer. It has been indicated that RRM2 is involved in the pathogenesis of pancreas adenocarcinoma. However, its role in colorectal cancer has been addressed in several studies55,56. KRAS-mediated upregulation of RRM2 is vital for the proliferation of colorectal cancer cell lines57.

The protein encoded by MCM6 is one of the extremely conserved mini-chromosome maintenance proteins (MCM) that are necessary for the beginning of eukaryotic genome replication. The MCM complex consisted of this protein, as well as MCM2, MCM4, and MCM7. This complex has been shown to have DNA helicase activity and act as a DNA unwinding enzyme. The phosphorylation of the complex by CDC2 kinase decreases the helicase activity, signifying a role in the regulation of DNA replication. Huang et al. mentioned that the interaction between RAD51 and MCM complex is indispensable for the formation of RAD51 foci in colon cancer HCT116 cells58. Also, its significance has been shown in other types of cancers59,60. Accordingly, the protein DEPDC1B has some significant roles in pathways p75 NTR receptor-mediated signaling and Signaling by Rho GTPases. An important paralog of this gene is DEPDC1, and it is overexpressed in the case of tumor progression. Our computations suggest that the genes mentioned above have a critical role in colon carcinoma; however, additional experimental validations are needed to approve these markers.

Conclusion

In this research, we employed multilayer networks to model colon adenocarcinoma and investigated its functional core components. We used the transcriptome-to-interactome integrative approach, and different omics data sources to reconstruct disease network and study its foundations. Then, we utilized an extended community detection algorithm and achieved two modules with centroid genes USF1 and E2F1, which are dense subnetworks, and their genes have functional linkage similarities. Both modules showed a significant overlay with COAD-related genes and pathways; however, the module E2F1 contained statistically meaningful differentially expressed genes, and it had a marked effect on the survival of patients with COAD. We selected suitable DEGs as potential biomarkers and examined their regulatory cascade flow. Results of the literature mining suggest that the candidate genes play roles in critical pathways associated with cell cycle, apoptosis, and COAD progression; however, their role in the development and pathogenesis of cancer should be approved by experimental approaches in the future. The approach employed here is a general framework applicable to other problems in this context; however, the construction of the multilayer network is the core part of the procedure that must be constructed based on the phenotype-specific transcriptomic dataset. Modules extracted in this study are dedicated to colon adenocarcinoma, which should be confirmed experimentally.