Introduction

It is well known that the interaction of predator species and prey species is an important topic in biology and mathematical ecology. Since the classical works of Lotka and Volterra1,2, the research on the dynamical behavior of predator-prey models has become a crucial research field for mathematicians and biologists. In the natural ecosystem, different biological populations take certain measures such as group defense, refuging, escaping and so on, to maintain their own survivals or search for food. To further grasp the law of interaction of predator species and prey species, many scholars pay much attention to the group defense mechanism of the prey. For example, Falconi et al.3 investigated the stability and global dynamic of a predator-prey model with group defense, Raw et al.4 reveal the complex dynamical behavior of prey-predator system with group defense, Xu et al.5 discussed the global dynamics of a predator-prey system with defense mechanism. In details, one can see6,7,8,9.

In 2013, Venturino and Petrovskii10 put up the following predator-prey model with group defense:

$$\left\{\begin{array}{l}{\dot{u}}_{1}(t)={\gamma }_{1}\left[1-\frac{{u}_{1}(t)}{\kappa }\right]{u}_{1}(t)-{\gamma }_{2}{u}_{1}^{\sigma }(t){u}_{2}(t),\\ {\dot{u}}_{2}(t)=-{\gamma }_{3}{u}_{2}(t)+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }(t){u}_{2}(t),\end{array}\right.$$
(11)

where u1 and u2 stand for the densities of prey and predator population, respectively. γ1 represents the logistic growth rate, γ2 stands for the search efficiency of predator for prey, γ3 stands for the mortality rate of predator species, γ4 stands for the biomass conversion coefficient, κ is the carrying capacity of the environment, and σ denotes aggregation efficiency. All the parameters γi(i = 1, 2, 3, 4), κ are positive. Considering that the harvesting play an important role in describing the evolution process of a population, Kumar and Kharbanda11 introduced the Michaelis-Menten type harvesting into predator-prey model (1.1). Then they established the following predator-prey model with group defense and Michaelis-Menten type harvesting:

$$\left\{\begin{array}{l}{\dot{u}}_{1}(t)={\gamma }_{1}\left[1-\frac{{u}_{1}(t)}{\kappa }\right]{u}_{1}(t)-{\gamma }_{2}{u}_{1}^{\sigma }(t){u}_{2}(t)-\frac{{\rho }_{1}{\rho }_{2}{u}_{1}(t)}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}(t)},\\ {\dot{u}}_{2}(t)=-{\gamma }_{3}{u}_{2}(t)+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }(t){u}_{2}(t),\end{array}\right.$$
(12)

where u1 and u2 stand for the densities of prey and predator population, respectively, ρ1, ρ2 stand for the catchability parameter, the effort applied to harvest the prey species, respectively, ρ3 and ρ4 denote appropriate real constants, γi(i = 1, 2, 3, 4), κ have the same implication as those in model (1.1). Based on the biological viewpoint, we assume that all the parameters are positive. Kumar and Kharbanda11 discussed detailedly the stability and Hopf bifurcation of model (1.2).

As is known to us, fractional calculus is a generalization of classical ordinary differentiation and integration12,13,14,15,16. For a long time, the fractional calculus has been maintained a slow development state due to the lack of practical background and technical means. Recently, fractional calculus has been found to be widely applied in numerous areas such as chemical engineering, viscoelasticity, biomedical Science, robotics, physics, mechanics and control science and so on17,18,19,20,21. Moreover, fractional-order differential equations can better describe the real objective phenomena than integer-order differential equations since they possess memory and hereditary natures of different materials and processes. Thus we think that the investigation on dynamical behavior of fractional-order differential equations have important theoretical significance and broad potential value.

Model formulation

Considering that fractional calculus is a more suitable tool to describe memory and hereditary properties of numerous processes and materials and fractional-order equations are closely connected with memory for predator-prey systems22,23. Based on this viewpoint and inspired by the analysis in Section 1, we modify model (1.2) as the following fractional-order version:

$$\left\{\begin{array}{l}{D}^{\theta }{u}_{1}(t)={\gamma }_{1}\left[1-\frac{{u}_{1}(t)}{\kappa }\right]{u}_{1}(t)-{\gamma }_{2}{u}_{1}^{\sigma }(t){u}_{2}(t)-\frac{{\rho }_{1}{\rho }_{2}{u}_{1}(t)}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}(t)},\\ {D}^{\theta }{u}_{2}(t)=-{\gamma }_{3}{u}_{2}(t)+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }(t){u}_{2}(t),\end{array}\right.$$
(21)

where Dθ denotes the Caputo fractional derivative and 0 < θ < 1. We give the initial value of model (1.2) as follows: u1(t0) = u10 ≥ 0, u2(t0) = u20 ≥ 0. Denote \({R}_{+}^{2}=\{({u}_{1},{u}_{2})\in {R}^{2}| {u}_{1}\ \ge \ 0,{u}_{2}\ \ge \ 0\}\). \(\Theta =\{({u}_{1},{u}_{2})\in {R}^{2}:\max \{| {u}_{1}| ,| {u}_{2}| \} < K\}\).

The key task of this manuscript is to handel two aspects: (1) seek the sufficient conditions to ensure the existence, uniqueness and boundness of solution, the stability of equilibrium point and the existence of Hopf bifurcation for system (2.1); (2) reveal the effect of fractional order on the stability and the existence of Hopf bifurcation of model (2.1).

The bright spots of the manuscript include the following four aspects:

  • Based on the earlier works, a new fractional-order predator-prey model with group defense is established.

  • Several sufficient criteria to ensure the existence, uniqueness and boundness of solution, the stability of equilibrium point and the existence of Hopf bifurcation of the involved predator-prey model are presented. The investigation reveals that fractional-order is an pivotal parameter in affecting the Hopf bifurcation of the involved fractional-order predator-prey model.

  • Skillfully constructing a suitable Lyapunov function to prove the boundness of solution has achieved great success.

  • The research approach of this paper will provide useful ideas for future investigation on numerous fractional-order differential systems.

This article is planned as follows. In Sect. 2, a fractional-order predator-prey model is established. In Sect. 3, few necessary definitions and lemmas are prepared. In Sect. 4, the existence, uniqueness and boundness of solution of model (2.1) is analyzed. In Sect. 5, the stability of equilibrium point of system (2.1) is discussed in detail. Hopf bifurcation analysis is carried out in Sect. 6. Some related computer simulations are given to check effectiveness of the main findings in Sect. 7. We ends the article with a simple conclusion in Sect. 8.

Preliminary results

In this section, we give few definitions and lemmas.

Definition 3.124 The Caputo fractional derivative of order θ is defined as follows:

$${D}^{\theta }h(\zeta )=\frac{1}{\Gamma (l-\theta )}{\int }_{{\zeta }_{0}}^{\zeta }\frac{{h}^{(l)}(\tau )}{{(\zeta -\tau )}^{\theta -l+1}}d\tau ,$$

where h(ζ) ∈ ([ζ0, ∞), R), ζ ≥ ζ0 and l ∈ N and satisfies l − 1 ≤ θ < l.

Give the following Caputo fractional differential system:

$${D}^{\theta }U(t)=h(t,U(t)),U({t}_{0})={U}_{0},$$
(3.1)

where \(U(t)={({u}_{1}(t),{u}_{2}(t),\cdots ,{u}_{n}(t))}^{T}\in {R}^{n}\) and \(h:\left[{t}_{0},\infty \right)\times \Phi \to {R}^{n}\) is piecewise continuous function with respect to t and satisfies locally Lipschitz continuous in U on \(\left[{t}_{0},\infty \right)\times \Phi ,\Phi \subset {R}^{n}.\)

Definition 3.225,26 We say that U* is an equilibrium point of system (3.1) if and only if h(t, U*) = 0. 

Lemma 3.126,27 Let J(U*) be the Jacobian matrix of model (3.1) near U*and λi(i = 1, 2, ⋯ , n) the eigenvalues of J(U*). If some eigenvalues of λi satisfy \(| arg({\lambda }_{i})| > \frac{\theta \pi }{2}\) and some other eigenvalues of λi satisfy \(| arg({\lambda }_{i})| < \frac{\theta \pi }{2}\), then the equilibrium point U* is a saddle point.

Lemma 3.226,27 Let U*, J(U*) be equilibrium point, Jacobian matrix of system (3.1), respectively, and λi be the eigenvalues of Jacobian matrix J(U*) of system (2.1).

  1. (1)

    U* is locally asymptotically stable ⇔ \(| arg({\lambda }_{i})| > \frac{\theta \pi }{2}\) for all λi(i = 1, 2, ⋯ , n).

  2. (2)

    U* is stable ⇔ \(| arg({\lambda }_{i})| \ \ge \ \frac{\theta \pi }{2}\) for all λi(i = 1, 2, ⋯ , n) and the eigenvalues with \(| arg({\lambda }_{i})| =\frac{\theta \pi }{2}\) have the same geometric multiplicity and algebraic multiplicity.

  3. (3)

    U* is unstable ⇔ ∃ λi such that \(| arg({\lambda }_{i})| < \frac{\theta \pi }{2}\).

Lemma 3.3 26,28If the following conditions hold:

  1. (1)

    the Jacobian matrix J(U*) of system (3.1) near the equilibrium point has a pair of complex conjugate eigenvalues with positive real part;

  2. (2)

    \(p(\theta )=\frac{\theta \pi }{2}-{\min }_{1\le i\le 2}| arg({\lambda }_{i})| =0;\)

  3. (3)

    \(\frac{dp(\theta )}{d\theta }{| }_{\theta ={\theta }_{0}}\ne 0,\)

then system (3.1) undergoes a Hopf bifurcation near the equilibrium point U* when θ crosses the critical value θ0.

Existence, uniqueness and boundness of solution

In this segment, we will discuss the existence, uniqueness and boundness of solution of model (2.1).

Theorem 4.1 System (2.1) with initial value (u10, u20) has a unique solution (u1(t), u2(t)) ∈ Θ for all t ≥ t0. 

Proof Let

$$\left\{\begin{array}{l}{F}_{1}(u)={\gamma }_{1}\left[1-\frac{{u}_{1}(t)}{\kappa }\right]{u}_{1}(t)-{\gamma }_{2}{u}_{1}^{\sigma }(t){u}_{2}(t)-\frac{{\rho }_{1}{\rho }_{2}{u}_{1}(t)}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}(t)},{F}_{2}(u)=-{\gamma }_{3}{u}_{2}(t)+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }(t){u}_{2}(t),\end{array}\right.$$
(41)

where u = (u1, u2). Define a mapping as follows:

$$F(u)=({F}_{1}(u),{F}_{2}(u)).$$
(4.2)

\(\forall u,{\bar{u}}\in \Theta \), one has

$$\begin{array}{lll}| | F(u)-F({\bar{u}})| | & = & | {F}_{1}(u)-{F}_{1}({\bar{u}})| +| {F}_{2}(u)-{F}_{2}({\bar{u}})| \\ & = & \left|\left\{{\gamma }_{1}\left[1-\frac{{u}_{1}({t}_{1})}{\kappa }\right]{u}_{1}({t}_{1})-{\gamma }_{2}{u}_{1}^{\sigma }({t}_{1}){u}_{2}({t}_{1})-\frac{{\rho }_{1}{\rho }_{2}{u}_{1}({t}_{1})}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}({t}_{1})}\right.\right.\\ & & \left.\left.-\,\left\{{\gamma }_{1}\left[1-\frac{{u}_{1}({t}_{2})}{\kappa }\right]{u}_{1}({t}_{2})-{\gamma }_{2}{u}_{1}^{\sigma }({t}_{2}){u}_{2}(t)-\frac{{\rho }_{1}{\rho }_{2}{u}_{1}({t}_{2})}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}({t}_{2})}\right\}\right\}\right|\\ & & +| -{\gamma }_{3}{u}_{2}({t}_{1})+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }({t}_{1}){u}_{2}({t}_{1})-[-{\gamma }_{3}{u}_{2}({t}_{2})+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }({t}_{2}){u}_{2}({t}_{2})]| \\ & & \le | {u}_{1}({t}_{1})-{u}_{1}({t}_{2})| \left|{\gamma }_{1}\left[1-\frac{{u}_{1}({t}_{1})}{\kappa }\right]-{\gamma }_{2}{u}_{1}^{\sigma -1}({t}_{1}){u}_{2}({t}_{1})-\frac{{\rho }_{1}{\rho }_{2}}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}({t}_{1})}\right|\\ & & +\max \{| {u}_{1}({t}_{1})| ,| {u}_{1}({t}_{2})| \}\left|\left\{{\gamma }_{1}\left[1-\frac{{u}_{1}({t}_{1})}{\kappa }\right]-{\gamma }_{2}{u}_{1}{({t}_{1})}^{\sigma -1}{u}_{2}({t}_{1})-\frac{{\rho }_{1}{\rho }_{2}}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}({t}_{1})}\right\}\right.\\ & & -\left.\left\{{\gamma }_{1}\left[1-\frac{{u}_{1}({t}_{2})}{\kappa }\right]-{\gamma }_{2}{u}_{1}^{\sigma -1}({t}_{2}){u}_{2}({t}_{2})-\frac{{\rho }_{1}{\rho }_{2}}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}({t}_{2})}\right\}\right|\\ & & +| {u}_{2}({t}_{1})-{u}_{2}({t}_{2})| | -{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }({t}_{1})| \end{array}$$
$$\begin{array}{ll} & +\max \left\{| {u}_{1}({t}_{1})| ,| {u}_{1}({t}_{2})| \right\}| (-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }({t}_{1}))-(-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{u}_{1}{({t}_{2})}^{\sigma })| \\ & \le | {u}_{1}({t}_{1})-{u}_{1}({t}_{2})| \left|{\gamma }_{1}\left[1-\frac{{u}_{1}({t}_{1})}{\kappa }\right]-{\gamma }_{2}{u}_{1}^{\sigma -1}({t}_{1}){u}_{2}({t}_{1})-\frac{{\rho }_{1}{\rho }_{2}}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}({t}_{1})}\right|\\ & +K\max \{| {u}_{1}({t}_{1})-{u}_{1}({t}_{2})| ,| {u}_{2}({t}_{1})-{u}_{2}({t}_{2})| \}\left(\frac{{\gamma }_{1}}{\kappa }+{\gamma }_{2}{K}^{\sigma -1}+\frac{{\rho }_{1}{\rho }_{4}}{{\rho }_{4}}\right)\\ & +| {u}_{2}({t}_{1})-{u}_{2}({t}_{2})| | -{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }({t}_{1})| \\ & +K\max \{| {u}_{1}({t}_{1})-{u}_{1}({t}_{2})| ,| {u}_{2}({t}_{1})-{u}_{2}({t}_{2})| \}2{\gamma }_{2}{\gamma }_{4}{K}^{\sigma }\\ & \le | {u}_{1}({t}_{1})-{u}_{1}({t}_{2})| \left|{\gamma }_{1}\left[1+\frac{K}{\kappa }\right]+{\gamma }_{2}{K}^{\sigma }-\frac{{\rho }_{1}{\rho }_{2}}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}K}\right|\\ & +K\max \{| {u}_{1}({t}_{1})-{u}_{1}({t}_{2})| ,| {u}_{2}({t}_{1})-{u}_{2}({t}_{2})| \}\left(\frac{{\gamma }_{1}}{\kappa }+{\gamma }_{2}{K}^{\sigma -1}+\frac{{\rho }_{1}{\rho }_{4}}{{\rho }_{4}}\right)\\ & +| {u}_{2}({t}_{1})-{u}_{2}({t}_{2})| | -{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{K}^{\sigma }| \\ & +K\max \{| {u}_{1}({t}_{1})-{u}_{1}({t}_{2})| ,| {u}_{2}({t}_{1})-{u}_{2}({t}_{2})| \}2{\gamma }_{2}{\gamma }_{4}{K}^{\sigma }\\ & \le \vartheta | u-{\bar{u}}| ,\end{array}$$
(43)

where

$$\vartheta =\max \left\{\left|{\gamma }_{1}\left(1+\frac{K}{\kappa }\right)+{\gamma }_{2}{K}^{\sigma }-\frac{{\rho }_{1}{\rho }_{2}}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}K}\right|+K\left(\frac{{\gamma }_{1}}{\kappa }+{\gamma }_{2}{K}^{\sigma -1}+\frac{{\rho }_{1}{\rho }_{4}}{{\rho }_{4}}\right)+2{\gamma }_{2}{\gamma }_{4}{K}^{\sigma +1}\right\}.$$
(4.4)

Then F(u) satisfies the Lipschitz condition with respect to u. Thus we can conclude that system (2.1) with initial value (u10, u20) has a unique solution (u1(t), u2(t)) ∈ Θ for all t ≥ t0. The proof is completed.

Theorem 4.2 Every solution (u1(t), u2(t)) of system (2.1) with the initial condition (u1(t0), u2(t0)) is uniformly bounded and non-negative.

Proof Let U(t) = γ4u1(t) + u2(t). Then

$$\begin{array}{lll}{D}^{\theta }U(t) & = & {\gamma }_{4}{D}^{\theta }{u}_{1}(t)+{D}^{\theta }(t){u}_{2}\\ & = & {\gamma }_{4}\left\{{\gamma }_{1}\left[1-\frac{{u}_{1}(t)}{\kappa }\right]{u}_{1}(t)-{\gamma }_{2}{u}_{1}^{\sigma }(t){u}_{2}(t)-\frac{{\rho }_{1}{\rho }_{2}{u}_{1}(t)}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}(t)}\right\}\\ & & -\ {\gamma }_{3}{u}_{2}(t)+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }(t){u}_{2}(t)\\ & = & {\gamma }_{4}{\gamma }_{1}{u}_{1}(t)-\frac{{\gamma }_{4}{\gamma }_{1}}{\kappa }{u}_{1}^{2}(t)-\frac{{\gamma }_{4}{\rho }_{1}{\rho }_{2}{u}_{1}(t)}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}(t)}-{\gamma }_{3}{u}_{2}(t)\\ & = & {\gamma }_{4}{\gamma }_{1}{u}_{1}(t)-\frac{{\gamma }_{4}{\gamma }_{1}}{\kappa }{u}_{1}^{2}(t)-\frac{{\gamma }_{4}{\rho }_{1}{\rho }_{2}{u}_{1}(t)}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}(t)}-{\gamma }_{3}U(t)+{\gamma }_{3}{\gamma }_{4}{u}_{1}(t)\\ & \le & ({\gamma }_{1}+{\gamma }_{3}){\gamma }_{4}{u}_{1}(t)-\frac{{\gamma }_{4}{\gamma }_{1}}{\kappa }{u}_{1}^{2}(t)-{\gamma }_{3}U(t)\end{array}$$
(4.5)

Then

$$\begin{array}{lll}{D}^{\theta }U(t)+{\gamma }_{3}U(t) & \le & ({\gamma }_{1}+{\gamma }_{3}){\gamma }_{4}{u}_{1}(t)-\frac{{\gamma }_{4}{\gamma }_{1}}{\kappa }{u}_{1}^{2}(t)\\ & = & \frac{{\gamma }_{4}{\gamma }_{1}}{\kappa }{\left[{u}_{1}(t)-{\left(\frac{{\gamma }_{1}+{\gamma }_{3}}{2{\gamma }_{1}}\right)}^{2}\right]}^{2}+\frac{{\gamma }_{4}{({\gamma }_{1}+{\gamma }_{3})}^{2}}{4\kappa {\gamma }_{1}}\\ & \le & \frac{{\gamma }_{4}{({\gamma }_{1}+{\gamma }_{3})}^{2}}{4\kappa {\gamma }_{1}}.\end{array}$$
(4.6)

In view of the results in29, one has

$$U(t)\le U(0){E}_{\theta }(-{\gamma }_{3}{t}^{\theta })+\frac{{\gamma }_{4}{({\gamma }_{1}+{\gamma }_{3})}^{2}}{4\kappa {\gamma }_{1}}{t}^{\theta }{E}_{\theta ,\theta +1}(-{\gamma }_{3}{t}^{\theta }),$$
(47)

where Eθ is the Mittag-Leffler function. In view of Lemma 5 and Corollary 6 of29, we have

$$U(t)\le \frac{{\gamma }_{4}{({\gamma }_{1}+{\gamma }_{3})}^{2}}{4\kappa {\gamma }_{1}},t\to \infty .$$
(4.8)

Thus every solution (u1(t), u2(t)) of system (2.1) with the initial condition (u1(t0), u2(t0)) is uniformly bounded.

Equilibria and stability

In this section, we consider the equilibria and their stability. In order to obtain the equilibrium point of system (2.1), we can solve the following equations:

$$\left\{\begin{array}{l}{D}^{\theta }{u}_{1}(t)=0\\ {D}^{\theta }{u}_{2}(t)=0.\end{array}\right.$$
(5.1)

Namely,

$$\left\{\begin{array}{l}{\gamma }_{1}\left[1-\frac{{u}_{1}(t)}{\kappa }\right]{u}_{1}(t)-{\gamma }_{2}{u}_{1}^{\sigma }(t){u}_{2}(t)-\frac{{\rho }_{1}{\rho }_{2}{u}_{1}(t)}{{\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}(t)}=0,\\ -\ {\gamma }_{3}{u}_{2}(t)+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }(t){u}_{2}(t)=0.\end{array}\right.$$
(5.2)

It is not difficult to obtain the following equilibria of system (2.1): \({E}_{1}(0,0),{E}_{2}({u}_{1}^{(1)},0),{E}_{3}({u}_{1}^{(2)},0),{E}_{4}({u}_{1\ast },{u}_{2\ast }),\) where

$$\left\{\begin{array}{lll}{u}_{1}^{(1)} & = & \frac{\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)+\sqrt{{\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}^{2}-4\left(\frac{{\rho }_{1}{\rho }_{2}}{{\gamma }_{1}{\rho }_{4}\kappa }-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}}{2},\\ {u}_{1}^{(2)} & = & \frac{\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)-\sqrt{{\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}^{2}-4\left(\frac{{\rho }_{1}{\rho }_{2}}{{\gamma }_{1}{\rho }_{4}\kappa }-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}}{2},\\ {u}_{1\ast } & = & {\left(\frac{{\gamma }_{3}}{{\gamma }_{2}{\gamma }_{3}{\kappa }^{\sigma }}\right)}^{\frac{1}{\sigma }},\\ {u}_{2\ast } & = & {u}_{1\ast }^{1-\sigma }\left(1-{u}_{1\ast }-\frac{{\rho }_{1}{\rho }_{2}}{{\gamma }_{1}({\rho }_{2}{\rho }_{3}+{u}_{1\ast }{\rho }_{4}\kappa )}\right).\end{array}\right.$$
(53)

Theorem 5.1 (1) System (2.1) always has the zero equilibrium point E1(0, 0).

(2) If \({\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}^{2} < 4\left(\frac{{\rho }_{1}{\rho }_{2}}{{\gamma }_{1}{\rho }_{4}\kappa }-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)\), then system (2.1) has no boundary equilibrium points.

(3) If \({\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}^{2}=4\left(\frac{{\rho }_{1}{\rho }_{2}}{{\gamma }_{1}{\rho }_{4}\kappa }-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)\) and \(\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa } < 1,\) then system (2.1) has a unique boundary equilibrium points \({ {\tilde{E}} }_{1}({ {\tilde{u}} }_{1}^{(1)},0)\), where \({ {\tilde{u}} }_{1}^{(1)}=\frac{1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }}{2}\).

(4) If \({\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}^{2} > 4\left(\frac{{\rho }_{1}{\rho }_{2}}{{\gamma }_{1}{\rho }_{4}\kappa }-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)\) and \(\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa } < 1,\) then system (2.1) has two boundary equilibrium points \({ {\tilde{E}} }_{1}^{\ast }({ {\tilde{u}} }_{1}^{(1\ast )},0)\) and \({ {\tilde{E}} }_{1}^{\ast \ast }({ {\tilde{u}} }_{1}^{(1\ast \ast )},0)\) where

$${ {\tilde{u}} }_{1}^{(1\ast )}=\frac{\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)+\sqrt{{\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}^{2}-4\left(\frac{{\rho }_{1}{\rho }_{2}}{{\gamma }_{1}{\rho }_{4}\kappa }-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}}{2}$$

and

$${ {\tilde{u}} }_{1}^{(1\ast \ast )}=\frac{\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)-\sqrt{{\left(1-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}^{2}-4\left(\frac{{\rho }_{1}{\rho }_{2}}{{\gamma }_{1}{\rho }_{4}\kappa }-\frac{{\rho }_{2}{\rho }_{3}}{{\rho }_{4}\kappa }\right)}}{2}.$$

(5) If (1 − u1*)γ1(ρ2ρ3 + u1*ρ4κ) > ρ1ρ2, then system (2.1) has the interior equilibrium pointE4(u1*, u2*).

Since the proof of Theorem 5.1 is simple in view of (5.3). Here we omit it.

Next we discuss the stability of the equilibrium points. The Jacobian matrix of system (2.1) near the equilibrium point (u1, u2) is

$$J({u}_{1},{u}_{2})=\left[\begin{array}{ll}{\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1}}{\kappa }-{\gamma }_{2}\sigma {u}_{1}^{\sigma -1}{u}_{2}-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1})}^{2}} & -{\gamma }_{2}{u}_{1}^{\sigma }\\ \sigma {\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma -1}{u}_{2} & -{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{u}_{1}^{\sigma }\\ \end{array}\right].$$
(5.4)

Theorem 5.2 The equilibrium point E1(0, 0) of system (2.1) is locally asymptotically stable if \({\gamma }_{1}-\frac{{\rho }_{1}}{{\rho }_{3}} < 0\) and is a saddle point if \({\gamma }_{1}-\frac{{\rho }_{1}}{{\rho }_{3}} > 0\).

Proof In view of (5.4), one can get

$$J(0,0)=\left[\begin{array}{ll}{\gamma }_{1}-\frac{{\rho }_{1}}{{\rho }_{3}} & 0\\ 0 & -{\gamma }_{3}\\ \end{array}\right]$$
(5.5)

It follows that the eigenvalues of J(0, 0) are \({\lambda }_{1}={\gamma }_{1}-\frac{{\rho }_{1}}{{\rho }_{3}},{\lambda }_{2}=-{\gamma }_{3}.\) When \({\gamma }_{1}-\frac{{\rho }_{1}}{{\rho }_{3}} < 0\), then λ1 < 0, λ2 < 0 and hence arg(λi) = π(i = 1, 2) and \(| arg({\lambda }_{i})| > \frac{\theta \pi }{2}(i=1,2)\). Thus the equilibrium point E0(0, 0) of system (2.1) is locally asymptotically stable if \({\gamma }_{1}-\frac{{\rho }_{1}}{{\rho }_{3}} < 0\). When \({\gamma }_{1}-\frac{{\rho }_{1}}{{\rho }_{3}} > 0\), then λ1 > 0, λ2 < 0 and hence arg(λ1) = 0 and \(| arg({\lambda }_{1})| < \frac{\theta \pi }{2}\). Thus the equilibrium point E0(0, 0) of system (2.1) is a saddle point if \({\gamma }_{1}-\frac{{\rho }_{1}}{{\rho }_{3}} > 0.\) The proof of Theorem 5.2 is completed.

Theorem 5.3 (1) The equilibrium point \({E}_{2}({u}_{1}^{(1)},0)\) of system (2.1) is locally asymptotically stable if \({\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1}^{(1)}}{\kappa }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}^{(1)})}^{2}} < 0\) and \(-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{({u}_{1}^{(1)})}^{\sigma } > 0\)

(2) The equilibrium point\({E}_{2}({u}_{1}^{(1)},0)\)of system (2.1) is a saddle point if \(\left({\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1}^{(1)}}{\kappa }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}^{(1)})}^{2}}\right)\) \((-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{({u}_{1}^{(1)})}^{\sigma }) < 0\).

(3) The equilibrium point\({E}_{2}({u}_{1}^{(1)},0)\)of system (2.1) is a saddle point if \({\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1}^{(1)}}{\kappa }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}^{(1)})}^{2}} > 0\)and \(-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{({u}_{1}^{(1)})}^{\sigma } > 0\).

Proof In view of (5.4), one can get

$$J({u}_{1}^{(1)},0)=\left[\begin{array}{cc}{\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1}^{(1)}}{\kappa }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}^{(1)})}^{2}} & -{\gamma }_{2}{({u}_{1}^{(1)})}^{\sigma }\\ 0 & -{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{({u}_{1}^{(1)})}^{\sigma }\\ \end{array}\right]$$
(56)

It follows that the eigenvalues of \(J({u}_{1}^{(1)},0)\) are \({\lambda }_{1}={\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1}^{(1)}}{\kappa }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}^{(1)})}^{2}},{\lambda }_{2}=-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{({u}_{1}^{(1)})}^{\sigma }.\) Under the assumptions of (1), (2) and (3) of Theorem 5.3, we can easily conclude that the conclusion of Theorem 5.3 holds true. The proof of Theorem 5.3 is completed.

In a same way, we get the following result on the equilibrium point \({E}_{3}({u}_{1}^{(2)},0)\) of system (2.1).

Theorem 5.4 (1) The equilibrium point \({E}_{3}({u}_{1}^{(2)},0)\) of system (2.1) is locally asymptotically stable if \({\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1}^{(2)}}{\kappa }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}^{(2)})}^{2}} < 0\) and \(-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{({u}_{1}^{(2)})}^{\sigma } > 0\)

(2) The equilibrium point \({E}_{3}({u}_{1}^{(2)},0)\) of system(2.1)is a saddle point if \(\left({\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1}^{(2)}}{\kappa }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}^{(2)})}^{2}}\right)\)\((-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{({u}_{1}^{(2)})}^{\sigma }) < 0\).

(3) The equilibrium point \({E}_{3}({u}_{1}^{(2)},0)\) of system (2.1) is a saddle point if \({\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1}^{(2)}}{\kappa }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1}^{(2)})}^{2}} > 0\)and \(-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{({u}_{1}^{(2)})}^{\sigma } > 0\).

Theorem 5.5 (1) If the one of following inequalities is satisfied: (a) α ≤ 0 (b) α > 0, α2 − 4β < 0 and \(\frac{\sqrt{4\beta -{\alpha }^{2}}}{\alpha } > \tan \frac{\theta \pi }{2}\). Then the equilibrium point E4(u1*, u2*) of system (2.1) is locally asymptotically stable.

Proof In view of (5.4), we have

$$J({u}_{1\ast },{u}_{2\ast })=\left[\begin{array}{ll}{\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1\ast }}{\kappa }-{\gamma }_{2}\sigma {u}_{1\ast }^{\sigma -1}{u}_{2\ast }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1\ast })}^{2}} & -{\gamma }_{2}{u}_{1\ast }^{\sigma }\\ \sigma {\gamma }_{2}{\gamma }_{4}{u}_{1\ast }^{\sigma -1}{u}_{2\ast } & -{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{u}_{1\ast }^{\sigma }\\ \end{array}\right].$$
(57)

Let

$$\left\{\begin{array}{l}{a}_{11}={\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1\ast }}{\kappa }-{\gamma }_{2}\sigma {u}_{1\ast }^{\sigma -1}{u}_{2\ast }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1\ast })}^{2}},\\ {a}_{12}=-{\gamma }_{2}{u}_{1\ast }^{\sigma },\\ {a}_{21}=\sigma {\gamma }_{2}{\gamma }_{4}{u}_{1\ast }^{\sigma -1}{u}_{2\ast },\\ {a}_{22}=-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{u}_{1\ast }^{\sigma }.\end{array}\right.$$
(58)

Then (5.7) becomes

$$J({u}_{1\ast },{u}_{2\ast })=\left[\begin{array}{ll}{a}_{11} & {a}_{12}\\ {a}_{21} & {a}_{22}\end{array}\right].$$
(59)

The eigenvalues of J(u1*, u2*) are

$${\lambda }_{1}=\frac{\alpha +\sqrt{{\alpha }^{2}-4\beta }}{2},{\lambda }_{2}=\frac{\alpha -\sqrt{{\alpha }^{2}-4\beta }}{2},$$
(5.10)

where

$$\alpha ={a}_{11}+{a}_{22},\beta ={a}_{11}{a}_{22}-{a}_{12}{a}_{21}.$$
(5.11)

If α ≤ 0, then we consider three cases:

  1. (i)

    If α = 0, then the eigenvalues of J(u1*, u2*) are a pair of complex conjugate λ1 and \({\bar{\lambda }}_{1}\). Hence \(Re({\lambda }_{1})=Re({\bar{\lambda }}_{1})=0\) and \(arg({\lambda }_{1})=\frac{\pi }{2},arg({\bar{\lambda }}_{1})=-\frac{\pi }{2}\). Thus \(| arg({\lambda }_{1})| > \frac{\theta \pi }{2}\) and \(| arg({\bar{\lambda }}_{1})| > \frac{\theta \pi }{2}\). In view of Lemma 3.2, we can conclude that the equilibrium point E4(u1*, u2*) of system (2.1) is locally asymptotically stable.

  2. (ii)

    If α < 0, α2 − 4β ≥ 0, then the both eigenvalues of J(u1*, u2*) are λ1 < 0 and λ2 < 0. Hence \(| arg({\lambda }_{i})| =\frac{\pi }{2} > \frac{\theta \pi }{2}(i=1,2)\). In view of Lemma 3.2, we can conclude that the equilibrium point E4(u1*, u2*) of system (2.1) is locally asymptotically stable.

  3. (iii)

    If α < 0, α2 − 4β < 0, then the eigenvalues of J(u1*, u2*) are a pair of complex conjugate λ1 and \({\bar{\lambda }}_{1}\). Hence \(\,{\rm{Re}}\,({\lambda }_{1})=\,{\rm{Re}}\,({\bar{\lambda }}_{1}) < 0\) and \(arg({\lambda }_{i}) > \frac{\pi }{2}\). In view of Lemma 3.2, we can conclude that the equilibrium point E4(u1*, u2*) of system (2.1) is locally asymptotically stable.

If \(\alpha > 0,{\alpha }^{2}-4\beta < 0,\frac{\sqrt{4\beta -{\alpha }^{2}}}{\alpha } > \tan \frac{\theta \pi }{2}\), then the both eigenvalues of J(u1*, u2*) are λ1 and \({\bar{\lambda }}_{1}\) satisfy \(\,{\rm{Re}}\,({\lambda }_{1})=\,{\rm{Re}}\,({\bar{\lambda }}_{1}) > 0,\,{\rm{Im}}\,({\lambda }_{1})=-{\rm{Im}}\,({\bar{\lambda }}_{1})=\frac{\sqrt{4\beta -{\alpha }^{2}}}{2} > 0.\) Hence

$$\frac{\,{\rm{Im}}\,({\lambda }_{1})}{\,{\rm{Re}}\,({\lambda }_{1})} > \tan \frac{\theta \pi }{2},-\frac{{\rm{Im}}\,({\bar{\lambda }}_{1})}{\,{\rm{Re}}\,({\bar{\lambda }}_{1})} > \tan \frac{\theta \pi }{2}.$$

Then \(| arg({\lambda }_{1})| > \frac{\alpha \pi }{2},| arg({\bar{\lambda }}_{1})| > \frac{\alpha \pi }{2}.\) In view of Lemma 3.2, we can conclude that the equilibrium point E4(u1*, u2*) of system (2.1) is locally asymptotically stable.

Theorem 5.6 (1) If the one of following inequalities is satisfied: (a) α > 0, α2 − 4β ≥ 0 (b) α2 − 4β < 0, α > 0 and \(\frac{\sqrt{4\beta -{\alpha }^{2}}}{\alpha } < \tan \frac{\theta \pi }{2}\). Then the equilibrium point E4(u1*, u2*) of system (2.1) is unstable.

Proof In view of (5.4), we have

$$J({u}_{1\ast },{u}_{2\ast })=\left[\begin{array}{ll}{\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1\ast }}{\kappa }-{\gamma }_{2}\sigma {u}_{1\ast }^{\sigma -1}{u}_{2\ast }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1\ast })}^{2}} & -{\gamma }_{2}{u}_{1\ast }^{\sigma }\\ \sigma {\gamma }_{2}{\gamma }_{4}{u}_{1\ast }^{\sigma -1}{u}_{2\ast } & -{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{u}_{1\ast }^{\sigma }\end{array}\right].$$

Let

$$\left\{\begin{array}{l}{a}_{11}={\gamma }_{1}-\frac{2{\gamma }_{1}{u}_{1\ast }}{\kappa }-{\gamma }_{2}\sigma {u}_{1\ast }^{\sigma -1}{u}_{2\ast }-\frac{{\rho }_{1}{\rho }_{2}^{2}{\rho }_{3}}{{({\rho }_{2}{\rho }_{3}+{\rho }_{4}{u}_{1\ast })}^{2}},\\ {a}_{12}=-{\gamma }_{2}{u}_{1\ast }^{\sigma },\\ {a}_{21}=\sigma {\gamma }_{2}{\gamma }_{4}{u}_{1\ast }^{\sigma -1}{u}_{2\ast },\\ {a}_{22}=-{\gamma }_{3}+{\gamma }_{2}{\gamma }_{4}{u}_{1\ast }^{\sigma }.\end{array}\right.$$

Then (5.7) becomes

$$J({u}_{1\ast },{u}_{2\ast })=\left[\begin{array}{ll}{a}_{11} & {a}_{12}\\ {a}_{21} & {a}_{22}\end{array}\right].$$

The eigenvalues of J(u1*, u2*) are

$${\lambda }_{1}=\frac{\alpha +\sqrt{{\alpha }^{2}-4\beta }}{2},{\lambda }_{2}=\frac{\alpha -\sqrt{{\alpha }^{2}-4\beta }}{2},$$

where

$$\alpha ={a}_{11}+{a}_{22},\beta ={a}_{11}{a}_{22}-{a}_{12}{a}_{21}.$$
(5.12)

(i) If α > 0, α2 − 4β≥0, then the both eigenvalues of J(u1*, u2*) are λ1 > 0 and λ2 > 0. Hence \(| arg({\lambda }_{i})| < \frac{\theta \pi }{2}(i=1,2)\). In view of Lemma 3.2, we can conclude that the equilibrium point E4(u1*, u2*) of system (2.1) is unstable.

(ii) If α > 0, α2 − 4β < 0 and \(\frac{\sqrt{4\beta -{\alpha }^{2}}}{\alpha } < \tan \frac{\theta \pi }{2}\), then the eigenvalues of J(u1*, u2*) are a pair of complex conjugate λ1 and \({\bar{\lambda }}_{1}\). Hence \(\,{\rm{Im}}\,({\lambda }_{1})=-{\rm{Im}}\,({\bar{\lambda }}_{1}) > 0\), \(\,{\rm{Re}}\,({\lambda }_{1})=\,{\rm{Re}}\,({\bar{\lambda }}_{1})=\alpha > 0.\) Then

$$\frac{\,{\rm{Im}}\,({\lambda }_{1})}{\,{\rm{Re}}\,({\lambda }_{1})} < \tan \frac{\theta \pi }{2},-\frac{\,{\rm{Im}}\,({\bar{\lambda }}_{1})}{\,{\rm{Re}}\,({\bar{\lambda }}_{1})} < \tan \frac{\theta \pi }{2}.$$

Thus \(| arg({\lambda }_{1})| < \frac{\alpha \pi }{2},| arg({\bar{\lambda }}_{1})| < \frac{\alpha \pi }{2}.\) In view of Lemma 3.2, we can conclude that the equilibrium point E4(u1*, u2*) of system (2.1) is unstable.

Bifurcation analysis

In this section, we will establish the sufficient condition that guarantees the existence of Hopf bifurcation of system (2.1).

Theorem 6.1 If α2 − 4β > 0 and α > 0, then a Hopf bifurcation of system (2.1) will appear around E4(u1*, u2*) when the fractional order θ crosses the critical value \({\theta }_{0}=\frac{2}{\pi }\arctan \frac{\sqrt{| {\alpha }^{2}-4\beta | }}{\alpha }\).

Proof Denote \({\vartheta }=\frac{\alpha }{2}\) and \(\psi =\frac{\sqrt{| {\alpha }^{2}-4\beta | }}{2}\). In view of the assumption α > 0, one get ϑ > 0. By the assumption α2 − 4β > 0 and (4.10), the the eigenvalues of J(u1*, u2*) of system (2.1) are a pair of complex conjugate λ1,2 = ϑ ± iψ. Next, \(p({\theta }_{0})=\frac{{\theta }_{0}\pi }{2}-{\min }_{1\le i\le 2}| arg({\lambda }_{i})| =\frac{{\theta }_{0}\pi }{2}-arg\left(\frac{\psi }{\vartheta }\right)=arg\left(\frac{\psi }{\vartheta }\right)-arg\left(\frac{\psi }{\vartheta }\right)=0.\) Finally, \(\frac{dp(\theta )}{d\theta }{| }_{\theta ={\theta }_{0}}=\frac{\pi }{2}\ne 0.\) In view of Lemma 3.3, we can conclude that a Hopf bifurcation of system (2.1) will appear around E4(u1*, u2*) when the fractional order θ crosses the critical value \({\theta }_{0}=\frac{2}{\pi }\arctan \frac{\sqrt{| {\alpha }^{2}-4\beta | }}{\alpha }\). The proof of Theorem 6.1 is completed.

Remark 6.1 In11, the authors studied the stability, Hopf bifurcation and chaotic behavior of integer order predator-pry system. In this article, we mainly focus on the existence, uniqueness and boundness of solution, the stability of equilibrium point and the existence of Hopf bifurcation of fractional order predator-prey model. The research method and theoretical findings are different from those in11. According to this viewpoint, the results of this paper complete the works of Kumar and Kharbanda11.

Numerical simulation

Example 7.1 We give the fractional-order system as follows:

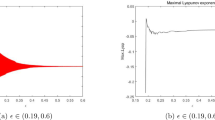
$$\left\{\begin{array}{l}{D}^{\theta }{u}_{1}(t)=\left(1-{u}_{1}(t)\right){u}_{1}(t)-{u}_{1}^{0.25}(t){u}_{2}(t)-\frac{0.2{u}_{1}(t)}{0.3+{u}_{1}(t)},\\ {D}^{\theta }{u}_{2}(t)=-0.2{u}_{2}(t)+0.25{u}_{1}^{0.25}(t){u}_{2}(t),\end{array}\right.$$
(71)

where γ1 = 1, γ2 = 1, γ3 = 0.2, γ4 = 0.25, κ = 1, σ = 0.25, ρ1 = 0.2, ρ2 = 1, ρ3 = 0.3, ρ4 = 1. Obviously, system (7.1) has a unique coexistence equilibrium point E3(0.4096, 0.1580). By direct computation, one has θ0 = 0.83. Let θ = 0.78. We can easily check that all the assumptions of Theorem 5.4 and Theorem 6.1 are fulfilled. Thus the equilibrium point E3(0.4096, 0.1580) of system (7.1) is locally asymptotically stable. This fact is depicted in Figs. 1–4. When the parameter θ crosses the critical value θ0, then a Hopf bifurcation will appear. This result can be shown in Figs. 5–8 (here let θ = 0.9). If θ = 1 (integer order), a Hopf bifurcation appears near the equilibrium point E3(0.4096, 0.1580). This result can be illustrated in Figs. 9–12.

Figure 1
figure 1

The trajectories of system (7.1) with γ1 = 1, γ2 = 1, γ3 = 0.2, γ4 = 0.25, κ = 1, σ = 0.25, ρ1 = 0.2, ρ2 = 1, ρ3 = 0.3, ρ4 = 1, θ = 0.78. The equilibrium point (0.4096, 0.1580) of system (7.1) is asymptotically stable. The relation of t and u1(t).

Full size image
Figure 2
figure 2

The trajectories of system (7.1) with γ1 = 1, γ2 = 1, γ3 = 0.2, γ4 = 0.25, κ = 1, σ = 0.25, ρ1 = 0.2, ρ2 = 1, ρ3 = 0.3, ρ4 = 1, θ = 0.78. The equilibrium point (0.4096, 0.1580) of system (7.1) is asymptotically stable. The relation of t and u2(t).

Full size image
Figure 3
figure 3

The trajectories of system (7.1) with γ1 = 1, γ2 = 1, γ3 = 0.2, γ4 = 0.25, κ = 1, σ = 0.25, ρ1 = 0.2, ρ2 = 1, ρ3 = 0.3, ρ4 = 1, θ = 0.78. The equilibrium point (0.4096, 0.1580) of system (7.1) is asymptotically stable. The relation of u1(t) and u2(t).

Full size image
Figure 4
figure 4

The trajectories of system (7.1) with γ1 = 1, γ2 = 1, γ3 = 0.2, γ4 = 0.25, κ = 1, σ = 0.25, ρ1 = 0.2, ρ2 = 1, ρ3 = 0.3, ρ4 = 1, θ = 0.78. The equilibrium point (0.4096, 0.1580) of system (7.1) is asymptotically stable. The relation of t, u1(t) and u2(t).

Full size image
Figure 5
figure 5

The trajectories of system (7.1) with γ1 = 1, γ2 = 1, γ3 = 0.2, γ4 = 0.25, κ = 1, σ = 0.25, ρ1 = 0.2, ρ2 = 1, ρ3 = 0.3, ρ4 = 1 and θ = 0.9 > θ0 = 0.83. Hopf bifurcation of system (7.1) appears from the equilibrium point (0.4096, 0.1580). The relation of t and u1(t).

Full size image
Figure 6
figure 6

The trajectories of system (7.1) with γ1 = 1, γ2 = 1, γ3 = 0.2, γ4 = 0.25, κ = 1, σ = 0.25, ρ1 = 0.2, ρ2 = 1, ρ3 = 0.3, ρ4 = 1 and θ = 0.9 > θ0 = 0.83. Hopf bifurcation of system (7.1) appears from the equilibrium point (0.4096, 0.1580). The relation of t and u2(t).

Full size image
Figure 7
figure 7

The trajectories of system (7.1) with γ1 = 1, γ2 = 1, γ3 = 0.2, γ4 = 0.25, κ = 1, σ = 0.25, ρ1 = 0.2, ρ2 = 1, ρ3 = 0.3, ρ4 = 1 and θ = 0.9 > θ0 = 0.83. Hopf bifurcation of system (7.1) appears from the equilibrium point (0.4096, 0.1580). The relation of u1(t) and u2(t).

Full size image
Figure 8
figure 8

The trajectories of system (7.1) with γ1 = 1, γ2 = 1, γ3 = 0.2, γ4 = 0.25, κ = 1, σ = 0.25, ρ1 = 0.2, ρ2 = 1, ρ3 = 0.3, ρ4 = 1 and θ = 0.9 > θ0 = 0.83. Hopf bifurcation of system (7.1) appears from the equilibrium point (0.4096, 0.1580). The relation of t, u1(t) and u2(t).

Full size image
Figure 9
figure 9

The trajectories of system (7.1) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\)and θ = 1. Hopf bifurcation appears near the equilibrium point (0.4168, 0.1465). The relation of t and u1(t).

Full size image
Figure 10
figure 10

The trajectories of system (7.1) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\)and θ = 1. Hopf bifurcation appears near the equilibrium point (0.4168, 0.1465). The relation of t and u2(t).

Full size image
Figure 11
figure 11

The trajectories of system (7.1) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\)and θ = 1. Hopf bifurcation appears near the equilibrium point (0.4168, 0.1465). The relation of u1(t) and u2(t).

Full size image
Figure 12
figure 12

The trajectories of system (7.1) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\)and θ = 1. Hopf bifurcation appears near the equilibrium point (0.4168, 0.1465). The relation of t, u1(t) and u2(t).

Full size image

Example 7.2 We give the fractional-order system as follows:

$$\left\{\begin{array}{l}{D}^{\theta }{u}_{1}(t)=\left(0.999-0.998{u}_{1}(t)\right){u}_{1}(t)-{u}_{1}^{0.255}(t){u}_{2}(t)-\frac{0.22{u}_{1}(t)}{0.25+{u}_{1}(t)},\\ {D}^{\theta }{u}_{2}(t)=-0.2{u}_{2}(t)+0.25{u}_{1}^{0.255}(t){u}_{2}(t),\end{array}\right.$$
(72)

where \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,{\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1.\) Obviously, system (7.2) has a unique coexistence equilibrium point E3(0.4168, 0.1465). By direct computation, one has θ0 = 0.778. Let θ = 0.65. We can easily check that all the assumptions of Theorem 5.5 and Theorem 6.1 are fulfilled. Thus the equilibrium point E3(0.4168, 0.1465) of system (7.2) is locally asymptotically stable. This fact is depicted in Figs. 13–16. When the parameter θ crosses the critical value θ0, then a Hopf bifurcation will appear. This result can be shown in Figs. 10–20 (here let θ = 0.823). If θ = 1 (integer order), a Hopf bifurcation appears near the equilibrium point E3(0.4168, 0.1465). This result can be illustrated in Figs. 21–24.

Figure 13
figure 13

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\)and θ = 0.65. The equilibrium point (0.4168, 0.1465) of system (7.2) is asymptotically stable. The relation of t and u1(t).

Full size image
Figure 14
figure 14

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\)and θ = 0.65. The equilibrium point (0.4168, 0.1465) of system (7.2) is asymptotically stable. The relation of t and u2(t).

Full size image
Figure 15
figure 15

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\)and θ = 0.65. The equilibrium point (0.4168, 0.1465) of system (7.2) is asymptotically stable. The relation of u1(t) and u2(t).

Full size image
Figure 16
figure 16

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\)and θ = 0.65. The equilibrium point (0.4168, 0.1465) of system (7.2) is asymptotically stable. The relation of t, u1(t) and u2(t).

Full size image
Figure 17
figure 17

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\) and θ = 0.823 > θ0 = 0.778. Hopf bifurcation of system (7.2) appears from the equilibrium point (0.4168, 0.1465). The relation of t and u1(t).

Full size image
Figure 18
figure 18

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\)and θ = 0.823 > θ0 = 0.778. Hopf bifurcation of system (7.2) appears from the equilibrium point (0.4168, 0.1465). The relation of t and u2(t).

Full size image
Figure 19
figure 19

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\) and θ = 0.823 > θ0 = 0.778. Hopf bifurcation of system (7.2) appears from the equilibrium point (0.4168, 0.1465). The relation of u1(t) and u2(t).

Full size image
Figure 20
figure 20

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\) and θ = 0.823 > θ0 = 0.778. Hopf bifurcation of system (7.2) appears from the equilibrium point (0.4168, 0.1465). The relation of t, u1(t) and u2(t).

Full size image
Figure 21
figure 21

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\) and θ = 1. Hopf bifurcation of system (7.2) appears neasr the equilibrium point (0.4168, 0.1465). The relation of t and u1(t).

Full size image
Figure 22
figure 22

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\) and θ = 1. Hopf bifurcation of system (7.2) appears neasr the equilibrium point (0.4168, 0.1465). The relation of t and u2(t).

Full size image
Figure 23
figure 23

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\) and θ = 1. Hopf bifurcation of system (7.2) appears neasr the equilibrium point (0.4168, 0.1465). The relation of u1(t) and u2(t).

Full size image
Figure 24
figure 24

The trajectories of system (7.2) with \({\gamma }_{1}=0.999,{\gamma }_{2}=0.9,{\gamma }_{3}=0.2,{\gamma }_{4}=\frac{25}{9},\kappa =\frac{500}{499},\sigma =0.255,\) \({\rho }_{1}=0.2,{\rho }_{2}=1.1,{\rho }_{3}=0.25,{\rho }_{4}=1\) and θ = 1. Hopf bifurcation of system (7.2) appears neasr the equilibrium point (0.4168, 0.1465). The relation of t, u1(t) and u2(t).

Full size image

Conclusions

In this article, we have discussed a fractional order predator-prey model with group defense. Some sufficient conditions that guarantee the the existence, uniqueness and boundness of solution, the stability of equilibrium point and the existence of Hopf bifurcation of the considered fractional order predator-prey model are established. The study shows that under some suitable parameter conditions, the various equilibrium points are locally asymptotically stable, when the parameter θ cross the critical value, the Hopf bifurcation will appear. The research also reveal that the fractional order has an important effect on the stability and the existence of Hopf bifurcation of the involved fractional order predator-prey model. At last, computer simulations are performed to illustrate the theoretical results. Numerical simulation results show that Hopf bifurcation value of Example 7.1 is θ0 = 0.83 and Hopf bifurcation value of Example 7.2 is θ0 = 0.778. The obtained results of this article can be applied to keep the coexistence of biological populations and maintain ecological balance. In addition, we must point out that time delay often exist in predator-prey system. But we still do not consider this case. We will deal with the dynamical behavior of fractional order delayed predator-prey models in the near future.