Introduction

Recognition of the potential of artificial intelligence (AI) techniques for clinical modelling and decision-making in medicine and psychiatry is increasing. Simultaneously, there is growing interest in understanding psychological disorders as complex systems, with emergence of the network approach to psychopathology1,2. Novel statistical methods reflecting the multifarious influences on, and dynamic nature of, psychopathology are needed to provide greater insight in complex mental health trajectories3. McGorry et al.3 highlight the need for new diagnostic and early identification strategies to overcome limitations of current analytic approaches, calling for innovative modelling and prediction strategies for mental health outcomes. Bayesian methods are increasingly employed in various statistical frameworks in psychology and related disciplines, including hypothesis testing, item response theory, and structural equation modelling4. Bayesian networks (BN) offer a systems approach to modelling risk and supporting decision making in complex domains, such as mental health trajectories5,6. Here we present a prototype BN for risk of psychological distress, based on self-reported lifestyle and psychosocial variables from a community-derived cohort of 12-year-old adolescents.

Network perspective on psychopathology

The network approach to psychopathology is experiencing a surge of interest since its emergence in the last 10–15 years7,8,9, conceivably due to factors such as an exponential rise in data availability and moves in science and medicine away from reductionism and towards a systems perspective. The approach is based on the view that mental disorders arise as a result of complex interactions between psychological, biological and sociological elements, in conjunction with risk factors and symptoms. Patterns of interaction can be observed in a network structure, in which variables (e.g., symptoms, comorbidities, environmental or risk factors) are represented as nodes connected by arcs, implying the existence of a statistical association. Freese and Baer-Bositis10 describe psychopathology as networks of ‘problems’—adverse social, psychological, and genetic influences in individuals—connected by causal arcs, with the network approach facilitating focus on priority interventions or treatment targets to prevent propagation of problems. Isvoranu11 also suggests that personalised network modelling could be beneficial for intervention planning in psychotic disorders.

Bayesian networks (BN)

BN are powerful risk assessment tools, particularly valuable for reasoning under uncertainty5,12, and are increasingly recognised as useful for prediction in complex systems such as environmental and health domains13. Importantly, Bayesian methods are able to produce reasonable results even with small to moderate sample sizes, particularly when robust prior information is available14,15.

A BN is a probabilistic graphical model representing a set of variables and their conditional dependencies via a directed acyclic graph (DAG). The variables, represented as nodes, are connected by directed arcs implying causality5,6,12. In a DAG, nodes with no parents are referred to as root nodes. If there is a directed arc from node Y to node Z, Y is said to be a parent of Z; likewise, Z is called a child of Y. Chance nodes in a BN have a number of user-defined ‘states’ that can be qualitative or discrete (e.g., ‘Yes/No, ‘High/Low’, ‘ > 5/ ≤ 5’). Conditional probabilities are assigned to each state, derived from data, simulation, or expert opinion, and algorithms compute the joint probability distribution of the network. Once quantified, BN can simulate multiple risk pathways or intervention scenarios, providing conditional probability of mental health outcomes. This interactive function of BN is achieved by changing the evidence ‘conditions’ in the network, wherein the BN is instantly updated. The many applications of BN models include comparing relative risks of scenarios, studying interactions between variables, quantifying the strength of associations, revealing obscure relationships and identifying sensitivities for target nodes.

BN are widely used in medicine for individual-level risk estimation and decision support16, and are increasingly employed in psychology, psychiatry and neuroscience17,18,19,20,21. BN offer a systems approach to decision making under uncertainty in complex domains5,6 boasting several advantages over traditional analytical techniques. In a comparative evaluation of frequentist and machine learning methods (BN) in a clinical trial of pravastatin, Cleophas and Zwinderman22 concluded that, compared with frequentist methods (t-tests, linear regressions), the machine learning methods provided better sensitivity of testing, were robust with respect to overfitting, efficient in describing multivariate distributions, and were more informative.

The longitudinal adolescent brain study

The Longitudinal Adolescent Brain Study (LABS) commenced in July 2018 with the goal of monitoring changes in social, demographic, cognitive and psychological factors thought to influence or reflect mental health status in adolescents. Building on our precedent work23, the current paper examines interactions between risk and protective factors from participants’ self-report data, with the aim of better understanding the inter-relationships of self-reported states and influences on mental health. We present a prototype BN for risk of psychological distress for a community-derived sample of 12-year old adolescents, based on early findings from data in the first year of LABS. The BN explores relationships between risk factors able to be externally modulated (sleep, physical activity, social connectedness, eating behaviours), measures of internal homeostasis (impulsivity, metacognition, mindfulness), and an established measure of psychological distress (Kessler Psychological Distress Scale; K10), with the aim of exploring influences on risk of psychological distress in this sample.

Method

Study design and setting

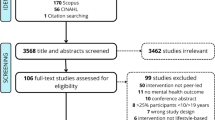
The LABS enrols young people from the general population who are in their first year of high school (grade 7), from a range of public, private and independent schools in the local community. Young people and their caregivers are invited to contact LABS if they are interested in participating in the study. The study protocol was approved by the Human Research Ethics Committee, University of the Sunshine Coast (A181064). Informed consent was obtained from individual participants and their caregivers and the study was conducted in accordance with the Declaration of Helsinki. Participants were assessed at baseline and invited to return for assessments every four months for five years during the high school years. This paper focuses on data from the self-report questionnaire collected at baseline, during the first eight months of the study, at which point this paper was written. At this time in the study, 129 expressions of interest in participating had been received. Of these, 94 potential participants were screened, and 68 participants were enrolled in the study. At the time of this paper, n = 64 participants had completed their baseline assessment.

Inclusion and exclusion criteria

Young people aged 12 years 0 months to 12 years 11 months, living in the Sunshine Coast region were included in the study. Young people with a major neurological disorder (e.g., epilepsy), intellectual disability, major medical illness, or who had sustained head injury with loss of consciousness > 30 min were excluded from the study.

Data collection and preparation

The self-report questionnaire was administered to participants on a touch screen tablet, using the Qualtrics survey platform (Qualtrics, Provo, UT, USA 2019). The SPSS version 24.0 (IBM Corp 2016) was used for data preparation in conjunction with the Python programming package SciPy 1.4.124.

Variables used in the current study

The selection of variables for the current study was informed by our previous work23, examining associations between intrinsic and extrinsic variables thought to influence, or be influenced by, psychological distress. Variables from the LABS used in the current study are described in Table 1. The complete set of variables from the LABS self-report questionnaire is detailed elsewhere23.

Table 1 LABS variables used to model risk of psychological distress.
Full size table

Model structure and parameterisation

A conceptual model was created using GeNIe 2.3.3828.0 (BayesFusion, LLC; http://www.bayesfusion.com/). Selection of variables for the conceptual model in the current study was informed initially by our previous work23, examining associations between measures of intrinsic homeostasis and extrinsic modulators thought to influence (or be influenced by) psychological distress. The structure of the conceptual model was developed iteratively from the complete suite of LABS self-report variables, guided by the domain knowledge of the LABS team, with the primary aim of studying the interacting effects of self-reported risk and protective factors on chance of psychological distress. Parsimony, a primary goal in BN design, where the simplest structure to describe the system being studied is the best31, was a guiding principle in model development.

The primary outcome measure chosen was psychological distress, measured by the K10, with other self-report variables used as inputs to the model. Dichotomous states were chosen for all variables except the outcome variable, K10, where established categories were used28,32. Threshold ranges for node states (Table S1, supplementary file) were selected where possible from validated ranges in the literature. Eleven measures without validated ranges were discretised using percentiles of the possible range for each measure (< 50th, and ≥ 50th for low and high categories, respectively). The states of parentless or root nodes were parameterised using frequency distributions from the LABS data. The conditional probabilities underlying child nodes in the BN were derived using Bayes' theorem, which evaluates the probability of an event, based on conditions that are thought to influence the event. Mathematically, Bayes’ theorem is represented by:

$$ \begin{array}{*{20}c} {P\left( {B{|}A} \right) = \frac{{P\left( {A{|}B} \right)P\left( B \right)}}{P\left( A \right)} } \\ \end{array} $$
(1)

where \(P\left( {B|A} \right)\) is the conditional probability of event \(B\), given that event \(A\) is true. Parameterisation of the states of child nodes was accomplished by calculating conditional probabilities from the data set. The BN model structure, and discretisation and parameterisation of nodes was reviewed and modified by domain experts from the disciplines of psychology and neurobiology and validated by mental health clinicians.

Model validation

The BN was evaluated through inference, scenario analysis and sensitivity analysis. Validation of model behaviour was accomplished by cross-checking the probabilities in the network with each other for consistency, such that if the probabilities in one node of the network were changed, the subsequent changes in probabilities of other nodes followed approximately as expected. Sensitivity analysis, described in the next section, completed the model validation procedures, in the absence of other Bayesian networks in this domain with which to compare model output33.

Baseline network and sensitivity assessment

The network in Fig. 1 presents the prior probability distribution of each node, computed from the relationships of influence and resulting conditional probabilities. Figure 1 thus represents the reference point for the network, i.e., before any further evidence is added. The value ascribed to a node state represents the chance that the node will be in that state. For example, in the study population at the baseline assessment, the chance of a participant being psychologically well as indicated by the psychological distress node is 83%, and as indicated in the physical activity node, the chance that a participant is less active is 11%. Sensitivity analysis of the model priors was conducted using an algorithm proposed by Kjaerulff and van der Gaag34 to give an indication of the relative importance of model inputs in terms of precision. The assessment showed that, in the absence of introduced evidence, the target node psychological distress was most sensitive to the modifiable node eating behaviours, followed by social connectedness, indicating that small changes in these nodes may lead to a large change in the posterior of the target node.

Figure 1
figure 1

Baseline Bayesian network for risk of psychological distress.

Full size image

Scenarios

An established practice in BN modelling is consideration of various scenarios (or queries), by setting evidence in input nodes, in order to draw conclusions about another node under those conditions. Evidence is introduced in a single node by selecting a node state. To complete model verification, the probability distribution in the outcome node is observed in response to varying combinations of parameters in input nodes. Multivariate scenarios are presented in the Results, demonstrating modelling of multiple influences on risk of psychological distress.

Statistical analysis

Categorical variables were described in terms of frequencies and percentages; continuous variables were summarised as means ± standard deviation (SD). To study the effect of new evidence introduced into the network on the chosen outcome measures, the percent change (\({\Delta }_{\%}\)) in each response node state was calculated as

$$ {{\Delta }_{\% } = \frac{{P_{\text{evidence}}- P_{\text{baseline}}}}{{P_{{{\text{baseline}}}} }} \times 100\% } $$
(2)

where \(P_{{{\text{baseline}}}}\) is the probability of occurrence of response node states under baseline network conditions before new evidence is introduced and \(P_{{{\text{evidence}}}}\) is the probability of a state occurring after new evidence is introduced into the network35.

Results

Sample description

64 participants aged 12 years and in grade 7 were recruited between July 2018 and February 2019. Forty seven percent (n = 30) of participants were female. The mean (SD) height for the sample was 157 (6.8) cm, the mean (SD) weight was 47 (9.5) kg and mean (SD) BMI was 19 (3.0). Fifty two percent of participants (n = 33) attended government schools, 20% of participants (n = 13) attended independent schools, 27% of participants (n = 17) attended religious schools and 1 participant attended distance education. Thirty one percent of participants (n = 20) had consulted a mental health professional at least once in their lifetime. Of these, seven participants had formal diagnoses for a developmental disorder—four participants had a diagnosis of autism spectrum disorder and three participants had been diagnosed as having ADHD. Four participants were taking psychopharmacological medication. Summary data (n = 64) from LABS used in the BN are presented in Table 2.

Table 2 LABS summary data used in BN for risk of psychological distress.
Full size table

Scenario analyses

Scenario 1 ‘certainty for psychological wellness’

In the first instance, it is of interest to determine the conditions for certainty that a participant will be psychologically well, simulated by setting the psychological distress node to 100% ‘well’. To ensure the query constraint, multiple parameters in the network changed simultaneously (Fig. 2). Table 3 summarises the percent change in each input node in response to the query constraint. The variables amenable to external modulation with the largest changes required to achieve the target of 100% certainty for a participant to be well were eating behaviours, social connectedness and physical activity. Risk factors such as cyberstrife and sleep were not as influential in achieving psychological wellness in this sample. This scenario, and the next, ‘certainty for severe psychological distress’, are examples of the ‘backwards reasoning’ ability of BN, whereby the required state in the outcome node psychological distress is specified, and the states of the network required to obtain the required outcome are determined using priors and Bayes' theorem.

Figure 2
figure 2

Bayesian network for Scenario 1 ‘certainty for psychological wellness’.

Full size image
Table 3 Scenario 1 ‘certainty for psychological wellness’, displaying changes in Bayesian network node states to achieve certainty of a participant being psychologically well.
Full size table

Scenario 2 ‘certainty for severe psychological distress’

We next explored network conditions for certainty of a participant having severe psychological distress, modelled by setting the psychological distress node to ‘100% severe’ (Fig. 3). The changes in states observed in ‘upstream’ nodes in response to this evidence are shown in Table 4. The modifiable variable with the largest influence in this scenario was social connectedness. With certainty of severe psychological distress, the chance of low social connectedness increased by 178%. At the same time the chance of the participant experiencing cyberstrife decreased by 18%, feasibly due to the influence of decreased social connectedness. These findings are reflected in the QOL social relationships node, where the chance of low quality of life regarding social relationships increased by 850%. Also of note in this scenario, high levels of impulsivity and metacognition increased by 113% and 213%, respectively.

Figure 3
figure 3

Bayesian network for Scenario 2 ‘certainty for severe psychological distress’.

Full size image
Table 4 Scenario 2 ‘certainty for severe psychological distress’, displaying changes propagated in Bayesian network with query constraint of severe psychological distress.
Full size table

Scenario 3 ‘certainty for less healthy eating behaviours’

Increasing the chance of a participant adopting less healthy eating behaviours to certainty (100%) had a marked effect on the chance of a participant being psychologically well, which decreased by 27% (Fig. 4). The chance of a participant having psychological distress of moderate severity increased more significantly, by 600%. Certainty for less healthy eating behaviours also had a significant effect on the chance of a participant having low quality of life with respect to physical health, which increased from baseline by 1550%. The changes in affected nodes are shown in Table 5.

Figure 4
figure 4

Bayesian network for Scenario 3 ‘certainty for less healthy eating behaviours’.

Full size image
Table 5 Changes from baseline in affected nodes with Scenario 3 ‘certainty for less healthy eating behaviours’.
Full size table

Scenario 4 ‘certainty for low social connectedness’

Setting the social connectedness node to ‘100% low’, indicating certainty for low social connectedness had the ‘downstream’ effect of increasing the chance of cyberstrife by 26%, increasing the chance of low quality of life with respect to social relationships by 850% and reducing the chance of a participant being psychologically well by 11%. Notably, certainty for low social connectedness also increased the chance of severe psychological disorder by 200%. The changes in affected nodes are shown in Table 6.

Table 6 Changes from baseline in affected nodes with Scenario 4 ‘certainty for low social connectedness’.
Full size table

Discussion

Using Bayesian analyses, this study sought to explicate the complex interactions between influences on mental health. Important findings that emerged were the conditions necessary for a participant to be certain of being psychologically well (Scenario 1). These conditions included a decrease in the chance of unhealthy eating behaviours by 33%; reduction in low social connectedness of 11%; and a decrease in the chance of less physical activity by 9%. Conversely, network conditions under which a participant was certain to be experiencing severe psychological distress (Scenario 2) included a 178% increase in the chance of low social connectedness, albeit accompanied by a decrease in the chance of cyberstrife by 18%.

The interactions between the social connectedness and cyberstrife nodes were particularly interesting. Certainty for low social connectedness (Scenario 4) alone resulted in an increased chance of cyberstrife. This result is consistent with the finding by McLoughlin et al.36, that cyberbully-victims experienced lower levels of social connectedness than those who had never been involved in cyberbullying as victim or bully. Nonetheless, the network conditions required for the query constraint in Scenario 3 (severe psychological distress), included an increased chance of low social connectedness, and decreased chance of cyberstrife. This situation, wherein evidence entered in a node varies in its effect depending upon network conditions, is illustrative of the ability of a BN to model the mutual distribution of all states in all nodes in the network, considering node dependencies and any new evidence introduced to the network simultaneously. Thus, regardless of model response to evidence introduction in a single node, the same evidence may prompt a different response in a multivariate scenario, contingent on the combination of evidence in other nodes. Notably, our study findings highlighted the substantial effect of eating behaviours on psychological distress as measured by the K10. Modelling a participant adopting less healthy eating behaviours by setting the ‘less healthy’ eating behaviours node state to certainty had the effect of decreasing the chance of the participant being psychologically well by 27%. This result corroborates other evidence supporting links between food and mood in adolescents, from Australia37,38,39 and elsewhere40,41,42.

Examination of the LABS data on eating behaviour showed that 38% (n = 24) of participants did not eat fruit every day; 52% of participants (n = 33) ate vegetables more than once a day, every day; 73% (n = 47) of participants ate sweets (candy or chocolate) more than once per week; 14% (n = 9) of participants had soft drinks containing sugar more than once a week; 35% (n = 22) of participants didn’t have breakfast on at least one weekday, and 25% (n = 16) skipped breakfast on at least one weekend day. These insights, in conjunction with the probabilistic modelling of the interaction between eating behaviour and psychological distress evident in our community-derived sample of 12-year-olds, are indicative of strong potential for risk reduction strategies.

As we have shown, modelling of psychosocial and lifestyle data using BN provides rich insights into networks of risk and protective factors for psychopathology in young adolescents. BN can be built and estimated in several ways and used to examine simultaneous changes in variables and relative risks during scenario comparisons. A BN can reveal obscure relationships between variables and generate sensitivity profiles for different target nodes. BN probabilities are updated immediately when evidence is entered and the interactive, visual platform presents scenario outcomes plainly to users, regardless of their discipline. The ability of BN to present and evaluate multivariate scenarios is particularly beneficial in analysing complex systems. Hence BN, when used as probabilistic decision support systems, can complement clinician judgement in mental disorders with prediction and weighing treatment options43,44. The full potential of the BN methodology in a complex systems approach to psychopathology, with benefits for multidisciplinary teams, has yet to be realised.

Limitations in the current study suggest potential future directions for BN modelling in psychopathology research. Firstly, the network developed for the purposes of this study was constructed using variables derived from a self-report questionnaire administered to a self-selected sample of 12-year-old adolescents; our inferences about model behaviour must therefore be qualified accordingly. Secondly, the current study employs data from a single timepoint; incorporation of longitudinal data would enable assessment of the temporal role on risk and protective factors, symptoms and neurobiology. Thirdly, the BN presented here is a simple prototype, developed to demonstrate the potential of the approach in this domain. Further research could include inputs from other dimensions, such as indicators of functional impairment, neuroimaging biomarkers, measures of cognition, clinical inputs such as formal diagnoses, lifestyle factors such as screen time, and demographic variables such as family history of mental illness. Input nodes such as eating behaviours which are shown to have large impacts on target nodes can be modelled in more detail, with inclusion as sub models.

Lastly, small sample size is a limitation in the current study. However, LABS is a longitudinal study, aiming to recruit 500 participants in total. The BN presented here should be replicated, with a larger sample size. A larger sample size will also enable examination of gender differences.

The BN modelling in this study yielded both novel and previously validated findings regarding influences and risk factors for risk of psychological distress in adolescents. BN are sophisticated tools which can optimise use of multidimensional data in our understanding of psychopathology, transcending reductionism and biomedical approaches, and producing new perspectives and actionable insights in an indisputably complex field.