Introduction

Heat transfer process is the process which is concerned with conversion and exchange of thermal energy and heat between the systems. Heat transfer is classical field into various mechanisms such as thermal convection, transfer of energy by phase changes, thermal convection, and thermal radiation. The transfer of heat occurs due to bulk movement of the fluid (liquid and gasses) which carries along them with flow of matter in the fluid. On the other side mass transfer is collective movement of the mass form one location, usually meaning stream, fraction or components phase changes to one another. Mass transfer occurs in many processes such as evaporation, drying, absorption, precipitation, membrane filtration and distillation. The combined phenomena of heat and mass transfer occur in engineering for physical processes which are concerned with diffusive and convective transport of chemical species. The term of Arrheniuous activation energy was introduced by Svante Arrhenius in 1889.This is the energy which is required to produce the chemical reaction with potential reactants. Exothermic chemical reactions are the processes which require or give off. Highly exothermic chemical reactions are needed to thrust spacecraft into air. White plumes following the craft are reaction produce gasses dispersing aluminum oxide. The combination of mixed convection flow and catalytic chemical reactions has so many applications in engineering especially in chemical engineering, thermal engineering and industry. The above said mechanisms attracted much attention of the researchers on different flow geometries and flow conditions.

Pop and Thakar1 encountered the phenomena of free convection flow over the curved surface theoretically. A note on mechanism of self-similar natural convection flow from a heated curved surface has been considered by Magyari et al.2. Maleque3 focused on magnetohydrodynamics natural convection flow numerically. He included the effects of radiation, exothermic/endothermic chemical reaction, activation energy and magnetic field simultaneously in his study. Similarity solutions of mixed convection flow along a vertical plate with slip flow conditions are computed by Krishnendu et al.4. Bachok et al.5 investigated numerically the mixed convection flow along the vertical flat plate in the external fluid flow considering the effects of viscous dissipation. Hayat et al.6 proposed the novel study of Marangoni mixed convection flow coupled with radiation and Joule heating effects. They also took into account the impacts of inclined magnetic field and viscous dissipation impacts. MHD mixed convection flow along the vertical plate with convective boundary conditions along with heat source and chemical has analyzed by Rajeswari and Manjum7. The numerical investigations on unsteady mixed convection flow along the surface of a sphere with dissipation effects have been studied by Ashraf et al.8. Okehi et al.9 addressed the boundary layer flow induced by exponentially stretched curved surface in the presence of dissipation effects. They solve the self-similar equations by using shooting and R–K methods.

Theoretical analysis on boundary layer flow along the curved stretching surface under the convective boundary conditions of heat and mass transfer has been conducted by Hayat el al.10. Computational treatment of natural convection flow along the curved surface in the presence of catalytic chemical reaction has been done by Ashraf et al.11. Unsteady mixed convection flow along the infinite length with the combined impacts of activation energy and binary chemical reaction has been addressed by Dhlamini et al.12 and highlighted the influences of thermophoresis, Brownian motion and viscous dissipation. Discussion on mixed convection flow coupled with and thermophoresis phenomena along with the effects of temperature dependent viscosity, thermal conductivity, and heat generation effects along the surface of a sphere has been conducted in13,14,15,16. The fluid flow of nanofluid due to rotating disk with the consideration of activation energy and magnetic field has been addressed in by Alghamdi17. Uzma and Ashraf18 tackled the problem of natural convection flow under the impact of exothermic catalytic chemical reaction along with the viscous dissipation effects on curved surface. Zia et al.19 have taken in to account the problem of mixed convection oscillatory flow along the non-conducting cylinder under the influence of thermal stratification. Chudhary and Kanika20 studied the phenomena of nanofluid flow along the particle shape over exponential temperature with the effect of thermal radiation, magnetic field and viscous dissipation. Heat and mass transfer analysis of MHD flow through porous medium along infinite plate has been conducted by Krishna et al.21. Saeed et al.22 focused their attention on nanofluid flow along the curved surface in the presence of magnetic field, chemical reaction and Arrhenius activation energy. Muhammad et al.23 proposed the model of fully developed flow Darcy–Forchheimer mixed convection flow along the curved surface in the presence of activation energy and entropy generation. Khan et al.24 investigated theoretically the phenomena of mixed convection flow equipped with entropy optimization, electric field, magnetic field and second order slip conditions. The computational study of heat transfer in mixed convection flow of blood based carbon nanotubes over the curved stretching surface has been conducted by Hayat et al.25.

Being motivated from the above said applications and literature review the current study is concerned with the mixed convection flow coupled with the exothermic catalytic chemical reaction along a curved surface. In the coming sections the mathematical model for the proposed problem will be established in terms of nonlinear partial differential equations and then the developed model will besolved by using finite difference method. The obtained numerical results in terms of the effects of different parameters on velocity profile, temperature distribution, mass concentration, skin friction, heat and mass transfer are displayed graphically. The novelty of the current work is to highlight the behavior above mentioned quantities along the curved surface.

Statement of the problem and mathematical formulation mathematical model and solution methodology

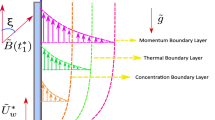
Consider steady, two dimensional, incompressible and mixed convection fluid flow along the curved surface in the presence of exothermic chemical reaction. The horizontal axis on the curved surface is assumed along x-axis and normal axis is taken along y-axis. The velocity components along horizontal and normal axis are u and v respecively. The graphical vision of the problem and the coordinate system of such a flow model are manifested in Fig. 1. The dimensionless flow model in terms of system of the coupled partial differential equations given as below:

Figure 1
figure 1

Coordinate system and flow configuration of the proposed model.

Full size image
$$\frac{\partial \stackrel{-}{u}}{\partial \stackrel{-}{x}}+\frac{\partial \stackrel{-}{v}}{\partial \stackrel{-}{y}}$$
(1)
$$\stackrel{-}{u}\frac{\partial \stackrel{-}{u}}{\partial \stackrel{-}{x}}+\stackrel{-}{v}\frac{\partial \stackrel{-}{u}}{\partial \stackrel{-}{y}}+\frac{{\stackrel{-}{u}}^{2}}{2x}\left(P(\stackrel{-}{x})+Q(\stackrel{-}{x})\right)=\frac{{\partial }^{2}\stackrel{-}{u}}{\partial {\stackrel{-}{y}}^{2}}+{\lambda }_{T}\theta +{\lambda }_{C}\phi$$
(2)
$$\stackrel{-}{u}\frac{\partial \theta }{\partial \stackrel{-}{x}}+\stackrel{-}{v}\frac{\partial \theta }{\partial \stackrel{-}{y}}=\frac{1}{Pr}\frac{{\partial }^{2}\theta }{\partial {\stackrel{-}{y}}^{2}}+\beta {\lambda }^{2}\left(1+n\gamma \theta \right)\theta {e}^{\frac{-E}{1+\gamma \theta }}$$
(3)
$$\stackrel{-}{u}\frac{\partial \phi }{\partial \stackrel{-}{x}}+\stackrel{-}{v}\frac{\partial \phi }{\partial \stackrel{-}{y}}=\frac{1}{Sc}\frac{{\partial }^{2}\phi }{\partial {\stackrel{-}{y}}^{2}}+{\lambda }^{2}\left(1+n\gamma \theta \right)\phi {e}^{\frac{-E}{1+\gamma \theta }}$$
(4)

Dimensionless form of boundary conditions satisfied by the system of equations given in (1)–(4)

$$\begin{gathered} \bar{u} = 0, \quad \bar{v} = 0, \quad \theta = 1, \quad \phi = 1 \quad at \quad \bar{y} = 0 \hfill \\ \bar{u} \to 1, \quad \hat{\theta } \to 0, \quad \phi \to 0 \quad as \quad \bar{y} \to \infty . \hfill \\ \end{gathered}$$
(5)

These are the dimensionless variables used in the above equations

$$\begin{aligned} & \bar{x} = \frac{x}{l},\quad \bar{y} = \frac{y}{l}Re_{L} ^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} ,\quad \bar{u} = \frac{u}{{U_{s} }},\quad \bar{v} = \frac{v}{{U_{\infty } }}Re_{l} ^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} , \\ & \theta = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\quad \phi = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}. \\ \end{aligned}$$
(6)

We also define the velocity scale, Grashof number and Reynolds number as

$$\begin{aligned} & \Delta T = T_{w} - T_{\infty } ,\quad \Delta C = C_{w} - C_{\infty } ,\quad U_{s} = \left( {g_{x} \beta \Delta Tl} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} ,\quad Gr = \frac{{g_{x} \beta \Delta Tl^{3} }}{{\nu ^{2} }}, \\ & Gr^{*} = \frac{{g_{x} \beta \Delta Cl^{3} }}{{\nu ^{2} }},\quad Re_{l} = \frac{{U_{s} l}}{\nu } \\ \end{aligned}$$

In the above equations, \({\lambda }_{T}=\frac{{Gr}_{l}}{{Re}_{l}^{2,}}\) is the mixed convection parameter, also known as, \({\lambda }_{C}=\frac{{Gr}_{l}^{*}}{{Re}_{l}^{2}}\) is the modified mixed convection parameter, \(\beta =1\) is the exothermic. The symbol \({\lambda }^{2}=\frac{{k}_{r}^{2}l}{{U}_{s}}\) is the dimensionless chemical reaction rate constant,where \({k}_{r}^{2}\) is the chemical reaction rate constant, \(l\) is the characteristic length. The notations \(\gamma =\frac{{T}_{w}-{T}_{\infty }}{{T}_{\infty }}\) is the temperature relative parameter, \(E=\frac{{E}_{a}}{k{T}_{\infty }}\) is the dimensionless activation energy, with \({E}_{a}\) as the activation energy and \(k=1.380649\times {10}^{-23}\) JK−1 is the Boltzman constant. Moreover, Pr = \(\frac{\nu }{\alpha }\) is the Prandtl number and Sc = \(\frac{\nu }{{D}_{m}}\) is the Schmidt number respectively.

Also \(P(\stackrel{-}{x})\), the wall temperature function and the body shape function \(Q(\stackrel{-}{x})\) are defined as (see detail5)

$$P\left( {\bar{x}} \right) = \frac{{dlnT_{s} }}{{dlnxl}},\quad Q\left( {\bar{x}} \right) = \frac{{dlng_{x} }}{{dlnxl}}$$
(7)

where It is important to point out that the system of partial differential equations given in (1)–(4) formulates a general mathematical form which is suitable for mixed convection flow over heated body of an arbitrary curved shape in the presence of exothermic catalytic chemical reaction. For the special case in which both \(P(x)\) and \(Q(x)\) are constants namely, \(m\) and \(n\), which satisfy the relation \(m+n=1\) (see5). Thus we have the following power functions along \(x\)-axis of the surface temperature and the tangential component of acceleration

$$g_{x} \sim x^{n} ,\quad \Delta T\sim ~x^{m}$$
(8)

Under the conditions given in (7) and (8), the conservation Eqs. (2)–(4) along with boundary conditions (5) (by dropping bars) take the following form

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$
(9)
$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\stackrel{\sim }{n}\frac{{u}^{2}}{2x}=\frac{{\partial }^{2}u}{\partial {y}^{2}}+{\lambda }_{T}\theta +{\lambda }_{C}\phi ,$$
(10)
$$u\frac{{\partial \theta }}{{\partial x}} + v\frac{{\partial \theta }}{{\partial y}} = \frac{1}{{Pr}}\frac{{\partial ^{2} \theta }}{{\partial y^{2} }} + \beta \lambda ^{2} \left( {1 + n\gamma \theta } \right)\theta e^{{\frac{{ - E}}{{1 + \gamma \theta }}}} ,$$
(11)
$$u\frac{\partial \phi }{\partial x}+v\frac{\partial \phi }{\partial y}=\frac{1}{Sc}\frac{{\partial }^{2}\phi }{\partial {y}^{2}}+{\lambda }^{2}\left(1+n\gamma \theta \right)\phi {e}^{\frac{-E}{1+\gamma \theta }}$$
(12)

Subject to the boundary conditions

$$\begin{aligned} & u = 0,\quad v = 0,\quad \theta = 1,\quad \phi = 1\quad at\quad y = 0 \\ & u \to 1,\quad \theta \to 0,\quad \phi \to 0\quad as\quad y \to \infty . \\ \end{aligned}$$
(13)

Primitive variable formulation

To create the straight forwardness in the above equations for numerical algorithm on computer, we use the following transformation variables known as primitive variable formulation. The primitive variables formulation for dependent and independent variables is given below:

$$u = U\left( {X,Y} \right),\quad v = x^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} V\left( {X,Y} \right),\quad x = X,\quad y = x^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Y,\quad \theta = \Theta \left( {X,Y} \right),\quad \phi = \Phi \left( {X,Y} \right)$$
(14)

By using Eq. (14) into Eqs. (9)–(12), we have

$$X\frac{{\partial U}}{{\partial X}} - \frac{Y}{2}\frac{{\partial U}}{{\partial Y}} + \frac{{\partial V}}{{\partial Y}} = 0,$$
(15)
$$\frac{n}{2}U^{2} + XU\frac{{\partial U}}{{\partial X}} + \left( {V - \frac{{YU}}{2}} \right)\frac{{\partial U}}{{\partial Y}} = \frac{{\partial ^{2} U}}{{\partial Y^{2} }} + \lambda _{T} \Theta + \lambda _{C} \Phi ,$$
(16)
$$XU\frac{{\partial \Theta }}{{\partial X}} + \left( {V - \frac{{YU}}{2}} \right)\frac{{\partial \Theta }}{{\partial Y}} = \frac{1}{{Pr}}\frac{{\partial ^{2} \Theta }}{{\partial Y^{2} }} + \beta \lambda ^{2} \left( {1 + n\gamma \Theta } \right)\left( {1 - E + E\gamma \Theta } \right)\Theta ,$$
(17)
$$XU\frac{{\partial \Phi }}{{\partial X}} + \left( {V - \frac{{YU}}{2}} \right)\frac{{\partial \Phi }}{{\partial Y}} = \frac{1}{{Sc}}\frac{{\partial ^{2} \Phi }}{{\partial Y^{2} }} + \lambda ^{2} \left( {1 + n\gamma \Theta } \right)\left( {1 - E + E\gamma \Theta } \right)\Phi .$$
(18)

The transformed boundary conditions are

$$\begin{aligned} & U = 0,\quad V = 0,\quad \Theta = 1,\quad \Phi = 1\quad at\quad Y = 0 \\ & U \to 1,\quad \Theta \to 0,\quad \Phi \to 0\quad as\quad Y \to \infty \\ \end{aligned}$$
(19)

Discretization

The above system of transformed boundary layer equations are solved with application of finite difference method. With the use of finite difference method the differential equations are transformed into algebraic system of equations which are kwon as discretized form of equations

$$\frac{{\partial U}}{{\partial X}} = \frac{{U_{{i,j}} - U_{{i,j - 1}} }}{{\Delta X}},\quad \frac{{\partial U}}{{\partial Y}} = \frac{{U_{{i + 1,j}} - U_{{i - 1,j}} }}{{2\Delta Y}},\quad \frac{{\partial ^{2} U}}{{\partial Y^{2} }} = \frac{{U_{{i - 1,j}} - 2U_{{i,j}} + U_{{i + 1,j}} }}{{\Delta Y^{2} }}$$
(20)
$${V}_{i+1,j}={V}_{i-1,j}-2\frac{\Delta Y}{\Delta X}{X}_{i}\left({U}_{i,j}-{U}_{i,j-1}\right)+\frac{{Y}_{j}}{2}\left({U}_{i+1,j}-{U}_{i-1,j}\right),$$
(21)

Momentum equation

$$A_{1} U_{{i - 1,j}} + B_{1} U_{{i,j}} + C_{1} U_{{i + 1,j}} = D_{1} ,$$
(22)

where

$${A}_{1}=1+\frac{\Delta Y}{2}\left({V}_{i,j}-\frac{{U}_{i,j}{Y}_{j}}{2}\right),$$
$${B}_{1}=\left[\frac{1}{2}-\frac{{X}_{i}}{\Delta X}\right]\Delta {Y}^{2}{U}_{i,j}-2,$$
$${C}_{1}=1-\frac{\Delta Y}{2}\left({V}_{i,j}-\frac{{U}_{i,j}{Y}_{j}}{2}\right),$$
$$D_{1} = - \frac{{X_{i} }}{{\Delta X}}\Delta Y^{2} U_{{i,j}} U_{{i,j - 1}} - \Delta Y^{2} \left( {\lambda _{T} \Theta _{{i,j}} + \lambda _{C} \Phi _{{i,j}} } \right).$$

Energy equation

$$A_{2} \theta _{{i - 1,j}} + B_{2} \theta _{{i,j}} + C_{2} \theta _{{i + 1,j}} = D_{2} ,$$
(23)

where

$${A}_{2}=\frac{1}{Pr}+\frac{\Delta Y}{2}\left({V}_{i,j}-\frac{{U}_{i,j}{Y}_{j}}{2}\right),$$
$$B_{2} = - \frac{2}{{Pr}} - \frac{{X_{i} }}{{\Delta X}}\Delta Y^{2} U_{{i,j}} + \beta X_{i} \lambda ^{2} \Delta y^{2} \left( {1 + n\gamma \Theta _{{i,j}} } \right)\left( {1 - E + E\gamma \Theta _{{i,j}} } \right),$$

\({C}_{2}=\frac{1}{Pr}-\frac{\Delta Y}{2}\left({V}_{i,j}-\frac{{U}_{i,j}{Y}_{j}}{2}\right),\)

$$D_{2} = - \frac{{X_{i} }}{{\Delta X}}\Delta Y^{2} U_{{i,j}} \Theta _{{i,j - 1}}$$

Mass equation

$$A_{3} \Phi _{{i - 1,j}} + B_{3} \Phi _{{i,j}} + C_{3} \Phi _{{i + 1,j}} = D_{3} ,$$
(24)

where

$${A}_{3}=\frac{1}{Sc}+\frac{\Delta Y}{2}\left({V}_{i,j}-\frac{{U}_{i,j}{Y}_{j}}{5}\right),$$
$$B_{3} = - \frac{2}{{Sc}} - \frac{{{\text{X}}_{{\text{i}}} }}{{\Delta X}}\Delta Y^{2} U_{{i,j}} + X_{i} \lambda ^{2} \Delta y^{2} \left( {1 + n\gamma \Theta _{{i,j}} } \right)\left( {1 - E + E\gamma \Theta _{{i,j}} } \right),$$
$${C}_{3}=\frac{1}{Sc}-\frac{\Delta Y}{2}\left({V}_{i,j}-\frac{{U}_{i,j}{Y}_{j}}{5}\right),$$
$$D_{3} = - \frac{{X_{i} }}{{\Delta X}}\Delta Y^{2} U_{{i,j}} \Phi _{{i,j - 1}} .$$

The discretized boundary conditions are

$$\begin{aligned} & U_{{i,j}} = 0,\quad {\text{V}}_{{{\text{i}},{\text{j}}}} = 0,\quad \theta _{{{\text{i}},{\text{j}}}} = 1,\quad \Phi _{{{\text{i}},{\text{j}}}} = 1\quad {\text{at}}\quad {\text{Y}}_{{\text{j}}} = 0 \\ & U_{{i,j}} \to 1,\quad \theta _{{i,j}} \to 0,\quad \Phi _{{i.j}} \to 0\quad as\quad Y_{j} \to \infty . \\ \end{aligned}$$
(25)

The foregoing governing equations together with the boundary conditions are solved numerically on a uniform mesh using Gauss elimination algorithm developed in previous study18. The discretization of the partial differential equations basically involved in second order central difference approximation for all diffusion terms and quick approximation for convective terms. The iterative calculations were continued until a relative convergence criterion of \({10}^{-5}\) was satisfied by all the field variables of the problem.

The obtained value of \(\left( {\frac{{\partial \uptheta }}{{\partial {\text{Y}}}}} \right)_{{{\text{Y}} = 0}}\) is compared with Pop and Takhar1 in the presence of mass transfer to ensure the validity of the procedure. The comparison results are demonstrated in Table 1 and found to be in very good agreement.

Table 1 The comparison of obtained results for \(\left( {\frac{{\partial \uptheta }}{{\partial {\text{Y}}}}} \right)_{{{\text{Y}} = 0}}\) by the present result and Pop and Takhar1 for Pr = 1.0 by keeping other parameters constant.
Full size table

Results and discussion

The current section is devoted for the detailed discussion about the physical behavior of the unknown physical quantities such as velocity profile \(U\), temperature distribution \(\theta\) and mass concentration \(\phi\) for several values of the appeared pertinent parameters in the flow model. The physical parameters involved in the flow model are body shape parameter \(n\), mixed convection parameter \({\lambda }_{T}\), modified mixed convection parameter \({\lambda }_{C}\), Prandtle number Pr, exothermic parameter \(\beta\), chemical reaction parameter \({\lambda }^{2}\), temperature relative parameter \(\gamma\), activation energy parameter \(E\), and Schmidt number Sc for which the numerical results of considered properties are computed and demonstrated graphically in Figs. 2, 3, 4, 5, 6, 7 and 8.

Figure 2
figure 2

Dimensionless (a) Velocity U, (b) Temperature \(\theta\) and (c) mass distribution \(\phi\) for different values of \({\lambda }_{T}=1.0,\) 10.0, 20.0, 50.0 while \(n=0.3,\) \(E=0.2\), \(\gamma =0.1\), \(\lambda =0.5\), \(\beta =0.5\), \({\lambda }_{c}=20\), Pr = 7.0, Sc = 0.6.

Full size image
Figure 3
figure 3

Dimensionless (a) Velocity \(U\), (b) temperature \(\theta\) and (c) mass distribution \(\phi\) for different values of \({\lambda }_{c}=0.1,\) 0.3, 0.5, 0.7 while \(n=0.3\), \(E=0.2\), \(\gamma =0.1\), \(\lambda =0.5\), \(\beta =0.5\), \({\lambda }_{T}=20\), Pr = 7.0, Sc = 0.6.

Full size image
Figure 4
figure 4

Dimensionless (a) Velocity \(U\), (b) temperature \(\theta\) and (c) mass distribution \(\phi\) for different values of \(n=0.1,\) 0.3, 0.35, 0.4 while \(E=0.5\), \(\gamma =0.1\), \(\lambda =0.5\), \(\beta =0.3\), \({\lambda }_{T}=1.0\), \({\lambda }_{c}=0.4\), Pr = 7.0, Sc = 0.2.

Full size image
Figure 5
figure 5

Dimensionless (a) Velocity \(U\), (b) temperature \(\theta\) and (c) mass distribution \(\phi\) for different values of Pr \(=0.1,\) 0.71, 1.0, 7.0 while \(n=0.3\), \(E=0.5\), \(\gamma =0.1\), \(\lambda =0.5\), \(\beta =0.5\), \({\lambda }_{T}=15.0\), \({\lambda }_{c}=10.0,\) Sc = 0.2.

Full size image
Figure 6
figure 6

Dimensionless (a) Velocity \(U\), (b) temperature \(\theta\) and (c) mass distribution \(\phi\) for different values of \(\beta =0.1,\) 0.3, 0.5, 0.7 while \(n=0.3\), \(E=0.2\), \(\gamma =0.2\), \(\lambda =0.4\), \({\lambda }_{T}=10.0\), \({\lambda }_{c}=10.0,\) Pr = 7.0, Sc = 0.2.

Full size image
Figure 7
figure 7

Dimensionless (a) Velocity \(U\), (b) temperature \(\theta\) and (c) mass distribution \(\phi\) for different values of \(\gamma =0.01,\) 0.25, 0.03, 0.05 while \(n=0.3\), \(E=0.8\), \(\gamma =0.2\), \(\lambda =0.5\), \(\beta =0.5\), \({\lambda }_{T}=15.0\), \({\lambda }_{c}=10.0,\) Pr = 7.0, Sc = 0.2.

Full size image
Figure 8
figure 8

Dimensionless (a) Velocity \(U\), (b) temperature \(\theta\) and (c) mass distribution \(\phi\) for different values of \(E=0.01,\) 0.03, 0.05, 0.1 while \(n=0.3\), \(\gamma =0.1\), \(\lambda =0.4\), \(\beta =0.5\), \({\lambda }_{T}=20.0\), \({\lambda }_{c}=8.0\), Pr = 7.0, Sc = 0.2.

Full size image

Figure 2a–c highlighted the physical behavior of profiles of velocity, temperature and concentration for various values of \({\lambda }_{T}\) keeping other dimensionless parameters fixed. The increase of mixed convection parameter clearly leads to significant increase in velocity profile and decrease in temperature distribution and mass concentration observed. It is interesting to note that the maximum values of velocity distribution at \({\lambda }_{T}=50.0\), temperature distributionat \({\lambda }_{T}=1.0\) and mass concentrationat \({\lambda }_{T}=1.0\) are achieved, and the obtained graphical results are satisfying the given boundary conditions at the surface and far from the surface in asymptotic manner. The fact is that the an increase \({\lambda }_{T}\) increase the buoyancy force which effect the speed of the fluid flow due to the ratio of temperature difference and inertial force. The graphical illustration of the above said properties for several values of modified mixed convection parameter \({\lambda }_{c}\) is presented in Fig. 3a–c. It is pertinent to highlight that as \({\lambda }_{c}\) is enhanced the velocity of the fluid reduces but opposite behavior for temperature and mass concentration is observed. The noted behavior of velocity was expected because as \({\lambda }_{C}\) is increased diffusion force increases which causes friction in velocity field. At \({\lambda }_{c}=0.1,{\lambda }_{c}=0.5\) and \({\lambda }_{c}=0.5\) the highest magnitudes for velocity distribution, temperature distribution and concentration profile are noted.

In Fig. 4a–c the effects of increasing values of body shape parameter \(n\) on the distribution of velocity and temperature along with mass concentration profile are highlighted. We can note from the obtained results that the decrease in velocity profile \(U\) but reverse mechanisms for temperature and mass concentration are observed.

The impact of different values of Pr on velocity profile, temperature and mass concentration are shown in Fig. 5a–c. It is concluded from the geometrical interpretation that velocity and temperature of the flow domain slow down but mass concentration is improved gradually.

Figure 6a–c, we have shown the variation of the corresponding velocity field, temperature distribution and mass concentration for several values of exothermic parameter \(\beta\). These functions are greatly influenced by the exothermic parameter \(\beta\), as \(\beta\) is increased, the velocity profile is maximum for \(\beta =0.1\) and minimum for \(\beta =0.3\), where the temperature and mass concentration are increased gradually.

The influence of temperature relative parameter \(\gamma\) on the velocity, temperature field and mass concentration is shown in Fig. 7a–c. We see that the velocity profile is maximum for \(\gamma =0.05,\) and this parameter shows its constant behavior for \(\gamma\) = 0.03, 0.05 in the case of temperature field and mass concentration. Finally, the variation of the velocity, temperature field and mass concentration with activation energy parameter E is illustrated in Fig. 7a–c. It can be seen that the velocity exceed for E = 0.05, and slight changes is noted for values of E in the case of mass concentration. Table 2 represents the effects of different values of mixed convection parameter \({\lambda }_{T}\), it is noted that for the increasing values of this parameter the skin friction is increased and rate of heat and mass transfer are decreased. Table 3 highlights the effect of body shape parameter n, it is observed that skin friction is maximum for n = 0.3 but rate of heat and mass transfer are maximum at n = 02. Table 4 shows the effects of different values of activation parameter E, it is estimated that the skin friction, rate of heat and mass transfer are increased simultaneously.

Table 2 Numerical results of skin friction \(\left( {\frac{{\partial {\text{U}}}}{{\partial {\text{Y}}}}} \right)_{{{\text{Y}} = 0}}\), rate of heat transfer \(\left( {\frac{{\partial \uptheta }}{{\partial {\text{Y}}}}} \right)_{{{\text{Y}} = 0}}\) and rate of mass transfer \(\left( {\frac{{\partial \upphi }}{{\partial {\text{Y}}}}} \right)_{{{\text{Y}} = 0}}\) for different values of \(\uplambda _{{\text{T}}}\) when Pr = 7.0, n = 0.3, \(\uplambda _{{\text{c}}} = 0.6\), \(\upgamma = 0.1\), \(\upbeta = 0.5\), \(\uplambda = 0.3,{\text{E}} = 0.4\).
Full size table
Table 3 Numerical results of skin friction \(\left( {\frac{{\partial {\text{U}}}}{{\partial {\text{Y}}}}} \right)_{{{\text{y}} = 0}}\), rate of heat transfer \(\left( {\frac{{\partial \uptheta }}{{\partial {\text{Y}}}}} \right)_{{{\text{Y}} = 0}}\) and rate of mass transfer \(\left( {\frac{{\partial \upphi }}{{\partial {\text{Y}}}}} \right)_{{{\text{Y}} = 0}}\) for different values of n when Pr = 7.0, \(\uplambda _{{\text{T}}} = 10.0\), \(\uplambda _{{\text{c}}} = 0.6\), \(\upgamma = 0.1\), \(\upbeta = 0.5\), \(\uplambda = 0.3\), E = 0.4.
Full size table
Table 4 Numerical results of skin friction \(\left( {\frac{{\partial {\text{U}}}}{{\partial {\text{Y}}}}} \right)_{{{\text{y}} = 0}}\), rate of heat transfer \(\left( {\frac{{\partial \uptheta }}{{\partial {\text{Y}}}}} \right)_{{{\text{Y}} = 0}}\) and rate of mass transfer \(\left( {\frac{{\partial \upphi }}{{\partial {\text{Y}}}}} \right)_{{{\text{Y}} = 0}}\) for different values of E when Pr = 7.0, \(\uplambda _{{\text{T}}} = 10.0\), \(\uplambda _{{\text{c}}} = 0.6\), \(\upgamma = 0.1\), \(\upbeta = 0.5\), \(\uplambda = 0.3\), n = 0.3.
Full size table

Conclusions

The numerical simulations have been conducted in order to examine the effects of different parameters involved in the flow model on some pertinent quantities that is velocity profile, temperature distribution, mass concentration, skin friction, heat and mass transfer along the curved surface by using finite difference method. The main findings are summarized as follows.

  • The increase in \({\lambda }_{T}\) increase the buoyancy force like pressure gradient thus the velocity profile is increased for highest value of \({\lambda }_{T}=50.0\), temperature profile, mass concentration are maximum for lower value \({\lambda }_{T}=1.0\). In addition, It is observed that skin friction increased, heat and mass transfer are decreased for increased values of \({\lambda }_{T}\).

  • The increase in \({\lambda }_{c}\) enhance the ratio mass concentration difference to dynamic viscosity which reduced the velocity of the fluid but opposite trend for temperature and mass concentration has observed.

  • For increasing values of body shape parameter \(n\) the velocity of the fluid is decreased and reverse mechanism for temperature profile and mass concentration has noted due to tangential effects of gravity. On the other hands, very interesting behavior for skin friction, heat and mass transfer have noted; the skin friction is maximum at n = 0.3, the heat and mass transfer are maximum for n = 0.2.

  • The velocity profile, temperature distribution and mass concentration are significantly influenced by the exothermic parameter \(\beta\), as \(\beta\) is increased, the velocity profile is maximum for \(\beta =0.1\) and minimum for \(\beta =0.3\), where the temperature and mass concentration are increased gradually.

  • It is observed that the velocity profile is maximum for \(\gamma =0.05,\) and this parameter shows its constant behavior for \(\gamma\) = 0.03, 0.05 in the case of temperature field and mass concentration.

  • It can be seen that the velocity exceed for energy activation parameter E = 0.05, and slight changes is noted for the case of temperature distribution and mass concentration. Further, it is very interesting to note that magnitude of skin friction, rate of heat and mass transfer are increased very prominently.