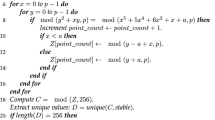Introduction

Information security is the protection of information and information systems from unauthorized access and manipulation. Block cipher has been a standout amongst the most reliable options by which data security is accomplished1,2. Block ciphers are deterministic cryptographic algorithms that operate on a plaintext block of n bits, to produce a block of cipher text of m bits. Here n and m length are not necessarily to same. Block cipher contains repeating rounds of key mixing, permutation and substitution layers, which make it difficult for cryptanalysis or attacks. Data Encryption Standard (DES) and Advanced Encryption Standard (AES) are the most famous examples of block cipher. For block ciphers such as AES and DES, linear and differential cryptanalysis attacks are considered as powerful attacks. These cryptanalysis attacks are based on probabilistic characteristics of cipher parameters and output. Such an attack identifies the strength of the encryption algorithm by exponentially growing the number of rounds. For example, a differential attack examines how the differences in input reflect as differences in output. The ultimate goal of the attacker is to find the non-random behavior of the output which helps the attacker to attack the algorithm. For this purpose, attacker tries to put specific set of inputs to trace the differences in the output of every round. In linear cryptanalysis, the attacker tries to learn the probabilistic linear relations between the parity bits of plaintext, cipher text, and the key, by running the cipher several times3,4. Responsibility to make the correlation between cipher text and the key, as undetectable as possible, is on Substitution box (S-box). An S-box is an m x n mapping S: {0, 1}m \(\to\){0, 1}n, transforming input vector x = [xn−1, xn−2, xn−3 … x0] into output vector y = [yn−1, yn−2, yn−3 … y0].

The noise of medical imaging which captured from multi sensors, multi-sources is an inevitable random phenomenon caused by the numerous intrinsic and inevitable switching factors including sensors temperature, spectral density, trap state, mobility fluctuation, charge trapping, free carriers, thermal motion of the ions, pulse sequence, field strength, charged particles scattering, optical density fluctuation and so on. Correlation and distribution of noise values captured from a single sensor, a single source of medical images is noticeably different from noise values that are captured from the multi-sensors, multi-sources. Noise captured from a single sensor and a single source has cohesiveness, more patterns, less uniform distribution compare to noise captured from the multi-sensors, multi-sources.

Remaining paper is organized as follows; "Contribution" section presents our core contribution; "Weaknesses in existing S-box designs" section describes weaknesses in existing s-box designs. "Proposed information fusion design" section explains the proposed multilevel information fusion for the construction of S-boxes. "Results and evaluation: S-box analysis" section presents the results and its evaluation; "Conclusion" section gives the concluding remarks.

Contribution

The main contribution of this research is summarized in the following:

  1. 1.

    First-time multilevel information fusion is introduced to construct the cryptographic substitution boxes.

  2. 2.

    Extraction of true random numbers from the inevitable random noise of medical imaging, to synthesize the multi-level information fusion, for the construction of substitution boxes.

  3. 3.

    We introduce a novel nonlinear multi features whitening technique.

  4. 4.

    The proposed design passes all substitution box security evaluation criteria including Nonlinearity, Bit Independence Criterion (BIC), Strict Avalanche Criterion (SAC), Differential Approximation Probability(DP), Linear Approximation Probability(LP), and Statistical tests including resistance to Differential Attack, Correlation Analysis, 2D,3D histogram analysis.

  5. 5.

    The substitution-boxes constructed from our proposed design does not bear weaknesses of algebraic structures and chaotic systems.

Weaknesses in existing S-box designs

In literature, extensively algebraic structures and chaotic systems-based methods are available for designing the S-boxes. Although algebraic and chaotic systems base approaches provide favourable characteristics for the S-box design, but researchers have also pointed weaknesses in these approaches. S-box designs of pure algebraic structures are jeopardized due to the intrinsic algebraic structure. Various algebraic attacks are available for algebraic construction of S-boxes including linear and differential attacks3,4,5,6,7,8,9,10,11,12,13,14,15,16,17, interpolation attacks18,19,20,21, Gröbner basis attack22,23,24,25,26,27,28, side-channel attacks29,30,31,32,33,34,35,36,37, SAT solver38,39,40,41,42,43,44,45, XSL attack18,46,47,48,49,50,51,52,53,54,55, XL attacks56,57,58,59,60.

Similarly, chaotic systems widely adopted in the designs of substitution boxes61,62,63,64,65,66,67,68,69,70,71,72,73,74. But due to the inherent algorithmic evolution of control parameters and periodic nature of chaotic maps, many weaknesses also exist in the literature, including discontinuity in chaotic sequences1,67,75,76,77,78, non-uniform distribution of chaotic sequences1,75,76,79,80, predictability66,81,82,83,84,85,86,87,88,89,90,91, finite precision effect1,75,78,92,93, dynamical degradation of chaotic systems61,78,92,93,94, small number of control parameters79,82,83,95, frail chaos67,94, short quantity of randomness1,11,67,75,76,77,79,80,84,92,93,96,97,98,99 Inherent intrinsic evolution of algebraic structures and its automorphism nature is an essential problem. Alternatively, researchers endorse the true random sequences for cryptography due to the fact that these sequences rely on the strength of naturally occurring processes to generate the true randomness100,101,102,103,104,105,106,107. True random sequences are irreversible, unpredictable, and unreproducible, even if their internal structure and response history are known to adversaries.

The objective of this research is extraction of true random numbers from the inevitable random noise of medical imaging, to synthesize the multi-level information fusion, for the construct of cryptographically strong substitution boxes.

Proposed information fusion design

The proposed design of multilevel information fusion for substitution boxes construction have four layers Multi Sources, Multi Features, Nonlinear Multi Features Whitening and Substitution Boxes Construction. The whole design is thoroughly explained in the following layers and depicted in Fig. 1.

Figure 1
figure 1

Multilevel information fusion for substitution boxes construction.

Full size image

Multi sources (L0: DAI-DAO)

This layer takes multiple medical imaging objects as input and gives raw objects to layer 1. One hundred medical imaging objects of random sources and random organs are taken from the UACI, Kaggle, SpineWeb, softnetaMedDream, OASIS, TCIA repositories.

Multi features (L1: DAI-FEO)

Noise is an inevitable random phenomenon caused by the numerous intrinsic and inevitable switching factors including sensors temperature, spectral density, trap state, mobility fluctuation, charge trapping, free carriers, thermal motion of the ions, pulse sequence, field strength, charged particles scattering, optical density fluctuation and so on. In this layer primary four types of noise features are extracted from the raw objects of layer 1. First type is Thermal noise which is an inevitable energy equilibrium fluctuation phenomenon caused by the thermal agitation of electrons in resistances. Thermal noise always presents in medical imaging sensors and devices pre-eminently in multimodality imaging. The spectrum of thermal noise is flat over a wide range of frequencies. Features of the thermal noise extracted using108,109. Second is shot noise which is caused by the fact that current flowing across a junction isn’t smooth but is comprised of individual electrons arriving at random times. This non-uniform flow gives rise to broadband white noise that gets worse with increasing average. Features of the shot noise extracted using106. Third is speckle noise, which is a multiplicative noise that accompanies all coherent imaging modalities, in which images are produced by interfering echoes of a transmitted waveform and backscattered reflection. Forth is impulse noise, which is the most common noise that exists in medical modalities. Normally, impulse noise generated during the image acquisition, storage and transmission. In impulse noise some of the pixels are replaced by outliers while the rest remain unchanged. This layer gives features of these four noises to layer 2. Features of the speckle noise and impulse noise extracted using88,110,111,112 respectively.

Nonlinear multi features whitening (L2: FEI-FEO)

Inherently various characteristics of the true randomness are existing in the noise features of medical imaging, which captured from multi sensors, multi-sources but these characteristics are unable to pass each NIST statistical randomness tests. In Table 1, we can see that various NIST randomness criteria failed, thus requiring a technique that is able to decrease the correlation, cohesiveness, and periodicity among multi-features, creating a highly random output that appears independent from multi-sources and uniformly distributed. To adhere to these requirements, we propose a technique called the “Nonlinear Multi Features Whitening”, which takes Multi features of the noise as input and returns uniformly distributed output that has no cohesiveness and calculable periodicity. The output of the proposed scheme has good statistical properties, including the elimination of statistical autocorrelation among multi-features. Thus, making the suggested multi-features fusion technique suitable for symmetric encryption.

Table 1 Noise features of medical imaging objects.
Full size table

The nonlinear multi features whitening design has two basic transformations: horizontal permutation and vertical permutation. This layer takes multi noise features including thermal, speckle, shot and impulse from the layer-1 and returns highly random output that appears independent from the input features. This layer also decreases the correlation, cohesiveness, and periodicity among the input features. The whole design of nonlinear multi features whitening thoroughly explained in the following steps and depicted in L2 of the Fig. 1.

Horizontal permutation

  • Step 1: Convert Thermal noise \(\left( {{\text{T}}_{{{\text{nf}}}} } \right)\), Speckle noise \(\left( {{\text{Sp}}_{{{\text{nf~}}}} } \right)\), Shot \(\left( {{\text{Sh}}_{{{\text{nf~}}}} } \right)\),Impulse noise \(\left( {{\text{I}}_{{{\text{nf}}}} } \right)\) values into their respective binary representation. Where vector \(x\) holds \({\text{T}}_{{{\text{nf}}}}\) binaries, vector \(z\) holds \({\text{Sp}}_{{{\text{nf~}}}}\) binaries, vector \(y\) holds \({\text{Sh}}_{{{\text{nf~}}}}\) binaries and \(w\) holds \({\text{I}}_{{{\text{nf}}}}\) binaries.

  • Step 2: Select the LSB of the \(x_{i}\) and check if the selected bit is ‘0’ then execute step-3 to step-8 and if the selected bit is ‘1’ then execute step-9 to step-14. A visual representation of the vector \(x,y\) pair and vector \(z,w\) pair are depicted in Fig. 2.

  • Step 3: If the frequency of 0's in leftmost 6 bits of \(x_{i}\) are greater than frequency of 0's in leftmost 6 bits of \({\text{y}}_{{\text{i}}}\) then permute twice the \(x_{i}\), \(z_{i}\), \(y_{i}\), \(w_{i}\) from left to right respectively.

  • Step 4: If the frequency of 0's in leftmost 6 bits of \(x_{i}\) are less than frequency of 0's in leftmost 6 bits of \(y_{i}\) then permute twice the \(y_{i}\), \(w_{i}\), \(x_{i}\), \(z_{i}\) from right to left respectively.

  • Step 5: If the frequency of 0's in leftmost 6 bits of \(x_{i}\) and leftmost 6 bits of \(y_{i}\) are the same then execute step-6 or step-7, accordingly.

  • Step 6: If the frequency of 0's in leftmost 6 bits of \(z_{i}\) are greater than frequency of 0's in leftmost 6 bits of \({\text{w}}_{{\text{i}}}\) then permute twice the \(z_{i}\), \(y_{i}\), \(w_{i}\), \(x_{i}\) from left to right respectively.

  • Step 7: If the frequency of 0's in leftmost 6 bits of \(z_{i}\) are less than frequency of 0's in leftmost 6 bits of \(w_{i}\) then permute twice the \(w_{i}\), \(y_{i}\), \(z_{i}\), \(x_{i}\) from right to left respectively.

  • Step 8: If the frequency of 0's in leftmost 6 bits of \(z_{i}\) and leftmost 6 bits of \({\text{w}}_{{\text{i}}}\) are same then discard the \(x_{i}\), \(z_{i}\), \(y_{i}\), \(w_{i}\).

  • Step 9: If the frequency of 1's in leftmost 6 bits of \(x_{i}\) are greater than frequency of 1's in leftmost 6 bits of \({\text{y}}_{{\text{i}}}\) then permute twice the \(x_{i}\), \(z_{i}\), \(y_{i}\), \(w_{i}\) from left to right, respectively.

  • Step 10: If the frequency of 1's in leftmost 6 bits of \(x_{i}\) are less than frequency of 1's in leftmost 6 bits of \(y_{i}\) then permute twice the \(y_{i}\), \(w_{i}\), \(x_{i}\), \(z_{i}\) from right to left respectively.

  • Step 11: If the frequency of 1's in leftmost 6 bits of \(x_{i}\) and leftmost 6 bits of \(y_{i}\) are the same then execute step-12 or step-13 accordingly.

  • Step 12: If the frequency of 1's in leftmost 6 bits of \(z_{i}\) are greater than frequency of 1's in leftmost 6 bits of \({\text{w}}_{{\text{i}}}\) then permute twice the \(z_{i}\), \(y_{i}\), \(w_{i}\), \(x_{i}\) from left to right respectively.

  • Step 13: If the frequency of 1's in leftmost 6 bits of \(z_{i}\) are less than frequency of 1's in leftmost 6 bits of \(w_{i}\) then permute twice the \(w_{i}\), \(y_{i}\), \(z_{i}\), \(x_{i}\) from right to left respectively.

  • Step 14: If the frequency of 1's in leftmost 6 bits of \(z_{i}\) and leftmost 6 bits of \({\text{w}}_{{\text{i}}}\) are also same then discard the \(x_{i}\), \(z_{i}\), \(y_{i}\), \(w_{i}\).

Figure 2
figure 2

Pairs of vectors \(x,y\) and vector \(z,w\).

Full size image

Vertical permutation

  • Step 1: Assign fused octet values according to the following:

    • 1st bit ← 2nd bit of \({\text{z}}_{{\text{i}}}\)

    • 2nd bit ← 1st bit of \(z_{{i + 1}}\)

    • 3rd bit ← 3rd bit of \(z_{{i - 1}}\)

    • 4th bit ← 4th bit of \(w_{{i + 1}}\)

    • 5th bit ← 5th bit of \(w_{{i - 1}}\)

    • 6th bit ← 6th bit of \(y_{{i + 1}}\)

    • 7th bit ← 7th bit of \(y_{{i - 1}}\)

    • 8th bit ← 8th bit of \(y_{i}\)

      A visual representation of vertical permutation depicted in Fig. 3.

  • Step 2: For variable ‘K’: Parse left-most 6 bits of the fused byte into corresponding decimal value.

  • Step 3: If 1st bit of the fused octet is ‘0’ then K times cyclically permute the \(column_{x}\) in the top to bottom manner.

  • Step 4: If 1st bit of the fused octet is ‘1’ then K times cyclically permute the \(column_{y}\) in the bottom to top manner.

  • Step 5: If 2nd bit of the fused octet is ‘0’ then K times cyclically permute the \(column_{z}\) in the top to bottom manner.

  • Step 6: If 2nd bit of the fused octet is ‘1’ then K times cyclically permute the \(column_{w}\) in the bottom to top manner.

Figure 3
figure 3

Vertical permutation.

Full size image

Substitution boxes construction (L3: FEI-DEO)

This layer takes highly correlated true random numbers from the L2 and generates substitution boxes. The complete design of this layer is thoroughly described in the following steps:

  • Step 1: Traverse each value of \(column_{x}\), \({\text{~}}column_{y}\), \({\text{~}}column_{z}\), and \({\text{~}}column_{w}\), row by row and then concatenate the subsequent rows in a one dimensional vector. A visual representation of steps 2 to 11 is depicted in Fig. 4.

  • Step 2: Split one-dimensional vector into blocks of 6 bytes. If the length of last block is less than 6 then exclude last block.

  • Step 3: Convert each block of step-2 into binary representation and then split into blocks of 3 bits.

  • Step 4: Get frequency of 0’s in every block which are obtained from step-3.

  • Step 5: Consider the block-0 to block-3 values of step-4 as the 1st row of matrix Map1.

  • Step 6: Consider the block-4 to block-7 values of step-4 as the 2nd row of matrix Map1.

  • Step 7: Consider the block-8 to block-11 values of step-4 as the 3rd row of matrix Map1.

  • Step 8: Consider the block-12 to block-15 values of step-4 as the 4th row of matrix Map1.

  • Step 9: To create the matrix Map2 : Traverse Map1 in the Z-order format. Consider quadrant NW as a 1st column, quadrant NE as a 3rd column, quadrant SW as 2nd column and quadrant SE as a 4th column of Map2.

  • Step 10: Traverse first 4 unique values of Map2 from row-major order.

  • Step 11: Sublevel-1 indexes assignment: Consider the values of step-10 as indexes of the first-4 unique elements which are obtained from step-2. A visual representation of the steps 12 to 14 is shown in the sublevel-1 of Fig. 5.

  • Step 12: To Get 1st \(right_{{index}}\): Use each index of the left most block to select a row of Map1 and the second left-most index of a block to select a column of Map1.

  • Step 13: To Get 2nd \(right_{{index}} {\text{~}}\): For first parameter, take index from step-12 and for second parameter, take the index of third left-most element which gained from step-11. Use first and second parameters to select a row and column of Map1.

  • Step 14: To Get 3rd \(right_{{index}}\): For first parameter, take index from step-13 and for second parameter, take the index of fourth left-most element which gained from step-11. Use first and second parameters to select a row and column of Map1.

  • Step 15: Get 1st permutated element of sublevel-2: To obtain index, execute the step-12 over Map2, except Map1, and get permutated element through the retrieved index. A visual representation of the steps 15 to 19 is shown in the sublevel-2 of Fig. 5.

  • Step 16: Get 2nd permutated element of sublevel-2: To obtain index, execute the step-13 over Map2, except Map1, and get permutated element through the retrieved index.

  • Step 17: Get 3rd permutated element of sublevel-2: To obtain index, execute the step-14 over Map2, except Map1, and get permutated element through the retrieved index.

  • Step 18: To Get 4th \(right_{{index}} {\text{~}}\): For first parameter, take the index of output of the step-15 and for second parameter, take the index of output of the step-16. Use first and second parameter to select a row and column of Map1.

  • Step 19: To Get 5th \(right_{{index}} {\text{~}}\): For first parameter, take the index of output of the step-18. For second parameter, take the index of output of the step-17. Use first and second parameters to select a row and column of Map1.

  • Step 20: Get 1st permutated element of sublevel-3: To obtain index, execute the step-14 over Map2, except Map1, by passing resultant values of step-18 and step-19 as parameters. Fetch permutated element through the retrieved index.

  • Step 21: To Get 6th \(right_{{index}} {\text{~}}\): Take index of the 1st permutated element of sublevel-3

  • Step 22: To acquire arbitrary bits of permutated elements: Obtain indexes from step-12 to step-14, step-18 to step-19, and step-21. Acquire the respective bits of permutated elements from these indexes.

  • Step 23: Get a most significant bit and least significant bit from the permutated element of step-15.

  • Step 24: Subsequently, generate σi, βi, γi, δi: Concatenate the bits of step-22 and step-23 thus parse these bits into their particular decimal value.

  • Step 25: Put values of σi, βi, γi, δi in linear fraction transform f (\(z_{i}\)) \(\mapsto\) (σi \(z_{i}\) + βi)/(γi \(z_{i}\) + δ1) where γi \(z_{i}\) =  − δ1 and σiδ1 − βiγi, ≠ 0. Remove repeating elements from the f (\(z_{i}\)) block of 256 size and transformed elements in a s-box of size 8 × 8.

Figure 4
figure 4

Visual representation of steps 2 to 11.

Full size image
Figure 5
figure 5

Visual representation of steps 15 to 19.

Full size image

Results and evaluation: S-box analysis

This section covers the results and evaluation of the results. The resultant S-boxes evaluated through the standard S-box evaluation criteria65,69,74,113,114,115,116,117,118,119,120,121,122,123,124 including Strict Avalanche Criterion (SAC), Bit Independence Criterion (BIC), Linear Approximation Probability(LP), Differential Approximation Probability(DP), Nonlinearity, and through the statistical tests including resistance to Differential Attack, Correlation Analysis, 2D, 3D histogram analysis. From the proposed design the total number of 4562 S-boxes constructed, where the nonlinearity of 821 S-boxes are less-than 109, the nonlinearity of 3728 S-boxes are equal to 110 and the nonlinearity of 13 S-boxes is equal to 112. Two S-boxes picked randomly from the resultant S-boxes as samples and shown in the Table 2a, b. The nonlinearity of S-boxes which are shown in Table 2a, b are 110 and 112 respectively.

Table 2 (a) Substitution box 1. (b) Substitution box 2.
Full size table

Nonlinearity

The nonlinearity is the ability of substitution box that provides immunity from the linear cryptanalysis and it is exhibited by the nonlinearity score1,128,129,142,145,154,155,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175. The nonlinearity of a substitution box h(x) described as the Walsh spectrum (WS):

$$ N_{h} = 2^{{m - 1}} \left( {1 - 2^{{ - m}} ~~max~\left| {S_{{\left( g \right)}} \left( w \right)} \right|} \right) $$
(1)

The WS, h(x) defined as:

$$ S_{{\left\langle h \right\rangle }} \left( x \right) = \mathop \sum \limits_{{{\text{x~}} \in {\text{~GF}}\left( {2^{n} } \right)}}^{n} \left( { - 1)^{{h\left( x \right) \oplus x \cdot X}} } \right) $$
(2)

where \({\text{x}} \in {\text{GF}}\left( {2^{n} } \right)\) and \(x \cdot X\) is the dot product of \(x\) and \(~X\), which is defined as:

$$ x \cdot X = x_{1} \oplus X_{1} + x_{2} \oplus X_{2} + \cdots + x_{{\text{n}}} \oplus X_{{\text{n}}} $$
(3)

The nonlinearity score of substitution box-1 and substitution box-2 is 110 and 112 respectively. We observed that the Nonlinearity score of both these S-boxes are better than to the thirty state-of-the-art (2018 to 2020 year) S-boxes, mentioned in Table 3.

Table 3 Nonlinearity of the state-of-the-art S-boxes.
Full size table

Bit independence criterion (BIC)

One of the desirable characteristic of substitution box is bit independent criterion. BIC property is defined as all the avalanche variables should be pair-wise independent for a given set of avalanche vectors, created by complementing of only one plaintext bit. Bit independent criterion is examined by altering every input bit from the plaintext1. Suppose Boolean functions are S1, S2, . . . Sn and if two Boolean functions output bits, Sj and Sk satisfy BIC, the nonlinearity and SAC must be met by Sj ⊕ Sk (j ≠ k, 1 ≤ j, k ≤ n). The average of BIC-SAC matrix of the S-box1 is 0.499 and the S-box2 is also 4.99, which is very close to 0.5. Result shows that our proposed S-boxes are competent enough to fulfil the bit independent criteria. BIC results of the S-box1 and S-box2 are presented in Table 4a, b, respectively.

Table 4 (a) Bit independence criterion of the S-box1. (b) Bit independence criterion of the S-box2.
Full size table

Strict avalanche criterion (SAC)

The confusion strength of the substitution box is examined through the strict avalanche criteria. SAC determines how many output bits changed when a single change is made in input1. It is defined as: \(f:{\text{~}}F_{2}^{n} \to F_{2}\) satisfies if \(f\left( x \right) \oplus f\left( {x \oplus \alpha } \right)\) is balanced for α = 1. Variance, Maximum, Minimum and Average SAC results of the S-box1 are 0.041869, 0.593750, 0.390625 and 0.503174, respectively. Variance, Maximum, Minimum and Average SAC results of the S-box2 are 0.032103, 0.578125, 0.437500 and 0.500488, respectively. The average SAC value of S-box1 and Sbox-2 dependency matrix are 0.503174 and 0.500488 which are exactly same to the ideal SAC. So, our proposed S-boxes satisfy the avalanche criteria. S-box1 and S-box2 results of the SAC are presented in Table 5a, b, respectively.

Table 5 (a) Strict Avalanche Criterion of the S-box1. (b) Strict Avalanche Criterion of the S-box2.
Full size table

Linear approximation probability (LP)

The imbalance of an event among input and output bit is identified by LP79,80. LP is the biggest disparity of an event, in which parity of the output bits is equal to the parity of the input bits. Here parity of the input bits is selected by the mask Ωx and parity of the output bits is selected by the mask Ωy.56,74. 2n is the number of elements and X is the set of all feasible inputs. Maximum LP of our S-box1 is 0.140625 and S-box2 is 0.1171875, which satisfy the LP criteria.

$$ LP_{f} = max_{{\Omega x,\Omega y \ne 0}} \left| {\frac{{\left\{ {\left. {x \in X} \right|x \cdot \Omega x = {\text{S}}\left( {\text{x}} \right) \cdot \Omega {\text{y}}} \right\}}}{{2^{n} }} - \frac{1}{2}} \right| $$
(4)

Differential approximation probability (DP)

Differential uniformity of substitution box is measured through the differential approximation probability. For any change in the input either sequence or value, there has to be a change in the output. In DP, the input differential Δ \(x_{i}\) should uniquely map to an output differential Δ \(y_{i}\), therefore ensuring a uniform mapping probability for each \(i\). In Table 6a, b we can see that the results of our S-box1 and S-box2 fully fills the DP criteria, represented as follows1:

$$ DP~\left( {\Delta x \to \Delta y} \right) = \left[ {\frac{{\# \{ \left. {x \in X} \right|({\text{S~}}\left( {\text{x}} \right) \oplus S\left( {x \oplus \Delta x} \right) = \Delta y\} }}{{2^{n} }}} \right] $$
(5)
Table 6 (a) DP of the S-box1. (b) DP of the proposed S-box2.
Full size table

Evaluation: statistical analysis

Resistance to differential attack

Number of changing pixel rate (NPCR) and Unified Averaged Changed Intensity (UACI) are the performance indicators that have the ability to assess the resilience of cipher against differential attacks9,74. Mathematically they are defined in Eqs. (6) and (7).

$$ NPCR~ = \frac{{\mathop \sum \nolimits_{{i,j}} ~D\left( {i,j} \right)}}{{N \times M}} \times 100\% $$
(6)
$$ UACI~ = \frac{1}{{N \times M}} \times \left[ {\mathop \sum \limits_{{i,j}} \times \frac{{\left| {C_{1} \left( {i,j} \right) - C_{2} \left( {i,j} \right)} \right|}}{{255}}} \right] \times 100\% $$
(7)

In Eq. (8) \(C_{1} \left( {i,j} \right)\) and \(C_{2} \left( {i,j} \right)\) are two encrypted images obtained from plaintext images that are slightly different. where \({\text{N}}\) is the width, \({\text{M}}\) is height of the encrypted image and \(D\left( {i,j} \right)\) is the difference function between encrypted images. Difference is given as:

$$ f\left( x \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if}}\;{\text{C}}_{1} \left( {{\text{i}},{\text{j}}} \right) = {\text{C}}_{2} \left( {{\text{i}},{\text{j}}} \right),} \hfill \\ {1,} \hfill & {{\text{if}}\;{\text{C}}_{1} \left( {{\text{i}},{\text{j}}} \right) \ne {\text{C}}_{2} \left( {{\text{i}},{\text{j}}} \right),} \hfill \\ \end{array} } \right. $$
(8)

To evaluate the impact of pixels change, in the plain images over the encrypted images various test images are evaluated through the NPCR and UACI measures. Experimental results of the NPCR and UACI for each channel (R, G, B) of baboon, cameraman,parrot and fruits are presented in Table 7. Constantly NPCR values of our results are close to 99.9 which is the perfect value. Similarly, all the values of UACI are greater than 33.5 which is also the perfect value.

Table 7 NPCR and UACI.
Full size table

Histogram analysis

Here histogram analysis is used to examine the resistance of encryption algorithm against the statistical attacks. It shows, how plain image pixels scatter after the encryption process and it indicates the frequency distribution of encrypted pixels. Ideal encryption technique reconstructs the plain image into encrypted image that bears the random pixel values and sequences. We examined the 2D and 3D histograms of various color images.

Test images of fruit and parrot with their corresponding encrypted images are shown in Figs. 6 and 7 respectively. Two-dimensional histogram of the plain test images (fruit Fig. 8g, parrot Fig. 9g) over RGB channels are shown in Figs. 8c–e and 9c–e and their corresponding encrypted images histograms are shown in Figs. 8h–j and 9h–j respectively. Histogram of the test images (Figs. 8a and 9a) and their corresponding encrypted images histograms are shown in Figs. 8b,f and 9b, f respectively.

Figure 6
figure 6

Plain and encrypted images of fruit. (a) R channel; (b) G channel; (c) B channel; (d) Encrypted R channel; (e) Encrypted G channel; (f) Encrypted B channel.

Full size image
Figure 7
figure 7

Plain and encrypted images of parrot. (a) R channel; (b) G channel; (c) B channel; (d) Encrypted R channel; (e) Encrypted G channel; (f) Encrypted B channel.

Full size image
Figure 8
figure 8

Plain and encrypted images of fruit. (a) Color image; (b) Histogram of color image; (c) Plain R channel; (d) Plain G channel; (e) Plain B channel; (f) Encrypted color image; (g) Histogram of encrypted image; (h) Encrypted R channel; (i) Encrypted G channel; (j) Encrypted B channel.

Full size image
Figure 9
figure 9

Plain and encrypted images of parrot. (a) Color image; (b) Histogram of color image; (c) Plain R channel; (d) Plain G channel; (e) Plain B channel; (f) Encrypted color image; (g). Histogram of encrypted image; (h) Encrypted R channel; (i) Encrypted G channel; (j) Encrypted B channel.

Full size image

Three-dimensional histogram of the plain test images (fruit, parrot) over RGB channels are shown in Figs. 10b–d and 11b–d and their corresponding encrypted images histograms are shown in Figs. 10f–h and 11f–h respectively. Histogram of the color plain test images (fruit, parrot) are shown in Figs. 10a and 11a and their corresponding encrypted images histograms are shown in Figs. 10e and 11e respectively.

Figure 10
figure 10

Three-dimensional histogram of fruit. (a) Color plain image; (b) R channel of plain image; (c) G channel of plain image; (d) B channel of plain image; (e) Color encrypted image; (f) R channel of encrypted image; (g) G channel of encrypted image; (h) B channel of encrypted image.

Full size image
Figure 11
figure 11

Three-dimensional histogram of parrot. (a) Color plain image; (b) R channel of plain image; (c) G channel of plain image; (d) B channel of plain image; (e) Color encrypted image; (f) R channel of encrypted image; (g) G channel of encrypted image; (h) B channel of encrypted image.

Full size image

It is clearly visible that the proposed algorithm shows a uniform two dimensional and 3-dimensional histogram for encrypted image. The uniformity of random pixels indicates a good encryption and resist against several types of statistical attacks. So, histogram analysis fails to provide any clue about encrypted image.

Correlation-coefficient analysis

Adjacent pixels of the plain images are highly correlated, that provides significant visual traits to the attacker. Strong cipher should reduce the correlation of adjacent pixels. Adjacent pixel pairs in every direction of the sailboat image are plotted in Figs. 12, 13, and 14 From the plain images and from the encrypted images, 103 adjacent pixels are selected in the horizontal, vertical and diagonal directions to calculate their correlation coefficients by using Eqs. (9), (10), (11). The results of the Correlation-coefficient analysis for each channel (R, G, B) of Peppers, parrot, baboon, and sailboat are presented in Table 8. It is clear that the distribution of adjacent pixel pairs in every direction and in every channel (R, G, B) are entirely changed after the encryption. Correlation coefficients are calculated by the following formulas:

$$ r_{{xy}} = cov\left( {x,y} \right)/\left( {\sqrt {\psi \left( x \right)} \sqrt {\psi \left( y \right)} } \right. $$
(9)
$$ cov\left( {x,y} \right) = \frac{1}{N}\mathop \sum \limits_{{i = 1}}^{N} \left( {x_{i} - E\left( x \right)} \right)\left( {y_{i} - E\left( y \right)} \right) $$
(10)
$$ \psi \left( x \right) = \frac{1}{N}\mathop \sum \limits_{{i = 1}}^{N} \left( {x_{i} - E\left( x \right)} \right)^{2} ,~E\left( x \right) = \frac{1}{N}\mathop \sum \limits_{{i = 1}}^{N} x_{i} $$
(11)
Figure 12
figure 12

Red channel scatter plots of the Sailboat, to indicate the correlation-coefficient analysis of neighbouring pixels. (a) Plain image horizontal direction; (b) Plain image vertical direction; (c) Plain image diagonal direction; (d) Encrypted image horizontal direction; (e) Encrypted image vertical direction; (f) Encrypted image diagonal direction.

Full size image
Figure 13
figure 13

Green channel scatter plots of the Sailboat, to indicate the correlation-coefficient analysis of neighbouring pixels. (a) Plain image horizontal direction; (b) Plain image vertical direction; (c) Plain image diagonal direction; (d) Encrypted image horizontal direction; (e) Encrypted image vertical direction; (f) Encrypted image diagonal direction.

Full size image
Figure 14
figure 14

Blue channel scatter plots of the Sailboat, to indicate the correlation-coefficient analysis of neighbouring pixels. (a) Plain image horizontal direction; (b) Plain image vertical direction; (c) Plain image diagonal direction; (d) Encrypted image horizontal direction; (e) Encrypted image vertical direction; (f) Encrypted image diagonal direction.

Full size image
Table 8 Correlation-coefficient analysis.
Full size table

where x, y shows 2 adjacent pixels (whatever diagonal, vertical, or horizontal), N is the total size of \(x_{i}\) and \(y_{i}\) acquired form the image. \(E\left( x \right)\) is the mean value of \(x_{i}\) and, \(E\left( y \right)\;is\;the\;mean\;value\;of\) \(y_{i}\).

Results presented in Table 8 show that before encryption, correlation-coefficient values of plain images are close to 1 and after encryption, these values are close to 0 which validates that correlation-coefficient analysis fails to provide any clue of plain images.

Assume that our proposed S-box and any existing s-box (such as the AES) are identical, even in this case our proposed S-box does not hold those vulnerabilities which are highlighted in above "Weaknesses in existing S-box designs" section. Instead of well-understood mathematical principles, we introduce the true random numbers for the design of S-boxes due to the reason that, true random numbers are irreversible, unpredictable, and unreproducible, even if their internal structure and response history are known to adversaries.

The asymptotic computational complexity of our technique is O(n2), detailed derivation is attached in Annexed C. The asymptotic computational complexity of1 and75 is O(n4) and O(n5) respectively. The asymptotic computational complexity of125,126,127 is O(n3).

Conclusion

Protecting confidential data is a major worldwide challenge and block ciphers has been a standout amongst the most reliable option by which data security is accomplished. Block cipher strength against various attacks rely on substitution box. Various weakness in the algebraic and chaos-based S-box designs are pointed in the literature. On the other hand, researchers endorse the true random sequences for cryptography due to the fact that these sequences rely on the strength of naturally occurring processes to generate the true randomness. The objective of this research is extraction of inevitable random noise from the medical imaging, and to synthesize the multi-level information fusion for the construction of strong substitution boxes. Various security evaluation criteria, statistical tests and comparison with various very recent state-of-the-art techniques validate our proposed technique. In future, we will extend our proposed information fusion design for the construction of lattice cryptographic primitive.