Abstract
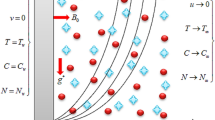
This study presents the magnetized and non-magnetized Casson fluid flow with gyrotactic microorganisms over a stratified stretching cylinder. The mathematical modeling is presented in the form of partial differential equations and then transformed into ordinary differential equations (ODEs) utilizing suitable similarity transformations. The analytical solution of the transformed ODEs is presented with the help of homotopy analysis method (HAM). The convergence analysis of HAM is also presented by mean of figure. The present analysis consists of five phases. In the first four phases, we have compared our work with previously published investigations while phase five is consists of our new results. The influences of dimensionless factors like a magnetic parameter, thermal radiation, curvature parameter, Prandtl number, Brownian motion parameter, Schmidt number, heat generation, chemical reaction parameter, thermophoresis parameter, Eckert number, and concentration difference parameter on physical quantities of interests and flow profiles are shown through tables and figures. It has been established that with the increasing Casson parameter (i.e. \(\beta \to \infty\)), the streamlines become denser which results the increasing behavior in the fluid velocity while on the other hand, the fluid velocity reduces for the existence of Casson parameter (i.e. \(\beta = 1.0\)). Also, the streamlines of stagnation point Casson fluid flow are highly wider for the case of magnetized fluid as equated to non-magnetized fluid. The higher values of bioconvection Lewis number, Peclet number, and microorganisms’ concentration difference parameter reduces the motile density function of microorganisms while an opposite behavior is depicted against density number.
Similar content being viewed by others
Introduction
Magnetohydrodynamic (MHD) flow is a fluid flow that interacts with an applied magnetic field. Newtonian and non-Newtonian versions are used to engage the fluid. Commonly well-known Newtonian fluids are gasoline, alcohol, water, and minerals. When it comes to the study of MHD, the inferred fluid model will serve as the electrical conductor. To better understand the significance of MHD flows, scientists suggested linking the integrated magnetic field with Navier–Stokes equations, and the final results identify appropriate remarks in both engineering and industrial areas such as electrolytic Hall cells, plasma welding, casting processes, defensive eccentricities, and thermal transmission characteristics are some examples. Numerous researchers and scientists expressed their perspectives on the role of magnetic field participation like Walker and Hua1 discussed the interaction of magnetic field over rectangular ducts. Chaturvedi2 addressed the MHD flow of viscous fluid with variable suction through a porous plate. Aldoss3 used a vertical cylinder to investigate the influence of magnetic field using the non-Darcian model. He discovered that when a magnetic field is introduced, both normal and forced convection regimes produce a reverse effect. Nanousis4 signified the time-dependent MHD flow of viscous fluid though an oscillatory surface. The MHD flow of electrically conducting fluid over a thermally stratified medium was addressed by Chamkha5. The heat transfer in MHD stagnation point flow of micropolar fluid over a three-dimensional frame was addressed by Gupta and Bhattacharyya6. The micropolar fluid flow with Joule heating and magnetic impacts is represented by Hakiem et al.7. The mass and heat transfer characteristics of MHD micropolar fluid flow through a circular cylinder was analyzed by Mansour et al.8. The thermal transmission characteristics of MHD fluid flow in the existence of thermal radiation were proposed by Sadeek9. The flow of micropolar fluid with MHD and constant suction impacts was presented by Amin10. The MHD flow of Oldroyd-B fluid was addressed by Hayat et al.11. The MHD flow of Casson fluid through a shrinking surface was discussed by Nadeem et al.12. Thammanna et al.13 addressed the chemically reactive MHD flow of Casson fluid through an unsteady stretching sheet with convective boundary conditions. Ramesh et al.14 presented the MHD Casson fluid flow with Cattaneo–Christov heat theory heat absorption/generation. The MHD flow of nanofluid past an unsteady contracting cylinder with convective condition and heat generation/absorption was investigated by Ramesh et al.15. Bilal et al.16 presented the numerical analysis of MHD viscoelastic fluid past an exponentially extending sheet. The related studies towards this development can be seen in Refs.17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46.
Because of its useful applications in engineering and industry, a study of stratification phenomena in non-Newtonian fluids has got a lot of interest. Temperature fluctuations, composition variations, or a combination of different liquids of varying thicknesses causes stratification of the medium. For instance, thermal rejection into the atmosphere, storage systems of heat energy, geophysical flows, etc. In short, stratification takes place in both natural and industrial phenomena. Using thermal and solutal stratifications many attempts have been performed like Yang et al.47 analyzed the convective fluid flow over a thermally stratified medium. The buoyance flow over a stratified medium was discussed by Jaluria and Gebhart48. The mixed convection fluid flow over a stratified medium was introduced by Ishak et al.49. The thermally stratified flow of micropolar fluid over a vertical plate constant and uniform heat flux was examined by Chang and Lee50. The incompressible and electrically conducting viscous fluid flow through an inclined plate was presented by Singh and Makinde51. The MHD flow of dissipative fluid with heat generation and second-order chemical reaction was introduced by Malik and Rehman52. The incompressible and mixed convective flow of viscous fluid through a thermally stratified stretching cylinder was introduced by Mukhopadhyay and Ishak53. Cheng et al.54 investigated the mass and heat transmission in a power-law fluid through a stratified medium. The heat transmission in a boundary layer flow through a stratified vertical plate was presented by Ibrahim and Makinde55. Furthermore, related analyses are mentioned in Refs.56,57,58,59,60.
Our contribution to the field of non-Newtonian fluids consists of Casson fluid flow containing gyrotactic microorganisms through a stratified stretching cylinder. Furthermore, stagnation point, Joule heating, heat absorption/generation, thermal stratification, mass stratification, motile stratification, nonlinear thermal radiation, magnetic field, and chemical reaction are taken into account. Also, the fluid flow is treated for magnetized and non-magnetized conditions. The present analysis consists of five phases. In the first four phases, we have compared our work with previously published investigations while phase five is consists of our new results.
At the end of this analysis, we will be able to answer that:
-
How the streamlines behave for non-Newtonian (Casson) and Newtonian fluid?
-
How the streamlines behave for magnetized and non-magnetized Casson fluid flow under the stagnation point?
-
What are the impacts of bioconvection Lewis number, Peclet number, and microorganisms’ concentration difference parameter on Casson fluid flow?
-
What are the impacts of bioconvection Lewis number, Peclet number, and microorganisms’ concentration difference parameter on density number?
Problem formulation
The mathematical model for Casson fluid containing gyrotactic microorganisms through a stretching cylinder is modeled under the effects of various parameters like stagnation point, Joule heating, heat absorption/generation, thermal stratification, mass stratification, motile stratification, thermal radiation, magnetic field, and chemical reaction.
For an isotropic and incompressible flow of Casson fluid, the rheological equation is stated as61:
where \(\tau_{ij}\) is the \(\left( {i,j} \right){\text{th}}\) component of stress tensor, \(\pi = e_{ij} e_{ij}\) and \(e_{ij}\) are the \(\left( {i,j} \right){\text{th}}\) component of the deformation rate, \(p_{y}\) is the fluid yield stress, and \(\mu_{B}\) is the plastic dynamic viscosity of the non-Newtonian fluid, \(\pi\) is the product of component of deformation rate with itself and \(\pi_{c}\) is the critical value of this product.
According to these assumptions the leading equations are38,57,60:
with boundary conditions57:
The conversion parameters are defined as:
Using (7), (2–6) are reduced as:
with transformed boundary conditions:
where \(\kappa = \frac{1}{R}\sqrt {\frac{\nu L}{{U_{0} }}}\) is the curvature parameter,\(\gamma = \sqrt {\frac{{\sigma B_{0}^{2} }}{a\rho }}\) is the magnetic parameter,\(A = \frac{{a^{*} }}{a}\) is the ratio of velocities, \(Rd = \frac{{4\sigma^{*} T_{\infty }^{3} }}{{kk^{*} }}\) is the thermal radiation parameter, \(\Pr = \frac{\nu }{\alpha }\) is the Prandtl number,\({\text{Nb}} = \frac{{\tau D_{B} \left( {C_{w} - C_{\infty } } \right)}}{\nu }\) is the Brownian motion parameter,\({\text{Nt}} = \frac{{\tau D_{T} \left( {T_{w} - T_{\infty } } \right)}}{{\nu T_{\infty } }}\) is the thermophoresis parameter,\(\delta_{1} = \frac{c}{b}\) is the temperature stratification parameter,\(\delta_{2} = \frac{e}{d}\) is the concentration stratification parameter, \(\delta_{3} = \frac{h}{g}\) is the motile density stratification parameter,\(Q = \frac{{Q_{0} L}}{{\rho c_{p} U_{0} }}\) is the heat generation parameter,\({\text{Sc}} = \frac{\nu }{{D_{B} }}\) is the Schmidt number,\(R_{c} = \frac{{LR_{0} }}{{U_{0} }}\) is the chemical reaction parameter, \({\text{Le}} = \frac{\alpha }{{D_{n} }}\) is bioconvection Lewis number, and \({\text{Ec}} = \frac{{xU_{0} }}{{Lc_{p} \left( {T_{w} - T_{\infty } } \right)}}\) is Eckert number, \({\text{Pe}} = \frac{{bW_{c} }}{{D_{n} }}\) is the bioconvection Peclet number, \(\Omega = \frac{{N_{\infty } }}{{N_{\infty } - N_{0} }}\) is the concentration difference parameter.
Engineering quantities of interests
Skin friction (SF)
At the cylindrical surface, the SF is specified by:
In view of Eq. (7), the dimensionless form of SF is written as:
where \({\text{Re}}_{x} = \frac{{U_{0} x^{2} }}{\nu L}\) is the local Reynolds number.
Nusselt number (NN)
At the surface of cylinder, the NN is given by:
In view of Eq. (7), the dimensionless form of NN is written as:
Sherwood number (SN)
At the surface of cylinder, the SN is given by:
In view of Eq. (7), the dimensionless form of SN is written as:
Density number (DN)
At the surface of cylinder, the DN is given by:
In view of Eq. (7), the dimensionless form of SN is written as:
HAM solution and convergence
An analytical of the modeled problem is solved with the help of HAM. The initial guesses and linear operators are taken as:
with

where  are the arbitrary constants.
are the arbitrary constants.
The convergence analysis of HAM is presented in Fig. 1a,b. The convergence area for \(f^{\prime\prime}\left( 0 \right)\) is \(- 0.1 \le \hbar_{f} \le 0.1\) as shown in Fig. 1a. Similarly, the convergence areas for \(\theta^{\prime}\left( 0 \right)\), \(\phi^{\prime}\left( 0 \right)\) and \(\chi^{\prime}\left( 0 \right)\) are \(- 1.75 \le \hbar_{\theta } \le 1.50\), \(- 0.75 \le \hbar_{\phi } \le 1.60\) and \(- 1.75 \le \hbar_{\chi } \le 1.20\) respectively, as shown in Fig. 1b.
Phases of study
This paper contains the generalized mathematical formulation for both magnetized and non-magnetized Casson fluid flow with gyrotactic microorganisms over a stratified cylinder. So the present analysis divides the proposed study into sub-phases in order to analyze the Casson fluid flow under different situations. It should be noted that in the current investigation, we have ignored the mixed convection phenomena. The present analysis consists of five phases. In the first four phases, we have compared our work with previously published investigations while phase five is consists of our new results.
Phase 1
Ignoring the suspended nanoparticles assumptions, stagnation point, Joule heating, thermal radiation, concentration distribution, and motile distribution the comprehensive formulation compact to the problem described in Ref.38. In this study, the comparative analysis of MHD mixed convective flow of Casson fluid through the stratified flat and cylindrical stretching surfaces are analyzed. The obtained variations were found to be surprisingly large for cylindrical geometry as particularly in comparison to plane surface geometry. The SF is found the heightening function of \(\kappa\),\(\Pr\),\(\beta\) and \(\delta_{1}\) whereas a reducing function of \(Q\). The NN is found the heightening function of \(\kappa\) and \(\Pr\) whereas a diminishing function of \(Q\),\(\delta_{1}\) and \(\beta\). By applying the assumptions reported in Ref.38, an analytical solution is proposed in order to verify the current model. An outstanding comparison is found with Ref.38 as shown in Table 1. The mathematical formulation designed in Ref.38 is given as:
with transformed boundary conditions:
Phase 2
In the absence of suspended nanoparticles assumptions, Joule heating, thermal radiation, stagnation point, and motile distribution the comprehensive formulation compact to the problem described in Ref.56. In this analysis, a stratified flow of Casson fluid through an inclined cylinder was presented. It was concluded that the SF is reduced with \(K\),\(\beta\),\(\Pr\) and \(\delta_{1}\) whereas the opposite trend in SF was found due to \(\delta_{2}\) and \(Q^{*}\). Furthermore, the NN has reduced with \(\beta\),\(\delta_{1}\),\(Q^{*}\) however the NN has increased with \(K\) and \(\Pr\). Additionally, it was also concluded that the higher \(K\),\(\delta_{2}\),\(R_{c}\) and \(Sc\) have increasing impacts on SN. By applying the assumptions reported in Ref.56, an analytical solution is proposed in order to verify the current model. An outstanding comparison is found with Ref.56 as shown in Tables 2 and 3. The mathematical formulation designed in Ref.56 is given as:
with transformed boundary conditions:
Phase 3
In the absence of suspended nanoparticles assumptions, Joule heating, thermal radiation, stagnation point, magnetic field, concentration distribution, motile distribution, and with the condition when \(\beta \to \infty\), the comprehensive formulation condensed to the problem reported in Ref.53. It was found that the buoyancy force escalates the SF and the thermal stratification parameter increases the NN. In addition, it was claimed that the SF and NN are highly impressed for a cylinder in contrast with plate. The mathematical formulation designed in Ref.53 is given as:
with transformed boundary conditions:
Phase 4
By ignoring the Joule heating and motile distribution, the comprehensive formulation condensed to the problem reported in Ref.57. In this examination, the authors found that the SF reduces with \(K\) and \(\beta\). Furthermore, the NN increases with \(K\) and \(\Pr\) whereas as reduces with \(\delta_{1}\). Also, the SN reduces with \(K\),\(\delta_{2}\) and increases with \({\text{Le}}\) and \(\Pr\). An outstanding comparison is found with Ref.57 as shown in Tables 4, 5 and 6. The mathematical formulation designed in Ref.57 is given as:
with transformed boundary conditions:
Phase 5
Ignoring the mixed convection phenomena and considering all other assumptions defined in Refs.38,56,57 with gyrotactic microorganisms through a stratified stretching cylinder is presented in this phase. The generalized mathematical modeling is given in (8–11) with boundary conditions (12). Here, we are interested to study the behavior of swimming microorganisms in a Casson fluid flow and to study the variation in Casson fluid flow through a stratified medium due to bioconvection Peclet number, bioconvection Lewis number, and concentration difference parameter. Furthermore, to analyze the flow of both magnetized and non-magnetized Casson fluid in the presence and absence of stagnation point. The physical quantities of interests like SF, NN, and SN are compared with the previous studies and have found quite similar results by which we have verified our study. Furthermore, the DN is calculated in Table 7. Here we have found that the DN increases with \(K\), Pe, Le and \(\Omega\) while the opposite trend in found via \(\delta_{3}\).
Graphical results
Figure 2a shows the variations in the streamlines of Newtonian fluid velocity for magnetized stratified medium under the stagnation point. Here, with the increasing Casson parameter (i.e.\(\beta \to \infty\)), we have observed that the streamlines become denser which results the increasing behavior in the fluid velocity, while on the other hand the fluid velocity reduces for the existence of Casson parameter (i.e.\(\beta = 1.0\)) as shown in Fig. 2b. Figure 3a–f show the variations in the streamlines of Casson fluid velocity for both magnetized and non-magnetized stratified medium under the region of stagnation point. Figure 3a,b are plotted for both non-magnetized and magnetized stratified medium when \(A = 0.5\) respectively. We can see that the streamlines are wider for the case of magnetized Casson fluid as equated to non-magnetized fluid. Figure 3c,d are plotted for both non-magnetized and magnetized stratified medium when \(A = 1.0\) respectively. Here, we observed that the streamlines are stifled for the case for the case of magnetized Casson fluid as equated to non-magnetized case. This conduct is due to the Lorentz force which always provides the contrasting force to the fluid flow. Figure 3e,f are plotted for both non-magnetized and magnetized stratified medium when \(A = 1.5\) respectively. A similar impact of magnetic field is depicted as observed in Fig. 3a–d. Thus, we have concluded that the magnetic field plays a significant role in streamlines of Casson fluid flow. Figure 4 shows the influence of bioconvection Lewis number Le on motile density function. Here, we concluded that the higher values of Le reduce the motile density function. Figure 5 shows the influence of bioconvection Peclet Pe number on motile density function. The greater Peclet number reduces the diffusivity of microorganisms which conclude a reducing influence in motile density function. Thus, the greater Pe reduces the motile function of the microorganisms. Figure 6 shows the effect of microorganisms’ concentration difference parameter \(\Omega\) on motile function. The increase in microorganisms’ concentration difference parameter heightens the microorganisms’ in the ambient liquid which consequently reduces the motile density function.
Final comments
The mathematical model for both magnetized and non-magnetized Casson fluid containing gyrotactic microorganisms through a stretching cylinder is modeled under the effects of various parameter like stagnation point, Joule heating, heat absorption/generation, thermal stratification, mass stratification, motile stratification, nonlinear thermal radiation, magnetic field, and chemical reaction. We have studied the Casson fluid under different situations in order to analyze the flow behavior. The final comments are listed as:
-
The increasing Casson parameter (i.e.\(\beta \to \infty\)) the streamlines become denser which results the increasing behavior in the fluid velocity, while on the other hand the fluid velocity reduces for the existence of Casson parameter (i.e.\(\beta = 1.0\)).
-
The streamlines of stagnation point Casson fluid flow are highly wider for the case of magnetized fluid as equated to non-magnetized fluid.
-
The motile function of microorganisms is reducing with higher values of bioconvection Lewis number, Peclet number, and microorganisms’ concentration difference parameter.
-
The DN increases with higher values of curvature parameter, bioconvection Lewis number, Peclet number, and microorganisms’ concentration difference parameter while reduces with motile density stratification parameter.
References
Hua, T. Q. & Walker, J. S. MHD flow in rectangular ducts with inclined non-uniform transverse magnetic field. Fusion Eng. Des. 27, 703–710 (1995).
Chaturvedi, N. On MHD flow past an infinite porous plate with variable suction. Energy Convers. Manag. 37, 623–627 (1996).
Aldoss, T. K. MHD mixed convection from a vertical cylinder embedded in a porous medium. Int. Commun. Heat Mass Transf. 23, 517–530 (1996).
Nanousis, N. D. The unsteady hydromagnetic thermal boundary layer with suction. Mech. Res. Commun. 23, 81–90 (1996).
Chamkha, A. J. MHD-free convection from a vertical plate embedded in a thermally stratified porous medium with Hall effects. Appl. Math. Model. 21, 603–609 (1997).
Bhattacharyya, S. & Gupta, A. S. MHD flow and heat transfer at a general three-dimensional stagnation point. Int. J. Non. Linear. Mech. 33, 125–134 (1998).
El-Hakiem, M. A., Mohammadein, A. A., El-Kabeir, S. M. M. & Gorla, R. S. R. Joule heating effects on magnetohydrodynamic free convection flow of a micropolar fluid. Int. Commun. Heat Mass Transf. 26, 219–227 (1999).
Mansour, M. A., El-Hakiem, M. A. & El Kabeir, S. M. Heat and mass transfer in magnetohydrodynamic flow of micropolar fluid on a circular cylinder with uniform heat and mass flux. J. Magn. Magn. Mater. 220, 259–270 (2000).
Seddeek, M. A. The effect of variable viscosity on hydromagnetic flow and heat transfer past a continuously moving porous boundary with radiation. Int. Commun. Heat Mass Transf. 27, 1037–1046 (2000).
El-Amin, M. F. Magnetohydrodynamic free convection and mass transfer flow in micropolar fluid with constant suction. J. Magn. Magn. Mater. 234, 567–574 (2001).
Hayat, T., Hutter, K., Asghar, S. & Siddiqui, A. M. MHD flows of an Oldroyd-B fluid. Math. Comput. Model. 36, 987–995 (2002).
Nadeem, S., Haq, R. U. & Lee, C. MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci. Iran. 19, 1550–1553 (2012).
Thammanna, G. T., Ganesh Kumar, K., Gireesha, B. J., Ramesh, G. K. & Prasannakumara, B. C. Three dimensional MHD flow of couple stress Casson fluid past an unsteady stretching surface with chemical reaction. Res. Phys. 7, 4104–4110. https://doi.org/10.1016/j.rinp.2017.10.016 (2017).
Ramesh, G. K., Gireesha, B. J., Shehzad, S. A. & Abbasi, F. M. Analysis of heat transfer phenomenon in magnetohydrodynamic casson fluid flow through cattaneo-christov heat diffusion theory. Commun. Theor. Phys. 68, 91. https://doi.org/10.1088/0253-6102/68/1/91 (2017).
Ramesh, G. K., Ganesh Kumar, K., Gireesha, B. J., Shehzad, S. A. & Abbasi, F. M. Magnetohydrodynamic nanoliquid due to unsteady contracting cylinder with uniform heat generation/absorption and convective condition. Alex. Eng. J. 57(4), 3333–3340. https://doi.org/10.1016/j.aej.2017.12.009 (2018).
Bilal, S. et al. Numerical investigation on 2D viscoelastic fluid due to exponentially stretching surface with magnetic effects: An application of non-Fourier flux theory. Neural Comput. Appl. 30, 2749–2758. https://doi.org/10.1007/s00521-016-2832-4 (2018).
Ali, U., Malik, M. Y., Alderremy, A. A., Aly, S. & Rehman, K. U. A generalized findings on thermal radiation and heat generation/absorption in nanofluid flow regime. Phys. A Stat. Mech. its Appl. 553, 124026. https://doi.org/10.1016/j.physa.2019.124026 (2020).
Ramesh, G. K., Shehzad, S. A., Rauf, A. & Chamkha, A. J. Heat transport analysis of aluminum alloy and magnetite graphene oxide through permeable cylinder with heat source/sink. Phys. Scr. 95, 095203. https://doi.org/10.1088/1402-4896/aba5af (2020).
Ramesh, G. K. et al. Hybrid (ND-Co3O4/EG) nanoliquid through a permeable cylinder under homogeneous-heterogeneous reactions and slip effects. J. Therm. Anal. Calorim. https://doi.org/10.1007/s10973-020-10106-1 (2020).
Rehman, K. U., Alshomrani, A. S., Malik, M. Y., Zehra, I. & Naseer, M. Thermo-physical aspects in tangent hyperbolic fluid flow regime: A short communication. Case Stud. Therm. Eng. 12, 203–212. https://doi.org/10.1016/j.csite.2018.04.014 (2018).
Hayat, T., Awais, M. & Asghar, S. Radiative effects in a three-dimensional flow of MHD Eyring-Powell fluid. J. Egypt. Math. Soc. 21, 379–384 (2013).
Khan, W. A., Makinde, O. D. & Khan, Z. H. MHD boundary layer flow of a nanofluid containing gyrotactic microorganisms past a vertical plate with Navier slip. Int. J. Heat Mass Transf. 74, 285–291 (2014).
Shahzad, A. & Ramzan, A. L. I. MHD flow of a non-Newtonian Power law fluid over a vertical stretching sheet with the convective boundary condition. Walailak J. Sci. Technol. 10, 43–56 (2012).
Shahzad, A. & Ali, R. Approximate analytic solution for magneto-hydrodynamic flow of a non-Newtonian fluid over a vertical stretching sheet. Can. J. Appl. Sci. 2, 202–215 (2012).
Masood, K., Ramzan, A. L. I. & Shahzad, A. MHD Falkner-Skan flow with mixed convection and convective boundary conditions. Walailak J. Sci. Technol. 10, 517–529 (2013).
Ahmed, J., Shahzad, A., Khan, M. & Ali, R. A note on convective heat transfer of an MHD Jeffrey fluid over a stretching sheet. AIP Adv. 5, 117117 (2015).
Hayat, T., Muhammad, T., Shehzad, S. A., Chen, G. Q. & Abbas, I. A. Interaction of magnetic field in flow of Maxwell nanofluid with convective effect. J. Magn. Magn. Mater. 389, 48–55 (2015).
Nejad, M. M., Javaherdeh, K. & Moslemi, M. MHD mixed convection flow of power law non-Newtonian fluids over an isothermal vertical wavy plate. J. Magn. Magn. Mater. 389, 66–72 (2015).
Eid, M. R. Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation. J. Mol. Liq. 220, 718–725 (2016).
Babu, D. H. & Narayana, P. V. S. Joule heating effects on MHD mixed convection of a Jeffrey fluid over a stretching sheet with power law heat flux: A numerical study. J. Magn. Magn. Mater. 412, 185–193 (2016).
Ahmed, J., Begum, A., Shahzad, A. & Ali, R. MHD axisymmetric flow of power-law fluid over an unsteady stretching sheet with convective boundary conditions. Results Phys. 6, 973–981 (2016).
Ahmed, J., Shahzad, A., Begum, A., Ali, R. & Siddiqui, N. Effects of inclined Lorentz forces on boundary layer flow of Sisko fluid over a radially stretching sheet with radiative heat transfer. J. Braz. Soc. Mech. Sci. Eng. 39, 3039–3050 (2017).
Ali, F., Sheikh, N. A., Khan, I. & Saqib, M. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: A fractional model. J. Magn. Magn. Mater. 423, 327–336 (2017).
Shankar, B. M., Kumar, J. & Shivakumara, I. S. Magnetohydrodynamic stability of natural convection in a vertical porous slab. J. Magn. Magn. Mater. 421, 152–164 (2017).
Rashad, A. M. Impact of thermal radiation on MHD slip flow of a ferrofluid over a non-isothermal wedge. J. Magn. Magn. Mater. 422, 25–31 (2017).
Pal, D. & Mandal, G. Thermal radiation and MHD effects on boundary layer flow of micropolar nanofluid past a stretching sheet with non-uniform heat source/sink. Int. J. Mech. Sci. 126, 308–318 (2017).
Soid, S. K., Ishak, A. & Pop, I. MHD flow and heat transfer over a radially stretching/shrinking disk. Chin. J. Phys. 56, 58–66 (2018).
Rehman, K. U., Qaiser, A., Malik, M. Y. & Ali, U. Numerical communication for MHD thermally stratified dual convection flow of Casson fluid yields by stretching cylinder. Chin. J. Phys. 55, 1605–1614 (2017).
Rehman, K. U., Malik, M. Y., Zahri, M. & Tahir, M. Numerical analysis of MHD Casson Navier’s slip nanofluid flow yield by rigid rotating disk. Results Phys. 8, 744–751 (2018).
Ahmad, M. W. et al. Darcy-Forchheimer MHD couple stress 3D nanofluid over an exponentially stretching sheet through cattaneo-christov convective heat flux with zero nanoparticles mass flux conditions. Entropy 21, 867 (2019).
Muhammad, R. et al. Magnetohydrodynamics (MHD) radiated nanomaterial viscous material flow by a curved surface with second order slip and entropy generation. Comput. Meth. Prog. Biomed. 189, 105294 (2020).
Dawar, A. et al. Chemically reactive MHD micropolar nanofluid flow with velocity slips and variable heat source/sink. Sci. Rep. 10, 20926. https://doi.org/10.1038/s41598-020-77615-9 (2020).
Shah, Z. O., Alzahrani, E., Dawar, A., Alghamdi, W. & Zaka Ullah, M. Entropy generation in MHD second-grade nanofluid thin film flow containing CNTs with cattaneo-christov heat flux model past an unsteady stretching sheet. Appl. Sci. 10, 2720 (2020).
Alreshidi, N. A. et al. Brownian motion and thermophoresis effects on MHD three dimensional nanofluid flow with slip conditions and joule dissipation due to porous rotating disk. Molecules 25, 729 (2020).
Dawar, A., Shah, Z. & Islam, S. Mathematical modeling, and study of MHD flow of Williamson nanofluid over a nonlinear stretching plate with activation energy. Heat Transf. https://doi.org/10.1002/htj.21992 (2020).
Dawar, A. et al. Joule heating in magnetohydrodynamic micropolar boundary layer flow past a stretching sheet with chemical reaction and microstructural slip. Case Stud. Therm. Eng. https://doi.org/10.1016/j.csite.2021.100870 (2021).
Yang, K. T., Novotny, J. L. & Cheng, Y. S. Laminar free convection from a non-isothermal plate immersed in a temperature stratified medium. Int. J. Heat Mass Transf. 15, 1097–1109 (1972).
Jaluria, Y. & Gebhart, B. Stability and transition of buoyancy-induced flows in a stratified medium. J. Fluid Mech. 66, 593–612 (1974).
Ishak, A., Nazar, R. & Pop, I. Mixed convection boundary layer flow adjacent to a vertical surface embedded in a stable stratified medium. Int. J. Heat Mass Transf. 51, 3693–3695 (2008).
Chang, C. L. & Lee, Z. Y. Free convection on a vertical plate with uniform and constant heat flux in a thermally stratified micropolar fluid. Mech. Res. Commun. 35, 421–427 (2008).
Singh, G. & Makinde, O. D. Computational dynamics of MHD free convection flow along an inclined plate with Newtonian heating in the presence of volumetric heat generation. Chem. Eng. Commun. 199, 1144–1154 (2012).
Malik, M. Y. & Rehman, K. U. Effects of second order chemical reaction on MHD free convection dissipative fluid flow past an inclined porous surface by way of heat generation: A Lie group analysis. Inf. Sci. Lett. 5, 35–45 (2016).
Mukhopadhyay, S. & Ishak, A. Mixed convection flow along a stretching cylinder in a thermally stratified medium. J. Appl. Math. (2012).
Cheng, C. Y. Combined heat and mass transfer in natural convection flow from a vertical wavy surface in a power-law fluid saturated porous medium with thermal and mass stratification. Int. Commun. Heat Mass 36, 351–356 (2009).
Ibrahim, W. & Makinde, O. D. The effect of double stratification on boundary layer flow and heat transfer of nanofluid over a vertical plate. Comput. Fluids 86, 433–441 (2013).
Rehman, K. U., Malik, A. A., Malik, M. Y., Sandeep, N. & Saba, N. U. Numerical study of double stratification in Casson fluid flow in the presence of mixed convection and chemical reaction. Results Phys. 7, 2997–3006 (2017).
Rehman, K. U., Saba, N. U., Malik, M. Y. & Zehra, I. Nanoparticles individualities in both Newtonian and Casson fluid models by way of stratified media: A numerical analysis. Eur. Phys. J. E 41, 37 (2018).
Ali, U., Alqahtani, A. S., Rehman, K. U. & Malik, M. Y. On Cattaneo-Christov heat flux analysis with magneto-hydrodynamic and heat generation effects in a Carreau nanofluid over a stretching sheet. Rev. Mex. Fis. 65(5), 479–488 (2019).
Kannan, R. M., Pullepu, B. & Shehzad, S. A. Numerical solutions of dissipative natural convective flow from a vertical cone with heat absorption, generation, MHD and radiated surface heat flux. Int. J. Appl. Comput. Math. 5(1), 24 (2019).
Eswaramoorthi, S., Jagan, K. & Sivasankaran, S. MHD bioconvective flow of a thermally radiative nanoliquid in a stratified medium considering gyrotactic microorganisms. J. Phys: Conf. Ser. 1597, 012001. https://doi.org/10.1088/1742-6596/1597/1/012001 (2020).
Nakamura, M. & Sawada, T. Numerical study on the flow of a non-newtonian fluid through an axisymmetric stenosis. J. Biomech. Eng. 110(2), 137–143. https://doi.org/10.1115/1.3108418 (1988).
Acknowledgements
“The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT”. Moreover, this research project is supported by Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2021 under Project Number 64A306000005.
Author information
Authors and Affiliations
Contributions
A.D. and Z.S. modeled and solved the problem. S.I. and A.D. wrote the manuscript. Z.S. contributed in the numerical computations and plotting the graphical results. P.K. and H.M.A. contributed in revised version. All authors finalized the manuscript after its internal evaluation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dawar, A., Shah, Z., Alshehri, H.M. et al. Magnetized and non-magnetized Casson fluid flow with gyrotactic microorganisms over a stratified stretching cylinder. Sci Rep 11, 16376 (2021). https://doi.org/10.1038/s41598-021-95878-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-95878-8
This article is cited by
-
Magnetic field impact on gyrotactic microorganisms slip flow over a stretching cylinder: insights of Hall current, and Darcy–Forchheimer dynamics
Multiscale and Multidisciplinary Modeling, Experiments and Design (2025)
-
A numerical study of heat and mass transfer characteristic of three-dimensional thermally radiated bi-directional slip flow over a permeable stretching surface
Scientific Reports (2024)
-
Impact of thermal radiation in a mixed convective magnetize Casson fluid flow through a porous bulb-shaped enclosure
Journal of Thermal Analysis and Calorimetry (2024)
-
Rheology of bioconvective stratified Eyring-Powell nanofluid over a surface with variable thickness and homogeneous-heterogeneous reactions
Biomass Conversion and Biorefinery (2024)
-
Numerical Simulation of Electroosmotic Sutterby Hybrid Nanofluid Flowing Through an Irregularly Mild Stenotic Artery with an Aneurysm
Arabian Journal for Science and Engineering (2024)