Introduction

The analysis of heat and mass transmission, as well as boundary layer flow across a starching substrate, is an interesting subject of study due to its numerous applications in various industries and metal extraction processes1,2. Sivaraj and Kumar3 evaluated the consequences of mixed convection on time-dependent MHD dusty viscous fluid flow with thermal conduction through the impermeable irregular surface. The streamlines of dusty fluids are found to be greater than the velocity distribution of dust particulates. Alharbi et al.4 reported the three-dimensional ferrofluid flow across an impermeable upright surface, as well as the impacts of slips in a porous medium with hybrid nanoparticles. It's has been discovered that as the volume proportion of nanoparticles (Nps) increases, the rate of heat transport enhances. Ullah et al.5 described the flow variations in the near area of and inside irregular surfaces. Bilal et al.6 investigated the effect of inconsistent 2D & 3D sharpness on instability by simulating fully developed flows over two distinct rough substrates. The two designs are created by superimposing sinusoidal functions with various wavelengths and random amplitudes. Gul et al.7 and Zhou et al.8 established a numerical model that compared the comportment of simple and hybrid NPs moving over an extending sheet. When compared to simple nanofluid, the hybrid nanofluid (HNF) is more efficacious in heat flux due to its excellent thermal properties. Iyyappan and Singh9 examined the flow of a force convective laminar boundary layer on an irregular diverging channel when magnetic field influences were employed. Bilal et al.10 studied the Casson fluid flow under the upshot of magnetic flux over an expanding surface. It has been shown that the variation of the magnetic field, Marangoni factor, and unsteadiness component decreases the fluid velocity. Some advanced research have been reported by11,12,13,14.

Non-Newtonian fluids come in a wide variety of types, each with its own set of characteristics. Non-Newtonian fluids are being examined by scientists and researchers due to a broad range of implementations, like drug companies, fiber new tech, cables sealant, food items, crystal growth, psychology and many more. Jeffrey fluid is the most well-known and easiest-to-understand. The Jeffrey fluid parameter and the time retardation parameter elevates this fluid to the top of the non-Newtonian fluids list15. Ullah et al.16 evaluated the Jeffrey fluid flow across porous horizontal sheet. The velocity of an unsteady Jeffrey fluid flow over an inestimable plane permeable plate is inspected by Algehyne et al.17. The results reveal that as the magnetic parameter, the ratio of retardation and relaxation times and Jeffrey fluid parameter increase, the fluid velocity decreases. In the response to an ambient magnetic field, Ali et al.18 calculated the upshot of energy conduction on the flow of a Jeffery fluid with immersed NPs through a dynamic flexible substrate. Alrabaiah et al.19 inspected the peristaltic transmission of MHD Jeffery fluid flow through channel. Saleem et al. evaluated MHD Jeffrey fluid flows with mass and energy transport on an indefinitely circulating inverted cone.20. Azlina et al.21 proposed a numerical calculation of the MHD Jeffrey fluid flow through plates in a translucent sheet. Bilal et al.22 investigate the 2D Jeffrey fluid flow across a continuously extending disc. Kumar et al.23 discussed the influence of an applied magnetics flux on an irregular 2D Jeffrey fluid flow. A theoretical investigation is carried out by Yadav et al.24 to determine the upshot of a magnetic flux and mixed convection on the Jeffrey fluid flow. The results show that increasing the Jeffrey fluid parameter reduces system stability while increasing magnetic field parameters has the reverse effect. Recently many researchers have worked on this topic25,26,27,28.

The MHD flow plays a vital role in manufacturing heavy machinery, astrophysics, electrical power generation solar power equipment, space vehicle and many other fields. Kumar et al.29 explore the thermal energy transference in a HNF flow through an extending cylinder while considering magnetic dipoles. Nanoliquid flow across curved stretched sheets is studied numerically by Dhananjaya et al.30 to determine the effect of magnetic fields on Casson nanoliquid flow. The findings indicated that enhancing the curvature parameter positively affects the velocity profile, but that it has the opposite impact on the thermal gradient. Chu et al.31 scrutinise Maxwell nano liquid’s radiative flow along with a cylinder by taking into consideration the magnetic effect. The fluid flow and temperature fluctuations of nanofluid flow with the Hall upshot are discussed by Acharya et al.32. A moving plate with Joule heating is used to demonstrate Magnetohydrodynamic hybrid nanofluid flow with temperature distribution is solved numerically by Lv et al.33. Kodi et al.34 presented an analytical assessment of Casson fluid flows with heat and mass transmit. This analysis revealed that intensifying the Newtonian heating effect shrinks heat transport at the plate surface. The influence of a porous surface and magnetic flux on the Jeffery fluid flow has been reported by Abdelhameed35. Ellahi et al.36 investigated the upshots of MHD and velocity slip on sliding flat plate. The obtained outcomes exposed that the velocity contour improves for different values of the slip variable. Recently, a large number of studies have been reported by the implying magnetic effect on the fluid flow37,38,39,40.

The Jeffrey fluid model effectively describes the stress relaxation behavior of non-Newtonian fluids, which is something that the standard viscous fluid model can't. The Jeffrey fluid model may accurately explain a class of non-Newtonian fluids. The main purpose of this research is to look into the impact of MHD and thermal radiation on the 3D Jeffery fluid flow over an irregular stretching surface. The Darcy effect, varying thickness, and chemical reaction are all taken into account. The results are obtained through computational strategy PCM.

Mathematical formulation

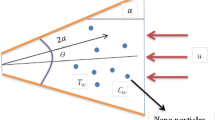
The influence of a tridimensional steady MHD Jeffery fluid flow on an irregular surface immersed in an absorbent medium is considered. Figure 1 described a schematic description of the model. The magnetic effect \(B\) is imposed in the z-direction. When the fluid is stationary at \(t = 0,\) the sheet is impulsively stretched in the x and y directions with velocities \(u_{w}\) and \(v_{w}\). The effects of solar radiation on the sheet's surface as well as chemical reaction are considered. Under the above description, the principal equations are expressed as14:

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} + \frac{\partial w}{{\partial z}} = 0, $$
(1)
$$ u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} + w\frac{\partial u}{{\partial z}} = \frac{\nu }{{1 + \Lambda_{1} }}\frac{\partial }{\partial z}\left( {\frac{\partial u}{{\partial z}} + \Lambda_{2} \left( {u\frac{{\partial^{2} u}}{\partial x\partial z} + v\frac{{\partial^{2} u}}{\partial y\partial z} + w\frac{{\partial^{2} u}}{{\partial z^{2} }}} \right)} \right) - \left( {\frac{{\sigma B_{0}^{2} }}{\rho } + \frac{\nu }{{k_{p} }}} \right)u - Fu^{2} , $$
(2)
$$ u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}} + w\frac{\partial v}{{\partial z}} = \frac{\nu }{{1 + \Lambda_{1} }}\frac{\partial }{\partial z}\left( {\frac{\partial v}{{\partial z}} + \Lambda_{2} \left( {u\frac{{\partial^{2} v}}{\partial x\partial z} + v\frac{{\partial^{2} v}}{\partial y\partial z} + w\frac{{\partial^{2} v}}{{\partial z^{2} }}} \right)} \right) - \left( {\frac{{\sigma B_{0}^{2} }}{\rho } + \frac{\nu }{{k_{p} }}} \right)v - Fv^{2} , $$
(3)
$$ u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} + w\frac{\partial T}{{\partial z}} = \left( {\frac{{k_{f} }}{{(\rho C_{p} )_{f} }} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \rho C_{p} }}} \right)\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{Q}{{\left( {\rho C} \right)_{f} }}\left( {T - T_{\infty } } \right), $$
(4)
$$ u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} + w\frac{\partial C}{{\partial z}} = D\frac{{\partial^{2} C}}{{\partial y^{2} }} - k_{1} (C - C_{\infty } ). $$
(5)
Figure 1
figure 1

Fluid flow over an irregular permeable surface.

Full size image

Here \(\left( {u,v,w} \right)\) determine the velocity factors in x, y and z direction. \(k_{p}\) is the permeability of the porous medium, \(k_{f}\) is the thermal conductivity, T is the temperature of the fluid, \(\nu\) is the kinematic viscosity, Q the heat absorption/generation term, F is the non-uniform inertia factor, where, Cb is the drag coefficient. \(D\) is the molecular diffusivity and \(\Lambda_{1} ,\Lambda_{2}\) is the period of relaxation and time retardation respectively.

The boundary conditions are14,41:

$$ \begin{gathered} u - u_{w} (x) = 0,\,\,\,\,v - v_{w} (x) = 0,\,\,\,\,T - T_{w} (x) = 0,\,\,\,\,C - C_{w} (x) = 0\,\,\,{\text{as}}\,\,\,\,z = A\delta^{{\frac{1 - n}{2}}} , \hfill \\ u \to 0,\,\,\,\,v \to 0,\,\,\,\,\,\frac{\partial u}{{\partial z}} \to 0,\,\,\,\,\,\frac{\partial v}{{\partial z}} \to 0,\,\,\,\,T - T_{\infty } ,\,\,C - C_{\infty } \,\,\,\,\,{\text{as}}\,\,\,\,z \to \infty . \hfill \\ \end{gathered} $$
(6)

where

$$ \zeta _{1} = \frac{{k_{B} T}}{{\sqrt 2 \pi d^{2} p}},\quad \Omega = x + y + z,\quad \zeta _{2} = \left( {\frac{{2\gamma }}{{\gamma + 1}}} \right)\frac{{\zeta _{1} }}{{Pr}},\quad B = B_{0} \Omega ^{{\frac{{n - 1}}{2}}} ,u_{w} = a\Omega ^{{\frac{{n - 1}}{2}}} ,\quad v_{w} = a{\mkern 1mu} \Omega ^{n} ,\quad T_{w} - T_{\infty } = T_{0} \Omega ^{{\frac{{1 - n}}{2}}} \quad n \ne 1. $$

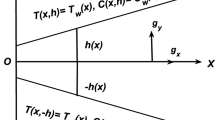
In the above equation, we supposed as \(n \ne 1\) (i.e., \(n = 1\) denotes the surface shape to flat sheet). Where, \(n > 1\) and \(n < 1\) are yields to surface curviness, inner convex and outer convex due to reduction and increment of wall thicknesses respectively. \(T_{0} ,T_{\infty }\) reference atmospheric liquid temperature \(f_{1}\) specify the Maxwell coefficient, \(b\) shows the thermal adaptation coefficient, \(\zeta_{1} ,\,\zeta_{2}\) are the constant number, \(\lambda\) specific heat ratio.

Similarity transformation

The similarity variables are:

$$ \begin{gathered} \zeta = \Omega^{{\frac{n - 1}{2}}} \left( {\frac{{(n + 1)U_{0} }}{{2\nu_{f} }}} \right)^{\frac{1}{2}} z,\,\,\,\psi = \Omega^{{\frac{n + 1}{2}}} \left( {\frac{{2\nu_{f} U_{0} }}{n + 1}} \right)^{\frac{1}{2}} F(\zeta ),\,\,\,\theta (\zeta ) = \frac{{\theta - \theta_{\infty } }}{{\theta_{w} - \theta_{\infty } }},\,\,\phi (\zeta ) = \frac{{\phi - \phi_{\infty } }}{{\phi_{w} - \phi_{\infty } }}, \hfill \\ u = U_{0} \Omega^{\prime \prime}f^{\prime}(\zeta ),\,\,v = V_{0} \Omega^{\prime \prime}g^{\prime}(\zeta ),\,\,w = \left( {\frac{{2\nu_{f} U_{0} }}{n + 1}} \right)^{\frac{1}{2}} \hfill \\ \Omega^{{\frac{n - 1}{2}}} \left[ {\frac{n + 1}{2}\left( {f(\zeta ) + g(\zeta ) + \frac{n - 1}{2}\zeta (f^{\prime}(\zeta ) + g^{\prime}(\zeta ))} \right)} \right], \hfill \\ \end{gathered} $$
(7)

By applying the above similarity transformation, Eq. (1) is identically satisfied while Eq. (2–5) take the form as:

$$ f^{\prime \prime \prime} + (\Lambda_{1} + 1)\left( {\left( {g + f} \right)f^{\prime \prime} - \frac{2n}{{n + 1}}\left( {Frf^{{\prime}{2}} + f^{\prime}g^{\prime}} \right)} \right) + D\left( {\left( {\frac{3n - 1}{2}} \right)\left( {g^{\prime \prime} + f^{\prime \prime}} \right)f^{\prime \prime} + \left( {n - 1} \right)\left( {f^{\prime} + g^{\prime}} \right)f^{\prime \prime \prime}} \right) - D\left( {\frac{n + 1}{2}(g + f)f^{\prime \prime \prime} + \frac{2}{n + 1}(1 + \Lambda_{1} )(M_{F}^{2} + P_{0} )f^{\prime}} \right) = 0, $$
(8)
$$ g^{\prime \prime \prime} + (1 + \Lambda_{1} )\left( {(g + f)g^{\prime \prime} - \frac{2n}{{n + 1}}(Frg^{{\prime}{2}} + g^{\prime}\,f^{\prime})} \right) + D\left( {\left( {\frac{3n - 1}{2}} \right)(g^{\prime \prime} + f^{\prime \prime})g^{\prime \prime} + (n - 1)(f^{\prime} + g^{\prime})g^{\prime \prime \prime}} \right) - D\left( {\frac{n + 1}{2}(g + f)g^{\prime \prime \prime} + \frac{2}{n + 1}(1 + \Lambda_{1} )(M_{F}^{2} + P_{0} )g^{\prime}} \right) = 0, $$
(9)
$$ (1 + R)\theta^{\prime \prime} + (f + g)Pr\theta^{\prime} + Hs\theta = 0, $$
(10)
$$ \phi^{\prime \prime} + Sc\left( {(f + g)\phi^{\prime} - \frac{2}{n + 1}C_{r} \phi } \right) = 0. $$
(11)

The reduced conditions are:

$$ \left. \begin{aligned} g(\eta ) & = f(\eta ) = \Lambda \left( {\frac{1 - n}{{1 + n}}} \right),\quad f^{\prime}(\eta ) = \phi (\eta ) = g^{\prime}(\eta ) = \theta (\eta ) = 1\;{\text{as}}\;\eta \to 0 \\ f^{\prime}(\eta ) & = g^{\prime}(\eta ) \to 0,\quad f^{\prime \prime}(\eta ) = g^{\prime \prime}(\eta ) = \phi^{\prime}(\eta ) = \theta^{\prime}(\eta ) \to 0\;{\text{as}}\;\eta \to \infty . \\ \end{aligned} \right\} $$
(12)

Here, D and \(M_{F}\) is the Deborah number and magnetic field, Hs is the absorption & generation term, \(P_{0}\) is the porosity factor, R is the thermal radiation, Pr and Sc is the Prandtl and Schmidt numbers, Fr is the Darcy Forchhemier term, \(C_{r}\) is the chemical reaction and \(\Lambda\) wall thickness factor. Mathematically we have

$$ \left. \begin{gathered} P_{0} = \frac{{v_{f} }}{{k_{p} U_{0} \Omega^{n - 1} }},\,\,\,Pr = \frac{{\mu_{f} (C_{p} )_{f} }}{{k_{f} }},\,\,\,\Lambda = z\left( {\frac{{(n + 1)U_{0} }}{2\nu }} \right)^{\frac{1}{2}} ,\,\,M_{F} = \frac{{\sigma B_{0}^{2} }}{{\rho U_{0} \Omega^{n - 1} }}, \hfill \\ Hs = \frac{xQ}{{u\rho C_{p} }},\,\,\,\,D = \Lambda_{2} U_{0} \Omega^{n - 1} ,\,\,\,\,\,Fr = \frac{{xC_{b} }}{{k^{*1/2} }},\,\,\,\,\,C_{r} = \frac{{k_{1} }}{{U_{0} \Omega^{n - 1} }},\,\,\,\,\,Sc = \frac{{\nu_{f} }}{D}. \hfill \\ \end{gathered} \right\} $$
(13)

The friction factor towards x and y direction are:

$$ Cf_{x} = \frac{{\tau_{xz} }}{{\rho U_{w}^{2} }},\,\,\,Cf_{y} = \frac{{\tau_{yz} }}{{\rho U_{w}^{2} }}, $$
(14)

where

$$ \begin{gathered} \tau_{xz} = \frac{\mu }{{1 + \Lambda_{1} }}\left[ {\frac{\partial u}{{\partial z}} + \left( {u\frac{{\partial^{2} u}}{\partial x\partial z} + v\frac{{\partial^{2} u}}{\partial y\partial z} + w\frac{{\partial^{2} u}}{{\partial z^{2} }}} \right)\Lambda_{2} } \right], \hfill \\ \tau_{yz} = \frac{\mu }{{1 + \Lambda_{1} }}\left[ {\frac{\partial v}{{\partial z}} + \left( {u\frac{{\partial^{2} v}}{\partial x\partial z} + v\frac{{\partial^{2} v}}{\partial y\partial z} + w\frac{{\partial^{2} v}}{{\partial z^{2} }}} \right)\Lambda_{2} } \right]. \hfill \\ \end{gathered} $$
(15)

Here the physical quantities are:

$$ Nu_{x} = \frac{{\Omega q_{w} }}{{k_{f} (T_{w} - T_{\infty } )}},\quad {\text{where}}\quad q_{w} = - \left( {k_{f} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}} \right)\frac{\partial T}{{\partial z}}. $$
(16)
$$ Sh_{x} = \frac{{\Omega j_{w} }}{{D(C_{w} - C_{\infty } )}},\quad {\text{where}}\quad j_{w} = - D\frac{\partial C}{{\partial z}}, $$
(17)

The skin friction, heat and mass allocation expression are as follows:

$$ {\text{Re}}_{x}^{0.5} Cf_{x} = \frac{1}{{1 + \Lambda_{1} }}\left( {\frac{n + 1}{2}} \right)^{0.5} \left( {f^{\prime \prime}(0) + D\left( {\frac{3n - 1}{2}f^{\prime \prime}(0)(f^{\prime}(0) + g^{\prime}(0)) - \frac{n + 1}{2}f^{\prime \prime \prime}(0)(g(0) + f(0))} \right)} \right), $$
(18)
$$ {\text{Re}}_{y}^{0.5} Cf_{y} = \frac{1}{{1 + \Lambda_{1} }}\left( {\frac{n + 1}{2}} \right)^{0.5} \left( {g^{\prime \prime}(0) + D\left( {\frac{3n - 1}{2}g^{\prime \prime}(0)(f^{\prime}(0) + g^{\prime}(0)) - \frac{n + 1}{2}(g(0) + f(0))g^{\prime \prime \prime}(0)} \right)} \right), $$
(19)
$$ Nn_{x} {\text{Re}}_{{}}^{\frac{1}{2}} = - \left( {\frac{n + 1}{2}} \right)\theta^{\prime}(0),\,\,\,\,\,\,\,\,Sh_{x} {\text{Re}}_{{}}^{{\frac{ - 1}{2}}} = - \left( {\frac{n + 1}{2}} \right)\phi^{\prime}(0).\, $$
(20)

Here \({\text{Re}} = \frac{{\Omega U_{w} }}{{\nu_{f} }}\) is the Reynold’s number.

Numerical solution

The basic methodology steps of PCM approach are as follow17,42,43,44,45,46:

Step 1: simplification to 1st order ODE

$$ \left. \begin{aligned} \hbar_{1} & = f(\eta ),\;\hbar_{3} = f^{\prime\prime}(\eta ),\;\hbar_{5} = g^{\prime}(\eta ),\;\hbar_{7} = \theta (\eta ),\;\hbar_{9} = \phi (\eta ), \\ \hbar_{2} & = f^{\prime}(\eta ),\;\hbar_{4} = g(\eta ),\;\hbar_{6} = g^{\prime \prime}(\eta ),\;\hbar_{8} = \theta^{\prime}(\eta ),\;\hbar_{10} = \phi^{\prime}(\eta ). \\ \end{aligned} \right\} $$
(21)

By putting Eq. (21) in Eqs. (12)–(15) & (16), we get:

$$ \left( {1 - D\frac{{n + 1}}{2}(\hbar _{1} + \hbar _{4} ) + D(n - 1)(\hbar _{2} + \hbar _{5} )} \right)\hbar _{3}^{\prime } + (1 + \Lambda _{1} )\left( {(\hbar _{1} + \hbar _{4} )\hbar _{3} - \frac{{2n}}{{n + 1}}(Fr\hbar _{2}^{2} + \hbar _{2} \hbar _{5} )} \right)\quad + D\frac{{3n - 1}}{2}(\hbar _{3} + \hbar _{6} )\hbar _{3} - \frac{{2D}}{{n + 1}}(1 + \Lambda _{1} )(M_{F}^{2} + P_{0} )\hbar _{2} = 0, $$
(22)
$$ \left( {1 - D\frac{{n + 1}}{2}(\hbar _{1} + \hbar _{4} ) + D(n - 1)(\hbar _{2} + \hbar _{5} )} \right)\hbar _{6}^{\prime } + (1 + \Lambda _{1} )\left( {(\hbar _{4} + \hbar _{5} )\hbar _{6} - \frac{{2n}}{{n + 1}}(Fr\hbar _{5}^{2} + \hbar _{2} \hbar _{5} )} \right)\quad + D\frac{{3n - 1}}{2}(\hbar _{2} + \hbar _{6} )\hbar _{6} - D\frac{2}{{n + 1}}(1 + \Lambda _{1} )(M_{F}^{2} + P_{0} )\hbar _{5} = 0, $$
(23)
$$ (1 + R)\hbar^{\prime}_{8} + (\hbar_{1} + \hbar_{4} )Pr\hbar_{8} + Hs\hbar_{7} = 0, $$
(24)
$$ \hbar^{\prime}_{10} + Sc\left( {(\hbar_{1} + \hbar_{4} )\hbar_{10} - \frac{2}{n + 1}C_{r} \hbar_{9} } \right) = 0. $$
(25)

with the corresponding boundary conditions.

$$ \left. \begin{gathered} \hbar_{1} (\eta ) = \hbar_{4} (\eta ) = \Lambda \left( {\frac{1 - n}{{1 + n}}} \right),\,\,\,\hbar_{2} (\eta ) = \,\hbar_{5} (\eta ) = \hbar_{7} (\eta ) = \hbar_{9} (\eta ) = 1\,\,\,\,{\text{as}}\,\,\,\,\,\eta \to 0 \hfill \\ \hbar_{2} (\eta ) = \hbar_{5} (\eta ) = 0,\,\,\,\,\,\hbar_{3} (\eta ) = \hbar_{6} (\eta ) = \hbar_{8} (\eta ) = \hbar_{10} (\eta ) = 0\,\,\,\,\,{\text{as}}\,\,\,\,\,\eta \to \infty . \hfill \\ \end{gathered} \right\} $$
(26)

Step 2: familiarizing the embedding constraint p in Eqs. (22)–(25)

$$ \begin{gathered} \left( {1 - D\frac{n + 1}{2}(\hbar_{1} + \hbar_{4} ) + D(n - 1)(\hbar_{2} + \hbar_{5} )} \right)\hbar^{\prime}_{3} + \left( {(1 + \Lambda_{1} )(\hbar_{1} + \hbar_{4} ) + D\frac{3n - 1}{2}(\hbar_{3} + \hbar_{6} )} \right)(\hbar_{3} - 1)p \hfill \\ - \frac{{2n(1 + \Lambda_{1} )}}{n + 1}(Fr\hbar_{2}^{2} + \hbar_{2} \hbar_{5} ) - \frac{2D}{{n + 1}}(1 + \Lambda_{1} )(M_{F}^{2} + P_{0} )\hbar_{2} = 0, \hfill \\ \end{gathered} $$
(27)
$$ \begin{gathered} \left( {1 - D\frac{n + 1}{2}(\hbar_{1} + \hbar_{4} ) + D(n - 1)(\hbar_{2} + \hbar_{5} )} \right)\hbar^{\prime}_{6} + \left( {(1 + \Lambda_{1} )(\hbar_{4} + \hbar_{5} ) + D\frac{3n - 1}{2}(\hbar_{2} + \hbar_{6} )} \right)(\hbar_{6} - 1)p \hfill \\ - \frac{{2n(1 + \Lambda_{1} )}}{n + 1}(Fr\hbar_{5}^{2} + \hbar_{2} \hbar_{5} ) - D\frac{2}{n + 1}(1 + \Lambda_{1} )(M_{F}^{2} + P_{0} )\hbar_{5} = 0, \hfill \\ \end{gathered} $$
(28)
$$ (1 + R)\hbar^{\prime}_{8} + (\hbar_{1} + \hbar_{4} )Pr(\hbar_{8} - 1)p + Hs\hbar_{7} = 0, $$
(29)
$$ \hbar^{\prime}_{10} + Sc\left( {(\hbar_{1} + \hbar_{4} )(\hbar_{10} - 1)p - \frac{2}{n + 1}C_{r} \hbar_{9} } \right) = 0. $$
(30)

Step 3: solving the Cauchy principal

Numerical implicit scheme is employed for the above modeled equations, which is defined as below:

$$ \frac{{U^{i + 1} - U^{i} }}{\Delta \eta } = \rlap{---} \Delta U^{i + 1} ,\,\,\,\,\frac{{W^{i + 1} - W^{i} }}{\Delta \eta } = \rlap{---} \Delta W^{i + 1} . $$
(31)

Finally, we get:

$$ U^{i + 1} = (I - \Delta \rlap{---} \Delta \eta )^{ - 1} U^{i} ,\,\,\,\,\,\,\,\,W^{i + 1} = (I - \Delta \rlap{---} \Delta \eta )^{ - 1} (W^{i} + \Delta \eta R). $$
(32)

Results and discussion

The section revealed the physics behind each figure and table. The subsequent trends have been observed:

Velocity profile

Figures 2, 3, 4, 5, 6, 7, 8 explained the presentation of axial \(f^{\prime}\left( \eta \right)\) and radial \(g^{\prime}\left( \eta \right)\) velocity profile versus the variation of porosity term P0, power-law index n, magnetic field constraint MF, Darcy Forchhemier term Fr, Deborah number D, wall thickness term \(\Lambda\) and the ratio of relaxation time to retardation term \(\Lambda_{1}\) respectively. Figures 2 & 3 shows that the velocity curve declines with the growth of porosity term, while augmented with the flourishing upshot of power index constraint. Physically, the number of pours increases with the porosity parameter effect, which resists the fluid flow, so causes the reduction in the velocity outline. Figures 4 and 5 reported that the rising frequency of both constraints magnetic field and Darcy Forchhemier effect deduce the velocity distribution. Because the opposing force, which is created due to magnetic effect, resist the flow field, as a result such trend observed. Figures 6 and 7 described that the impact of local Deborah number and wall thickness parameter augmented the velocity field. Figure 8 displays that the upshot of thermal relaxation term, reduce the energy profile.

Figure 2
figure 2

Velocity profile versus porosity term P0.

Full size image
Figure 3
figure 3

Velocity profile versus power law index n.

Full size image
Figure 4
figure 4

Velocity profile versus magnetic field constraint MF.

Full size image
Figure 5
figure 5

Velocity outline versus Darcy Forchhemier term Fr.

Full size image
Figure 6
figure 6

Velocity outline versus local Deborah number D.

Full size image
Figure 7
figure 7

Velocity profile versus wall thickness term \(\Lambda\).

Full size image
Figure 8
figure 8

Velocity profile versus ratio of relaxation time to retardation term \(\Lambda_{1}\).

Full size image

Energy profile

Figures 9, 10, 11, 12, 13, 14 explained the appearance of energy contour \(\theta \left( \eta \right)\) versus the variation of porosity term P0, power-law index n, thermal radiation R, heat source term Hs, Deborah number D, thermal relaxation term \(\Lambda_{1}\). Figures 9 and 10 shows that the energy contour amplifies with the increment of porosity term while diminishing with the flourishing upshot of power index constraint. Physically, the number of pours increases with the porosity parameter effect, which resists the fluid flow, so triggers an expansion in the heat. Figures 11 and 12 illustrated that the thermal field boosts with the mounting values of R and Hs. The effect of both constraints generates an additional heat inside the fluid, which scores in the advancement of the temperature field \(\theta \left( \eta \right)\). Figures 13 and 14 presented that Deborah number D decreases the thermal energy field, while the impact of thermal relaxation term \(\Lambda_{1}\) enhances the energy distribution.

Figure 9
figure 9

Energy profile versus the porosity term P0.

Full size image
Figure 10
figure 10

Energy profile versus the power law index n.

Full size image
Figure 11
figure 11

Energy profile versus the thermal radiation R.

Full size image
Figure 12
figure 12

Energy profile versus the heat source term Hs.

Full size image
Figure 13
figure 13

Energy profile versus the local Deborah number D.

Full size image
Figure 14
figure 14

Energy profile versus the ratio of relaxation time to retardation term \(\Lambda_{1}\).

Full size image

Concentration profile

Figures 15, 16 and 17 elaborated the exhibition of mass outline \(\phi \left( \eta \right)\) versus CR, Deborah number D and Schmidt number Sc respectively. Figures 15, 16 and 17 assessed hat the mass transmission profiles reduce with the intensifying upshot of chemical reaction, Deborah number and Schmidt number. Physically, the influence of the Sc enhances the kinetic viscosity of the fluid, while lessen the molecular diffusion, which causes the reduction in mass profile. Similarly, the consequences of chemical reaction and Deborah number also declines the concentration profile \(\phi \left( \eta \right).\)

Figure 15
figure 15

Mass profile versus the chemical reaction CR.

Full size image
Figure 16
figure 16

Mass profile versus the Deborah number D.

Full size image
Figure 17
figure 17

Mass profile versus the Schmidt number Sc.

Full size image

Error analysis

In Fig. 18, we performed the error analysis, to ensure that our results are accurate up to the lowest residual error scale. Until evaluating and providing physical forecasts, we analyze an error to determine the accuracy of the proposed method.

Figure 18
figure 18

Residual error for velocity, energy and concentration profile.

Full size image

Tables 1 and 2 illustrated the statistical outcomes for skin friction, Nusselt and Sherwood number versus several physical constraints respectively. Table 3 highlighted the comparative assessment of the present results versus the existing works. The results of Table 3 verify the accuracy of the current analysis.

Table 1 The arithmetical results for skin friction along x and y direction.
Full size table
Table 2 The statistical outputs of Sherwood and Nusselt numbers.
Full size table
Table 3 Relative evaluation of current results with the available literature for \(- f^{\prime \prime}(0)\).
Full size table

Conclusion

We have numerically analyzed the energy conveyance through Jeffery fluid flow over an irregular extensible sheet with a porous medium. The consequences of the Darcy effect, variable thickness and chemical reaction are also considered. The phenomena have been modeled as a system of PDEs. Using similarity substitution, the modeled equations are reduced to a dimensionless system of ODEs. The computational technique is used to determine the numerical solution to the obtained sets of nonlinear differential equations. The key conclusions are:

  • The velocity profiles \(\left( {f^{\prime}\left( \eta \right),\,\,g^{\prime}\left( \eta \right)} \right)\) both decline with the increment of porosity term, magnetic field, Darcy Forchhemier and thermal relaxation factor while augmented with the flourishing upshot of power index and local Deborah number.

  • The energy profile \(\theta \left( \eta \right)\) magnifies with the increment of porosity term, thermal radiation and heat source term, while diminishing with the flourishing upshot of power index and Deborah number.

  • The mass transfer profiles reduce with the rising upshot of CR, Deborah number and Schmidt number.

  • The porosity term and wall thickness parameter enhance the skin friction.