Introduction

Phosphate glasses excel with desirable properties such as a low melting point, high thermal expansion coefficient, and high ultraviolet transmission in contrast to common oxide glasses1,2,3. The open structure of the phosphate chain allows incorporating property modifiers such as heavy metals, transition or rare earth elements which greatly improve the glass's thermal stability and toughness as well as its chemical resistance. Phosphate glasses have achieved unique magnetic, optical, and electrical properties which meet the requirements of many modern applications1,2,3. Recently, phosphate glasses are considered promising as new solid-state electrolytes owing to their structure that permits a high mobility for protons4,5.

Many prior studies on phosphate glass have focused on the effect of both alkalis and alkaline earth oxides on its structure and properties in the context of improving its optical, physical, and electrical qualities6,7,8. Li2O-P2O5 glass was found to be an outstanding fast-conducting glass for Li+ ions. Depending on the concentration of Li2O, the addition of Li2O can improve phosphate glass's ionic conductivity6,7. Strontium oxide was also used to improve the durability of phosphate glass9,10. SrO may be useful in improving the electrical conductivity of phosphate glasses. Furthermore, Bouabdalli et al.10 Found that adding SrCO3 and Li2CO3 to the boro-phosphate matrix reduces the phonon energy via the exchange of BO4 ↔ BO3 and PO3 ↔ PO2, resulting in improved fluorescence efficiency and a longer lifetime.

MgO is utilized as a glass modifier. Its molecules break the random glass network creating bonding defects which result in free paths8,11. Because lithium ions are light and tiny, they can move freely across the glass network. The ionic conductivity of glass is affected by this phenomenon. Mg2+ ions occupy the glass system's interstitial sites and disintegrate the P-O-P bonds, generating bonding deformations. This process leads to empty cavities and easy tracking by facilitating the doped ions' movement8,11. As a result, MgO plays a crucial role in improving the samples' dielectric features.

Molybdenum oxide and P2O5 combine to generate binary glasses with a broad and continuous glass-forming range. The structure of molybdenum phosphate glass systems has received a lot of attention12,13. The presence of molybdenum ions in two different valence states Mo5+ (which occupy octahedral sites) and Mo6+ (which occupy tetrahedral and octahedral sites) was identified, and the redox [Mo5+/Mo6+] ratio increased with MoO3 concentration increase12,13. Molybdenum's six-coordinated environment was further identified in the Na2O-MoO3-P2O5 glass structure14. The electrical properties of sodium and lithium phosphate glasses were studied by impedance spectroscopy to evaluate the electronic and ionic contributions to conduction. It indicated that there is no correlation between the variation in electronic or ionic conductivity and the maximum Mo5+/Motot and Mo5+/Mo6+ ratio in these glasses14,15. An optical absorption investigation shows that increasing the MoO3 content up to 0.3 mol% results in the conversion of molybdenum ions from tetrahedral sites to octahedral sites. While the concentration of molybdenum ions that exceed 0.3 mol% assists in glass network formation16. Molybdenum phosphate glasses have received major concern for their ionic and electronic transport properties2,17,18. As known, pure ionic-conducting glasses can be used as solid electrolytes in electrochemical cells, whilst mixed ionic-electronic glass conductors have the potential to be useful as cathode materials19.

Optical and electrical properties are suitable for describing glass structure as a function of its composition and network connectivity. Previous literature indicated that reports on optical and electrical properties of glasses containing combined SrO and Li2O are limited. To the best of our knowledge, ternary P2O5, MoO3, and MgO glass systems doped with both SrO and Li2O have not been investigated.

In the current work, the structural properties of studied glasses in the system 40 P2O5, 20 MoO3, 15 MgO, (25-x) Li2O, x SrO where 0 ≤ x ≤ 20 mol% are examined based on XRD analysis, density measurements, molar volume calculations, hardness and FTIR spectroscopy. The optical properties as a function of structural changes induced by SrO addition are assessed. Moreover, the effect of SrO concentration on the electrical properties of these glasses has been reported, which may be suitable for use in opto-electronic devices.

Experimental

Glass preparation

The glass samples were obtained by melting a mixture of calculated proportions of pure materials NH4H2PO4, SrCO3, Li2CO3, MoO3, MgO in porcelain crucibles in a SiC-heated furnace (Vecstar, UK) at 1200 °C for 2 h with repeated rotation of the melts to ensure perfect blending and homogeneity. The completed molten of each sample was cast into warmed stainless-steel molds to get the desired dimensions (2 cm × 1cm). These samples were then transferred to a regulated muffle furnace at 320 °C for annealing. Keeping the samples in the furnace for 1 h, the furnace was switched off and allowed to cool at 30 °C/h to room temperature.

XRD

X-ray diffraction (XRD) was measured on fine powders of the obtained samples. Samples were ground and the fine powder was examined using a diffractometer adopting Ni-filter and Cu-target. The X-ray diffraction patterns were obtained using a Philips PW 1390 X-ray diffractometer. The diffraction patterns were identified with comparison with standard ASTM cards and published related data. The diffractometer with Cu radiation (λ = 1.5405 Å) operating at 40 kV, 30 mA, at room temperature was used. The acquired diffraction patterns are ranging from 5° to 80° for 2θ values.

Density and molar volume, microhardness

Density of glasses was measured at room temperature, using the suspended weight method based on Archimedes principle according to the following formula,

$$\uprho \, = \, \left[ {{\text{ a}}/\left( {{\text{a}} - {\text{b}}} \right)} \right] \, \times \, 0.{86 } = {\text{ g/cm}}^{{3}}$$
(1)

where ρ is the density of the glass sample, a and b are the weights of the glasses in the air and in xylene respectively, and 0.86 is the density of xylene at 20 °C. Molar volume of the glasses was calculated using the following formula:

$${\text{Vm}} = {\text{ M}}/\uprho \, = {\text{ m}}^{{3}} /{\text{mol}}$$
(2)

where, M is the molar mass of elements in each glass sample individually, and ρ is the glass density. The specific volume of the glasses was calculated by using the inverse formula of density values.

The hardness was measured by using a Knoop diamond (KHN), under a load of 25 g, applied for 10 s (HMV microhardness tester; Shimadzu Type-M Tokyo, Japan). Three sequences of five indentations were performed.

FTIR

Fourier transform infrared spectroscopy was measured by (FT-IR- Brucker Vertex 8V, Germany), in the range of 1600 to 400 cm−1 wavenumbers with a resolution of 4 cm−1, to identify the structural network groupings.

Optical measurements

The diffuse reflectance spectra (DR) of the glass powders were recorded within the range of 200–1750 nm utilizing a UV–Vis near-infrared spectrometer (UV-3150, Shimadzu, Tokyo, Japan) equipped with the ISR-3100 integrated sphere. Spectra were measured at room temperature with a 0.3-nm resolution. The Kubelka–Munk function F(R) is directly proportional to absorbance. Hence, F(R) values were altered to the linear absorption coefficient α using the next relation:

$$\upalpha \, = {\text{ F}}\left( {\text{R}} \right)/{\text{t}}$$
(3)

where t is the thickness of the sample.

In the limiting case of infinitely thick samples, neither thickness nor sample holder affect reflectance (R). In this case, the Kubelka–Munk equation at any wavelength becomes the following20,21:

$${\text{F }}\left( {\text{R}} \right) = \left( {{1} - {\text{ R }}} \right)^{{2}} /{\text{2R}}$$
(4)

where R = Rsample/Rstandard. As a result, the following relational expression was applied as proposed by Tauc et al.20,21.

$$\upalpha {\text{hv }} = {\text{ A}}_{{1}} \left( {{\text{hv }} - {\text{ E}}_{{\text{g}}} } \right)^{{\text{n}}}$$
(5)

where h is Planck's constant, ν is frequency of vibration, α is absorption coefficient, Eg is band gap n is the type of transition (1/2 in the case of direct transition or 2 in the case of indirect transition) and A1 is proportional constant.

Diffuse reflectance spectra were transformed to the Kubelka–Munk function. Thus, the vertical axis became F(R), whose value corresponded to the absorption coefficient. Then α in the Tauc equation, it is replaced with F(R). So, in the actual experiment the relational expression develops into22,23:

$$\left[ {{\text{F}}\left( {\text{R}} \right){\text{hv}}} \right]^{{{1}/{\text{n}}}} = {\text{ A}}_{{2}} \left( {{\text{hv }} - {\text{ Eg}}} \right)$$
(6)

Consequently, getting F(R) from Eq. (4) and plotting the [F(R)hν]1/n against hν, the band gap Eg of powder samples can be obtained simply, where A2 is proportional constant.

ESR

The prepared glasses' ESR spectra were measured using an EMX spectrometer (X-band). The cavity selected was a standard Bruker ER 4102 rectangular cavity, Germany. The operating parameters were as follows: microwave power 0.796 mV, modulation amplitude 5 Gauss, time constant 81.92 ms and conversion time 20.48 ms. The powder of samples was inserted into ESR tubes and measured at the mentioned parameters. All ESR measurements were performed at 25 °C during a single scan.

Electrical measurements

The AC conductivity (σac) of the prepared samples was measured with LRC Hi-Tester (HIOKI, 3532-50), Japan, in a frequency range from 0.042 kHz to 1 MHz, and at temperatures ranging from 298 to 473 K. Temperature rising was achieved via increasing the input voltage from a variac transformer connected to a wire-wound resistance heater. In close proximity to the sample, a copper/constantan thermocouple was used to determine the temperature. The capacitance, C, and the dissipation factor, tan δ, are acquired instantly from the instrument for the samples. The AC conductivity, σac, is calculated using the relation:

$$\upsigma_{{{\text{ac}}}} = \, \upomega \varepsilon_{o} \varepsilon \prime {\text{ tan }}\updelta ,$$
(7)

where ω is the angular frequency, εο is the free‐space permittivity and ε′ is the dielectric constant which is determined from the expression

$$\varepsilon \prime \, = {\text{ C d}}/\varepsilon_{o} {\text{A}},$$
(8)

where d is the thickness of the sample and A is the cross‐sectional area24.

Results and discussion

X-ray diffraction analysis (XRD)

XRD is a crucial experimental method for determining structure, grain size, lattice strains, and other aspects of material characterization. The produced samples lack sharp peaks and are amorphous25 and are verified to be non-crystalline. All produced samples' XRD patterns support amorphicity as depicted in Fig. 1.

Figure 1
figure 1

X-ray pattern of samples Sr0 and Sr20.

Full size image

Density, molar volume and microhardness

Density measurement has been extensively studied to understand how composition affects glass structure. The network compactness, change in geometrical arrangement, cross-link density, and molar mass of the components are the primary determinants of glass density26.

The variation in measured density and calculated molar volume values of the glass samples is shown in Fig. 2, Table 1. It is observed that the successive partial substitution of Li2O with SrO results in a rearrangement and change in the geometrical configuration of the atoms in the host glass lattice. The density increased gradually up to 20 mol% SrO while the molar volume decreased as increasing SrO oxide content replacing Li2O oxide. The density increase might be explained by the fact that Li has a smaller molar mass (6.941 g/mol) than Sr (87.6200 g/mol). From another standpoint, SrO (4.7 g cm−3) has a heavier density than Li2O (2.01 g cm−3). Furthermore, the density increase (decrease in molar volume) was accompanied by the existence of varying structural units of PO2, PO3, and PO4. The conversion of some MoO6 into MoO4 and the potential increase in non-bridging oxygen support the increase in density.

Figure 2
figure 2

Density and molar volume of prepared samples.

Full size image
Table 1 The chemical composition and some physical properties of studied glasses.
Full size table

Glass hardness is one of its most crucial qualities since it gauges how dense the structure is. Microhardness values show how different cation substitutions affect glass. Table 1 lists the values. The microhardness values of glass samples were raised when Li2O was replaced with SrO leading to an increase in glass network coherence. The increased glass microhardness may be attributed to the strontium-oxygen connection strength being higher than that of the lithium-oxygen link27. As known, Sr2+ has a stronger cationic field strength (0.29 A−2) than Li+ (0.26 A−2)27,28.

FTIR studies

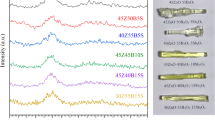
Oxide glass FTIR investigations provide information on structure as well as the compound's oxygen coordination number, network formers, and change in oxygen bonds of the framework that is also produced by the cation modifiers. Figure 3 demonstrates the FTIR absorption spectra of the current series of molybdenum phosphate glass samples that are doped with successive increasing SrO content on expense of Li2O. It is reasonable that vibrational signals originate mostly from the phosphate matrix as it is the most predominant composition. The addition of alkali or divalent oxides induces linear chain structure of the phosphate molecule29. This structure is created by cleaving P–O–P bonds and creating non-bridged oxygens (NBOs). These divalent ions act as ionic crosslinks among NBOs of two different chains. This action is typically carried out by alkaline cations such as (Ca2+, Sr2+, Ba2+). But there are some divalent oxides such as (ZnO, MgO) form structural units (ZnO4, MgO4). As mentioned, molybdenum ions get into the glass network as a former and/or modifier when bound to four or six oxygen ions to form tetrahedral coordinated MoO4 and octahedral coordinated MoO6 units. Molybdate structural units (isolated MoO4) revealed infrared absorption at wavenumbers 920–900, 850–830, 800 and 430–410 cm−1 as established in previous published data30. Moreover, symmetric and asymmetric vibrations of Mo–O–Mo links can be noticed near 600 and 450 cm−1, respectively. Accordingly, FTIR infrared absorption spectra measurements are expected to show a clearer image of the structural lattice of the investigated phosphate glasses with varied modifier cations. The phosphate species in phosphate glasses mainly occur within the wavenumber range 1600–400 cm−1. Considering the deconvoluted FT-IR data, the current glass network has a broad spectrum of IR-active bands. Based on the literature the origin of the identified bands can be explained as follows29,30,31,32,33,34,35,36.

  • The absorption peaks in the wavenumber region below 600 cm−1 are related to the vibrations of modifying cations (such as Ca+, Sr2+, Na+ and Li+) at different interstitial locations. The band around 469 cm−1 corresponds to the bending oscillations of O–P–O groups, δ (PO2) modes of (PO2−)n chain units. In addition, symmetric and asymmetric Mo–O–Mo links vibration, vibrations of Mg2+ cations in their sites.

  • The presence of the absorption band at 575 cm−1 correlates with the fundamental frequency of PO4–3 or to P=O bending vibrations. The existing mode at 755 cm−1 is ascribed to υs (P–O–P) linkages in the pyrophosphate group (P2O7)4−, while those around 920 and 858 cm−1 are accredited to υas (P–O–P) linkages besides isolated MoO4.

  • The bands around 1087 and 1170 cm−1 are determined from asymmetric stretching vibration of the (PO3)2− terminal group, υas (PO3)2−.

Figure 3
figure 3

FTIR absorption spectra of (a) prepared samples and (b–d) the deconvolution spectra of some Sr0, Sr10 and Sr20 samples.

Full size image

It was observed that the location, widening and intensity of absorption bands are affected by Sr ions’ entrance. The band at 441 cm−1 disappeared with Li2O decrease. The peaks in the wavenumber range 400–580 cm−1 became one medium broad peak at wavenumber around 511 cm−1 by SrO addition. Moreover, vibrations spanning between 1000 and 1300 cm−1 and the disappearance of the band at 850–860 cm−1 illustrate the modification behavior of SrO in the phosphate lattice. This is done through the formation of different anionic groups or NBOs. These groups are categorized as PO2−, PO32−, and PO43−, found in Q2, Q1, and Q0, respectively35,36. The observed peaks at 1240-1290 and 1013 cm−1 with different SrO contents are ascribed to asymmetric stretching oscillations of O-P-O links of (PO2−)as and (PO32−)as located in Q2 and Q1 units, respectively35,36. Thus, all the vibration bands detected in the infrared spectrum are within the framework of the modification of the molybdenum phosphate glass network. This modification is associated with the strontium oxide content.

Optical properties

The normalized absorption spectra of 40% P2O5, 20% MoO3, 15% MgO, (25-x) Li2O, and x % SrO are shown in Fig. 4. Based on the Kubelka–Munk function, these spectra were transformed from diffuse reflectance spectra as clarified elsewhere23. Optical absorption data indicate interesting variations upon continuous substitution of specific ratios of Li2O with SrO. This is correlated to the strong effect of the existing alkaline oxides, magnesium, and strontium oxide on the optical characteristics of the studied glass lattice. Whereas the incorporation of alkaline earth elements into the glass matrix depolymerizes the glass network then stimulates the formation of non-bridging oxygen species (NBO). Furthermore, the presence of MgO and successive addition of SrO at expense of Li2O, is expected to cause variations in the ligand field around the Molybdenum probe ion owing to alterations in the oxygen ion polarizability that surrounding molybdenum ion as well as its reliance on the field strength of the glass matrix37,38. Otherwise, some previous studies39,40,41 focused on UV–visible investigations of molybdenum ions in glass. They realized that it is acceptable for molybdenum ions to exist in the glass matrix as either trivalent, tetravalent, pentavalent, hexavalent, or a mixture of some of them. Weyl42 attributed the green color of phosphate glass to pentavalent molybdenum ions under severely reducing conditions and suggest that the Mo-doped glasses display blue-green, green, brown, violet, and faint yellow resulting from Mo6+, Mo5+, Mo4+, and Mo3+ ions. ElBatal et al.42,43 and others34,44 investigated the structure and optical features of some phosphate glasses doped with MoO3. They reached to that the presence of Mo6+, Mo5+, Mo4+ and Mo3+ ions together within the studied glasses. In addition, each valence state of molybdenum ions is characterized by a specific visible absorption band. Mo3+ and Mo5+ions display absorption bands at 350–370 nm and 420–450 nm, Mo4+ ions are assigned at 550–580 nm beside the visible absorption in the wavelength range 700–960 nm is correlated to Mo5+ ions.

Figure 4
figure 4

The normalized absorption spectra of prepared glasses.

Full size image

As depicted in Fig. 4 the present glasses reveal an appearance of UV–visible absorption bands with some changes associated with the consecutive substitution of Li2O with SrO. The first sample with 0 SrO content shows UV-near visible absorption peaks at about 216, 260, and 322 nm accompanied by a visible absorption peak at 480 nm plus weak broad absorption in the 800–1000 nm wavelength range. The UV-near visible spectrum range in the glass samples with 10–20 mol% SrO extended and show extra absorption peaks at 346 and 390 nm. With SrO content increases the absorption intensity of the band at 480 nm increases and shifts to higher wavelength at 557 and 510 nm in 10% and 15% SrO. The broad visible absorption at 800–1000 nm reached the highest intensity and shifted to lower wavelength centered at 765 nm in the highest SrO content glass sample. The identified absorption in UV region could be clarified as it was studied by many researchers, and they attribute it to trace iron impurities (Fe3+) that are indeed contaminate the raw materials45,46. Urbach47 attributes this UV absorption edge to electron transitions between oxygen 2p and transition metal ion 3d states. It is noteworthy, the highest intensity of the broad band observed in the spectrum of glass sample that contains 20% SrO suggests that this glass includes the highest concentration of Mo5+ ions. It is expected that such Mo5+ ions will form Mo5+O3− molecular orbital states and take part in the depolymerization of the glass matrix44,48, leading to more bonding defects and non-bridged oxygens (NBO’s). It is obvious that glass samples' absorption spectra comprise expanded UV-near visible peaks alongside the observed wide peak centered at about 760 nm. It is clear from this that the investigated molybdenum phosphate glasses reveal absorption bands which elucidate that the valences of molybdenum ions (Mo3+, Mo4+, Mo5+ and Mo6+) substantially exist with varied ratios. While the hexavalent state of Mo ions (d0) exhibit UV band that may interfere with strong charge transfer peaks due to trace iron contaminants, it cannot be excluded39.

Diffuse reflectance spectroscopy, especially the bandgap energy, is valuable for probing optically induced transitions. Furthermore, it provides information on the structural characteristics of glass. Figure 5 illustrates the diffuse reflectance (DR) spectra of the prepared glasses within wavelength range of 200–1800 nm. DR spectra demonstrate that the samples behave in the same manner as reflectivity increases at wavelengths higher than 800 nm. Additionally, different DR peaks of the samples can be seen in the UV–visible range at λ ≈ 300 to 800 nm reflects the electronic transformations of Molybdenum ions in glass matrices.

Figure 5
figure 5

The diffuse reflectance (DR) spectra of the prepared glasses.

Full size image

The determination of the optical transition (optical band gap) relates to the optical absorption coefficient (α) which was derived as aforementioned from Kubelka–Munk relation20,21,22,23.

$$\upalpha hv = C_{{1}} \left( {hv - E_{g} } \right)^{{\text{n}}}$$
(9)

where n determines the nature of electronic transition. It is well known that optical transitions take place directly (n = 1/2) or indirectly (n = 2) across the region between conduction and valence bands (optical band gap). These transitions in vitreous materials like glass, are almost indirect transitions, i.e., the effects of glass forming anions on the conduction band and cations, play a significant role in indirect transition which is always associated with absorbing or releasing phonons49. Figure 6 depicts (αhν)1/2 versus photon energy (hν) for studied samples. The linear extrapolation of the curves to the hν axis at (αhν)1/2 = 0 gives the value of the optical energy band gap for indirect Eopt transitions.

Figure 6
figure 6

(αhν)1/2 as a function of (hν).

Full size image

SrO and the base glass lattice affect the optical band gap energy in the present glass system. By increasing the SrO concentration, the indirect transition values decreased from 3.22 to 2.17 eV. It has been acknowledged that the oxygen bond strength forming the glass network directly influences the absorption edge location. These links are broken with network modifiers resulting in non-bridged oxygen. One end of the glass network structural unit is partially associated with these oxygen ions, which are partially negative in charge. Thus, the change in Eopt can be correlated with the change in the glass lattice, which influences cross-linking density50. The Fig. 7 shows how the bandgap energy Eg declines as the SrO content increases. This reduction may be attributed to the increase in non-bridged oxygen within the glass matrix, caused by replacing Li2O with SrO. These oxygens significantly contribute to the valence band due to their energy. Since non-bridging oxygens are more energetic and active than bridging oxygens, valence band energy rises and Eg decreases. Additionally, with a higher atomic number, coordination number, and ionic radius, the conduction band moves down more frequently. By creating non-bridging oxygen and decreasing glass structural tightness, Eg is lowered38,50.

Figure 7
figure 7

The variation of the gap energy Eg vs SrO content.

Full size image

ESR results

ESR spectroscopy was used to confirm the status of molybdenum ions in glass samples and approve the UV–visible findings. Figure 8 displays ESR spectra at room temperature of the studied molybdenum phosphate glasses where successive portions of Li2O were replaced by SrO. The spectra exhibit a hyperfine structure with resonance lines have g-values, parallel at g||= 1.91716 and perpendicular at g⊥ = 1.93602 which are corresponding to octahedrally coordinated Mo5+ ions paramagnetic active species, the octahedron being trigonally distorted51. It is observed that with an increase in SrO content in glass composition from 0 to 20 mol%, there is no change in g-values. However, there is a noticeable increase in signal intensity. The increase may be due to the charge transition transfer between Mo6+ and Mo5+41,51.

Figure 8
figure 8

ESR spectra of the studied glasses.

Full size image

Electrical conductivity

Figure 9 illustrates the logarithmic variation of AC conductivity (log σac) as a function of frequency for all samples at room temperature (298 K) covering a frequency range from 0.042 kHz to 1 MHz. At lower frequencies, a plateau region of independent frequency appears which corresponds to DC conductivity52. However, in higher frequency regions, AC conductivity is more frequency-dependent. According to Fig. 9, the AC conductivity of the samples increases with frequency, implying that they are of a semiconducting character53. The increase in AC conductivity of the material with increasing frequency can be attributed to the release of space charges caused by a decrease in the material's barrier properties54. As an example, sample Sr5 exhibits an AC conductivity value of approximately 1.43 × 10–5 S cm−1 at lower frequencies, up to about 50 kHz, which then increases to 1.84 × 10–4 S cm−1 at 1 MHz, as detailed in Table 2.

Figure 9
figure 9

Variation of log σac as a function of frequency measured at 298 K for glass samples.

Full size image
Table 2 The DC activation energy (Ea(dc)), the DC conductivity (σdc) at room temperature (RT) and the AC conductivity (σac) at 1 MHz and at RT for all glass samples.
Full size table

The frequency dependence of conductivity (σac) for samples Sr5 and Sr15 (chosen as representative samples) is illustrated in Fig. 10a,b at different temperatures. It is evident from the figure that the σac increases with increasing frequency. Furthermore, as the temperature increases the values of conductivity rise. This observation strongly suggests that the electrical conductivity of the material is a thermally activated process55.

Figure 10
figure 10

Variation of log σac as a function of frequency for glass samples (a) Sr5 and (b) Sr15 at different temperatures.

Full size image

Figure 11 displays the temperature-dependent DC electrical conductivity of glass samples with the composition 40 P2O5 − 20 MoO3 − 15 MgO-(25-x) Li2O-x SrO, featuring varying SrO content. The electrical conductivity σdc is thermally activated process and follows the Arrhenius relation

$$\upsigma_{{{\text{dc}}}} = \, \upsigma_{{\text{o}}} {\text{exp }}\left( { - {\text{E}}_{{\text{a}}} /{\text{ kT}}} \right),$$
(10)

where σo is the pre-exponential factor, Ea is the activation energy for conduction, T is the absolute temperature and k is the Boltzmann constant. The figure reveals that the electrical conductivity (σdc) of these glasses increases with temperature across the entire temperature range, indicating their semiconducting nature56. At the high temperature region ranging from 413 to 473 (K), the DC activation energies (Ea(dc)) are determined from the slopes of the straight lines of the log σdc plots versus 1000/T plots and the values are listed in Table 2. The range of activation energy values falls between 0.13 and 2.15 (eV).

Figure 11
figure 11

The variation of Log σdc versus 1000/T for glass samples of the composition 40 P2O5 − 20 MoO3 − 15 MgO-(25-x) Li2O-x SrO at different contents of SrO (mol%). Error bars are determined.

Full size image

In addition, in Fig. 11, it can be noticed that the σdc of the samples Sr0 and Sr5 exhibits a non-linear increase with rising the measuring temperature, featuring two distinct regions. These two regions are formed by two different mechanisms. The first region, at lower temperatures ranging from room temperature up to approximately 373 K, is characterized by low activation energy. This behavior is attributed to electronic transition mechanisms, likely facilitated by the presence of molybdenum ions in multivalent states (Mo3+, Mo4+, Mo5+, and Mo6+)57 as confirmed by UV–visible spectra. While the second mechanism observed at higher temperatures (413–473 K) exhibits higher activation energy. This is primarily due to ionic movement mechanisms driven by the mobility of charge carriers, specifically Li+ ions.

Furthermore, for samples Sr10, Sr15, and Sr20, it is evident that the electrical conductivity (σdc) increases linearly with rising temperature, accompanied by relatively low activation energies ranging from 0.13 to 0.37 eV. The substantial decrease in Li+ concentration due to the substitution of lithium ions with alkaline-earth metal ions is expected to lead to a reduction in the number of ionic carriers, consequently resulting in decreased ionic conductivity. Moreover, the replacement of Li2O by SrO is found to increase the presence of non-bridging oxygen (NBO) ions, a finding confirmed by UV–visible spectra. This increase in NBO ions, in turn, enhances the mobility of charge carriers, primarily electrons. This explains the decrease of the Ea(dc) with the addition of SrO and suggests that the conduction in glass samples Sr10, Sr15 and Sr20 is mainly electronic.

Figure 12 illustrates the variations in both room temperature DC electrical conductivity (σdc) and activation energies (Ea(dc)) as a function of SrO concentration (in mol%). It is evident from this figure that σdc decreases from 1.10 × 10–6 to 8.31 × 10–8 (S/cm) as the SrO concentration increases from 0 to 20 mol%. Notably, the plot exhibits a maximum value when x = 5 mol% of SrO. To elucidate this behavior, it is worth noting that various studies suggest that alkali ions contribute more significantly to the conductivity of oxide glasses doped with alkali and alkaline earth ions, whereas alkaline earth ions have a less pronounced effect58,59. As a result, Li2O ion species exhibit greater mobility and ease of diffusion compared to SrO ion species within the glass matrix. Consequently, in the present study, the initial replacement of SrO concentration (at 5 mol%) leads to an increase in σdc, reaching 1.64 × 10–5 S/cm, accompanied by a decrease in activation energy.

Figure 12
figure 12

The Variation of the σdc at 298 K and high temperature activation energy, Ea(dc), with mole fractions of SrO for all glass samples. Error bars are determined.

Full size image

Additionally, the increase in conductivity can be attributed to structural modifications within the phosphate network. The presence of SrO is known to induce a loosening effect on the glass matrix10,60. Consequently, this structural change facilitates the migration of conducting ions (Li+ ions), which are smaller (90 pm) compared to Sr2+ ions (132 pm). This size disparity enhances ion mobility, resulting in increased conductivity. In this context, both Li+ ion concentration and the introduction of non-bridging oxygen species, a result of adding the modifier oxide SrO9, can influence glass conductivity. This effect is especially notable during the initial replacement with 5 mol% SrO in sample Sr5, leading to an increase in conductivity.

With further replacement of SrO, both the conductivity and activation energy decrease. This drop in conductivity is attributed to the increased presence of less mobile SrO ions at the expense of more mobile Li2O ions, resulting in reduced conductivity for the glass samples Sr10, Sr15, and Sr20. However, the increased number of non-bridging oxygens (NBO) with a higher concentration of SrO suggests the dominance of electronic conduction with lower activation energy. The nonlinear variation of activation energy and DC conductivity within the studied glass compositions is attributed to the occurrence of a mixed cation effect58.

Conclusions

Improved molybdenum phosphate glasses with the composition 40 P2O5, 20 MoO3, 15 MgO, (25-x) Li2O, x SrO where 0 ≤ x ≤ 20 mol % were prepared via the melt-quenching technique. Increasing the strontium oxide content leads to enhanced packing of coordination polyhedra in the glass network, resulting in increased glass density and hardness. This compactness arises from Sr2+ ions occupying interstitial spaces within the network structure. FTIR of the base glass Sr0 displayed the characteristic absorption bands of oscillation modes of the basic building blocks of the glass lattice PO2, PO3, PO4−, MoO4−. The introduction of SrO into the glass network led to modifications as phosphate chains depolymerized, driven by the modifying behavior of Sr2+ ions. FTIR deconvoluted spectra confirmed structural network modifications associated with increasing SrO content, up to 20 mol%. The optical measurements revealed the presence of diverse active molybdenum ion species incorporated into the glass network. They explained the role of modifier ions in the structural network leading to an increase in non-bridging oxygen. Consequently, the bandgap energy decreased, transforming the glass from an insulator with its characteristic features into a material exhibiting semiconductor properties. Temperature dependent DC electrical conductivity was investigated. The samples' electrical conductivities increase with temperature, revealing semiconducting behavior. It was observed that the conductivity of Sr0 and Sr5 samples was the highest. This may be due to the dominance of lithium ions over their conductivity. As the concentration of strontium oxide increases beyond 5 mol%, the observed conductivity may be mainly electronic, which can be attributed to the hopping of electrons between multivalent states of molybdenum in addition to the enhanced electrons created by the increasing number of NBO ions. For samples with SrO ˃ 5 mol%, the dominance of electronic mechanism over the ionic transfer ones may present good candidates for semiconductor materials in electronic devices. In addition, the investigated glass compositions exhibited favorable optical and electrical properties, enhancing their suitability for applications in opto-electronic devices.