Abstract
The paper examines the dynamics of asymmetric thin shell wormholes that connect two distinct spacetimes using the cut and paste technique. The focus is on analyzing the linear stability of these wormholes by considering radial perturbations and utilizing the modified generalized Chaplygin gas equation of state. The specific case of an asymmetric wormhole connecting Schwarzschild–Rindler spacetime to Schwarzschild–Rindler–de Sitter space–time is analyzed using this formalism. Our investigation uncovers the existence of both stable and unstable regions, which are contingent upon the appropriate selection of various parameters within the metric spacetime and equation of state. Additionally, we determine that stability regions exist as a consequence of the square speed of sound. By increasing the value of the cosmological constant, the stability region is expanded. Furthermore, the stability regions are augmented by the influence of Rindler parameters, while the stability regions are also affected by adjustments in the equation of state parameters, leading to their enlargement.
Similar content being viewed by others
Introduction
An asymmetric Schwarzschild–Rindler–de Sitter (SRdS) thin shell wormhole (TSW) is a theoretical geometric structure in general relativity that proposes the existence of a special type of wormhole composed of a thin, asymmetric shell mediating between two regions of four-dimensional spacetime with different characteristics. These theoretical structures have been studied by various researchers in the field of general relativity and wormholes, and theoretical analyses and complex calculations have shown that this type of wormhole could be theoretically possible according to Einstein’s equations1,2. The asymmetric thin-shell wormhole differs from other wormholes in its presence in a varying environment, where it exists in spacetime influenced by different forces such as gravity and cosmic expansion. This type of wormhole has been proposed for theoretical purposes and has not been extensively studied from a practical or experimental standpoint. The theoretical studies of asymmetric TSWs are part of ongoing research into understanding spacetime geometry and enigmatic phenomena like wormholes. By studying these theoretical structures, we can deepen our understanding of the nature of the universe and non-equilibrium fields in general relativity.
In 1966, a set formalism of invariant junction conditions at the surface of discontinuity was introduced by Israel3. There are two types of surfaces, such as boundary surfaces and surface layers. They play an important role in gravitational theory, both Newtonian and relativistic, and also in electromagnetic theory. Afterward, Visser4 investigated the idea of TSWs connecting two regions of different spacetimes or the same spacetimes by using cut and paste approach. These two regions are related by Israel junction conditions. Afterward, several authors discussed the construction and stability of TSWs in different theories with different equations of state (EoS). For instance, Poisson and Visser5 studied TSWs of two identical copies of Schwarzschild spacetimes. Gerica et al.6 studied the generic TSWs in relativity. The stability of various types of TSWs with different EoS has been extensively investigated by several researchers. Eiroa7 examined TSWs supported by a generalized Chaplygin gas (GCG) and studied their stability. Mazharimousavi et al.8 analyzed the stability of cylindrical TSWs. In another work, Mazharimousavi et al.9 analyzed the stability of TSW with a variable EoS. Varela10 investigated the stability of Schwarzschild TSWs with a variable EoS. Eid11 discussed the stability of cylindrical TSWs with Phantom energy. Eiroa12 conducted a stability analysis of TSWs in general. Kokubu and Harada13 discussed TSWs in the context of the Einstein-Gauss-Bonnet theory of gravity. Eid1 explored TSW stability in f(R) theory. Rahaman et al.14 studied the stability of TSWs in the context of Heterotic string theory. Finally, Eid15 investigated TSW stability in the Einstein-Hoffman-Born-Infeld theory. Recent studies have focused on analyzing the stability of asymmetric TSWs that exhibit different manifolds in the two regions of the throat. Forghani et al.16 investigated the stability of such asymmetric TSWs and addressed the issue of discontinuity in linear stability. They discussed the challenges associated with maintaining stability in these configurations. Additionally, Forghani et al.17 further explored the discontinuity in the linear stability of TSWs. In a related study, Eid2 examined asymmetric TSW stability with a variable EoS, shedding light on its behavior under different conditions.
In a series of papers Javed et al.18,19,20,21,22,23 have discussed thin shells in different physical contexts and different modified theories, e.g., the effect of a scalar field on the dynamical evolution of thin shell with hairy Schwarzschild black hole, the quantum corrected charged black hole solution bounded by quintessence, thin shell dynamics in regular charged black hole through T-duality, the stability of nonlinear electrodynamics thin shell wormholes via variable equations of state, new generic wormhole models with stability analysis via thin shell, stability analysis of new thin shell wormhole in teleparallel gravity. Also, Mustafa and coworkers24,25 have discussed the stability of thin shell wormholes within string cloud and quintessential field via the van der Waals and polytropic EOS, and also the construction of thin-shell around new wormhole solutions via solitonic quantum wave dark matter. In addition, Javed26 studied the geometric structure of a thin shell within the context of metric-affine gravity. Also, he studied the stability and dynamics of scalar field thin-shell for renormalization group improved Schwarzschild black holes27. Waseem et al.28 discussed the stability constraints of d-dimensional charged thin-shell wormholes via quintessence and a cloud of strings. Sharif and Javed29 studied the stability of charged thin-shell gravastars with quintessence. Moreover, Godani30 studied the linear and nonlinear stability of charged thin-shell wormholes in f(R) gravity. Mishra et al.31 studied the traversable wormhole models in f(R) gravity. Mazharimousavi32 discussed the thin shell wormhole satisfying the null-energy condition unconditionally. Hernández-Almada et al.33 discussed the cosmological constraints on the alternative model to Chaplygin fluid revisited. Debnath et al.34 analyzed the modified cosmic chaplygin AdS black hole. Bambi and Stojkovic35 discussed the astrophysical wormholes. De Celis and Simeone36 studied the traversability of thin-shell wormholes.
Recently, Grumiller37 investigated a new kind of model for the gravity of a central object at large scales. He obtained an extra new term that generates acceleration, similar to the ones observed in various abnormal systems in nature, called Rindler acceleration. Carloni et al.38 conducted a study examining the constraints imposed by the solar system on Rindler acceleration within the framework of general relativity. They investigated how Rindler acceleration, a concept related to the acceleration experienced by an observer in flat spacetime, affects the behavior of gravitational systems in our solar system. In a separate study, Sakalli and Mirekhtiary39 explored the influence of Rindler acceleration effects on Grumiller black hole (GBH) spectroscopy. They examined how the presence of Rindler acceleration, which is associated with non-inertial frames of reference, impacts the spectroscopic features of GBHs. This research sheds light on the connection between Rindler acceleration and the observable characteristics of black holes within the Grumiller model. Moreover, Sakalli and Ovgun40 studied the deflection of light and Hawking radiation from a Rindler- modified Schwarzschild BH. Afterward, Alestas et al.41 analyzed the stability of Schwarzschild–Rindler-anti de Sitter TSWs. Also, Muniz et al.42 studied the scalar particles around a Rindler-Schwarzschild wormhole.
Motivated by the aforementioned considerations, in the present our work is to investigate the dynamical and stability analysis of asymmetric TSW within the background geometry of Schwarzschild- Rindler- de Sitter spacetime under linear radial perturbation around the static solution via the modified generalized Chaplygin gas (MGCG) EoS. The paper is constructed as follows. In “Stability analysis of asymmetric Schwarzschild–Rindler–de Sitter TSW” section we display the dynamics and the stability analysis of asymmetric TSW under linear perturbation supported by MGCG EoS. Finally, a remarking conclusion is discussed in “Conclusion” section.
Stability analysis of asymmetric Schwarzschild–Rindler–de Sitter TSW
Grumiller37 introduced an effective model called Rindler-modified Schwarzschild black hole geometry. He found a new term that generates acceleration (called Rindler acceleration) and leads to an abnormal acceleration in the geodesic of the test particle. The action describes the generic effective theory given by Grumiller,
where \(g=det\left({g}_{\mu \nu }\right),\) \(\Phi ,\) and \(\Lambda\) are the determinants of the metric tensor, the scalar (dilaton) field, and the cosmological constant, with \(R\) being the Ricci scalar curvature and \(b\) representing the Rindler acceleration parameter.
Due to studying the influence of cosmological constant and Rindler acceleration on the stability of TSWs, regarding the background of static spherically symmetric line elements whose interior (−) and exterior (+)Schwarzschild–Rindler–de Sitter (SRdS) line elements are described by
and
In the given context, the variables \(m_{ \pm }\), \({b}_{\pm }\) and \({\Lambda }_{\pm }\) represent the mass of the central black hole object, the Rindler acceleration parameter, and the cosmological constant associated with both sides, respectively. When b equals zero, the solution of Schwarzschild-de Sitter is recovered. In the case where b and Λ are both zero, the solution of the Schwarzschild black hole is recovered. Furthermore, the metric (3) reduces to the two-dimensional Rindler metric, when m and Λ are equal to zero.
The stability of a static solution of radius \({r}_{^\circ }\) considering \(\text{G}({r}_{^\circ })>0\), so that no event horizon is present when \(\text{r}>{r}_{h}\). Also, for \(\text{r}={r}_{h}\), the metric function (3) becomes \(G\left(\text{r}\right)=0.\) In addition, the metric function can be written in the form: \(G\left(\text{r}\right)=\frac{2b}{r} \left(\text{r}-{r}_{h}\right)\left(\text{r}-{r}_{n}\right),\) where \({r}_{n}=-\frac{1}{4b} \left(1+\sqrt{1+16bm}\right),\) 40. Thus, from a negative value of \({r}_{n}\), it cannot be explained as the horizon. So, the RMS metric possesses only the event horizon, \({r}_{h}=\frac{1}{4b} \left(-1+\sqrt{1+16bm}\right).\)
Moreover, the metric (3) with \((1>9{m}^{2}{\Lambda }_{ext}>0)\) becomes zero at two positive values of \(\text{r}\) corresponding to two real positive roots. When \({m}^{2}{\Lambda }_{ext}>\frac{1}{9}\), the metric function becomes negative, so let \({m}^{2}{\Lambda }_{ext}\le \frac{1}{9},\) 7.
Thus, if \(\left(0<\Lambda {m}^{2}\le \frac{1}{9}\right),\) the metric has two horizons one is the event horizon and the second is the cosmological horizon. For increasing \(m\), \({r}_{h}\) and keeping \({\Lambda }_{ext}\) constant, the cosmological horizon will decrease. Therefore, both horizons coincide at \(r={r}_{h}= {r}_{c}=3m.\) In most cases, we let \({m}_{-}=1\), so the cosmological horizon becomes dimensionless and equal \(\Lambda {m}_{-}^{2}\). Consequently, the radius of the throat is always considered in the region outside the event horizon of BH (\(\text{r}>{r}_{h}\)). Therefore, for the considered parameter values there is no \({r}_{c}\) but only \({r}_{h}.\)
Afterward, the geometry of TS surrounding wormhole spacetime is developed by the cut-and-paste approach.
The single manifold \(M\), bounded by hypersurface \(\Sigma\) is obtained by gluing together the two regions \({M}^{+}\) and \({M}^{-}\) at their boundaries, \(M={M}^{+}\cup {M}^{-},\) with natural identification of the boundaries (hypersurface) \(\Sigma \equiv {\Sigma }^{+}={\Sigma }^{-}.\)
For the time-like hypersurface \(\Sigma \equiv {\Sigma }^{\pm }=\left\{{r}^{\pm }=a|a>{r}_{h}\right\}\). We set the values of \(a\) (radius of the throat) greater than the event horizon radius \({r}_{h}\) to avoid the presence of horizons and singularities in the line element (2),43.
Assuming that \(h_{ + } = h_{ - } = r^{2}\) is at the location of the throat, and the time evolution \(a(\tau )\) is described by the throat radius \({r}_{\pm }=a(\tau )\), with the proper time \(\tau\) along the hypersurface. Consequently, on the hypersurface \(\Sigma ,\) the induced (intrinsic) metric is defined by
Furthermore, according to the Darmois–Israel formalism introduced by Israel3, the extrinsic curvature across the hypersurface Σ, can be expressed as follows,
where \(\xi^{i}\) and \({\chi }_{\pm }^{\alpha }\) are the coordinates on Σ and coordinates in \({M}^{\pm }\), while \({\Gamma }_{\alpha \beta }^{\gamma }\) and \(n_{\gamma }^{ \pm }\) correspond to Christoffel symbols and the four-unit normal vector.
Moreover, the extrinsic curvatures of the metric (3) are described by
in which the dot and the prime represent the derivatives of \(\tau\) and \(a\), respectively.
Accordingly, the surface stress-energy tensor \({S}_{j}^{i}=diag(-\sigma ,{p}_{\theta },{p}_{\varphi })\), related to the discontinuity of \({K}_{ij}^{\pm }\) at Σ, is described by the Lanczos equation5,
with \(\left[ K \right]\) representing the trace of \(\left[ {K_{ij} } \right] = K_{ij}^{ + } - K_{ij}^{ - }\), while \(\sigma\) and \(p\) represent the surface energy density and pressure, respectively. Therefore, Lanczos equations become
Consequently, by inserting (6) into (8) and (9) to obtain
It is observed that the negative sign of (\(\sigma < 0\)) in Eq. (10) and the flare-out condition \(\stackrel{`}{h}>0,\) indicate that the matter at the throat is exotic. There are several energy conditions applied to the matter of the theory depending on the source of the energy–momentum tensor. It represents a common property to the states of matter and the field. It means that the distribution of matter at the throat violates the weak energy condition (\(\sigma \ge 0\), \(\sigma + p \ge 0\)) because \(\sigma\) is negative44. The null energy conditions require only that (\(\sigma + p \ge 0\)), from a static solution of (10) and (11) that \(\sigma +p<0\), this condition is violated. While the strong energy condition holds by \(\sigma +3p\ge 0\) and \(\sigma + p \ge 0\) is satisfied for \(\Lambda <0\) and violated for \(\Lambda >0\).
The recent cosmological observations, such as the cosmic microwave background radiation, type Ia supernovae (SNIa), and large-scale redshift structure, confirmed that our universe is undergoing a phase of accelerated expansion. The source of this acceleration is described by an exotic type of fluid with negative pressure called dark energy. The simplest two candidates of dark energy (DE) are the universe filled with exotic fluid and the second one is the cosmological constant. One exotic matter is Chaplygin gas (CG) which behaves like a pressureless fluid at an era and a cosmological constant at a later era.
Thus, a universe may be described starting from the radiation stage to the dominated stage by DE consistently. Consequently, the general modification of CG (called MGCG) is suitable to describe the evolution of the universe over a wide range epoch. And also, MGCG is a fluid model which unifies DE and dark matter depending on the suitable choices of involved parameters34.
Therefore, to study the stability analysis within the context of RMSdS spacetime, we consider an exotic background fluid called MGCG whose EoS, Debnath et al.45, is described by
where \(0<\beta \le 1\), \(\alpha <0\), and \(\gamma \ge 0\) are free parameters.
When \(\alpha =0\) and \(\beta =1\) Eq. (12) is reduced to Chaplygin gas and reduced to generalized Chaplygin gas with \(\alpha =0\). Also, a cosmological constant emerges by setting \(\beta =0\) and \(\gamma =1+\alpha\). While, for \(\gamma =0\) it reduces to an EoS which describes a phantom energy with \(\alpha =-\delta\) and a quintessence fluid with \(\alpha =\delta\).
Furthermore, using the Eqs. (10), (11) and (12), the dynamical evolution becomes
Alternatively, the continuity equation is described by
and can be written in the form:
Accordingly, using Eqs. (12) and (15) to obtain
Thus, the second derivative of \({\sigma }^{\prime}\) becomes
As a result, the solution of Eq. (16) is determined by
with \(n=(\alpha +1)(\beta +1)\).
In addition, from Eq. (10) the dynamical equation becomes
in which the effective potential \(H(a)\) is described by
Consequently, a linearization is going to be done to determine whether and in what conditions the static solution with a radius \({a}_{\circ }\) is stable under a linear radial perturbation about \({a}_{\circ }\). To analyze the stability, the Taylor expansion up to the second order at \({a}_{\circ }\) of the effective potential is employed
Moreover, the first and second derivatives of \(\text{H}(a)\) take the following form:
where \(W=\frac{2h}{{h}^{\prime}}\sigma\), \(A=\frac{1}{2}({G}_{+}+{G}_{-})\) and \(T=({G}_{+}-{G}_{-}{)}^{2}\).
Inserting Eqs. (15), (17) and \(h={a}^{2}\) into Eq. (23) to obtain:
where \(\upvarepsilon ^{2} ( = {\text{dp}}/{\text{d}}\upsigma )\) is called the squared speed of sound.
From this perspective, the effective potential is approximated as a linear function around \(a={a}_{\circ }\). Thus, the necessary general conditions for the existence and stability of a static fluid shell \(\text{H}({a}_{\circ })=0\) and \({\text{H}}^{\prime}({a}_{\circ })=0\) are satisfied. As a result, the dynamical equation can be expressed as \({\dot{a}}^{2}\left(\tau \right)=-\frac{1}{2}{\text{H}}^{^{\prime\prime} }({a}_{\circ })(a-{a}_{\circ }{)}^{2}+O\left[(a-{a}_{\circ }{)}^{3}\right]\). The stability condition is examined by considering a linear perturbation and depends on the sign of \({\text{H}}^{^{\prime\prime} }({a}_{\circ })\) at the throat radius. A stable configuration is achieved when \({\text{H}}^{^{\prime\prime} }({a}_{\circ })>0\), while \({\text{H}}^{^{\prime\prime} }({a}_{\circ })<0\) indicates instability.
Consequently, from Eq. (24), the square speed of sound \({\upvarepsilon }^{2}\) takes the form:
Afterward, it is worth noting that the static solution (\(\ddot{a}=\dot{a}=0\)) of Eqs. (10) and (11) simplifies to
Furthermore, the dynamical evolution (13) becomes
Consequently, in the case of SRdS and Rindler-Schwarzschild (RS) spacetimes, let us assume that: \(m_{ - } = m{ ,}\) \(m_{ + } = \left( {1 + \omega } \right)m\), \(b_{ \pm } = b\), \({\Lambda }_{ - } = 0,\) and \({\Lambda }_{ + } = {\Lambda ;}\) therefore, the metric (3) takes the following form
Moreover, by plugging the Eq. (29) into (27) and (28), to obtain
Also, by inserting (29) into (20) to get
Meanwhile, inserting Eqs. (29), (30) and (31) into (25) to become
with,
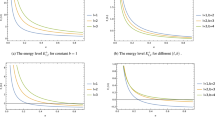
The graph of \({\varepsilon }^{2}\) against \(a\) is presented in Fig. 1, having different values of \(m,\omega ,b,\) and \(\Lambda\) as free parameters.
The graph of \({\varepsilon }^{2}\) against \(a\) with \(m=1\) and different values of: (a) \(\Lambda =-0.1,\omega =1,\) \(b=0, -0.04, -0.1, -1,\) (b) \(\Lambda =0.1,\) \(\omega =1\) \(, b=0, -0.04, -0.1, -1,\) (c) \(\Lambda =-0.1,\) \(\omega =1,\) \(b=0, 0.04, 0.1, 1,\) (d) \(\Lambda =0.1,\) \(\omega =1,\) \(b=0, 0.04, 0.1, 1,\) (e) \(\Lambda =-0.1,\) \(\omega =0.5,\) \(b=0, -0.04,- 0.1,- 1,\) (f) \(\Lambda =-0.1,\) \(\omega =0.5,\) \(b=0, 0.04, 0.1, 1,\) (g) \(\Lambda =-0.1,-\text{1,0.1,1},\) \(\omega =1,\) \(b=0.04,\) (h) \(\Lambda =-0.1,-\text{1,0.1,1},\) \(\omega =1,\) \(b=- 0.04,\) (i) \(\Lambda =-0.1,\) \(\omega =\text{0.5,1},\text{1.5,2},\) \(b=-0.04,\) (j)\(\Lambda =-0.1,\) \(\omega =\text{0.5,1},\text{1.5,2},\) \(b= 0.04.\)
The graphical representation of the effective potential \(\text{H}\left(a\right)\) against \(a\), obtained from Eqs. (32) and (18), is presented in Fig. 2. Various values of \(m,{b,a}_{\circ },{\sigma }_{^\circ },\omega ,\alpha ,\gamma ,\beta\) and \(\Lambda\) are considered as free parameters.
The graph of \(\text{H}\left(a\right)\) against \(a\) according to \(m=1, {a}_{\circ }=1,\) and \({\sigma }_{\circ }=1\) for different values of: (a) \(\Lambda =1,\omega =1,\) \(\gamma =1, \beta =1,b=0.04,\) \(\alpha =-0.01,- 0.1, -0.5, -1.1,\) (b) \(\Lambda =1,\omega =1, \gamma =1, \beta =1, b=0.04,\) \(\alpha =0.01, 0.1,\) \(0.5, 1.1,\) (c) \(\Lambda =1,\omega =0.5,\) \(\gamma =1, \beta =1,b=0.04,\) \(\alpha =-0.01,- 0.1, -0.5, -1.1,\) (d) \(\Lambda =1,\omega =1, \gamma =\text{0.1,0.5,1},2, \beta =1, b=-0.04,\) \(\alpha =- 1.1,\) (e) \(\Lambda =1,\omega =1,\) \(\gamma =1, \beta =\text{0.01,0.1}, \text{0.5,1}, b=-0.04,\) \(\alpha = -1.1,\) (f) \(\Lambda =1,\omega =1, \gamma =1, \beta =1, b=-0.04,\) \(\alpha =-0.01,-0.1-0.5,- 1.1.\)
The graphs of \({\varepsilon }^{2}\) versus \(a\) are given in Fig. 1 for different values of \(m,\upomega ,\text{b},\) and \(\Lambda\) as free parameters. The stability configuration increases due to increasing \(\Lambda ,\) in both cases of \(\Lambda >0\) and \(\Lambda <0\). Also, the stability configuration in the case of \(\Lambda <0\) is greater than the stability in the case of \(\Lambda >0.\) Similarly, the stability region increases by increasing \(\upomega\). Furthermore, the stability region decreases by decreasing the Rindler parameter \(\text{b}\) in the case of \(b <0,\) while for \(\text{b}>0,\) the stable region increases by decreasing b.
Furthermore, the variation between \(\text{H}\) and \(a\) is given in Fig. 2. The stability configurations can be extended by changing the value of the parameter \(\alpha\). The graphs are not changed with \(\Lambda\) and \(b\) parameters. While the stability configurations can be slightly extended due to \(\upomega\). Moreover, the graphs exhibit notable changes with changing \(\upbeta\) and \(\upgamma\) parameters.
To obtain a comparison for the stability configuration of the Schwarzschild, Schwarzschild–Rindler, Schwarzschild-de Sitter, and Schwarzschild–Rindler–de Sitter metrics, we graph Figs. 3 and 4, and the results are tabulated in Table 1.
The graph of \({\varepsilon }^{2}\) against \(a\) with \(m=1\) and different values of \(\Lambda ,b,\) and \(\omega .\) Fig. 3–1: \(\omega =1\) and (a) \(b=0,\) \(\Lambda =0,\) (b) \(b=0.1,\) \(\Lambda =0,\) (c) \(b=0,\) \(\Lambda =-0.1,\) (d) \(b=0.1,\) \(\Lambda =-0.1.\) Fig. 3–2: \(\omega =2\) and (a) \(b=0,\) \(\Lambda =0,\) (b) \(b=0.1,\) \(\Lambda =0,\) (c) \(b=0,\) \(\Lambda =-0.1,\) (d) \(b=0.1,\) \(\Lambda =-0.1.\) Fig. 3–3: \(\omega =0.5\) and (a) \(b=0,\) \(\Lambda =0,\) (b) \(b=0.1,\) \(\Lambda =0,\) (c) \(b=0,\) \(\Lambda =-0.1,\) (d) \(b=0.1,\) \(\Lambda =-0.1.\) Fig. 3–4: \(\omega =0\) and (a) \(b=0,\) \(\Lambda =0,\) (b) \(b=0.1,\) \(\Lambda =0,\) (c) \(b=0,\) \(\Lambda =-0.1,\) (d) \(b=0.1,\) \(\Lambda =-0.1.\)
The graph of \(\text{H}\left(a\right)\) against \(a\) with \(m=1\) and different values of \(\Lambda ,b,\) and \(\omega .\) Fig. 4–1: \(\omega =1\) and (a) \(b=0,\) \(\Lambda =0,\) (b) \(b=0.1,\) \(\Lambda =0,\) (c) \(b=0,\) \(\Lambda =-0.1,\) (d) \(b=-0.1,\) \(\Lambda =-0.1.\) Fig. 4–2: \(\omega =2\) and (a) \(b=0,\) \(\Lambda =0,\) (b) \(b=0.1,\) \(\Lambda =0,\) (c) \(b=0,\) \(\Lambda =-0.1,\) (d) \(b=-0.1,\) \(\Lambda =-0.1.\) Fig. 4–3: \(\omega =0.5\) and (a) \(b=0,\) \(\Lambda =0,\) (b) \(b=0.1,\) \(\Lambda =0,\) (c) \(b=0,\) \(\Lambda =-0.1,\) (d) \(b=-0.1,\) \(\Lambda =-0.1.\) Fig. 4–4: \(\omega =0\) and (a) \(b=0,\) \(\Lambda =0,\) (b) \(b=0.1,\) \(\Lambda =0,\) (c) \(b=0,\) \(\Lambda =-0.1,\) (d) \(b=-0.1,\) \(\Lambda =-0.1.\)
The graph of \({\varepsilon }^{2}\) against \(a\) is plotted in Fig. 3, with different values of \(m,\omega ,b,\) and \(\Lambda\) as free parameters.
The graphical representation of the effective potential \(\text{H}\left(a\right)\) against \(a\), obtained from Eqs. (32) and (30), is plotted in Fig. 4. Various values of \(m,\omega ,b,\) and \(\Lambda\) are considered free parameters.
The stability of thin shell wormholes for Schwarzschild, Schwarzschild–Rindler, Schwarzschild-de Sitter, and Schwarzschild–Rindler–de Sitter metrics is given in Table 1.
Conclusion
The study focuses on the dynamics of asymmetric traversable wormholes that connect two distinct spacetimes, namely the RS metric and the SRdS metric. The analysis is conducted using cut-and-paste techniques within the framework of the Darmois-Israel formalism. Additionally, the stability analysis of these asymmetric TSWs is investigated by considering linear radial perturbations and incorporating the modified generalized Chaplygin gas EoS. Furthermore, new results regarding the stability and dynamics of these asymmetric TSWs are presented. It may be that the asymmetric TSW is stable at \({\text{H}}^{^{\prime\prime} }({a}_{\circ })>0\), while at \({\text{H}}^{^{\prime\prime} }\left({a}_{\circ }\right)<0\) it turns out to be unstable. It is observed that the stable configurations depend on the appropriate values of different parameters included in the metric spacetimes and the MGCG EoS. We have found that the stability regions are greatly affected by the presence of the Rindler parameter as well as the cosmological constant. In summary, we concluded that the influence of the Rindler parameter increases the stability configurations, and the stability configurations are also extended by increasing the value of the cosmological constant. Also, the influence of changing the EoS parameters increases the stability regions.
Data availability
The data sets used and analyzed during the present study are available from the corresponding author upon reasonable request.
References
Eid, A. Stability of thin shell wormhole in f(R) theory of gravity. Phys. Dark Univ. 30, 100705 (2020).
Eid, A. Stability of asymmetric thin shell wormhole with a variable equation of state. Mod. Phys. Let. A 35(26), 2050215 (2020).
Israel, W. Singular hypersurfaces and thin shells in general relativity. Nuovo Cimento B 44, 1 (1966).
Visser, M. Traversable wormholes: Some simple examples. Phys. Rev. D 39, 3182 (1989).
Poisson, E. & Visser, M. Thin-shell wormholes: Linearization stability. Phys. Rev. D 52, 7318 (1995).
Garica, N. M., Lobo, F. S. N. & Visser, M. Generic spherically symmetric dynamic thin-shell traversable wormholes in standard general relativity. Phys Rev. D 86, 044026 (2012).
Eiroa, E. F. Thin-shell wormholes with a generalized Chaplygin gas. Phys. Rev. D. 80, 044033 (2009).
Mazharimousavi, S. H., Halilsoy, M. & Amirabi, Z. Stability of generic cylindrical thin shell wormholes. Phys. Rev. D 89(8), 084003 (2014).
Mazharimousavi, S. H., Halilsoy, M. & Amen, S. N. H. Stability of spherically symmetric time like thin-shells in general relativity with a variable equation of state. Int. J. Mod. Phys. D 26(14), 1750158 (2017).
Varela, V. Note on linearized stability of Schwarzschild thin-shell wormholes with variable equations of state. Phys. Rev. D 92, 044002 (2015).
Eid, A. Cylindrical thin-shell wormholes supported by phantom energy. Eur. Phys. J. Plus 131, 298 (2016).
Eiroa, E. F. Stability of thin-shell wormholes with spherical symmetry. Phys. Rev. D 78, 024018 (2008).
Kokubu, T. & Harada, T. Thin-shell wormholes in Einstein and Einstein–Gauss–Bonnet theories of gravity. Universe 6, 197 (2020).
Rahaman, F., Kalam, M. & Chakraborty, S. Thin-shell wormhole in the heterotic string theory. Int. J. Mod. Phys. D 16, 1669 (2007).
Eid, A. Stability of thin shell wormholes with a modified Chaplygin gas in Einstein–Hoffman–Born–Infeld theory. Ind. J. Phys. 91(11), 1451 (2017).
Forghani, S. D., Mazharimousavi, S. H. & Halilsoy, M. Thermodynamic stability of a Schwarzschild thin-shell wormhole. Eur. Phys. J. C 78, 469 (2018).
Forghani, S. D., Mazharimousavi, S. H. & Halilsoy, M. Discontinuity problem in the linear stability analysis of thin-shell wormholes. Eur. Phys. J. Plus 134, 342 (2019).
Javed, F. & Mustafa, G. Övgün Ali, The effect of scalar field on dynamical evolution of thin shell with hairy Schwarzschild black hole. Eur. Phys. J. Plus 138(8), 706 (2023).
Javed, F., Waseem, A. & Almutairi, B. Quantum corrected charged thin-shell wormholes surrounded by quintessence. Eur. Phys. J. C. 83(9), 811 (2023).
Javed, F., Mumtaz, S., Mustafa, G., Atamurotov, F. & Ghosh, S. G. Exploring thin-shell dynamics in regular charged black hole through T-duality. Chin. J. Phys. 88, 55 (2024).
Javed, F., Fatima, G., Mustafa, G. & Ovgun, A. Effects of variable equations of state on the stability of nonlinear electrodynamics thin-shell wormholes. Int. J. Geom. Meth. Mod. Phys. 20(1), 2350010 (2023).
Javed, F., Sadiq, S., Mustafa, G. & Hussain, I. A comparative study of new generic wormhole models with stability analysis via thin-shell. Phys. Scr. 97(12), 125010 (2022).
Javed, F., Mumtaz, S., Mustafa, G., Hussain, I. & Liu, W.-M. New wormhole models with stability analysis via thin-shell in teleparallel gravity. Eur. Phys. J. C. 82, 825 (2022).
Mustafa, G., Javed, F., Maurya, S. K. & Ray, S. Possibility of stable thin-shell around wormholes within string cloud and quintessential field via the van der Waals and polytropic EOS. Chin. J. phys. 88, 32 (2024).
Mustafa, G., Maurya, S. K., Ray, S. & Javed, F. Construction of thin-shell around new wormhole solutions via solitonic quantum wave dark matter. Ann. Phys. 460, 169551 (2024).
Javed, F. Computational analysis of thin-shell with scalar field for class of new black hole solutions in metric-affine gravity. Ann. Phys. 458, 169464 (2023).
Javed, F. Stability and dynamics of scalar field thin-shell for renormalization group improved Schwarzschild black holes. Eur. Phys. J. C. 83, 513 (2023).
Waseem, A., Javed, F., Zeeshan Gul, M., Mustafa, G. & Errehymy, A. Impact of quintessence and cloud of strings on self-consistent d-dimensional charged thin-shell wormholes. Eur. Phys. J. C. 83(11), 1088 (2023).
Sharif, M. & Javed, F. Stability of charged thin-shell gravastars with quintessence. Eur. Phys. J. C. 81, 47 (2021).
Godani, N. Linear and nonlinear stability of charged thin-shell wormhole in f(R) gravity. Eur. Phys. J. Plus 137(1), 883 (2022).
Mishra, B., Agrawal, A. S., Tripathy, S. K. & Ray, S. Traversable wormhole models in f(R) gravity. Int. J. Mod. Phys. A 37(05), 2250010 (2022).
Mazharimousavi, S. H. Thin-shell wormhole satisfying the null-energy condition unconditionally. Eur. Phys. J. C 82, 496 (2022).
Hernández-Almada, A., Magaña, J., García-Aspeitia, M. A. & Motta, V. Cosmological constraints on alternative model to Chaplygin fluid revisited. Eur. Phys. J. C 79, 12 (2019).
Debnath, U., Pourhassan, B. & Sakallı, I. Modified cosmic Chaplygin AdS black hole. Mod. Phys. Lett. A 37(14), 2250085 (2022).
Bambi, C. & Stojkovic, D. Astrophysical wormholes. Universe 7, 136 (2021).
De Celis, E. R. & Simeone, C. About the traversability of thin-shell wormholes. Eur. Phys. J. C 81, 937 (2021).
Grumiller, D. Model for gravity at large distances. Phys. Rev. Let. 105, 211303 (2010).
Carloni, S., Grumiller, D. & Preis, F. Solar system constraints on Rindler acceleration. Phys. Rev. D 83, 124024 (2011).
Sakalli, I. & Mirekhtiary, S. F. Spectroscopy of Rindler modified Schwarzschild black hole. Astrophys. Space Sci. 350, 727 (2014).
Sakalli, I. & Ovgun, A. Hawking radiation and deflection of light from Rindler modified Schwarzschild black hole. Lett. J. Explor. Front. Phys. 118, 60006 (2017).
Alestas, G., Kraniotis, G. V. & Perivolaropoulos, L. Existence and stability of static spherical fluid shells in a Schwarzschild–Rindler-anti-de Sitter Metric. Phys. Rev. D 102, 104015 (2020).
Muniz, G. R., Christianssen, H. R., Cunha, M. S., Furtado, J. & Bezerra, V. B. Scalar particles around a Rindler–Schwarzschild wormhole. Universe 8(12), 616 (2022).
Alestas, G., Kraniotis, G. V. & Perivolaropoulos, L. Stable, spherical and thin fluid shells. Phys. Sci. Forum 2, 24 (2021).
Kim, S.-W. The physical properties of exotic matter. J. Korean Phys. Soc. 54(6), 2196 (2009).
Debnath, U., Banerjee, A. & Chakraborty, S. Role of modified Chaplygin gas in accelerated universe. Class. Quantum Gravity 21, 5609 (2004).
Author information
Authors and Affiliations
Contributions
A.A, A.E. and M.M. wrote the main manuscript text and M.A. prepared figures. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eid, A., Alkaoud, A., Khader, M.M. et al. Stability of asymmetric Schwarzschild–Rindler–de Sitter thin shell wormhole. Sci Rep 14, 12696 (2024). https://doi.org/10.1038/s41598-024-63342-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-63342-y