Introduction

White matter tracts in the brain have always been of interest to neuroscientists, who studied both their anatomy and their function1,2. Due to their organization in networks, connectomic analyses have been carried out to further understand brain function and plasticity3. While these approaches carry great potential to unravel new insights, it is of utmost importance to choose physical quantities that actually describe the connections that are made by axons in white matter tracts between different brain regions. However, little data exists to address this question, especially in the presence of brain tumors4,5.

Information in the brain travels along axons on an electrical basis and is transferred in synapses, which are mostly chemical6. When a larger number of axons travels together, they form a white matter tract, which gains its volume due to the surrounding myelin sheaths. These sheaths electrically isolate the axons and form a diffusion barrier that causes diffusion tensors to point in the tract direction when measured with diffusion tensor imaging (DTI) sequences in magnetic resonance imaging (MRI). Diffusion tensors can be used to create tractograms by using highly sophisticated algorithms that are able to consider crossing fibers as well as the presence of tumors, while still relying on expert interaction in the workflow7. Further, diffusion markers like fractional anisotropy (FA) can be calculated per voxel. FA is a measure of the directedness of diffusion and can take on values between 0 and 1. As of now, it is the most robust marker of white matter integrity8,9,10,11,12,13,14.

Tractograms usually consist of streamlines, describing the probability that a white matter tract is present along their coordinates12. This spatial information can then be used to define volumes of the depicted tracts15. While a great number of connectomic studies use streamline count or its derivates to measure structural connectivity, its biological relevance has not yet been proven16. On the other hand, diffusion measures like the mean FA of voxels in a tract volume have been shown to relate to outcome and function17,18,19.

Since automatic tractography methods are within reach to become feasible for routine data analysis, machine learning algorithms are of growing interest to handle the expansive amount of data15. However, feature selection is essential for the successful analysis of high-dimensional data20.

In order to safely resect high-grade gliomas, the expansion of our knowledge about functional white matter measurement is critical. This concerns surgical planning and navigation as well as the preparation of informed feature selection for machine learning in the future. We therefore analyzed the statistical relation of different white matter markers of the corticospinal tract (CST) with CST function and morphological CST affection.

Methods

Patients

This study was approved by the ethics committee of Leipzig University (297/21-ek) and was performed in accordance with the relevant guidelines and regulations. Informed consent was waived by the ethics committee due to the retrospective pseudonymized nature of the study. We retrospectively searched the database of our institution for all patients who were operated for a malignant glioma (WHO grade 3 and 4) and underwent preoperative MRI with DTI sequence between January 1, 2020 and December 31, 2021. Diagnostic criteria for tumor grading were based on integrated histomolecular classification and followed the WHO classification of 201621. Inclusion criteria were an MRI including DTI within 7 days before surgery and age of at least 18 years.

Contralateral paresis was measured according to the MRC scale and recorded dichotomously as "yes" or "no" according to clinical neurological examination of the patient22.

Imaging

MRI was conducted within seven days prior to surgery with a 3 T system (Ingenia, Philips, Eindhoven, Netherlands) using a single-shot echo-planar imaging diffusion tensor imaging (DTI) sequence (TR/TE = 7010/102 ms; FOV = 222 × 222 mm2; matrix 112 × 112; 50 slices without gap; slice thickness 2.7 mm; 32 non-collinear directions, b-value = 1000 s/mm2) and contrast-enhanced T1 weighted MPRAGE 3D dataset (TR/TE = 8.1/3.7 ms; FOV = 222 × 222 mm2; matrix = 512 × 512; 170 slices without gap, thickness 1 mm) using a dedicated head coil. The data was preprocessed with the dwipreproc23 command in MRtrix3 (www.mrtrix.org)24 including eddy correction and underwent a visual quality check. CST tractography was performed first manually with MRtrix317, and also automatically in TractSeg. 15 Tractography parameters included an FA cutoff of 0.15, a maximum length of 250 mm, a minimum length of 60 mm, and 106 seeds. The seed region was placed in the mesencephalon, and the target region in the internal capsule. An experienced neurosurgeon and an experienced neuroradiologist removed false-positive streamlines that were identified as collaterals to other tracts or showed clear signs of noise. CST affection was assessed in comparison to the contralateral CST by an experienced neuroradiologist and an experienced neurosurgeon, who were blinded for patient data, with: 0—unaffected (symmetric), 1—dislocated (asymmetric), 2—compressed (reduced volume), 3—infiltrated (contact or overlap with tumor). We recorded mean and median FA and streamline count from manual tractograms, and radiomic parameters from automatic tractograms25.

Radiomics

Radiomics were calculated upon the volumes of the respective tractograms of the CST. The space was defined in the FA map, so that voxel based calculations used the respective FA. A complete description is available under https://pyradiomics.readthedocs.io/en/latest/features.html25.

FA energy

Energy is a measure of the magnitude of all voxel values within the respective volume, where a larger value marks a larger sum of the squares25.

$${\text{energy}}=\sum_{i=1}^{{N}_{p}}({\text{X}}(i)+c{)}^{2}$$

FA kurtosis

Kurtosis measures the shape of the distribution of values, where a lower kurtosis marks a high concentration of values in form of a peak near the mean.

$${\text{kurtosis}}=\frac{{\mu }_{4}}{{\sigma }^{4}}=\frac{\frac{1}{{N}_{p}}\sum_{i=1}^{{N}_{p}}({\text{X}}(i)-\overline{X}{)}^{4}}{{(\frac{1}{{N}_{p}}\sum_{i=1}^{{N}_{p}}({\text{X}}(i)-\overline{X}{)}^{2})}^{2}}$$

Maximum 2D diameter column

This is the maximum slice diameter of the CST in the axial plane. It is defined as the largest pairwise distance between volume surface mesh vertices in this plane.

Maximum 3D diameter

This is defined as the largest pairwise Euclidean distance between volume surface mesh vertices, also known as the Feret Diameter.

Minor axis length

This is the second largest axis of the enclosing ellipsoid and calculated with the largest principal component λminor.

Elongation

Elongation reflects the ratio of the two largest principal components of the respective volume, where λminor and λmajor are the lengths of these components. It can take values between 0 and 1 and is defined as the inverse of true elongation for computational reasons.

$${\text{elongation}}=\sqrt{\frac{{\lambda }_{minor}}{{\lambda }_{major}}}$$

Surface area

Surface area is calculated with a mesh of triangles around the respective volume.

$$A=\sum_{i=1}^{{N}_{f}}{A}_{i}$$
$$\begin{array}{c}\begin{array}{c}{A}_{i}=\frac{1}{2}\left|{\text{a}}_{i}{\text{b}}_{i}\times {\text{a}}_{i}{\text{c}}_{i}\right|\end{array}\end{array}$$

Voxel volume

This volume is calculated through multiplication of the single voxel volume Vk with the number of voxels in the respective volume. It is less precise than mesh volume and is not used in further calculations.

$${V}_{voxel}=\sum_{k=1}^{{N}_{v}}{V}_{k}$$

Mesh volume

This volume is calculated from the mesh of triangles around the respective space by calculating the volume Vi of the tetrahedrons within that space defined by the origin O and the points ai, bi, and ci.

$$\begin{array}{c}\begin{array}{c}{V}_{i}=\frac{O{a}_{i}\cdot (O{b}_{i}\times O{c}_{i})}{6}\\ V=\sum\limits_{i=1}^{{N}_{f}}{V}_{i}\end{array}\end{array}$$

Surface volume ratio

This ratio is calculated with surface area A and mesh volume V.

$$\text{surface volume ratio}=\frac{A}{V}$$

Statistics

Statistical analysis was carried out with SPSS Statistics 27 (IBM, Armonk, NY, USA). FA values of all tracts were tested for normal distribution after D'Agostino-Pearson yielding non-normal distribution in all cases. Correlations were tested by bivariate non-parametric Spearman's rank order for significance. P-values < 0.05 were considered statistically significant. Receiver-operating-characteristics analysis was applied to report area under the curve (AUC), sensitivity, and specificity for each variable. For further investigation, the analyzed variables were sorted by their respective p-value. Significant correlations were then plotted in a diagram with the dependent variable.

Results

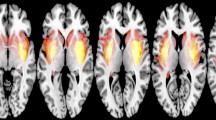
Screening of 42 patients yielded 24 patients (42% female) with high-grade glioma (five grade 3, 19 grade 4). Median time between preoperative imaging and surgery was one day (range 1–5 days). Six patients suffered from preoperative contralateral paresis. Epidemiological data is shown in Table 1. Example tractograms are shown in Fig. 1. In morphological affection rating, CSTs were dislocated by glioma growth in four patients, compressed in six and considered to be infiltrated in five. In the remaining nine patients CSTs were marked unaffected.

Table 1 Baseline data.
Full size table
Figure 1
figure 1

Example tractograms of the CST. Top row: Manual tractography result with MRTrix3 in coregistered contrast-enhanced T1 weighted MPRAGE 3D dataset. Bottom row: Automatic tractography result with TractSeg in a coregistered skull-stripped FA map. Left: coronal view. Right: sagittal view. Orientation in radiological convention.

Full size image

CST affection correlated most significantly with energy (based on FA, p = 0.002), median and mean FA (p = 0.008), and surface-volume ratio (p = 0.014). Contralateral paresis showed a significant correlation with 2D column diameter (p = 0.005), minor axis length (p = 0.006), kurtosis (based on FA, p = 0.008), median FA (p = 0.015) and mean FA (p = 0.026). Correlations sorted by their respective p-values are shown in Tables 2 and 3. Scatterplots of significant correlations are shown in Figs. 2 and 3.

Table 2 Markers of radiological affection.
Full size table
Table 3 Markers of motor function.
Full size table
Figure 2
figure 2

Scatter plots of significant correlations and streamline count with CST affection.

Full size image
Figure 3
figure 3

Scatter plots of significant correlations and streamline count with paresis.

Full size image

Discussion

This work analyzed the relation of different white matter parameters with clinical presentation in both radiological and clinical examination. The corticospinal tract (CST) was chosen due to its anatomical size and clinical importance in a large portion of neurological functions26. Damage to the CST is easily detectable and can be quantified in clinical presentation while being routinely demonstrated in MRI and more so in MRI tractography.

Furthermore, neurological deficits show significant correlations with overall survival in high-grade glioma, since a certain level of neurological function is always required for adjuvant treatment27,28. Neurological function and explicitly motor function is on the other hand important for maintaining quality of life in the treatment of high-grade glioma29.

The growing field of tractography studies motivates both clinicians and researchers to find better tools for patient evaluation and patient counseling by depicting and measuring different tracts or whole connectomes in patients with stroke, multiple sclerosis, or brain tumors5,30,31. The depiction of tract anatomy is becoming increasingly precise, which enables analyses of higher orders like connectomics32. However, surrogate variables of tract damage should be evaluated for their respective value before drawing conclusions from them in higher order analyses. Although FA has been shown to be a feasible marker of white matter integrity, streamline count is often used in the analysis of tractography or connectomes33.

In the presented analysis of high-grade glioma patients, we found no significant correlations of streamline count with radiological or clinical CST affection, which is well visible in the scatter plots of our data. Interestingly, different measurements of FA and CST volume showed different correlations with CST affection. Mean and median are easily applicable in both clinical and experimental setups, and have been demonstrated in our screening approach to indicate functional CST affection in imaging and neurological examination. This holds also true for mesh volume, voxel volume, surface area, and energy. While the latter is derived from FA values, it is interesting that its correlation with both radiological and clinical CST affection is stronger than mean and median. Since energy is the sum of the squared values of every voxel, it is volume-confounded, which may be the cause of its stronger correlation with CST integrity.

It is visible in the scatter-plots that voxel volume, maximum 3D diameter, mesh volume, and surface area correlate foremost with CST compression. This is to expect, since a reduced volume was the definition for compression in our data. Nevertheless, these variables correlate also with contralateral paresis, which points both towards intervariable correlations and overlapping effects of compression, infiltration, and function.

Surprisingly, three geometric variables correlate significantly only with paresis. Maximum 2D diameter column, minor axis length, and elongation seem to indicate CST function by its shape, independent from radiological CST affection. They may therefore be useful in automatic categorization of CST affection that is not easily assessable by expert interaction.

The fact that FA kurtosis is a strong indicator of CST function, but not radiological affection, is in line with previously published studies that mentioned postoperative FA in the CST to be more condensed around the mean. Interpreted together, it could indicate higher kurtosis and better motor function16.

Limitations

The data was retrospectively collected. Further, different MRI scanners and different tractography algorithms may deliver different results, which remains to be disproven. Therefore, prospective multicenter studies with comparison of different scanners and algorithms would be needed for confirmation or rebuttal of comparability. Also, CST affection was measured manually, which leaves room for uncertainty of the measurement. However, we believe, that reproducibility is given by following the thorough description of affection rating. Nevertheless, further studies which may apply machine learning approaches should analyze larger cohorts.

Conclusions

Our results confirm earlier studies that found FA to be a good indicator of white matter integrity and expand this finding for high-grade glioma. It is further shown that FA-derived radiomics like energy and kurtosis, as well as geometric radiomics like volume and elongation, are suitable indicators of tract integrity and can be used in further research on the functional relevance of white matter tracts. Streamline count should not be used for functional analysis.