Abstract
This study aimed to investigate body physical parameters as substitutes for water equivalent diameter (Dw) while calculating size-specific dose estimates (SSDEs) during adult chest computed tomography (CT). A retrospective analysis was conducted on 776 patients. Patients were divided into training set (542 patients) and validation set (234 patients) according to a ratio of 7:3. The correlations between physical parameters and Dw were analyzed. The differences between SSDEsubstitutes and the reference SSDE (SSDEreference) were compared. Strong positive correlations were observed between body mass index (BMI) and Dw as well as between weight and Dw in overall, male, and female patients (all p < 0.001). The correlations between BMI and Dw were stronger than those between weight and Dw in overall, male, and female subjects (all p < 0.001). SSDEweight and SSDEBMI were not significantly different from SSDEreference (p > 0.05). The RMSEs of overall patients between SSDEweight and SSDEreference as well as between SSDEBMI and SSDEreference were 0.237 and 0.2, respectively. The use of sex-specific regression equations for BMI caused a slightly reduction in RMSE. Weight and BMI can be used as surrogate parameters for Dw when calculating SSDE in adult chest CT exams, with BMI being the preferred substitute parameter.
Similar content being viewed by others
Introduction
Computed tomography (CT) is widely used in modern medical examinations for disease diagnosis, follow-up, and health assessments. The 2007 Recommendations of the International Commission on Radiological Protection stated that CT delivers the highest dose of ionizing radiation exposure in medical imaging1. Some studies2,3 have revealed an increased risk of cancer from radiation exposure. Therefore, ensuring an accurate assessment of the radiation dose delivered during CT scanning is crucial for evaluating radiation risks. Currently, the most common indicators for evaluating radiation dose in CT are volume CT dose index (CTDIvol) and dose-length product (DLP)4,5,6,7. CTDIvol, which indicates the radiation output within standard head and body phantoms, is a standardized index for comparing radiation output levels among different CT scanners using a reference phantom8. DLP is computed by multiplying CTDIvol with the length of the scan volume8. Both indices are affected by tube voltage, tube current, gantry rotation time, pitch, and other parameters8. However, notably, the actual radiation dose received by the human body is influenced by patient body size and X-ray attenuation properties of the examined tissue. Consequently, interpreting CTDIvol as the patient dose may result in either actual dose overestimation or underestimation, thereby causing inaccurate radiation risk estimates9.
Radiologists have been increasingly interested in radiation dose assessment methods that consider patient body size because of the limitations of CTDIvol in assessing radiation dose. In 20118, the American Association of Medical Physicists (AAPM) published a report (204) describing the use of dimensional measures, such as patients’ anterior–posterior (AP) diameter, lateral (LAT) diameter, AP + LAT diameter, and effective diameter (ED), in combination with CTDIvol to determine the size-specific dose estimate (SSDE) for CT scan. However, the abovementioned body diameters do not consider the impact of X-ray attenuation of tissue on the radiation dose. In 201410, the AAPM published report No. 220, introducing the use of water equivalent diameter (Dw) for calculating SSDE. According to AAPM 220, Dw = 2 \([\sqrt{\frac{1}{1000} \overline{CT(x,y)} ROI]+\frac{\text{AROI}}{\pi }}\), where \(\overline{CT(x,y)}ROI\) is the mean CT number in the region of interest (ROI), AROI is the total area of the ROI. Wang et al.11 confirmed that ED, which considers only geometry, in a chest phantom was 4.3–21.5% larger than Dw. Thus, Dw considers the effect of both patient body size and X-ray attenuation of the examined tissue on the radiation dose, which is a more appropriate parameter to evaluate SSDE, especially during chest CT. Many studies on the calculation and measurement of SSDE have been reported in recent years12,13,14,15,16,17,18,19. These studies use different methods to consider the influence of tissue attenuation12,13, body size14,15,16, and scanning parameters17,18,19 on the radiation dose, thereby improving the accuracy and precision of SSDE estimation. However, in these studies, it was necessary to measure organ density or body diameter based on CT localization image or axial image, which are only obtained after performing CT scan and have complex measurement methods. This is because the measurement method requires capturing the circumference of the patient’s entire body within the field of vision. This can be challenging for patients with obesity or under specific scanning conditions, such as spine examinations, wherein the entire body circumference cannot be accurately captured. Some commercial software programs20,21 have been used to calculate SSDE, but the accuracy and reliability may vary depending on the software and algorithms. Additionally, the cost of commercial software may be relatively high, leading to economic constraints for some backward regions or medical institutions, which may limit its wide application. Hence, easily achievable physical parameters would be beneficial for calculating SSDE instead of relying solely on the patient’s body diameter.
Therefore, this study aimed to explore whether easily achievable physical parameters, such as height, weight, and body mass index (BMI), can be an alternative for Dw to calculate SSDE. If feasible, doctors may develop personalized scanning protocols for patients based on their physical parameters before CT scan, thus optimizing the received radiation dose as much as possible.
Methods
Clinical data
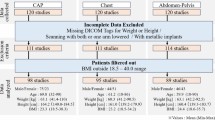
This study was approved by our Medical Ethics Committee (2021 WZ No. 003) and was conducted following the guidelines of the Declaration of Helsinki. This study included patients who underwent CT exams at our institution and provided informed consent. For the training set, we retrospectively analyzed the relevant data of patients who received CT exams in our hospital from May to July 2021. For the validation set, data on patients who underwent CT examination in our hospital between June and July 2022 were continuously analyzed. The inclusion criteria were as follows: (1) patients who underwent chest CT examination for illness or health examination purposes; (2) those aged > 18 years; (3) those with complete height and weight data; (4) those whose examination site included only the chest; and (5) those in whom the same protocol was used for each exam. The exclusion criteria were as follows: (1) patients with metal foreign bodies on the body surface or in the chest or metal internal fixators in the body, which could interfere with dose estimation; (2) those with pacemakers; (3) uncooperative patients; (4) and those with a cross-sectional image but with no entire body circumference data. Finally enrolled patients were divided into training set and validation set according to a ratio of 7:3. The regression equation between physical parameters and Dw was established using the training set data. Validation set data were used to verify the reliability of the regression equation.
CT examination
A SOMATOM Definition Flash scanner (Siemens, Germany) was used to conduct CT examinations. Care KV and Care Dose 4D were activated for all patients, Which can automatically select the appropriate KV and mAs for patients according to body size. The preset parameters were tube voltage of 80–120 kV, quality reference of 100 mAs, detector collimation of 128 × 0.6 mm, acquisition matrix of 512 × 512, field-of-view of 314 × 314 mm, gantry rotation time of 0.5 s, pitch of 1.5, reconstruction source image slice thickness of 1 mm, and interslice spacing of 1 mm. The reference mAs is the initial mAs value preset by the device based on the scanning conditions and can be used as a guide to adjust and optimize the radiation dose. All patients were placed in the supine position, with the head first entering the scanner. The scanning region ranged from the lung apex to adrenal glands.
Data collection and calculation
After completing the scan, the patient’s image and demographics (including sex and age) were automatically transmitted to the Picture Archiving and Communications System (PACS). The CTDIvol reference for a 32-cm diameter phantom and DLP were automatically output by the CT scanner console and transmitted to the PACS. The patient’s physical parameters, including height and weight, were routinely measured by CT technicians before examination and were recorded in the PACS. The equation provided by the World Health Organization22 BMI = weight (kg)/height (m)2, was used to calculate the BMI. The patient’s images and dose data were imported into the previously validated23 software tool “Teamplay Dose” (Siemens Healthineers), and Dw and SSDE were automatically calculated. In training set, correlations between physical parameters (including height, weight, and BMI) and Dw were analyzed, and their respective regression equations were established. In the validation set, Dwheight, Dwweight, and DwBMI were calculated using the regression equations between height and Dw, weight and Dw, and BMI and Dw. The AAPM 2049 and 22010 reports provide the following Eqs. (1) and (2) for calculating SSDE. We used Dwweight, Dwheight, and DwBMI instead of Dw in Eqs. (1) and (2) to calculate the corresponding SSDEweight, SSDEheight, and SSDEBMI. We then compared SSDEsubstitutes (including SSDEweight, SSDEheight, and SSDEBMI) with the reference SSDE (SSDEreference) calculated via “Teamplay Dose.” The root mean square errors (RMSEs) between SSDEweight and SSDEreference, SSDEheight and SSDEreference, and SSDEBMI and SSDEreference were evaluated using the following Eq. (3).
where f is the size-dependent factor pertinent to the 32-cm diameter CTDIvol reference phantom, n is the number of patient.
Statistical analyses
Statistical Package for the Social Sciences (version 22, IBM Inc., NY, USA) was used to perform all data analyses. The Kolmogorov–Smirnov normality test and Levene’s test for homogeneity of variance were used for all data. Regarding data that satisfied normal distribution and homogeneity of variance, the mean ± standard deviation is used to represent the data, and an independent sample t-test is used to compare the differences between the two groups. Regarding data that do not satisfy normal distribution, non-parametric tests are used. P-value of 0.05 was considered to indicate statistical significance. Age, height, weight, BMI, Dw, CTDIvol, DLP and SSDE data did not show a normal distribution; therefore, these parameters were represented by median ± interquartile range (M ± IQR). Spearman correlation analysis was used to analyze the correlation of height, weight, and BMI with Dw, as well as the correlation of age with height, weight, BMI, Dw, CTDIvol, and SSDE. The absolute value of the correlation coefficient within the range of 0.8 to 1 indicates a very strong correlation, 0.6 to 0.8 indicates a strong correlation, 0.4 to 0.6 indicates a moderate correlation, 0.2 to 0.4 indicates a weak correlation, and 0 to 0.2 indicates a very weak correlation. Simple linear regression analysis was used to predict Dwweight, Dwheight, and DwBMI, and correlation regression formulas were established. Fisher’s Z transformation was used to compare the differences in correlation coefficients. The Mann–Whitney U test was used to compare the differences between CTDIvol and SSDE as well as between SSDEsubstitutes and SSDEreference.
Results
Basic patient information and dose data
A total of 776 patients (378 males and 398 females) were enrolled, including 542 patients (247 males and 295 females) in the training set and 234 patients (131 males and 103 females) in the validation set. Weak or moderate correlations were found between age with height, weight, BMI, Dw, CTDIvol and SSDE for all patients, male patients, and female patients (all p < 0.05). Table 1 shows the correlation coefficients between age and body size and radiation dose. Figure 1 shows the flowchart of patient selection. The Dw of all patients was 23.77 ± 2.54 cm, which was lower than the phantom diameter (32 cm). The median CTDIvol and SSDEreference for all patients were 3.03 ± 0.83 mGy and 4.62 ± 0.92 mGy, respectively. Notably, CTDIvol was 34.42% lower than SSDEreference (Z = − 30.927, p < 0.001). Furthermore, male patients exhibited significantly higher Dw, CTDIvol, DLP, and SSDE values than female patients. Table 2 shows the basic information and dose data of the patients. The CTDIvol (2.92 ± 0.72 mGy) and SSDE (4.56 ± 0.74 mGy) in the training set were lower than those in the validation set with CTDIvol = 3.33 ± 1 mGy and SSDE = 5.11 ± 1.62 mGy, all p < 0.001. The Dw (23.3 ± 2.96 cm) in the training set was lower than that (24.56 ± 1.76) in the validation set, p < 0.001.
Correlation between physical parameters and Dw in training set
A weak correlation was observed between height and Dw in overall and female patients (r = 0.151, 95% confidence interval [CI] 0.06 to 0.235, p < 0.001; r = − 0.164, 95% CI − 0.282 to 0.036, p = 0.01, respectively). Male patients demonstrated no significant linear correlation between height and Dw (r = 0.056, 95% CI − 0.065 to 0.187, p = 0.379). However, in overall, male, and female patients, a strong positive correlation was noted between weight and Dw (r = 0.779 [95% CI 0.739 to 0.815], 0.834 [95% CI 0.831 to 0.891], and 0.71 [95% CI 0.633 to 0.774], respectively; all p < 0.001) as well as between BMI and Dw (r = 0.868 [95% CI 0.836 to 0.891], 0.903 [95% CI 0.876 to 0.924], 0.806 [95% CI 0.741 to 0.859], respectively; all p < 0.001). Figures 2 and 3 show the scatter plots of body physical parameters with Dw of patients.
Notably, the correlation between BMI and Dw was stronger than that between weight and Dw, regardless of overall, male, or female patients, as evidenced by statistical analysis (z = 7.685, 6.546, and 3.185, respectively; all p < 0.001). Table 3 shows the regression equations of weight with Dw, regression equations of BMI with Dw for overall, male, and female patients.
Comparison of SSDEweight, SSDEBMI, and SSDEreference in validation set
In the validation set, SSDEweight and SSDEBMI were not significantly different from SSDEreference in overall, male, and female patients (Table 4). The RMSE of overall patients between SSDEweight and SSDEreference as well as between SSDEBMI and SSDEreference were 0.237 and 0.2, respectively. When sex-specific regression equations were used for male patients, the RMSE between SSDEweight and SSDEreference as well as between SSDEBMI and SSDEreference were reduced to 0.217 and 0.18, respectively. When sex-specific regression equations for BMI were used for female patients, the RMSE between SSDEBMI and SSDEreference was reduced to 0.19. However, when sex-specific regression equation for weight was used for female patients, the RMSE between SSDEBMI and SSDEreference was increased to 0.24.
Discussion
This study divided patients into training set and validation set. Training set investigated the correlation between body physical parameters (height, weight, and BMI) and Dw. The results revealed a strong positive correlation of weight and BMI with Dw. The correlation between BMI and Dw was significantly higher than that between weight and Dw. The verification set verified the reliability of the results of the training group. The results showed that the calculated SSDEweight and SSDEBMI, based on the regression equation of weight and BMI, demonstrated statistically insignificant difference compared with SSDEreference. These results indicated that weight and BMI can be used as alternative parameters for Dw while calculating SSDE in adult chest CT examination. This facilitates doctors to estimate the radiation dose based on the patient’s weight or BMI without using complex calculation methods. This estimation can be performed before CT scan, thereby providing a reference for the doctors to personalize the scan plan and optimize radiation dose management.
Our study revealed that the Dw of all patients was 23.77 ± 2.54 cm, which was lower than the body phantom diameter (32 cm); moreover, CTDIvol was lower than SSDE. Our results were consistent with those of previous studies24,25,26. Valeri et al.26 revealed that CTDIvol tended to underestimate the radiation dose received by smaller patients. Klosterkemper et al.27 reported that CTDIvol was greater than SSDE when the Dw of chest and abdomen CT ranged from 37 to 43 cm. CTDIvol tends to overestimate the radiation dose in patients with obesity. As mentioned previously, Dw considers the effect of both patient’s body size and X-ray attenuation of the examined tissues on the radiation dose. The use of SSDE, which is calculated based on Dw, allows a more realistic estimation of the radiation exposure dose during CT examinations.
Our study revealed that weight and BMI have a strong positive correlation with Dw, consistent with the findings of previous studies28,29,30,31,32,33. Iriuchijima et al.29 revealed a positive linear correlation between body weight and Dw in chest and abdomen CT. Similarly, O’Neill et al.31 reported that ED has a good correlation with BMI in abdominal CT. Studies conducted by Khawaja32 and Kritsaneepaiboon33 revealed a strong correlation between body weight and body diameter. Although the results of our study are similar to those of previous studies, there are some differences in our study. First, most previous studies used geometric dimensions such as AP, LAT, or ED to calculate SSDE. However, in our study, Dw was used to calculate SSDE. Wang et al.11 confirmed that ED in a chest phantom was 4.3%–21.5% larger than Dw. This discrepancy arises from the fact that ED solely considers geometric factors and excludes the impact of X-ray attenuation of tissue on the radiation dose. Consequently, it causes an overestimation of the patient body size and an underestimation of SSDE. Khatonabadi’s34 study compared the correlation between Dw with lung dose, and ED with lung dose, and they confirmed that the correlation between Dw and lung dose was better than that between ED and lung dose. According to the calculation formula of Dw10, Dw takes into account both the average CT value within the entire perimeter range of the patient examined area, which represents tissue attenuation of X-rays, and the total area of the scanned region, which represents the patient's body size. Therefore, the radiation dose can be estimated more accurately when patient attenuation is taken into account. Second, most of the previous studies only analyzed the relationship between weight and body diameter, and did not analyze the relationship between BMI and body diameter. BMI takes into account both weight and height, providing a better representation of the patient's body size. Our study found that the correlation between BMI and Dw was consistently stronger than that between weight and Dw, regardless of sex. This indicates that BMI, which considers both weight and height, is a more accurate alternative parameter for Dw while calculating SSDE during chest CT examination. Third, some of the previous studies have focused on underage patients, who exhibit significant variations in body size across different age groups. Therefore, the findings of those studies may only be applicable to a specific age group. In contrast, our study focuses on adult patients whose physical development has reached a stable state, the results are more pragmatic and generalizable. Fourth, this study divides the data into training set and validation set. The reliability of the research results was verified by the validation set data. The results were more generalizable.
At the same time, we revealed a weak positive correlation between height and Dw in overall patients and female patients, which was consistent with a previous study28. However, male patients demonstrated insignificant linear correlation between height and Dw. These results indicate that considering height as an alternative parameter for Dw is inappropriate.
In order to verify the long-term stability of the regression equation, and better evaluate the performance of the regression equation in practical applications, we selected patients from different time periods as the validation set. Our results revealed that SSDEweight and SSDEBMI did not significantly differ from SSDEreference, with the RMSE between SSDEBMI and SSDEreference being lower than that between SSDEweight and SSDEreference. This finding revealed that these equations may be reliable tools for calculating SSDE in clinical practice. Additionally, when sex-specific regression equations of weight and BMI for males and BMI for females were used, the RMSEs were slightly reduced. However, when sex-specific regression equation of weight for females was used, the RMSE increased from 0.237 to 0.24 without significant change. In general, based on physiological and sexual characteristics, males have wider thorax and greater muscle mass than females. Hence, X-ray attenuation differs between male and female patients during chest CT. Therefore, to minimize errors, sex-specific regression equation of weight and BMI for males and BMI for females are recommended when calculating SSDE.
This study has several limitations. First, this study included data that were obtained from a single CT model and single medical institution. Therefore, incorporating data from different institutions and CT models is necessary to further validate the accuracy of the results. Second, this study only focused on chest CT, and it remains unclear whether the findings can be applied to examinations of other body parts. Third, all patients in this study were adults. To determine whether the results can be applied to children, relevant data specifically for pediatric populations must be collected for further research and confirmation. Finally, owing to the fact that most Asians tend to have smaller body sizes, the Dw of patients in this study was lower than the diameter of the standard phantom. Therefore, further research is warranted by including more patients who have a larger Dw than the diameter of the standard phantom to expand our understanding in this area.
Conclusions
Weight and BMI can be alternative parameters for Dw while calculating SSDE in adult chest CT. We recommend BMI as a substitute parameter for Dw and suggested that a further reduction in RMSE can be achieved using sex-specific regression equations to calculate SSDE. These results may provide a more simplified SSDE calculation method for clinical practice. Additionally, personalized scanning protocols and radiation dose management can be developed according to the patient’s weight, BMI, and sex.
Data availability
The datasets generated during and analysed during the current study are available from the corresponding author on reasonable request.
References
ICRP. The 2007 recommendations of the international commission on radiological protection. Ann. ICRP 103, 2–4 (2007).
Pedrosa, K. F. S., Engler, C. & Nogueira, M. S. Cancer risk in healthy patients who underwent chest tomography comparing three different technologies. Appl. Radiat. Isot. 193, 110625. https://doi.org/10.1016/j.apradiso.2022.110625 (2023).
Ghetti, C., Ortenzia, O., Maddalo, M., Altabella, L. & Sverzellati, N. Dosimetric and radiation cancer risk evaluation of high resolution thorax CT during COVID-19 outbreak. Phys. Med. 80, 119–124. https://doi.org/10.1016/j.ejmp.2020.10.018 (2020).
Karmazyn, B. et al. How accurate is size-specific dose estimate in pediatric body CT examinations?. Pediatr. Radiol. 46(9), 1234–1240. https://doi.org/10.1007/s00247-016-3604-0 (2016).
Bernardo, M. et al. Chest CT using in COVID-19 pneumonia: Multicenter study on radiation doses and diagnostic quality in Brazil. Radiat. Prot. Dosim. 197(3–4), 135–145. https://doi.org/10.1093/rpd/ncab171 (2021).
Urikura, A. et al. Patient dose increase caused by posteroanterior CT localizer radiographs. Radiography 29(2), 334–339. https://doi.org/10.1016/j.radi.2023.01.009 (2023).
Inoue, Y. et al. Automatic exposure control attains radiation dose modulation matched with the head size in pediatric brain CT. Tomography. 8(6), 2929–2938. https://doi.org/10.3390/tomography8060246 (2022).
American Association of Physicists in Medicine. Size-Specific Dose Estimates (SSDE) in Pediatric and Adult Body CT Examinations (Task Group 204) (American Association of Physicists in Medicine, 2011).
Dixon, R. L. & Boone, J. M. Cone beam CT dosimetry: A unified and self-consistent approach including all scan modalities—with or without phantom motion. Med. Phys. 37(6), 2703–2718. https://doi.org/10.1118/1.3395578 (2010).
McCollough, C. et al. Use of water equivalent diameter for calculating patient size and size-specific dose estimates (SSDE) in CT: The report of AAPM task group 220. AAPM Rep. 2014, 6–23 (2014).
Wang, J. et al. Attenuation-based estimation of patient size for the purpose of size specific dose estimation in CT. Part I. Development and validation of methods using the CT image. Med. Phys. 39(11), 6764–6771. https://doi.org/10.1118/1.4754303 (2012).
Funashima, K., Abiko, S. & Sato, K. Novel method for calculating the effective dose using size-specific dose estimates conversion factors in abdomen-pelvis computed tomography. Radiol. Phys. Technol. https://doi.org/10.1007/s12194-023-00738-x (2023).
Mihailidis, D., Tsapaki, V. & Tomara, P. A simple manual method to estimate water-equivalent diameter for calculating size-specific dose estimate in chest computed tomography. Br. J. Radiol. 94(1117), 20200473. https://doi.org/10.1259/bjr.20200473 (2021).
Burton, C. S. Method of determining geometric patient size surrogates using localizer images in CT. J. Appl. Clin. Med. Phys. 21(3), 178–183. https://doi.org/10.1002/acm2.12814 (2020).
Li, X., Marschall, T. A., Yang, K. & Liu, B. Technical note: Advancing size-specific dose estimates in CT examinations: Dose estimates at longitudinal positions of scans. Med. Phys. 49(2), 1303–1311. https://doi.org/10.1002/mp.15402 (2022).
Anam, C. et al. An improved method for automated calculation of the water-equivalent diameter for estimating size-specific dose in CT. J. Appl. Clin. Med. Phys. 22(9), 313–323. https://doi.org/10.1002/acm2.13367 (2021).
Burton, C. S., Malkus, A., Ranallo, F. & Szczykutowicz, T. P. Technical note: Model-based magnification/minification correction of patient size surrogates extracted from CT localizers. Med. Phys. 46(1), 165–172. https://doi.org/10.1002/mp.13251 (2019).
Li, X., Marschall, T. A., Yang, K. & Liu, B. Calculation of scan length and size-specific dose at longitudinal positions of body CT scans using dose equilibrium function. Med. Phys. 50(2), 1096–1104. https://doi.org/10.1002/mp.15959 (2023).
Kuriyama, K. et al. Effect of table height displacement and patient center deviation on size-specific dose estimates calculated from computed tomography localizer radiographs. Phys. Eng. Sci. Med. 43(2), 665–672. https://doi.org/10.1007/s13246-020-00874-3 (2020).
Boos, J. et al. Accuracy of size-specific dose estimate calculation from center slice in computed tomography. Radiat. Prot. Dosim. 178(3), 343. https://doi.org/10.1093/rpd/ncx119 (2018).
Heilmaier, C., Zuber, N., Bruijns, B., Ceyrolle, C. & Weishaupt, D. Implementation of dose monitoring software in the clinical routine: First experiences. Rofo. 188(1), 82–88. https://doi.org/10.1055/s-0041-106071 (2016).
World Health Organization. Obesity: Preventing and managing the global epidemic: Report a WHO consultation. in WHO Technical Report Series 894. (World Health Organization, 2000).
Hu, X., Gou, J., Lin, W., Zou, C. & Li, W. Size-specific dose estimates of adult, chest computed tomography examinations: Comparison of Chinese and updated 2017 American College of Radiology diagnostic reference levels based on the water-equivalent diameter. PLoS ONE. 16(9), e0257294. https://doi.org/10.1371/journal.pone.0257294 (2021).
Alrehily, F. A. et al. Establishing local diagnostic reference levels for computed tomography examinations using size-specific dose estimates. Saudi Med. J. 44(8), 761–766. https://doi.org/10.15537/smj.2023.44.8.20230230 (2023).
El Mansouri, M. et al. Size-specific dose estimates for thoracic and abdominal computed tomography examinations at two Moroccan hospitals. J. Digit. Imaging. 35(6), 1648–1653. https://doi.org/10.1007/s10278-022-00657-0 (2022).
Valeri, G. et al. Evaluating the appropriateness of dosimetric indices in body CT. Radiol. Med. 120(5), 466–473. https://doi.org/10.1007/s11547-014-0476-y (2015).
Klosterkemper, Y. et al. Tailoring CT dose to patient size: Implementation of the updated 2017 ACR size-specific diagnostic reference levels. Acad. Radiol. 25(12), 1624–1631. https://doi.org/10.1016/j.acra.2018.03.005 (2018).
Boos, J. et al. Does body mass index outperform body weight as a surrogate parameter in the calculation of size-specific dose estimates in adult body CT?. Br. J. Radiol. 89(1059), 20150734 (2016).
Iriuchijima, A., Fukushima, Y., Nakajima, T., Tsushima, Y. & Ogura, A. Simple method of size-specific dose estimates calculation from patient weight on computed tomogyaphy. Radiat. Prot. Dosim. 128(2), 208–212. https://doi.org/10.1093/rpd/ncx100 (2018).
Xu, J., Wang, X., Yang, P., Luo, K. & He, X. Size-specific dose estimates of radiation based on body weight and body mass index for chest and abdomen-pelvic CTs. Biomed. Res. Int. 2020, 6046501. https://doi.org/10.1155/2020/6046501 (2020).
O’Neill, S. et al. Using body mass index to estimate individualised patient radiation dose in abdominal computed tomography. Eur. Radiol. Exp. 2(1), 38. https://doi.org/10.1186/s41747-018-0070-5 (2018).
Khawaja, R. D. et al. Simplifying size-specific radiation dose estimates in pediatric CT. AJR Am. J. Roentgenol. 204(1), 167–176. https://doi.org/10.2214/AJR.13.12191 (2015).
Kritsaneepaiboon, S., Eng-Chuan, S. & Yoykaew, S. Can patient’s body weight represent body diameter for pediatric size-specific dose estimate in thoracic and abdominal computed tomography?. J. Clin. Imaging Sci. 9, 24. https://doi.org/10.25259/JCIS-7-2019 (2019).
Khatonabadi, M. et al. Calculating size specific dose estimates (SSDE): The effect of using water equivalent diameter (WED) vs. effective diameter (ED) on organ dose estimates when applying the conversion coefficients of TG 204. in 55th Annual AAPM Meeting. (2013).
Funding
This work was funded by Chengdu Medical Research Project, Chengdu Municipal Health Commission, Grant Number: 2022202.
Author information
Authors and Affiliations
Contributions
Y.F analyzed the correlation between physical parameters and Dw. H.XY and G.J collected patient physical parameters data, dose data, and validated the validation set. H.XY was a major contributor in writing the manuscript. G.DJ reviewed the findings and the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Hu, X., Gou, J., Yang, F. et al. Body physical parameters instead of water equivalent diameter to calculate size-specific dose estimate in adult chest CT. Sci Rep 14, 17053 (2024). https://doi.org/10.1038/s41598-024-66657-y
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-024-66657-y