Introduction

Clayey soil is widely employed in the construction of impermeable barriers within landfills or tailings repositories, attributed to its superior permeability characteristics1,2,3. These impermeable barriers function as crucial containment systems, mitigating the spread of leachates across the region, which includes the base, slopes, and cover layers of landfills or tailings4. The potential ramifications of leachate on impermeable systems could pose a threat to the long-term stability of landfills or tailings. Upon occurrence of an initial leakage event, there is a risk of significant problems arising, including groundwater and surface water contamination, vegetation diebacks, and potential health hazards to residents. However, it's important to note that these processes are irreversible5,6,7.

In recent years, numerous incidents of leakage and structural failures have been documented in both operational and decommissioned landfills or tailings in seasonally frozen regions8,9,10. Although these failures are commonly attributed to factors such as improper site selection, defective design, inadequate management, or non-conformist operational practices, the impact of freeze–thaw cycles on these structures is often neglected in research. Comprehensive studies have consistently shown that freeze–thaw cycles significantly impact the engineering properties of soils in varying degrees11,12,13. Triaxial tests reveal that soils undergoing freeze–thaw cycles exhibit a notable decrease in both elastic modulus and failure strength, compared to their unfrozen counterparts14. The influence of freeze–thaw cycles on diminishing soil modulus and strength is observed to ultimately stabilize. For various clayey soils, cohesion initially declines during the initial freeze–thaw cycles, stabilizing after about 5–9 cycles. Simultaneously, the internal friction angle escalates, peaking between 5 and 7 cycles, thereafter maintaining relative stability15,16,17,18,19.

The freeze–thaw cycle is a prevalent phenomenon in regions with seasonally frozen soils, leading to significant changes in soil structure and consequently impacting the mechanical properties of the soil. Numerous methods and techniques have been employed to explore the configuration of soil particle structures, notably including scanning electron microscopy (SEM)20,21,22, time domain reflectometry (TDR)23,24 and nuclear magnetic resonance (NMR) techniques25,26,27. Recently, the pulsed NMR technique has gained widespread acceptance in geotechnical engineering for its ability to evaluate actual soil pore size distribution (PSD), ascertain the local structure of rock matrices, and measure the unfrozen water content in frozen soils28,29. Due to frost heave, water between soil particles induces the development of pores and fissures within the soil, with these pores expanding notably during freeze–thaw cycles. Consequently, this instigates significant alterations in soil structure, compromising overall stability. The NMR technique reliably quantifies the number of protons in water molecules and precisely capture mesostructured details, including shifts in pore distribution within the porous medium. The surrounding pore structure is accurately depicted by the distributions of proton transverse relaxation time T2.

Following a failure in clay soils, the strength can be partially recovered during extended rest periods, effectively limiting further deformation30,31,32. Carrubba and Fabbro33 conducted a series of experiments to assess the impact of rest periods on the recovery strength of Montona flysch and Rosazzo flysch, revealing that recovery strength can exceed residual strength, contingent upon the duration of the rest period and the applied vertical stress. Recovery strength demonstrated a 20 to 30% increase following a prolonged rest period of one month. Bhat et al.34 elucidated the mechanisms underlying the strength recovery in both highly and lowly plastic soils in a residual state, recommending that both recovery and residual strengths be integrated into the design of clayey soil structures. Xu et al.35 explored the effects of shear rate, over-consolidation ratio (OCR), plasticity index, and multi-stage shear mode on residual strength, finding that plasticity index and normal stress exert a more pronounced influence on residual strength compared to shear rate and OCR. Zheng et al.32 observed that recovery strength increased with rising OCR under constant normal stress following a brief rest period, yet this gain was negated by minor shear displacement. The findings also suggest that fully leveraging both residual and recovery strengths can effectively mitigate and manage slow-moving structural changes in clayey soils. The repeated direct shear test is extensively utilized to measure the recovery and residual strength of a soil. It effectively simulates the cyclic loading conditions encountered by soil in actual engineering applications, allowing for the assessment of cumulative damage and performance decline under repetitive loading36. By conducting repeated loading tests, engineers can forecast the long-term performance of soil under cyclic loads. In comparison to other intricate soil mechanics tests, the repeated direct shear test stands out for its simplicity, ease of implementation, and ability to yield reproducible data. This facilitates scientific analysis and comparison37,38.

While significant research has been conducted on residual and recovery strengths in clayey soils, there still exist research gaps regarding these strengths after undergoing multiple freeze–thaw cycles. The primary objective of this study is to investigate the recovery and residual strengths of Jilin ball clay after undergoing six freeze–thaw cycles. A series of repeated direct shear tests were conducted on remolded soil samples, varying in dry densities and subjected to different normal stresses. Then, the pore structure characteristics of the Jilin ball clay, subjected to multiple freeze–thaw cycles, were analyzed using a series of NMR tests. The variations in the pore characteristics of Jilin ball clay, resulting from freeze–thaw cycles, are quantitatively delineated. This research furnishes a theoretical foundation for the construction and management of impermeable clayey soil structures in seasonally frozen areas.

Jilin ball clay

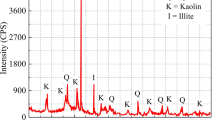
The ball clay used in the remoulded samples originated from Dakouqin, Jilin Province, China, as depicted in Fig. 1. Table 1 respectively presents the chemical composition of the Jilin ball clay. As illustrated in Fig. 2, the Jilin ball clay features pronounced peaks of quartz, alongside considerable quantities of kaolinite and minor traces of illite. The particle size distribution is shown in Fig. 3. The findings indicate that the Jilin ball clay possesses small, uniform particle sizes and a substantial specific surface area, identifying it as a natural nanoscale and high-activity raw clay material. Table 2 displays the fundamental physical properties of the Jilin ball clay. Then the Jilin ball clay is defined as CL (Cohesive soil) according to the Unified Soil Classification System.

Figure 1
figure 1

Study area of Jilin, Jilin province, China (ArcGIS 10.8 https://www.esri.com/en-us/arcgis/products/arcgis-desktop/resources).

Full size image
Table 1 Chemical component of Jilin ball clay with particle size small than 2 μm.
Full size table
Figure 2
figure 2

The XRD spectrum of Jilin ball clay.

Full size image
Figure 3
figure 3

Particle size distribution of the Jilin ball clay.

Full size image
Table 2 Basic physical property of Jilin ball clay.
Full size table

Comprehensive analysis of strength recovery characteristics of Jilin ball clay

Quality control of compaction is a crucial aspect of earthwork construction in engineering. Dry density is a commonly utilized property for monitoring compaction quality39. The dry density of soil plays a vital role in influencing both the soil–water characteristic curve and the mechanical properties of the soil. In the realm of unsaturated soil engineering, fluctuations in dry density can have a profound impact on the stability and deformation characteristics of the soil40.To investigate the strength recovery characteristics of Jilin ball clay following the stabilization of the freeze–thaw cycle effects, samples with three different dry densities (1.60 g/cm3, 1.65 g/cm3, and 1.70 g/cm3) were tested using a repeated direct shear instrument equipped with an automatic shear apparatus, after undergoing six freeze–thaw cycles.

Sample preparation and test procedure

First, distilled water was incorporated into the powdered Jilin ball clay in accordance with the water content at the plastic limit, thoroughly mixed, and then covered with plastic film to rest for 24 h, ensuring an even moisture distribution throughout. Following a 24-h rest period, the sample was structured in two layers employing the layered compaction method, adhering to specific target masses and heights for each layer. Finally, the samples achieving target dry densities of 1.60, 1.65, and 1.70 g/cm3 were positioned within a ring knife (20mm height and 61.8mm diameter) and set up for the freeze–thaw cycle. To prevent moisture loss through evaporation during the six freeze–thaw cycles, the samples were sealed with fresh-keeping film and subsequently frozen in a low-temperature environmental box. Each freeze–thaw cycle involved 12 h of freezing at ‒30 °C, succeeded by 12 h of thawing at an ambient room temperature of 15 ± 1 °C. After completing six freeze–thaw cycles, the sample was inserted into the repeated direct shear instrument to commence preparation for the experimental procedures (see Fig. 4).

Figure 4
figure 4

Repeated direct shear instrument.

Full size image

Each type of dry density of sample is subjected to four repeated direct shear tests under normal stresses of 50, 100, 150, and 200kPa, respectively (12 groups of samples in total). The repeated direct shear test comprises three main steps to assess the strength recovery characteristics of Jilin ball clay: (1) Executing the direct shear test procedure. This procedure is performed at a shear rate of 0.06 mm/min, rendering the pore water pressure effects negligible. Experimental data are captured every 0.2 mm of shear displacement. Upon reaching 8 mm of shear displacement, the upper shear box is retracted in the opposite direction at a shear rate of 0.5 mm/min; data collection is suspended during this phase. (2) Replicating step 1 twice to enable the sample to attain a complete residual state. (3) Following a 100-s rest period, shearing resumes as per step 1, after which the sample undergoes subsequent rest periods. The sequence of rest periods for one test group includes 100 s, 50 min, 150 min, 12 h, and 24 h. This series of tests encompasses five iterative direct shearing operations (as per step 1) following varying rest periods. Normal stress remains constant throughout the entire series of tests for each group, while the shear rate is precisely regulated by an automated motor display system. Petroleum jelly is strategically applied to the junction between the upper and lower shear boxes to mitigate moisture loss throughout the shearing and resting phases.

Residual and recovery strength

A Fig. 5 presents the results of the repeated direct shear tests conducted on Jilin ball clay after six freeze–thaw cycles, with rest periods ranging from 100 s to 24 h. As illustrated in Fig. 5, three key characteristics of the shearing mode can be summarized as follows: (1) The recovery strengths are significantly lower than the maximum shear strengths throughout the entire rest period; (2) There is a marked increase in recovery strength during the 12-h and 24-h rest periods, whereas the recovery strength observed during the 100-s, 50-min, and 150-min rest periods is negligible; (3) Both residual and recovery strengths are influenced by the dry density; specifically, these strengths increase as the dry density rises. As the dry density increases, the soil structure becomes more compact, leading to intensified particle occlusion. However, this trend is not particularly pronounced when the normal stress is at 50kN/m2.

Figure 5
figure 5

Recovery strength of Jilin ball clay after 6 freeze–thaw cycles and rest period ranging from 100 s to 24 h.

Full size image

It is noteworthy that the recovery strength of the sample with a dry density of 1.70 g/cm3 during the 24-h rest period exhibits a distinct peak at very small relative displacements under a normal stress of 100kN/m2. Upon further displacements, the strength rapidly declines to its residual value. As the normal stress increases to 200 kN/m2, peak strengths successively emerge in samples with dry densities of 1.65 and 1.60 g/cm3 during the 24-h rest period. Notably, a peak strength also manifests during the 12-h rest period in the sample with a dry density of 1.70 g/cm3 under a normal stress of 200 kN/m2.

Although the peak strength dissipates rapidly and exerts minimal influence on the residual strength, analogous findings were reported by Carrubba and Fabbro33 and Zheng32. The underlying causes of this peak strength are still under investigation. Schofield41 discovered that remolded, reconsolidated fine-grained soil with high water content could dilate during shearing, a result stemming from volume changes as water content varied. This was based on interpretations by Terzaghi and Hvorslev of peak strength data from shearing samples. Xu et al.35 proposed that plasticity indexes significantly impact both the peak and residual strengths of clayey samples. An earlier study by Bhat et al.34 also indicated that the peak values of recovery strength from the residual shear state are higher in high-plasticity soils than in low-plasticity soils. Typically, normally consolidated soil samples (OCR = 1) exhibit no peaks during shearing42; however, Zheng et al.32 observed that peak values of recovery strength appeared in repeated shearing tests for both normally and over-consolidated soil samples, and these values escalated with increasing OCR. From the analysis above, numerous factors can influence the occurrence of peak strength in recovery strength assessments. As demonstrated in Fig. 5, although the peak strengths become increasingly pronounced as dry density, normal stress plays a far more fundamental role compared to dry density and rest periods.

Influence of rest period, normal stress and dry density

A Fig. 6a,b show the test results for Jilin ball clay in terms of τremax/σv, Δτ/σv under repeated shearing tests, respectively, where τremax represents the maximum recovery strength at each rest period, Δτ denotes the difference between the maximum recovery strength τremax and the residual strength τres; and σv is the normal stress. Previous discussions have demonstrated that strength recovery consistently increases with normal stress and dry density, indicative of a time-dependent process. However, during the same rest period, both τremax/σv and Δτ/σv values decrease as the normal stress σv increases. As demonstrated in Fig. 6, τremax/σv and Δτ/σv with respect to the time of the rest period t evolve according to a power law

$$ \tau_{re\max } /\sigma_{v} = \beta t^{\alpha } $$
(1)
$$ \Delta \tau /\sigma_{v} = \varepsilon t^{\theta } $$
(2)

where α, β, θ, and ε represent the parameters of the power law, which are contingent upon both the dry density and normal stress. According to the power law relationship between τremax/σv and t, recovery strength initially develops over a short rest period and subsequently increases with slowing increase rates; similarly, Δτ/σv exhibits a comparable trend.

Figure 6
figure 6

Recovery strength for Jilin ball clay versus time of rest period and normal stress.

Full size image

Several researchers30,33,34,43,44 have reached similar conclusions across various types of clayey soil; however, a precise theoretical framework that fully explains this phenomenon remains elusive. Czarnecki and Dabroś45 posited that the strength recovery mechanism in clayey soils is primarily due to van der Waals forces acting on the shear surfaces. Mitchell and Soga46 theorized that the neutralization or exchange of cations in clay particles, leading to the precipitation of cementing agents, is the primary driver of strength recovery. Consequently, the observed recovery strength in experiments is significantly lower than the maximum shear strength, due to the limited time available for these processes to occur. According to the results depicted in Fig. 6a, the dry density of samples distinctly influences the maximum recovery strengths τremax. Integrating the insights proposed by Bhat et al.34, who conducted ring shear experiments, the increase in strength is likely attributable to particle rearrangement during rest periods and dilatancy effects during shearing. As the dry density increases, the occlusion among particles within the sample intensifies, enhancing the extent of rearrangement and the impact of dilatancy effects.

Recovery in internal frictional angle and cohesion

When clayey soil undergoes significant deformation, it is commonly assumed that cohesion diminishes to zero, and residual strength is derived solely from the internal friction angle. Increases in internal frictional angles (Δφ) and cohesion (Δc) are detailed in Table 3. For the same rest period, both internal friction angle and cohesion increase as dry density rises. During the 100-s rest periods, there are negligible increases in internal frictional angles and only slight increases in cohesion across all three dry densities. Relative to internal friction angle, the recovery in cohesion becomes more pronounced as the duration of the rest period extends. Figure 7 illustrates the growth rates of the internal frictional angle and cohesion. The growth rate of the internal frictional angle increases with both the time of rest period and dry density. Conversely, the growth rate of cohesion increases with the time of rest period but decreases with dry density. Higher dry density samples exhibit more compact particles, resulting in a more pronounced early-stage recovery of cohesion. However, samples with lower dry densities demonstrate greater increases in cohesion due to more comprehensive adjustment and interaction between particles over time of rest period. As depicted in Fig. 7, the growth rates for Δφ across three dry densities are 8.09%, 9.44%, and 9.69% respectively, after a 24-h rest period; conversely, the growth rates for Δc are 31.02%, 26.73%, and 22.44%, respectively. Therefore, based on the data from Table 3 and Fig. 7, the increase in cohesion for Jilin ball clay is more pronounced and occurs earlier compared to the internal friction angle.

Table 3 Summary of strength recovery in terms of internal frictional angle and cohesion.
Full size table
Figure 7
figure 7

The growth rates of internal frictional angle and cohesion (φ and c are initial internal frictional angle and cohesion).

Full size image

Pore structure characteristics of frozen-thawed Jilin ball clay

NMR experiment methods and sample

To investigate the pore structure characteristics of Jilin ball clay after multiple freeze–thaw cycles, a series of NMR tests were conducted on saturated samples following various cycles. A 23-MHz MiniMR system, developed by the Institute of Rock and Soil Mechanics of the Chinese Academy of Sciences and Niumag Corporation, China, was utilized in these experiments. As illustrated in Fig. 8a, the complete NMR system comprises a sample tube, a magnet unit, an RF system, and a data acquisition and analysis system. The sample must be saturated with water prior to testing, as the NMR signal intensity of pore water in saturated samples and their relaxation times under a magnetic field correlate directly with the pore structure47,48,49. The T2 spectrum relaxation time indicates the size and distribution of the sample's internal pores; the specific correlation between the T2 relaxation time and the pore size (R) is outlined as follows:

$$ R = \rho_{2} \times F \times T_{2} $$
(3)
Figure 8
figure 8

Nuclear magnetic resonance (NMR) equipment and samples.

Full size image

Here, R denotes the pore radius, ρ2 represents the surface relaxivity of the pore walls within the pore media, and F is the shape geometry factor. Feng50 suggested that the ρ2 × F was taken as 0.2μm/ms.

All samples were prepared within the laboratory setting. Initially, a sufficient quantity of Jilin ball clay in dry powder form was thoroughly mixed with water to achieve a 17.0% moisture content in a plastic bag, left for 24 h to ensure even moisture distribution. To investigate the impact of dry density on pore structure characteristics after multiple freeze–thaw cycles, samples were prepared with three distinct dry densities: 1.60, 1.65, and 1.70g/m3, respectively. All samples were methodically prepared in three layers using the layered compaction technique to achieve the targeted dry densities in the sample rings. Given the effective area of the sample tube (60mm × Φ60mm) and to minimize the influence of iron on the magnetic field, a special plastic membrane, measuring 40mm in height and 50mm in inside diameter and made from Teflon, was utilized instead of the traditional steel odometer ring. All samples were saturated using the vacuum saturation method for 24 h before being subjected to freeze–thaw cycles in a low-temperature environmental box. The samples were encapsulated in fresh-keeping film to prevent moisture loss through evaporation across multiple freeze–thaw cycles. Each freeze–thaw cycle involved 12 h of freezing at ‒30 °C, followed by 12h of thawing at ambient room temperature of 15 ± 1 °C. The details of the experimental plan are illustrated in Table 4. Figure 8b shows the samples after several times of freeze–thaw cycles.

Table 4 The details of the experimental plan.
Full size table

Correlation between T2 distribution curve and number of freeze thaw cycle

Drawing from the research of Harmer et al.51, Li52 et al., and Li et al.53, pore diameters are classified based on T2 relaxation times: T2 ≤ 10ms are considered micropores, 10ms < T2 ≤ 100ms are mesopores; and T2 > 100ms are macropores. Using the T2 distribution curves results for a density of ρd = 1.65g/cm3 as an example, Fig. 9 illustrates the T2 distribution curves for samples subjected to 0, 1, 2, 4, 6, 10, and 15 freeze–thaw cycles. The curves display a single peak, and the pore diameter corresponding to this peak slightly shifts to the right as the number of freeze–thaw cycles increases. This indicates a gradual increase in pore diameter. However, the pore diameter consistently remains within the micropores range, and no distinct peak for mesopores is observed throughout the freeze–thaw cycles. This is attributed to Jilin ball clay's small and uniform particle size (mean particle diameter: 0.67μm) and large specific surface area54, which result in similarly small pore diameters. Building upon the foundational study by Chen et al.55, which delineated the T2 relaxation times for diverse classes of pore water, such as bulk, capillary, and bound water, it is posited that capillary water predominates within the Jilin ball clay, a hypothesis substantiated by the pronounced physicochemical interactions occurring within the pore water and soil granules, specifically within the T2 relaxation window of 100ms to 101ms. In contrast to the T2 distribution profiles of clayey soils documented in extant literature27,56,57,58, the T2 distribution curves characteristic of Jilin ball clay exhibit remarkable resilience to freeze–thaw cycles, maintaining microporous integrity throughout.

Figure 9
figure 9

T2 distribution curves for sample with 1.65 g/cm3 (Y-axis indicates NMR signal intensity which is dimensionless).

Full size image

Figure 10 delineates the T2 relaxation time distribution curves for samples characterized by varying dry densities ρd, after being subjected to a series of freeze–thaw cycles. As illustrated in Fig. 1, each curve manifests a congruent pattern, predominantly distinguished by a solitary peak within the T2 interval of 100‒101ms, indicative of the micropores' presence. Prior to the initiation of freeze–thaw cycles (C1, 2, 3–0), the apex of the T2 peaks evidences a rightward trend correlating with a decrement in ρd. Additionally, the T2 distribution curve for group C1 exhibits an incremental convergence with that of group C2 with the escalation in the number of freeze–thaw cycles. Significantly, subsequent to the 15th freeze–thaw cycle, the T2 distribution profiles of groups C1 and C2 approach near complete superposition. From Fig. 9, two salient features of the T2 distribution curves can be discerned: (1) the T2 distribution curves corresponding to samples with divergent dry densities are similar in shape, with peak values (T2) showing a regular distribution at a lower number of freeze–thaw cycles. However, the curves representative of groups C1 and C2 tend toward superposition with the progressive increase in the freeze–thaw cycle count; (2) the peak shapes of all the T2 distribution evolve from a flatter to a sharper morphology with the accumulation of freeze–thaw cycles, which intimates a progression towards a more homogeneous microstructure within the samples subsequent to multiple freeze–thaw cycles.

Figure 10
figure 10

T2 distribution curves for samples (Y-axis indicates NMR signal intensity which is dimensionless).

Full size image

Correlation between porosity and number of freeze thaw cycle

While the pore diameter within the sample consistently resides within the microporous range, exhibiting enhanced uniformity throughout the freeze–thaw cycles, the soil structure has been subject to pronounced alterations, most notably reflected in the sample's porosity53,59,60,61. Figure 11 graphically delineates the fluctuations in porosity and the integral areas of the T2 curves, as ascertained through NMR testing, in correlation with the number of freeze–thaw cycles. Post completion of the freeze–thaw sequence, the derived porosity metrics from the three groups conspicuously surpass the initial measurements. The initial porosity values were recorded at 0.428, 0.410, and 0.392, corresponding to the three distinct dry densities of 1.60, 1.65, and 1.70g/cm3, respectively. Upon culminating the 15th freeze–thaw cycle, the porosity values ascended to 0.470, 0.464, and 0.461 for each respective dry density. The most substantial percentage rise in porosity was observed in the sample with a dry density of 1.70 g/cm3, followed by 1.65g/cm3, with the most modest increase noted in the sample of 1.60g/cm3. Liu et al.61 advanced a theoretical framework that serves to elucidate the underlying mechanisms driving pore formation within soil matrices subjected to freeze–thaw cycles. In addition to the presence of minuscule quantities of unfrozen water film, the pore water exhibits a migration tendency towards the freezing front concomitant with temperature diminution. Concurrent with the phase transition of pore water into ice crystals, the soil undergoes a morphological transformation, yielding spherical and cylindrical pores under the impetus of frost heaving stress. Upon the melting of the ice crystals, consequent to a rise in temperature, the pores retain their structure within the soil. This investigation reveals that inter-particle junctions within the clay manifest greater laxity in samples exhibiting relatively lower dry densities, culminating in more pronounced pore distributions, although the soil's structural integrity remains largely unscathed by the stresses imparted by frost heave. Nevertheless, the soil structure exhibits heightened variability with an escalation in dry density. In comparison to samples with lower dry densities, the porosity of higher dry density samples may become augmented as a consequence of the freeze–thaw cycles, owing to the likelihood that particles may not revert to their precise original positions throughout the freeze–thaw cycles, and the particle-to-particle bonding capacity may be diminished, thereby making the soil structure slightly looser than prior to the freezing process.

Figure 11
figure 11

Variation of the porosities and integral areas with the number of freeze–thaw cycles.

Full size image

Viklander62 introduced the concept of the residual void ratio as a means to articulate the observed phenomenon whereby the void ratio of initially loose soils diminishes, whereas that of initially dense soils augments, both converging towards a residual void ratio subsequent to the first to third freeze–thaw cycles. In the present investigation, the integral area demarcated by the T2 distribution curve and the horizontal axis is representative of the soil's water content, the emergent pattern of variations within the integral areas corresponding to the three disparate dry densities of the sample further substantiates the aforementioned conclusion, as is exhibited in Fig. 11. It is of particular note that the increment in porosity is not inexhaustible, for specimens with dry densities of 1.60g/cm3, the degree of porosity enhancement post the fourth freeze–thaw cycle is not marked, comparatively, analogous conditions are discerned at the sixth and tenth freeze–thaw cycles for the dry densities of 1.65g/cm3 and 1.70 g/cm3, respectively.

Discussion

According to the findings from the repeated direct shear test and NMR test of Jilin ball clay presented herein, this study facilitates an analysis of one causal factor underlying the incidents of leakage and structural failure observed in impermeable constructs commonly employed in landfills or tailings within seasonally frozen territories. The substantial diminution in the strength of clayey soil attributable to freeze–thaw cycles is principally due to the initial pore structure is destroyed by the phenomena of freezing, thawing, and migratory activities within the pore water, which weaken the bonding ability between the particles. Alterations in pore attributes progressively accumulate, culminating in a zenith during the fourth to the tenth freeze–thaw cycles. This suggests that impermeable structures may be predisposed to leakage and failure over the course of several years, independent of operational and stress condition variations, thereby posing significant safety risks to the anti-seepage system. However, for the disrupted clayey soil, a modicum of strength recuperation is achievable upon stabilization of the freeze–thaw effects. Subsequent to the disruption of clayey soil, any substantial restoration of strength may necessitate an extended duration. The synthesis of research outcomes from this study may serve as a reference for the edification and management of impermeable infrastructures within landfills and tailings located in seasonally frozen zones.

Conclusion

The study examined the recovery and residual strengths of Jilin ball clay after undergoing six freeze–thaw cycles at three different dry densities, using a series of repeated direct shear tests. Analysis of NMR test results revealed alterations in the pore structure of Jilin ball clay following multiple freeze–thaw cycles. The conclusions are as follows:

  1. 1.

    Shorter rest periods show less recovery strength compared to longer rest periods of 12 and 24 h, with peak values increasing as dry density, normal stress, and rest period duration increase. Normal stress plays a more important role than dry density and rest period duration. τremax/σv and Δτ/σv decrease with increasing normal stress during identical rest periods, following a power law with respect to the time of rest period.

  2. 2.

    As dry densities increase, both cohesion and internal friction angle increase with the same rest period. After a 24-h rest period, cohesion increases more significantly (31.02%, 26.73%, and 22.44%) and earlier than the internal friction angle (8.09%, 9.44%, and 9.69%) for Jilin ball clay at different dry densities.

  3. 3.

    The T2 distribution curves of Jilin ball clay remain stable during freeze–thaw cycles, with pore sizes consistently in the microporous range. After 15th freeze–thaw cycles, initial porosities increase for three dry densities.

The final analysis offers significant insights for the design and maintenance of impermeable barriers in landfills or tailings repositories located in regions with seasonal freezing. The integration of findings from this study serves as a practical guide for engineering applications. It is recommended that impermeable barriers made of clayey soil in landfills or tailings repositories within seasonally frozen areas undergo monitoring and evaluation following the initial freeze–thaw cycle, with reinforcement techniques such as geosynthetics being potential options to enhance their effectiveness. Although this study does not account for the influence of engineering geological conditions, soil composition, water content, solution pH value, and cation exchange capacity, these parameters will be the focus of our future research.