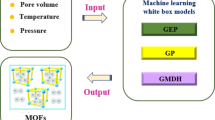
Abstract
Over time, with the increase in population and the subsequent increase in energy consumption and also due to the non-renewability of fossil fuels, the study of alternative fuels has increased. One of these fuels is biodiesel, which is a suitable alternative to fossil fuels such as diesel and received much attention from researchers today. For this reason, measuring the physical properties of biodiesel is of great importance. Due to the high cost and time-consuming nature of laboratory methods, numerical methods are used to estimate material properties. The novelty of this research was the use of two white box models, including Group method of data handling (GMDH) and Gene expression programming (GEP), which work on the basis of artificial intelligence. By using these models, two simple mathematical equations with high accuracy were presented to predict the surface tension of biodiesel. These models can be used at different temperatures and molecular weights. To do modeling, 78 laboratory data available in the literature were gathered and the data were randomly divided into two groups, train and test, in a ratio of 80 and 20. The input parameters include mass fraction of fatty acid ethyl esters and temperature (T), and esters are divided into three groups according to their molecular weight: less than 200 (Mw1), between 200 and 300 (Mw2), and greater than 300 (Mw3). The statistical error parameters were calculated for the two models developed in this research and after comparing the results, it was found that the GMDH model estimates the surface tension of biodiesel with a higher accuracy. The average absolute relative error for GMDH and GEP models was reported as 0.97 and 1.89, respectively. Also, other statistical error parameters of GMDH such as RMSE, SD, and R2 for the GMDH model were obtained as 0.444, 0.000233, and 0.9233, respectively. Moreover, sensitivity analysis showed that temperature has the highest impact on the surface tension of biodiesel, which is also an inverse effect. Finally, suspicious laboratory and outlier data points were identified using the Leverage technique. According to this analysis, only five data points were identified as outliers and suspicious laboratory data.
Similar content being viewed by others
Introduction
Today, the problems caused by non-renewable energies have been widespread in the world. The production of greenhouse gases is due to the high consumption of fossil fuels, which makes the Earth warmer1,2,3. Many measures have been taken to control the production of greenhouse gases4. It exists as one of the most popular sources of fuel that causes less damage to nature5. By combining fatty acid alkyl esters, biodiesel is produced. Transesterification of fats is carried out catalytically by different alcohols. Catalysts increase the reaction rate6. The reason why biodiesel is known as a clean fuel is the presence of a small amount of sulfur in its composition, which reduces the production of greenhouse gases7. Among other uses of biodiesel in diesel engines, it can be mentioned to increase the life of the engine due to its high fluidity8. However, the use of biodiesel compared to petroleum-based fuels has disadvantages such as oxidation stability, higher viscosity, and production cost9. Nowadays, due to the importance of biofuels, the focus on their properties and applications has increased, and many experimental relationships and modeling have been done to determine these properties10. One of the important features of biodiesel is surface tension which is used in atomization, so atomization quality increases with the reduction of surface tension10. Surface tension is one of the important issues in diesel fuels that affects economic and environmental issues.
In the following, an overview of thermodynamic models, artificial intelligence, and experimental studies conducted for forecasting biodiesel and fossil fuels surface tension is presented:
At first, Queimada et al.11 established a model to estimate fuels’ viscosity and surface tension. Then, a smart model for predicting brine interfacial tension utilizing the least-squares method of support vector machine (SVM) was presented by Barati-Harooni et al.12 In this model, the inputs were water salinity, temperature, and pressure. Also, Rostami et al.13 presented a model using genetic programming algorithm for estimating water and hydrocarbon surface tension, and the value of R2 for this model was reported as 0.91. Next, a model was presented by Pratas et al.14 for predicting biodiesel density with an error of 0.25–2.96%. Then a smart model was developed by Gahek et al.15 to approximate alkane density with an average absolute error of 0.6%. After that, a model using ANN methods was presented by Miraboutalebi et al.16. R2 value and root mean square error (RMSE) for this model were reported as 0.95 and 2.53, respectively. Then cetane number of biodiesel was estimated by Hosseinpour et al.17 using SVM. R2 and RMSE values for this model were reported as 0.99 and 0.72. Then Mostafaei18 predicted the cetane number using the logical phase neural system. Bemani et al. developed models for estimating the cetane number of biodiesel based on FAME properties of experimental data. The LSSVM algorithm was used and coupled with three models: Genetic algorithm (GA), particle swarm optimization (PSO), and a hybrid of GA and PSO (HGAPSO) algorithms. R2 values for LSSVM-GA, LSSVM-PSO, and LSSVM-HGAPSO were reported as 0.965, 0.966, and 0.978, respectively19,20,21. Razavi et al. developed a precise model using LSSVM-PSO algorithm to predict biodiesel properties such as pour point, cloud point, iodine value, and kinematic viscosity based on fatty acid composition that the accuracy of test data of biodiesel properties are 0.99995, 0.99981, 0.99848 and 0.99930, respectivly22,23,24,25. Baghban et al. developed TLBO-NN and PSO-NN to improve the prediction of cetane number of FAMEs based on biodiesel. This study showed that the TLBO-NN was more accurate than PSO-NN and the R-squared and mean square of errors are 0.973 and 3.538 and 0.951 and 6.324, respectively26. Nabipour et al. presented four advanced models, including Least Square Support Vector Machine (LSSVM), Radial Basis Function Artificial Neural Network (RBF-ANN), Multi-layer Perceptron Artificial Neural Network (MLP-ANN), and Adaptive Network-based Fuzzy Inference System (ANFIS), for forecasting biofuel density. These models leverage intermolecular interactions and the van der Waals radii of atoms in their predictions. The LSSVM model is more accurate than other models and the R-squared of this model is 0.847. This investigation demonstrates the potential efficacy of employing the LSSVM model as a proficient means of estimating biofuel density, thereby presenting a viable alternative to conventional thermodynamic modeling approaches27.
In the following, studies on the biodiesel’s surface tension approximation will be reviewed. In order to predict the surface tension of pure FAME and biodiesel, Phankosol et al.28 presented two relations in terms of Gibbs free energy and, the error value of these models was reported as 1.84% and 1.21% for 10 & 8 distinct biodiesel FAME. Further, Thangaraja29 proposed a relationship in the temperature range of 306–353 with 7% absolute error for the approximation of biodiesel and vegetable oil surface tension. The relationships presented by Miller and Macleod-Sugden were again examined by An et al.30 and it was concluded that the relationships presented by Miller have a higher performance than the Macleod-Sugden relationship. Then, in order to forecast fatty acid ethyl esters surface tension, Valk31 used Brock and Rari/Olivier models and reported the following accuracies of 7.5% and 2.4%, respectively, for each correlation. Also, models utilizing intelligent methods to predict the surface tension of different oils in different temperature ranges by Melo-Espinosa et al.32 were presented. According to the results, it can be seen that artificial neural network (ANN) is more accurate than multilevel regression (MLR) in predicting surface tension. Moreover, ANN and thermodynamic models were developed by Hosseini et al.33 for approximation of the surface tension of 3 biodiesel and FAME at different temperatures with accuracies of 0.44 and 1.82%. Salehi et al.34 used machine learning methods to model the interfacial tension of N2/CO2 mixture + n-alkanes of oils. Their model estimated laboratory data with high accuracy with an average absolute relative error of 0.77%34. Also, biodiesel surface tension was predicted utilizing the models of Ceriani et al., Ferrando et al., and Marrero et al.35,36,37. Also, Oliveira38 presented a model for predicting esters surface tension for a distinct temperature range by combining the gradient theory and the equation of cubic plus state (CPA). The accuracy value of the model for independent and temperature-dependent parameters was reported as 5.44% and 1.5%. Some of the properties of biodiesel that have been investigated experimentally are given below:
The soybean oil biodiesel density in the temperature range of 298.15–393.15 K and pressures up to 140 MPa was experimentally measured by Aitbelale et al.39. Next, the surface tension of three different types of biodiesel was measured by Chehtri40 at a pressure of 7 MPa and a temperature of 473 K. And finally, the surface tension, viscosity, and density of biodiesel were measured for an extensive temperature range by Blangino et al.41 and they used these data to validate their proposed models. The models presented above require accurate thermophysical properties and have long calculations and insufficient accuracy in predicting the desired parameter. Also, experimental studies conducted in the laboratory require a lot of time and money. Due to the great importance of biodiesel, we need an accurate method to predict its properties.
Other investigations have explored biodiesel production utilizing supercritical methanol (SCM), employing the LSSVM model and ANFIS model42,43,44,45,46.
The Novelty of this research was the use of two white box models, including Group method of data handling (GMDH) and Gene expression programming (GEP), which work on the basis of artificial intelligence, and by using these models, two simple mathematical equations with high accuracy were presented to predict the surface tension of biodiesel, which these models are for the range different temperature and molecular weight can be used. The data used in this research are 78 surface tension laboratory data collected from the literature. The input parameters in this research were temperature and fatty acid ethyl esters mass fraction. Also, the effect of input parameters on the surface tension was evaluated using sensitivity analysis. Finally, the suspicious laboratory data and outlier data points were identified by leverage technique.
Theory and methods
Data gathering
To approximate biodiesel surface tension, 78 laboratory data were collected from the literature41. The statistical parameters related to the input data are given in Table 1. Input data includes temperature and mass fraction of fatty acid ethyl esters. In order to reduce the dimensions of the input data, esters are divided into three groups according to their molecular weight: less than 200 (Mw1), between 200 and 300 (Mw2), and greater than 300 (Mw3). The input parameters in the presented models and correlations are displayed with the abbreviations T, Mw1, Mw2, and Mw3. Also, the data was divided into a 20/80 ratio for testing and training.
Gene expression programming (GEP)
GEP is a well-known Evolutionary Algorithm (EA), that uses the development of computer programs to address user-defined problems47. GEP was verified to be efficient in the search for accurate and concise software. GEP is separated into numerous distinct sections. For simplicity, These are organized into eight groups in this survey. GEP includes encoding design, design of the evolutionary mechanism, design of adaptation, design of cooperative coevolution, design of continual creation, design of parallel systems, theoretical research, and, last but not least, design of the applications of GEP. The design of the encoding has a significant impact on GEP performance, as it determines the research space of genotypes and phenotypes. Traditional evolutionary mechanisms GEP adopts multiple operators based on genetic algorithm (GA), such as random mutation and crossing a point, to make chromosomes evolve48. Adaptation design refers to the design of adaptive control mechanisms for GEP parameters. It’s important to note that the GEP incorporates a number of control variables, such as population size, chromosomal length, and mutation rate. EAs are frequently enhanced with cooperative coevolutionary (CC) design when dealing with complex optimization issues. An optional GEP operator called constant creation searches for numerical constants to build precise GEP solutions. Further GEP processing time reduction by integrating parallel design. Theoretical studies of GEP have received the most attention, including the estimation of convergence speed and the proof of convergence49. In the GEP strategy, an evolutionary algorithm is used to determine the most effective mathematical format47,50. As a result, the GEP approach was used in this investigation to relate the inputs to the output of how much asphaltene precipitated. The evolutionary algorithm (EA) is used to find the optimum solution for optimization problems. This is comparable to characteristic evolution. GEP is really thought of as an improved form of Genetic Programming (GP), which was created by Koza50,51. It addressed problems with GP, such as the use of just a few regression techniques47,50. Like other evolutionary algorithms, GEP searches for the optimum expression technique by formalizing and representing alternative solutions using chromosomes. In particular, the Expression Tree (ET), a crucial element, is introduced by GEP. The chromosomes are transformed into real ET contenders. Genes having a head and terminals containing functions are necessary for GEP. There is a set number of symbols for each gene that stand in for various operators, such as + , /, and log, as well as a terminal set, such as x, y, and z50.
Algorithm framework of GEP has many steps, and each step is explained separately in the next paragraph. The flowchart of the algorithm framework of GEP is shown in Fig. 1.
The initialization step aims to create the initial population and create a set of chromosomes at random. Depending on the kind of element, each fixed-length string’s chromosome in the initial population is randomly assigned to one of the elements. In fitness assessment, all of the population’s chromosomes have their fitness values assessed. The performance of the algorithm is significantly impacted by the problem-specific fitness evaluation function. Choice and Replication to create a new population for the following generation that this phase picks the population’s superior chromosomes. Many different selection techniques should be employed, such as the tournament selection strategy and the roulette wheel selection strategy, because these strategies perform better when addressing difficult problems49,52. Every component on each chromosome is randomly altered with a preset mutation rate (pm) during the mutation process, according to the mutation step53. The transposition step tries to swap out a section of the chromosome’s consecutive elements for a segment of the same chromosome’s consecutive elements. It consists of three sub-steps that are each carried out with a probability of pis, pris, and pg. A section of consecutive elements in the chromosome is known as an insertion sequence (IS). An IS is chosen at random in this step’s sub-step54. Then, a copy of the IS is generated and randomly placed into a gene’s head. So, the name of this step is IS-transposition. The RIS-transposition step has a group of subsequent items that begins with a function known as a root insertion sequence (RIS)55. So, genes’ heads are used to select RISs. The chromosome, the gene that will be changed, the start location of the RIS, and the length of the RIS are all determined at random in this sub-step56. As part of the IS transposition process, after a RIS is chosen, a copy of the RIS is created and put into the root of the chosen gene. In gene transposition, the chromosome that will be changed is picked at random. Then, a randomly chosen gene except for the first gene from the predetermined chromosome is picked and moved to the start of the chromosome57. The purpose of the recombination process is to create two offspring by exchanging the gene information from the two parent chromosomes. Gene recombination involves the random selection of a gene from one parent58. The chosen gene is then switched for its counterpart from the other parent, producing two children. The three sub-steps in the recombination are carried out with a probability of as follows: pc1, pc2, and pcg. A new population, similar in size to the parent population is produced following the recombination procedure. The evolutionary process continues until the termination conditions (such as producing a good result or reaching the maximum generation) are met, at which point the algorithm moves on to the fitness evaluation phase49.
GEP mechanism is briefly described as follows:
In the GEP algorithm, predictive models are generated through the use of genetic ideas. First, an initial population of predictive models is randomly generated as a set of genetic members. Then, these models are evaluated based on their performance in predicting the training data. Models that perform better are more likely to survive and reproduce in the next generation, while models with poorer performance are less likely to survive59. This iterative process continues to arrive at new generations of models that perform better in predicting new data. Also, in each generation, genetic operators such as mutation and combination are used to increase population diversity and generate new models with different combinations of features. This process ensures improved performance and accuracy of models in predicting new data49.
Advantages and disadvantages have been reported for the GEP model, which are described as follows:
Advantages of GEP model:
-
The ability to generate prediction models with complex structures and the ability to explore the space of different models.
-
The possibility of using genetic operators to improve and adapt models to input data.
-
Ability to quickly adapt and change models in response to changes in data or issues under investigation.
Disadvantages of the GEP model:
-
Complexity in interpreting the resulting models, especially when using more complex structures.
-
The need to adjust genetic parameters appropriate to the problem in order to improve the performance of the model.
-
The possibility of encountering problems related to lack of training data or incorrect selection of genetic parameters that can lead to inferable models60.
Group method of data handling (GMDH)
Basically, Volterra-Kolmogorov-Gabor (VKG) polynomials (Eq. (1)) are used to model complex systems61.
where x = x1,x2,…,xn are the input vectors, y is the output of the model, and ai are polynomial constants. VKG polynomials are estimated by means of quadratic polynomials. These quadratic polynomials are built based on binary mixtures of network inputs. Utilizing knowledge as a learning technique, the GMDH algorithm has been introduced to model complex systems61,62.
The GMDH neural network has the construction of a multi-layered and forward network and contains a set of neurons that are formed by connecting dissimilar input couples to complete a second-degree polynomial. Every layer in this network contains one or more processor parts, every of which has two inputs and one output. These parts truly play the role of model formation constituents and are presumed in the form of a second-degree polynomial (Eq. (2))63.
The unidentified parameters of GMDH algorithm are the polynomial constants of Eq. (2). In order to estimate the output value yi for each input vector x = xi1,xi2,…,xin based on Eq. (6), the mean square error of Eq. (3) must be minimized60.
To find the minimum error value, the partial derivative of Eq. (3) is used. By replacing Eq. (2) in this partial derivative, a matrix equation (Aa = y) is gained. In the equation, a = (a0,a1,a2,a3,a4,a5) and Y = (y1,…,ym)T is matrix A according to Eq. (4) 50.
A solution method for this matrix equation (Aa = y) is to use the Singular Value Decomposition (SVD) method. If using the SVD method, the unknown \(\alpha\) is estimated from Eq. (5).
In Eq. (1), AT is the term of matrix A. By utilizing the method, the solution of the unidentified can be computed in any case. As long as the matrix (ATA) is not invertible, the Thikhonov method will be utilized to resolve the equation.64. In the design of GMDH neural network, the goal is to avoid the growth of network divergence and to relate the shape and construction of the network to one or more numerical parameters, so that the network structure changes with the change of this parameter. To generalize GMDH neural networks, the condition of using the conjoining layer in building the next layer should be removed. This form of neural network is called GS and it uses all the former layers (including the input layer) to build a new layer65.
The structure of the GMDH model is shown in Fig. 2.
Briefly, the mechanism of GMDH is written in several lines:
In the GMDH algorithm, simple mathematical models are automatically created by the algorithm when the process starts. These models include linear combinations of input variables. Then, by evaluating the performance of each of these models on the training data, models that show better performance than other models are selected50. The selected models are then combined with each other to create more complex models with better predictive ability. This process continues iteratively and models with better performance are added to the new models. Finally, the model with the best performance on the test data is selected to predict the new data more accurately. This process continues to improve the performance and prediction accuracy of the models to provide an optimal final model65.
The GMDH model has advantages and disadvantages, including the following:
Advantages of GMDH model:
-
The ability to create predictive models with variable complexity and the ability to adapt to different input data.
-
Ability to automate the process of selecting and combining models based on their performance.
-
Good performance in cases where there are more complex relationships between variables66.
Disadvantages of the GMDH model:
-
The need for larger training data volumes in order to create more accurate models.
-
High computational processing to combine and upgrade models, which may be time-consuming and complex.
-
The complexity of the resulting models may be difficult to interpret for non-expert users67.
Results and discussion
In the research, using GMDH and GEP, two models were developed to approximate biodiesel surface tension with high accuracy. The proposed correlations in the research to forecast biodiesel surface tension are presented in Table 2. The details related to each model, including the execution time and hyper-parameters set to achieve the desired accuracy, are listed in Table 3. As mentioned previously, model input parameters include 78 laboratory data including temperature and mass fraction of fatty acid ethyl esters and esters are divided into three groups according to their molecular weight: less than 200 (Mw1), between 200 and 300 (Mw2), and greater than 300 (Mw3). Classification of mass fractions is one of the methods of reducing the dimensions of input parameters, and input parameters with similar characteristics are placed in one category, and the similarity of the input parameters in this research was considered molecular weight. Among 78 laboratory data, 63 data were designated as train subset, and 15 points were randomly selected as test data for checking the precision and perfection of the presented models.
Determinant error parameters
The precision of the presented models was assessed utilizing the statistical parameters introduced below68:
Average percent relative error:
Root mean square error
Average absolute percent relative error
Standard deviation
R-squared
In the correlations that were presented above, ST, \(\overline{ST}\) and N represent the surface tension, average surface tension and the number of data, respectively, and the predicted and experimental surface tension are shown with superscript cal and act.
Determinant error diagrams
One of the methods of evaluating the presented models is the use of error-determining diagrams. The error-determining diagrams in this research include the relative error distribution diagram, cross-plot diagram, and bar chart diagrams. In the relative error distribution diagram, the deflection of the data from the zero error line is shown. In the cross-plot diagram, the degree of deflection of the data from the X = Y line is shown, and in both diagrams, the degree of compatibility of the experimental data with the predicted data by the model is checked.
Precisions and validities of the models
To check the accuracy of the developed models in this research, the statistical parameters were presented in Table 4, which shows the accuracy of these models. In this table, the training, test and total error values for both proposed models in this research were calculated. As mentioned in the table, the AAPRE value for the GMDH model is the lowest value and is equal to 0.97%, which indicates the high accuracy of this model. Also, other error parameters for this method are as follows:
It should be noted that between two introduced models, the GEP model reports a higher error than GMDH with AAPRE equal to 1.89%. Considering the amount of AAPRE for the GMDH model, which is equal to 0.97%, it can be concluded that this model has a high ability to forecast biodiesel surface tension.
It is also clear that the amount of SD for two models reports a small value, which shows the robustness and accuracy of the presented models. Also, the values of APRE for two models, GMDH and GEP, are estimated to be − 0.07 and 0.13, respectively, and according to these values, it can be said that no overestimate or underestimate occurred in any of the models.
In the following, the accuracy of the established models is checked in the form of a diagram. Figure 3 displays the cross-plot diagram for the developed models in the research for two training and testing data sets. As it is clear, both models report high accuracy and their R2 values are close to 1. According to the cross-plot diagram, the laboratory data have a good match and overlap with the predicted data. Also, the density and high accumulation of data around the line with a slope of 1 are high, and this indicates the high accuracy of the presented models in this research. Also, another diagram has been drawn to check the accuracy of the models in Fig. 4 called the relative error distribution diagram. In this diagram, it can be perceived that the dispersion of the data around the zero error line is low and the density of the data around this line is high. The highest density around this line is related to the GMDH model, which has high accuracy. It is also worth mentioning that there was no over-fitting or under-fitting in these models. When the accumulation of data is high below the zero error line, it can be understood that the model has under-fitting, and also when the accumulation of data is above the zero error line, the model predicts the value of the desired parameter much more than the experimental data.
Also, in order to compare the models presented in this research with the existing models in the literature to measure biodiesel surface tension, Table 5 was presented69,70. The statistical parameter used to compare these models was considered R2. It is clear that both presented models in this research are more precise than the models in the literature and their R2 value is close to 1.
Compatibility and overlapping of laboratory data and data predicted by the model are of great importance. In order to check this purpose in detail, Fig. 5a,b was presented. In this diagram, the horizontal axis represents the index of data points and the vertical axis represents the experimental and predicted surface tension by the GMDH. Also, Fig. 5a is for checking the training data and Fig. 5b is for checking the compatibility of the test data. Finally, it can be concluded that the data predicted by the GMDH follows the same trend as the laboratory data.
In order to specify the data that report the highest amount of absolute error, a three-dimensional diagram was used. Figure 6 shows a cumulative chart for the models developed in this research to compare their efficiency and accuracy. The absolute error of each model is shown on the X-axis of this diagram, and the Y-axis shows the cumulative frequency. In this graph, the steeper the slope of the graph and converges towards the Y axis, the less error the model reports. According to the explanations mentioned and according to this graph, the line related to the GMDH model reports an accuracy of about 4% for 95% of the data. Also, according to the graph related to the GEP model, it can be found that this model reports an error of 4% for 80% of the data.
Trend analysis
In general, liquids’ surface tension reduces with growing temperature and reaches zero when the critical temperature is reached. The cause for decreasing surface tension with increasing temperature is that when the temperature rises, the kinetic energy of the molecules increases and leads to a diminution in the energy of attraction between molecules71. As it is clear in Fig. 7, with the increase in temperature, the value of surface tension decreases and the data predicted by the model follow the same trend as the laboratory data and have high overlap and accuracy.
Sensitivity analysis
In order to check the effectiveness of the output of the most accurate model in this research of the input parameters, sensitivity analysis is used. The basis of this method is to use the relevancy factor function64. The purpose of this function is to find the effect of inputs on the output, and the values obtained by this function are between − 1 and 1, where the positive value indicates the direct behavior of the input with the output, while the negative value indicates the inverse behavior of the input parameter with the output67. The relevancy factor is measured based on the relationships presented below59.
Inpk,i and Inpk represent the ith and kth average values of the input, respectively. In this relationship, ST represents the predicted value of surface tension and \(\overline{ST}\) represents the average value of surface tension. Also, k can be any of the input parameters including temperature or mass fractions. The outcomes of the mentioned method are given in Fig. 8. According to the diagram, temperature has the highest relevancy factor, and it can be concluded that surface tension is more affected by temperature than other input parameters, and the negative value of temperature indicates the inverse effect of temperature on surface tension. Also, the mass fractions related to esters, esters with molecular weight of less than 200 have the greatest effect, and esters with molecular weight of more than 300 report the least effect on surface tension.
Detection of outliers and suspected data
William’s chart was used to find outlier data and suspicious experimental data. In the chart, the horizontal axis indicates Hat values and the vertical axis demonstrates the value of standardized residuals. How to calculate the cap and Standardized Residuals is as follows60,67:
In Fig. 9, the vertical line drawn in the middle of the graph represents the Hat*, which is determined by the value of the Hat*of outlier data. According to the figure, it is clear that only three data points of their hat are more than the Hat* and they are out of the applicable range of the model. This shows the uniformity and validity of the dataset used, as well as the reliability of the models provided by this dataset. Also, suspicious laboratory data are data that their standardized residuals are out of the range of 3– − 3. According to the graph, only three data points from the dataset have been identified as suspicious laboratory data. It can also be seen that there is a large amount of data within the range of the model validity area and reliability, and their Hats are less than the Hat*, and their standardized residuals are between 3 and − 3.
Conclusions
It is clear that one of the sources of clean fuels for energy production is biodiesel. For this reason, the importance of this fuel is clear to everyone, and measuring its properties is of considerable importance. In this research, the surface tension of biodiesel was approximated by GMDH and GEP methods. The input parameters include mass fraction of fatty acid ethyl esters and temperature (T), and esters are divided into three groups according to their molecular weight: less than 200 (Mw1), between 200 and 300 (Mw2), and greater than 300 (Mw3). The advantage of this model compared to the presented models in the literature is the higher accuracy and ease of use of these models. The presented models in this research are white boxes and are available for use, while the presented models in the literature are all black boxes and special software and codes are needed to use them. After performing calculations to check the accuracy of the presented models, it was concluded that the GMDH model with the value of AAPRE = 0.97% and R2 = 0.9233 has higher accuracy than the GEP method. Also, the accuracy of the presented models in this research was checked using the error-determining diagram including the cross-plot diagram and the relative error distribution diagram, in which satisfactory results were observed. Then, the surface tension behavior of biodiesel was investigated at different temperatures and it was concluded that the surface tension of biodiesel decreases with increasing temperature, which was well predicted by the model. As well as that, the effect of input parameters on the surface tension obtained from the GMDH method was investigated and it was found that the maximum effect of the input parameters on the surface tension of biodiesel is related to temperature. Finally, only five data points were identified as outliers and suspicious laboratory data using the Leverage technique.
Data availability
The datasets generated and/or analyzed during the current study are available from the corresponding author upon reasonable request.
References
Montzka, S. A., Dlugokencky, E. J. & Butler, J. H. Non-CO2 greenhouse gases and climate change. Nature 476, 43–50 (2011).
Cao, L., Bala, G., Caldeira, K., Nemani, R. & Ban-Weiss, G. Importance of carbon dioxide physiological forcing to future climate change. Proc. Natl. Acad. Sci. 107, 9513–9518 (2010).
Mahmoudvand, M. & Ashoorian, S. Carbon dioxide injection enhanced oil recovery and carbon storage in shale oil reservoirs. Gas Inject. Methods, 199–257 (2023).
Sandler, T. Environmental cooperation: Contrasting international environmental agreements. Oxford Econ. Papers 69, 345–364 (2017).
Demirbas, A. & Karslioglu, S. Biodiesel production facilities from vegetable oils and animal fats. Energy Sources, Part A 29, 133–141 (2007).
Srivastava, A. & Prasad, R. Triglycerides-based diesel fuels. Renew. Sustain. Energy Rev. 4, 111–133 (2000).
Datta, A. & Mandal, B. K. Use of Jatropha biodiesel as a future sustainable fuel. Energy Technol. Policy 1, 8–14 (2014).
Knothe, G. & Steidley, K. R. Lubricity of components of biodiesel and petrodiesel. The origin of biodiesel lubricity. Energy Fuels 19, 1192–1200 (2005).
Verduzco, L. F. R. Density and viscosity of biodiesel as a function of temperature: Empirical models. Renew. Sustain. Energy Rev. 19, 652–665 (2013).
West, Z. J. et al. Investigation of water interactions with petroleum-derived and synthetic aviation turbine fuels. Energy Fuels 32, 1166–1178 (2018).
Queimada, A. et al. Prediction of viscosities and surface tensions of fuels using a new corresponding states model. Fuel 85, 874–877 (2006).
Barati-Harooni, A. et al. Experimental and modeling studies on the effects of temperature, pressure and brine salinity on interfacial tension in live oil-brine systems. J. Mol. Liquids 219, 985–993 (2016).
Rostami, A., Ebadi, H., Arabloo, M., Meybodi, M. K. & Bahadori, A. Toward genetic programming (GP) approach for estimation of hydrocarbon/water interfacial tension. J. Mol. Liquids 230, 175–189 (2017).
Pratas, M. J. et al. Biodiesel density: Experimental measurements and prediction models. Energy Fuels 25, 2333–2340 (2011).
Gakh, A. A., Gakh, E. G., Sumpter, B. G. & Noid, D. W. Neural network-graph theory approach to the prediction of the physical properties of organic compounds. J. Chem. Inf. Comput. Sci. 34, 832–839 (1994).
Miraboutalebi, S. M., Kazemi, P. & Bahrami, P. Fatty acid methyl ester (FAME) composition used for estimation of biodiesel cetane number employing random forest and artificial neural networks: A new approach. Fuel 166, 143–151 (2016).
Hosseinpour, S., Aghbashlo, M., Tabatabaei, M. & Khalife, E. Exact estimation of biodiesel cetane number (CN) from its fatty acid methyl esters (FAMEs) profile using partial least square (PLS) adapted by artificial neural network (ANN). Energy Convers. Manag. 124, 389–398 (2016).
Mostafaei, M. Prediction of biodiesel fuel properties from its fatty acids composition using ANFIS approach. Fuel 229, 227–234 (2018).
Bemani, A. et al. Modeling of cetane number of biodiesel from fatty acid methyl ester (FAME) information using GA-, PSO-, and HGAPSO-LSSVM models. Renew. Energy 150, 924–934 (2020).
Parveen, N., Zaidi, S. & Danish, M. Artificial intelligence (AI)-based friction factor models for large piping networks. Chem. Eng. Commun. 207, 213–230 (2020).
Parveen, N., Zaidi, S. & Danish, M. Development and analyses of data-driven models for predicting the bed depth profile of solids flowing in a rotary kiln. Adv. Powder Technol. 31, 678–694 (2020).
Razavi, R., Bemani, A., Baghban, A., Mohammadi, A. H. & Habibzadeh, S. An insight into the estimation of fatty acid methyl ester based biodiesel properties using a LSSVM model. Fuel 243, 133–141 (2019).
Parveen, N., Zaidi, S. & Danish, M. Comparative analysis for the prediction of boiling heat transfer coefficient of R134a in micro/mini channels using artificial intelligence (AI)-based techniques. Int. J. Modell. Simul. 40, 114–129 (2020).
Parveen, N., Zaidi, S. & Danish, M. Support vector regression: A novel soft computing technique for predicting the removal of cadmium from wastewater. Indian J. Chem. Technol. (IJCT) 27, 43–50 (2020).
Nusrat, P., Sadaf, Z. & Mohammad, D. Support vector regression (SVR)-based adsorption model for Ni (II) ions removal. Groundw. Sustain. Dev. 9, 100232 (2019).
Baghban, A., Kardani, M. N. & Mohammadi, A. H. Improved estimation of Cetane number of fatty acid methyl esters (FAMEs) based biodiesels using TLBO-NN and PSO-NN models. Fuel 232, 620–631 (2018).
Nabipour, N. et al. Estimating biofuel density via a soft computing approach based on intermolecular interactions. Renew. Energy 152, 1086–1098 (2020).
Phankosol, S., Sudaprasert, K., Lilitchan, S., Aryusuk, K. & Krisnangkura, K. Estimation of surface tension of fatty acid methyl ester and biodiesel at different temperatures. Fuel 126, 162–168 (2014).
Thangaraja, J., Anand, K. & Mehta, P. S. Predicting surface tension for vegetable oil and biodiesel fuels. RSC Adv. 6, 84645–84657 (2016).
An, H., Yang, W., Maghbouli, A., Chou, S. & Chua, K. Detailed physical properties prediction of pure methyl esters for biodiesel combustion modeling. Appl. Energy 102, 647–656 (2013).
Wallek, T., Rarey, J., Metzger, J. O. & Gmehling, J. Estimation of pure-component properties of biodiesel-related components: Fatty acid methyl esters, fatty acids, and triglycerides. Ind. Eng. Chem. Res. 52, 16966–16978 (2013).
Melo-Espinosa, E. A. et al. Surface tension prediction of vegetable oils using artificial neural networks and multiple linear regression. Energy Procedia 57, 886–895 (2014).
Hosseini, S. M. & Pierantozzi, M. Molecular thermodynamic modeling of surface tensions of some fatty acid esters and biodiesels. J. Mol. Liquids 281, 431–443 (2019).
Salehi, E. et al. Modeling interfacial tension of N2/CO2 mixture+ n-alkanes with machine learning methods: Application to EOR in conventional and unconventional reservoirs by flue gas injection. Minerals 12, 252 (2022).
Ceriani, R. & Meirelles, A. J. Predicting vapor–liquid equilibria of fatty systems. Fluid Phase Equilibria 215, 227–236 (2004).
Ferrando, N., Lachet, V. & Boutin, A. Transferable force field for carboxylate esters: Application to fatty acid methylic ester phase equilibria prediction. J. Phys. Chem. B 116, 3239–3248 (2012).
Marrero, J. & Gani, R. Group-contribution based estimation of pure component properties. Fluid Phase Equilibria 183, 183–208 (2001).
Oliveira, M., Coutinho, J. & Queimada, A. Surface tensions of esters from a combination of the gradient theory with the CPA EoS. Fluid Phase Equilibria 303, 56–61 (2011).
Aitbelale, R. et al. High-pressure soybean oil biodiesel density: Experimental measurements, correlation by Tait equation, and perturbed chain SAFT (PC-SAFT) modeling. J. Chem. Eng. Data 64, 3994–4004 (2019).
Chhetri, A. & Watts, K. Surface tensions of petro-diesel, canola, jatropha and soapnut biodiesel fuels at elevated temperatures and pressures. Fuel 104, 704–710 (2013).
Blangino, E., Riveros, A. & Romano, S. Numerical expressions for viscosity, surface tension and density of biodiesel: Analysis and experimental validation. Phys. Chem. Liquids 46, 527–547 (2008).
Baghban, A. Computational modeling of biodiesel production using supercritical methanol. Energy Sources, Part A Recover. Util. Environ. Effects 41, 14–20 (2019).
Guo, J. & Baghban, A. Application of ANFIS strategy for prediction of biodiesel production using supercritical methanol. Energy Sources, Part A Recover. Util. Environ. Effects 39, 1862–1868 (2017).
Parveen, N., Zaidi, S. & Danish, M. Modeling of flow boiling heat transfer coefficient of R11 in mini-channels using support vector machines and its comparative analysis with the existing correlations. Heat Mass Transf. 55, 151–164 (2019).
Parveen, N., Zaidi, S. & Danish, M. Development of SVR-based model and comparative analysis with MLR and ANN models for predicting the sorption capacity of Cr (VI). Process Saf. Environ. Prot. 107, 428–437 (2017).
Parveen, N., Zaidi, S. & Danish, M. Support vector regression prediction and analysis of the copper (II) biosorption efficiency. Indian Chem. Eng. 59, 295–311 (2017).
Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. arXiv preprint cs/0102027 (2001).
Mohammadi, M.-R. et al. On the evaluation of crude oil oxidation during thermogravimetry by generalised regression neural network and gene expression programming: Application to thermal enhanced oil recovery. Combust. Theory Modell. 25, 1268–1295 (2021).
Zhong, J., Feng, L. & Ong, Y. Gene expression programming: A survey [Review Article]. IEEE Comput. Intell. Mag. 12, 54–72. https://doi.org/10.1109/MCI.2017.2708618 (2017).
Hadavimoghaddam, F. et al. Modeling thermal conductivity of nanofluids using advanced correlative approaches: Group method of data handling and gene expression programming. Int. Commun. Heat Mass Transf. 131, 105818 (2022).
Koza, J. R. Genetic Programming II: Automatic Discovery of Reusable Programs (MIT Press, 1994).
Jinghui, Z., Xiaomin, H., Jun, Z. & Min, G. in International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06). 1115–1121.
Rezaei, F., Jafari, S., Hemmati-Sarapardeh, A. & Mohammadi, A. H. Modeling viscosity of methane, nitrogen, and hydrocarbon gas mixtures at ultra-high pressures and temperatures using group method of data handling and gene expression programming techniques. Chin. J. Chem. Eng. 32, 431–445 (2021).
Cao, B. et al. Multiobjective evolution of the explainable fuzzy rough neural network with gene expression programming. IEEE Trans. Fuzzy Syst. 30, 4190–4200 (2022).
Shah, H. A., Rehman, S. K. U., Javed, M. F. & Iftikhar, Y. Prediction of compressive and splitting tensile strength of concrete with fly ash by using gene expression programming. Struct. Concr. 23, 2435–2449 (2022).
Khan, M. A. et al. Compressive strength of fly-ash-based geopolymer concrete by gene expression programming and random forest. Adv. Civ. Eng. 2021, 6618407 (2021).
Khan, M. A., Zafar, A., Akbar, A., Javed, M. F. & Mosavi, A. Application of gene expression programming (GEP) for the prediction of compressive strength of geopolymer concrete. Materials 14, 1106 (2021).
Ahmad, A. et al. Compressive strength prediction via gene expression programming (GEP) and artificial neural network (ANN) for concrete containing RCA. Buildings 11, 324 (2021).
Mazloom, M. S. et al. Artificial intelligence based methods for asphaltenes adsorption by nanocomposites: Application of group method of data handling, least squares support vector machine, and artificial neural networks. Nanomaterials 10, 890 (2020).
Moosanezhad-Kermani, H., Rezaei, F., Hemmati-Sarapardeh, A., Band, S. S. & Mosavi, A. Modeling of carbon dioxide solubility in ionic liquids based on group method of data handling. Eng. Appl. Comput. Fluid Mech. 15, 23–42 (2021).
Ivakhnenko, A. G. Polynomial theory of complex systems. IEEE Trans. Syst., Man, Cybern. 4, 364–378 (1971).
Madala, H. R. Inductive Learning Algorithms for Complex Systems Modeling (CRC Press, 2019).
Mohammadi, M.-R. et al. Toward predicting SO2 solubility in ionic liquids utilizing soft computing approaches and equations of state. J. Taiwan Inst. Chem. Eng. 133, 104220 (2022).
Rezaei, F. et al. On the evaluation of interfacial tension (IFT) of CO2–paraffin system for enhanced oil recovery process: Comparison of empirical correlations, soft computing approaches, and parachor model. Energies 14, 3045 (2021).
Mulashani, A. K., Shen, C., Nkurlu, B. M., Mkono, C. N. & Kawamala, M. Enhanced group method of data handling (GMDH) for permeability prediction based on the modified Levenberg Marquardt technique from well log data. Energy 239, 121915 (2022).
Rezaei, F., Akbari, M., Rafiei, Y. & Hemmati-Sarapardeh, A. Compositional modeling of gas-condensate viscosity using ensemble approach. Sci. Rep. 13, 9659 (2023).
Rezaei, F., Jafari, S., Hemmati-Sarapardeh, A. & Mohammadi, A. H. Modeling of gas viscosity at high pressure-high temperature conditions: Integrating radial basis function neural network with evolutionary algorithms. J. Pet. Sci. Eng. 208, 109328 (2022).
Mohammadi, M.-R. et al. Application of robust machine learning methods to modeling hydrogen solubility in hydrocarbon fuels. Int. J. Hydrogen Energy 47, 320–338 (2022).
Mousavi, N. S., Romero-Martínez, A. & Ramírez-Verduzco, L. F. Predicting the surface tension of mixtures of fatty acid ethyl esters and biodiesel fuels using UNIFAC activity coefficients. Fluid Phase Equilibria 507, 112430 (2020).
Cao, Y., Du, J., Bai, Y., Ghadiri, M. & Mohammadinia, S. Towards estimating surface tension of biodiesels: Application to thermodynamic and intelligent modeling. Fuel 283, 118797 (2021).
Sugden, S. VI.—The variation of surface tension with temperature and some related functions. J. Chem. Soc., Trans. 125, 32–41 (1924).
Author information
Authors and Affiliations
Contributions
F.R.: Investigation, Data curation, Methodology, Writing–original draft, M.R.A.J.: Visualization, Methodology, Writing–original draft, M.K.M.:Methodology, Validation, Writing-Review & Editing, Y.R.: Methodology, conceptualization, Visualization, Writing-Review & Editing, M.S.: Visualization, validation, Writing-Review & Editing, M.A.: Visualization, conceptualization, Writing-Review & Editing, A.H.: Supervision, Validation, conceptualization, Writing-Review & Editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Rezaei, F., Arab Juneghani, M.R., Keshavarz Moraveji, M. et al. On the evaluation of surface tension of biodiesel. Sci Rep 14, 18253 (2024). https://doi.org/10.1038/s41598-024-68064-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-68064-9