Introduction

The successful application of hydraulic fracturing techniques in the field has greatly promoted the development of unconventional oil and gas1,2. The propagation laws of hydraulic fracture were widely studied through laboratory physical experiments, numerical simulation, and theoretical analyses3,4,5,6,7,8,9,10,11. It was found that in-situ stress is the main controlling factor determining the fracture propagation direction and morphology. The laboratory experiment is an effective way to study fracture propagation by simulating the actual formation conditions, in which the fracture morphology could be directly observed. The laboratory hydraulic fracturing experiment started in 1957. Hubbert and Willis12 studied the relationship between the orientation of hydraulic fractures and in-situ stress state. They concluded that hydraulic fracture propagates perpendicular to the direction of minimum principal stress. Daneshy et al.13 conducted hydraulic fracturing experiments on layered rock to study the influences of physical properties and weak surfaces on fracture propagation. Since then, the effects of different parameters on fracture propagation were extensively investigated, including the discontinuities such as natural fractures and beddings, rock mechanical properties, pumping modes, and injection parameters (fluid viscosity and injection rate)14,15,16,17,18. Recently, with the exploitation of shale and coalbed methane reservoirs, the fracture propagation behaviors in shale and coal were increasingly studied through fracturing experiments19,20,21,22. However, the well-developed beddings, joints, and cleats in shale and coal lead to inaccurate simulated in-situ stress, which directly affects the experimental results. Although lots of physical experiments have been conducted, the similarity between laboratory experiments and field tests lacks detailed discussion. De Pater et al.23 established the 2-D hydraulic fracturing similarity criterion through dimensional analysis to determine similar proportions of fracturing specimen similar to that under reservoir condition. Liu et al.24 derived a new similarity criterion through equation analysis in similarity theory, which was consistent with De Pater's results. Guo et al.25 derived the 3-D similarity criterion for perforated Wells and obtained similar proportions among various physical quantities. The above similarity criteria were derived based on linear elastic assumptions, ignoring the similarity of in-situ stress conditions between laboratory experiments and field tests. In laboratory experiments, the true triaxial loading mode is often used to simulate the magnitude and direction of in-situ stress, generally assuming that the stress applied to the specimen surface could immediately transfer to the interior, and the stress distribution inside the specimen is uniform. However, microcracks, cleats, beddings, and other discontinuities exist in the rock, affecting the stress transfer to the interior of the specimen. The stress transfer process is accompanied by the stress redistribution inside the specimen26,27,28, resulting in inconsistency with the in-situ stress conditions. Therefore, it is necessary to further clarify the stress transfer process in laboratory experiments to ensure the reliability of hydraulic fracturing experimental results.

There are limited publications reporting the stress redistribution inside rocks under continuous stress loading conditions, mainly focusing on the creep behavior. Bazant and Wittmann26, Taha et al.27, and Ma28 found that the concrete material creeps under a long-term loading process, accompanying stress redistribution inside the specimen. Wang et al.29 used stress sensors to monitor the real-time stress variations inside the coal specimen and found that the stress applied to the specimen surface would not be uniformly transferred to the interior, and the stress transfer process was affected by cracks in the coal specimens. However, the stress sensor used is relatively large in size and is only suitable for monitoring the internal stress of large-size specimens. In laboratory experiments, it is difficult to monitor the stress variation inside rocks due to the smaller specimen size. Therefore, it is necessary to establish a new stress monitoring method to study the stress redistribution process of rocks.

At present, there are many methods for monitoring stress and strain in rocks, mainly including the overscoring technique, hollow inclusion stress gauge, flat jack, strain gauge, and earth pressure box30,31,32,33. However, the precision of these methods is not high enough for monitoring the stress inside smaller-size specimens. Compared with traditional stress monitoring methods, Fiber Bragg Grating (FBG) has the advantages of simple structure, small size, high reliability, high tensile strength, real-time monitoring of multiple measurement points, high sensitivity, and so on39,40. In recent years, FBG has been increasingly used to monitor stress and strain. Mendez et al.34 and Nanni et al.35 used FBG strain sensors to measure the strain inside concrete material. Chen et al.36 and Yang et al.37 embedded optical fiber sensors into concrete specimens to measure the change of the strain inside specimens and hydraulic fracture width. Cai et al.38 used FBG earth pressure sensors to monitor confining stress change in the tunnel for a long time.

In this study, a stress monitoring method based on FBG sensing technique was proposed to quantitatively analyze the stress transfer process during the true triaxial stress loading experiments of the concrete-like specimens. It was observed that the stress is difficult to transfer from the surface to the interior of the specimen in a short time. The stress transfer mechanism was analyzed, and a 3-D Bungers model was modified to describe the stress transfer process. This study is helpful to standardize the simulation of in-situ stress in the laboratory hydraulic fracturing experiments.

True triaxial stress loading experimental methods

Stress monitoring based on FBG sensing technique

FBG has been widely used to measure parameters such as strain, temperature, and pressure since Hill et al.41 produced the first FBG sensor in the world. In this study, a stress monitoring method based on FBG sensing technique was proposed to study the stress transfer process, which converts the strain measured by FBG sensor into the stress. We note that the strain measured by FBG sensor differs from the actual strain inside the specimen42. Therefore, the calibration experiment was conducted to obtain the relationship between FBG strain and the actual strain. This method can monitor the multi-point stress change inside the specimen in real-time. Therefore, it is suitable for the stress monitoring of laboratory specimens with different sizes. Moreover, the strain measured by FBG sensor differs from the actual strain inside the specimen42. Therefore, the calibration experiment was conducted to obtain the relationship between FBG strain and the actual strain.

FBG monitoring principle

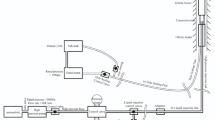
The measurement principle of FBG sensor is shown in Fig. 1. As a quasi-distributed optical fiber, FBG uses the photosensitive optical fiber to produce a photoinduced refractive index change effect under ultraviolet light irradiation and periodically refracts light waves of different wavelengths into the fiber core. Only the incident light waves that meet the diffraction conditions are reflected at the fiber grating, and a peak appears in the reflection spectrum39.

Figure 1
figure 1

Measurement principle of FBG sensor.

Full size image

The demodulation instrument emits light waves to the fiber grating and receives the reflection spectra. The wavelength of the reflection spectra \(\lambda\) is calculated as Eq. (1). FBG is affected by external factors such as temperature, strain, and pressure during the experiment. The effective refractive index \(n\) and pitch change accordingly, resulting in changes in the wavelength of the reflection spectrum. The relationship between wavelength variation \(\Delta \lambda\) and strain is described in Eq. (2)37.

$$\lambda = 2n\Lambda$$
(1)
$$\Delta \lambda = K_{{\upvarepsilon }} \varepsilon_{g} + K_{{\text{T}}} \Delta T$$
(2)

where \(K_{{\upvarepsilon }}\) is the strain optical sensitivity coefficient, \({\upvarepsilon }_{g}\) is FBG strain, \(K_{{\text{T}}}\) is the temperature sensitive optical coefficient, and \(\Delta T\) is the temperature variation.

Calibration experiment

This experiment used Portland cement and quartz sand (the ratio is 1:1) to prepare a calibration specimen with the height of 102 mm and diameter of 51.6 mm, as shown in Fig. 2. FBG sensor was embedded into the calibration specimen during the preparation. The grating length direction is parallel to the height direction of the specimen, with the length of 10 mm. After the specimen pouring was completed, regular water spraying was applied to cure the specimen to ensure that the specimen and FBG sensor were cemented as completely as possible. The calibration process consists of three steps: (1) Connecting FBG with the calibration specimen. (2) Applying axial load to the calibration specimen at a 0.02 mm/min rate. (3) Using FBG and LVDT sensors to monitor the strain in real-time.

Figure 2
figure 2

Schematic diagram of the calibration specimen.

Full size image

The FBG strain is different from the actual strain of the specimen, which is measured by the LVDT strain. Therefore, we use the strain transfer coefficient \(\alpha\) to calibrate FBG strain, which is defined as the ratio of LVDT strain to FBG strain, as shown in Eq. (3). The precision and measuring range of FBG sensor are 1 micro-strain and 7000 micro-strain, and LVDT sensor is 1 micro-strain and 20,000 micro-strains, respectively.

$$\alpha = \varepsilon_{{\text{m}}} /\varepsilon_{g}$$
(3)

The variation curves of the strain transfer coefficient and FBG strain with LVDT strain are plotted in Fig. 3. As can be seen, the strain transfer coefficient shows an approximately linear relationship with LVDT strain, as shown in Eq. (4), with the correlation coefficient of 0.9791. During the initial loading process, the strain transfer coefficient fluctuates frequently due to the deformation adjustment of the specimen, and the linear relationship is not applicable when LVDT strain exceeds 0.007.

$$\alpha = 11.5 - 1463.4\varepsilon_{{\text{m}}}$$
(4)
Figure 3
figure 3

Variation of the strain transfer coefficient and FBG strain with LVDT strain.

Full size image

According to Eqs. (5) and (6), the relationship between LVDT strain and FBG strain is derived, as shown in Eq. (7).

$$\varepsilon_{{\text{m}}} = \varepsilon_{{\text{g}}} (11.5 - 1463.4\varepsilon_{{\text{m}}} )$$
(5)
$$\varepsilon_{{\text{m}}} (1 + 1463.4\varepsilon_{{\text{g}}} ) = 11.5\varepsilon_{{\text{g}}}$$
(6)
$$\varepsilon_{{\text{m}}} = 11.5\varepsilon_{{\text{g}}} /(1 + 1463.4\varepsilon_{{\text{g}}} )$$
(7)

Stress calculation

This study assumes that the specimen is an isotropic linear elastic material. The strains generated in the three principal stress directions are equal under hydrostatic pressure. The stress–strain relationship could be expressed as (8)–(10)43.

$$\sigma_{{\text{p}}} = \sigma_{x} = \sigma_{y} = \sigma_{z}$$
(8)
$$\varepsilon_{{\text{m}}} = \varepsilon_{x} = \varepsilon_{y} = \varepsilon_{z}$$
(9)
$$\sigma_{{\text{p}}} = 3\left( {\frac{{11.5\varepsilon_{{\text{g}}} }}{{1 + 1463.4\varepsilon_{{\text{g}}} }}} \right)\left( {\lambda + \frac{2}{3}G} \right)$$
(10)

where \(\sigma_{{\text{p}}}\) is the hydrostatic pressure, \(\sigma_{x}\), \(\sigma_{y}\), and \(\sigma_{z}\) are the stresses on x, y, and z axes, and \(\varepsilon_{x}\), \(\varepsilon_{y}\), and \(\varepsilon_{z}\) are the corresponding strains, respectively.

Experimental facilities and specimen preparation

The true triaxial loading system designed by China University of Petroleum-Beijing adopts a rigid loading mode with a maximum loading stress of 50 MPa and an accuracy of 0.01 MPa (Fig. 4a). The MOI si155 fiber grating demodulation instrument is used to monitor the stress change inside the specimen (Fig. 4b).

Figure 4
figure 4

Experimental facilities: (a) True triaxial loading system; (b) Fiber grating demodulation instrument.

Full size image

To ensure the repeatability of experimental results, all concrete-like specimens were prepared using the same formula and method. The specimens were composed of Portland cement and quartz sand, the ratio is 1:1. FBG sensors were embedded into the specimens during the specimen preparation. The specimens were cured with water spraying after it was poured, ensuring that FBG sensor and the concrete-like specimen were completely cemented. This study prepared two concrete-like specimens containing FBG fiber strings, as schematically shown in Fig. 5. FBG sensor in specimen 1 has three monitoring points (A1, A2, and A3), and the vibrator is not used in the specimen preparation process, resulting in many defects, such as microcracks and pores inside the specimen. FBG sensor in specimen 2 has two monitoring points (B1 and B2), and the vibrator is used to minimize the defects inside the specimen. The grating length of the fiber string is 10 mm, and the pitch is 40 mm. We note that this study mainly focuses on the stress transfer process inside the specimen, and the number of monitoring points won’t affect the experimental results.

Figure 5
figure 5

Schematic diagram of FBG sensor layout: (a) Specimen 1; (b) Specimen 2; (c) concrete-like specimen.

Full size image

True triaxial stress loading scheme

The experimental parameters are listed in Table 1. As can be seen, with the increase of curing time, the mechanical properties of the specimens change. To thoroughly analyze the stress transfer process in different rocks, the specimens with different curing times were used in this study. In addition, three different loading stresses were applied to analyze the stress transfer process, which are 9 - 9 - 9 MPa, 20 - 20 - 20 MPa, and 30 - 30 - 30 MPa, corresponding to low, medium, and high stress conditions, respectively. For specimen 1, the first stress loading experiment was conducted after it was cured for 7 days. Afterward, it was further cured for 23 days before conducting the second stress loading experiment.

Table 1 Mechanical parameters of the specimen and experimental conditions.
Full size table

For specimen 2, it was cured for 15, 30, 36, and 37 days, and four stress loading experiments were conducted accordingly. The loading ways were the same for all experiments.

The testing process consists of three steps: (1) Loading the specimen until it reaches the preset stress value. (2) Keeping the three-way stress constant for a period of time. (3) Using FBG sensor to monitor the real-time stress changes inside the specimen.

Experimental results of stress transfer in concrete-like materials

FBG strain is monitored in real-time during the stress loading, which is then converted into stress accordingly. As shown in Fig. 6, the stress inside specimen 1 increases gradually with the loading time. The stresses at the end of loading are listed in Table 2. It is observed that the stress is non-uniformly distributed in the specimen, which increases from monitoring points A1 to A3 for both conditions cured for 7 days and 30 days. The potential reason is that many defects, such as microcracks and pores, exist in specimen 1, and the applied three-way stress (9 - 9 - 9 MPa) is not high enough to transfer from the surface to the interior in a short time.

Figure 6
figure 6

Variation of stresses inside specimen 1 with the loading time: (a) Curing for 7 days, stress 9 - 9 - 9 MPa; (b) Curing for 30 days, stress 9 - 9 - 9 MPa.

Full size image
Table 2 The stresses at A1, A2, and A3 at the end of loading.
Full size table

Four stress loading experiments were conducted on specimen 2 after curing for 15, 30, 36, and 37 days. The stress variation inside specimen 2 with the loading time is plotted in Fig. 7. The stress redistribution process can be divided into two stages. The stage I is the stress adjustment stage. With the loading time, the stress at B1 gradually increases, while the stress at B2 slowly decreases (Fig. 7 a, c), indicating the stress redistribution process. The reason may be that microcracks and other defects inside the specimen gradually close with time. The stage II is the stress balance stage. The stress distribution inside the specimen reaches a relatively uniform state. The criteria for dividing the two stages are: (1) The stress remains almost unchanged with the loading time. (2) The stresses at the two monitoring points are the same. The reason for the stress redistribution will be discussed in the fourth section.

Figure 7
figure 7

Variation of stresses inside specimen 2 with the loading time: (a) Curing for 15 days, stress 9 - 9 - 9 MPa; (b) Curing for 30 days, stress 9 - 9 - 9 MPa; (c) Curing for 36 days, stress 20 - 20 - 20 MPa; (d) Curing for 37 days, stress 30 - 30 - 30 MPa.

Full size image

The experimental results of stress transfer in specimen 2 after curing for 15 and 30 days are depicted in Fig. 7a and b. The three-way stress (9 - 9 - 9MPa) remains unchanged, and the stress adjustment time for specimen 2 cured for 15 days is 1 h. However, the stress adjustment time for specimen 2 cured for 30 days exceeds 5 h. In addition, the stress at B2 does not decrease monotonically with the loading time (Fig. 7a). The reason may be that defects such as microcracks and pores inside the specimen change with the hardening of concrete-like material44,45, ultimately affecting the stress transfer process. Due to the stress concentration near defects (pores and microcracks), the monitoring points near these defects initially experience high stress levels that gradually decrease with the loading time. On the contrary, when there are fewer defects near the monitoring point, the stress will increase slowly with the closure of microcracks. Figure 7c and d shows the stress variations inside specimen 2 under the loading conditions of 20 - 20 - 20 MPa and 30 - 30 - 30 MPa. The times required for stress adjustment decrease significantly with the increase of compression stress, which are 12 h and 1.5 h for the two loading conditions, respectively. In addition, the stress unloading process is shown in Fig. 8. When the stress is completely unloaded (stress is zero), the strain is as small as 0.0001 and gradually decreases to almost zero, which indicates that the concrete-like material exhibits obvious viscoelastic properties under hydrostatic pressure. Therefore, repeated loading of the specimen has little effect on subsequent experiments.

Figure 8
figure 8

Strain variation inside the specimen during stress unloading.

Full size image

As shown in Table 3, the stresses at B1 and B2 are almost the same as the stress applied to the specimen surface under different loading conditions. However, the stresses at B1 and B2 under the loading condition of 30 - 30 - 30 MPa are 28.5 and 28.6 MPa respectively, which are slightly less than 30 MPa. The reason may be that the friction between the pressurized steel plate and the specimen surface is larger, which directly affects the stress transfer process.

Table 3 The stresses at B1 and B2 during stress balance stage.
Full size table

The stress transfer mechanism of concrete-like materials

The true triaxial stress loading experiments were conducted on concrete-like specimens to study the stress transfer process. It is found that the stress applied to the specimen surface requires a certain loading time to transfer to the interior. Concrete-like material shows obvious viscoelastic properties instead of damage under hydrostatic pressure with the loading time. However, it is generally believed that rock creep occurs only under a certain stress difference, ignoring the rock creep behavior under hydrostatic pressure. The commonly used creep models for concrete-like material include the Burgers model, B3 model, and ACI 209 model46,47,48, in which the Burgers model characterizes the viscoelastic properties of rocks and is suitable for describing the first two stages of rock creep. The Burgers model consists of the Maxwell model and the Kelvin model in series. The creep equations of the Maxwell model and Kelvin model are expressed as Eqs. (11) and (12), respectively. The 1-D Burgers model is obtained by using the superposition principle, as shown in Eq. (13)49.

$$\varepsilon = \frac{{\sigma_{1} }}{{E_{1} }} + \frac{{\sigma_{1} }}{{\eta_{1} }}t$$
(11)
$$\varepsilon = \frac{{\sigma_{2} }}{{E_{2} }}[1 - \exp ( - \frac{{E_{2} }}{{\eta_{2} }}t)]$$
(12)
$$\varepsilon = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{\eta_{1} }}t + \frac{\sigma }{{E_{2} }}[1 - \exp ( - \frac{{E_{2} }}{{\eta_{2} }}t)]$$
(13)

where \(\sigma\) and \(\varepsilon\) are the stress and strain of the components under 1-D condition, \(E_{1}\) and \(\eta_{1}\) the elastic modulus and viscosity coefficient of the components in the Maxwell model. \(E_{2}\) and \(\eta_{2}\) the elastic modulus and viscosity coefficient of the components in the Kelvin model.

The 1-D Burgers model is derived to the 3-D model by analogy method50. The expression of the modified 3-D model is shown in Eq. (14).

$$\varepsilon_{{{\text{ij}}}} = \frac{{I_{1} }}{9K}\delta_{{{\text{ij}}}} + \frac{{s_{{{\text{ij}}}} }}{2G} + \frac{{\sigma_{{{\text{ij}}}} }}{{2H_{1} }}t + \frac{{\sigma_{{{\text{ij}}}} }}{{2G_{2} }}[1 - \exp ( - \frac{{G_{2} }}{{H_{2} }}t)]$$
(14)

where \(\sigma\) and \(\varepsilon\) represent \(\sigma_{{{\text{ij}}}}\) and \(\varepsilon_{{{\text{ij}}}}\), \(E = 2G\), and \(\eta = 2H\). \(G\) is the shear modulus, and \(H\) is the viscosity coefficient in the 3-D model. \(\sigma /E_{1} = \delta_{{{\text{ij}}}} I_{1} /9K + s_{{{\text{ij}}}} /2G\), \(\sigma t/\eta_{1} = \sigma_{{{\text{ij}}}} t/2H_{1}\), and \(\sigma [1 - \exp ( - E_{2} t/\eta_{2} )]/E_{2} = \sigma_{{{\text{ij}}}} [1 - \exp ( - G_{2} t/H_{2} )]/2G_{2}\). \(I_{1}\) is the first stress invariant, \(K\) is the volume modulus. \(G_{1}\) and \(G_{2}\) are the shear modulus of the components, \(H_{1}\) and \(H_{2}\) are the viscosity coefficient of the components.

The true triaxial stress loading condition in this work is the hydrostatic pressure. The modified 3-D Burgers model under the hydrostatic pressure is obtained by substituting \(s_{{{\text{ij}}}} = 0\) into Eq. (14), as shown in Eq. (15).

$$\varepsilon_{1} = \frac{{I_{1} }}{9K} + \frac{{\sigma_{1} }}{{2H_{1} }}t + \frac{{\sigma_{1} }}{{2G_{2} }}[1 - \exp ( - \frac{{G_{2} }}{{H_{2} }}t)]$$
(15)

where \(\sigma_{1}\) and \(\varepsilon_{1}\) are hydrostatic pressure and strain, respectively.

A modified 3-D Burgers model was used to describe the stress transfer process. The experimental data was fitted by the least-square method51. The fitting results of specimen 2 under different loading conditions are plotted in Fig. 9. Under the conditions of 9 - 9 – 9 MPa, 20 - 20 - 20 MPa, and 30 - 30 - 30MPa, the fitting results of the modified 3-D Burgers model show good agreements with the experimental results, indicating that the modified model is suitable for different loading conditions. Under hydrostatic pressure, the strain rate gradually decreases to zero with the loading time, and only primary creep occurs, which is mainly caused by the closure of microcracks inside rock52,53,54. The fitting and experimental results indicate that the specimen creeps with the loading time, accompanied by the closure of microcracks and the stress redistribution inside the specimen. When the microcracks are completely closed, the stress inside the specimen reaches a uniform state.

Figure 9
figure 9

Strain–time and fitting curves inside specimen 2 under different loading conditions: (a) Curing for 15 days, stress 9 - 9 - 9 MPa; (b) Curing for 36 days, stress 20 - 20 - 20 MPa; (c) Curing for 37 days, stress 30 - 30 - 30 MPa.

Full size image

The creep parameters in the modified 3-D Burgers model are divided into two categories. The first kind of parameters are dependent on the intrinsic properties of rock materials, namely \(K\) and \(G_{1}\). The other reflects the creep properties, namely \(H_{1}\) and \(H_{2}\), which directly affect the stress transfer process of rock materials. The larger \(H_{1}\) and \(H_{2}\), the longer time is required for the stress transfer to the interior. In addition, some other factors, such as specimen size and pore structure, also affect the stress transfer process. The influence of the boundary effect can be effectively reduced by increasing the specimen size. However, the larger the specimen size, the more defects such as microcracks and pores inside the specimen55,56. The stress transfer chain induced by the stress concentration around the pore is strongly related to the pore structures. As the disorder degree of pore arrangement increases, the distribution heterogeneity of the stress transfer chain increases. When pores are completely closed, the stress transfer chain disappears, meaning that the stress is transferred to the interior57,58.

Implications of stress transfer for hydraulic fracturing experiments

This study shows that it takes a certain loading time for the stress to transfer from the surface to the interior of the specimen. Under the loading conditions of 20 - 20 - 20 MPa and 30 - 30 - 30 MPa, it takes 12 h and 1.5 h for the stress to be completely transferred to the interior. For the former condition, it takes only 2 h for 90% of the applied stress to transfer to the interior. Therefore, it is recommended to preload concrete specimens for at least 2 h to accurately simulate in-situ stress conditions. In addition, for the specimens with geological discontinuity, such as natural fractures, cleats, and beddings, the stress transfer to the interior requires a longer preloading time.

A method for determining the preloading time is proposed according to the modified 3-D Burgers model, as shown in Fig. 10. Firstly, the standard cylindrical samples are obtained from the target fracturing formation. Then, the creep experiments are conducted on the cylindrical samples according to the in-situ stress conditions, and the creep parameters are obtained by the modified 3 D Burgers model. Finally, the time required for the primary creep stage is calculated by the derivative of \(\varepsilon_{{{\text{ij}}}} (t)\), i.e. the preloading time.

Figure 10
figure 10

Flow chart for determining the preloading time.

Full size image

A group of experiments is designed to verify the stress transfer phenomenon during hydraulic fracturing of coal rocks. The in-situ stress is set as 20 - 25 - 30 MPa, and the specimen size is 30 cm × 30 cm × 30 cm (Fig. 11a). The first fracturing specimen is preloaded for 5 h, while the other is not preloaded. The injection pressure curves are shown in Fig. 11b. Due to the well-developed cleat inside coal, fracture initiation primarily overcomes \(\sigma_{{\text{h}}}\). The initiation pressure (17 MPa) for the specimen preloaded for 5 h is closes to \(\sigma_{{\text{h}}}\) , while that for the specimen without preloading is 9 MPa, much lower than \(\sigma_{{\text{h}}}\), indicating that sufficient preloading is necessary to simulate the in-situ stress. The experimental results demonstrate that there is an obvious stress transfer phenomenon during laboratory experiments, which directly affects fracture initiation and propagation. This work standardizes the simulation of in-situ stress in laboratory hydraulic fracturing experiments.

Figure 11
figure 11

(a) coal specimen; (b) Injection pressure–time curves.

Full size image

In laboratory hydraulic fracturing experiments, concrete-like material, core from target formation, and natural outcrop are commonly used as specimens for fracturing59,60. These specimens have numerous microcracks and pores, which directly affect the stress transfer process, resulting in inconsistency with the in-situ stress conditions, making it impossible for the laboratory experimental results to effectively provide a reference for on-site hydraulic fracturing. This work aims to standardize the simulation of in-situ stress. In addition, understanding the rock mechanical behavior under in-situ geological conditions is also of reference significance. Rock is susceptible to damage due to stress release during coring. Applying long-term stress loading to the core can make the stress state of the core closer to the in-situ stress state, thus allowing it to obtain the in-situ mechanical properties of rock61.

Conclusions

In this study, the true triaxial stress loading experiments were conducted on the concrete-like specimens to study the stress transfer process, in which FBG sensors were used to monitor the real-time stress variations inside the specimen. Then, the stress transfer mechanisms were analyzed. Finally, the stress transfer phenomenon during hydraulic fracturing was verified through coal fracturing experiments. The following conclusions can be drawn:

  1. (1)

    The relationship between FBG strain and the actual strain of the specimen was obtained by calibrating FBG strain. A method for monitoring stress based on FBG sensing technique was proposed, which is suitable for real-time stress measurement inside multi-size specimens.

  2. (2)

    It takes a certain loading time for the stress applied on the specimen surface to transfer to the interior. The required loading time decreases with the increase of compression stresses. Under the loading conditions of 20 - 20 - 20 MPa and 30 - 30 - 30 MPa, the required loading times are 12 h and 1.5 h, respectively.

  3. (3)

    The stress transfer process in rock materials is determined by creep. The closure of microcracks results in stress redistribution inside the specimen during creep. In addition, a 3-D Burgers model is modified to describe the stress transfer process and calculate the preloading time of the fracturing specimen. For concrete-like materials, it is recommended that the preloading time is at least 2 h.