Introduction

Machining is defined as the macron scale metal removal on work material by using various source of energy (chemical, laser and mechanical). The machining techniques such as tool based machining, laser based machining, water based machining and chemical based machining processes are commercially used to achieve the machining. Electrical Discharge Machining (EDM) still remains a competitive process to other machining processes from the time of invention to today. EDM is an electro-thermal operation used in many sectors like medical, military, aerospace and automotive industry. Processing is performed without the contact of electrodes (tool) with the work material. Therefore, neither cutting forces nor stress is involved during the machining. Electrodes with low thermal conductivity are also used for machining hard and tough materials. During machining, electrode wear is an inevitable issue that should be addressed in order to achieve desired component quality. Hence, electrode wear can be reduced by adopting certain methods like uniform electrode wear method1, real-time electrode wear method2, or by measures like selection of electrode materials3,4, dielectric jacket on electrodes5. The above described procedures have been slowly improved by researchers. In the EDM, both the work-piece and electrode remove material using erosion process. Due to this erosion effect, the degradation of electrode shape greatly affects the desired shape of the work material. For this reason, the focus of research is on reducing square electrode wear by changing the EDM parameters and also varying the size of square shaped electrodes. Generally, the electrode wear is strongly associated to thermal properties, thermal diffusivity, wear resistance, size effect and thermal conductivity of electrodes. Therefore, electrodes with higher thermal conductivity, higher thermal diffusivity, better wear resistance and larger diameter are recommended to reduce electrode wear. The performance of carbon nano-tube infused copper electrodes and pure copper electrodes on work material using EDM are analyzed. Results show that EDM produces a minimum electrode wear rate 0.00047 mm3/s for 1 µs pulse duration, 6 µs pulse interval and 3 A current. In another study on reduction of wear rate of copper electrode, EDM is performed on tool steel by varying drill diameter and current. The observed results reveal that electrode wear decreases with increase in electrode diameter and current6. In addition, different electrode materials such as brass, aluminium, copper and copper-tungsten are also tested to compare their performances in reducing electrode wear in the machining of steel. Hence, proper selection of thermal conductivity and melting point of electrodes also plays an important role in reducing electrode wear. In yet another method, the design of experiment is also used to assess reduce the electrode wear. In addition, a comparative study is performed between the performances of copper and graphite electrodes on tool steel. Results show that the relative volumetric wear of copper and graphite decreases on decreasing the current from 8 to 3 A and the discharge duration from 10 to 50 µs. Copper and graphite electrodes show equal machining performances over tool steel7. Another comparative study was conducted on the drilling performances of copper, brass and graphite exhibits lower tool wear than brass and graphite8. On comparing the performances of brass, copper and tungsten electrodes over that of copper electrodes in ultrafast drilling of Inconel 718, a copper electrode wear rate of 40% and a surface roughness of 11.716 µm are observed by using 115 A current and 50 A current respectively9.

Wear analysis of square copper electrode for sizes 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm have not been studied by using EDM parameters for far. Therefore, in this work, the square electrode wear analysis is conducted for different hole sizes that have been micro-drilled on Hastelloy B2 by EDM process and the process has then been analyzed in different aspects. The similar results observed in the previous work10. Also, a square electrode wear analysis is carried out by considering Electrode Taper Angle (ETA), Electrode Radius (ER), Electrode Wear Length (EWL) and Cutting Time (CT) as responses. Due to limitations of the grey system theory, the research scope of grey relational analysis has not been developed in recent years. Also, the existing GRA models are all based on distance perspective, slope perspective and area perspective. In view of this, the present work applies Taguchi based VIKOR method to find the optimum process parameters of EDM process and compares the results with Taguchi based GRA method for validation. Also, alternative methods are required to provide better results compared to the Taguchi based GRA method. Therefore, Taguchi based Višekriterijumsko Kompromisno Rangiranje (VIKOR)11 and Taguchi based GRA12 are implemented on the process for obtaining unique optimum parameters. In the recent studies, the square blind holes were fabricated in a titanium alloy. It found that 0.02 mm lower taper, 0.04 mm filet radius 0.127 mm corner radius13. The effect of square electrode size on performance measures of Inconel studied using nano-SiC powder mixed EDM. Results found that high square electrodes had a low wear14. Ion Nitriding (IN), Surface Hardening by Laser (LSH) and Hybrid Process (IN + LS + LSH) were used for reducing the copper electrodes in the name of electrode wear in frontal and lateral. Analysis proved that the electrode wear was reduced by 30% for frontal and 76% for lateral using a hybrid method15. The electrode wear was studied by using the rotating tool and vibrating workpiece. The result found that a high vibration electrode produced a smaller electrode wear16. In this past literature works, the research gap was found that the few works were performed the micron level square holes analysis of superalloys and study the performance of square hole and electrode wear. In recent days, micron level products were developed. Hence, in order to achieve the micro level features such as microhole, microslot, microgear and micropump. There was a need for microhole fabrication using microelectrode and its studies.

Experimental details

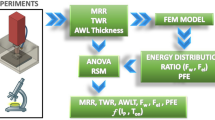
A series of micro-drilling experiments are performed in EDM (Model: Sodick AD30 linear motor). The schematic diagram of EDM, photo-shoot of EDM and machined work material is shown in Fig. 1. The experiments are carried out at ambient temperature. The copper electrodes in the form of solid squares are fabricated through a vertical machining center. Hastelloy B2is a new high performance superalloy. Table 1 shows the chemical composition of Hastelloy B2. It is combination of two alloy properties (nickel-molybdenum). This combination of properties makes them an ideal choice for many corrosive environments. Compared to similar materials, Hastelloy be offers superior mechanical strength at ambient and elevated temperature and excellent formability and weldability. Hence, the alloy is used hazardous applications like chemical environments, oil and gas. Hastelloy B2 is a difficult to cut by conventional machining process such as turning, milling and grinding. Hence, EDM is selected for machining.Square shaped micron scale square holes are fabricated on Hastelloy B2, a difficult task due to the selection of process parameters. The mechanical properties of Hastelloy B2 and copper electrode are shown in Table 2. In earlier literature, selection of process parameters and problems observed on selecting those process parameters are also shown in Table 3. By using the MINITAB software, the design of experiment is created based on the number of factors and levels. MINITAB software URL is given in the Reference. Hence, the through square hole was selected as priority for selection of parameters. EDM oil with dielectric fluid pressure is selected as 0.6 kg/cm2 and is maintained constant in all tests. Square holes are processed on Hastelloy B2 according to design of experiments to study the effects of different machining process parameters on the electrode taper angle, electrode radius, electrode wear length and cutting time using EDM. The parameters, Current (A), Pulse duration (µs), Duty cycle (%) and Servo voltage (V) for EDM are selected as input factors for EDM. The actual photographic view of square electrode is shown in Fig. 2. A video measuring system and scanning electron microscope were used to measure the response. The schematic diagram for worn out electrode is shown in Fig. 3.

Figure 1
figure 1

Photo-shoot of EDM with square copper electrode.

Full size image
Table 1 Chemical composition of Hastelloy B2.
Full size table
Table 2 Mechanical properties of Hastelloy B2 and Copper electrode.
Full size table
Table 3 Selection of process parameters.
Full size table
Figure 2
figure 2

Fresh copper square electrode size of 0.5 mm.

Full size image
Figure 3
figure 3

Optical microscopic image of worn out electrode size of 0.5 mm.

Full size image

Methodologies of optimization techniques

There are two optimization techniques used in this work. One is VIKOR and another one is GRA. The procedure of VIKOR and GRA are given below.

Vikor method

VIKOR method is presented as follows:

Step 1: As per weight assumtions, the beneficial criteria and non-beneficial criteria are decided.

Step 2: Calculate the best and worst value of criterions.

(a) best fi+ and worst fi- value for each criterion by using Eq. (1)

$${f}_{i}^{+ }= {f}_{ij, }{f}_{i}^{- }= {f}_{ij}$$
(1)

(b) Compute the values Si and Ri using Eqs. (2), (3), respectively; i = 1, 2 ,…, m,

$${S}_{i }= {\sum }_{j=1}^{n}\frac{{W}_{j}\left({f}_{j}^{+}- {f}_{ij}\right)}{\left({f}_{j}^{+}- {f}_{j}^{-}\right)}$$
(2)
$${R}_{i }={W}_{j }\frac{\left({f}_{j}^{+}- {f}_{ij}\right)}{\left({f}_{j}^{+}- {f}_{j}^{-}\right)}$$
(3)

Step 3:Compute S*, R* and Qi using Eqs. (4), (5) and (6), respectively.

$${S}^{*}= {s}_{i, }{S}^{-}= {s}_{i,}$$
(4)
$${R}^{*}= {R}_{i, }{R}^{-}= {R}_{i,}$$
(5)
$${Q}_{i}=v ({s}_{i }- {s}^{* })/ ({s}^{-}- {s}^{* })+\frac{\left(1-v\right)\left({R}_{i }- {R}^{* }\right)}{{R}^{-}- {R}^{*}}$$
(6)

Here, ʋ is denoted as the weight of strategy (ʋ = 0.5).

Step 4:Rank and sort by the values S, R and Q in decreasing order.

Step 5: Find the best alternatives by minimum Q with C1 and C2 conditions satisfied using Eqs. (7), (8) and (9).

C1: Acceptable advantage

$$ Q(A^{^{\prime\prime}} ) - Q(A^{\prime} ) \ge DQ $$
(7)
$$DQ= 1/\left(m-1\right)$$
(8)

If only condition C2 is not satisfied, select the alternatives A’ and A”.

If the conditions C1 is not satisfied, find the AM

$$ Q \left( {A^{\left( M \right) } } \right) - Q \left( {A^{^{\prime} } } \right) < DQ $$
(9)

GRA method

The procedure of GRA is given below.

Step 1:To calculate the S/N Ratio of response using Eqs. (10),(11)with respect to its quality characteristics.

Larger is better;

$$ {\raise0.7ex\hbox{$S$} \!\mathord{\left/ {\vphantom {S N}}\right.\kern-0pt} \!\lower0.7ex\hbox{$N$}} ratio = - 10*\log \left( \frac{1}{n} \right)\mathop \sum \limits_{i = 1}^{n} 1/y_{ij}^{2} $$
(10)

Smaller is better;

$$ {\raise0.7ex\hbox{$S$} \!\mathord{\left/ {\vphantom {S N}}\right.\kern-0pt} \!\lower0.7ex\hbox{$N$}} ratio = - 10*\log \left( \frac{1}{n} \right)\mathop \sum \limits_{i = 1}^{n} y_{ij}^{2} $$
(11)

Step 2: To find the normalized S/N ratio using Eqs. (12),(13) with respect to their quality characteristics.

$${For\, lower\, the\, better, N}_{i}^{*}\left(k\right)=\frac{{max y}_{i}\left(k\right)- {y}_{i}(k)}{max {y}_{i}\left(k\right)-{min y}_{i}(k)}$$
(12)
$${For\, higher\, the\, better, N}_{i}^{*}\left(k\right)=\frac{{ y}_{i}\left(k\right)-min{y}_{i}\left(k\right)}{max {y}_{i}\left(k\right)-{min y}_{i}(k)}$$
(13)

Step 3:Calculate Grey relational Coefficient from the normalized S/N ratio values using Eq. (14).

$${\epsilon }_{i}\left(k\right)=\frac{\Delta min+\tau \Delta max}{{\Delta }_{oi}\left(k\right)+\tau \Delta max}$$
(14)

Step 4: To calculate the Grey relational grade from grey relational coefficients using Eq. (15).

$$GRG=\left(\frac{1}{m}\right)\sum {\epsilon }_{i}\left(k\right)$$
(15)

where \(\overline{{\gamma_{j} }}\)is the grey relational grade; jth experiment and k is the number of performance characteristics.

Step 5: Find the optimal factor and its level combination using Eq. (16)

$$ E_{i} = \, \max \, \left( {AGV_{ij} } \right){-}\min \, \left( {AGV_{ij} } \right) $$
(16)

Results

The through square holes are made on Hastelloy B2 through design of experiments. After drilling, the square copper electrodes are worn out at surfaces and edges. The responses such as electrode taper angle, electrode radius and electrode wear length for 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm square copper electrodes are measured. The cutting times are also measured and the design layout and responses are shown in Table 4. The rank of the parameter is identified on the basis of delta value. The delta value for each response is calculated by difference between the maximum and minimum values. The most significant parameters are identified through the highest delta value/first rank value in the process parameters. In order to evaluate performance measures of EDM, an analysis is performed on the most significant parameters over electrode taper angle, electrode radius, electrode wear length and cutting time.

Table 4 Design layout and its experimental results for 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm square electrode.
Full size table

Electrode taper angle

A taper angle is formed on the square electrode in all experimental conditions due to the worn out surfaces and edges of electrodes. Table 5 tabulates mean ETA calculations. The square electrode taper angle (ETA) of 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm is found to increase on increasing the significant parameters, which is shown in Fig. 4a. The electrode surfaces and edges are less worn out than work material while achieving the desired square holes.Also, the electrode wear is found to be minimized by lowering the current and voltage17. The reason for selecting the maximum electrode taper angle is because it produces minimum electrode wear. Thereby, the maximum electrode taper angle is selected as objective. Similarly, the square electrode of 0.5 mm is found to have minimum electrode taper angle on giving a 3 A current input.

Table 5 Mean ETA calculations.
Full size table
Figure 4
figure 4

Significant parameters over: (a) Electrode taper angle, (b) Electrode radius, (c) Electrode wear length, and (d) cutting time.

Full size image

Electrode radius

After drilling, the square electrode is found to attain a hemispherical shape at the electrode end in all experiments. This is attributed to a high degree of short-circuit developed particularly in the machining of micro features and also the square electrode area and skin effect. A large amount of heat is stacked at the electrode corner resulting in a strong wear off. The influence of EDM process parameters and square electrodes of sizes0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm on worn out electrode radius (ER) at the end is studied and it is shown in Fig. 4b. The effect of EDM process parameters and square electrodes of sizes of 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm on EWL is studied which is shown in Fig. 4c. In this electrode radius analysis, the most significant parameter was identified as pulse duration for 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm square electrodes. A similar procedure is followed for calculating ER and the results are shown in Table 6. The ER was found to improve up to 34.48% (the range varying from 0.259 to 0.169 mm) for 0.5 mm square electrode, up to 34.94% (the range varying from 0.346 to 0.225 mm) for 0.6 mm square electrode, up to 34.22% (the range varying from 0.393 to 0.258 mm) for 0.7 mm square electrode and up to 34.23% (the range varying from 0.435 to 0.286 mm) for 0.8 mm square electrode by increasing the pulse duration. Therefore, the 0.8 mm square electrode is found to exhibit maximum electrode radius with a 300 µs pulse duration.

Table 6 Mean ER calculations.
Full size table

Electrode wear length

The schematic diagram of electrode wear length along the length (y-direction) and cross-section (x-direction) is shown in Fig. 5. After drilling, the length of electrode wear is observed to be more along the y-direction than along the cross-section of the electrode in the x-direction. This is due to the thickness of work material being less than the length of the copper electrode, resulting in producing more machining contact area in the y-direction. In additional reason is poor heat transformation. EWL is measured along the y-direction of square electrodes. It is calculated from the difference between the fresh electrode length and worn out electrode length. In this EWL analysis, the most significant parameter is identified as current for 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm square electrodes and which is shown in Table 7. The EWLs for 0.6 mm, 0.7 mm and 0.8 mm square electrodes are found to increase gradually by increasing current on account of the increased number of unstable sparks generated from the square electrode on work material. Similarly, the EWL is found to improve up to 7.85% for 0.5 mm square electrode, up to 15.95% for 0.6 mm square electrode, up to 18.32% for 0.7 mm square electrode and up to 19.88% for 0.8 mmsquare electrode on increasing the current. Therefore, the 0.8 mm square electrode exhibits minimum EWL for 3 A current.

Figure 5
figure 5

Schematic diagram: (a) Fresh electrode, (b) Partially worn out electrode, and (c) Full worn out electrode.

Full size image
Table 7 Mean EWL calculations.
Full size table

Cutting time

The cutting time is measured by obtaining through a square hole on work material. The effect of EDM process parameters and square electrodes of sizes 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm on CT is analyzed which is shown in Fig. 4d In this CT analysis, the most significant parameter is identified as the duty cycle for 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm square electrodes which is also identified in Table 8. The CTs for 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm square electrodes are found to decrease corresponding to an increase in duty cycle. The duty cycle is found to directly depend on the pulse duration. Also, pulse duration directly affects the metal removal rate of both work material and electrode. Thereby, CT decreases on increasing the duty cycle. Also, the area and skin effects are causative factors for decrease in cutting time. Similar results are observed in other work too18. Similarly, the CT is found to improve of 79.2% for 0.5 mm square electrode, 83.6% for 0.6 mm square electrode, 77.1% for 0.7 mm square electrode and 78.2% for 0.8 mm square electrode by increasing the duty cycle. Therefore, the 0.6 mm square electrode exhibits minimum CT by using 8% DC.

Table 8 Mean CT calculations.
Full size table

Analysis of variance

The purpose of this ANOVA is to determine the significant parameters for ETA, ER, EWL and CT at 95% confidence interval. It was performed in MINITAB 19 trail version software19 and results are shown in Table 9. The p-value is less than 0.05 which is identified as a significant factor. In ETA, the highest contributing factor/significant factor is current. In ER, the most significant factor is a pulse duration. Similarly, the most important factors are current for EWL and duty cycle for CT. The experimental errors are observed to be less than 5% for EWL and CT and the results provide good for further prediction. More variances are observed in the ERs model due to the R-Sq and R-Sq (Adj) being lower than 95%. This is due to the debris movement and secondary discharge developed in the side of holes resulting in non-uniform wear effect on ER.

Table 9 ANOVA for ETA, ER, EWL and CT.
Full size table

Electrode surface analysis

The front and bottom views of surfaces worn out by copper electrode are shown in Figs. 6, 7 respectively. The square electrodes with sharp edges are fully transformed into hemispherical shape at end electrodes due to the unstable sparks generated from edges and surfaces with diffusion of heat on the work material. Also, the electromagnetic effect, generated by the passage of current, plays a major role in the skin effect and tip effect. Therefore, the square shape of electrode drastically transforms into a hemispherical shape at electrode end on increasing the current and pulse duration. Results are comparable with literature data20. The strong wear on the electrode corner and edges are due to the thermal conductivity, density, specific heat, melting point and boiling point of electrode21. The low thermal conductivity of electrodes is the reason behind observation of rounded corners and it is highly related to diffusion of heat. In the bottom view of electrode, a hemispherical shape of diameter 0.190 mm is observed for 0.5 mm square electrode, a hemispherical diameter of 0.299 mm for 0.6 mm square electrode, a hemispherical diameter of 0.579 mm for 0.7 mm square electrode and a hemispherical diameter of 0.639 mm for 0.8 mm square electrode on increasing the current.

Figure 6
figure 6

Worn out electrode at front view for optimum parameter: (a) 0.5 mm electrode, (b) 0.6 mm electrode, (c) 0.7 mm electrode, and (d) 0.8 mm electrode.

Full size image
Figure 7
figure 7

Worn out electrode at bottom view for optimum parameter: (a) 0.5 mm electrode, (b) 0.6 mm electrode, (c) 0.7 mm electrode, and (d) 0.8 mm electrode.

Full size image

Determination of optimum parameters setting

In this VIKOR method, there are 16 alternatives (experimental number varies from 1 to 16) and four criteria (ETA, ER, EWL and CT). The purpose of this research is to select alternative process parameters that have maximum ETA and ER and minimum EWL and CT. All the criteria are assigned equal weightages (0.25). The rank is formed based on the minimum Si, Ri and Qi which are represented as optimum points. Based on the experimental results of 0.5 mm square electrode, the VIKOR calculations are performed for 0.5 mm square electrode which is shown in Table 10. The third experimental number has been selected as the best alternative for all the square electrodes based on the minimum Qi, Ri and Si. Grey Relational Analysis (GRA) is yet another multi-objective optimization technique which is widely used in manufacturing sector. In order to evaluate the best optimization technique, comparison is made between optimum process parameters selected through VIKOR and GRA. The GRA calculation is shown in Table 11. The S/N ratio for responses is calculated. The purpose of normalization is to convert high value into 0—1 value. The normalization of S/N ratio for responses is calculated. The grey relational coefficient is calculated. The grey relational grade is calculated. The highest GRG is considered as optimum parameters. The confirmation test of 0.5 mm square electrode for VIKOR and GRA is carried out on Hastelloy B2 and it is shown in Table 12. The optimum process parameters for VIKOR method are 3 A current/225 µs pulse duration/6% duty cycle/ 80 V servo voltage. The optimum process parameters for GRA method are 12 A current/300 µs pulse duration/2% duty cycle/ 80 V servo voltage. The current and pulse duration are directly related to metal removal of work material and electrode. VIKOR method establishes that lesser electrothermal energy is sufficient to enhance ETA, ER and EWL of electrode, compared to GRA. The electrothermal energy is induced between work material and electrode based on the density, thermal conductivity and melting point of the material. Hence, the combined effect of 3 A current, 225 µs pulse duration, 6% duty cycle 80 V servo voltage in VIKOR method yields better performance method than GRA optimum parameters. It may therefore be inferred that the VIKOR method is better suited to provide process parameters for better electrode performance.

Table 10 VIKOR method for 0.5 mm square hole.
Full size table
Table 11 GRA method for 0.5 mm square hole.
Full size table
Table 12 Confirmation experiment for 0.5 mm square electrode.
Full size table

Discussions

The effect of process parameters and square electrode size on electrode taper angle, electrode radius, wear length and electrode surface are discussed on the basis of previous studies. In ETA result20. The least electrode taper angle of 14º is obtained in the copper electrode using a current value of 27.4 A. The present ETA results of 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm square electrode found that the ETA ranges from 0.24º to 5.185º as observed by using 3 A current. Variations in the ETA are due to erosion resistance of electrodes and work material. The erosion resistance is an index to evaluate EDM machinability of material. Generally, erosion resistance of electrodes is directly proportional to thermal conductivity of electrodes. The formula for erosion resistance is cλƟ2. Here, the c, λ and Ɵ are denoted as specific heat, thermal conductivity and melting point, respectively. The copper electrode has higher erosion resistance than the Hastelloy B2. Therefore, the higher erosion resistance and higher electrode size end to lower electrode wear. Normally, the electrodes wear decreases on increasing the round shape electrode diameter6. The present results produce inverse effects due to the skin effect. The skin effect is identified through fluctuation of discharge energy. Compared to other electrode radius results, the electrode radius in this case is shown to increase from 0.773 mm to 0.702 mm by varying current from 27.4 A to 33.4 A. In the electrode surface analysis, more debris and micro-crater are formed on the worn out electrode surface due to the fluctuating discharge energy developed from the EDM process parameters with unstable spark generated.

Conclusion

Hastelloy B2 is used in microchannel reactors and high corrosion-resistant equipments. These components need a square holes for their applications. Therefore, square hole drilling has been performed on Hastelloy B2. In this research, the effects of process parameters and square electrodes of sizes 0.5 mm, 0.6 mm, 0.7 mm and 0.8 mm on electrode taper angle, electrode radius, electrode wear length and cutting time of Hastelloy B2 are studied by using EDM. The results are shown below:

  • The size of electrode and length are most important factor with electrode wear.

  • The current has the most influential parameter that affects the electrode taper angle and electrode wear length.

  • The electrode radius is found to decrease above 225 µs pulse duration due to the irregular sparking.

  • The duty cycle has the most influential parameter for affecting cutting time.

  • The square electrodes with sharp edges are fully transformed into hemispherical shapes at end electrodes due to the unstable spark generated.

  • The debris and micro-crater are formed on the worn out surface of the electrode.

  • Taguchi based VIKOR method is found to improve the process performance of electrodes compared to Taguchi based GRA.