Introduction

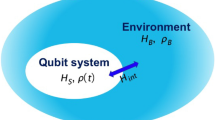
Quantum system’s interaction with their surrounding environment causes the exchange of information, potentially resulting in energy dissipation and the loss of quantum coherence1,2,3,4,5,6. However, the process does not need to be monotonic as the quantum system may temporarily regain some of the lost energy or information due to memory effects during the evolution7,8,9,10,11,12,13,14,15,16,17,18,19,20. This dynamic behavior, known as non-Markovianity, can manifest in different quantum information tasks such as teleportation involving mixed states21, boosting channel capacity in quantum systems22, optimal entanglement protocols23,24,25, and extracting work from an Otto cycle26.

In the context of information flow in open quantum systems, the dynamics involving the system’s interaction with its environment are divided into two categories8,27,28: Markovian and non-Markovian dynamics. If information flows continuously from the system to the surrounding environment, it is referred to as Markovian dynamics. Conversely, information backflow to the system from the environment at some time intervals due to quantum memory effects is known as non-Markovian dynamics.

Research on the non-Markovianity of dynamics in quantum systems has been extensively studied8,9,29,30. Some important witnesses of non-Markovianity effects have been proposed based on different dynamical metrics such as quantum mutual information31, the flow of quantum Fisher information (QFI)32,33, and simple tool of Hilbert-Schmidt speed (HSS)34. Another approach is to probe temporary increases in the entanglement shared between the open quantum system and an isolated ancilla via measuring the deviation from complete positivity (CP) divisibility of the dynamical map that represents the system’s evolution, which was first suggested by Rivas et al.35. The next key approach relies on assessing the distinguishability of two optimal initial states evolving through the same quantum channel or resource and investigating any nonmonotonicity (backflows of information) is quantified by the trace distance (TD) as first proposed by Breuer et al.27,36. Moreover, negative time-dependent decoherence rates in the standard shape of the master equation37, local quantum uncertainty38, coherence39,40, fidelity of the quantum states41,42, channel capacities43, quantum interferometric power44,45,46, Choi states47, changing in the volume of the set of accessible states in the evolved system48, correlation measures49, spectral analysis50, quantum evolution speedup51,52,53, and entropy production rates54. This array of witnesses and approaches highlights the diverse nature of non-Markovian behavior, making it challenging to attribute to a single system-environment interaction feature, hindering its characterization with a single tool for this phenomenon. Therefore, searching for new witnesses to detect non-Markovianity effects in various situations within open quantum systems is beneficial.

In this article, we aim to introduce a method for witnessing and measuring non-Markovianity using the Bhattacharyya distance (BD)55,56, which is a particular case of the quantum statistical distance57. The advantage of this witness is a simple form for computation, as it does not require the calculation of the evolved density matrix. It only computes through the initial and final states of the system, thereby leading to an improvement in quantum metrology. Moreover, we examine the BD-based non-Markovianity witness detects memory effects, in total agreement with witnesses based on the QFI, Bures distance, and HSS therefore identifying system-environment information backflows. This proposal is studied based on the two open quantum systems including the two and three-level atoms interacting with single and two-mode fields, respectively, and two effective two-level atoms interacting locally with two independent environments.

The article is structured as follows: In section “Preliminaries”, the preliminaries of non-Markovianity witnesses are discussed, and the suggested BD witness is introduced. Additionally, in section “The physical models”, the theoretical models are presented. Finally, in section “Discussion and results”, we outline the key discoveries and discussions such that the sensitivity of this measure for identifying memory effects is studied.

Preliminaries

Non-Markovianity witnesses

Quantum Fisher information (QFI)

One of the most crucial witnesses of non-Markovianity is quantum Fisher information (QFI)32. The QFI can serve as a tool for quantum estimation of the desired parameter \(\vartheta\). For instance, we can utilize the QFI to estimate phase in an open quantum system. Considering the quantum Cramer-Rao bound58, one can obtain the smallest resolvable change in the parameter \(\vartheta\) by

$$\begin{aligned} \delta \vartheta =\left( 1 / \sqrt{\mathcal {F}_{\vartheta }}\right) , \end{aligned}$$
(1)

where \(\mathcal {F}_{\eta }\) represents the QFI and for pure states can be simply defined by59

$$\begin{aligned} \mathcal {F}_{\vartheta }=4\left[ \langle \dot{\psi } \mid \dot{\psi }\rangle -|\langle \psi \mid \dot{\psi }\rangle |^{2}\right] . \end{aligned}$$
(2)

in which \(|\dot{\psi }\rangle =(\partial / \partial \vartheta )|\psi \rangle\). The theory of quantum estimation suggests that an increase in QFI signifies an improvement in the optimal accuracy of estimation. Therefore, QFI is a useful measure of the maximum information on parameter \(\vartheta\) that can be obtained from a measurement process.

Hilbert-Schmidt speed (HSS)

Hilbert-Schmidt speed (HSS) is recognized as another potent tool for improving quantum parameter estimation in quantum information theory. As suggested in34,60, the HSS can be utilized as a non-Markovianity witness that identifies memory effects.

To introduce the HSS, we can consider the Hellinger distance criteria d(p, q), defined by \([d(p, q)]^2=\frac{1}{2} \sum _x\left| p_x-q_x\right| ^2\)57, such that \(p=\left\{ p_x\right\} _x\) and \(q=\left\{ q_x\right\} _x\) represent the probability distributions corresponding to the desired parameter \(\vartheta\), which results in characterizing the classical statistical speed (CSS) \(s\left[ p\left( \vartheta _0\right) \right] =\frac{d}{d \theta } d\left( p\left( \vartheta _0+\vartheta \right) , p\left( \vartheta _0\right) \right)\). To expand to the quantum case, one can assume a pair of quantum states \(\rho\) and \(\sigma\), and define \(p_x={\text {Tr}}\left[ \Pi _x \rho \right]\) and \(q_x={\text {Tr}}\left[ \Pi _x \sigma \right]\) where these are the measurement probabilities corresponding to the positive operator-valued measure (POVM) \(\left\{ \Pi _x \ge 0\right\}\) fulfilling \(\sum _x \Pi _x=\mathbb {I}\).

To determine the corresponding quantum statistical distance known as the Hilbert-Schmidt distance61 represented by \(D_{H S}(\rho , \sigma ) \equiv \max _{\left\{ \Pi _x\right\} } d(p, q)=\sqrt{\frac{1}{2} {\text {Tr}}\left[ (\rho -\sigma )^2\right] }\), we maximize the classical statistical distance d(p, q) over all possible measurements of POVMs62. In the same way, the related quantum statistical speed (QSS) is determined by maximizing the CSS over all possible measurements of POVMs57,63. Hence, assuming the quantum state \(\rho (\vartheta )\), one can define the HSS as34,57,64

$$\begin{aligned} HSS(\vartheta )=\max _{\left\{ \Pi _x\right\} } s[p(\vartheta )]=\sqrt{\frac{1}{2}\text {Tr}\Bigg [\frac{d\rho (\vartheta )}{d\vartheta }\Bigg ]^2}. \end{aligned}$$
(3)

Bures distance

As mentioned in65, another popular witness for quantifying non-Markovianity is the Bures distance. In a similar method for determining the HSS, for an assumed pair of quantum states \(\rho _{in}\) and \(\rho _{fi}\), maximizing the classical distance over all possible choices of POVMs, one can define the Bures distance as56,57,66

$$\begin{aligned} D_{Bures}(\rho _{in},\rho _{fi})=\sqrt{2-2\sqrt{f(\rho _{in},\rho _{fi})}}. \end{aligned}$$
(4)

where \(f(\rho _{in},\rho _{fi})=\Bigg (Tr \Big [\sqrt{\sqrt{\rho _{in}}\rho _{fi}\sqrt{\rho _{in}}}\Big ]\Bigg )^2\) denotes fidelity67,68. It should be noted that we can use the distances to quantify the distinguishability between two quantum states.

Bhattacharyya distance (BD)

We now introduce a new distance that then we can use to identify non-Markovianity for pure quantum states. Considering two arbitrary probability distributions p and q, one can determine the classical Bhattacharyya distance (BD) or geodesic distance as55,56,69,70

$$\begin{aligned} d_{B}(p,q)=\cos ^{-1}\left( \sum _{i=1}^n \sqrt{p_i q_i}\right) , \end{aligned}$$
(5)

The right-hand side of the equation is called the Bhattacharyya coefficient, and it bears a striking resemblance to the scalar product in quantum mechanics. Its square is referred to as classical fidelity. Moreover, it is clear that the Hellinger distance is a monotone function of the Bhattacharyya distance.

To expand to the quantum case, we assume two states of \(|\psi _{in}\rangle\) and \(|\psi _{fi}\rangle\). Consider an operator A, and observe that it has \(n+1\) orthogonal eigenstates \(|e_i\rangle\) in terms of which we can expand as

$$\begin{aligned} |\psi _{in}\rangle =\sum _{i=0}^n \sqrt{p_i} e^{i \mu _i}\left| e_i\right\rangle , \quad |\psi _{fi}\rangle =\sum _{i=0}^n \sqrt{q_i} e^{i \nu _i}\left| e_i\right\rangle , \end{aligned}$$
(6)

where we suppose \(p_i\) and \(q_i\) are non-negative real numbers in such a way

$$\begin{aligned} \sum _{i=0}^n p_i=\sum _{i=0}^n q_i=1, \end{aligned}$$
(7)

It means that our states are normalized. Here, \(\mu _i, \nu _i\) represent the phase factors. The probability \(p_i\) to obtain a given measurement outcome is obtained through the standard interpretation of quantum mechanics for the i th outcome to happen when the state is \(|\psi _{in}\rangle\). According to the mentioned method in56 the BD between the given states \(\psi _1\) and \(\psi _2\), can be determined from the square roots of the probabilities:

$$\begin{aligned} \cos (d_B)=\sum _{i=0}^n \sqrt{p_i} \sqrt{q_i}=\sum _{i=0}^n|\langle \psi _{in} \mid i\rangle ||\langle \psi _{fi} \mid i\rangle |, \end{aligned}$$
(8)

Concerning the definition of distance between quantum states, we should choose operator A so that \(d_B\) is maximized, making the right-hand side as small as possible. However, we have the inequality as follows

$$\begin{aligned} \sum _{i=0}^n|\langle \psi _{in} \mid i\rangle ||\langle \psi _{fi} \mid i\rangle | \ge |\langle \psi _{in} \mid \psi _{fi}\rangle |, \end{aligned}$$
(9)

Therefore, the quantum BD which is the distance in the space of pure states can be reduced as

$$\begin{aligned} D_{Bhatt}(\psi _{in},\psi _{fi})=\cos ^{-1}\Big (|\langle \psi _{in} \mid \psi _{fi}\rangle |\Big ), \end{aligned}$$
(10)

This distance is sometimes called the quantum angle between two pure states. Furthermore, the threshold of BD is \(\pi /2\).

Non-Markovianity measure based on Bhattacharyya distance

It is well known that non-Markovian effects can lead to quicker quantum evolution from an initial state to a subsequent state51,71,72,73,74,75. The Bhattacharyya distance criterion can effectively determine memory effects in system dynamics. Here, we emphasize exploiting the Bhattacharyya distance55,56,70 as a valuable witness of the non-Markovian aspect of quantum evolutions, leading to practical benefits in analysis.

Regarding the idea that a nonmonotonic speed (positive acceleration) of quantum dynamics indicates memory effects in the system dynamics, a non-Markovianity witness based on BD can be introduced as

$$\begin{aligned} \mathcal {I}(t):=\frac{d D_{Bhatt}(t)}{d t}>0, \end{aligned}$$
(11)

If the system interacts with its surrounding environment, i.e. there is a system-environment information exchange, the \(D_{Bhatt}\) decreases monotonically, then dynamics is known as Markovian. So, we have for some time intervals \(\mathcal {I}(t)<0\). In contrast, every positive value of \(\mathcal {I}(t)>0\) denotes a witness of non-Markovianity.

According to this witness, similar to what has been done for other measures27,34,36,42,76, a determiner of the degree of non-Markovianity can be defined as

$$\begin{aligned} \mathcal {N}:=\max \int _{\mathcal {I}(t)>0} \mathcal {I}(t) d t, \end{aligned}$$
(12)

where the maximization is carried out over all possible parameterizations of the initial state. It is essential to note this point that in this article we evaluate the quantity presented in Eq. (12) according to the quantities of Bhattacharyya distance, Bures distance, Hilbert-Schmidt speed, and quantum Fisher information, which expresses the degree of non-Markovian system dynamics.

We aim to only investigate non-Markovian effects using \(D_{Bhatt}\) based on the witness, where the actual value is irrelevant and no optimization is performed on the initial state parameters.

The physical models

Two-level atom

We assume the interaction between a single-mode radiation field with frequency v and a two-level atom (as illustrated in Fig. 1). Suppose \(|a\rangle\) and \(|b\rangle\) denote the upper and lower level states of the atom, such that they are eigenstates of the unperturbed part of the Hamiltonian \(\mathcal {H}_0\) with the eigenvalues \(\hbar \omega _a\) and \(\hbar \omega _b\), respectively. We can write the wave function of a two-level atom as the following form

Figure 1
figure 1

Schematic of the interaction of a two-level atom with a single-mode field.

Full size image
$$\begin{aligned} |\psi (t)\rangle =C_a(t)|a\rangle +C_b(t)|b\rangle , \end{aligned}$$
(13)

in which \(C_a\) and \(C_b\) denote the probability amplitudes of finding the atom in states \(|a\rangle\) and \(|b\rangle\), respectively. The corresponding Schrödinger equation is defined as

$$\begin{aligned} |\dot{\psi }(t)\rangle =-\frac{i}{\hbar } \mathcal {H}|\psi (t)\rangle , \end{aligned}$$
(14)

with the Hamiltonian of the system

$$\begin{aligned} \mathcal {H}=\mathcal {H}_0+\mathcal {H}_1, \end{aligned}$$
(15)

where \(\mathcal {H}_0\) and \(\mathcal {H}_1\) are the unperturbed and interaction terms of the Hamiltonian, respectively. Utilizing the completeness relation \(|a\rangle \langle a|+| b\rangle \langle b|=\textbf{1}\), one can write the unperturbed part as77

$$\begin{aligned} \mathcal {H}_0 =(|a\rangle \langle a|+| b\rangle \langle b|) \mathcal {H}_0(|a\rangle \langle a|+| b\rangle \langle b|)=\hbar \omega _a|a\rangle \left\langle a\left| +\hbar \omega _b\right| b\right\rangle \langle b|, \end{aligned}$$
(16)

such that we used \(\mathcal {H}_0|a\rangle =\hbar \omega _a|a\rangle\) and \(\mathcal {H}_0|b\rangle =\hbar \omega _b|b\rangle\). Also, another term of the Hamiltonian \(\mathcal {H}_1\) representing the atom’s interaction with the radiation field can be expressed as

$$\begin{aligned} \begin{aligned} \mathcal {H}_1&=-e x E(t) \\&=-e(|a\rangle \langle a|+| b\rangle \langle b|) x(|a\rangle \langle a|+| b\rangle \langle b|) E(t) \\&=-\left( \wp _{a b}|a\rangle \left\langle b\left| +\wp _{b a}\right| b\right\rangle \langle a|\right) E(t), \end{aligned} \end{aligned}$$
(17)

where \(\wp _{a b}=\wp _{b a}^*=e\langle a|x| b\rangle\) represents the matrix element of the electric dipole moment and E(t) denotes the field at the atom. We suppose the electric field is linearly polarized along the x-axis and in the dipole approximation such that \(E(t)=E \cos (vt)\), where E depicts the amplitude and \(v=c k\) represents the field frequency.

The motion equations of the system can be written as

$$\begin{aligned} \begin{aligned}{}&\dot{C}_a=-i \omega _a C_a+i \Omega _R e^{-i \phi } \cos (v t) C_b, \\&\dot{C}_b=-i \omega _b C_b+i \Omega _R e^{i \phi } \cos (v t) C_a, \end{aligned} \end{aligned}$$
(18)

where \(\Omega _R=\frac{\left| \wp _{b a}\right| E}{\hbar }\) is the Rabi frequency, and \(\phi\) represents the phase of the dipole matrix element \(\wp _{b a}=\left| \wp _{b a}\right| \exp (i \phi )\).

To solve for \(C_a\) and \(C_b\), we begin by considering the motion equations for the slowly varying amplitudes:

$$\begin{aligned} \begin{aligned}{}&c_a=C_a e^{i \omega _a t}, \\&c_b=C_b e^{i \omega _b t} . \end{aligned} \end{aligned}$$
(19)

It next obeys from Eq. (18) that

$$\begin{aligned} \begin{aligned}{}&\dot{c}_a=i \frac{\Omega _R}{2} e^{-i \phi } c_b e^{i(\omega -v) t}, \\&\dot{c}_b=i \frac{\Omega _R}{2} e^{i \phi } c_a e^{-i(\omega -v) t}, \end{aligned} \end{aligned}$$
(20)

where \(\omega =\omega _a-\omega _b\) denotes the atomic transition frequency. After some straight calculations and ignoring the terms \(\exp [ \pm i(\omega +v) t]\), the solutions for ca and cb can be obtained as

$$\begin{aligned} \begin{aligned}{}&c_a(t)=\left( a_1 e^{i \Omega t / 2}+a_2 e^{-i \Omega t / 2}\right) e^{i \Delta t / 2}, \\&c_b(t)=\left( b_1 e^{i \Omega t / 2}+b_2 e^{-i \Omega t / 2}\right) e^{-i \Delta t / 2}, \end{aligned} \end{aligned}$$
(21)

where we have \(\Delta =\omega -v\), \(\Omega =\sqrt{\Omega _R^2+(\omega -v)^2}\), and \(a_1, a_2, b_1, b_2\) are constants of integration which are determined from the initial conditions:

$$\begin{aligned} \begin{aligned}{}&a_1=\frac{1}{2 \Omega }\left[ (\Omega -\Delta ) c_a(0)+\Omega _R e^{-i \phi } c_b(0)\right] , \\&a_2=\frac{1}{2 \Omega }\left[ (\Omega +\Delta ) c_a(0)-\Omega _R e^{-i \phi } c_b(0)\right] , \\&b_1=\frac{1}{2 \Omega }\left[ (\Omega +\Delta ) c_b(0)+\Omega _R e^{i \phi } c_a(0)\right] , \\&b_2=\frac{1}{2 \Omega }\left[ (\Omega -\Delta ) c_b(0)-\Omega _R e^{i \phi } c_a(0)\right] . \end{aligned} \end{aligned}$$
(22)

Finally, we can write as follows

$$\begin{aligned} \begin{aligned} c_a(t)= \left\{ c_a(0)\left[ \cos \left( \frac{\Omega t}{2}\right) -\frac{i \Delta }{\Omega } \sin \left( \frac{\Omega t}{2}\right) \right] \right. \left. +i \frac{\Omega _R}{\Omega } e^{-i \phi } c_b(0) \sin \left( \frac{\Omega t}{2}\right) \right\} e^{i \Delta t / 2}, \\ c_b(t)= \left\{ c_b(0)\left[ \cos \left( \frac{\Omega t}{2}\right) +\frac{i \Delta }{\Omega } \sin \left( \frac{\Omega t}{2}\right) \right] \right. \left. +i \frac{\Omega _R}{\Omega } e^{i \phi } c_a(0) \sin \left( \frac{\Omega t}{2}\right) \right\} e^{-i \Delta t / 2} . \end{aligned} \end{aligned}$$
(23)

such that \(\left| c_a(t)\right| ^2+\left| c_b(t)\right| ^2=1\). If we assume that the atom is initially in the state \(|a\rangle\) the we have \(c_a(0)=1\) and \(c_b(0)=0\).

Three-level atom

We suppose a three-level atom in the \({\Lambda }\) configuration interacting with two electromagnetic fields with frequencies \({\nu }_{1}\) and \({\nu }_{2}\). As shown in Fig. 2, two lower levels \(|b\rangle\) and \(|c\rangle\) are commonly coupled to an upper level \(|a\rangle\).

Figure 2
figure 2

Schematic of a three-level atom in the \(\Lambda\) configuration which are driven by two fields of frequencies \(\nu _1\) and \(\nu _2\).

Full size image

The system’s Hamiltonian in the rotating-wave approximation is described by Eq. (15), in which

$$\begin{aligned} \left. {\mathcal {H}}_0\mathrm {=}\mathrm {\hbar }{{{\omega }}}_a{{|}}a\right\rangle \left\langle a{{|}}\mathrm {+}\left. \mathrm {\hbar }{{{\omega }}}_b{{|}}b\right\rangle \left\langle b{{|}}\left. \mathrm {+}\mathrm {\hbar }{{{\omega }}}_c{{|}}c\right\rangle \left\langle c{{|}}\right. \right. \right. \end{aligned}$$
(24)

represents the unperturbed Hamiltonian having eigenvalues \(\left\{ \hbar \omega _{a},\hbar \omega _{b},\hbar \omega _{c}\right\}\), and

$$\begin{aligned} {\mathcal {H}}_1\mathrm {=}\mathrm {-}\frac{\mathrm {\hbar }}{\textrm{2}}({{{\Omega }}}_{R1}e^{-i{{\phi }}_1}e^{-i{{\nu }}_1t}|a\rangle \langle b{{|}}\mathrm {+}{{{\Omega }}}_{R2}e^{-i{{\phi }}_2}e^{-i{{\nu }}_2t}\big |a\rangle \big \langle c|)+H.C. \end{aligned}$$
(25)

denotes the Hamiltonian that describes the interaction between the atom and fields. Furthermore, \({{{\Omega }}}_{R1}e^{-i{{\phi }}_1}\) and \({{{\Omega }}}_{R2}e^{-i{{\phi }}_2}\) are the complex Rabi frequencies corresponding to the coupling of the field modes with the frequencies \(\nu _1\) and \(\nu _2\) to the atomic transitions \(|a\rangle\) \(\mathrm {\rightarrow }\) \(|b\rangle\) and \(|a\rangle\) \(\mathrm {\rightarrow }\) \(|c\rangle\), respectively. Moreover, \(\phi _1\) and \(\phi _2\) are phases of the fields with Rabi frequencies. We only assume \(|a\rangle\) \(\mathrm {\rightarrow }\) \(|b\rangle\) and \(|a\rangle\) \(\mathrm {\rightarrow }\) \(|c\rangle\) transitions are permissible dipole.

If the system is prepared in the initial atomic state

$$\begin{aligned} |\psi _{in}\rangle =\text {cos}\Big (\frac{\theta }{2}\Big )|b\rangle +e^{-i\psi }\text {sin}\Big (\frac{\theta }{2}\Big )|c\rangle , \end{aligned}$$
(26)

that is a superposition of the two lower levels \(\{|b\rangle ,|c\rangle \}\), and consider the fields are in the resonant state with the transitions of \(|a\rangle\) \(\mathrm {\rightarrow }\) \(|b\rangle\) and \(|a\rangle\) \(\mathrm {\rightarrow }\) \(|c\rangle\), i.e, \(\omega _{ab}=\nu _1\) and \(\omega _{ac}=\nu _2\), then one can write the evolved state of the system as77

$$\begin{aligned} |\psi _{fi}(t)\rangle =c_a(t)e^{-i\omega _{a}t}|a\rangle +c_b(t)e^{-i\omega _{b}t}|b\rangle +c_c(t)e^{-i\omega _{c}t}|c\rangle , \end{aligned}$$
(27)

such that using the probability amplitude method, the probability amplitudes of finding the atom in states \(|a\rangle\), \(|b\rangle\), and \(|c\rangle\) are given by

$$\begin{aligned} \begin{aligned}{}&c_a=\frac{i~\text {sin}({{\Omega }}t/2)}{2}\Big [{{{\Omega }}}_{R1}e^{-i{{\phi }}_1}\textrm{cos}\mathrm {}(\frac{{\theta }}{2})+{{{\Omega }}}_{R2}e^{-i{({\phi }}_2+{\psi })}\textrm{sin}\mathrm {}(\frac{{\theta }}{2})\Big ], \\&c_b=\frac{1}{{{{\Omega }}}^2}\Bigg \{\left[ {{{\Omega }}}^2_{R2}+{{{\Omega }}}^2_{R1}\text {cos}\left( \frac{{{\Omega }}t}{2}\right) \right] {\textrm{cos} \left( \frac{{\theta }}{2}\right) \ } -2{{{\Omega }}}_{R1}{{{\Omega }}}_{R2}e^{i{({\phi }}_1-{{\phi }}_2-{\psi })}{\text {sin}}^2\left( \frac{{{\Omega }}t}{4}\right) \text {sin}\left( \frac{{{\theta }}}{2}\right) \Bigg \}, \\&c_c=\frac{1}{{{{\Omega }}}^2}\Bigg \{-2{{{\Omega }}}_{R1}{{{\Omega }}}_{R2}e^{-i{({\phi }}_1-{{\phi }}_2)}{\text {sin}}^2\left( \frac{{{\Omega }}t}{4}\right) \text {cos}\left( \frac{{{\theta }}}{2}\right) +\left[ {{{\Omega }}}^2_{R1}+{{{\Omega }}}^2_{R2}\text {cos}\left( \frac{{{\Omega }}t}{2}\right) \right] {e^{-i{\psi }}\textrm{sin} \left( \frac{{\theta }}{2}\right) \ }\Bigg \}. \end{aligned} \end{aligned}$$
(28)

in which \(\Omega =\sqrt{\Omega ^2_{R1}+\Omega ^2_{R2}}\). where \(\theta\) and \(\psi\) are the amplitude and phase of the initial state. Besides, \(\phi _1\) and \(\phi _2\) are the initial phases of the fields.

Throughout this paper, we consider \(\hbar =1\) and all parameters are nondimensionalized to plot the figures as mentioned in Refs.78,79.

Two effective two-level atoms

The system contains two effective two-level atoms that are considered as two similar qubits A and B interacting locally with two independent environments \(R_1\ and\ R_2\), respectively, such that are modeled as bosonic reservoirs at zero temperature. The schematic of two two-level atoms at this configuration is illustrated in Fig. 3. We consider the qubit system in each environment interacts with the environment’s field through degenerate two-photon transitions in the presence of the Stark shift. The transition frequencies of the environment modes \(\omega _{k j},(j=1,2)\) corresponding to \(R_1\ and\ R_2\). Besides \(\omega _0\) represents the transition frequency of the two qubits. In the rotating wave approximation, the effective Hamiltonian for the current model is written by \((\hbar =1)\)80,81:

Figure 3
figure 3

Schematic of the configuration of two effective two-level atoms (qubits A, and B) interacting independently with their reservoirs \(R_1\), and \(R_2\). There is no interaction between the two subsystems.

Full size image
$$\begin{aligned} \begin{aligned} \hat{H}_{\text{ eff } }=&\omega _0\left( \hat{\sigma }_{+}^A \hat{\sigma }_{-}^A+\hat{\sigma }_{+}^B \hat{\sigma }_{-}^B\right) +\sum _{k_1} \omega _{k_1} \hat{a}_{k_1}^{\dagger } \hat{a}_{k_1}+\sum _{k_2} \omega _{k_2} \hat{a}_{k_2}^{\dagger } \hat{a}_{k_2} \\&+\sum _{k_1} g_{k_1}\left( \hat{a}_{k_1}^{\dagger ^2} \hat{\sigma }_{-}^A+\hat{a}_{k_1}^2 \hat{\sigma }_{+}^A\right) +\sum _{k_1} \hat{a}_{k_1}^{\dagger } \hat{a}_{k_1}\left( \beta _{k_1} \hat{\sigma }_{-}^A \hat{\sigma }_{+}^A+\eta _{k_1} \hat{\sigma }_{+}^A \hat{\sigma }_{-}^A\right) \\&+\sum _{k_2} g_{k_2}\left( \hat{a}_{k_2}^{\dagger ^2} \hat{\sigma }_{-}^B+\hat{a}_{k_2}^{2} \hat{\sigma }_{+}^B\right) +\sum _{k_2} \hat{a}_{k_2}^{\dagger } \hat{a}_{k_2}\left( \beta _{k_2} \hat{\sigma }_{-}^B \hat{\sigma }_{+}^B+\eta _{k_2} \hat{\sigma }_{+}^B \hat{\sigma }_{-}^B\right) . \end{aligned} \end{aligned}$$
(29)

where \(\hat{\sigma }_{ \pm }^{A, B}\) denote atomic raising and lowering operators of the qubits A, and B. Besides, \(\hat{a}_{k_j}^{\dagger }\) and \(\hat{a}_{k_j}\) represent the creation and annihilation operators of the k th mode of the j th environment \((j=1,2)\). Moreover, \(g_{k_1}\) and \(g_{k_2}\) determine the effective two-photon strength of the qubit environment corresponding to the modes \(k_1\) and \(k_2\), respectively. Furthermore, \(\beta _{k_j}\) and \(\eta _{k_j}\) are the effective Stark shift coefficients82. Rewriting the previous Hamiltonian in the interaction picture is convenient:

$$\begin{aligned} \begin{aligned} \hat{H}_{\text{ int } }=&\sum _{k_1} g_{k_1}\left( \hat{a}_{k_1}^{\dagger ^2} \hat{\sigma }_{-}^A \textrm{e}^{-\textrm{i}\left( \omega _0-2 \omega _{k_1}\right) t}+\hat{a}_{k_1}^2 \hat{\sigma }_{+}^A e^{i\left( \omega _0-2 \omega _{k_1}\right) t}\right) \\&+\sum _{k_1} \hat{a}_{k_1}^{\dagger } \hat{a}_{k_1}\left( \beta _{k_1} \hat{\sigma }_{-}^A \hat{\sigma }_{+}^A+\eta _{k_1} \hat{\sigma }_{+}^A \hat{\sigma }_{-}^A\right) \\&+\sum _{k_2} g_{k_2}\left( \hat{a}_{k_2}^{\dagger ^2} \hat{\sigma }_{-}^B \textrm{e}^{-\textrm{i}\left( \omega _0-2 \omega _{k_2}\right) t}+\hat{a}_{k_2}^2 \hat{\sigma }_{+}^B\right) e^{i\left( \omega _0-2 \omega _{k_2}\right) t} \\&+\sum _{k_2} \hat{a}_{k_2}^{\dagger } \hat{a}_{k_2}\left( \beta _{k_2} \hat{\sigma }_{-}^B \hat{\sigma }_{+}^B+\eta _{k_2} \hat{\sigma }_{+}^B \hat{\sigma }_{-}^B\right) . \end{aligned} \end{aligned}$$
(30)

We assume the system is in the initial state as:

$$\begin{aligned} |\phi (0)\rangle =\left( \chi |0\rangle _A|1\rangle _B+\sqrt{1-\chi ^2}|1\rangle _A|0\rangle _B\right) \otimes \left| 0_{k_1}\right\rangle _{R_1}\left| 0_{k_2}\right\rangle _{R_2}, \end{aligned}$$
(31)

in which \(\chi \in [0,1]\), where \(\left| 0_{k_j}\right\rangle _{R_j}\) represents the vacuum state of the j th environment, and \(|0\rangle _j,|1\rangle _j(j=A, B)\) denote the ground and excited states of the two-level atoms. The number of excitations in the total system is preserved, thus the time evolution of the total system can be obtained by

$$\begin{aligned} \begin{aligned} |\phi (t)\rangle =&\left( c_1(t)|1\rangle _A|0\rangle _B+c_2(t)|0\rangle _A|1\rangle _B\right) \left| 0_{k_1}\right\rangle _{R_1}\left| 0_{k_2}\right\rangle _{R_2} \\&+\sum _{k_1} c_{k_1}(t)|0\rangle _A|0\rangle _B\left| 2_{k_1}\right\rangle _{R_1}\left| 0_{k_2}\right\rangle _{R_2} \\&+\sum _{k_2} c_{k_2}(t)|0\rangle _A|0\rangle _B\left| 0_{k_1}\right\rangle _{R_1}\left| 2_{k_2}\right\rangle _{R_2}, \end{aligned} \end{aligned}$$
(32)

where \(\left| 2_{k_j}\right\rangle _{R_j}\) denotes excitations of two photons in the mode k for the j th environment. It’s worth noting that the two-photon process is considered, and then the j th environment has only two states \(\left| 0_{k_j}\right\rangle\) and \(\left| 2_{k_j}\right\rangle\). Using the probability amplitude method, Laplace technique, and the similar method given by Refs.80,81, the probability amplitude coefficients can be written as:

$$\begin{aligned} c_1(t)=\chi \xi (t), \quad c_2(t)=\sqrt{ } 1-\chi ^2 \xi (t), \end{aligned}$$
(33)

with

$$\xi (t)=e^{-\frac{(\lambda +2 \textrm{i} \beta ) t}{2}}\left[ \cosh \left( \frac{\varrho t}{2}\right) +\frac{\lambda +2 \textrm{i} \beta }{\varrho } \sinh \left( \frac{\varrho t}{2}\right) \right] ,$$

and

$$\varrho =\sqrt{-4 \gamma _0 \lambda +(\lambda +2 \textrm{i} \beta )^2} .$$

We are facing two regimes, i.e. weak (\(\gamma _0<\lambda / 2\)) and strong (\(\gamma _0>\lambda / 2\)) coupling regimes83. In the weak coupling regime, the relaxation time is more than the reservoir correlation time, where the behavior of the qubit-reservoir system is Markovian and a decay process arises in the time. In contrast, when the reservoir correlation time exceeds the relaxation time, non-Markovian dynamics emerge, leading to a strong coupling regime. The entanglement revival, accompanied by oscillations due to the reservoir memory effect, becomes observable.

Consider the Hermitian matrix \(\hat{H}=\hat{\rho } \hat{\rho }_s\), in which \(\hat{\rho }\) indicates the reduced density matrix of the pair of qubits A, B and \(\hat{\rho }_s=\left( \hat{\sigma }_y^A \otimes \hat{\sigma }_y^B\right) \rho ^*\left( \hat{\sigma }_y^A \otimes \hat{\sigma }_y^B\right)\), with \(\rho ^*\) as the complex conjugate of \(\hat{\rho }\) and \(\hat{\sigma }_y^A, \hat{\sigma }_y^B\) as the usual Pauli matrices for the qubits. Assuming the atomic basis \(\left\{ |1\rangle _A|1\rangle _B,|1\rangle _A|0\rangle _B,|0\rangle _A|1\rangle _B,|0\rangle _A|0\rangle _B\right\}\), one can calculate the time-dependence of the reduced density matrix as80,81:

$$\begin{aligned} \rho (t)=\left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \left| c_1(t)\right| ^2 &{} c_1(t) c_2^*(t) &{} 0 \\ 0 &{} c_1^*(t) c_2(t) &{} \left| c_2(t)\right| ^2 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1-\left| c_1(t)\right| ^2-\left| c_2(t)\right| ^2 \end{array}\right) . \end{aligned}$$
(34)

Discussion and results

Here we display that memory effects can be extracted by faithful witnesses of non-Markovianity based on the Bhattacharyya distance. As illustrated in Fig. 4, using straightforward expressions in Appendix A, we compare the qualitative behaviors of the Bhattacharyya distance (\(D_{Bhatt}\)), the Bures distance (\(D_{Bures}\)), Hilbert-Schmidt speed (\(HSS_{\phi }\)), and quantum Fisher information (\(\mathcal {F}_{\phi }\)) with respect to the phase of the dipole matrix element for a two-level atom scenario. We can clearly see that the qualitative behavior of \(D_{Bhatt}\) is completely similar to other quantities so that the maximum and minimum points of the curves coincide with each other. As mentioned in Refs.32,34, a flow of QFI and HSS, i.e., \(\frac{d(\mathcal {F}_{\phi })}{dt}>0\) and \(\frac{d(HSS_{\phi })}{dt}>0\), in which the QFI and HSS have been calculated with respect to the phase \(\phi\), can detect the non-Markovianity effects. Hence the positive changing rate of the Bhattacharyya distance, i.e., \(\frac{d(D_{Bhatt})}{dt}>0\), can also detect the memory effects. This non-Markovianity witness is in total agreement with other witnesses based on Bures distance, QFI, and HSS thus identifying the information backflows.

Figure 4
figure 4

Comparison between the dynamics of the Bhattacharyya distance (\(D_{Bhatt}\)), Bures distance (\(D_{Bures}\)), Hilbert-Schmidt speed (\(HSS_{\phi }\)), and quantum Fisher information (\(\mathcal {F}_{\phi }\)) with respect to the phase of the dipole matrix element for the two-level atom scenario when \(\Omega _R=0.5\) and \(\Delta =1\).

Full size image

Next, we expand the efficiency of our witness to the system with higher dimensions. In Fig. 5, the qualitative behaviors of the Bhattacharyya distance (\(D_{Bhatt}\)) and the Bures distance (\(D_{Bures}\)) for the three-level atom scenario are demonstrated. Here we see that the general agreement of the similar behaviors of the two quantities \(D_{Bhatt}\) and \(D_{Bures}\) for a three-level atom system still stands.

Figure 5
figure 5

Comparison between the temporal variations of the Bhattacharyya distance (\(D_{Bhatt}\)) and Bures distance (\(D_{Bures}\)) for the three-level atom scenario when \(\Omega _{R1}=1, \Omega _{R2}=2, \omega _a=\omega _b=\omega _c=1, \varphi =2\pi , \phi _1=\phi _2=\psi =\pi\) and \(\theta =\pi /2\). Here, \(BT=1.57\) represents the Bhattacharyya distance threshold.

Full size image

Furthermore, we show the comparison between time evolutions of the \(D_{Bhatt}\), \(D_{Bures}\), \(HSS_{\phi 1}\), and \(\mathcal {F}_{\phi 1}\) with respect to the phase of the fields for the three-level atom scenario in Fig. 6. The result that can be obtained from this figure is that the qualitative behaviors of the \(D_{Bhatt}\), \(D_{Bures}\), \(HSS_{\phi 1}\), and \(\mathcal {F}_{\phi 1}\) in high dimensions systems are exactly similar. These results are also valid for other different values of the system parameters. In addition, these results can be extended to other models.

Figure 6
figure 6

Comparison between the qualitative behaviors of the Bhattacharyya distance (\(D_{Bhatt}\)), the Bures distance (\(D_{Bures}\)), Hilbert-Schmidt speed (\(HSS_{\phi 1}\)), and quantum Fisher information (\(\mathcal {F}_{\phi 1}\)) with respect to the phase of the fields in terms of scaled time for the three-level atom scenario when \(\Omega _{R1}=0.3, \Omega _{R2}=1, \omega _a=0.9,\omega _b=\omega _c=1, \varphi =\phi _1=\phi _2=\psi =\pi\) and \(\theta =\pi /4\).

Full size image

In Fig. 7, we investigate the qualitative behaviors of the \(D_{Bhatt}\), \(D_{Bures}\), and concurrence for the two effective two-level atoms system. The concurrence measure84 is employed as an entanglement criterion defined as \(Concurrence=max \left\{ 0,\sqrt{\lambda _1}-\sqrt{\lambda _2}-\sqrt{\lambda _3}-\sqrt{\lambda _4}\right\}\) where \(\lambda _i\,\,(i=1,\ldots ,4)\) represents the eigenvalues of the evolved density matrix Eq. (34). In Fig. 7, we observe that the qualitative behaviors of the \(D_{Bhatt}\), \(D_{Bures}\), and concurrence are similar such that the minimum and maximum points of the behaviors coincide. This allows \(D_{Bhatt}\) to examine the entanglement dynamics of the system along with non-Markovian effects, making it highly beneficial in quantum computing. In a weak coupling regime (\(\gamma _0<\lambda / 2\)), Fig. 7a, the monotonicity decrease of \(D_{Bhatt}\), \(D_{Bures}\), and concurrence is obvious. Here, the relaxation time is more than the reservoir correlation time, where the behavior of the qubit-reservoir system is Markovian and a decay process arises in the time. While in a strong coupling regime (\(\gamma _0>\lambda / 2\)), Fig. 7b, the \(D_{Bhatt}\), \(D_{Bures}\), and concurrence revivals, accompanied by oscillations due to the reservoir memory effect, becomes observable. It means that the reservoir correlation time exceeds the relaxation time, leading to non-Markovian dynamics emerging.

Figure 7
figure 7

Comparison between the temporal variations of the Bhattacharyya distance (\(D_{Bhatt}\)), the Bures distance (\(D_{Bures}\)), and concurrence for two effective two-level atoms system for (a) Markovian reservoir when \(\lambda =10,\beta =0,\gamma _0=1,\chi =\frac{1}{\sqrt{2}}\), (b) Non-Markovian reservoir \(\lambda =0.1,\beta =0,\gamma _0=1,\chi =\frac{1}{\sqrt{2}}\).

Full size image

Therefore, it can be easily stated that Bhattacharyya quantum distance can well detect the non-Markovian dynamics caused by quantum memory effects. As stated in Appendix A, it can be seen that this distance does not require heavy calculations in pure states, and only by having the initial and final states of the system, the effects of quantum memory can be detected. This point is important in high-dimension systems because of difficult calculations.

Conclusion

In this article, we have determined a relation between the positive changing rate of the Bhattacharyya distance (BD), a particular type of quantum statistical distance, and the non-Markovian dynamics of open quantum systems. The concept behind this suggestion is based on the idea that the nonmonotonic speed (positive acceleration) of quantum evolutions indicates memory effects in the dynamics of the system interacting with its environment. Through the introduction of a BD-based quantifier, a quantitative witness of memory effects in system dynamics can be defined.

In an extensive case study analysis, we have demonstrated that the suggested witness is as useful as the well-known witnesses of quantum Fisher information (QFI), Bures distance, and Hilbert-Schmidt speed (HSS) in identifying non-Markovianity. The models analyzed in our paper include various paradigmatic open quantum systems (two and three-level atoms interacting single and two-mode fields, respectively, and two effective two-level atoms interacting locally with two independent environments) and provide proof of the sensitivity of our BD witness to system-environment information backflows. We note that non-Markovianity witness of the BD does not require the computation of the density matrix, but only determines it from the initial and final states of the system thereby leading to the improvement of the quantum metrology. One crucial finding in this article is that the BD measure can be used as a measure of entanglement like the Bures distance. Therefore, a quantifier with this characteristic would be highly sought after.

This article motivates further analysis of the role of non-Markovian effects in different open quantum systems and their relationship to quantum statistical distances.