Introduction

With the economic development in China, individuals’ interests investing and financing through stock trading has increased. Stock trading has emerged as a fundamental investment method available to investors1. Within the stock investment market, risk and return coexist, emphasizing the importance of acquiring more accurate stock prices to enable investors to effectively mitigate certain risks. Being a significant component of the financial realm, the stock market shares a close correlation with a country's economic activities. Price fluctuations can significantly impact a nation's economic development, and stock market trends reflect the fluctuations in a country's economic landscape. Predicting stock price trends through technical means holds substantial value in guiding financial management and enhancing investment efficiency as they contribute to the stable growth of the stock market and the global economy. Consequently, individuals strive to forecast stock price trends utilizing various algorithms in pursuit of greater financial gains2. However, the stock market is a complex nonlinear dynamic system, and data generation is a result not only of historical market behavior but is also influenced by multiple factors such as corporate financial reports, financial news, macroeconomics, and investor sentiment3. The availability of rich data sources enhances the comprehension of the stock market, resulting in more precise forecasts. Certain methodologies can establish connections between historical data and future movements in stock prices, utilizing past data to predict future trends4. Furthermore, the predictability of stocks heavily relies on market analysis, the comprehensive collection and derivation of information, the potential integration of available data points, the identification of relevant information features, and the selection and optimization of predictive models and hyperparameters.

In the nascent stages, stock price movements were described by random fluctuations, domestic and international scholars used traditional statistical models to describe stock behavior. Traditional statistical models include Exponential Smoothing (ES)5, Multiple Linear Regression (MLR)6, Autoregressive Moving Average (ARMA)7 and Autoregressive Integrated Moving Average (ARIMA)8. Due to the large number of factors influencing stock prices and the complexity of the influencing mechanisms, the problem of forecasting time series with insufficient information, regional heterogeneity and complex patterns is difficult for traditional statistical models. Therefore, it is often difficult to achieve good forecasting accuracy using these simple mathematical models9.

The ascent of artificial intelligence has steered researchers' attention toward machine learning methods for their adeptness in modeling non-linear time series. These methods construct predictive models by discerning underlying data patterns, offering superior adaptability with fewer presumptive models. As of late, researchers have increasingly turned to machine learning approaches to address the limitations of numerical models in stock price forecasting. Prominent among these methods are Support Vector Machine (SVM)10, Decision Tree (DT)11, and Random Forest (RF)12. For instance, Nayak et al.13 introduced a hybrid framework that melds Support Vector Machine (SVM) and K-Nearest Neighbors (KNN) methods to forecast Indian stock market indices. Their study delves into a comprehensive analysis of these indices, employing technical analysis tools such as closing prices, volatility, and stock market momentum. The experimental outcomes underscore the superior predictive performance of the hybrid SVM-KNN model compared to existing models, showcasing its efficacy in forecasting Indian stock market indices. Zhang et al.14 employed an unsupervised heuristic algorithm to segment stock trading data into multiple segments based on the shapes of their closing prices. They utilized random forest, unbalanced learning, and feature selection to train a prediction model on these segments. The experimental results showcased the system's effectiveness in predicting stock price trends. In another approach, Zhang et al.15 introduced the "state box method," which assesses current stock price trends and predicts future price changes by categorizing stock data into boxes with three distinct states. Machine learning techniques were then applied to classify these boxes, using their states to forecast stock price movements. Experimental results highlighted the method's high classification accuracy and its success in addressing imbalances in stock turning point classification. Vijh et al.16 leveraged Random Forest and Artificial Neural Network models to forecast the following day's closing prices across various industries. They evaluated the model using standard strategy metrics like RMSE and MAPE, both of which demonstrated low values, indicating the model's effectiveness in predicting stock closing prices. Additionally, Chen et al.17 devised a novel portfolio construction approach using a machine learning-based hybrid model for stock prediction in conjunction with mean–variance (MV) for portfolio selection. Employing the Shanghai Stock Exchange as their study sample, their findings showcased that the proposed method outperformed traditional and benchmark methods in terms of both return and risk. The stock market's nonlinearity, noise, non-stationarity, and intricate influencing factors pose significant challenges for traditional machine learning methods18. These methods encounter difficulties in capturing nonlinear trends, contending with data noise, and combatting overfitting. They exhibit several limitations, notably in modeling complex nonlinear relationships and typically necessitate manual intervention for feature selection. Furthermore, these models often operate with low demands for extensive data and computational resources, which restricts their efficacy in handling high-dimensional data and large-scale tasks of a more intricate nature.

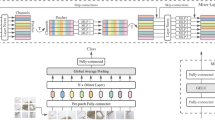
In contrast, deep learning models are able to capture complex relationships more efficiently and train large neural networks effectively through parallel computing19. As a result, more sophisticated models such as deep learning are beginning to gain attention. They can automatically learn complex feature representations from non-smooth, non-linear stock price data. At the same time, they compensate for the shortcomings of machine learning, which can only achieve local optimization. Convolutional Neural Networks (CNN)20,21, Recurrent Neural Networks (RNN)22,23, Long Short-Term Memory Networks (LSTM)24,25 and Transformer26,27 and many other deep learning methods have been applied to stock price prediction and have shown excellent performance. Zhang et al.28 first explored the application of deep learning in the stock market by using two deep learning models, Convolutional Neural Network (CNN) and Long Short-Term Memory Network (LSTM), in conjunction with technical indicators and financial news articles to make predictions. Rezaei et al.29 proposed CEEMD-CNN-LSTM and EMD-CNN-LSTM algorithms which can extract deep features and time series and ultimately be used for one step ahead forecasting. The results of practical studies confirm this claim and show that the combination of CNN with LSTM, CEEMD or EMD can improve the prediction accuracy and outperform other similar algorithms. Liu et al.30 proposed a new stock price prediction model called VML, in order to train the initial Long Short-Term Memory (LSTM) network with good generalization ability using the parameters of the unrelated meta-learning (MAML) algorithm, a method to divide the decomposed subsequence into multiple tasks is proposed. Experimental results show that the proposed method improves the prediction accuracy. Teng et al.31 applied local descriptors to stock trend prediction for the first time. Their method introduces diversified local descriptors by employing sliding windows of various scales on stock price series. This process enriches multi-scale information, followed by the integration of time-dependent and multi-scale interactions through a hierarchical attention mechanism and a multi-branch LSTM structure. Experimental results validate the model's high effectiveness. Liu et al.32 proposed a distinctive stock price prediction method, named CapTE, leveraging a Transformer Encoder model. This approach extracts deep semantic features from social media using the Transformer Encoder, while capturing text structural relationships via capsule networks, ultimately enhancing stock movement prediction performance. Zhou et al. 33significantly enhanced stock price prediction by devising an efficient Transformer-based LSTF model named Informer. Notably, this model employs the ProbSparse self-attention mechanism, self-attention distillation, and a generative decoder, markedly improving prediction accuracy and inference speed for extended sequences. While the above study achieved good results and demonstrated the feasibility of LSTM and Transformer family for temporal sequence prediction tasks, their focus primarily centered on short sequence recognition. They overlooked exploring the correlation between significant long time series features and the network structure. Additionally, these studies didn't delve into the impact of mutation points within the strain data on prediction accuracy. Figure 1 illustrates a comparison of three time series prediction network architectures. The standard self-attention mechanism used by Transformer poses a challenge due to its O(L^2) time complexity, making it less adept at handling lengthy stock data sequences. On the other hand, LSTM, based on recurrent neural networks, heavily relies on hidden states to capture sequence dependencies, but it faces challenges of gradient vanishing and explosion in longer sequences. However, there remains a critical need for further research in the realm of stock prediction to unearth deeper insights into time series features and enhance the network's capabilities. Consequently, we have chosen Informer as a benchmark network for our related work, aiming to address these pivotal gaps and advance the field.

Figure 1
figure 1

Comparison of three timing prediction models.

Full size image

In the current landscape of stock prediction, three notable challenges persist:(1) Existing stock price prediction models often overlook the effects of other stocks within the market and the impact of mutation points on the accuracy of predicting the target stock. As depicted in Fig. 2, the presence of mutation points in stock price data results in significant discrepancies between predicted and actual values. Failure to accurately capture these changes or market trends due to mutation points can detrimentally affect prediction accuracy. (2) Long time series encompass numerous time steps, imposing a burden on models by requiring them to manage extensive data points. This substantially escalates the computational resources and time necessary for training and inference, leading to increased computational costs. Utilizing overly lengthy input sequences in stock market forecasting can adversely affect predictive performance. (3) Conventional hybrid models struggle to consider the relative positions of elements within lengthy sequences. These models lack a comprehensive understanding of relationships and dependencies among different elements in the sequence. Consequently, increasing the layers can exacerbate issues like overfitting and result in poor generalization.

Figure 2
figure 2

Bank of Communications and RoyalFlush Stock Weekly Opening Price Chart.

Full size image

In response to these challenges, several research approaches offer insights that could potentially inform our solutions. To mitigate the impact of mutation points on prediction accuracy, Tao et al.34 introduced a novel knowledge graph coupled with a deep learning method. This method identifies mutation points based on price change ranges, constructs mutation point distance weight matrices, and extracts mutation point information features through graph convolutional networks. Jiang et al.35 developed two distinct CNN models to extract individual stock features and related stock features separately. Employing an MLP model for final interval-valued stock price prediction significantly improved prediction accuracy. Addressing the issue of excessively long input sequences, Faraz et al.36 utilized an auto-encoding long short-term memory network (AE-LSTM) to sequentially predict closing prices, achieving accurate predictions for extended sequences. Zhou et al.33 efficiently dealt with extremely long input sequences by adding self-attention distillation to Informer to halve the cascade layer inputs to highlight the dominant attention, and by adding a generative decoder to carry out a single forward operation to predict the time series. To enhance the model's learning of relative positions and dependencies between elements, Wen et al.37 integrated the MODWT method into a deep learning network framework and explored the interrelationships and different importance of subsequences. Zhang et al.38 fused the Transformer model with multiple attention mechanisms for stock motion prediction, using the Transformer model to the fusion method of extracting the deep features of small samples and using multiple attention mechanisms to capture inter-element dependencies and obtain key information improves the feature fusion efficiency of the model and improves the prediction accuracy. For long sequence elements, the Transformer model incorporating the multiple attention mechanism can capture the temporal dependence of the data and use the multiple attention mechanism to model the correlation between long-term and short-term data. However, the multiple attention mechanism is more sensitive to the noise and outliers present in the time series data, which can affect the stability and accuracy of the network prediction and lead to some overfitting. Therefore, we address this issue in the position coding and optimizer.

The contributions of this paper are as follows:

  • (1) We have developed a comprehensive dataset encompassing stocks from six distinct industries (JT, THS, GL, HR, KM, BYD) spanning from January 2018 to September 2023. This dataset serves as a rich resource for extracting diverse stock trend features, facilitating a nuanced understanding of industry-specific market dynamics.

  • (2) The PPA module is an innovative addition designed to enhance the understanding of stock sequences. It first augments the positional information of input sequences using positional coding. Subsequently, it generates initial contextual information by sampling cross terms from query keys. Finally, the module computes attention-weighted contextual information in combination with the sequence data. This multifaceted approach allows for a more nuanced capture of stock sequence relationships and inter-element dependencies.

  • (3) We introduce MTFC to improve the network's capability in processing complex features of long sequences. This approach involves taking input time series in two dimensions—time step and feature—and performing multi-scale convolution and gated convolution operations. This methodology allows for a more thorough extraction of stock price information.

  • (4) The APSO is a novel approach that merges the Ant Colony Algorithm (ACO) with the Particle Swarm Algorithm (PSO), leveraging both global and local search characteristics. This hybrid method enables the network to identify optimal solutions more rapidly and accurately, especially in handling mutation points present in the data.

  • (5) Our empirical studies show that the PMANet model significantly outperform existing models, such as the Informer model, in stock prediction tasks. Specifically, the PMANet model achieves a 43.9% improvement in Mean Squared Error (MSE) and a 24.8% improvement in Mean Absolute Error (MAE) metrics. These results underscore PMANet's enhanced ability to accurately capture the fluctuations and trends of stock prices.

Materials and methods

Data acquisition

The study aims to forecast the opening prices of prominent stocks across four distinct industries: Bank of Communications (JT), RoyalFlush (THS), Hengrui Pharmaceuticals (HR), and Gree Electric Appliances (GL). These industries span finance, information technology, pharmaceuticals, and manufacturing, commanding significant market influence and attention. Data for this study is sourced from the Wind Economics database, renowned for its comprehensive, accurate, and timely financial data and information services. For the preliminary investigation, daily stock data was selected for each entity from January 2, 2018, to September 14, 2023, encompassing a total of 5,534 data points. Commonly used in stock price forecasting, the stock price series includes both price data (e.g., opening price, closing price) and trading data (e.g., P/E ratio, P/S ratio). Price data directly mirrors stock price trends, while trading data reflects stock trends through activities and profitability, considered high-quality data in stock forecasting, capturing diverse information impacting stock price trends. Each stock's dataset involves seven primary price factors: opening price (Open), high price (High), low price (Low), closing price (Close), price-earnings ratio (PE), price-to-book ratio (PB), and price-to-sales ratio (PS). Here, the opening price serves as the target variable for prediction, while the remaining six attributes act as characteristic variables. The High, Low, and Close signify stock price fluctuations, representing maximum demand, minimum supply, and overall market valuation of the stock, respectively. These data influence market perceptions regarding a stock's potential upside, downside risk, and yield, thereby impacting the stock's opening price. On the other hand, PE, PB, and PS reflect a stock's valuation level, signifying market expectations concerning a company's profitability, net worth, and sales capacity. These expectations shape market perceptions of a company's future prospects, consequently influencing the stock's opening price. Hence, the High, Low, Close, PE, PB, and PS attributes are chosen as characteristic variables to predict the stock's opening price.

Method

Probabilistic positional attention (PPA)

The integration of attention mechanisms into models for stock prediction is crucial due to the complex interplay of multiple factors influencing stock trends. Attention mechanisms have gained prominence in various neural network architectures, such as Convolutional Neural Networks (CNNs), Recurrent Neural Networks (RNNs), and Transformers. These mechanisms are particularly adept at processing financial data, time series data, and natural language data. However, a key challenge arises when current attention mechanisms are applied to excessively long sequences. In such scenarios, these mechanisms often struggle to fully comprehend the relationships and dependencies between sequence elements, leading to issues like overfitting and poor generalization. To address these limitations, previous work like SE38 has focused on modeling the significance of each feature channel. By enhancing the attention and expressiveness of different channel features, SE not only improves network performance but also effectively reduces redundant information between channels, thereby enhancing network stability. Building on this, CBAM39 incorporated spatial attention into SE, thereby enriching the representation of features both spatially and channel-wise. This is achieved by efficiently extracting spatial patterns and variations in time series data. Despite these advancements, solely relying on channel attention (like SE) or spatial attention often falls short in intensive prediction tasks such as stock volume prediction. The reason is the lack of localization or comprehensive feature information. CBAM attempted to address this by synthesizing information, but it still lacks in capturing interactions and dependencies between elements. To overcome these shortcomings, we introduce the Probabilistic Positional Attention (PPA). PPA is designed to provide a more nuanced understanding of the positional relationships and dependencies within sequence elements. The structure of PPA, as depicted in Fig. 3-PPA, represents a significant advancement in attention mechanisms, offering a more sophisticated approach to handling the complexities inherent in stock volume prediction tasks. This approach ensures not only the extraction of relevant features but also the preservation of their contextual and positional s.

Figure 3
figure 3

PMANet network structure (The Softmax function is used in multi-classification, converting input vectors into probability distributions for each category.)

Full size image

We first add positional encodings to the input data to enable the model to understand the order of elements in the sequence. These positional encodings, later added to the input data, help the model distinguish between elements at different positions in the sequence. The positional encodings are calculated as in Eqs. (1) and (2).

$$PE(pos,2i) = \sin \left( {\frac{pos}{{10000^{\frac{2i}{m}} }}} \right)$$
(1)
$$PE(pos,2i + 1) = \cos \left( {\frac{pos}{{10000^{\frac{2i}{m}} }}} \right)$$
(2)

where pos is the position, from 0 to the maximum length of the sequence. i is the index of the dimension in which the position is encoded, typically from 0 to m-1 (m is the hidden state dimension of the model). PE(pos, 2i) is the position encoded value for position pos and dimension 2i. PE(pos, 2i + 1) is the position-coded value for position pos and dimension 2i + 1.

Next, we integrate a multi-head attention mechanism into the PPA module. In this mechanism, attention is divided into multiple 'heads', each of which independently processes different representational subspaces of the input data, and then combines the results of these processes. This allows the model to capture features of the sequence from multiple perspectives, improving the model's understanding of the input data.

In addition, we implement a cross-attention mechanism, which is particularly important when dealing with sequence-to-sequence tasks. In this mechanism, the model pays attention not only to its own input sequence but also to the information of another sequence. For example, in machine translation, the attention layer of the decoder pays attention to the sequence output by the encoder to capture the correspondence between the source and target languages.

Next, we combine a new mechanism for computing sampled query key interactions with the _prob_QK function. This sampling mechanism helps to reduce computational complexity and increase efficiency while capturing important information. The output of the attention mechanism is scaled by a factor and optionally includes positional encoding, and the mask_flag parameter determines whether a mask should be applied during the attention computation. This module allows regularised attention scores to be discarded. The output can also include detailed attention weights if the output_address flag is set.

Specifically, the relevant information in the input sequence is captured by computing the sampled query key cross terms (Q_K sampling) using a combination of sampled query key interactions, scaling, positional coding, and optional masking. To reduce computational complexity and increase efficiency, Q_K sampling is computed as in Eq. (3).

$$Q\_K\_sample = Q*K\_sample^{ \wedge } T$$
(3)

After computing the sparsity measure M, the top n_top queries with the highest sparsity measure are selected. This selection initializes the context information, pivotal for subsequent computation of attention-weighted contextual information. The context initialization process varies based on the mask_flag value. When mask_flag is enabled, the context is initialized using the cumulative sum; otherwise, the average of the values is computed to initialize the context. The sparsity measure M is calculated according to (4)

$$M = \max (Q\_K\_sample) - (sum(Q\_K\_sample)/L\_K)$$
(4)

The integration of positional encoding with multi-attention, cross-attention capabilities, and computational sampling of query key interactions significantly enhances the model's proficiency in processing sequence data. This multifaceted approach not only deepens the model's understanding of the relationships and dependencies between sequence elements but also empowers it to efficiently discern and leverage intricate patterns within sequence data. Such capability is especially crucial in tasks that involve analyzing complex time series, like stock market forecasting, where comprehending and predicting temporal dynamics is essential.

In subsection "Effectiveness of PPA" of this paper, we conduct a detailed analysis of the PPA module's impact. The comparative experiments demonstrate a notable performance enhancement over the baseline model. This empirical evidence not only validates the theoretical soundness of the proposed improvements but also confirms their superior performance in practical applications. The results underscore the efficacy of the PPA module in enriching the model's analytical capabilities, thereby making it a valuable tool for complex sequence analysis tasks, particularly in the realm of financial forecasting.

Multi-scale timing feature convolution (MTFC)

The input of too long sequences in stock forecasting leads to an increase in computational resources and a decrease in model generalisation ability.The convolution operation of the encoder in the Informer model can effectively capture local patterns and trends in stock time series data, which can improve the model's ability to perceive local features.However, a single one-dimensional convolutional feature extraction is limited and cannot effectively handle too long input sequences, and it may result in the dimensionality of the output features being too high, which increases computational complexity. Therefore, to avoid the problem of reduced model generalisation ability when the input sequence is too long, this paper proposes a Multi-scale Timing Feature Convolution (MTFC), the structure of which is shown in Fig. 3- MTFC.

While the common 3 × 3 convolution has been able to capture time series information in regular stock datasets, the mapping range of the fixed convolutional layers is limited, which does not capture all the information in large datasets and affects the accuracy of the predictions. In addition, a fixed convolutional filter considers all sampling points in the time series equally, which can limit the ability of the model to express features of the time series. To address this issue, we use MTFC instead of one-dimensional convolution in Encoder to construct the convolutional layer. First, we draw on the core idea of coordinate attention (CA)40, due to the specificity of the input time series data, we decompose it into two dimensions, time step and feature, for feature extraction separately by two parallel pooling layers, and through this operation, the model can focus on which changes are more significant at different points in time, which is particularly important for understanding the dynamic characteristics of stock prices over time.

Owing to the dynamic characteristics of stock market data across multiple time scales, important information may be concealed within different time scales in time series analysis. To address this, we have designed a multi-scale convolution structure consisting of three branches. Convolution kernel size of 1 × 1, 3 × 3 and 5 × 5 is used for computation in this structure. Subsequently, three normalization layers stabilize the network, preventing dispersion. The results are then concatenated.

Regarding the feature dimension, traditional convolution processes all features simultaneously, increasing the network's computational load and potentially reducing generalization ability. To mitigate this, we use a gating mechanism to categorize features as important or unimportant. Important features undergo a more comprehensive 3 × 3 convolution to fully capture temporal information. In contrast, unimportant features are processed with a more cost-effective 1 × 1 convolution to conserve computational resources. After convolution normalization and sigmoid activation, we obtain the final output feature sequence.

Specifically, we first use AvgPool to process the input vector sequence and decompose it into two dimensions, time step and feature. Then, we input the time-step feature sequences of the two dimensions into two specially designed convolutions and use multi-scale convolution operation and gated convolution operation to extract features from the two dimensions. Finally, we output the extracted time-series feature sequences, which are spliced and processed into the time-series prediction network to perform accurate feature extraction of long time-series multiscale sequences using the multiscale convolution and gated convolution operations, which are used to perform the next prediction task. Experiments on MTFC are described in subsection "Effectiveness of MTFC".

Ant particle swarm optimization (APSO)

In stock prediction tasks, mutation points in the data significantly impact the prediction network. In deep learning tasks, the selection of an efficient optimizer is pivotal. An adaptive learning rate adjustment strategy can help the model converge to the optimal solution more swiftly, crucial for achieving accurate segmentation of edge-blurred images. The earlier Stochastic Gradient Descent (SGD)41 optimizer, which updates parameters by randomly selecting samples and optionally incorporates a momentum parameter to expedite the learning process, proves effective in scenarios involving high curvature, small but consistent gradients, or noisy gradients. Subsequently proposed was Adam's optimizer42, which is more advanced. It commences by computing the exponential moving average of the gradient, incorporating prior gradient information. Following this, it calculates the exponential moving average of the squared gradient to normalize the gradient. The optimizer will then correct for the bias in the estimation of the first and second order moments of the slope. Finally, it updates the parameters based on the ratio of the square root of the corrected first order moment estimate to the square root of the second order moment estimate. This intricate process allows for fine-tuning the learning rate of each parameter, enabling a more rapid convergence to the optimal solution.

At sudden change points in stock data, time series prediction models often struggle to process these data points correctly, leading to reduced robustness and incorrect predictions. During these instances, optimizers with adaptive learning rates, such as Adam, can face difficulties in accurately estimating the gradient, which in turn affects the learning and generalization process of the model. To tackle this challenge, we introduce a novel optimization algorithm: Ant Particle Swarm Optimization (APSO). APSO enhances the identification of mutation points within the entire market data by synergizing the Ant Colony Algorithm (ACO) and Particle Swarm Algorithm (PSO). This combination facilitates the exploration of a broader potential solution space, thus addressing the limitations posed by sudden changes in stock data.

The optimization parameter process in APSO involves several key steps: Initially, a colony of ants is established, with each ant symbolizing a path (and consequently, a solution). The positions of these ants and their respective chosen paths are initialized. Then, during each iteration of training, the velocity of the ants (representing the divergence between their current paths and the optimal paths) is updated. The current paths of the ants are denoted as P_current. Furthermore, the term P (global best) is used to represent the globally optimal path. The formula for updating P (global best) is described in the subsequent section.

$$W = \sum\limits_{i = 1}^{n} \delta (P_{current} [i],P_{globalbest} [i])$$
(5)

where δ(x,y) is an indicator function that takes the value 1 if x ≠ y and 0 otherwise, this formula calculates the number of points where the two paths do not coincide at all positions.

The path update is performed based on the current path and a set probability (assumed to be 0.5), and for each point P_current [i] on the ant's path, the set probability determines whether it is updated to the corresponding point P_(global best) [i] on the global best path, which can be expressed as

$$P_{current} [i] = \left\{ {\begin{array}{*{20}l} {P_{globalbest} [i]} \hfill & {{\text{if random}}({0},{1}) < {0}.{5}} \hfill \\ {P_{current} [i]} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(6)

Then the process of exploring new paths and updating the global optimal paths is carried out by repeating this process for the number of iterations (N), thus balancing between the global optimal solution and the current solution, in this way the algorithm is able not only to maintain the search for the current optimal solution, but also to explore new solutions and to explore more efficiently in the space of multimutant points, for experiments on APSO see subsection "Effectiveness of APSO".

Robust regression loss function (RRLF)

Stock prediction presents a multifaceted challenge, influenced by a myriad of factors encompassing economic, market, and political realms. The inherent uncertainty and volatility in this domain necessitate the precise adjustment of network parameters in deep learning models. This optimization aims to align the model's output as closely as possible with real values. Presently, the majority of deep learning models adopt the mean square error (MSE) as their loss function. However, the MSE loss function exhibits a drawback: its partial derivative is directly proportional to the error magnitude. Consequently, as the error diminishes, so does the partial derivative, resulting in a slowdown of the model's convergence speed when nearing the optimal solution. To overcome this limitation, an improved loss function, the SmoothL1 loss function, emerges as a solution. It amalgamates the strengths of both the L1 and L2 loss functions, offering smoothness and differentiability through a segmented function structure. Moreover, to specifically tackle the challenge of mutation points prevalent in stock data, this paper proposes a Robust Regression Loss function. This function amalgamates the beneficial aspects of MSE and SmoothL1, defining a comprehensive formulation as presented in Eq. (7):

$$Loss = \left\{ {\begin{array}{*{20}l} {\frac{1}{2}\left[ {\frac{1}{N}\sum\limits_{S = 1}^{N} {\left( {\hat{y}_{i} - y_{i} } \right)^{2} } + \frac{1}{2}\left( {\hat{y}_{i} - y_{i} } \right)^{2} } \right],} \hfill & {\left| {\hat{y}_{i} - y_{i} } \right| < 1} \hfill \\ {\frac{1}{2}\left[ {\frac{1}{N}\sum\limits_{S = 1}^{N} {\left( {\hat{y}_{i} - y_{i} } \right)^{2} } + \left| {\hat{y}_{i} - y_{i} } \right| - 0.5} \right],} \hfill & {\left| {\hat{y}_{i} - y_{i} } \right| \ge 1} \hfill \\ \end{array} } \right.$$
(7)

This paper introduces a novel segmented loss function designed to optimize inventory forecasting models. The distinctive feature of this loss function lies in its differential approach to varying error intervals. When the discrepancy between the model's predicted values and actual values is minimal, the loss function's gradient diminishes as the error decreases. This characteristic aids in maintaining high accuracy and prevents over-tuning when the model nears the optimal solution. Conversely, for larger errors, the gradient of this loss function is capped at an upper limit of 0.75. This cap serves to shield the model from excessive disruptions caused by outliers or extreme values, thereby enhancing its robustness. In comparison to the conventional smooth L1 loss, the segmented loss function proposed in this paper retains a certain gradient level without dwindling to zero when handling large errors. This attribute is particularly beneficial for expediting the model's convergence during training. It provides a more effective and stable training methodology for analyzing complex time-series data, such as stock market forecasting. The segmented loss function thereby represents a significant advancement in the field, offering an improved approach for managing the intricacies of time-series analysis.

Results and analysis

This section demonstrates the superiority of the model by experimentally verifying that PARNet resolves the challenges posed by the difficulty of understanding the correlation of the stock data elements, the lack of accuracy of overly long sequences, and the difficulty of handling mutation points in the stock prediction task. The remaining subsections are divided into: (1) Describing the experimental environment and setup, including the hardware and software environments. (2) Evaluating the experimental metrics. (3) Analyzing the performance of PMANet and verifying the superiority of the model in this thesis. (4) Evaluating the performance of individual modules and exploring the effectiveness of each module. (5) Performing ablation experiments on PMANet and verifying the validity of the methodology proposed in this paper. (6) Comparing PMANet with other deep learning network models and performing generalization experiments to intuitively analyze the sophistication of the model and prove the superiority and generalization ability of PMANet.

Experimental environment and training details

To ensure consistent experimental conditions and prevent variance from different environments, all experiments detailed in this paper are conducted within an identical hardware and software setup. The primary hardware utilized in these experiments comprises the NVIDIA GeForce RTX 3060 Laptop GPU and 11th Gen Intel(R) Core (TM) i5-11400H @ 2.70 GHz. Although the versions of Python, CUDA, and CUDNN are not influential on the experiment results, their compatibility with the software and hardware is crucial. PMANet implementation relied on PyTorch 1.11.0. Please refer to Table 1 for specific hardware specifications.

Table 1 Experimental Hardware and Software Parameter.
Full size table

Evaluation indicators

As stock price prediction constitutes a regression task, the evaluation of our proposed prediction model's performance relied on several commonly used metrics in stock price forecasting. These metrics include relative squared error (RSE), absolute mean error (MAE), mean square error (MSE), root mean square error (RMSE), and mean absolute percentage error (MAPE).

The MAE computes the average absolute error between the predicted and actual values of the model. Being less influenced by outliers, the MAE serves as an indicator of the model's robustness. A lower MAE value signifies better prediction accuracy. The formula is as follows:

$$MAE = \frac{1}{n}\sum\limits_{i = 1}^{n} | y_{i} - \hat{y}_{i} |$$
(8)

The MSE stands as a prevalent regression performance metric, assessing the average of the mean squared error between the model's predictions and the actual stock values. It accentuates larger errors more significantly, and within the realm of stock forecasting, these sizable errors directly impact accuracy and investment profitability. The formula is as follows:

$$MSE = \frac{1}{n}\sum\limits_{i = 1}^{n} {(y_{i} - \hat{y}_{i} )^{2} }$$
(9)

The RSE, relative to the MSE, provides a comparison between the MSE and the variance of the actual data. It serves to evaluate the enhancement in model performance concerning data volatility. The formula is as follows:

$$RSE = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {(y_{i} - \hat{y}_{i} )^{2} } }}{{\sum\limits_{i = 1}^{n} {(y_{i} - \overline{y}_{i} )^{2} } }}}$$
(10)

The RMSE is calculated by averaging the squares of the errors and then taking the square root as follows:

$$RMSE = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^{m} {(y_{i} - \hat{y}_{i} )^{2} } }$$
(11)

where is the average price, is the forecast price and is the actual price.

Performance analysis

To assess PMANet's enhancement over Informer, we utilized the Bank of Communications stock dataset (JT) as a case study, conducting a comprehensive series of performance evaluation experiments outlined in Table 2. The evaluation aimed to comprehensively scrutinize the network model's capabilities. The results showcased a significant enhancement in accuracy for both MSE and MAE metrics. This improvement can be attributed partly to PMANet's superior feature extraction and fusion capabilities, augmented by the integration of PPA, which enhances the interconnectedness of elements within the time series. Moreover, our comparison between the two models during the prediction process, depicted in Fig. 4 with the change curve of their predicted values, distinctly illustrates PMANet's superior fit in the prediction results. This suggests PMANet's better alignment with the inherent characteristics of the stock data. Collectively, PMANet markedly boosts detection accuracy without a substantial increase in parameter count.

Table 2 Model Performance Comparison.
Full size table
Figure 4
figure 4

PMANet vs. Informer's 24-h vs. 48-h forecasts of real stock prices.

Full size image

Module effectiveness experiments.

Effectiveness of PPA

In this study, we introduced positional encoding into all attention layers within the Informer backbone network, forming what we term 'Probabilistic Positional Attention'. To ascertain the effectiveness of this attention mechanism, we introduced various alternative attention mechanisms into the network for comparative experiments. The outcomes of these experiments are presented in Table 3.

Table 3 Exploring Optimal Attention.
Full size table

The experimental findings illustrate that PPA enhances the accuracy of predicting future stock trends and significantly improves the model's comprehension of relationships and dependencies among sequence elements. In conclusion, the Probabilistic Positional Attention (PPA) mechanism presents distinct advantages over traditional attention models by incorporating positional encodings for a deeper understanding of sequence order, integrating multi-head and cross-attention mechanisms for enhanced feature extraction, and employing sampling strategies for efficiency. These innovations not only improve computational efficiency but also significantly bolster the model's ability to capture complex patterns in tasks such as stock market prediction. Our experimental comparisons demonstrate that PPA markedly outperforms baseline models, validating its theoretical soundness and practical efficacy in handling intricate time-series data. Hence, PPA was chosen as the attention mechanism for PMANet.

Effectiveness of MTFC

To explore the performance advantages of MTFC over other convolutions, we introduced other convolutions at the same positions in the net. The results of this study are reported in Table 4.

Table 4 Explore the best convolution.
Full size table

The experimental results indicate that Ghost Convolution and DSC exhibit a moderate ability to address the impact of excessively long sequences on prediction; however, their effectiveness is limited. Conversely, Atrous Convolution and Involution demonstrate inadequate predictive performance, attributed to the gridding effect and the additional inner product operation, resulting in a lack of correlation among convolution results. Dynamic Convolution, while displaying potential, demands increased computational resources and parameters, heightening the model training complexity and adversely affecting time series prediction results.

Effectiveness of APSO

To explore the performance advantage of APSO over other algorithms, we compare four cases, Adam, AdamW, Lion, RMSprop and APSO, in our experiments. The results of the study are shown in Table 5.

Table 5 Exploring the optimal loss function.
Full size table

In the volatile and intricate realm of stock market forecasting, gradient-based optimizers like Adam, AdamW, Lion, and RMSprop offer rapid, data-driven optimization pathways. However, these methods are not without their drawbacks, including a propensity for overfitting, sensitivity to initial parameter settings, and limitations in handling global optimization tasks. Such challenges are particularly pronounced in the complex, non-linear, and dynamic context of stock market data. In contrast, Ant Particle Swarm Optimization (APSO), which amalgamates global and local search methodologies, exhibits superior global search capabilities and adaptability in navigating complex and irregular search spaces. This distinction renders APSO more proficient than traditional gradient-based optimizers for tasks like stock market forecasting. APSO's strengths are especially evident in identifying globally optimal solutions and effectively managing mutation points in the data. Its ability to cope with the nonlinearities and dynamism of the stock market underscores its potential as a robust alternative to conventional gradient-based optimization techniques in complex and constantly evolving environments.

Ablation experiments

Verification of the validity of the method in this document, we conducted ablation experiments on PMANet based on the Bank of Communications (BOC) dataset (JT), and the results of the experiments are shown in Fig. 5. We used the control variable method to add PPA, RRL and APSO sequentially, and conducted 8 sets of ablation experiments on these three modules in combination with PMANet. It can be seen from the figure that PPA is able to perform better feature extraction and significantly improves the accuracy of the model. While APSO filters out the interfering information in the stock dataset, the performance of MTFC is the most significant. It works alone and achieves the best results for both MSE and MAE. Taken together, compared to Informer, PMANet improves MSE and MAE by 43.9% and 24.8% respectively with a small number of parameters and without introducing a larger number of parameters. Meanwhile, the comparative results of 8 sets of experiments fully demonstrate the effectiveness of PPA, RRL and MTFC in improving model accuracy. Therefore, PMANet is more suitable than Informer for stock forecasting.

Figure 5
figure 5

Graph of ablation experiment results.

Full size image

Figure 5 shows that our proposed PPA can significantly improve the segmentation performance of the network compared to Informer's ProbSparse self-attention method, and MTFC improves the MAE and MSE by 5% and 14% respectively under the same conditions, which proves that MTFC is able to better understand and process the input long sequences to more accurately extract the features of the inventory data. In addition, we also used PPA and APSO to optimise the network, and although their improvement in network performance is relatively small, they are still effective. In summary, each module of PMANet has a positive impact on the stock prediction model, confirming that our proposed substitutions of PPA, MTFC and APSO are beneficial.

Contrast experiment of the model

At first, we curated a selection of four stocks spanning the banking, computer, pharmaceutical, and electrical appliance industries—namely JT, THS, HR, and GL—for training purposes. We conducted comparative experiments with various classical and contemporary advanced target detection methods within an identical test environment and prediction duration. "Dynamic graph construction via motif detection for stock prediction "52 proposes to divide the whole dataset into 6 smaller datasets, i.e., 6 phases of training, validation, and testing on a timeline of 1218 trading days to determine the effectiveness of the model in different volatility phases. Inspired by this, we expanded the dataset and used the price factor selection method in "Fuzzy hypergraph network for recommending top-K suitable stocks"53. we expanded the dataset from the original 4 dimensions (finance, information technology, pharmaceuticals, and manufacturing) to 6 dimensions, adding Kweichow Maotai, which represents high-end consumer goods, and BYD, which represents new automotive energy. In this way, the dataset was expanded from 4 to 6 dimensions, further enriching and improving our dataset to enhance the precision and comprehensiveness of the experiment. The comparative experimental results are shown in Table 6. In addition, we have plotted a visualisation of the results of the Bank of Communications opening price forecasts in Fig. 6. On this basis, we re-selected the price factors. We not only selected the opening price, closing price, high price, low price, and quantity factors from the inventory data, but also added static factors such as price-to-earnings (PE), price-to-book (PB), and market capitalization (MC) to augment the existing dataset. The comparative experimental results are shown in Table 7. The experimental results show that our model has made effective improvements after using the methods mentioned above.

Table 6 Comparative Experiments.
Full size table
Figure 6
figure 6

Forecast Chart of the 24-h and 48-h Opening Prices for Bank of Communications.

Full size image
Table 7 Comparative experiment of re-selected price factors.
Full size table

In the realm of inventory prediction using Transformer-like networks, temporal dependencies are predominantly established through the encoder-decoder structure and the self-attention mechanism. However, Transformers often lack sensitivity to non-linear temporal data, rendering them susceptible to anomalies and distribution shifts, thus diminishing prediction stability. Autoformer on the contrary, decomposes sequences into trend and period components through a deep decomposition architecture. It iteratively decomposes sequences and refines prediction results, aiming for progressive decomposition to maintain stability. Nonetheless, Autoformer heavily relies on the series' periodicity, which might not align well with the unpredictable nature of stock data, where series periodicity can be unstable. This dependency on periodicity could lead Autoformer's autocorrelation mechanism to misguide predictions. Fedformer utilizing Fourier transformation, converts time domain series into frequency domain series. Subsequently, it conducts random sampling and attention computations in the frequency domain to enhance computational efficiency and robustness. However, operations involving frequency domain sampling and complementation in Fedformer might lead to information loss or noise introduction, potentially impacting prediction accuracy.

Within the LSTM architecture applied to stock forecasting, long-term dependencies within the time series are primarily captured using Long Short-Term Memory cells (LSTM cells), instrumental in storing and updating time series information. CEEMD-CNN-LSTM adopts the CEEMD method to decompose input stock series data into a set of Intrinsic Mode Functions (IMFs) and a residual phase. These are then channeled into CNN for feature extraction and dimensionality reduction, capturing comprehensive global features embedded in the stock sequence. Throughout the prediction process, the selection of CEEMD parameters and the number of IMFs exert substantial influence. These selections vary across datasets, impacting the quality of decomposition and subsequently affecting prediction performance.

Generalization experiment of the model

The fundamental objective of stock prediction models is to assist investors in decision-making. Therefore, the practicality and credibility of these models are paramount. Generalization experiments play a crucial role in verifying the adaptability of the model to diverse industry characteristics and data features. It assesses whether the model can discern hidden patterns and trends within the data, offering reliable and reasonable prediction results and ultimately enhancing the model's practicality and credibility. For the generalization experiments, we selected power transformer temperature data provided by the State Grid, spanning from January 1, 2016, to January 1, 2018, and another dataset covering December 1, 2015, to December 1, 2017. These experiments were conducted to further analyze the performance of PMANet. Comparative experiments and generalization experiments were executed alongside several classical and contemporary advanced target detection methods in the same test environment and prediction period. The details of the test data can be found in Table 8.

Table 8 Generalization experiments.
Full size table

PMANet emerges as the most suitable model for stock forecasting among its counterparts in the table. Several reasons contribute to its superior performance:(1) PMANet innovates upon the Informer model by integrating efficient techniques like adaptive attention mechanisms, multi-scale encoders, and probabilistic predictions. These advancements significantly enhance prediction accuracy, efficiency, and overall performance. (2) The MTFC integration within PMANet significantly boosts its ability to identify target sequences, markedly improving its predictive capabilities. (3) The addition of PPA within the model's architecture, particularly within the neck, effectively filters out interference information prior to the fusion of time series features. This process enhances the precision of predictions. (4) The use of a self-generated dataset in this paper eliminates missing values and outliers, ensuring a more complete and more accurate dataset, At the same time, the method in "Dynamic graph construction via motif detection for stock prediction"38 is used to expand the data set. This refinement greatly benefits the model training process, leading to an overall improvement in performance.

Discussion and conclusion

Discussion

The paper introduces and evaluates the PMANet model for long-term stock price forecasting, comparing its performance with other Transformer-based models. It highlights certain advantages of the PMANet model in terms of both accuracy and efficiency in forecasting stock prices. The PMANet model stands out due to its incorporation of PPA, which significantly enhances its ability to handle the interdependence and correlation among elements in time series data. This augmentation leads to improved information utilization and aggregation within the model. Moreover, the PMANet model leverages MTFC to capture the temporal characteristics inherent in long time series data. This utilization enhances the model's flexibility and accuracy in forecasting, particularly regarding long-term trends. Lastly, by employing APSO, the PMANet model effectively processes mutation points within time series data, thereby enhancing the stability and reliability of its forecasting outcomes.

Certainly, the PMANet model, although effective for long-term forecasting, might have limitations in short-term stock prediction that necessitate further refinement. Primarily, its reliance on the Transformer's encoder-decoder structure might pose challenges. This structure could struggle with non-smooth time series data and overlook interactions among various variables. To investigate this possibility, we deployed the PMANet model to short-term stock data (Wanchen Bio: WC, Wanxing Technology: WX, and China Science and Technology: ZG) obtained from the Wind Economics database from 1 January 2022 to 30 December 2022. The datasets feature a daily time interval, with a forecast period of 12 h. The experimental findings are detailed in Table 9 and Fig. 7.

Table 9 Experiments on short-time data sets.
Full size table
Figure 7
figure 7

Comparison of predicted values on short-term data sets.

Full size image

The comparison between the MSE and MAE metrics highlights the PMANet model's higher accuracy and stability in predicting the prices of four stocks (JT, GL, THS, HR) compared to predicting three other stocks (WC, WX, ZG). This discrepancy suggests an opportunity to enhance PMANet's predictive performance for shorter time series data. Future research endeavors could focus on improving and expanding the PMANet model in several ways. Firstly, integrating additional time series features and contextual information could enhance the model's capacity to handle shorter time series data. Secondly, devising a more balanced attention mechanism that effectively manages information utilization and aggregation could further refine the model's performance. Lastly, exploring more efficient prediction methodologies could bolster prediction speed and efficacy.

Conclusion

To explore optimized methods for stock price prediction, we introduce an approach using PMANet for predicting stock prices and trends. Initially, we propose PPA to improve the model's learning and comprehension of the dependencies and correlations between elements in time series sequences. Subsequently, we employ MTFC for feature extraction in long time series. Finally, APSO is introduced for adaptive learning rate adjustment, aiding the model in converging more rapidly to the optimal solution and more effectively identifying data mutation points, thereby improving prediction accuracy. Most importantly, PMANet optimizes the accuracy of the Informer model in the domain of stock prediction and aligns more closely with the characteristics of stock data during training. This provides a new reference for deep learning in the prediction of stock opening prices. Overall, PMANet significantly enhances detection accuracy without excessively increasing the number of parameters and computational load, outperforming other test methods and proving the effectiveness of our improved approach.

Stock forecasting is an important technique used in financial and investment decision making that provides accurate information about stock market conditions and helps investors assess the price movement and risk of stocks. This technique helps investors keep abreast of market conditions and stock performance so that they can make more informed investment decisions. In doing so, it can significantly improve portfolio management efficiency and investment returns, while reducing investment risk and promoting financial health and wealth growth. However, stock prediction also faces some challenges, such as insufficient relationships and dependencies between data elements in ordinary networks, long input time series, and mutation points in time series data. In response to these problems, this document proposes a new informer segmentation network, PMANet, which achieves better results in stock prediction.

a. Ablation experiments show that PPA, MTFC and APSO are more effective for stock prediction with + 1.9%, + 8.5% and + 5.9% MSE respectively. With the same experimental setup, PMANet improves the MSE by 18.1% and the MAE by 10.7% compared to Informer.

b. For the 24-h prediction of the JT dataset, PMANet achieves an MSE of 0.412 and an MAE of 0.431 compared to the current mainstream and prediction algorithm pairs. b. The method shows excellent performance, not only in terms of significant improvement in prediction accuracy, but also in dealing with excessively long input sequences and data mutation points. c. In the 24-h prediction of the JT dataset, PMANet achieves an MSE of 0.412 and an MAE of 0.431 compared to Informer.

In this paper, we propose an innovative stock market forecasting method (called PMANet). This approach significantly improves the ability to detect stock market features by effectively extracting and fusing features at different scales and levels, thereby improving the consistency of stock price predictions. In a series of experiments, PMANet performs well on two key performance indicators, MSE and MAE. These results not only demonstrate the superior performance of PMANet in stock prediction, but also highlight its excellent generalization ability. The successful application of this stock prediction method is of great importance to investors and financial professionals. By accurately predicting stock price movements and market trends, PMANet is able to provide investors with critical information to help them make smarter investment strategies and decisions. This helps to reduce investment risk, increase investment returns and promote the financial health and long-term growth of individual and institutional portfolios. In addition, we will explore the use of more advanced techniques to introduce more diverse time series data to further improve the accuracy and processing efficiency of PMANet.