BD-YOLOv8s: enhancing bridge defect detection with multidimensional attention and precision reconstruction

Abstract

The YOLO (You Only Look Once) series has recently demonstrated remarkable effectiveness in the domain of object detection. However, deploying these networks for concrete bridge defect detection presents multiple challenges, such as insufficient accuracy, missed detections, and false positives. These complications arise chiefly from the complex backgrounds and the significant variability in defect characteristics observed in bridge imagery. This study presents BD-YOLOv8s, an advanced methodology utilizing YOLOv8s for bridge defect detection. This approach augments the network’s adaptability to a broad spectrum of bridge defect images through the integration of ODConv into the second convolutional layer, processing information within a four-dimensional kernel space. Furthermore, incorporating the CBAM module into the first two C2F architectures leverages spatial and channel attention mechanisms to focus on critical features, thus enhancing the accuracy of detail detection. CARAFE replaces traditional upsampling methods, improving feature map reconstruction and significantly reducing blurs and artifacts. In performance assessments, BD-YOLOv8s attained 86.2% mAP@0.5 and 56% mAP@0.5:0.95, surpassing the baseline by 5.3% and 5.7%. This signifies a considerable decrease in both false positives and missed detections, culminating in an overall improvement in accuracy.

Introduction

The challenge of aging infrastructure has become critical with global industrialization. The ‘2023 Bridge Report’ by the American Road & Transportation Builders Association¹ indicates over 222,000 spans in the U.S. need repairs, with 76,600 bridges requiring replacement, and 42,400 classified as ‘structurally deficient.’ At the current pace, these repairs could take nearly 75 years. In China, by the end of 2022, there were 1.0332 million highway bridges, totaling 85.7649 million linear meters². Approximately 40% of these bridges have been in service for over 20 years, with 30% showing deterioration and over 100,000 classified as hazardous. These bridges were designed mainly based on load-carrying capacity limit states, often neglecting long-term deterioration. Bridges face environmental erosion, construction defects, vehicle overloading, and natural aging, leading to structural integrity decline³. Manifestations like cracks⁴, spalling⁵, rebar exposure⁶, and corrosion⁷ can lead to catastrophic failures, impacting the national economy and public safety. Bridge safety is essential for modern development, human transportation, and regional economic connectivity. Thus, visual inspection of bridge structures is fundamental in their operation and maintenance^8,9.

Bridge defect detection heavily relies on manual visual inspection and basic instrumental measurements, which are subjective and influenced by various factors, resulting in false positives and missed detections^10,11. To address these challenges, digital image processing techniques have been proposed¹². Advanced equipment such as drones and wall-climbing robots facilitate image acquisition^13,14. After suitable preprocessing, mathematical statistical and machine learning techniques are used to extract image features. Two prevalent methods are threshold segmentation and edge detection. Threshold segmentation, an early method in bridge crack detection, involves manually setting detection thresholds¹⁵. For example, Talab et al.¹⁶ employed the Otsu method with various filters to enhance crack extraction, mitigating environmental effects but with limited applicability. Edge detection, frequently used in defect detection, utilizes local grayscale and gradient data to identify edges¹⁷. Ayenu-Prah et al.¹⁸ proposed Sobel edge detection for crack detection, which is suitable for pronounced crack features. Although traditional image processing has yielded favorable results, it requires further enhancement. These methods rely on manual parameter adjustments and laborious preprocessing, lacking the robustness needed for comprehensive end-to-end defect identification.

Recently, deep learning has made significant advances in detection due to its ability to learn data characteristics and update parameters directly, thus avoiding the need for manual design of complex algorithms. These methods, based on multi-layer neural network training, exhibit high robustness and detection accuracy, surpassing traditional image-processing technologies^19,20. Detection methods using deep learning can be categorized based on network architecture into dual-stage and single-stage detection algorithms. Dual-stage algorithms, such as Fast R-CNN²¹ and Faster R-CNN²², use regional convolutional neural networks to generate candidate boxes, a complex and computationally intensive process²³. Single-stage algorithms, such as SSD²⁴ and YOLO²⁵, combine feature extraction and prediction in a single step, enhancing detection efficiency. However, SSD faces challenges with feature extraction and relies on manual judgment. YOLOv3²⁶, YOLOv4²⁷, YOLOv5²⁸, and YOLOv8 have improved detection rates and accuracy, surpassing other algorithms. However, bridge defects are characterized by complex background environments and significant variability in defect features. When previous generations of target detection algorithms are directly applied to bridge defect detection, issues such as missed detections and false positives arise, often due to inadequate feature extraction of the defects. Notably, YOLOv3 improved detection accuracy and speed with a multi-scale feature pyramid but struggled with intricate backgrounds and noise, resulting in false detections and missed detections. YOLOv4 enhanced feature representation with CSPDarknet53 and the Mish activation function but still struggled to detect small, subtle features in complex backgrounds. YOLOv5 increased speed and accuracy with an automatic anchor box mechanism but remained inadequate for detecting small cracks on bridge surfaces. YOLOv6 introduced PAFPN and the SIoU loss function enhancements but still faced challenges with multi-scale and irregularly shaped defects. YOLOv8, with advanced feature extraction networks like EFPN and CSPNet, efficient training strategies, and optimized algorithms, offers significant improvements in accuracy and speed, making it better suited for practical applications. It performs well on some public datasets, such as the COCO²⁹ (Common Objects in Context) dataset, but there is still room for improvement in detecting bridge surface defects with complex data characteristics. Consequently, this study aims to explore enhancements to the YOLOv8s algorithm and its applicability in bridge defect detection tasks.

Related work

Related research

Recently, deep learning has significantly advanced concrete defect detection in structural health monitoring. Zhang et al.³⁰ utilized a multi-task compressed sampling algorithm for real-time crack detection, leveraging generative models’ sparsity patterns to enhance accuracy and reduce data compression. Yu et al.³¹ optimized deep convolutional neural networks with an enhanced chicken swarm algorithm, thereby improving crack detection accuracy and efficiency. Fernandez et al.³² applied distributed fiber optic sensing for monitoring concrete structures, thereby increasing detection sensitivity. Tang et al.³³ utilized deep transfer learning to identify defects in prefabricated structures, thereby improving reliability. Rao et al.³⁴ integrated Attention R2U-Net with a random forest regressor for crack detection, demonstrating high accuracy. Despite these advances, challenges remain in handling complex backgrounds and subtle features. This study proposes an improved YOLOv8s network (BD-YOLOv8s) incorporating Multi-dimensional Attention Mechanism (ODConv), Channel and Spatial Attention Mechanism (CBAM), and Content-Aware ReAssembly of FEatures (CARAFE) to enhance detection accuracy and robustness.

YOLOv8 network architecture

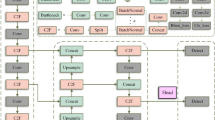
The YOLOv8 architecture consists of four main components: Input, Backbone, Neck, and Head, as depicted in Fig. 1. The Input utilizes Mosaic data augmentation, which is deactivated during the last 10 epochs to enhance real-world data adaptability. An anchor-free mechanism is employed for direct object center prediction, reducing anchor box predictions and enhancing NMS efficiency³⁵. Hyperparameters are fine-tuned for different model sizes, with MixUp and CopyPaste augmentations applied in larger models to enhance diversity and generalization. The Backbone extracts image information and incorporates Conv and C2f. modules, culminating in an SPPF layer. Conv modules extract and organize feature maps, while the C2f. structure, inspired by YOLOv7³⁶, enriches gradient flow and adjusts channels based on model scale, thereby improving performance. The SPPF layer expands the receptive field and fuses multi-scale features to enhance detection. The Neck combines multi-scale features using PANet, integrating FPN³⁷ and PAN³⁸ to improve spatial information retention and detection capability. The Head employs a decoupled structure for separate classification and detection tasks, thereby improving performance. The anchor-free method enhances detection speed by directly predicting object centers.

Figure 1

YOLOv8 structure diagram.

Methodology

The following enhancements have been implemented to address the challenges posed by complex background environments and significant variability in defect characteristics in bridge defect imagery. Initially, the second convolutional layer of the backbone network has been substituted with ODConv (Omni-Dimensional Dynamic Convolution)³⁹. ODConv employs a multi-dimensional attention mechanism to learn across the four dimensions of the kernel space concurrently. Compared to traditional CNN convolutional layers, ODConv is more adept at adapting to and learning the diverse and complex features of bridge defect images, particularly in handling background noise and irregularities. This leads to a significant enhancement in detection accuracy for various defect forms. Secondly, integrating CBAM (Convolutional Block Attention Module)⁴⁰ into the initial two C2F architectures of YOLOv8 further augments the model’s feature recognition and focusing capabilities. This integration optimizes the feature integration process, heightens detection accuracy for small targets like leaky bars, and bolsters the model’s generalization capacity. Consequently, the model becomes more efficient and precise in handling complex bridge defect environments. Finally, substituting the traditional upsampling method in YOLOv8 with CARAFE (Content-Aware ReAssembly of FEatures)⁴¹ has resulted in a more refined reconstruction of feature maps. CARAFE’s content-aware mechanism not only enhances the detection of minor defects but also effectively minimizes blur and artifacts in the upsampling process, preserving edge and detail information, thereby significantly improving the accuracy and efficiency of bridge defect detection.

A Multi-dimensional dynamic convolution

The traditional convolutional layer in YOLOv8 exhibits several critical limitations in processing complex bridge defect imagery:

• 1. The fixed size and number of convolution kernels constrain the model’s flexibility in capturing complex or irregular features, such as cracks and corrosion.

• 2. The local receptive fields of standard convolutional layers may insufficient so as to capture key defect features that are either widely distributed or resemble the background.

• 3. Traditional convolutional layers exhibit limited generalization capabilities in feature extraction, leading to potential fluctuations in model performance when confronted with diverse and intricate defect features.

• 4. These layers lack the capacity for dynamic adjustment and optimization based on input data characteristics, posing a significant challenge in processing bridge defect images with high variability.

This study reveals that integrating ODConv for identifying complex bridge defect imagery enhances the performance of the YOLOv8s model. This enhancement is primarily attributed to ODConv’s multi-dimensional dynamic attention mechanism and parallel processing strategy. Evolving from CondConv, ODConv not only broadens the scope of dynamic convolution but also incorporates factors such as spatial dimensions, input channel count, and output channel count, thereby achieving more comprehensive dynamic characteristics. ODConv’s multi-dimensional attention mechanism, which discerns complementary attention across the four dimensions of kernel space, enables a more precise focus on key image areas, thereby improving detection accuracy. Concurrently, ODConv’s parallel strategy augments its multi-dimensional dynamics, enhancing processing efficiency through simultaneous attention learning in different dimensions, ensuring complementarity and synergy. This capability allows the model to thoroughly capture and utilize critical image information, which is crucial for accurately identifying and pinpointing subtle variances in bridge defects. Furthermore, this fine-grained, feature-focused mechanism enables the model to utilize parameters more efficiently, diminishing its reliance on an extensive parameter set. This allows ODConv to be paired with a single convolutional kernel, yet still achieve performance comparable to or even surpassing that of existing multicore dynamic convolutions.

Figure 2 illustrates the operational workflow of the ODConv module. Global average pooling (GAP) initially transforms the input feature X into a compressed feature vector. Subsequently, it is mapped to a low-dimensional space via a fully connected layer (FC), with a reduction ratio of 1/16, to diminish the module's complexity. The ReLU function is then utilized to eliminate negative values, paving the way for constructing four attention scalars. The ODConv module comprises four branches dedicated to attention learning in distinct dimensions: spatial position, input channel, output channel, and convolution kernel weight. These branches, via the FC layer, predict corresponding weights and output feature vectors, which are instrumental in locating bridge defect areas, analyzing structural features, and refining local features. The first three branches undergo normalization using the Sigmoid function, whereas the fourth branch employs the Softmax function to ensure the summation of weights equals one. The ODConv formula is delineated in Eq. (1):

$$ Y = \left( {\mathop \sum \limits_{i = 1}^{n} \alpha_{\omega i} \cdot \alpha_{ci} \cdot \alpha_{fi} \cdot \alpha_{si} \cdot W_{i} } \right) * X $$

(1)

where ${\varvec{\alpha}}_{wi} \in {\mathbb{R}}$ represents the attention scalar of the entire convolution kernel ${\varvec{W}}_{i}$,${\varvec{\alpha}}_{si} \in {\mathbb{R}}^{k \times k}$ represents the attention scalar introduced along the spatial dimension of the convolution kernel ${\varvec{W}}_{i}$, ${\varvec{\alpha}}_{ci} \in {\mathbb{R}}^{Cin}$ represents the attention scalar introduced along the input channel dimension of the convolution kernel ${\varvec{W}}_{i}$, ${\varvec{\alpha}}_{fi} \in {\mathbb{R}}^{Cout}$ represents the attention scalar introduced along the output channel dimension of the convolution kernel ${\varvec{W}}_{i}$, $\cdot$ represents multiplication operations along different dimensions of the kernel space, $*$ means convolution operation, $X$ represents the input feature, $Y$ represents the output feature.

Figure 2

Flow chart of ODConv convolution operation.

In ODConv, for convolution kernel ${\varvec{W}}_{i}$, ${\varvec{\alpha}}_{si}$ assigns different attention scalars to the convolution parameters at the spatial location of $k \times k$. ${\varvec{\alpha}}_{ci}$ assigns different attention scalars to the convolution filters of different input channels. ${\varvec{\alpha}}_{fi}$ assigns different attention scalars to the convolution filters of different output channels.${\varvec{\alpha}}_{wi}$ assigns different attention scalars to $n$ ensemble convolutions. Figure 3a–d shows the process of multiplying these four types of attention by convolution kernels. Essentially, these four distinct attention types synergistically enhance one another by progressively applying multiplicative attention across the dimensions of position, channel, filter, and kernel. This approach allows the convolution operation to adapt uniquely in each dimension for every input, thereby capturing more comprehensive contextual information and consequently yielding enhanced performance.

Figure 3

Illustration of multiplying four types of attentions in ODConv to convolutional kernels progressively. (a) ODConv Convolution attention operations along spatial dimensions, (b) ODConv Convolution attention operations along the in-put channel dimension, (c) ODConv filters convolution attention operations along the output channel dimension, (d) ODConv convolutions attention operations along the spatial dimension of the convolution kernel kerne.

Leveraging its multi-dimensional dynamic attention mechanism, ODConv fine-tune the convolution kernel in response to input features, adapting to the diversity and complexity of bridge defect imagery. This enhancement bolsters the model’s ability to learn intricate features, thereby improving detection accuracy.

A channel and space joint attention module

The experimental analysis revealed that the C2F architecture of the YOLOv8 model exhibits certain limitations in processing complex bridge defect imagery. While C2F can process multi-scale information, its capacity for delicate feature fusion proves inadequate in differentiating micro-defect features from intricate backgrounds. This limitation primarily stems from a lack of precision in integrating features across various levels, thereby constraining the detection of defects exhibiting significant size variations. Furthermore, C2F encounters challenges in minimizing background interference and enhancing its generalization capabilities. This issue may result in false detections or missed diagnoses, particularly when addressing unfamiliar defect types or variable environments. Consequently, while C2F offers a robust multi-scale feature processing framework, it necessitates further optimization to meet the specific demands of complex bridge defect detection. In response to these challenges, this study incorporated CBAM into the initial two C2F architectures of the YOLOv8s model. CBAM significantly bolsters the model’s proficiency in identifying key regions and features, courtesy of its spatial and channel attention mechanisms. This enhancement amplifies the model’s capabilities in multi-scale information processing and subtle defect detection and elevates its generalization, thereby better adapting it to various types of bridge defects.

CBAM represents a fusion-based attention mechanism module. The structural principle, as depicted in Fig. 4, illustrates that the CBAM module comprises two distinct sub-modules: the channel and spatial attention modules. Integrating attention modules in both the channels and spatial domains conserves parameters and computational resources and facilitates their incorporation into existing network architectures as plug-and-play modules. The CBAM module functions on feature mapping, extracting features with greater detail via the channel and spatial attention modules, thereby enhancing the model’s expressiveness.

Figure 4

Convolutional Block Attention Module.

The schematic representations of each attention sub-module within CBAM are depicted in Figs. 5 and 6. Initially, through parallel execution of average pooling and max pooling operations on the feature map, spatial information is aggregated, resulting in the generation of two distinct spatial descriptors: $F_{avg}^{c}$ and $F_{\max }^{c}$, represent average pooling features and maximum pooling features respectively. Secondly, these two descriptors are input into the shared fully connected layer, culminating in the generation of the channel attention feature map $M_{c}$, its size is C × 1 × 1, The calculation formula is shown in formula (2). The shared fully connected layer consists of a multilayer perceptron (MLP) and a hidden layer. In order to reduce parameters, the activation size of the hidden layer is set to $R^{{C/r \times {1} \times {1}}}$, r is the reduction rate.

$$ \begin{aligned} Mc(F) = & \sigma \left( {MLP\left( {AvgPool(F)} \right) + MLP\left( {MaxPool(F)} \right)} \right) \\ = & \sigma \left( {W_{1} (W_{0} (F_{{{\text{avg}}}}^{c} )) + W_{1} (W_{0} (F_{{{\text{max}}}}^{c} )))} \right. \\ \end{aligned} $$

(2)

where $\sigma$ represents the sigmoid function, $W_{0} \in R^{C/r \times 1}$,$W_{1} \in R^{C \times C/r}$,$W_{0}$ and $W_{1}$ represents the weight of the shared MLP, AvgPool and MaxPool represent average and max pooling operations respectively. The spatial attention module concentrates on pinpointing the location of feature information within the image, serving as a complement to the channel attention module. Initially, the spatial attention module employs average pooling and maximum pooling operations along the channel axis, resulting in the generation of two distinct feature maps, $F_{avg}^{s}$ and $F_{\max }^{s}$, and splice them into an effective feature descriptor. Finally, the convolution layer performs a convolution operation to obtain the corresponding spatial feature map. The specific formula is shown in formula (3).

$$ \begin{aligned} Ms(F) = & \sigma \left( {f^{7 \times 7} \left( {\left[ {AvgPool(F);MaxPool(F)} \right]} \right)} \right) \\ = & \sigma \left( {f^{7 \times 7} \left( {\left[ {F_{avg}^{s} ;F_{{{\text{max}}}}^{s} } \right]} \right)} \right) \\ \end{aligned} $$

(3)

where $f^{7 \times 7}$ is the convolution operation with a filter size of 7 × 7.

Figure 5

Channel Attention Module.

Figure 6

Spatial Attention Module.

Figure 7 shows the specific level at which CBAM is introduced into the C2F architecture, and Fig. 8 shows the position of the CBAM-C2F module in the entire network structure.

Figure 7

c2f_cbam structure.

Figure 8

Location of c2f_cbam module.

An enhanced up-sampling method

Given the complexity of edge information in bridge defects and significant background noise, traditional sampling techniques such as bilinear interpolation and nearest neighbor interpolation frequently result in the loss of details and blurred edges in enlarged feature maps. This issue complicates the accurate identification of crucial defect information. Feature maps produced by these methods could be better quality and replete with extraneous interference information. This study substituted the traditional upsampling method with CARAFE (Content-Aware ReAssembly of FEatures) in the Neck component of YOLOv8 to enhance the expressive capability of defect characteristic information output. CARAFE employs a content-aware feature reorganization mechanism to meticulously reconstruct upsampled feature maps, effectively addressing the limitations inherent in traditional upsampling algorithms regarding semantic information processing and receptive field size in feature maps. This is achieved while circumventing the need for excessive parameters and computations. Such enhancement facilitates increased accuracy and efficiency in bridge defect detection tasks. The operational workflow of CARAFE is elaborated in Fig. 9.

Figure 9

CARAFE Flow Chart.

CARAFE comprises two primary modules: the upsampling kernel prediction module and the feature reorganization module. Assuming an upsampling ratio of $\sigma$ and an input feature map of shape $H \times W \times C$, CARAFE initially employs the upsampling kernel prediction module to forecast the upsampling kernel, followed by the feature reorganization module to execute the upsampling, resulting in an output feature map of shape $\sigma H \times \sigma W \times C$. Within the upsampling prediction module, to minimize subsequent computational load, the feature map with input shape $H \times W \times C$ undergoes compression via 1 × 1 convolution, reducing the number of channels to $H \times W \times C_{m}$. Subsequently, content encoding and upsampling kernel prediction are conducted, utilizing the $K_{encoder} \times K_{encoder}$ convolution layer for upsampling kernel forecasting. The process involves $C_{m}$ input channels and yields an output of $\sigma^{2} K_{up}^{2}$, followed by an expansion of channels in the spatial dimension to acquire the upsampling kernel of shape $\sigma H \times \sigma W \times K_{up}^{2}$. A normalization operation is performed on the upsampling kernel, ensuring that the sum of its convolution kernel weights equals 1. Within the feature reorganization module, each position in the output feature map is mapped back to the input feature map, encompassing the area of $K_{up} \times K_{up}$ centered on it, followed by a dot product with the predicted sampling kernel at this point to derive the output value. Different channels at the same position share an identical upsampling kernel, culminating in the acquisition of the output feature map with output $\sigma H \times \sigma W \times C$.

The enhanced model, employing CARAFE upsampling, achieves more sophisticated feature reorganization and notably improves upsampling quality for bridge defect detection. This advancement significantly boosts the model’s accuracy and efficiency in processing intricate backgrounds and discerning subtle defect features. The structure of the finally implemented BD-YOLOv8s is shown in Fig. 10.

Figure 10

BD-YOLOv8s structure diagram.

Experimental results and analysis

Experimental environment and dataset

To ascertain the efficacy of the proposed method, this study’s experimental setup employed Ubuntu 20.4 as the operating system, PyTorch 1.13 as the deep learning framework, and YOLOv8s as the foundational network model. The detailed configuration of the experimental environment is delineated in Table 1.

Table 1 Configuration and training environment.

Uniform hyperparameters were maintained throughout the training process across all experiments. Table 2 enumerates the specific hyperparameters employed during the training phase.

Table 2 Hyperparametric configuration.

Few researchers in bridge defect detection have released datasets for experimental use. For example, Mundt et al.⁴² introduced the CODEBRIM dataset for bridge concrete defect detection in 2019. However, the image quality in this dataset is inadequate for developing the BD-YOLOv8s model. Therefore, this study collected images of four main defects: cracks, exposed rebar, spalling, and corrosion, using web crawlers, local bridge inspection reports, and manual collection. This dataset was created by filtering and augmenting these images, resulting in a total of 7684 images. The defect types are listed in Table 3. The images were divided into training and validation sets in an 8:2 ratio.

Table 3 Types and quantities of defects in the dataset.

The image samples of various diseases in the data set are shown in Fig. 11. Common bridge defect features include cracks, spalling, exposed rebar, and corrosion. Cracks are among the most common types of damage in bridge structures, typically caused by loads, temperature fluctuations, or material aging. Severe cracks can compromise the overall stability and load-bearing capacity of the bridge. Spalling refers to the detachment of concrete surface material, usually caused by rebar corrosion or freeze–thaw cycles. This damages the protective layer of the concrete, exposes the internal rebar to further corrosion, and reduces structural integrity. Exposed rebar occurs when rebar in reinforced concrete structures becomes exposed, typically due to concrete spalling, crack propagation, or insufficient protective layer thickness. This accelerates rebar corrosion, weakening the bridge’s load-bearing capacity and durability. Corrosion occurs due to the failure of the bridge’s waterproof layer or high concrete porosity, leading to water infiltration. This can cause concrete carbonation and rebar corrosion, compromising the bridge’s lifespan and safety. These damage features are interrelated: cracks can lead to spalling, spalling can cause exposed rebar, and exposed rebar and cracks together exacerbate corrosion, collectively compromising the structural safety and durability of the bridge.

Figure 11

Examples of different types of defects. (a) crack; (b) spallation; (c) exposed bars; (d) corrosions.

Evaluation metrics

In object detection algorithms, mean Average Precision (mAP) is a standard metric for assessing model performance. The confusion matrix, delineating the classification results of the binary classification problem, is illustrated in Table 4. The judgment results are categorized into four types based on the combination of their labeling and prediction classes: true positives, false positives, true negatives, and false negatives, corresponding to TP, FP, TN, and FN in Table 4, respectively.

$$ P = \frac{TP}{{TP + FP}} $$

(4)

$$ P = \frac{TP}{{TP + FN}} $$

(5)

Table 4 Confusion matrix for binary classification.

Precision (P) is defined as the ratio of the number of targets correctly predicted by the model to the total number of predicted targets. Recall (R) signifies the ratio of the number of targets accurately predicted by the model to the overall number of targets within the dataset. Each class’s Average Precision (AP) is represented by the area enclosed by the Precision-Recall (P-R) curve and the coordinate axis. The mean Average Precision (mAP) is the average area under the Precision-Recall (P-R) curve across all defect categories. mAP serves as a relatively robust metric for evaluation. The formulas for calculating AP and mAP are as follows:

$$ AP = \frac{{\sum {_{i = 1}^{N} } P_{i} }}{N} $$

(6)

$$ mAP = \frac{{\sum {_{j = 1}^{N} } AP_{j} }}{M} $$

(7)

where M denotes the total number of categories utilized for detection, while N signifies the number of images subjected to testing. The mAP encompasses mAP@0.5 and mAP@0.5:0.95, both of which are contingent upon the predetermined IoU threshold. The expression for this is as follows:

$$ mAP@0.5 = \frac{{\sum\limits_{j = 1}^{M} {AP@0.5_{j} } }}{M} $$

(8)

$$ mAP@0.5:0.95 = \frac{{\sum\limits_{k = 0}^{9} {mAP@(0.5 + 0.05k)} }}{10} $$

(9)

As discerned from Eqs. (8) and (9), mAP@0.5 represents the average accuracy at an IoU threshold of 0.5, illustrating the fluctuating trend of precision P and recall rate R. mAP@0.5:0.95 denotes the average accuracy across IoU thresholds ranging from 0.5 to 0.95 in increments of 0.05, reflecting the model’s comprehensive performance under varying IoU thresholds. A higher mAP@0.5:0.95 indicates the model’s more robust boundary regression capability and a more precise alignment between the prediction and labeling frames. Concurrently, the F1 score considers accuracy and recall, offering a more holistic reflection of the network’s overall performance. The harmonic mean of these two indicators is calculated with the expression as follows:

$$ F1 = 2\frac{Precision \times Recall}{{Precision + Recall}} $$

(10)

Additionally, model complexity is quantified using model parameters (Params) and computational load (GFLOPs). Frames per second (FPS) is the metric for assessing inference speed. FPS denotes the number of frames processed per second, with its value being contingent upon the algorithm’s complexity and the model’s design.

Comparison of different attention mechanism effects

A range of attention modules were integrated into the C2f. architecture to identify the most suitable attention mechanism for this research, as shown in Table 5. Experimental findings indicate that incorporating CBAM into the YOLOv8s model elevates the mAP@0.5 index from a baseline of 80.9% to 85.7%. This improvement markedly surpasses the impact achieved by other attention modules. After integrating the SE and EMA modules, the improvements were 3.8% and 3.5%, respectively, whereas the CA module’s enhancement was the most modest at only 2.6%. These outcomes suggest that CBAM, which amalgamates channel and spatial attention, is more efficacious than single-dimensional attention in applying attention mechanisms. Furthermore, the C2f. + CBAM model attains performance enhancement while preserving low computational overhead (GFLOPs of 28.9) and a modest parameter count (11.20M), akin to the baseline model’s size. Additionally, this model successfully sustains a high processing speed (103 FPS/HZ), aligning closely with real-time processing requisites. Moreover, the model approaches real-time processing standards with a processing speed of 103 frames per second, striking an optimal balance between efficiency and speed.

Table 5 Performance table of different attention modules.

Ablation experiment

A comprehensive series of ablation studies was undertaken to assess the influence of individual network structure branches within the enhanced YOLOv8s algorithm on its overall performance. This experimental approach is frequently employed to incrementally dissect the effects of various network branches on the overall model architecture. The performance of the original YOLOv8s model and its optimized variants, employing diverse combinations of enhancements, was compared and analyzed using the test dataset. The outcomes of these experiments are shown in Table 6.

Table 6 Improved YOLOv8s and YOLOv8s experiments performance.

Table 6 shows that incorporating ODConv enhances the model’s mAP@0.5, elevating it from a baseline of 80.9% to 86.6%. This underscores that optimizing the convolution layer bolsters the recognition accuracy of this model. Integrating the C2f_cbam module further amplifies the model’s capability to apprehend complex features, culminating in an increase of mAP@0.5 to 85.7%. While integrating the CARAFE module did not augment mAP@0.5, it resulted in a 1% enhancement in mAP@0.5:0.9, demonstrating the efficacy of feature upsampling in augmenting spatial resolution. Utilizing ODConv in tandem with C2f_cbam elevates the mAP@0.5:0.9 to 53.8%. It accentuates the synergistic interplay between the two technologies. Furthermore, the amalgamation of C2f_cbam with CARAFE elevates mAP@0.5 to 82.2% and boosts mAP@0.5:0.9 by 3.3%. The confluence of ODConv and CARAFE has enhanced the model’s mAP@0.5 and mAP@0.5:0.9 by 1.5% and 1.7%, respectively. Ultimately, the synergistic integration of ODConv, C2f_cbam, and CARAFE propelled the model to attain an optimal mAP@0.5 of 86.2% and a notable increase to 56% at mAP@0.5:0.9. While this combination marginally escalated the computational complexity (GFLOPs increased to 29.5), it culminated in a substantial enhancement of the F1 score to 89. This equilibrium effectively enhances the model’s overall performance while maintaining processing efficiency.

The Precision-Recall (P-R) curve has been employed to evaluate model efficacy, allowing for a more accurate assessment of the YOLOv8s algorithm and its enhanced variant’s performance. The abscissa of the P-R curve denotes the recall rate, its ordinate indicates the precision rate, and the area beneath the curve represents the category’s Average Precision (AP) value. A comparative analysis of the overall P-R curves for both algorithms is depicted in Fig. 11a. Furthermore, to visually ascertain the accuracy of both models, the mAP value of the BD-YOLOv8s model has been compared with that of the original model, as illustrated in Fig. 11b,c.

As evidenced in Fig. 12, the Precision-Recall (P-R) curve area of the BD-YOLOv8s algorithm is notably more extensive than that of YOLOv8s, demonstrating superior precision and recall rates in comparison to the YOLOv8s algorithm. Furthermore, the mAP@0.5 and mAP@0.5:0.95 metrics of the BD-YOLOv8s model are substantially higher than those of the original YOLOv8s model. This indicates enhanced feature extraction capabilities, making it more adept for tasks such as bridge defect detection.

Figure 12

(a) comparison of P-R curve; (b) comparison of mAP@0.5; (c) comparison of mAP@0.5:0.95.

Interpretability experiment

A thorough investigation into the interpretability of deep learning models is imperative for acquiring an intuitive grasp of their performance dynamics. The BD-YOLOv8s model and the standard YOLOv8s model were employed as verification models in this study, with their performance exhaustively assessed through meticulous analysis of their confusion matrices. The confusion matrices for both models are delineated in Fig. 13, facilitating a more lucid comparison of their performance.

Figure 13

Confusion matrix of the YOLOv8s model and BD-YOLOv8s model. (a) Confusion matrix of YOLOv8s; (b) Confusion matrix of BD-YOLOv8s.

The confusion matrix reveals that the BD-YOLOv8s model has enhanced the detection accuracy for the three structural defects—crack, corrosion, and spall—with an increment of 2%-4%. At elevated accuracy thresholds, this enhancement in precision underscores the efficacy of detailed model optimization.

To further ensure and demonstrate the model’s performance and reliability, Fig. 14 presents the loss conditions during the training and validation phases, including changes in box regression loss (box_loss), classification loss (cls_loss), and distribution focal loss (dfl_loss).

Figure 14

Convergence curves of different loss functions during training and validation.

The figure illustrates the convergence curves of different loss functions during the training and validation processes. It is evident that as the number of training epochs increases, the values of each loss function on the training and validation sets quickly decrease and then stabilize, indicating that the model’s performance on both training and validation data continuously improves during the learning process. Specifically, the loss curves during the training and validation phases exhibit consistent behavior, characterized by rapid initial declines followed by gradual stabilization. This demonstrates that the model’s optimization across various tasks is significant and that it possesses good generalization capabilities.

Self-built dataset performance experiment

A targeted performance test was executed using authentic bridge defect images to augment the validation of the BD-YOLOv8s model’s versatility. The images were captured at Northeast Forestry University, with the photography session conducted at 2:00 pm. The photograph was captured using a DJI M350RTK drone outfitted with an H20N camera, as depicted in Fig. 15. The camera settings were calibrated to an ISO speed of 100 and an aperture of f/2.8. The captured images had a resolution of 1280 × 960 pixels. A variety of sample images were collected to assess the model’s performance. The detailed test results are illustrated in Fig. 16.

Figure 15

DJI M350RTK.

Figure 16

(a–h) Detection results from self-collected data.

The detection outcomes depicted in Fig. 16 underscore the efficacy of the BD-YOLOv8s model in real-world scenarios, emphasizing its formidable generalization capacity and robustness. Nevertheless, occurrences of false detections are still present. As illustrated in Fig. 16a, the model erroneously classifies two distinct cracks as a single continuous entity owing to the high similarity between the crack’s color, surrounding environment, and its relatively small size. In Fig. 16e, when the model encountered dense defects of various sizes and shapes, it failed to detect the inconspicuous exposed rebar. In Fig. 16f, the model mistakenly identified the white edge of the concrete on the left as corrosion. In Fig. 16g, the model misidentified distant bushes as spalling. In Fig. 16h, the model failed to accurately detect the entire area of corrosion. These false detections and missed detections may be attributed to insufficient training samples, indicating that the model’s robustness needs further improvement when handling data with significant shape differences.

Comparison of performance of different models

This study’s enhanced network BD-YOLOv8s, along with other target detection algorithms like Faster RCNN, SSD, YOLOv5s, YOLOv4, YOLOv6s, YOLOv7-tiny, and YOLOv8s, were employed for training and testing in the defect identification task to thoroughly substantiate the advantages of the model developed in this study for bridge defect detection, maintaining the same dataset, as shown in Table 7.

Table 7 Comparison of different detection networks.

Table 7 indicates that Faster R-CNN has low accuracy (mAP@0.5 of 70.6%) and slow speed (8 FPS), making it unsuitable for real-time applications. SSD has the lowest accuracy (mAP@0.5 of 64.1%) despite its fast speed, failing to meet high-precision requirements. YOLOv4 has high accuracy (mAP@0.5 of 78.6%) but slow speed (28 FPS), making it inefficient. YOLOv5s is fast (108 FPS) and accurate but struggles with complex backgrounds. YOLOv6s performs well overall (mAP@0.5 of 80.4%) but is neither as fast nor as accurate as YOLOv5s. YOLOv7-tiny is the fastest but is less accurate and robust than YOLOv8s. YOLOv8s excels in both accuracy (mAP@0.5 of 80.9%) and speed (105 FPS), making it suitable for real-time use. BD-YOLOv8s, developed in this study, achieved an mAP@0.5 of 86.2% and an mAP@0.5:0.9 of 56%, surpassing traditional and other single-stage models, while maintaining similar parameters and computational complexity as YOLOv8s. This demonstrates its enhanced accuracy and efficiency for practical bridge defect detection.

Effectiveness of defect detection

As depicted in Fig. 17, panels (a, c, e, g, i, k, m, o, q) on the left and (b, d, f, h, j, l, n, p, r) on the right, respectively, illustrate the detection outcomes of the original YOLOv8s model and the enhanced BD-YOLOv8s model developed in this study. In Fig. 17a, the original model erroneously classifies black graffiti as a reinforcement leak attributable to background noise. Conversely, in Fig. 17b, the refined model circumvents this misdetection, demonstrating heightened accuracy. Figure 17c reveals that the original model cannot detect smaller leak-prone reinforcement targets under low-light conditions. Conversely, the enhanced model displayed in Fig. 17d exhibits precise detection of all pertinent pathologies. Figure 17e illustrates that the original model inaccurately delineates the corrosion’s edge area and fails to detect minor corrosion instances. In Fig. 17f, the BD-YOLOv8s model precisely identifies two distinct corrosion pathologies. Figure 17g demonstrates that the original model inaccurately interprets two adjacent cracks as a singular continuous crack. In contrast, Fig. 17h shows that the enhanced model accurately demarcates the two cracks' boundaries. Figure 17i illustrates that the original model misidentified black marks as cracks, whereas Fig. 17j demonstrates that the improved model accurately distinguishes between cracks and marks. In Fig. 17k, the complex background caused the original model to miss small cracks in the upper left corner, while Fig. 17l illustrates the improved model’s high accuracy in multi-scale crack detection. Figure 17m shows that under low-light conditions, the original model failed to fully detect cracks and missed detections where spalling and the concrete background were not clearly distinguished. In contrast, Fig. 17n demonstrates that the improved model can accurately detect all relevant defects. Figure 17o illustrates that in complex detection environments, the original model missed small target defects like exposed rebar. Figure 17p demonstrates that the improved model correctly detected the exposed rebar missed by the original model but still missed more subtle cracks in highly complex backgrounds. Figure 17q illustrates that the original model failed to comprehensively detect spalling and missed small cracks. Figure 17r demonstrates that the improved model effectively overcame these issues. In summary, the BD-YOLOv8s model, while sustaining comparable GFLOPs, achieved an increase in average accuracy mAP@0.5 by 5.3% and mAP@0.5:0.9 by 5.7%. This model effectively identifies a broader range of defects, with a reduced rate of false positives and missed detections, rendering it more suitable for superficial defect detection in concrete bridges.

Figure 17

Detect result of YOLOv8s and BD-YOLOv8s.

Conclusions and future research

To address the challenges of reduced accuracy, high false detection rates, and increased missed detections due to significant feature disparities and complex backgrounds in bridge defect detection, this study introduces BD-YOLOv8s, an advanced version of YOLOv8s. Incorporating ODConv enhances the model’s adaptability to bridge defect features, particularly in managing background noise and unusual defect shapes, thereby improving recognition precision. Adding CBAM to the initial two C2f. layers of YOLOv8s increases the model’s ability to identify small defects and enhances generalization in complex environments. Replacing traditional upsampling with CARAFE improves feature map reconstruction, significantly boosting precision in identifying fine defects and preserving edge details. The study demonstrates the feasibility and effectiveness of this approach through ablation studies, comparative analyses, and experiments. Results show that BD-YOLOv8s outperforms the baseline and other models in generalization and mean accuracy for bridge defect detection, achieving an mAP@0.5 of 86.2%, an mAP@0.5:0.9 of 56%, and an F1-Score of 89, demonstrating strong interpretability. Although BD-YOLOv8s excels, it still faces false detections in complex backgrounds and misses small defects. To further enhance the performance of the BD-YOLOv8s model in bridge defect detection, future research can consider the following directions: increasing data samples of small defects, using higher resolution images, and adopting multi-scale feature extraction techniques to improve detection accuracy; improving training strategies by collecting more data from different environments and diverse defect types to build larger datasets, while also exploring semi-supervised or unsupervised learning methods to enhance the model’s robustness and generalization capability; and introducing multi-modal data fusion techniques to provide a more comprehensive assessment of bridge health. These improvements will further enhance the performance of the BD-YOLOv8s model, making it more efficient, accurate, and reliable in practical bridge defect detection.