Introduction

As one of the most geologically hazardous regions in Xinjiang and one of the sixteen key geological disaster prevention areas in China, the Ili River Valley is well noted from its extensive loess distribution, mountainous landscape, and humid climate. It is essential to investigate the mechanisms behind loess landslides in this area1. The dust in the loess of the Ili River Valley primarily originates from the Central Asian desert to the west2, during which the abundant dust is carried eastward by near-surface westerly winds and accumulates to form the unique topography of the Ili River Valley3. The loess in the Ili area is distributed in a striped pattern, mainly found in low mountainous and hilly areas, mountain foothills, river terraces, and the edges of deserts4. The loess thickness varies from west to east with more development on the windward slopes than on the leeward slopes or wind gaps and the particle size of the loess gradually becomes finer5,6,7. Loess is a typical structural soil with significant water sensitivity characterized by properties such as wet subsidence, disintegration, and dissolution8. Most loess in this area belongs to the Late Pleistocene Malan Loess, which has coarser particles, a looser structure, and a higher porosity ratio compared to the loess of the Loess Plateau, resulting in greater wet subsidence9. These unique characteristics distinctly influence the disaster-forming mechanisms and modes of loess geological disasters in the Ili River Valley.

As a typical seasonal frozen area, the Ili River Valley experiences long-term freeze–thaw cycles (FTCs) that significantly weaken soil strength, leading to various geological hazards (e.g., the landslides and avalanches). Research in frozen soil mechanics is broadly divided into two categories: the impact of freeze–thaw actions (the freezing and swelling, thawing, and their effects on soil's physical and mechanical properties) and the mechanical properties of frozen soil (including strength, stress–strain relationships, and dynamic characteristics)10. This paper specifically examines the influence of FTCs on the physical and mechanical properties of the loess. For example, Zhao et al. conducted a series of unconsolidated-undrained triaxial compression tests on the Malan loess from Jing’yang, China after FTCs. They observed that the cohesive force initially decreased and then increased, while the internal friction angle initially increased and then gradually decreased11. Similarly, Xu et al. performed direct shear tests on both original and remodeled loess form Xi’an, China and found that the cohesive force diminished with FTCs. Notably, the cohesive force stabilizes around a constant value after five cycles, while the internal friction angle changes only within a limited range12. However, Liu et al. investigated the loess collected from the silt zone of the Loess Plateau and found that the cohesion of the loess decreases with FTCs, but the internal friction angle increases13. Han et al. investigated the saline soils obtained from the western Jilin, which suggested the steady decline in both shear strength and cohesive force under consolidated undrained triaxial compression tests as the number of FTCs increased14. Most studies have determined that the cohesion of soil will decrease after FTCs, while the internal friction angle will increase, decrease or change little15. These differences are mainly attributed to soil type, initial conditions, and variations in testing procedures16. The mechanism of soil shear strength characteristics influenced by FTCs is not fully understood and it is thus crucial to comprehend the variations in soil mechanical strength for engineering construction in areas with seasonal frozen soil.

Modern geomechanics has further expanded the foundational work pioneered by Coulomb and Mohr 17, apart from the consideration of the cohesive force and the internal friction angle, a comprehensive approach termed "Geomechanics from Micro to Macro" was consequently proposed. This approach begins with an examination of micro (particle) properties and aims to explore the complex macroscopic properties of geotechnical materials by understanding their fundamental mechanisms, for which the cross-scale correlation between macro and micro properties and advocates for multi-scale analysis methods were established18. Note that the Macro–micro geomechanics primarily focuses on analyzing soil microstructure, conducting research on soil microstructure, interparticle contact response, and particle fragmentation, which deepens the understanding of the macroscopic characteristics of the soil mass. The application of modern testing methods including the scanning electron microscopy (SEM), the X-ray computed tomography (CT), the nuclear magnetic resonance (NMR), the X-ray diffraction (XRD), the energy spectral analysis (EDS), the mercury intrusion porosimeter (MIP), and the nitrogen adsorption19 promote the development of the theory. Notably, SEM allows for the direct observation of particle and pore morphology on specimen surfaces, providing convenient and rapid analysis. The NMR technology is particularly useful in permafrost, hydrated soils, and unsaturated soils. The effective combination of these techniques helps to achieve multi-scale evaluation of soil structure characteristics13,20. Hu suggested that structural elements can be described using nine types of structural parameters: the particle size (diameter and distribution), the particle shape (flatness and roundness), the particle surface undulation, the particle orientation, the particle distribution, the pore size (pore size and relative pore size), the pore distribution, the contact zone morphology (distribution), as well as the interparticle linkage (connectivity), which set up a solid foundation for the quantitative analysis of microstructures21.

The primary methods used to analyze the correlation between physical, mechanical, and microstructural parameters of soil include the cluster analysis, the principal component analysis, the factor analysis, the regression analysis, and the gray correlation analysis22. Considering that each method has its own application conditions and limitations, selecting an appropriate analytical method should be based on the specific research objectives and the nature of the subject matter. The Gray correlation analysis is applicable and convenient, suitable for various sample sizes and types and the widespread applicability of which has led to its increasing application in permafrost research in recent years23,24,25. However, most scholars relied on a single analytical method and the correlation among various factors were generally overlooked26. Because that these correlations can significantly impact the engineering properties in practical applications27, ignoring these interrelationships can lead to multiple covariance, potentially causing substantial errors in the results. Both the integrating cluster analysis and the factor analysis can preserve the information from the original factors and mitigate the effects of multiple covariances28 and the integration will reduce unexpected errors and enhance the accuracy of the analysis results29,30.

The research methods employed by scholars worldwide to explore the macroscopic properties of soil are well-developed. Similarly, microscopic testing techniques for soil can support current research objectives, and numerous analytical methods exist to explore the macro–micro correlations in soil. However, studies on the effects of FTCs on soil microstructure and its correlation with shear behavior are more abundant in the Loess Plateau region of China rather than that in the Ili Valley. Further research to quantitatively analyze the microstructural characteristics of soil and uncover the mechanisms behind loess shear strength degradation at the microstructural level are requested to fill up this research gap31. When analyzing soil microstructures using scanning electron microscopy (SEM), binarization is crucial for the quantitative analysis of SEM images32. However, researchers often overlook factors that can interfere with SEM image acquisition, leading to potential errors in subsequent analyses33,34. The concept of pre-processing and optimizing images before binarization is not yet widely popularized31,32,33,34. Additionally, in analyzing macro–micro correlations of soil, most researchers tend to focus on the influence of a single micro-variable on the macro-properties. In practical engineering scenarios, however, it is common for multiple micro-variables to interactively affect the soil's engineering properties. When examining the correlation between multiple micro-variables and macroscopic parameters, relying solely on one analytical method can be limiting. Using two or more analytical methods to avoid their respective limitations could lead to a more effective and comprehensive analysis26,27,28,29,30.

This study aims to investigate the mechanism of shear strength deterioration of the loess under FTCs at the microscale. The natural loess from the Ili River Valley is selected to explore its mechanical response subjected to various numbers of FTCs (i.e., 0, 5, 10, 20, 30, 45, and 60 cycles). Images of the loess are captured through the scanning electron microscopy (SEM), which are then pre-processed for optimized imaging and binarization to facilitate quantitative analysis. Additionally, the research also employs nuclear magnetic resonance (NMR) was applied to obtain the porosity and pore size distribution of the specimens. To further analyze the macro–micro correlations, the gray correlation analysis is utilized for individual microstructural parameters and the cluster-principal component analysis for sets of microstructural parameters in relation to macroscopic mechanical was also carried out. The anticipated outcomes of this research will not only provide a theoretical foundation for understanding strength degradation mechanisms due to FTCs from a microstructural perspective, but also enhance the comprehension of the engineering disaster associated with the strength degradation of loess slopes in the Ili region suffering from FTCs.

Materials and methods

Basic physical tests

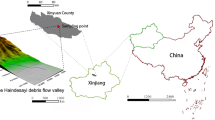
The sampling site for this study is located in Xinyuan County, Ili Region, Xinjiang, China (Fig. 1). Several tests were conducted to determine the basic physical properties of the soils (ie., the density, the moisture content, the bound moisture content, the particle size analysis), the value of which are presented in Table 1 for reference. The results of the particle analysis test (No.1, No.2, and No.3) by densimeter method and the compaction curves by compaction method were depicted in Figs. 2 and 3, respectively. The test results indiated that the sand content in the loess of Ili area is 32–39.5%, the silt content is 45–49%, and the clay content is 15–19%. According to the Unified Soil Classification System (USCS), the loess was low liquid limit clay (CL).

Figure 1
figure 1

A Schematic representation of the sampling location.

Full size image
Table 1 Basic physical properties of the natural loess.
Full size table
Figure 2
figure 2

Particle size distribution curve of loess in the study area.

Full size image
Figure 3
figure 3

Compaction curve of loess in the study area.

Full size image

Sample preparation

In order to avoid the interference of the difference between the initial damage of the sample on the test, the remolded loess sample was as the test object in the present research. Initially, blocks of disturbed soil are air-dried, and the soil is then crushed using a wooden mill and passed through a 2 mm sieve. Herein, wet soil is prepared at a moisture content of 17.4% via the spraying method and then stored in a shaded area for moistening over 24 h. The remodeled samples are compacted to achieve a maximum dry density of 1.86 g/cm3 and the diameter of the cylinder sample prepared for the triaxial compression test is 39.1 mm with a height of 80 mm. The diameter and height of the cylinder sample for the scanning electron microscopy test and the Nuclear magnetic resonance test are 50 mm 20 mm, respectively. These prepared loess samples are then located in the test chamber with constant temperature and humidity before the freeze–thaw tests. Because that there is no recognized standard for the temperature and duration of a single freeze–thaw cycle, the freezing temperature is set to −20 ℃ for 15 h and the thawing temperature to 15 ℃ for 9 h upon the previous statistical data24. In this case, the duration of the single freeze–thaw cycle is 24 h and the number of FTCs varied from 0 to 60 times.

Triaxial compression test of unsaturated soil in laboratory

The TFB-1 type stress–strain controlled triaxial apparatus designed for unsaturated soils was applied for the triaxail compression tests. Each group of tests consists of three samples, totaling seven groups of tests and 21 samples of triaxial compression tests. According to the Standard for geotechnical testing method and the Standard for unsaturated soil test method35,36, the consolidated-consolidated (CU) to determine the effective stress intensity parameters, which are crucial for analyzing the long-term stability of slope. The condition of consolidation termination is that the consolidation time is ≥ 72 h, and within 2 h, the volume variable does not exceed 6 mm3 and the displacement is ≤ 12 mm3. According to previous research results37, the net confining pressures for the test are set at 100, 200, and 300 kPa. The pore gas pressure is applied to the soil sample, and the pore water pressure is 0. At this time, the matrix suction of the soil sample is the applied pore gas pressure, and the matric suction was uniformly controlled at 80 kPa. After the consolidation, the sample was sheared with the constant loading speed of 0.1% per minute. During the shearing process, the peak point of the deviatoric stress on the stress–strain curve is taken as the failure point. If there is no peak, the deviatoric stress at 15% axial strain will be taken as the failure point. Note that the intensity index in this study was the effective stress.

Scanning electron microscopy test

An electron microscope scanner (No. German Zeiss Sigma300 field emission scanning electron microscope) is used for the scanning electron microscopy (SEM) test. This instrument utilizes secondary electron signal imaging to observe the surface morphology of the samples. Each group of tests consists of two samples, totaling seven groups of tests and 14 samples of scanning electron microscopy tests. First of all, the samples were polished into thin sheets and fixed on the electron microscope platform with conductive adhesive, and the surface soil was blown off and vacuumed. Then spray gold. This completes the preparation work before the test and specific areas of the microscopic specimens are then selected for scanning, where there are signs of freezing and thawing, such as particle cracking and agglomeration. During the scanning electron microscope test, the magnification should be determined according to the research purpose and the research object. For the soil with loose structure and large average particle size, a relatively small magnification should be selected. For the soil with dense structure, the magnification can be increased appropriately. In general, the larger the magnification, the more local and one-sided the information obtained38. It is necessary to coordinate the ratio between the magnification and the image quality. Considering the quality of the picture and the research object, the SEM image with a magnification of 800 times clearly reflecting the image of the research object is thus selected for processing and analysis. The image processing process is shown in Fig. 4.

Figure 4
figure 4

A Schematic representation of the workflow for SEM image preprocessing and binarization.

Full size image

At first, the SEM images obtained are pre-processed by Matlab software. Preprocessing is a fundamental aspect of image processing, particularly for soil SEM images. Due to variations in SEM equipment, the scanning quality can differ, each with its strengths and weaknesses. For instance, prolonged use of SEM can lead to filament displacement, causing uneven image brightness. Additionally, factors like unstable voltage and mechanical vibrations during scanning can introduce excessive noise and other issues. Upon examining numerous original soil SEM images, the most common problems are uneven image brightness, low contrast, and excessive noise. These issues can significantly affect subsequent quantitative analysis, leading to considerable errors. Image preprocessing aims to mitigate the impacts of these problems. This process involves three primary steps: removing uneven backgrounds, adjusting image contrast, and reducing noise.

Then, the preprocessed images are binarized by Matlab software. Image binarization involves converting the pixels of an original grayscale image to just two intensity values, 0 and 1, resulting in a black-and-white composition. In this binary format, 0 represents the black background, typically the pore regions, while 1 represents the white target particle areas. A crucial aspect of image analysis is selecting an appropriate threshold value. An incorrectly chosen threshold, either too high or too low, can distort the particle contours in the binarized image. Accurately selecting a threshold value to cover the particle region precisely can improve the precision of subsequent geometric parameter statistics based on the binary image. This study uses a manual intervention method—real-time observation and parameter adjustment—to set the threshold values manually. The optimal threshold, determined through visual inspection, provides the best coverage of the particles and is used for final image segmentation. In this study, the original dimensions of the SEM images are 1536 pixels in length and 2048 pixels in width. And thresholds are selected within the range of 80 to 128.

Finally, the small spots on the image are eliminated by the Matlab software, which is due to the different gray levels on the soil particles. The threshold is only one, which will identify the part of the soil particles that does not belong to the pore as the pore. If the small spots are not eliminated, it will cause large errors if they are calculated in quantitative statistics. Therefore, it is particularly important to eliminate these small white areas by means of morphological operations. The bwareaopen function is called in the Matlab soft armor, and the upper limit area X on the small target area is set to eliminate, so that any independent area less than the area X in the image is eliminated. Through repeated debugging, the value of X in this study was 120.

Nuclear magnetic resonance test

The pore radius distribution of the samples is determined via the application of a MesoMR23-60H-I medium-size NMR image analyzer. There are 14 samples prepared for the nuclear magnetic resonance tests and in each group there are two identical samples. The specimens required for NMR were compacted with correspondingly sized polyvinyl chloride (PVC) sleeves. Moreover, the sample sputtering time is 24h. This is achieved by converting the T2 spectra, obtainable through NMR testing39. It is known that three different relaxation mechanisms affect the fluid in the pores. However, surface relaxation is the dominant mechanism over free and diffused relaxation when the pore contains only water. Therefore, T2 is directly proportional to the pore radius. The relationship between a pore’s specific surface area and its radius can be expressed as S/V = FS/r. The equation for T2 is given as follows (Eq. 1):

$$\frac{{1}}{{T_{2} }} = \frac{1}{{T_{{2{\text{free}}}} }} + \frac{1}{{T_{{2{\text{surface}}}} }} + \frac{1}{{T_{{2{\text{diffusion}}}} }} \approx \frac{1}{{T_{{{\text{2surface}}}} }} = \rho_{{2}} \left( \frac{S}{V} \right)_{{{\text{proe}}}} = \rho_{2} \frac{{F_{{\text{s}}} }}{r}$$
(1)

where, T2 represents the transverse relaxation time of pore fluid measured by the CPMG sequence in NMR testing; T2surface represents the transverse relaxation time of fluids in sufficiently large containers (where container effects are negligible); T2free represents the transverse relaxation time induced by free relaxation; T2diffusion represents the transverse relaxation time due to diffusion under a magnetic gradient; \({\rho}_{2}\) represents the surface relaxation rate, measured in \({\mu m}/{ms}\); \({S}/{V}\) represents the specific surface area of the pores; \({{F}}_{{s}}\) represents the shape factor of the pores, a dimensionless quantity that varies with the pore model; and r represents the pore radius, in \({\mu m}\).

Both \({\rho}_{2}\) and \({{F}}_{{s}}\) are assumed constant for rock and soil, leading to the simplification \(\frac{1}{{\rho}_{2}{{{F}}}_{{s}}}= {C}\), then Eq. 1 can be expressed as: T2 = C × r. After obtaining the fixed value C, the T2 spectrum can be converted into a pore radius distribution map. This study focuses on the corresponding relationship between the main distribution of T2 spectrum and the main distribution of mercury pore throat radius. According to the difference between the distribution frequency of mercury pore throat radius and the distribution frequency of T2 spectrum, the weight is added in the calculation process of fitting error. The frequency distribution of T2 spectrum can reflect the proportion of pores of different sizes in the core. Therefore, this paper selects the frequency distribution of T2 spectrum as the weight \(\omega ({x}_{i})\) when calculating the error \(\delta\), and realizes the good correspondence between the main distribution of T2 spectrum and the main distribution of mercury injection pore throat radius. The fitting error calculation formula is as follows (Eq. 2):

$$\delta =\frac{\sqrt{\sum_{2}^{{n}}\omega ({x}_{i}){\left[{x}_{i}-\omega {x}_{i}\right]}^{2}}}{\sqrt{\sum_{2}^{{n}}\omega ({x}_{i})}}$$
(2)

where, \(\delta\) is the error, unit is μm; \({x}_{i}\) is mercury intrusion pore throat radius, unit is μm; \(\omega ({x}_{i})\) is the weight, dimensionless; \(\omega {x}_{i}\) is the pore radius obtained by the conversion of T2 spectrum under a certain C value, and the unit is μm; n is the number of pore throat radius distribution.

Figure 5 is the error curve after fitting, and the minimum error is the best conversion coefficient C, so the value of C is determined to be 2.5 \({ms}/{\mu m}\). Post-conversion, the T2 spectra closely match the MIP-measured pore throat radius distribution curves, displaying similar variation tendencies (Fig. 6). The relationship between the T2 spectra of the loess samples studied and their pore radius distributions is outlined in Eq. (3).

$${{r}} = \frac{{T_{2} }}{C} = \frac{{T_{2} }}{2.5} = 0.4T_{2}$$
(3)
Figure 5
figure 5

The curve of error fitting.

Full size image
Figure 6
figure 6

T2 spectra of loess samples and the pore radius distribution before and after conversion.

Full size image

The experimental flow of this study is presented in Fig. 7, including sample preparation, Laboratory triaxial compression test of unsaturated soil, Scanning electron microscopy test, and Nuclear magnetic resonance test.

Figure 7
figure 7

Diagram of the trial flow. (a) Sample preparation, (b) FTCs test, (c) Triaxial compression test of unsaturated soil in laboratory, (d) Scanning electron microscopy test, (e) Nuclear magnetic resonance test.

Full size image

Test results and analysis

Changes in the stress–strain curve of loess

The indoor triaxial compression test of unsaturated soil was carried out on the remolded loess after different FTCs, and the stress–strain relationship curve of the which are shown in Fig. 8. Most of them are strain hardening curves, and a few are strain softening curves. Only when σ3 = 200 kPa, the number of FTCs is 45 and 60 times, and σ3 = 300 kPa, the number of FTCs is 45 and 60 times, the stress–strain curve has a peak value, which is a softening stress–strain curve, and the rest is a hardening stress–strain curve.

Figure 8
figure 8

Stress–strain curves of loess under different FTCs. (a) σ3 = 100 kPa, (b) σ3 = 200 kPa, (c) σ3 = 300 kPa.

Full size image

Changes in the macroscopic mechanical strength of loess

Three Mohr circles are drawn by using the effective stress corresponding to the peak value of the softening stress–strain curve and the effective stress corresponding to the strain of 15% in the hardening stress–strain curve, and a straight line tangent to these three Mohr circles is obtained. The angle between this straight line and the Y axis is the internal friction angle, and the intercept with the X axis is the cohesive force. The cohesive force and internal friction angle of each soil sample are shown in Fig. 9. As the number of FTCs increases, the cohesive force of loess initially decreases, then increases and eventually stabilizes. Conversely, the internal friction angle generally increases initially, then decreases, and finally stabilizes. Specifically, during the first 0–10 FTCs, there is an obvious reduction in cohesive force, while the internal friction angle tends to increase. After 10 FTCs, the cohesive force of the soil samples begins to increase slowly, and the internal friction angle decreases tardily. At this time, the effect of FTCs on loess samples has gradually weakened. Therefore, the soil mechanical indexes after 10 FTCs can be used as reference values for engineering design in the seasonal frozen soil area of Ili River Valley.

Figure 9
figure 9

The variation of shear strength parameters of loess under different FTCs.

Full size image

Microstructure change of loess based on SEM

These 14 pre-processed, binarized and eliminated small spots images are imported into Image-Pro Plus software for quantitative analysis of the microscopic particle structure parameters in this research, to evaluate eight specific microstructural parameters listed in Table 2. The images are uploaded into Image-Pro Plus software for particle and pore identification. Subsequent measurements and calculations are performed to determine the precise values of these microstructural parameters.

Table 2 Definition and Structural Significance of Microstructural Parameter Images.
Full size table

According to the research statistics on loess in the Ili Basin by Li et al., the loess particles in this paper are classified into five categories based on size: clayey grains (< 5 µm), fine silt (5–10 µm), medium silt (16–32 µm), coarse silt (32–63 µm), and sandy grains (> 63 µm)40. The percentage of different particle sizes in various ranges is calculated using this classification, as shown in Fig. 10a. With an increasing number of FTCs, it is evident that the proportion of clay particles initially increases and then decreases, while the proportion of fine silt particles shows the opposite trend. The variation in the average particle size fractal dimension of loess is displayed in Fig. 10b. This dimension gradually increases, then fluctuates, and eventually stabilizes, indicating a slight overall increase. This suggests an increased complexity in loess particle morphology. The average abundance of loess particles is presented in Fig. 10c. Under non-freezing conditions, the average abundance is about 0.7, indicating a predominance of nearly rounded particles with fewer elongated particles. However, the average roundness decreases after the freeze–thaw action, suggesting a reduction in nearly equiaxed particles and an ongoing process of particle decomposition and aggregation during the FTCs. Figure 10d illustrates the changes in the orientation probability of loess particles. The entropy of orientation probability fluctuates with increasing FTCs, suggesting a weakening in orientation and a trend toward more disordered arrangement dimension, maximum pore size, pore size fractal dimension, porosity, and pore orientation fractal dimension.

Figure 10
figure 10

Quantitative analysis diagram of particle microstructure parameters: (a) average maximum particle size; (b) average particle size fractal dimension; (c) particle abundance; (d) average particle orientation probability entropy.

Full size image

The distribution of average maximum pore sizes in loess samples is shown in Fig. 11a. Initially, the average maximum pore diameter decreases, then increases, but ultimately shows an overall decreasing trend. This change is attributed to the decomposition and agglomeration of loess particles during FTCs. Decomposed soil particles fill the pores, reducing the maximum pore radius, although a subsequent increase in maximum pore diameter is observed. Figure 11b depicts the fluctuation in the fractal dimension of the average pore size. As the number of FTCs increases, the fractal dimension first rises then fall and rises again before ultimately declining. This pattern indicates a shift in pore morphology, which overall tended to simplify. As presented in Fig. 11c, the variation in the porosity of the loess samples shows an increase in the interstitial surface area as the number of FTCs grows. Lastly, it can be seen in Fig. 11d that the average pore orientation fractal dimension initially increases and then decreases with an increasing number of FTCs.

Figure 11
figure 11

Quantitative analysis diagram of pore microstructure parameters: (a) average maximum pore size; (b) average pore size fractal dimension; (c) porosity; (d) average pore orientation probability entropy.

Full size image

Microstructural changes in loess based on NMR

Figure 12 presents the T2 spectra distribution post-saturation. The loess sample's T2 spectra exhibit two peaks under varying FTCs (FTCs). The relaxation time for the first peak ranges from 0.1 to 10 ms. With an increasing number of FTCs, the peak height and NMR signal amplitude both rise and the T2 spectra shift rightward, indicating an increase in pore size after FTCs. The T2 spectra from NMR can be converted into pore radius values using Eq. (3). Following the classification by Lei et al.41, the pore radius was categorized into four types: micro-pores (< 1 µm), tiny pores (1–4 µm), medium pores (4–16 µm), and large pores (> 16 µm). The size distribution patterns of these pore types are illustrated in Fig. 13. With an increasing number of FTCs, the proportion of micro-pores decreases while the shares of tiny- and medium-pores increase. Conversely, the proportion of large pores first decreases, then increases, and ultimately stabilizes.

Figure 12
figure 12

T2 spectra from NMR under varying FTCs.

Full size image
Figure 13
figure 13

Pore distribution map of loess under different FTCs.

Full size image

Macro–micro correlation based on grey relational analysis method

The Grey Relational Analysis (GRA) method evaluates the relationship between factors in two systems, requiring the identification of these systems. The reference series, \({{X}}_{0}\) = {\({{x}}_{0}\) (1), \({{x}}_{0}\) (2), …, \({{x}}_{0}\) (n)}, represents the data series reflecting the behavior of the system. The comparative series, \({{X}}_{{i}}\) = {\({{x}}_{{i}}\) (1), \({{x}}_{{i}}\) (2), …, \({{x}}_{{i}}\) (n)} (\(i\)=1,2,…,m), consists of factors influencing the behavior of system. This method involves four main steps: identifying the analytical series, making variables dimensionless, calculating the correlation coefficients, and determining the correlation degree. The Grey Correlation Analysis classifies factors as strongly correlated if the grey correlation coefficient (\({\gamma }_{{i}}\)) is greater than or equal to 0.6; correlations are considered weak when \({\gamma }_{{i}}\) is less than 0.6. In this study, the reference sequence is the shear strength parameter of loess, and the comparative series comprises microstructural parameters obtained from SEM and NMR. The macro-microstructural parameters under various FTCs are presented in Table 3. The grey correlation between each microstructural parameter and the shear strength parameter are then calculated, with the results displayed in Table 4.

Table 3 Macro-microstructural parameters under various FTCs.
Full size table
Table 4 Correlation degree between shear strength parameters and microstructural parameters of loess under various FTCs.
Full size table

Table 4 reveals that under various freeze–thaw cycle conditions, the correlation between selected micro-parameters and the cohesive force of loess is ranked as follows (in descending order): particle abundance > particle size fractal dimension > particle orientation fractal dimension > porosity > average maximum pore size > average maximum particle size > pore size fractal dimension > pore orientation fractal dimension > T2 spectral area. Among these, the parameters of average maximum particle size, particle size fractal dimension, particle abundance, particle orientation fractal dimension, average maximum pore size, and porosity all have correlations greater than 0.6, indicating a strong influence on the cohesive force of the soil samples.

Similarly, the correlations between micro-parameters and the internal friction angle of loess are ranked as follows: particle abundance > particle orientation fractal dimension > average maximum particle size > pore orientation fractal dimension > average maximum pore size > pore size fractal dimension > porosity > particle size fractal dimension > T2 spectral area. Among these, particle abundance, particle orientation fractal dimension, average maximum particle size, and pore orientation fractal dimension all have correlations greater than 0.6 with the internal friction angle of loess, suggesting a strong relationship and their significant impact on the internal friction angle.

Macro–micro correlation based on cluster and principal component analysis

Cluster and principal component analysis

This paper employs factor analysis using independent variables: average maximum particle size (\({{X}}_{1}\)), particle size fractal dimension (\({{X}}_{2}\)), particle abundance (\({{X}}_{3}\)), particle orientation fractal dimension (\({{X}}_{4}\)), average maximum pore size (\({{X}}_{5}\)), pore size fractal dimension (\({{X}}_{6}\)), porosity (\({{X}}_{7}\)), pore orientation fractal dimension (\({{X}}_{8}\)), and T2 spectral area (\({{X}}_{9}\)). The dependent variables are the shear strength parameters including cohesive force (\({{Y}}_{1}\)) and the internal friction angle(\({{Y}}_{2}\)).

After standardizing the independent and dependent variables, clustering is performed, resulting in three groups as shown in Fig. 14a: Cluster 1–1 (\({{X}}_{2}\), \({{X}}_{3}\), \({{X}}_{6}\), \({{X}}_{8}\)), Cluster 1–2 (\({{X}}_{1}\)), and Cluster 1–3 (\({{X}}_{4}\), \({{X}}_{5}\), \({{X}}_{7}\), \({{X}}_{9}\)). Clusters 1–1 and 1–3, with more than one factor, undergo principal component analysis to extract principal components representing each subclass's microstructural parameters. The Kaiser–Meyer–Olkin (KMO) values for both clusters are above 0.5, and the significance probability (Sig) values are below 0.05, indicating their suitability for principal component analysis. In Cluster 1–1, one principal component (F1-1–1) is extracted with an eigenvalue of 3.33 and accounted for 83.30% of the variance. In Cluster 1–3, two principal components (F1-3–1, F1-3–2) are extracted with eigenvalues of 2.87 and 1.08, respectively, explaining 98.93% of the variance. These principal components, F, account for over 80% of their respective original independent variables X, signifying that they effectively represent their respective factor classes. The principal component analysis scree plots for Clusters 1–1 and 1–3 are shown in Fig. 14b,c. These plots visualize the number of common factors extracted. Cluster 1–2 shows a gradual decline in eigenvalues with an inflection point after the first principal component, while Cluster 1–3 exhibits a similar pattern but after the second principal component. This proves that the extracted principal components adequately capture the information of the original independent variables.

Figure 14
figure 14

Cluster analysis pedigree diagram of microstructure parameters and principal component analysis gravel diagram. (a) Dendrogram of microstructural parameter cluster analysis; (b) Principal component analysis scree plots for Clusters 1-1; (c) Principal component analysis scree plots for Clusters 1-3.

Full size image

The component matrices for F1-1-1, F1-3-1, and F1-3-2 under various FTCs are computed using IBM SPSS Statistics V26.0 software (https://www.ibm.com/software) and presented in Table 5. Analysis of the table reveals that principal component F1-1-1 effectively encompasses information regarding \({{X}}_{4}\) (particle orientation fractal dimension), \({{X}}_{7}\) (porosity), \({{X}}_{2}\) (particle size fractal dimension), and \({{X}}_{9}\) (T2 spectral area). Principal component F1-3-1 provides comprehensive coverage of particle abundance, pore orientation fractal dimension, and pore size fractal dimension. Meanwhile, F1-3-2 primarily covers the average maximum pore size.

Table 5 Component matrices.
Full size table

The scores for these principal components can be calculated using Eqs. (4) and (5), with the results detailed in Table 6.

Table 6 Scores of principal components.
Full size table
$${{F}}_{\mathrm{n}}={{w}}_{1{\mathrm{j}}}{{{X}}}_{1}{+}{{w}}_{2{\mathrm{j}}}{{\mathrm{X}}}_{2} + {\ldots} + {{w}}_{\mathrm{ij}}{{{X}}}_{\mathrm{i}}$$
(4)
$${{w}}_{{ij}}{=}\frac{{ \theta }_{{j}}}{\sqrt{{ \lambda }_{{i}}}}$$
(5)

In the equation, n represents the serial number 1-1-1, 1-3-1, 1-3-2; \({ \theta }_{{j}}\) represents the coefficient in the component matrix table; \({ \lambda }_{{i}}\) is the cumulative value of the eigenvalues.

Standardized regression coefficient analysis

The standardized regression coefficients for different numbers of FTCs are shown in Table 7. A negative correlation occurs when R2 is less than 0, a positive correlation when R2 is greater than 0, and a strong positive correlation when R2 exceeds 0.8. As Table 8 shows, the average maximum particle size(\({{X}}_{1}\)) of the three principal components F1-1-1, F1-3-1, and F1-3-2 demonstrate a strong positive correlation with both loess cohesive force and internal friction angle under varying FTCs. The correlation coefficients (R2) are 0.855 and 0.942, respectively. Using SPSS software, standardized linear regression calculations are performed on the three principal components F1-1-1, F1-3-1, F1-3-2, and average maximum particle size(\({{X}}_{1}\)) extracted under different freeze–thaw cycle conditions. These components were analyzed in relation to the cohesive force and internal friction angle of loess, with the results presented in Table 9. A comparison of the standardized coefficients reveals that under varying FTCs, the strongest correlation with cohesive force is found with F1-3-2 (which includes the average maximum particle size of \({{X}}_{5}\) and the particle size fractal dimension of \({{X}}_{6}\)). For the internal friction angle, the strongest correlation is with the average maximum particle size of \({{X}}_{1}\). Consequently, standard regression equations are established for the relationship between cohesive force and the average maximum particle size(\({{X}}_{1}\)) and F1-1-1, F1-3-1, F1-3-2 under different FTCs are represented by Eq. (6). Similarly, standard regression equations for the relationship between the internal friction angle and the average maximum particle size(\({{X}}_{1}\)) and F1-1-1, F1-3-1, F1-3-2 are presented in Eq. (7).

$$y_{1} = {5}.{{278e}}^{{ - {17}}} - 0.{876}F_{1 - 1 - 1} - 0.{789}F_{1 - 3 - 1} + 0.{675}F_{1 - 3 - 2} - 0.{249}X_{1}$$
(6)
$${{y}}_{{2}} = - {7}.{{469e}}^{{ - {17}}} - 0.{161}F_{1 - 1 - 1} + 0.0{43}F_{1 - 3 - 1} - 0.{587}F_{1 - 3 - 2} + 0.{399}X_{1}$$
(7)
Table 7 Standardized regression coefficients for different numbers of FTCs.
Full size table
Table 8 Correlation of standardized regression coefficients.
Full size table
Table 9 Results of standardized regression calculations under various FTCs.
Full size table

In the equation, F1-1-1 represents the common factor encompassing particle orientation fractal dimension, porosity, particle size fractal dimension, and T2 spectral area; F1-3-1 represents the common factor for particle abundance, pore orientation fractal dimension, and pore size fractal dimension. F1-3-2 represents the common factor for average maximum pore size and pore size fractal dimension. \({{X}}_{1}\) refers to the average maximum particle size.

Discussions

The FTCs significantly impact the mechanical strength and microstructure of loess, particularly affecting interparticle cementation and cohesive force, which has a crucial impact on the susceptibility and hazard of loess landslides in seasonal frozen zones42,43. Researching the deterioration mechanism of loess strength is essential for comprehending disaster support mechanisms in cold regions and provides a theoretical foundation for disaster prevention and management. This paper aims to explore the deterioration mechanism of loess shear strength in the Ili River Valley under FTCs at the micro-scale and to analyze the correlation between both single and multiple microstructural parameters with mechanical strength parameters.

The change mechanism of macroscopic mechanical strength of loess under FTCs

The results of this study are same as the loess in Jing'yang, China, where the cohesion gradually decreases and then stabilizes with an increase in the number of FTCs, and The internal friction angle increases first and then decreases gradually11. And The test results were similar to the loess found in Xi'an, China12. However, the results of this study are different from Malan loess in Yan'an, China, where the cohesive force and internal friction angle of loess shows an overall downward trend with the increase of FTCs13. The reason for the analysis is that the loess from the Ili River Valley, Jingyang and Xi 'an belong to clay soil, and the clay content of which is high. However, the loess in Yan 'an is a typical silty loess belt from the Loess Plateau. At the beginning of FTCs, the soil particles of the two loesses were cracked into small particles, the initial contact between the soil particles was destroyed, the adhesion was reduced, and the internal friction angle was increased. However, in the later stage of FTCs, because of the high content of clay particles, small particles agglomerate into large particles, and the decrease of contact area leads to the decrease of internal friction angle. The loess with high silt content continues to crack under freeze–thaw action, and small particles cannot agglomerate into large particles. Liu et al.'s study confirmed this point. After 10 FTCs, the soil particles in the scanning electron microscope (SEM) image became loosely arranged, with predominantly point-to-point contact, an increased total number of pores, and observed initial structure degradation13. At present, most of the research results show that FTCs mainly acting on cohesion rather than internal friction angle11,12,13.

The change mechanism of microstructure of loess under FTCs

It is apparent from the SEM test that, with the increase of FTCs, the clay particles of loess in Ili area increased first and then decreased, and the fine powder particles showed a trend of decreasing first and then increasing. It shows that the soil particles are cracked at the beginning of FTCs, and then the small particles are condensed to form large particles. The corresponding NMR test results also confirmed this point: as the number of FTCs increases, the total number of pores increases, and the pore arrangement becomes complicated and gradually simple. This study reveals that as for the loess of Ili River Valley, FTCs cause small particles to agglomerate into larger, more complex ones, decrease equiaxial particles, and lead to disordered arrangements. Loess particles continuously cleave to fill pore spaces, thereby expanding them and simplifying pore morphology. The total number of pores increases, initially becoming complex but then simplifying. Micropores first decrease and then increase with FTCs, while small, medium, and large pores slightly increase. Overall, the microstructure of loess from Ili River Valley undergoes a process of stability-instability-stability.

Macro–micro correlation of loess under FTCs

Through the method of grey association analysis, the study finds a strong correlation between particle abundance and cohesive force under various freeze–thaw conditions. Particle abundance, indicating the roundness of particles, shows a trend of increasing and then decreasing with the FTCs, stabilizing after 10 cycles. Freeze–thaw fundamentally involves water's action (mainly free and weakly bonded water). Freezing expands water volume, causing soil particle cracks and reducing particle abundance, leading to looser structural cohesive force. Conversely, during thawing, the cohesive effect of water increases the roundness of particles and the specimen's density, thus enhancing cohesive force. Both cohesive force and particle abundance tend to stabilize as freeze–thaw effects diminish. The correlation between particle abundance, particle orientation fractal dimension, and the internal friction angle is found to be the strongest under varying FTCs. Particle orientation fractal dimension reflects particle arrangement, which first increases, then decreases, and finally fluctuates as the cycles increase. The particle abundance and internal friction angle display the same trend. Post-freezing, as particles cleave and become disordered, the value of particle orientation fractal dimension increases. This disordered arrangement leads to more contact points and surfaces, thereby increasing friction and the internal friction angle. This finding aligns with studies on Malan loess from Jing'yang, China, where changes in particle shape are found to significantly affect shear strength during FTCs, followed by particle arrangement and distribution11.

According to the cluster and principal component analysis, it can be seen that there is the strongest correlation between the cohesive force and the average maximum pore size as well as the pore size. This correlation suggests that pore size and arrangement significantly influence soil cohesive force; smaller particle spacing indicates a more compact soil structure and enhancing cohesive force, while larger spacing implies a looser structure and reducing cohesive force. The strongest correlation with the internal friction angle is the average maximum particle size, likely because the principal components represent micro-parameters with similar trends.

The results of macro and micro correlation analysis by the grey correlation analysis, clustering and principal component analysis were different, the reason is that the extracted principal components represent a class of microscopic parameters with the same or similar change trend, but there may be a certain offset between them. The grey correlation analysis method focuses on the analysis of the correlation between individual factors, which is suitable for data analysis with large uncertainty. The combination of clustering and principal component analysis pays more attention to data dimensionality reduction and extraction of main information, which helps to simplify the data set and identify patterns in the data. In practical applications, the principal component analysis method can be used to reduce the dimension of the data, extract the main information, and then combine the gray correlation analysis method to study the correlation between factors, so as to more fully understand the characteristics and laws of the data.

Degradation mechanism of macroscopic mechanical strength of loess from micro perspective under FTCs

The mechanical deterioration of loess is the repeated frost heaving force and migration potential caused by FTCs44,45. These two mechanisms result in alterations in the soil's microstructure, leading to changes in the soil's macroscopic mechanical strength. It is worth noting that the particle roundness has a strong correlation with the cohesion and internal friction angle of loess. The mechanism of mechanical strength deterioration of loess is the repeated frost heave force and migration potential caused by FTCs. During FTCs, the soil particles are continuously broken and then agglomerated, which is a cyclical process. Among them, the frost heave stress extrusion destroys the coupling effect between particles, resulting in the gradual peeling off of some unstable particles, the increase of the distance between particles, the increase of pore radius, and the disorder of pore arrangement. This is verified by the strongest correlation between cohesion and average maximum pore size and pore size fractal dimension in principal component analysis. Meanwhile, the migration of water caused by the migration potential scours the surface of the soil particles, the soil particles become smooth, and the particle roundness increases. In the later stage, the roundness of the soil particles decreases after the freeze–thaw action.The internal friction angle mainly represents the anti-slip and interlocking characteristics between soil particles13. The moisture migration caused by the temperature gradient causes the finer particles in the soil to penetrate into the larger pores, and the arrangement of the particles becomes disordered. The increase of the contact area increases the internal friction angle, and the freeze–thaw cycle action is weakened in the later period. In summary, the dialectical analysis of the potential relationship between macro and micro effects shows that soil macro-degradation is an external manifestation of cumulative internal microstructure fatigue. Therefore, irreversible internal microstructural damage is a potential mechanism of soil macro-degradation. The schematic diagram of the strength degradation mechanism of the Ili loess under FTCs is shown in Fig. 15.

Figure 15
figure 15

The schematic diagram of loess microstructure change under different FTCs.

Full size image

The research comprehensively analyzes the deterioration mechanism of loess shear strength in the Ili River Valley at a microscopic scale, investigating the correlation between both single and multiple microstructural parameters and mechanical strength parameters. In the later stage, the prevention and control of freeze–thaw loess landslide in Ili area can be realized by changing the microstructure parameters, which provides a new idea for the prevention and control of loess landslide disaster in Ili area. This study extends the range of FTCs to 0–60, compared to previous studies limited to 30 or fewer, confirming that the impact of FTCs diminishes with an increased number of cycles. The number of FTCs in this study was significantly more than that in most previous studies, and the algorithm used in this study to process SEM images is rarely used in previous studies. But the total number of test samples in this study was not enough, which was the defect of this study.

Conclusions

This paper thoroughly analyzes the deterioration mechanism of the Ili loess subjected to the freeze–thaw cycles (i.e., FTCs) and the correlations between single and multiple microstructural parameters and mechanical strength parameters were investigated. The key conclusions are summerized as follows:

  • The cohesive force of the loess suffering from the freeze–thaw cycles exhibits an initial decrease and increases before the eventually stabilizes, while the internal friction angle shows the opposite development tendency.

  • The FTCs results in small loess particles to agglomerate into larger size with complex shapes, associated with the disordered arrangement and changes in pore structure. The overall number of pores increases with a tendency towards a simpler structure after initial complexity.

  • There is a strongest correlation between particle abundance and cohesive force under different numbers of FTCs, with changes in particle abundance directly impacting cohesive force. Similarly, the particle abundance and orientation fractal dimension showed the strongest correlation with the internal friction angle.

  • The strongest correlation between cohesive force and both average maximum pore size and pore size fractal dimension under various FTCs were observed. Whereas, the internal friction angle is closely related to the average maximum particle size.

  • Both the repeated frost heaving force and the migration potential caused by FTCs accelerated the deterioration of the loess.