Introduction

Major military powers worldwide attach great importance to the research in the field of signal confrontation, with communication signal reconnaissance being a focal point. Detecting crucial communication information and deciphering and disrupting it provide significant information and battlefield advantages for the side that conducts reconnaissance1,2. Digital signal modulation recognition technology serves as a critical component in communication signal reconnaissance, acting as the foundation and basis for signal demodulation3,4. In recent years, modulation methods and communication channels have become increasingly complex, posing new challenges to digital signal modulation recognition technology5. Therefore, researching the technology for recognizing digital signal modulation methods holds important research significance.

Before the invention of modern modulation recognition technology, the identification of signal modulation methods mainly relied on manual analysis using instruments such as oscilloscopes and spectrum analyzers. This involved analyzing various time–frequency domain characteristics of signals (such as instantaneous Amplitude, Frequency, and Phase) and determining the modulation method of the signal. This method was not only time-consuming but also lacked high accuracy in identification. In 1969, with the publication of the first literature discussing automatic modulation recognition technology6, this situation began to change, and more and more modulation recognition algorithms were proposed and validated. Currently, several mature modulation recognition algorithms can be broadly categorized into three types: those based on Decision Theory7, Feature Extraction8, and Machine Learning9.

In the realm of Decision Theory, Shi et al.10 explored a likelihood ratio construction algorithm based on the use of the phase probability witness function, achieving recognition of MPSK modulation methods. Zhu11, using likelihood function theory under the conditions of unknown symbol rate and carrier frequency, achieved the recognition of MQAM and MPSK modulation method signals. Chen et al.12 designed a maximum likelihood function estimator that could operate even in a fading channel environment. Shan et al.13 designed a likelihood algorithm based on the average likelihood ratio test method, independent of channel conditions and antenna numbers.

In terms of Feature Extraction, Nandi et al.14 extracted the instantaneous features of signals and used a Decision Tree Algorithm to achieve modulation method recognition. Fang15 and colleagues employed a recognition method based on Random Forests to automatically identify four underwater acoustic signal modulation methods: OFDM, 2FSK, 4FSK, and 8FSK. Wang16 and colleagues used Random Forests as classifiers, achieving a modulation method recognition accuracy of over 95% in underwater acoustic signals when the SNR was above -5dB. Sahidullah et al.17 proposed a speech recognition algorithm based on MFCC. Zheng et al.18 discussed in detail the factors that may affect the performance of MFCC. Shikha et al.19 utilized MFCC for gesture recognition. The results show that the proposed application of using MFCC for gesture recognition has very high accuracy.

Machine Learning-based modulation signal recognition also demonstrates good performance20. Compared to traditional pattern recognition algorithms, Deep Learning Algorithms can automatically extract more effective data features to obtain better classification results. Currently, Networks with structures such as Convolutional Neural Networks 21,22,23,24, Recurrent Neural Networks25,26, and others have achieved good results in the field of automatic modulation recognition.

The structure of this study is as follows: Section “Methodology” introduces the endpoint detection methods, denoising methods, and the overall logic of this study regarding modulation signal recognition. Section “Different feature parameters” provides an overview of the modulation signal recognition process. Section “Conclusions” presents the results of traditional modulation signal recognition and compares them with the methods proposed in this study. Section “Discussion” discusses the work completed in this study and outlines future work.

Methodology

Modulation signal endpoint detection

  1. (1)

    Short time energy method

Assuming the time-domain waveform of the i frame signal is represented as yi(n), the calculation method for the short time energy value E(i) of the i frame signal yi(n) is as follows:

$$ E(i) = \sum\limits_{n = 0}^{L - 1} {y_{i}^{2} } (n) $$
(1)

In the formula, L represents the frame length.

  1. (2)

    Spectral entropy method

The concept of entropy was originally applied in thermodynamics to represent the degree of disorder in molecules and later used to reflect the uncertainty of random events 27,28. With the interdisciplinary development and integration of various fields, entropy has also played a more significant role in the domain of signal detection and recognition. There is a clear positive correlation between the disorder level of a signal and its entropy value; typically, the entropy value is higher for useful signals compared to noise.

Assuming the original signal is denoted as x(n), and performing the Fourier transform on the framed signal, let Yi(k) represent the spectral value of the k spectral line of the i frame signal after Fourier transform. The normalized spectral density function pi(k) is then defined as:

$$ p_{i} (k) = Y_{i} (k)/\sum\limits_{l = 0}^{N/2} {Y_{i} } (l) $$
(2)

In the formula, pi(k) represents the spectral density value corresponding to the k spectral line of the i frame signal after FFT transformation, Yi(k) denotes the energy spectrum of the kth spectral line, and N is the FFT length. Therefore, the short-time spectral entropy value Hi of the i frame signal is defined as:

$$ H_{i} = - \sum\limits_{k = 0}^{N/2} {p_{i} } (k)\lg p_{i} (k) $$
(3)
  1. (3)

    Short time energy entropy ratio method

Through the introduction to the principles of the short time energy method and spectral entropy method, it is evident that the energy envelope of a signal segment and the entropy envelope tend to be opposite in the same interval. Utilizing the energy-entropy ratio can better highlight the respective characteristics and differences between useful signal segments and noise segments.

Assuming the original signal is denoted as x(n), and x(n) is framed, with the waveform of the i frame signal being xi(m), and the total number of frames being A, then the energy of each frame is given by:

$$ AMP_{i} = \sum\limits_{m = 1}^{A} {x_{i}^{2} } (m) $$
(4)

The short time energy entropy ratio of the signal can be expressed as:

$$ EEF_{i} = \sqrt {1 + \left| {EL_{i} /H_{i} } \right|} $$
(5)
  1. (4)

    Mel frequency cepstral coefficients method

Mel Frequency Cepstral Coefficients (MFCC) is a method for analyzing the spectrum of a signal 29,30, simulating the perceptual results of the human auditory system. The MFCC method has deep applications in signal recognition, as it extracts distinctive features from the signal. The human ear has varying perceptual sensitivity to signals in different frequency ranges. As the signal frequency gradually increases, the relationship between human ear perception and frequency slowly transitions from a linear to a logarithmic one. Additionally, in human perception, lower-frequency signals tend to mask higher frequency signals. To emulate these characteristics, a set of nonlinear filters called Mel filters has been designed. These filters exhibit sparse critical bandwidths in the high frequency region and tight critical bandwidths in the low frequency region, mimicking the masking effect in the human ear. The MFCC method employs these filters to filter the input signal, and the energy values of the resulting output are used as fundamental features of the signal. This feature is independent of prior knowledge, possesses good robustness, and performs well even in low SNR conditions.

Mel frequency reflects the relationship between perception and frequency f, and it can be expressed as:

$$ {\text{Mel}} (f) = 2595*\log (1 + f/700) $$
(6)

In the formula, f represents the frequency of the signal, and Mel(f) represents the corresponding Mel frequency, measured in Mel units.

Noise reduction methods for signals

  1. (1)

    Wavelet analysis for denoising

In recent years, wavelet theory has undergone continuous improvement and refinement, reaching a new level in understanding and application of wavelet analysis. It is applied in various fields of signal and image processing31. One major application of wavelet analysis in these fields is denoising one-dimensional signals. The following will briefly introduce the principles of wavelet denoising. A one-dimensional signal contaminated with noise can be represented as:

$$ s(i) = f(i) + \varepsilon * e(i) $$
(7)

In the formula, e(i) is the noise signal, s(i) is the signal with noise, and f(i) is the signal without noise, also known as the true signal.

The purpose and method of denoising the signal s(i) is to suppress the noise signal e(i) and highlight the true signal f(i). In practical applications, the audio noise signal is often of higher frequency, while the effective signal is usually composed of several low frequency stationary signals. The wavelet decomposition process generates a series of wavelet coefficients, with the noise signal primarily present in the high frequency coefficients. Therefore, selecting an appropriate threshold can filter and process the wavelet coefficients, eliminating the high frequency components and recombining the remaining parts to obtain the denoised signal.

Typically, the process of one-dimensional wavelet denoising is as follows:

  1. (1)

    Determine suitable wavelet basis and decomposition scales based on experience and experimentation, then perform wavelet decomposition.

  2. (2)

    Determine the threshold for wavelet coefficients to reduce the weight of high frequency components throughout the signal.

  3. (3)

    Reconstruct a new signal using the information from all wavelet coefficients based on the weights of low-frequency and high-frequency components, which becomes the denoised signal.

In the above steps, selecting appropriate thresholds and weights is crucial as it directly affects the quality of the wavelet denoising algorithm. There are several methods for setting thresholds in wavelet analysis:

  1. (1)

    Use the threshold provided by the ddencmp function in MATLAB software. This method is time-saving but may not perform well for specific signals.

  2. (2)

    Determine thresholds through empirical formulas and continuous experimentation. This method yields better denoising results than default thresholds but requires time and effort for derivation and experimentation, and this is the method employed in this study.

  3. (3)

    Set the weight of all high-frequency coefficients to zero. This method can eliminate the impact of noise signals but may distort the obtained denoised signal, resulting in the loss of information contained in the signal, so it is generally used less frequently.

  1. (2)

    Empirical mode decomposition denoising

Empirical Mode Decomposition (EMD) is a method for processing the time-domain part of a signal32. It decomposes the initial signal x(t) into a set of symmetric Intrinsic Mode Functions (IMF) ci, each with local mean, and a residual term rn:

$$ x(t) = \sum\limits_{i = 1}^{n} {c_{i} } + r_{n} $$
(8)

In this formula, each component of ci, known as IMF, is arranged in descending order of average frequency. These IMF components reflect some detailed temporal features of the signal.

EMD decomposition can reduce the impact of noise and interference on complex and dynamic signals, revealing the intrinsic characteristics of the signal and facilitating further extraction. The IMF components obtained through EMD decomposition are derived and computed directly from the signal itself, distinguishing it from methods such as FFT and wavelet transforms. This characteristic ensures that the analyzed signal is non-stationary.

Analyzing the envelope characteristics of modulated signals allows the extraction of information from high frequency modulated signals, revealing subtle features that contribute to spectral analysis. Unlike previous envelope analysis methods heavily reliant on prior knowledge, where the accuracy of filter center frequency and bandwidth significantly affects the analysis results, EMD decomposition includes high frequency resonance components in the IMF components. EMD decomposition is adaptive, requiring no prior knowledge of these details, and is capable of envelope analysis without significant distortion of the signal.

  1. (3)

    Intrinsic time decomposition denoising

Intrinsic Time Decomposition (ITD) is similar to EMD and is also a signal processing method applied in the time domain.

EMD method, compared to wavelet analysis, exhibits better adaptability to various non-stationary signals but has some issues such as mode mixing. ITD method is a new signal processing approach in the time domain that complements EMD, addressing the mode mixing phenomenon present in EMD. These two methods construct linear signals differently, where ITD employs a linear operator, effectively suppressing the mode mixing phenomenon observed in EMD. EMD uses a two-layer loop structure, while ITD improves upon this by utilizing a single-layer iteration, enabling faster analysis and processing of signals. ITD maintains the characteristics of IMF components seen in EMD, providing orthogonality and completeness. Additionally, ITD adapts dynamically to handle a large volume of signals, effectively reducing the time required for signal analysis.

The purpose of intrinsic time-scale decomposition is to decompose the data into a sum of a series of rotational components that characterize the signal features and a monotonic trend component, thereby obtaining meaningful instantaneous frequency and amplitude information.

Let Xt be the original signal, and define L as the baseline extraction operator. After applying L to the original signal, the remaining residue is defined as the intrinsic rotation. Therefore, if we denote the intrinsic rotation extraction operator as H, then H = 1 − L. his further decomposes Xt as33:

$$ X_{t} = Lx_{t} + (1 - L)x_{t} = L_{t} + H_{t} $$
(9)

In the formula, Lt and Ht are the baseline signal and the intrinsic rotation, respectively.

Optimization of MFSK signal recognition algorithm

Currently, there are two main methods used to distinguish between 2 and 4FSK signals. The first method involves using instantaneous parameters as feature parameters to differentiate MFSK signals. However, its recognition effectiveness is significantly influenced by the signal-to-noise ratio, making it challenging to serve as a reliable criterion for distinguishing MFSK signals, especially in low signal-to-noise ratio conditions. Another method is to calculate the number of peaks in the signal's cyclic spectrum, denoted as Pk, to differentiate between these two types of signals. However, simulation results in this study indicate that the cyclic spectrum of a 2FSK signal exhibits clear peaks, usually around 2, while the cyclic spectrum of a 4FSK signal lacks obvious peaks, and the number of peaks Pk fluctuates between 1 and 6, with the most common cases having 3 or 4 peaks.

This study optimizes the second method mentioned above. Instead of calculating the number of spectral peaks when the cyclic frequency α = 0, it now calculates the kurtosis coefficient Kur of the cyclic spectrum parameter matrix at α = 0 to distinguish between 2 and 4FSK modulated signals. The specific identification steps are as follows:

  1. (1)

    The input signal is subjected to one-dimensional discrete stationary wavelet denoising, and three levels of stationary wavelet coefficients are returned. Since Gaussian noise is mainly concentrated in the first two levels of wavelet coefficients, the third-level wavelet coefficients are taken as the denoised signal for subsequent steps.

  2. (2)

    Apply the time-domain smoothing cyclic method to calculate the cyclic spectrum parameter matrix \(S_{x}^{\alpha } (f)\) for the denoised signal obtained in step 1. Extract all the values at cyclic frequency \(\alpha = 0\) from the cyclic spectrum parameter matrix \(S_{x}^{\alpha } (f)\), and save the results as a new row vector matrix \(S_{\alpha = 0}\).

  3. (3)

    Calculate the Kur for the row vector matrix \(S_{\alpha = 0}\), and use the kurtosis coefficient Kur as the feature parameter T6* for identifying 2FSK and 4FSK modulation signals. The calculation method for kurtosis coefficient Kur is as follows:

    $$ T_{6*} = Kur = \frac{{\mu_{4} }}{{\sigma^{2} }} $$
    (10)

In the formula, \(\mu_{4}\) represents the fourth central moment of matrix \(S_{\alpha = 0}\), and \(\sigma^{2}\) represents the variance of matrix \(S_{\alpha = 0}\). Their calculation formulas are as follows:

$$ \mu_{4} = \frac{1}{n}\sum\limits_{1}^{n} {(S_{\alpha = 0} - \overline{{S_{\alpha = 0} }} )^{4} } $$
(11)
$$ \sigma^{2} = \frac{1}{n}\sum\limits_{1}^{n} {(S_{\alpha = 0} - \overline{{S_{\alpha = 0} }} )^{2} } $$
(12)

In the formula, n represents the number of elements in matrix \(S_{\alpha = 0}\), and \(\overline{{S_{\alpha = 0} }}\) represents the mean of matrix \(S_{\alpha = 0}\).

The identification process described above is illustrated in Fig. 1.

Figure 1
figure 1

Flowchart for distinguishing between 2 and 4FSK signals.

Full size image

Overall approach of this study

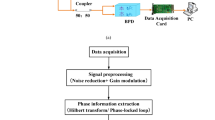
The overall technical approach of the modulation signal recognition method proposed in this study is shown in Fig. 2.

Figure 2
figure 2

Overall technology roadmap for modulated signal identification.

Full size image

As shown in Fig. 2, firstly, several commonly used endpoint detection methods are compared, and the method with the highest accuracy is selected for further optimization by feature extraction of the signal, so as to achieve the purpose of final signal recognition.

The specific process is as follows:

  1. (1)

    Simulate the modulation, communication, and reception process of digital modulation signals using MATLAB.

  2. (2)

    Preprocess the received signals to obtain the baseband signals.

  3. (3)

    Calculate feature parameter T1. Using the T1 value, differentiate the OFDM signal from the single-carrier modulated signals, dividing the signals into {OFDM} and {2ASK, 4ASK, 2FSK, 4FSK, 2PSK, 4PSK} categories.

  4. (4)

    Calculate feature parameter T2. Using T2, separate the signal set {2ASK, 4ASK, 2FSK, 4FSK, 2PSK, 4PSK} into {2ASK, 4ASK} and {2FSK, 4FSK, 2PSK, 4PSK} categories.

  5. (5)

    Calculate feature parameter T3. Using T3, divide the signal set {2FSK, 4FSK, 2PSK, 4PSK} into {2FSK, 4FSK} and {2PSK, 4PSK} categories.

  6. (6)

    Calculate feature parameter T4. Using T4, separate the signal set {2ASK, 4ASK} into {2ASK} and {4ASK} categories.

  7. (7)

    Calculate feature parameter T5. Using T5, divide the signal set {2PSK, 4PSK} into {2PSK} and {4PSK} categories.

  8. (8)

    Calculate feature parameter T6. Using T6, divide the signal set {2FSK, 4FSK} into {2FSK} and {4FSK} categories.

Different feature parameters

In this paper, feature extraction was performed using high-order cumulants34, the maximum value of the zero-center normalized instantaneous amplitude spectral density14,35, and the absolute amplitude standard deviation36,37.

Identification of feature parameter T 1 for OFDM signals

The theoretical values of cumulants for each digital modulation signal can be obtained from the method of calculating high-order cumulant theoretical values, as shown in Table 1. It is assumed that the energy value of the input signal is E.

Table 1 Theoretical values of cumulants for digital modulation signals.
Full size table

From Table 1, it can be observed that the cumulative values of OFDM signals are zero for the second order and higher, allowing for the distinction of OFDM from other signals based on this characteristic. Additionally, it is noteworthy that the cumulative values for 2FSK and 4FSK signals are the same, making it impossible to differentiate between these two signals using cumulative values.

In summary, we define the feature parameter T1:

$$ T_{1} = \left| {C_{42} } \right| $$
(13)

The table indicates that, except for OFDM signals, the T1 values for the remaining modulation signals are all greater than 0. Using the feature parameter T1 effectively distinguishes OFDM signals from other signals. In a Gaussian channel with a signal-to-noise ratio (SNR) ranging from 0 to 15 dB, the T1 values for the seven modulation signals were calculated. The simulation results, averaged over 500 repeated experiments, are shown in Fig. 3.

Figure 3
figure 3

T1 values for the 7 modulation signals.

Full size image

From Fig. 3, it can be observed that with the change in SNR, the T1 values for each modulation signal remain relatively stable, and they generally match the theoretical values in Table 1. The T1 value for OFDM signals stays close to 0, providing a clear distinction from the T1 values of other modulation signals. This indicates that OFDM signals can be effectively identified from the seven modulation signal types based on their T1 values.

Distinguishing feature parameter T 2 for MASK signals from MFSK and MPSK signals

From Table 1, it can be observed that the high-order cumulants for 2ASK signals are essentially the same as those for 2PSK signals. Relying solely on high-order cumulants as feature parameters is insufficient to effectively distinguish between these two types of signals. In this study, the maximum value \(\gamma_{\max }\) of the zero centered normalized instantaneous amplitude spectrum density is used as the feature parameter T2, enabling the discrimination of {2ASK, 4ASK} signals from the modulation signal set {2PSK, 4PSK, 2FSK, 4FSK}.

$$ T_{2} = \gamma_{\max } = \max \left| {FFT[a_{cn} (i)]^{2} /N_{s} } \right| $$
(14)

Simulations were conducted for the above modulation signals in a Gaussian channel with a SNR ranging from 0 to 15 dB. The T2 values were calculated for the received signals, and the results are shown in Fig. 4.

Figure 4
figure 4

T2 values for the 6 modulation signals.

Full size image

As shown in Fig. 4, by selecting a suitable threshold, {2ASK, 4ASK} can be distinguished from other modulation signals. With the increase in SNR, the distinctiveness of T2 values between {2ASK, 4ASK} and other signals also increases.

Distinguishing feature parameter T 3 for MFSK signals from MPSK signals

By analyzing the high-order cumulant values of MFSK and MPSK signals in Table 1, this study defines the feature parameter T3:

$$ T_{3} = \left| {C_{40} } \right|/\left| {C_{42} } \right| $$
(15)

Through calculations, the theoretical values of T3 for 2PSK and 4PSK modulation signals are 1, while the theoretical values of T3 for 2FSK and 4FSK modulation signals are 0. Feature parameter T3 can effectively distinguish between these two types of signals. Simulation verification is performed in the case of SNR from 0 to 15 dB, and the calculated T3 values for each received modulation signal are shown in Fig. 5.

Figure 5
figure 5

T3 values for the 6 modulation signals.

Full size image

As shown in Fig. 5, in the Gaussian channel with SNR ranging from 0 to 15 dB, the T3 values of various modulation signals remain relatively stable regardless of changes in SNR. Additionally, these values closely match the calculated values. The T3 value differentiation between the two types of modulation signals is significant, allowing for the effective distinction between PSK and FSK modulation signals using T3 values.

Identification of feature parameter T 4 for 2ASK and 4ASK signals

The absolute amplitude standard deviation is employed as the feature parameter T4 to distinguish the 2ASK signal from the modulation signal set {2ASK, 4ASK}.

$$ T_{4} = \sigma_{aa} = \sqrt {\frac{1}{c}\left( {\sum\limits_{{a_{n} (i){ > }a_{t} }} {a_{cn}^{2} (i)} } \right) - \frac{1}{c}\left( {\sum\limits_{{a_{n} (i){ > }a_{t} }} {\left| {a_{cn} (i)} \right|} } \right)^{2} } $$
(16)

Figure 6 shows the T4 values for various modulation signals, simulated in a Gaussian channel with a SNR ranging from 0 to 15 dB.

Figure 6
figure 6

T4 values for the 2 modulation signals.

Full size image

As shown in Fig. 6, under low signal conditions (SNR = 0 dB), it is challenging to effectively distinguish between these two signals. However, at higher SNR (SNR = 4dB), a suitable threshold (in this study, thr = 0.3) can be employed to separate 2ASK and 4ASK. With the increase in SNR, the discrimination between T4 values for 2ASK and 4ASK signals becomes more pronounced, facilitating a better separation of these two modulation signals.

Identification of feature parameter T 5 for 2PSK and 4PSK signals

By analyzing the high-order cumulant values of 2PSK and 4PSK signals in Table 1, this study defines the feature parameter T5:

$$ T_{5} = \left| {C_{30} } \right|^{3} /\left| {C_{42} } \right|^{2} $$
(17)

By calculation, the theoretical value of T5 for 2PSK modulation signal is 32, while the theoretical value of T5 for 4PSK modulation signal is 0. Using the feature parameter T5 can distinguish between these two signals. Experimental simulation in a Gaussian channel with SNR ranging from 0 to 15 dB was conducted, and the calculated T5 values for received modulation signals are shown in Fig. 7.

Figure 7
figure 7

T5 values for the 2 modulation signals.

Full size image

From Fig. 7, it can be observed that in the Gaussian channel with SNR ranging from 0 to 15 dB, the T5 values of various modulation signals basically remain unchanged with the change in SNR, and they are consistent with the theoretical values. The discrimination between the two types of modulation signals based on T5 values is significant, allowing us to distinguish between 2 and 4PSK signals using T5 values.

Optimization of MFSK signal recognition algorithm

  1. (1)

    MFSK Signal Recognition Based on Instantaneous Parameters

The traditional instantaneous parameter method uses the standard deviation \(\sigma_{af}\) of the zero centered normalized instantaneous frequency absolute value to distinguish between 2 and 4FSK modulation signals. This method was simulated in this study, and \(\sigma_{af}\) was employed as the feature parameter T6 to differentiate the 2FSK signal from the {2FSK, 4FSK} modulation signal set.

$$ T_{6} = \sigma_{af} = \sqrt {\frac{1}{c}\left( {\mathop \sum \limits_{{a_{n} (i) > a_{t} }} f_{NL}^{2} (i)} \right) - \frac{1}{c}\left( {\mathop \sum \limits_{{a_{n} (i) > a_{t} }} \left| {f_{NL} (i)} \right|} \right)^{2} } $$
(18)

Simulations were conducted on the above-mentioned modulation signals, with the SNR set in the range of 0 to 15 dB. The T6 values for the received signals are depicted in Fig. 8.

Figure 8
figure 8

T6 values for the 2 modulation signals.

Full size image

As shown in Fig. 8, when the SNR is relatively high (SNR = 10dB), it is possible to differentiate between 2 and 4FSK signals by selecting a suitable threshold (in this case, thr = 0.41). With increasing SNR, the distinctiveness of T6 values between 2 and 4FSK signals also improves, facilitating better differentiation between these two signals. However, at lower SNR values (e.g., SNR = 0 dB), distinguishing between these two modulation signals becomes challenging using the instantaneous parameter \(\sigma_{af}\).

As shown in Fig. 9, this recognition method achieves accurate identification of 2FSK and 4FSK signals when the SNR is greater than 10 dB, with recognition accuracy exceeding 95% for both types of signals. However, in an environment with a SNR of 5 dB, the algorithm based on instantaneous parameters has a lower recognition accuracy for 2FSK signals, reaching only 70%, and the recognition accuracy for 4FSK signals also falls short of the requirement at 83%. Comparing these results with those in Fig. 8, it can be inferred that when the SNR is too low, the distinction between the modulation signals of 2FSK and 4FSK using the instantaneous parameter \(\sigma_{af}\) becomes less obvious, making it challenging to accurately separate them using \(\sigma_{af}\).

Figure 9
figure 9

T6 values distinguishes between 2 and 4FSK signal recognition accuracy.

Full size image
  1. (2)

    MFSK signal recognition based on the number of peaks in the cyclo-spectrum

Currently, the mainstream method is to use the number of spectral peaks Pk in the cyclic spectral profile at cyclic frequency α = 0 to identify MFSK modulation signals. This study simulates and verifies this method, using the number of spectral peaks Pk as the feature parameter T6 to distinguish the {2FSK, 4FSK} modulated signal set.

$$ T_{6} = P_{k} $$
(19)

The theoretical values of the spectral peak count Pk for 2FSK and 4FSK modulated signals are known to be 2 and 4, respectively, based on references in the literature.

Simulations were conducted on the {2FSK, 4FSK} modulation signal set in a Gaussian channel. At a SNR of 0 dB, the cyclic spectrum cut of the 2FSK and 4FSK modulation signals is shown in Fig. 10. With SNR ranging from 0 to 15 dB, T6 values were calculated separately for 2FSK and 4FSK signals through 500 repeated experiments. The final simulation results are presented in Fig. 11.

Figure 10
figure 10

The cyclo-spectral sections of 2FSK and 4FSK signals at SNR of 0dB. (a) 2FSK signal cycle spectrum. (b) 4FSK signal cycle spectrum.

Full size image
Figure 11
figure 11

T6 values for the 2 modulation signals.

Full size image

As shown in Fig. 10, when the frequency f is greater than zero, (a) the spectral peaks of the 2FSK signal in the graph are more prominent and distinct, and the number of spectral peaks Pk is consistent with the theoretical value. (b) The spectral peaks of the 4FSK signal in the graph are not obvious, and the number of spectral peaks Pk is between 3 and 5, deviating from the theoretical value.

As shown in Fig. 11, under a Gaussian channel with a SNR ranging from 0 to 15 dB, the number of spectral peaks for the 2FSK signal remains around 2, which is consistent with the theoretical value. The number of spectral peaks for the 4FSK modulation signal fluctuates within the range of 3.4–3.7, showing a certain disparity from the theoretical value. However, they correspond to the figures in (b) of Fig. 10, confirming the insignificant issue of spectral peak quantity for the 4FSK modulation signal.

To further analyze the discrepancy between the simulated values and theoretical values for the occurrence of spectral peaks in the 4FSK modulation signal shown in Fig. 11, under a Gaussian channel with an SNR of 0 dB, the T6 values for randomly generated 4FSK modulation signals are calculated. This process is repeated 100 times in simulation experiments, and the occurrence of spectral peaks is recorded. The results are shown in Fig. 12.

Figure 12
figure 12

Occurrences of various T6 values for the 4FSK modulation signal at SNR of 0 dB.

Full size image

As shown in Fig. 12, the T6 values for the 4FSK modulation signal fluctuate between 1 and 6, with the majority (77%) falling in the range of 3–4. T6 values fluctuating between 1 and 2 occur 13 times, accounting for 13% of the total occurrences. When the T6 values for the 4FSK signal fluctuate between 1 and 2, identifying the 4FSK modulation signal based on the spectral peak count Pk may lead to a misclassification as 2FSK in the final output.

In a Gaussian channel with SNR ranging from 0 to 15 dB, the T6 values for 2FSK and 4FSK signals are calculated and compared with a threshold value (set to 2 in this study). Signals with T6 values greater than 2 are classified as 4FSK, while those less than or equal to 2 are classified as 2FSK. The simulation is independently repeated 1000 times, and the recognition accuracy for 2FSK and 4FSK modulation signals is depicted in Fig. 13.

Figure 13
figure 13

Recognition accuracy of 2FSK and 4FSK signals based on T6 values.

Full size image

As shown in Fig. 13, this recognition method achieves perfect identification of 2FSK signals in a Gaussian channel with a SNR greater than 2 dB, with a recognition accuracy of 100%. However, the recognition accuracy for 4FSK signals does not meet the requirements, reaching only around 85%. Comparing these results with Fig. 12, it can be predicted that the cyclic spectrum peaks of 4FSK modulated signals are not distinct, and some 4FSK signals are misclassified as 2FSK signals, resulting in a lower recognition accuracy for 4FSK signals.

  1. (3)

    MFSK signal recognition based on the kurtosis coefficient of the cyclo-spectrum

In summary, this study proposes an optimized approach for distinguishing the {2FSK, 4FSK} signal set based on the number of cyclic spectrum peaks Pk. The optimization involves not calculating the number of peaks at the cyclic frequency \(\alpha = 0\) but instead computing the kurtosis coefficient Kur of the cyclic spectrum parameter matrix at \(\alpha = 0\) to differentiate between 2 and 4FSK modulated signals. The recognition steps are outlined in Section “Optimization of MFSK signal recognition algorithm”.

In a Gaussian channel with a SNR ranging from 0 to 15 dB, the T6* values for received 2FSK and 4FSK signals were calculated according to the aforementioned procedure. The simulation results are depicted in Fig. 14.

Figure 14
figure 14

T6* values for the 2 modulation signals.

Full size image

From Fig. 14, it can be observed that in a Gaussian channel with a SNR ranging from 0 to 15 dB, the T6* values for both modulation signals remain relatively stable and are not sensitive to changes in the signal-to-noise ratio. There is a significant distinction in T6* values between the two modulation signals, allowing for effective differentiation between 2 and 4FSK signals. By setting a threshold value \(\eta = 30\), signals with T6* values greater than the threshold are considered as 2FSK signals, while those with values below the threshold are considered as 4FSK signals.

In a Gaussian channel with a SNR ranging from 0 to 10 dB, the T6* values for received 2FSK and 4FSK signals were calculated. These values were then compared with a set threshold value \(\eta\). The simulation was repeated 1000 times, and the recognition accuracy for 2FSK and 4FSK modulation signals is depicted in Fig. 15.

Figure 15
figure 15

Recognition accuracy of distinguishing 2FSK and 4FSK signals using T6* values.

Full size image

That algorithm can accurately distinguish these two signals when the SNR is greater than 1 dB, achieving a recognition accuracy of 92%. When the SNR is greater than 3 dB, this method can completely distinguish between 2 and 4FSK signals, with recognition accuracies exceeding 99% for both signals.

Table 2 shows the recognition accuracy of the instantaneous parameter algorithm, the peak number algorithm and the proposed algorithm under different SNR.

Table 2 Comparison of recognition accuracy of FSK signals by three algorithms.
Full size table

As shown in Table 2, the algorithm based on instantaneous parameter \(\sigma_{af}\) maintains a relatively high recognition accuracy at high SNR. However, in situations where the SNR is less than 5 dB, the recognition accuracy drops significantly. The algorithm based on the number of spectral peaks Pk in the cyclic spectrum exhibits extremely high recognition accuracy for 2FSK but falls short in recognizing 4FSK signals. The algorithm proposed in this study, which uses the kurtosis coefficient Kur of the cyclic spectrum as a substitute for the number of spectral peaks Pk, maintains a 99% recognition accuracy for 2FSK and 4FSK signals even at lower SNR. This algorithm demonstrates superiority when compared to the other two methods.

Conclusions

Simulation experiment

In the simulation testing of the overall modulation recognition design scheme, the symbol rate of the modulation signal is set to 5000 Baud, the sample length of the simulated waveform is 4 s, the carrier frequency is set to 20 kHz, and the sampling frequency of the receiving device is set to 120 kHz.

Under Gaussian channels with SNRs ranging from 1 to 10 dB, the six feature parameters are calculated for the received signals to identify the signal types. The recognition experiments for each signal are repeated 500 times at each SNR, and the recognition accuracy data for the seven modulation signals are saved. The results are shown in Fig. 16. It is worth noting that reducing the signal length may lead to a decrease in recognition accuracy.

Figure 16
figure 16

Recognition accuracy of various modulation signals.

Full size image

As shown in Fig. 16, when the SNR is 4 dB, the overall accuracy of the modulation recognition algorithm used in this study can reach over 92%. When the SNR is greater than 6 dB, the overall recognition accuracy of the algorithm can be maintained at over 95%. Specifically, when the SNR is greater than 2 dB, both 2FSK and 4FSK signals can be accurately identified, with recognition accuracy rates exceeding 97%.

Simulation experiment combined with endpoint detection

  1. (1)

    Comparison of the effects of several different endpoint detection algorithms

In a Gaussian channel, the endpoint detection effects of different endpoint detection algorithms for the same signal are studied. The SNR of the Gaussian channel is set to 0 dB, and the waveform of the signal before and after passing through the Gaussian channel is shown in Fig. 17.

Figure 17
figure 17

Initial signal waveform and noisy signal waveform.

Full size image

Endpoint detection is performed using Short Time Energy Entropy Ratio Method, Short Time Energy Zero Ratio Method, Short Time Spectral Entropy Method, and Short Time MFCC Distance Method. The results are illustrated in Fig. 18.

Figure 18
figure 18

Effectiveness of various endpoint detection algorithms. (a) Short time energy entropy ratio method result. (b) Short time energy zero ratio method result. (c) Short time spectral entropy method result. (d) Short time MFCC distance method result.

Full size image

As shown in Fig. 18, the envelope curve formed by the Short Time Energy Entropy Ratio method can best reconstruct the original waveform of the signal, making it suitable for further endpoint detection work. However, this simulation only verifies the detection effect of the Short Time Energy Entropy Ratio algorithm on general communication signals. For further research on the detection effect of the four endpoint detection algorithms on modulation signals, additional experiments are needed. By changing the modulation type of the signals, with the signal set {OFDM, 2ASK, 4ASK, 2FSK, 4FSK, 2PSK, 4PSK}, under a Gaussian channel with a SNR of 0 dB, the endpoint detection accuracy of the four algorithms is calculated for each signal type. Each signal type is experimented with 100 times, and the final endpoint detection accuracy is the average value. The experimental results are shown in Table 3.

$$ {\text{Endpoint}}\,{\text{Detection}}\,{\text{Accuracy}} = \left( {{\text{Total}}\,{\text{Frames}} - \left( {{\text{False}}\,{\text{Alarms}} + {\text{Missed}}\,{\text{Detections}}} \right)} \right)/{\text{Total}}\,{\text{Frames}} $$
Table 3 Average endpoint detection accuracy of various algorithms when the SNR of 0 dB.
Full size table

As shown in Table 3, under a Gaussian channel with a SNR of 0 dB, for these seven modulation signal types, the Short Time Energy Entropy Ratio algorithm performs the best, maintaining an endpoint detection accuracy of over 93%. This is superior to the Short Time Spectral Entropy Method, Short Time Energy Zero Ratio Method, and MFCC Distance Method. Additionally, the Short Time Energy Entropy Ratio algorithm is adaptable to various modulation signals. From Table 3, it can be observed that when the types of input modulation signals vary, the fluctuation range of the endpoint detection accuracy for the Short-Time Energy Entropy Ratio algorithm is the smallest, remaining around 2%, which is better than the other three algorithms.

  1. (2)

    Simulation of short time energy entropy ratio endpoint detection combined with denoising algorithms

In order to further improve the performance of the endpoint detection algorithm, an attempt was made to preprocess the signal with denoising before applying the Short Time Energy Entropy Ratio algorithm. Simulations were conducted for denoising effects using Empirical Mode Decomposition (EMD), Iterative Thresholding Decomposition (ITD), and Wavelet decomposition algorithms under a Gaussian channel. The time taken by each denoising algorithm was recorded.

In a Gaussian channel with SNR ranging from -20dB to 10dB, 300 Monte Carlo simulation experiments were conducted based on the Short-Time Energy Entropy Ratio and various denoising algorithms. The endpoint detection accuracy of each algorithm is shown in Fig. 19. The time taken by each denoising algorithm was 1.207 s, 0.023 s, and 0.003 s, respectively.

Figure 19
figure 19

Endpoint detection algorithm based on energy entropy ratio in gaussian channel.

Full size image

In Fig. 19, the ORI group serves as the control group without using denoising algorithms. The ITD group uses Intrinsic Time-Scale Decomposition, the EMD group uses Empirical Mode Decomposition, and the Wavelet group uses Wavelet decomposition as denoising algorithms.

From the graph, it can be observed that, in a Gaussian channel with a SNR greater than – 15 dB, the EMD denoising and Wavelet denoising algorithms outperform the ORI curve without denoising. Notably, the Wavelet denoising algorithm is superior to the EMD denoising algorithm. At a SNR of – 20 dB, the use of the Wavelet denoising algorithm is optimal, achieving a correctness rate of 90%, while the EMD denoising effect is similar to the control group without denoising. The ITD algorithm’s performance is inferior to the other three approaches. In the SNR range of – 20 dB to – 10 dB, the ITD denoising algorithm is less effective than the other three methods, possibly because the ITD decomposition disrupts some characteristic parameters of the input signal, degrading the Short Time Energy Entropy Ratio curve. When the SNR is greater than – 20 dB, the combination of the Wavelet denoising algorithm and the Short Time Energy Entropy Ratio-based endpoint detection algorithm achieves a 95% endpoint detection accuracy, meeting the requirements.

In the Gaussian channel, the EMD denoising algorithm takes the longest time, at 1.207 s, while the Wavelet denoising algorithm takes the shortest time, at 0.003 s. Combining the denoising algorithm’s endpoint detection accuracy under the Gaussian channel from Fig. 19, it can be concluded that, in a Gaussian channel, the denoising effect of the Wavelet denoising algorithm, in conjunction with the Short Time Energy Entropy Ratio algorithm, is the best, and this algorithm requires the shortest computation time.

  1. (3)

    Simulation of modulation recognition combined with endpoint detection

To evaluate the impact of the designed endpoint detection module on the overall modulation recognition system’s accuracy and verify the stability of the endpoint detection module in conjunction with the modulation recognition system, a simulation test was conducted by adding a preprocessing module (endpoint detection module) before the modulation recognition system. The testing steps are as follows:

  1. (1)

    Use MATLAB to generate corresponding test signals selected from the {2ASK, 4ASK, 2FSK, 4FSK, 2PSK, 4PSK, OFDM} signal set, as shown in Fig. 20A.

  2. (2)

    Add randomly sized blank signal segments before and after the generated modulation signals, resulting in mixed signal segments, as depicted in Fig. 20B.

  3. (3)

    Considering the information from Fig. 16, where overall modulation recognition accuracy is close to 95% in a Gaussian channel with SNR greater than 5 dB, simulate the channel environment with a Gaussian channel and SNR = 5 dB. The signal after adding Gaussian noise is illustrated in Fig. 20C.

  4. (4)

    Combine the foregoing, apply wavelet denoising to the noisy signal. Subsequently, use the endpoint detection algorithm based on short-time energy entropy to extract modulation signal segments. The resulting signal segments are shown in Fig. 20D.

  5. (5)

    Use the obtained signal segments as input to the entire modulation recognition system. Conduct a simulation to recognize the modulation type.

  6. (6)

    Vary the modulation signal types and repeat steps 1–5 for each of the 7 modulation signal types. Test each signal type 500 times.

Figure 20
figure 20

Simulation diagram of the endpoint detection process. (a) Modulate the signal. (b) Add blank segments before and after the modulatio signal. (c) Signal after Gaussian noise is added. (d) Endpoint detection intercepted signal.

Full size image

Present the overall modulation recognition results as shown in Table 4.

Table 4 Modulation recognition test accuracy.
Full size table

As shown in the results in Table 4, under a Gaussian channel with a SNR of 5 dB, the overall recognition accuracy of the modulation recognition system combined with the endpoint detection module is comparable to the ideal signal recognition accuracy shown in Fig. 16. The recognition accuracy fluctuates around 95% in both simulation tests. This indicates that the modulation signal segments, obtained through endpoint detection technology, do not undergo significant distortion and do not interfere with the subsequent recognition and classification of modulation signals. This validates the feasibility and stability of the entire modulation signal recognition scheme.

Result analysis

  1. (1)

    In a Gaussian channel with a SNR of 0 dB, the short time energy entropy ratio algorithm performs the best among the seven common modulation types, with an endpoint detection accuracy exceeding 93%. It outperforms the short time spectral entropy method, short time zero crossing rate method, and MFCC method. Additionally, the short time energy entropy ratio algorithm is adaptable to various modulation signals. When there is a change in the types of input modulation signals, the fluctuation range of the endpoint detection accuracy using the short-time energy entropy ratio algorithm is minimal, staying around 2%, which is superior to the other three algorithms.

  2. (2)

    In a Gaussian channel with a SNR greater than – 15 dB, the wavelet denoising algorithm is superior to the EMD denoising algorithm. When the SNR is – 20 dB, the wavelet denoising algorithm is optimal, achieving a correctness rate of 90%. In the SNR range of – 20 dB to – 10 dB, the ITD denoising algorithm performs poorly, possibly because ITD decomposition disrupts some characteristic parameters of the input signal, degrading the short time energy entropy ratio curve of the signal. In scenarios where the SNR is greater than – 20 dB, the combination of the wavelet denoising algorithm and the endpoint detection algorithm based on short time energy entropy ratio can achieve an endpoint detection correctness rate of 95%.

In a Gaussian channel, the EMD denoising algorithm takes the longest time, at 1.207 s, while the Wavelet denoising algorithm takes the shortest time, at 0.003 s.

  1. (6)

    In a Gaussian channel with a SNR of 5 dB, the overall recognition accuracy of the modulation recognition system combined with the endpoint detection module is basically consistent with the ideal signal recognition accuracy. The recognition accuracy fluctuates around 95% in both simulation tests. This indicates that the modulation signal segments obtained through endpoint detection technology do not undergo distortion and do not affect the subsequent recognition and classification of modulation signals. This validates the feasibility and stability of the entire modulation signal recognition scheme.

Discussion

This study analyzed the performance of four common endpoint detection techniques and found that the Short-Time Energy Entropy Ratio algorithm performs the best for detecting seven common modulation signals. In a Gaussian channel with a SNR of 0 dB, the correctness of endpoint detection is above 93%. Based on this, three different denoising algorithms were introduced to further enhance the performance of the Short Time Energy Entropy Ratio algorithm. The results indicate that the wavelet denoising algorithm achieves the greatest improvement in the performance of the Short Time Energy Entropy Ratio algorithm, with a short processing time. In a Gaussian channel with a SNR greater than -10dB, the endpoint detection correctness of this algorithm can be maintained at over 95%.

Furthermore, for accurate identification and differentiation between 2 and 4FSK signals, this study optimized the relevant algorithms in the cyclo-spectrum, using the kurtosis coefficient value Kur of the cyclo-spectrum parameter matrix at the cyclic frequency \(\alpha = 0\) to distinguish these two signals. The results show that under a SNR of 4 dB, the proposed modulation recognition algorithm can effectively differentiate these two signals, with an identification correctness rate of over 99%. Finally, this study compared the endpoint-detected signals with ideal signals, validating the feasibility and stability of the entire proposed modulation signal recognition scheme.

As the signals used for modulation recognition in this study are relatively stable and the noise source is relatively singular (white Gaussian noise added), in real-world applications, signals undergo more complex and varied noise and interference. In future work, the modulation recognition algorithm in complex channel environments needs to be further researched.