Abstract
To investigate the vibration isolation effect of composite vibration isolation walls on surface vibrations in suburban railway deep tunnels under various influencing factors, an integrated numerical model of the train was initially developed. This model solved the wheel-rail interaction force and was applied to a three-dimensional volume coupling model of the track soil. Subsequently, the model's reliability was validated through comparison with measured data. Afterward, the vibration isolation effects of various types of EPS material vibration isolation walls were examined, with a focus on exploring the impact of thickness, material proportion, and relative positioning of the materials within the vibration isolation wall composed of EPS material and concrete. Research indicates that with an increase in the burial depth of a single material vibration isolation wall, its effective vibration isolation frequency range gradually widens. When the burial depth of the vibration isolation wall exceeds the tunnel burial depth, the vibration isolation effect is optimal. Composite vibration isolation walls, with thicknesses smaller than single-material vibration isolation walls, exhibit superior vibration isolation effects compared to their single-material counterparts. The effective vibration isolation frequency band of composite vibration isolation walls differs from that of single-material vibration isolation walls. Using the optimal-size vibration isolation wall of a single material as a composite vibration isolation wall enhances the vibration isolation effect of peak acceleration in the frequency domain by 16.58% and peak velocity by 16.95%. Moreover, frequency domain peak displacement experiences a 30.73% improvement in the vibration isolation effect.
Similar content being viewed by others
Introduction
Vibrations generated during urban rail transit operations can adversely affect specialized buildings and the functionality of precision instruments1,2. To address these issues, vibration isolation measures are commonly implemented at the vibration source3,5, along the propagation path6,7,8,9,10, and at the vibration receiving structure11,12. Mitigation measures implemented against vibration sources include floating slab tracks13 and various types of ballast pads14. Vibration isolation barriers are frequently employed as mitigation measures for propagation paths. Mitigation measures for receiving structures include base isolation15 and room-within-room design16. Mitigation measures on the transmission path aim to prevent ground vibrations from propagating from the source to the receiving structure by altering the dynamic characteristics of the transmission path. This approach doesn't necessitate changing the dynamic characteristics of the vibration source and receiving structures, thereby averting potential safety issues at these locations that may arise from such alterations17.
Under the vibration excitation caused by the subway, waves propagate through the soil layer18,20. When elastic waves encounter a vibration isolation barrier, reflection waves, and transmitted waves are generated at the interface between the barrier and the soil due to the discontinuity between the two different media. After the wave passes through the barrier, it reduces the energy of soil vibration, thereby achieving a good vibration isolation effect21. The main types of vibration isolation barriers include empty trenches/filled trenches7,22, wall barrier23,24,25, pile barriers26,27, and wave-blocking blocks28,29. Existing research30,31 suggests that the most effective vibration isolation method is an empty trench. However, its applicability is limited due to the poor stability of the trench wall, making it feasible only for shallow trench depths. It has been noted that sheet piles are not as effective in mitigating vibrations as trenches32,33. Toygar et al.34 observed that sheet pile barriers effectively decreased vibration amplitudes by 44–79% within the frequency range of 30–80 Hz. Nonetheless, trenches still offer the best vibration isolation performance among sheet pile barriers. Wave-block vibration isolation barriers present challenges such as demanding construction specifications and unsuitability for certain construction scenarios. Consequently, wall barriers emerge as the optimal option for vibration isolation in deep tunnels.
There are currently various analysis methods employed to investigate the vibration isolation effectiveness of barriers, including numerical analysis methods35,36, finite element methods30,37,38,39,40,41,42,43, model tests, and field experiments44,45,46,47,48,49. Theoretical analyses, models, and field experimental studies are typically limited to simpler cases. In practical engineering, the vibration isolation problem is more intricate. Consequently, finite element analysis has emerged as the predominant research tool. Abdul Ahad Faizan et al50 utilized a simplified computational model to assess the impact of high-speed trains on environmental vibrations, studying the differences in vibration generation and wave propagation in various soil types. Ekanayake et al.51 constructed a three-dimensional finite element model to investigate the attenuation efficiency of various filling materials on ground vibration. Their findings revealed that polystyrene (EPS) geofoam exhibited the highest effectiveness among the fill materials, demonstrating attenuation efficiency comparable to trenching. Sitharam et al.52 assessed the impact of empty ditch parameters on reducing the amplitude of Rayleigh waves propagating through empty ditch using numerical simulations. Jazebi et al.53 performed a finite difference analysis on the effectiveness of filled geofoam barriers.
These researchers all employ a single material to fill the trench. However, when the tunnel is deeply buried, the vibration isolation efficacy of the trench is suboptimal, and wall barriers are better suited for vibration isolation. Therefore, this research plan employs a combination of numerical analysis methods and the finite element method to investigate the vibration isolation efficacy of composite vibration isolation walls on ground surface vibrations in deep tunnels of suburban railways. Firstly, the study focuses on assessing the impact of various types and sizes of EPS vibration isolation walls on the vibration isolation efficacy to identify the optimal burial depth for these walls. Subsequently, it investigates how factors such as the thickness of the vibration isolation wall, the proportion of materials used, and the relative position of these materials affect the vibration isolation efficacy when EPS material and C20 concrete are utilized as composite vibration isolation walls at the identified.
Establishment of the model
The model establishment in this study is divided into three steps. The first step involves creating a numerical model of the train to calculate the interaction force between the train's wheels and rails. In the second step, a finite element model of the rail-tunnel-soil coupling is established. Finally, the calculated wheel–rail interaction force is applied to the finite element model established in the second step.
Wheel–rail interaction force modeling
In the field of geotechnical earthquake engineering, researchers have long grappled with the challenge of addressing train loads. In establishing the numerical model of the train, we adopt the analytical method proposed by Wang54 to compute the wheel-rail interaction force of the train.
During routine operation, the wheels and rail remain in contact. By considering the continuity of vertical displacements between the wheel and rail, the wheel/rail interaction forces can be solved. The vertical displacement of a wheel axle is composed of the Hertz spring compression, wheel/rail irregularities, and vertical deformation of the rail. The vector collecting all displacements of alxes
in which the vector \(\widetilde{{\varvec{Z}}}(\Omega )={\left\{{e}^{i\Omega {a}_{1}/c},{e}^{i\Omega {a}_{2}/c},...,{e}^{i\Omega {a}_{M}/c}\right\}}^{T}\) represents the vertical harmonic roughness amplitudes at all M wheel/rail contact points of the train, and the diagonal matrix \({{\varvec{K}}}_{h}={\text{diag}}({k}_{h1},{k}_{h2},...,{k}_{hM})\) represents the Hertz contact stiffness at all wheel/rail contact points. Zw represents the vertical displacement of the wheel axis, Zr denotes the track displacement, and Ω stands for the train's vertical vibration frequency.
To obtain the wheel-rail interaction force, we first need to determine the values of Zw, Zr, and then substitute them into formula (1).
To obtain Zw and Zr, we can follow the steps below:
The vector Zv collects the displacements of all degrees of freedom of the vehicle. The matrix B = [0, IT is the degree of freedom transformation matrix, with I the identity matrix. Zw represents the vertical displacement of the wheel axle. Under the condition of uneven wheel/rail vertical harmonics, the vehicle exhibits vertical simple harmonic vibration, and the amplitude of the vertical displacement Zw of the wheel axle is determined as follows
in which the vehicle's transfer function matrix
and the overhead tilde notion represents the amplitude of a time-harmonic quantity.
According to Fourier series theory, any of the random roughness at the wheel/rail contact can be decomposed into a series of harmonic roughness components. For the ith component with an amplitude of zi, wave number of 2πβ, or wavelength of 1/(2πβ) = λi, when the train moves at a speed of c, the vertical vibration frequency of the train is Ωi = 2πc/λi. The vertical vibration of the train generates a series of wheel/rail interaction forces that vary harmonically with time at all the wheel/rail contact points. These forces can be represented as
Correspondingly, excited by the moving forces P(t), the vertical displacements of all of the moving contacts at the rail are given by
in which \({{\varvec{H}}}_{R}(\Omega )\) is the transfer function matrix of the track-ground system at the wheel/rail contact points.
Finite element model establishment
In real-world environments, machine vibrations and train-induced disturbances are unavoidable, and the complexity of the soil adds to the modeling challenges. Given these factors, we made several assumptions when establishing the model. We assumed that there were no other sources of disturbance during train operation, and we simplified the soil to a homogeneous condition. While these assumptions simplify the model, they help reduce the complexity of data collection and the large number of finite elements required.
The finite element model calculation domain is 200 m wide, 100 m long, and 30 m deep (Fig. 1). A total of 122,206 tennode tetrahedral elements were used to simulate the soil. The smallest element volume near the track was 5.75 e−5 m3, while the largest element volume at the model boundary was 88 m3. In this process, we considered a fixed axle spacing of 2 m and a train length of 13 m. The time interval for dynamic simulation was set to 0.005 s, with a total simulation duration of 15 s. Viscoelastic boundary conditions were applied at the model boundaries to minimize wave reflection near the boundaries. All surfaces, except for the ground surface, were fully constrained and employed viscoelastic artificial boundaries to ensure stress wave absorption. The equations are as follows:
where \({\sigma }_{\text{n}}^{0}\) and \({\tau }^{0}\) are the normal and tangential static stresses at the boundary of the main region, respectively. u and v are the normal and tangential displacements, respectively50.
The equilibrium equation for the entire model is as follows55,56:
where \([M]\) represents the mass matrix, \([C]\) represents the damping matrix, \([K]\) represents the stiffness matrix, and \(\{F(t)\}\) corresponds to the time-dependent load. \(\{\ddot{u}\}\), \(\{\dot{u}\}\)˙, and \(\{u\}\) are the acceleration vector, velocity vector, and displacement vector, respectively. The accuracy of the damping matrix \([C]\) is crucial as it directly affects the model’s vibration response. In the transient analysis of subsurface geotechnical structures, damping mainly manifests as internal friction and dissipation within the material. Therefore, Rayleigh damping is commonly used to calculate the damping matrix. Rayleigh damping theory simplifies the damping matrix as a linear combination of the mass matrix and stiffness matrix57.
where \(\alpha \) is the viscous damping component, and \(\beta \) is the hysteretic or solid or stiffness damping component. Combining the above equations, field investigation data, and the study by Ekanayake S.D51, it can be concluded that \(\alpha =2.128\) and \(\beta =4.1e-5\).
The tunnel is situated at a burial depth of 23 m, with an outer diameter of 8.5 m and an inner diameter of 7.7 m. Refer to Fig. 2 for detailed illustrations. Soil parameters are derived from geological exploration data; please consult Table 1 for specifics. The tunnel lining is constructed with C50 concrete material, while C20 concrete is utilized for the composite vibration isolation wall. Material properties are outlined in Table 2.
Verification of the model
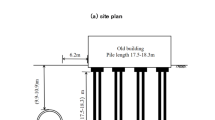
To facilitate model verification, measuring points are arranged on the ground surface and in the tunnels of the urban railway underground section for data collection. Select measuring point P0/P1/P2/P3/P4/P5/P6. The location relationship of each measuring point is depicted in Figs. 2 and 3. The left tunnel depicted in Fig. 3 is designated as a train tunnel, and it is specified that the vibration isolation wall is constructed 2 m away from the outer contour of the left tunnel. We employed the Donghua 2D001(Fig. 4a) accelerometer for data collection. The sensitivity of this sensor is 0.3 V·s2/m, with a maximum range of 20 m/s2, and a frequency response range from 0.25 Hz to 100 Hz. The data acquisition equipment used is the Donghua DH5922D (Fig. 4b) dynamic signal testing and analysis system.
Site diagram 58.
Data acquisition instrument 58.
According to the vehicle parameters and track structure parameters outlined in Tables 3 and 4, the wheel-rail interaction force is computed and then applied to the track within the finite element model. Subsequently, the power spectrum and maximum vertical vibration level of the data computed by the model were compared with the measured data to assess the reliability of the model. Refer to Figs. 5 and 6 for further details.
Comparison of measured and simulated power spectra at each measurement point. The black line represents the measured data, while the red line represents the simulated data. (a) Measurement point P0. (b) Measurement point P1. (c) Measurement point P2. (d) Measurement point P3. (e) Measurement point P4. (f) Measurement point P5. (g) Measurement point P6.
Analysis of the acceleration vibration effects of a single material vibration isolation wall at various frequencies
In numerous prior studies51,53, polystyrene foam (EPS) has served as a material for vibration isolation walls in investigating vibration isolation, demonstrating its effectiveness in this regard. Nonetheless, according to the American Society for Testing and Materials (ASTM) D6817 standard specification59, there exist 7 distinct types of EPS materials, each possessing significantly different properties, as depicted in Table 5. Therefore, drawing on prior research, we selected the measurement point 5 m away from the traffic tunnel to investigate the impact of varying the depth and thickness of vibration isolation walls made of different EPS materials on the frequency domain acceleration vibration isolation effect. We aimed to identify the optimal burial depth of the vibration isolation wall and determine which EPS material provides effective vibration isolation.
In Fig. 7, the frequency-domain acceleration curves under the influence of different isolation wall materials are largely overlapping. In Fig. 7d, except for the curve of EPS12, the curves for the remaining materials are almost identical to that of the EPS46 material.The findings depicted in Fig. 7 reveal that when the burial depth is 10 m, the peak acceleration in the frequency domain experiences not a reduction but rather an enhancement upon the installation of the vibration isolation wall. This amplification effect grows in magnitude with the thickness of the vibration isolation wall, reaching its maximum when the wall's thickness measures 2 m. Overall, variations in EPS materials exert minimal influence on the effective frequency band and peak acceleration of the vibration isolation wall. Nevertheless, the wall continues to demonstrate a notable attenuation effect on acceleration within the 32–52 Hz frequency range.
Frequency-domain acceleration at a depth of 10 m under the influence of EPS isolation walls of different thicknesses, with peak accelerations before and after applying isolation measures indicated. (a) Isolation wall thickness of 1 m. (b) Isolation wall thickness of 1.5 m. (c) Isolation wall thickness of 2 m. (d) Isolation wall thickness of 2 m.
In Fig. 8, the frequency-domain acceleration curves under the influence of different isolation wall materials are largely overlapping. In Fig. 8c, except for the curve of EPS22, the curves for the remaining materials are almost identical to that of the EPS46 material. In Fig. 8, when the vibration isolation wall is buried at a depth of 15 m, the peak acceleration in the frequency domain is enhanced only when the thickness of the wall is 2 m, while vibration reduction effects are observed at other thicknesses. However, the vibration isolation effect does not consistently improve with increasing thickness of the vibration isolation wall; the optimal effect is observed when the thickness is 1 m. Additionally, variations in EPS materials have minimal impact on the effective frequency band and overall vibration acceleration. Additionally, the vibration isolation wall demonstrates effective attenuation of acceleration within the 32–52 Hz frequency band.
Frequency-domain acceleration at a depth of 15 m under the influence of EPS isolation walls of different thicknesses, with peak accelerations before and after applying isolation measures indicated. (a) Isolation wall thickness of 1 m. (b) Isolation wall thickness of 1.5 m. (c) Isolation wall thickness of 2 m. (d) Isolation wall thickness of 2 m.
In Fig. 9, the frequency-domain acceleration curves under the influence of different isolation wall materials show significant overlap. In both Fig. 9b and d, except for the curve of EPS22, the curves for the remaining materials are almost identical to that of the EPS46 material. Similarly, in Fig. 9c, except for the curve of EPS39, the curves for the other materials are nearly identical to the curve of EPS46. In Fig. 9, with a burial depth of 20 m, all thicknesses of the vibration isolation wall exhibit notable vibration reduction effects. However, the efficacy of vibration reduction does not necessarily improve with increasing thickness. In fact, the optimal effect is achieved with a thickness of 1.5 m. Overall, variations in EPS materials show minimal impact on the vibration isolation effect. Moreover, the vibration isolation wall continues to demonstrate significant attenuation of acceleration within the 30–52 Hz frequency band.
Frequency-domain acceleration at a depth of 20 m under the influence of EPS isolation walls of different thicknesses, with peak accelerations before and after applying isolation measures indicated. (a) Isolation wall thickness of 1 m. (b) Isolation wall thickness of 1.5 m. (c) Isolation wall thickness of 2 m. (d) Isolation wall thickness of 2 m.
In Fig. 10, the frequency-domain acceleration curves under the influence of different isolation wall materials exhibit significant overlap. In Fig. 10, with the vibration isolation wall buried at a depth of 25 m, all thicknesses demonstrate effective vibration reduction. However, increasing the thickness of the vibration isolation wall does not necessarily improve its effectiveness. Optimal performance is achieved with a thickness of 2 m. Overall, while modifications in EPS materials may enhance the vibration isolation effect slightly, the overall improvement is marginal. Nevertheless, the vibration isolation wall continues to exhibit significant attenuation of acceleration within the 24–60 Hz frequency band.
Frequency-domain acceleration at a depth of 25 m under the influence of EPS isolation walls of different thicknesses, with peak accelerations before and after applying isolation measures indicated. (a) Isolation wall thickness of 1 m. (b) Isolation wall thickness of 1.5 m. (c) Isolation wall thickness of 2 m. (d) Isolation wall thickness of 2 m.
Based on the previous analysis, it was observed that when the burial depth of the vibration isolation wall is shallow, it may not effectively mitigate acceleration across all frequencies and could potentially lead to vibration amplification (e.g., when the burial depth is 10 m). As the burial depth of the vibration isolation wall increases, the enhancement effect of vibration gradually diminishes. Additionally, we observed that as the burial depth of the vibration isolation wall increases, its effective vibration isolation frequency range gradually expands. When the burial depth increases from 10 to 25 m, the effective vibration isolation frequency band expands from 32–52 Hz to 24–60 Hz.
The vibration isolation effect of composite vibration isolation walls under the influence of different proportions and relative positions
Based on the survey findings, it is evident that EPS materials incur relatively high costs. Constructing vibration isolation walls using significant quantities of EPS materials would thus entail substantial expenses. To reduce the cost of the vibration isolation wall, we opted to combine C20 concrete and EPS materials in specific thickness ratios for analysis of its vibration isolation performance. Additionally, we investigated the influence of different thickness ratios and the position of the vibration isolation wall material (Fig. 11) on the vibration isolation effect. For comparison purposes, we chose the data corresponding to the vibration isolation wall buried at a depth of 25 m, with EPS12 selected as the vibration isolation material.
We calculated the maximum peak acceleration, velocity, and displacement in the frequency domain for vibration isolation walls made of EPS12 at different thicknesses when buried at a depth of 25 m. To facilitate a comparison of the vibration isolation effects of single materials and composite walls with different thicknesses, we present the data in Table 6. In preparation for subsequent analysis, we categorize the thickness ratios of EPS materials and C20 concrete materials in composite vibration isolation walls as follows: EPS: C = 1:1, EPS: C = 2:1, EPS: C = 3:1, C: EPS = 1:1, C: EPS = 1:2 and C: EPS = 1:3. The positional arrangement of composite vibration isolation wall materials is as follows: “EPS: C” indicates the side of C20 concrete adjacent to the track, while “C: EPS” refers to the side of EPS material adjacent to the track.
To facilitate comparison of the enhanced vibration isolation effect achieved by increasing the thickness of a single material vibration isolation wall, we will calculate the isolation effect according to the following formula.
In the formula, a0 represents the maximum peak value in the frequency domain under a single material with a thickness of 1 m, and ai represents the maximum peak value in the frequency domain of vibration isolation walls with different material thicknesses.
Frequency domain peak acceleration vibration isolation effect of composite vibration isolation walls
It is evident from Fig. 12 that when the thickness ratio of the composite vibration isolation wall is 1:1, the thickness of the vibration isolation wall should not exceed 1.5 m; otherwise, the peak acceleration in the frequency domain will be enhanced, which will not achieve the same vibration isolation effect as using EPS material alone. Additionally, when using composite walls, the EPS material should be placed on the side away from the track. Additionally, combining vibration isolation walls of different thicknesses enhances the vibration isolation effect in certain frequency bands. Specifically, when the thickness of the vibration isolation wall is 1 m, the acceleration vibration isolation effect in the 35–46 Hz frequency band is enhanced. When the thickness of the vibration isolation wall is 1.5 m, the acceleration vibration isolation effect in the 32–38 Hz frequency band is enhanced. Similarly, with a wall thickness of 2 m, the acceleration vibration isolation effect in the 35–40 Hz frequency band is enhanced. Additionally, when the vibration isolation wall thickness is 2.5 m, the acceleration vibration isolation effect in the 43–50 Hz frequency band is enhanced.
It's observed from Fig. 13 that when the thickness ratio of the composite vibration isolation wall is 1:2 or 2:1, the thickness of the wall should not exceed 2 m, as it could lead to an increase in peak acceleration in the frequency domain. It’s worth noting that when constructing a composite vibration isolation wall, the section made of EPS material should be placed on the side close to the track. Additionally, composite vibration isolation walls with varying thicknesses can enhance the vibration isolation effect within specific frequency bands. With a thickness of 1 m, the acceleration vibration isolation improves in the 35–46 Hz frequency band. When the thickness reaches 1.5 m, the acceleration vibration isolation is enhanced in the 32–38 Hz and 61–71 Hz frequency bands. Similarly, a thickness of 2 m enhances the acceleration vibration isolation effect in the 35–40 Hz frequency band.
It is observed from Fig. 14 that when the thickness ratio of the composite vibration isolation wall is 1:3 or 3:1, the vibration isolation wall comprising EPS material should be positioned on the side closer to the track during construction. In addition, composite vibration isolation walls with different thicknesses can improve the vibration isolation effect in specific frequency bands. With a thickness of 1 m, the acceleration vibration isolation effect is enhanced in the 50–55 Hz frequency band; at 1.5 m thickness, the effect improves in the 35–38 Hz frequency band; at 2 m thickness, improvement is seen in the 28–42 Hz frequency band; and at 2.5 m thickness, enhancement is observed in the 44–50 Hz frequency band.
To streamline the analysis of the influence of the relative position of the vibration isolation material on the vibration isolation effect, we compute the effect using the following formula:
In the formula, a0 represents the peak acceleration in the frequency domain under a single material, while ai represents the peak acceleration in the frequency domain of the composite wall under different material thickness ratios and relative positions.
In Fig. 15, it's evident that the single-material vibration isolation wall achieves its optimal vibration isolation effect when the thickness is 2 m. Without altering the thickness and solely utilizing the composite vibration isolation wall, the vibration isolation effect can be enhanced by 16.58%. When employing a 1:2 composite vibration isolation wall with the EPS material positioned near the track, the optimal vibration isolation effect occurs at a thickness of 1.5 m, surpassing the effect of a single-material wall with a 2 m thickness. Moreover, it achieves a 28.8% enhancement in vibration isolation while consuming 1/3 less material. Conversely, when the EPS material is situated away from the track, the vibration isolation effect diminishes by -49.3%. In addition, when the ratio of the vibration isolation wall is 1:2 or 1:3, and the thickness of the vibration isolation wall is 1.5 m, the positional relationship of the materials has a huge impact on the vibration isolation effect. Improper material placement and improper composite isolation wall thickness can even enhance vibrations at the ground surface.
Frequency domain peak displacement vibration isolation effect of composite vibration isolation wall
According to standards60,61,62, most frequency domain analyses consider peak displacement as the allowable vibration threshold. Therefore, our analysis focused solely on peak displacement in the frequency domain. In Fig. 16, it's evident that the vibration isolation effectiveness of displacement increases with the thickness of a single material vibration isolation wall. The optimal performance is achieved with a thickness of 2.5 m. By maintaining this thickness and transitioning to a composite vibration isolation wall, the vibration isolation efficacy could further improve. Specifically, the potential enhancement could reach up to 30.73%.
When employing composite isolation walls, the isolation effect is influenced by both the proportions and thickness of the composite wall. After implementing composite vibration isolation walls, the reduction effect on peak displacement in the frequency domain typically surpasses that of single material vibration isolation walls. For ratios of vibration isolation walls at 1:1 or 1:2, positioning the EPS material near the track yields superior vibration isolation effects. The findings depicted in Fig. 16 indicate that compared to a composite vibration isolation wall with a thickness of 1 m, increasing its thickness yields diminishing enhancements in vibration isolation effects and may even lead to reduced effectiveness.
Frequency domain velocity vibration isolation effect of composite vibration isolation wall
In Fig. 17, when the composite wall ratio is 1:3 and EPS12 is positioned away from the trackside, the vibration isolation effect in other frequency bands surpasses that of a single-material vibration isolation wall, except for the frequency band near 12 Hz. At the same time, when EPS12 is positioned away from the track, the vibration isolation effect at frequency domain velocity is superior to that of single-material and composite vibration isolation walls of other proportions in the 2–5 Hz and 36–45 Hz frequency.
In Fig. 18, when the ratio of the composite vibration isolation wall is 1:3, its vibration isolation effect on frequency domain velocity is better than that of the single material vibration isolation wall in the frequency bands of 32–38 Hz and 60–72 Hz, and other proportions of composite isolation walls. When EPS12 is installed closer to the track, its vibration isolation effect in the frequency bands of 0–25 Hz and 42–70 Hz is better than when EPS12 is installed farther away from the track.
In Fig. 19, the composite vibration isolation wall exhibits a favorable vibration isolation effect in the 35–40 Hz frequency band. Furthermore, when EPS12 is positioned closer to the track, it also demonstrates an improved vibration isolation effect in the 62–72 Hz frequency band. When EPS12 is positioned closer to the track and the vibration isolation wall ratio is 1:1, it exhibits a favorable vibration isolation effect in the 17–40 Hz frequency band. When EPS12 is positioned closer to the track and the vibration isolation wall ratio is 1:3, it demonstrates a good vibration isolation effect in the 17–30 Hz and 32–55 Hz frequency bands.
According to the data depicted in Fig. 20, the optimal vibration isolation effect is achieved when the composite wall ratio is 1:1, with EPS12 positioned on the side away from the track. Moreover, when EPS12 is situated closer to the track, it also demonstrates a superior vibration isolation effect within the 42–60 Hz frequency band.
According to Fig. 21, when the thickness of a single-material vibration isolation wall is 2 m, the peak velocity in the frequency domain is the smallest. However, without changing the thickness of the vibration isolation wall and using only a composite vibration isolation wall, the vibration isolation effect can be improved by 16.95%. When the ratio of the composite vibration isolation wall is 1:1 and EPS12 is positioned on the side away from the track, the vibration isolation effect exhibits a consistent upward trend as the thickness of the vibration isolation wall increases. The vibration isolation effect increases significantly, reaching its peak when the vibration isolation wall is 2.5 m thick, achieving the optimal vibration isolation effect. The composite vibration isolation wall with a ratio of 1:1, particularly when EPS12 is positioned on the side away from the track, demonstrates a superior vibration isolation effect. Consequently, it is advisable to install EPS12 on the side away from the track.
Discussion
Through research, it was determined that the effectiveness of the vibration isolation wall increases progressively with the burial depth. Inappropriate burial depths may even exacerbate ground surface vibrations. When the vibration isolation wall is buried deeper than the tunnel, the variation in EPS material type has minimal impact on the wall's vibration isolation efficacy. Comparative analysis between single-material and composite vibration isolation walls reveals that composite structures typically exhibit superior vibration isolation properties. Additionally, when employing composite vibration isolation walls, the vibration isolation efficacy varies with the relative positioning of the composite materials.
Conclusion
This study initially developed a numerical model encompassing the train and the track plate to address the wheel-rail interaction force between the train and the rail. Subsequently, a finite element model incorporating the dynamic coupling of the rail-tunnel-soil was constructed, with the wheel-rail interaction force applied within this finite element model. The reliability of the model was verified by comparing simulation results with measured data. Next, the impact of single material EPS12 vibration isolation wall and composite vibration isolation wall (EPS12 and C20 concrete) on the vibration isolation frequency band and vibration isolation effect under different influencing factors was studied, and the following conclusions were drawn:
-
(1)
When the burial depth of the vibration isolation wall is shallow, it fails to effectively mitigate acceleration at all frequencies and may even amplify vibrations. However, as the burial depth of the vibration isolation wall increases, the vibration isolation effect gradually improves. Additionally, with the increasing burial depth of the vibration isolation wall, its effective vibration isolation frequency range gradually expands. The optimal vibration isolation effect is achieved when the burial depth of the vibration isolation wall surpasses that of the tunnel.
-
(2)
When the thickness of the single-material vibration isolation wall reaches 2 m, it exhibits a robust vibration isolation effect on both the peak acceleration and velocity in the frequency domain. Moreover, as the thickness of the single-material vibration isolation wall increases, the peak displacement gradually decreases.
-
(3)
The vibration isolation effect of a single-material vibration isolation wall is optimal when the thickness is 2 m, particularly evident in the peak acceleration within the frequency domain. Without altering the thickness, solely employing composite vibration isolation walls can enhance the vibration isolation effect by 16.58%. When the thickness of the single-material vibration isolation wall reaches 2 m, the peak velocity within the frequency domain is minimized. However, maintaining this thickness and transitioning solely to composite vibration isolation walls can enhance the vibration isolation effect by 16.95%. As the thickness of a single-material vibration isolation wall increases, the vibration isolation effect on displacement also increases, with the optimal effect observed at a thickness of 2.5 m. If the thickness remains constant and only a 2.5 m thick composite vibration isolation wall is employed, the vibration isolation effect can be enhanced by up to 30.73%. This illustrates that composite vibration isolation walls offer not only material savings and cost reduction but also an enhanced vibration isolation effect. Composite vibration isolation walls exhibit superior cost-effectiveness compared to single-material vibration isolation walls.
-
(4)
There are composite vibration isolation walls that are smaller in thickness than single-material vibration isolation walls, and their vibration isolation effect is better than that of single-material vibration isolation walls. This shows that, at appropriate proportions, composite vibration isolation walls have better vibration isolation performance than single material walls.
-
(5)
The effective vibration isolation frequency band of composite vibration isolation walls differs from that of single-material vibration isolation walls. Compared to single-material vibration isolation walls, when the thickness of the composite vibration isolation wall is 1 m, it exhibits a notable vibration isolation effect on both acceleration and velocity within the 35–46 Hz frequency band. Compared to single-material vibration isolation walls, when the thickness of the composite vibration isolation wall is 1.5 m, it demonstrates a significant vibration isolation effect on both acceleration and velocity within the 32–38 Hz frequency band. Compared to single-material vibration isolation walls, when the thickness of the composite vibration isolation wall is 2 m, it exhibits a notable vibration isolation effect on both acceleration and velocity within the 35–40 Hz frequency band.
-
(6)
When strict acceleration control requirements are mandated in the area necessitating the installation of a vibration isolation wall, it is advisable to employ a C: EPS12 = 1:2 composite vibration isolation wall with a thickness of 1.5 m, positioning the EPS material close to the trackside. If there are stringent acceleration control requirements in the area, necessitating the installation of a vibration isolation wall, a C: EPS12 = 1:1 composite vibration isolation wall with a thickness of 2.5 m, positioning the EPS material on the side away from the track, should be employed. If stringent displacement control requirements exist in the area and a vibration isolation wall is necessary, a 1:3 composite vibration isolation wall with a thickness of 2.5 m, positioning the EPS material close to the side of the track, should be employed.
Data availability
The data that support the findings of this study are available from the corresponding author, [F.T. Wang], upon reasonable request.
References
Yang, J. et al. Prediction and mitigation of train-induced vibrations of large-scale buildings constructed on subway tunnel. Sci. Total Environ. https://doi.org/10.1016/j.scitotenv.2019.02.397 (2019).
Ma, M., Xu, L., Du, L., Wu, Z. & Tan, X. Prediction of building vibration induced by metro trains running in a curved tunnel. J. Vib. Control https://doi.org/10.1177/1077546320930910 (2021).
Cheng, Z., Zhang, Q. & Shi, Z. Floating slab track with inerter enhanced dynamic vibration absorbers. Vehicle Syst Dyn. 61(2), 589–615. https://doi.org/10.1080/00423114.2022.2053170 (2022).
Ngo, T. & Indraratna, B. Mitigating ballast degradation with under-sleeper rubber pads: Experimental and numerical perspectives. Comput. Geotech. https://doi.org/10.1016/j.compgeo.2020.103540 (2020).
Zhao, Z., Wei, K., Ding, W., Du, W. & Li, H. UM-SIMULINK Co-simulation for the vibration reduction optimization of a magnetorheological damping steel-spring floating slab track. Constr. Build. Mater. https://doi.org/10.1016/j.conbuildmat.2021.124923 (2021).
Pan, P., Zeng, Y., Yang, J. & Zhang, D. Numerical study of isolation in the backfill zone of foundation pit method to reduce railway generated vibration in high-rise buildings. Struct. Des. Tall. Special Build. https://doi.org/10.1002/tal.1691 (2020).
Sitharam, T. G., Sebastian, R. & Fazil, F. Vibration isolation of buildings housed with sensitive equipment using open trenches—Case study and numerical simulations. Soil. Dyn. Earthq. Eng. https://doi.org/10.1016/j.soildyn.2018.08.033 (2018).
Zeng, Y., Pan, P., Zhang, D. & Yang, J. Experimental study of isolation in the backfill zone of the foundation pit (IBF) method to reduce ground-borne vibration in buildings. Eng. Struct. https://doi.org/10.1016/j.engstruct.2019.109740 (2020).
Sun, X., Ma, M., Jiang, B. & Cao, R. Ground vibration from freight railway: Environmental impact and potential mitigation measure at propagation path. Environ. Sci. Pollut. R https://doi.org/10.1007/s11356-022-18955-z (2022).
Cheng, Z. et al. Seismic vibrations attenuation via damped layered periodic foundations. Eng. Struct. https://doi.org/10.1016/j.engstruct.2020.110427 (2020).
Pan, P., Shen, S., Shen, Z. & Gong, R. Experimental investigation on the effectiveness of laminated rubber bearings to isolate metro generated vibration. Meas. J. Int. Meas. Confed https://doi.org/10.1016/j.measurement.2017.07.019 (2018).
Sheng, T. et al. Experimental study on a geosynthetics isolator for the base vibration isolation of buildings neighboring metro transportation. Geotext. Geomembr. https://doi.org/10.1016/j.geotexmem.2021.03.001 (2021).
Lombaert, G., Degrande, G. & Vanhauwere, B. The control of ground-borne vibrations from railway traffic by means of continuous floating slabs. J. Sound Vib. 297(3–5), 946–961. https://doi.org/10.1016/j.jsv.2006.05.013 (2006).
Costa, P. A., Calçada, R. & Cardoso, A. S. The control of ground-borne vibrations from railway traffic by means of continuous floating slabs. Soil Dyn. Earthq. Eng. 42, 137–150. https://doi.org/10.1016/j.soildyn.2012.06.014 (2012).
Talbot, J. P. & Hunt, H. E. M. A generic model for evaluating the performance of base-isolated buildings. J. Low Freq. Noise V A. 22(3), 149–160. https://doi.org/10.1260/026309203322986627 (2003).
Fiala, P., Degrande, G. & Augusztinovicz, F. Numerical modelling of groundborne noise and vibration in buildings due to surface rail traffic. J. Sound Vib. 301(3–5), 718–738. https://doi.org/10.1260/026309203322986627 (2007).
Zhang, X., Luo, W. L., Lin, B. H., Qin, J. F. & Liao, C. Vibration isolation effects of barriers filled with ceramsite and sand: Full-scale model test and numerical investigation. J. Constr. Build. Mater. 341, 127789 (2022).
Lai, C. G., Foti, S., Rix, G. J. & O’Neill, A. Propagation of data uncertainty in surface wave inversion. J. Environ. Eng. Geophys. https://doi.org/10.2113/JEEG10.2.219 (2005).
Kouretzis, G. P., Andrianopoulos, K. I., Sloan, S. W. & Carter, J. P. Analysis of circular tunnels due to seismic P-wave propagation, with emphasis on unreinforced concrete liners. Comput. Geotech. https://doi.org/10.1016/j.compgeo.2013.08.012 (2014).
Xu, L. & Ma, M. Analytical solution of ground-borne vibration due to a spatially periodic harmonic moving load in a tunnel embedded in layered soil. J. Zhejang Univ. Sci. A https://doi.org/10.1631/jzus.A2200385 (2023).
Yao, J. B., Zhao, R. T., Zhang, N. & Yang, D. J. Vibration isolation effect study of in-filled trench barriers to train-induced environmental vibrations. J. Soil Dyn. Earthq. Eng. https://doi.org/10.1016/j.soildyn.2019.105741 (2019).
Pu, X., Shi, Z. & Xiang, H. Feasibility of ambient vibration screening by periodic geofoam-filled trenches. Soil. Dyn. Earthq. Eng. https://doi.org/10.1016/j.soildyn.2017.10.022 (2018).
Coulier, P., Cuellar, V., Degrande, G. & Lombaert, G. Experimental and numerical evaluation of the effectiveness of a stiff wave barrier in the soil. Soil. Dyn. Earthq. Eng. https://doi.org/10.1016/j.soildyn.2015.04.007 (2015).
Dijckmans, A., Ekblad, A., Smekal, A., Degrande, G. & Lombaert, G. Efficacy of a sheet pile wall as a wave barrier for railway induced ground vibration. Soil Dyn. Earthq. Eng. 2016, 8455–8469. https://doi.org/10.1016/j.soildyn.2016.02.001 (1984).
Maleska, T., Nowacka, J. & Beben, D. Application of EPS geofoam to a soil–steel bridge to reduce seismic excitations. Geosciences https://doi.org/10.3390/geosciences9100448 (2019).
Xian-Jian, Y. & Prakash, S. Ground Vibration Isolated by Silo and Pile Barriers (University of Missouri-Rolla, Rolla, 1991).
Jiang, Y. et al. Vibration attenuation analysis of periodic underground barriers using complex band diagrams. Comput. Geotech. https://doi.org/10.1016/j.compgeo.2020.103821 (2020).
Takemiya, H. Field vibration mitigation by honeycomb WIB for pile foundations of a high-speed train viaduct. Soil. Dyn. Earthq. Eng. https://doi.org/10.1016/j.soildyn.2003.07.005 (2004).
Sheng, X., Jones, C. J. C. & Thompson, D. J. Prediction of ground vibration from trains using the wavenumber finite and boundary element methods. J. Sound. Vib. https://doi.org/10.1016/j.jsv.2005.08.040 (2006).
Shrivastava, R. K. & Rao, N. S. V. K. Response of soil media due to impulse loads and isolation using trenches. Soil. Dyn. Earthq. Eng. 22, 695–702. https://doi.org/10.1016/S0267-7261(02)00060-X (2002).
Celebi, E. et al. Field experiments on wave propagation and vibration isolation by using wave barriers. Soil. Dyn. Earthq. Eng. https://doi.org/10.1016/j.soildyn.2008.08.007 (2009).
Barkan, D. D. Dynamics of Bases and Foundations (McGraw-Hill, 1962).
Woods, R. D. Screening of surface wave in soils. J. Soil. Mech. Found. Div. 94(4), 951–979 (1968).
Toygar, O., Ulgen, D. & Fidan, N. B. Assessing vibration isolation performance of single and coupled wave barriers through field experiments. Constr. Build. Mater. 354, 129156 (2022).
Lee, V. W. A note on the scattering of elastic plane waves by a hemispherical canyon. Int. J. Soil Dyn. Earthq. Eng. 1, 122–129. https://doi.org/10.1016/0261-7277(82)90003-1 (1982).
Aviles, J. & Sanchez-Sesma, F. J. Piles as barriers for elastic waves. J. Geotech. Eng. 109, 1133–1146. https://doi.org/10.1061/(ASCE)0733-9410(1983)109:9(1133) (1983).
Saikia, A. Numerical study on screening of surface waves using a pair of softer backfilled trenches. Soil Dyn. Earthq. Eng. 65, 206–213. https://doi.org/10.1016/j.soildyn.2014.05.012 (2014).
Younesian, D. & Sadri, M. Performance analysis of multiple trenches in train-induced wave mitigation. J. Low Freq. Noise V A 33, 47–64. https://doi.org/10.1260/0263-0923.33.1.47 (2014).
Esmaeili, M., Zakeri, J. A. & Mosayebi, S. A. Investigating the optimized open V-shaped trench performance in reduction of train-induced ground vibrations. Int. J. Geomech. 14, 04014004. https://doi.org/10.1061/(ASCE)GM.1943-5622.0000331 (2013).
Zakeri, J. A., Esmaeili, M. & Mosayebi, S. A. Numerical investigation of the effectiveness of a step-shaped trench in reducing train-induced vibrations. P I Mech. Eng. F-J Rai 228(3), 298–306. https://doi.org/10.1177/0954409712473094 (2014).
Bo, Q., Ali, L. & Irini, D.-M. Numerical study of wave barrier and its optimization design. Finite Elem. Anal. Des. https://doi.org/10.1016/j.finel.2014.02.002 (2014).
Liyanapathirana, D. & Ekanayake, S. Application of EPS geofoam in attenuating ground vibrations during vibratory pile driving. Geotext. Geomembr. 44, 59–69. https://doi.org/10.1016/j.geotexmem.2015.06.007 (2016).
Hamdan, N., Laghrouche, O., Woodward, P. & Mahmood, M. Ground vibration reduction analysis using a frequency-domain finite element approach. Constr. Build. Mater. 92, 95–103. https://doi.org/10.1016/j.conbuildmat.2014.04.140 (2015).
Murillo, C., Thorel, L. & Caicedo, B. Ground vibration isolation with geofoam barriers: Centrifuge modeling. Geotext. Geomembr. 27, 423–434. https://doi.org/10.1016/j.geotexmem.2009.03.006 (2009).
Ulgen, D. & Toygar, O. Screening effectiveness of open and in-filled wave barriers: A full-scale experimental study. Constr. Build. Mater. 86, 12–20. https://doi.org/10.1016/j.conbuildmat.2015.03.098 (2015).
Xiong, W. & Li, Y. Seismic isolation using granulated tire-soil mixtures for less-developed regions: Experimental validation. Earthq. Eng. Struct. D 42, 2187–2193. https://doi.org/10.1002/eqe.2315 (2013).
Alzawi, A. & El Naggar, M. H. Full scale experimental study on vibration scattering using open and in-filled (GeoFoam) wave barriers. Soil Dyn. Earthq. Eng. 31, 306–317. https://doi.org/10.1016/j.soildyn.2010.08.010 (2011).
Celebi, E. et al. In-situ measurements and data analysis of environmental vibrations induced by high-speed trains: A case study in north-western Turkey. Soil Dyn. Earthq. Eng. 156(107211), 2. https://doi.org/10.1016/j.soildyn.2022.107211 (2022).
Coulier P, Dijckmans A, Cu’ellar V, Ekblad A, Smekal A, Degrande G, Lombaert G. Numerical and experimental study of stiff wave barriers for the mitigation of railway induced vibrations. Proceedings of ISMA. In Proc. International Conference on Noise and Vibration Engineering, 2014; 3429–3443.
Faizan, A. A., Kirtel, O., Celebi, E., Zulfikar, A. C. & Goktepe, F. Experimental validation of a simplified numerical model to predict train-induced ground vibrations. Comput. Geotech. 141, 104547. https://doi.org/10.1016/j.compgeo.2021.104547 (2022).
Ekanayake, S. D., Liyanapathirana, D. S. & Leo, C. J. Attenuation of ground vibrations using in-filled wave barriers. Soil Dyn. Earthq. Eng. 67, 290–300. https://doi.org/10.1016/j.soildyn.2014.10.004 (2014).
Sitharam, T. G., Sebastian, R. & Fazil, F. Vibration isolation of buildings housed with sensitive equipment using open trenches—case study and numerical simulations. Soil Dyn. Earthq. Eng. 115, 344–351. https://doi.org/10.1016/j.soildyn.2018.08.033 (2018).
Jazebi, M., Ahmadi, M. M. & Sahebalzamani, P. Efficiency of in-filled (geofoam) trenches in mitigating train-induced vibrations: A case study of Tehran-Tabriz railway. Constr Build Mater. 309, 125075. https://doi.org/10.1016/j.conbuildmat.2021.125075 (2021).
Wang, F. et al. Green’s function of multi-layered poroelastic half-space for models of ground vibration due to railway traffic. Earthq. Eng. Eng. Vib. 16, 311–328. https://doi.org/10.1007/s11803-017-0384-y (2017).
Du, X. L. Theories and Methods of Wave Motion for Engineering (Science Press, 2009).
Ma, H. W. & Wu, B. Elastic Dynamics and Its Numerical Methods (China Building Material Industry Publishing House, 2000).
Zhang, Q. L., Liu, L. Y. & Li, J. Y. Numerical analysis of ground vibration amplification phenomenon caused by subway operation. Noise Vib. Ctrl. 35(2), 116–120. https://doi.org/10.3969/j.issn.1006-1335.2015.02.027 (2015).
Cao, S. et al. Effects of train speed and passenger capacity on ground vibration of underground suburban railways. Sci. Rep. 14, 10531 (2024).
D6817/D6817M-17. Standard Specification for Rigid Cellular Polystyrene Geofoam. United States of America; 2021
GB50868, Allowable Vibration Standards for Construction Projects. China; 2013.
GB 50463, Engineering Vibration Isolation Design Standards. China; 2019.
GB 51076, Technical Specifications for Anti-Microvibration Engineering in the Electronics Industry. China; 2015.
Acknowledgements
This work was supported by the Fund of State Key Laboratory of Bridge Engineering Structural Dynamics (No. 202104), the Key Laboratory of Bridge Earthquake Resistance Technology, Ministry of Communications, PRC, the Scientific Research Fund of the Institute of Engineering Mechanics, China Earthquake Administration (No. 2021D32), the Heilongjiang Province Ecological Environment Protection Research Project (No. HST2023JC010).
Funding
Fund of State Key Laboratory of Bridge Engineering Structural Dynamics, No. 202104, Key Laboratory of Bridge Earthquake Resistance Technology, Ministry of Communications, PRC, the Scientific Research Fund of the Institute of Engineering Mechanics, China Earthquake Administration, No. 2021D32.
Author information
Authors and Affiliations
Contributions
D. Li: Formal analysis, Data curation, Investigation, Methodology, Software, Visualization, Writing—original draft; D.D Qian: Data curation, Investigation, Funding acquisition, Resources; S. S Cao: Investigation, Funding acquisition, Resources; C. Chen: Funding acquisition, Resources; J. L Yin: Data curation, Investigation; Z. J You: Data curation, Investigation; H. K Wang: Data curation, Investigation; L. Z Zhang: Funding acquisition, Resources; X. D Shi: Funding acquisition, Resources; F. T. Wang: Funding acquisition, Resources, Project administration, Funding acquisition.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Li, D., Qian, D., Cao, S. et al. Investigation of the vibration isolation effect of composite vibration isolation walls on ground surface vibrations in deep tunnels of suburban railways. Sci Rep 14, 19093 (2024). https://doi.org/10.1038/s41598-024-70098-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-70098-y