Introduction

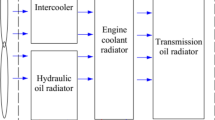
Engine bay thermal management is a critical measure for the vehicle performance development process. The design process considered the heat dissipation inside the engine bay including the cooling system coolant status and thermally sensitive components under extreme heating scenarios. This process also needs to ensure engine coolant temperature does not exceed the cut-off limitation at various operation scenarios while providing a normal operating temperature range for all electronic components1,2. A well-designed cooling system could allow the engine stays at optimal operating temperature. In a liquid cooling system, coolant flow through water channels extract heat from the cylinder head and body, then dissipate the heat to cooling air via the heat exchanger. The numerical investigation of a cooling system includes the air side and coolant side. On the airside, Computational Fluid Dynamics (CFD) is the main method to evaluate the cooling performance of underhood components. There are two main scenarios of cooling airflow, one is the ram air from high vehicle speed, and the other is the cooling fan when the vehicle speed is low. The path of cooling air could affect the air flow rate through the radiator hence affecting the engine's cooling capacity. Cooling air typically flows through components such as the grille, front bumper, condenser, radiator, fan, fan shield, and engine body. When cooling air approaches the front surface of the radiator, the flow resistance of the heat exchanger results in the airflow at lower momentum which helps the cooling air take way more heat.

Thermal management of engine bay can be divided into two types: steady state condition and soak condition. Steady state condition can quickly obtain the thermal performance of the vehicle when it reaches thermal balance. In the soak condition, key-off is carried out after the vehicle runs under high load to investigate the temperature change of the thermal sensitive element of the vehicle during the time in the whole soak condition, so as to evaluate the potential risk of thermal fatigue. Since the steady-state condition is to investigate the coolant temperature and the surface temperature of the thermal sensitive components when the vehicle reaches the state of thermal balance, this index cannot reflect the relationship with time, so the evaluation system of steady-state condition has certain limitations3,4. Thermal fatigue usually occurs after the engine is key-off, because a large amount of heat will gather in the engine bay for a short time during pre-soak, and after the cooling fan stops rotating, the main form of heat transfer in the engine bay will be changed into the natural convection mode driven by thermal buoyancy5,6. When the fan has fully stopped, buoyancy-driven natural convection takes over and becomes the main heat transfer drive which results in a heat rise in the engine bay. In addition, the thermally sensitive components keep receiving heat from the exhaust system which is still hot. Due to the lack of forced convection to take heat away from the engine bay, the thermally sensitive components may have a rapid temperature rise in a short period, then gradually cool down together with other engine parts7,8. Because of the material differences between components, the amount and duration of temperature rise are part-dependent. If a thermally sensitive component exceeds its temperature limit after the fan shut off and stays above limits for a while, this is known as a thermal fatigue state. Staying in the thermal fatigue state for a long period would result in component thermal failure. The purpose of studying hot soak is to simulate the temperature rise of the thermally sensitive components and obtain a temperature curve during this period9. This provides evidence to evaluate the whole vehicle's thermal performance.

Due to the transient property of the soak condition and the co-existence of various heat transfer phenomena (heat conduction, convection and radiation) between a large number of solid components and the coolant, there are huge challenges in the property development of the soak condition10. When using commercial software based on Navier–Stokes equations to simulate Soak conditions, it is necessary to simplify some small components in the engine bay, such as harnesses, pipelines, etc. Because the surface mesh used in this kind of software is a regular triangle mesh, the surface with large curvature change cannot be accurately restored. At the same time, the first layer of boundary layer mesh near the wall is generated by surface mesh, so the distribution of volume mesh will bring error or even non-convergence of calculation. Therefore, it is necessary to simplify the model in the engine bay. In addition, because the physical problem requires a long time transient simulation, and the Navier–Stokes method simulation needs to solve the strongly nonlinear convection term at each time step, the computational efficiency is low, and the numerical viscosity is high and the error is large. For many years, the industry has been trying to find reliable and efficient simulation tools and simulation methods to simulate this phenomenon11.

With the rapid development of fluid dynamics and computer hardware and software technology, CFD simulation has become an indispensable practical means to study the thermal management system of engine room. Through numerical simulation, not only can get the flow characteristic parameters required for product design in the early stage of new vehicle design, but also can master the detailed situation inside the flow field. When vehicle undergoes soak stage, the air flow and the associated convective heat transfer around and within the engine bay are driven by the buoyancy effect12,13. In the buoyancy flow, a non-dimensional parameter is usually used to correlate heat and mass transfer due to thermally induced natural convection, which is often described by the Grashof number, Gr, as defined in Eq. (1)

$$\begin{array}{c}Gr=g\beta \Delta T{L}^{3}{\upsilon }^{-2}\end{array}$$
(1)

where g is g is the gravitational acceleration due to Earth, \(\beta \) is the coefficient of thermal expansion, \(\Delta T\) is the average temperature difference between a solid surface and bulk fluid, L is the characteristic length, \(\upsilon \) is the kinematic viscosity. Grashof Number approximates the ratio of the buoyancy to the viscous force acting on a fluid. Like the Reynolds number (Re), the Gr number can categorize the natural convection to laminar flow, transition, and turbulence flow. The heat transfer coefficient h can be obtained from the Nusselt number from Eq. (2).

$$h=\left(Nu\cdot k\right)/L$$
(2)

The Nusselt number is a function of \(Pr\) and \(Gr\) such as in Eq. (3). And k is thermal conductivity of the fluid. Ra represents Rayleigh number which is the product of \(Pr\) and \(Gr\).

$$Nu=f\left(Ra,Pr\right)=f\left(Pr\cdot Gr,Gr\right)$$
(3)

where k is the thermal conductivity of the fluid. Ra, the Rayleigh number, is the product of Pr and Gr. For a vertical plate, Nu is expressed in Eq. (4)

$$Nu=\left\{\begin{array}{c}{0.59\left(Ra\right)}^\frac{1}{4},({10}^{4}<Ra<{10}^{9})\\ {0.1\left(Ra\right)}^\frac{1}{4},({10}^{9}<Ra<{10}^{13})\end{array}\right.$$
(4)

Chen et al.14 numerically investigated the buoyancy-driven flow structure in a simplified under-bonnet model with open enclosure mimicking the under-bonnet soak condition. A simplified engine block and exhaust cylinders were included to represent the heat sources. The Grashof numbers used in this study were around 3 × 108 and 4 × 105 at the nearby regions of the engine block and exhaust respectively. The transient simulation was carried out using ANSYS Fluent. The transient simulation with time-steps from 0.01 s to 0.001 s was run for 60 s of physical time before reaching a steady state result. The computing power used in this study was 32 CPUs with total running time of 12 and 85 h for coarse (with mesh size of 5 mm) and fine (of 1 mm) mesh cases, respectively. The buoyancy-driven flow and temperature fields modelled were compared with measurement data by particle image velocimetry and thermocouples15. An overall good agreement was found in the air velocities and engine block wall temperatures, although some discrepancies were observed in one side of the block attributed to the less restricted space that promoted larger recirculating motion calculated from the simulation. It was emphasised that the transient numerical approach was necessary to obtain meaningful buoyancy driven flow solution. Although buoyance-driven air flow was well evaluated, the heat transfer to the metal parts and the heat transfer from the metal parts to the internal fluids were not in the scope of the reported study.

In 2008, Weidmann from Daimler company proposed a coupled method to predict air and engine components. In this method, STAR-CD is used to calculate airflow and flow field temperature as a steady-state simulation while using RadTherm or PERMAS as a thermal solver to analyze solid temperature using the transient simulation method. The heat flux at the interface between the CFD solver and thermal solver is exchanged at a preset time step size using MPCCI16. This method reduced computational cost due to its steady state flow solving method, but simplified temperature and flow coupling. Even that took 10 days to calculate. In 2010, D.Mukutmoni published the Numerical Simulation of Transient Thermal Convection of Heated Plate17, which described the detailed transient simulation of heat transfer of a plate in an enclosed chamber, it is similar to an important such thermal scenario in vehicles is the so called key-off condition. In a key-off, a vehicle moving at a constant speed is stopped and the engine and fans are turned off. Such a scenario could lead to thermal issues of components that are close to heat sources. This is because while the convective cooling of these components is abruptly reduced immediately after key-off, the thermal radiation from the heat sources level off more gradually. As a result of the initial imbalance, the temperatures of some automotive components typically increase sharply at the onset before dropping. It is important to know from the design point of view, the value and duration of the elevated temperatures since these affect the durability and reliability of the components. However, when expanding the soak analysis of the engine room, it is necessary to consider the influence of the complex structure in the engine room, the material properties of the components and the processing technology on the soak condition. The simulation accuracy is still uncertain. In 2015, Tristan Donley published Thermal Design Evaluation of Construction Vehicles using a Simulation-Based Methodology18, which depicts the natural convection scenario of a stationary vehicle in key-off status. The article has a detailed description of the engine bay temperature profile and coolant temperature. The temperature difference of coolant obtained by this method is 4 °C, and the temperature difference of some components is 6 °C. At the same year, Minovski et al., upon the studies on the simplified engine bay geometry, the transient simulation method for the buoyance-driven convection flow in the engine bay was developed further to apply in passenger vehicles for unsteady thermal management19.

Utilizing the LBM for aero-thermal coupling simulations, with its numerical stability and robustness, allows for accurate transient thermal convection, thermal radiation, and analyze the heat transfer problem in the engine bay after the engine key-off. The research enables the assessment of potential risks of thermal damage and thermal fatigue within the engine bay.

Lattice Boltzmann methodology

The paper mainly researches the LBM method to analyze the heat transfer problem in the engine compartment after the engine key-off. Based on the advantages of LBM, the numerical analysis of long transient hot dip process is carried out to accurately predict the risk of thermal fatigue and thermal damage of thermal components and provide a scientific design reference for the subsequent operation time control strategy of cooling fan. The software developed by the LBM method is used to accurately solve the transient convection, radiation and heat conduction problems. At the same time, the material properties of the vehicle were calibrated based on the experimental results of pre-soak condition through the method of data origin management, so as to obtain the real material properties, and then simulate underhood cooling under the soak condition to identify the potential risk of thermal damage and thermal fatigue state.

At the same time, the material properties of the vehicle were calibrated based on the experimental results of pre-soak condition through the method of data origin management, so as to obtain the real material properties, and then simulate underhood cooling under the soak condition to identify the potential risk of thermal damage and thermal fatigue state.

The lattice Boltzmann method is used to simulate the flow field

Lattice Boltzmann Method (LBM) based commercial solver, PowerFLOW is used for fluid domain simulation to capture buoyancy-driven transient flow for engine bay soak. PowerFLOW uses a LBM approach. Different from the traditional CFD approach via solving the Navier–Stokes equations, LBM is based on statistical distribution function to describe the macroscopic behavior of fluid. LBM models the fluid consisting of fictive particles, and such particles perform consecutive propagation and collision processes over a discrete lattice. Bhatnagar Gross and Krook's (BGK) model for relaxation to equilibrium via collisions between the molecules of a fluid, is shown in Eq. (5)

$$f({\varvec{x}}+{\varvec{\xi}},t+1)-f({\varvec{x}},t)=\frac{1}{\tau }[f({\varvec{x}},t)-{f}^{eq}({\varvec{x}},t)]$$
(5)

where in \(f\equiv f\left({\varvec{x}},{\varvec{\xi}},t\right)\) described the sigle particle number density \(f\) at the time \(t\) and the position \(\overrightarrow{x}\) and also with the velocity \({\varvec{\xi}}\) , \(\tau \) is the relaxation time due to collision, and \({f}^{eq}\) are the equilibrium density which is described by the Maxwell–Boltzmann equation. As shown in Fig. 1, the Boltzmann Equation along with the BGK operator is discretized on a three-dimensional cubic lattice using a D3Q19 model.

Fig. 1
figure 1

Finite Difference scheme for Boltzmann Equation.

Full size image

Maxwell–Boltzmann equilibrium distribution function is shown in Eq. (6)

$${f}^{eq}\equiv \frac{\rho }{{\left(2\pi RT\right)}^\frac{D}{2}}\text{exp}\left[-\frac{{\left(\xi -{\varvec{u}}\right)}^{2}}{2\theta }\right]$$
(6)

where R is ideal gas constant, \(D\) is spatial dimension, \(\theta\) is standardized temperature based on \(\theta ={K}_{B}T/m\), where KB is Boltzmann constant, \(T\) is temperature and m particle mass. \(u\) is fluid velocity. LBM simulate gas and liquid based on microscopic models and mesoscopic kinetic equations. The macroscopic dynamics and density distribution is based on the Eq. (7)

$$\left\{\begin{array}{c}\rho ={\sum }_{i}{f}_{i}\left({\varvec{x}},t\right)\\ \rho u={\sum }_{i}{{\varvec{u}}}_{{\varvec{i}}}{f}_{i}\left({\varvec{x}},t\right)\\ \rho \varepsilon ={\sum }_{i}\frac{1}{2}{\left({{\varvec{\xi}}}_{{\varvec{i}}}-{\varvec{u}}\right)}^{2}{f}_{i}\left({\varvec{x}},t\right)\end{array}\right.$$
(7)

where \(\rho \) is density, \(u\) is velocity, \(\varepsilon \) is energy density and the index i = 0, 1, …, q−1 enumerates the direction. Three microscopic processes are used in LBM to simulate fluid behavior, including particle interaction, particle surface interaction and flow particle motion. The Lattice Boltzmann model used in Digital Physics20, particles exist at discrete locations in space, shown in the diagram (Fig. 2) where particles reside on a cubic lattice composed of voxels and surfels. Surfels are surface elements that occur where the surface (of which geometry can be arbitrary) of a body intersects the fluid. During the simulation, particles interact as they move from voxel to voxel during discrete intervals of time with discrete speeds. The particle density distribution functions are tracked when millions of particles move in each direction at each voxel. Particles in the same voxel collide and change speed and/or direction while conserving total mass, momentum and energy in the voxel (particle to particle interactions and advection). For the particle to surface interations and advection, particles that would hit a surfel whining a timestep are first gathered by the surfel. The surface-collision process enforces the conservation of mass while exchanging momentum and energy with desired boundary condition specification. The amount of momentum change corresponds to pressure and friction. After the described voxel-to-surface advection process, the gathered particles are reflected and returned to the fluid voxels.

Fig. 2
figure 2

Diagram of the particle/surfaces.

Full size image

Compared with existing commercial software, the advantages of LBM are as follows: (1) In terms of algorithm: The LBM algorithm is simple, which is a linear operation plus a relaxation process. It is easier to solve the nonlinear partial differential equation of N-S equation by using statistical method to study the motion law of particles. (2) High parallel computing efficiency: Because LBM is a linear equation, it is not necessary to calculate the strongly nonlinear convection term in the solution process, which is suitable for GPU acceleration technology. Compared with the N-S equation, the computational efficiency of the LBM is much higher than that of the N-S method at the same spatial discrete resolution. (3) Multi-physics coupling: LBM can conveniently simulate multi-physics coupling problems, such as fluid-thermal coupling and fluid–solid coupling. By adjusting the collision term and introducing different distribution functions, LBM can directly simulate heat conduction, diffusion and other phenomena. (4) Numerical stability and robustness: LBM has high numerical stability and robustness in high Reynolds number flow and nonlinear heat transfer problems. By adjusting the relaxation time and other parameters, the numerical error and stability can be controlled21.

PowerFLOW utilizes LBM solver and a modified RNG turbulence model to resolve the subgrid-scale. It is an inherently unsteady solver with very low artificial diffusivity. Thus, it resolved well for complex 3-D physics. In addition, the advanced wall function is also effective even for very low y +. These features make the method very robust at all grid resolutions and can accurately capture flow separation phenomena. Details on turbulence modeling are available in Chen.

The method can also solve buoyancy driven flow. The heat transfer coefficient (HTC) can be calculated through heat flux q, near wall temperature Twall and characteristic temperature Tref, according to the Eq. (8)

$$\begin{array}{c}HTC=q/({T}_{wall}-{T}_{ref})\end{array}$$
(8)

Here HTC is obtained by the CFD solver and passes the field value to the thermal solver which will handle conduction and radiation heat transfer.

Coupling simulation method

This study used the CFD solver coupled with a thermal solver to resolve both the fluid and solid model on the vehicle soak cooldown scenarios. In the coupled simulation, all surface heat transfer is calculated by the thermal solver while CFD calculates the fluid flow field, fluid temperature, and HTC. The wall boundary conditions for fluid are wall temperature coming from the thermal solver, while the near wall fluid temperature and near wall HTC are supplied to the thermal solver.

Heat transfer between fluid and solid driven by natural convection was simulated in the key-off soak condition. During the soak period, the flow field and temperature field both change with time ranging from minutes to hours. One particular challenge is the time scale involved in soak simulation can be very large. If the simulation accuracy is not guaranteed, it would not support product development. In addition, the long transient simulation is a challenging job itself. This is because finite volume-based CFD solvers typically used an under-relaxation factor to treat pressure-momentum coupling which could effectively solve steady-state flow. However, the under-relaxation method is not as effective for transient problems, as even with an implicit scheme, the time step size is still limited by CFL number, plus, the solver needs to solve the Poisson equation for pressure at each time step. This makes the computational cost of the long transient simulation too high to be practical. Hence we used PowerFLOW and PowerTHERM coupling to reduce computational cost. PowerTHERM is a thermal solver which considered heat conduction and radiation between solids. Figure 3 showed the flowchart of this transient simulation method.

Fig. 3
figure 3

Flow chart of computational methodology.

Full size image

The first step is to run the PowerFLOW simulation and use the results as initial conditions for the thermal transient simulation. The long-term thermal transient simulation as the next step is done by coupled PowerFLOW-PowerTHERM simulation. In the coupled simulation, PowerFLOW and PowerTHERM solve the flow field and surface temperature respectively. PowerFLOW solves the velocity and temperature in the fluid flow and then passes the near-wall heat transfer coefficient (HTC) and near-wall fluid temperature to a PowerTHERM model. PowerTHERM then calculates surface temperature with consideration of conduction and radiation and passes the temperature back to PowerFLOW. PowerTHERM solves transient temperature at a fixed time step size while PowerFLOW update HTC and temperature, this process iterates until the preset simulation duration.

When the coupled simulation was completed, we put together all HTC and near-wall temperature data into a standalone PowerTHERM file to run a thermal standalone simulation. This extra step can improve the thermal simulation accuracy level from first order to second order.

In this algorithm, the transient surface temperature is calculated by PowerTHERM, and the flow field is simulated by PowerFLOW, this makes the total simulation cost low. In addition, it is worth pointing out that PowerFLOW simulation needs to run sufficient time to achieve steady flow, especially at near wall region. Due to the innovative method in PowerFLOW, the simulation cost is lower compared to the traditional method.

In PowerFLOW, the variable resolution method is used to place refined voxels at the specified region as the user desired. In the present work, the finer voxels are placed near the wall flow region and wake region behind objects. Figure 4 shows visualized variable region. Placing finer voxels in the region of interest will be beneficial to the simulation without impacting the overall accuracy. In the present simulation cases, the time step of the first operating condition is 2.202e−06 s, and the Reynolds number is 1.60552e+06 and the Prandtl number is 0.707; the time step of the second operating condition is 1.856e−06 s, and the Reynolds number is 4.17436e+06 and the Prandtl number is 0.707.

Fig. 4
figure 4

Variable resolution regions for the thermal protection.

Full size image

Results analysis

Pre-soak results analysis

Before the soak testing of a vehicle, a pre-soak initialization is needed, that is, the test vehicle needs to undergo a harsh driving condition for a period before key-off. According to the OEM physical testing scenario. It is necessary to choose the condition with the maximum engine load as the presoak condition from the high-speed condition (130 km/h, 0°slope) and the low-speed climbing condition (50 km/h, 7.2°slope). Through the analysis and comparison of the thermal state in the engine bay under two operating conditions, the low-speed climbing condition was selected as the pre-soak condition, The boundary conditions of this simulation are shown in the Table 1.

Table 1 Boundary condition of pre-soak.
Full size table

The heat source distribution in pre-soak condition is shown in Fig. 5.

Fig. 5
figure 5

The heat source distribution in the simulation.

Full size image

The vehicle external flow field and engine bay heat transfer analysis is completed based on the coupled simulation method. Figure 6 shows the velocity distribution and temperature distribution at Y = 0 section in the engine bay when dynamic heat balance was achieved under low-speed climbing conditions and high-speed operating conditions. The results showed that the higher speed cooling airflow can take away more heat from the cooling module. At the same time, the faster the airflow speed flowing through the surface of the component, the greater the surface heat transfer coefficient, which means that the convection heat transfer effect is good. As shown in Fig. 7, the surface heat transfer coefficient is higher in high-speed conditions, and the temperature inside the engine bay is significantly lower than low-speed conditions.

Fig. 6
figure 6

The temperature and velocity distribution in the engine-bay at pre-soak condition (50 km/h climb and high speed).

Full size image
Fig. 7
figure 7

The HTC and Temperature distribution in the engine-bay at pre-soak condition (50 km/h climb and high speed).

Full size image

When the components in the engine bay are both close to the heat source and subjected to high-speed airflow, the dominant modes of heat transfer are radiation and convection, with conduction having a relatively minor impact. The heat analysis of components such as the battery, oxygen sensor wiring harness, and exhaust hanger are shown in Table 2.

Table 2 Heat transfer of measurement point of component (exhaust hanger, battery and oxygen sensor wiring).
Full size table

After analyzing the engine bay heat transfer of the vehicle under two heat balance states, the low-speed climbing condition with severe thermal environment was selected as the initial state of the key-off Soak for the heat accumulation in the engine bay. The simulation of the whole vehicle under low-speed hill climbing conditions also considers engine coolant temperature. The aim is to assess the risk of coolant overheating which could cause an A/C system cut-off or even a "boiling" phenomenon.

Comparison of simulation results and test data

This study simulated the low-speed hill climbing operating condition and compared simulation results against tests. The results are shown in Fig. 8. The engine coolant temperature has a good agreement with experiments with under 1 °C difference. The surface temperature of thermal-sensitive parts also showed good prediction with under a 5 °C difference. This comparison showed the coupled simulation successfully predicted both the engine coolant temperature and the component's surface temperature. This good prediction could also improve the accuracy of the soak simulation at the next step as it will be the initial condition of the soak simulation.

Fig. 8
figure 8

Comparison of the temperature between simulation and test at the pre-soak condition.

Full size image

This simulation method successfully compared the heat transfer characteristic of engine coolant and engine bay thermal sensitive parts against experiments at low-speed hill climbing operating conditions in this vehicle. At the thermal balance state, the engine coolant temperature showed under 1 °C deviation. The thermal-sensitive components can be largely affected by the actual manufacturing condition and the material thermal properties. Thus, surface temperature has bigger uncertainty. With PowerFLOW-PowerTHERM coupled simulation method, the temperature deviated is remain under 5 °C which ensured accuracy for soak simulation.

Heat transfer analysis and temperature performance of key components during soak

This section uses engine block temperature, cylinder head temperature, oil pan temperature, transmission temperature, and exhaust system temperature from the pre-soak condition as the heat source. Then, the heat dissipation of vehicle engine bay to the surrounding environment was solved by coupling simulation. Figure 9 shows the heat transfer between the vehicle and the surrounding environment during the soak period of 0 s, 60 s up to 400 s. The heat in the engine bay was first transferred from the intake grille and the wiper cover to the environment, and exchanged the heat with ambient air by convection. At the early stage of the soak (0–120 s), the engine cover was heated up through convection and radiation, and then carries out convection heat transfer with the environment, as shown in Fig. 9c, until 400 s, the convection heat transfer between the vehicle and the surrounding environment gradually decreased.

Fig. 9
figure 9

Comparison of the temperature between simulation and test at the pre-soak condition.

Full size image

The net values were normalized by the maximum net values among the three heat transfer mechanisms (radiation, conduction, convection) for each of engine surfaces (battery, oxygen sensor wiring harness, and exhaust hanger) separately for comparison during the soak process, as show in Fig. 10.

Fig. 10
figure 10

Comparison of the normalized net heat rates contribution by conduction, convection and radiation to the exhaust hanger, battery and oxygen sensor wiring during the 400 s vehicle soak.

Full size image

Convection was the main heat contribution at the early stage of the soak (0–60 s) for battery. Due to the battery is in front of the heat source, and the cooling air flow into the engine bay carries out convection heat transfer. During the period of 60–300 s, the heat transfer form of the engine bay changes after the cooling fan stops running. At this time, radiation took a major heat contribute and followed by convection heat transfer. The contribution of radiation and convection is consistent, and the role of conduction is negligible at the later stage of soak (300–400 s).

Convection also was the main heat contribution for oxygen sensor wire harness, followed by conduction. The temperature of the catalytic converter gradually decreases during soak and the conduction heat transfer of the oxygen sensor wire harness is weakened from 300 s, meanwhile the cooling air in the engine bay was heated and the convection heat transfer effect is enhanced. Radiation and conduction were the main heat contribution at the early stage of the soak (0–180 s) for exhaust hanger. However, the heat transfer capacity of these two forms gradually decreases with time. The results suggest that in order to accurately predict the thermal performance of the components in the engine bay, radiation and convection are important to be considered especially in the early stage of soak.

We performed a thermal analysis focused on the thermally sensitive components. This analysis considered conduction and radiation from the thermal solver and convective heat transfer of the heat exchanger from the flow solver. The comparison against experiments is shown in Fig. 11.

Fig. 11
figure 11

Comparison of test values and simulation values of monitoring points and their error bars (dash lines are the differences range).

Full size image

In the plots above, the red dash lines are uncertainty ranges from experiments. The results showed good agreement between simulation results and experiments data of the 400 s soak duration with an accuracy level under 10 °C. It is noticeable that all plots did not show significant temperature change in the first 30 s. This is because right after the key-off, the cooling fan is still operating powered by the car battery. Forced convection is still dominant in the engine bay which keeps the temperature of thermal sensitive parts stable. The sudden increase in temperature is due to the engine is key-off, the cooling fan stops rotating, and the heat transfer form in the engine bay is transformed into natural convection heat transfer driven by thermal buoyancy. A large amount of heat is accumulated in a short time, resulting in a sudden increase in temperature at the measuring point. However, with the development of time, the heat is gradually transferred to the surrounding environment and gradually cooled to the ambient temperature. If the temperature rises suddenly for a long time, it is easy to cause different degrees of thermal damage or thermal fatigue of the thermistors, and there are potential safety hazards.

Conclusion

The study simulates the cooling process of thermal-sensitive components in the engine bay within 400 s after the vehicle is turned off and compares it with real vehicle test data. The simulation results show that the developed simulation technology can accurately predict the heating conditions of coolant temperature and thermal-sensitive components. During the first 30 s after the engine is turned off, the surface temperature of thermal-sensitive components remains stable; subsequently, due to the cooling fan stopping, the heat transfer mode in the engine bay changes to less efficient natural convection, causing the temperature to rise sharply in the short term and then gradually fall back to ambient temperature.

The maximum net value normalization of three heat transfer forms of battery, oxygen sensor and Exhaust hanger were carried out to analyze their heat transfer characteristics in the process soak. In the early stage of soak (0–60 s), the main heat transfer modes of the engine bay are radiation and convection, and the conduction effect is relatively low, and only the parts close to the heat source have a significant effect on conduction heat transfer. During the 400 s soak process, the efficiency of radiation heat transfer continues to decline, while the convective heat transfer efficiency increases first and then decrease. According to the heating form of different components, the components subjected to high temperature radiation heat transfer can be added by thermal insulation measures to reduce the thermal risk, Alternatively, the convective heat transfer efficiency can be improved by increasing the velocity of the cooling airflow. For the components in contact with heat source, the convective heat transfer capacity can be increased or the materials with lower thermal conductivity can be changed to reduce the thermal risk.

The simulation technology successfully visualizes the airflow paths and temperature distribution around the engine bay. The difference between the predicted fluid temperature and the measured value is controlled within 1 °C, and the surface temperature error of thermal-sensitive components is within 5 °C, demonstrating the high accuracy of the simulation method.

This research not only provides new insights into the thermal behavior of SUVs under the key-off soak condition but also offers valuable data support for studying thermal fatigue and thermal failure mechanisms. This method provides an important reference for the control strategy of fan running time after key-off.