Multiple rogue wave, double-periodic soliton and breather wave solutions for a generalized breaking soliton system in (3 + 1)-dimensions

Abstract

We focused on solitonic phenomena in wave propagation which was extracted from a generalized breaking soliton system in (3 + 1)-dimensions. The model describes the interaction phenomena between Riemann wave and long wave via two space variable in nonlinear media. Abundant double-periodic soliton, breather wave and the multiple rogue wave solutions to a generalized breaking soliton system by the Hirota bilinear form and a mixture of exponentials and trigonometric functions are presented. Periodic-soliton, breather wave and periodic are studied with the usage of symbolic computation. In addition, the symbolic computation and the applied methods for governing model are investigated. Through three-dimensional graph, density graph, and two-dimensional design using Maple, the physical features of double-periodic soliton and breather wave solutions are explained all right. The findings demonstrate the investigated model’s broad variety of explicit solutions. All outcomes in this work are necessary to understand the physical meaning and behavior of the explored results and shed light on the significance of the investigation of several nonlinear wave phenomena in sciences and engineering.

Introduction

Currently, the nonlinear partial differential equations are widely utilized to determine the exact soliton solution of a variety of natural phenomena^1,2,3,4,5. Nonlinear phenomena use in various scientific fields such as, plasma physics, solid state physics, fluid dynamics, chemical kinetics and mathematical biology^6,7,8,9,10. The applications of nonlinear models cover physics^11,12, network¹³, computer science¹⁴, and many other fields¹⁵. Exact solutions can be evaluated without the effect of nonlinear resistances in propagation using Hirota derivatives. In the literature¹⁶, there are various viewpoints on the fractional derivative operator. However, numerous scholars and scientists have been investigating the potential of nonlinear operator for the past three decades such as Galerkin finite element technique¹⁷, Paul–Painlevé approach¹⁸, the Exp-function scheme¹⁹, the extended trial equation scheme²⁰, the $tan(\phi /2)$-expansion scheme²¹, etc. Based on the above methods, plenty of the exact solutions including different schemes have been worked, for example, the generalized exponential rational function method²², Gaussian traveling wave solution²³, seismic attenuation for geotechnical²⁴, the generalized trial equation scheme²⁵, a wavelet approach²⁶. Since the 1950s, the concept of soliton has been put forward in the study of nonlinear phenomena, which makes the study of nonlinear partial differential equations (NLPDEs) solution become a hot spot in nonlinear science including orthogonal frequency division multiplexing²⁷, Fluid inverse volumetric modeling²⁸, network governance step by step method²⁹ and the neural network method³⁰. However, due to the complexity of NLPDEs, the results of mathematical research have not provided a universally effective method to find the exact solution at present. With the emergence of a variety of solution methods, not only the past difficult to solve the equation has been solved, but also new, has important physical meaning of the solution has been discovered and applied in practice. Nonlinear differential equations have been widely employed to describe a wide range of physical processes, not just in mathematics but also in physics, biology, and engineering, for example: the conservation of mass, electrochemical analysis, groundwater flow problem, viscoelastic damping models, fractional quantum mechanics, classical mechanics, and propagation of acoustical waves^{31,32,33,34,35}. Several effective techniques have been established to find the clear and specific solutions of nonlinear models for instance such as machine learning methods³⁶, He’s variational direct technique³⁷, the discrete mean-field stochastic systems³⁸, bistable origami flexible gripper³⁹, the breather wave solutions⁴⁰. The nonlinear problems are characterized by dispersive and dissipative effects, advection, convection, and diffusion process such as N-lump solutions⁴¹, seismic wave attenuation⁴², the development of deep geothermal energy⁴³, hyperbolic shear polaritons⁴⁴, the modified Schrödinger’s equation via innovative approaches⁴⁵. A wide class of analytical techniques other schemes have been applied to solve nonlinear problems such as the parabolic dish solar collector⁴⁶, the renewable energy sources⁴⁷, a hybrid convolutional neural network⁴⁸, a hybrid robust-stochastic approach⁴⁹, a optimal chiller loading⁵⁰. Furthermore, many mathematical models have been constructed based on more theory and applied assumptions. Many researchers have constructed on these problems including the distributed series reactor⁵¹, an intelligent algorithm⁵², the deep learning method⁵³, the trigonometric quadrature rules⁵⁴, nonlinearities of SiGe bipolar phototransistor⁵⁵. Several researchers have studied the modified and optimization technique such as the robust optimization technique⁵⁶, random variables with Copula theory⁵⁷, and power systems⁵⁸. Jiand and co-workers studied the asymptotic properties for the drift parameter estimators in the fractional Ornstein-Uhlenbeck process with periodic mean function and long range dependence⁵⁹. Authors investigated the distinct types of the exact soliton solutions to an important model called the beta-time fractional (1 + 1)-dimensional nonlinear Van der Waals equation⁶⁰. The versatility of electrofabrication for the customized manufacturing of functional gradient soft matter was studied in⁶¹. The multiple soliton solutions for the generalized Bogoyavlensky–Konopelchenko equation along with solutions contain first-order, second-order, and third-order wave solutions were analyzed⁶².

A precise balance between the nonlinear and dispersion elements in the evolution system gives rise to the solitons, a typical nonlinear phenomenon. The soliton theory has a wide range of useful applications. For instance, optical soliton has unquestionably produced the basis for optical fibre communication and the current Internet era. Two and more solitons coexist and interact often in an evolution system. With the exception of phase, solitons interact and clash most frequently in an elastic manner, preserving their propagation speed, amplitude, and direction. Solitons may collide inelastically in some settings. Even in extremely uncommon situations, soliton fusion and fission can occur^63,64,65.

The primary goal of this research is to offer generalized breaking soliton system in (3 + 1)-dimensions arising in wave propagation a significant number of trustworthy analytical closed-form solutions. Additionally, wave designs from distinctive soliton solutions’ nonlinear behavior in 3D, 2D, and stage plane examination has been appeared. The express methods’ versatile profile structures are very unmistakable and supportive for basic forms. Only a very small number of findings from previous research have been released, and the resulting periodic and single soliton compositions are entirely original. Furthermore, this research could be seen as a complement to previous relevant articles.

For reasons known to all, the researchers of shallow water wave in various field is critical for further study in physical systems when we turn to mathematical physics, nonlinear optics, optical fibres and communication engineering in which the nonlinear evolution equation was recently developed. Feng et al.⁶⁶ obtained the exact analytical solutions and novel interaction solutions by Hirota bilinear method and symbolic computation. Ma et al.⁶⁷ obtained the localized interaction solutions based on a Hirota bilinear transformation. The multi-component Sasa-Satsuma integrable hierarchies was studied via an arbitrary-order matrix spectral problem, based on the zero curvature formulation⁶⁸. Analytical one-, two-, three- and four-soliton solutions of the (2 + 1)-dimensional variable-coefficient Sawada-Kotera equation were constructed based on its Hirota bilinear form⁶⁹. A fourth-order time-fractional partial differential equation with Riemann–Liouville definition was studied using the general method of separation of variables⁷⁰.

Although solitons theoretically possess unique properties that allow them to maintain their propagation shape, speed, and amplitude, in practical application scenarios, the propagation of solitons is often influenced by various complex factors such as common damping, initial or boundary perturbations, evolving dissipation, and variable nonlinearity⁷¹. These factors directly affect the soliton dynamics, leading to energy loss, amplitude attenuation, deformation, and deceleration during propagation. To address these issues, it is necessary to introduce certain physical factors mentioned above in nonlinear evolution systems, such as the multimodal vision-language learning paradigm method⁷², a complete language-vision interaction network⁷³, the multimodal hybrid parallel network method⁷⁴, a multi-scale channel-spatial attention⁷⁵, Fourier decomposition method⁷⁶.

In this paper, we will discuss the following generalized breaking soliton system in (3 + 1)-dimensions⁷⁷

$$\begin{aligned} \left\{ \begin{array}{ll} v_{t}+s_1u_{xxx}+s_2u_{xxy}+s_3u_{xxz}+ s_4uu_{x}+s_5uu_{y}+s_6uu_{z}+s_7u_xw=0,\\ v_x=u_x+u_y-\int u_{xx}\,dt,\\ w=\int (u_y+u_z)\,dx, \end{array} \right. \end{aligned}$$

(1)

with $u=u(t,x,y,z), v=v(t,x,y,z)$ and $w=w(t,x,y,z)$ and $s_j(j= 1, 2,\ldots ,7)$ are free parameters. System (1) is derived from the generalization of the following (2 + 1)-dimensional generalized breaking soliton system

$$\begin{aligned} \left\{ \begin{array}{ll} u_{t}+s_1u_{xxx}+s_2u_{xxy}+s_3uu_{x}+s_4uu_{y}+s_5u_xw=0,\\ w=\int u_y\,dx, \end{array} \right. \end{aligned}$$

(2)

where $u=u(t,x,y)$ and $w=w(t,x,y)$ and $s_j(j= 1, 2,\ldots ,5)$ are the nonzero parameters. System (2) is investigated by different methods in Refs.^78,79,80. Using $s_4=6s_1=\delta , s_2=s_3=s, s_5=s_6=s_7=3s$ and the following relation

$$\begin{aligned} u(x,y,z,t)=2(\ln T(x,y,z,t))_{xx}, \end{aligned}$$

(3)

then, the bilinear form B(T) of Eq. (1) will be arisen as

$$\begin{aligned} B(T):=\left( \delta \,D_x^4 +sD_x^3D_y+sD_x^3D_z+D_xD_t+D_yD_t-D_x^2\right) T. T=0, \end{aligned}$$

(4)

with the bilinear operator D

$$\begin{aligned} \prod _{i=1}^{4}D_{\varsigma _i}^{\beta _i}f. g=\left. \prod _{i=1}^{4}\left( \frac{\partial }{\partial \varsigma _i}-\frac{\partial }{\partial \varsigma _i'}\right) ^{\beta _i}f(\varsigma )g(\varsigma ')\right| _{\varsigma '=\varsigma }, \end{aligned}$$

(5)

in which $\varsigma =(x,y,z,t)$ and $\varsigma '=(x',y',z',t')$. Hence, we get

$$\begin{aligned} B(T)= 2\delta (TT_{xxxx}-4T_xT_{xxx}+3T_{xx}^2)+2s(T_{xxxy}-T_yT_{xxx}- 3T_xT_{xxy}+3T_{xx}T_{xy}+T_{xxxz}-T_zT_{xxx}- \end{aligned}$$

(6)

$$\begin{aligned}3T_xT_{xxz}+3T_{xx}T_{xz})+ 2(TT_{xt}-T_{x}T_{t})+2(TT_{yt}-T_{y}T_{t})-2(TT_{xx}-T_{x}^2). \end{aligned}$$

The (2 + 1)-dimensional Zoomeron model extensively was utilized the extended Jacobian elliptic function and the modified extended tanh techniques to derive the analytical solutions⁸⁷. The improved Kudryashov, the novel Kudryashov, and the unified methods were used to demonstrate new wave behaviors of the Fokas–Lenells nonlinear waveform arising in birefringent fibers⁸⁸. The linear stability technique and bifurcation analysis were employed to assess the stability of the fractional 3D Wazwaz–Benjamin–Bona–Mahony model⁸⁹. The novel waveforms and bifurcation analysis for the fractional Klein–Fock–Gordon structure were investigated in⁹⁰. N-solitons and interaction solution for the (3 + 1)-D negative-order KdV first structure that arises in shallow-water waves were studied⁹¹. The Hirota bilinear formation was used to analyze novel collision solutions between the lump and kinky waves of the (3 + 1)-D Jimbo–Miwa-like model⁹².

In essence, the generalized breaking soliton system characterizes the propagation of nonlinear dispersive waves within (3 + 1)-dimensions, embodying a balance between nonlinear convection effects and dispersive tendencies originating from the medium.

The structure of this paper is given as under:

The double-periodic soliton method is presented in the second section by plenty of the solutions. Application of breather wave is discussed in the third section. The result and discussion are investigated in fourth section. Fifth section points to the multiple rogue wave and its application on mentioned system. Finally, we approach some kind of results and conclusion in sixth section.

Double-periodic soliton solutions

Recently, “three-wave method” was revised for obtaining the double-periodic soliton solutions to NLPDEs⁸¹, such as the (2 + 1)- and (3 + 1)-dimensional BLMP equation⁸², the (2 + 1)-dimensional breaking soliton equation⁸³, the new (2 + 1)-dimensional KdV equation⁸⁴. Following the steps of this method, T(x, y, t) has a solution of the following form

$$\begin{aligned} T(x,y,z,t)=k_1e^{\alpha _1x+\beta _1y+\lambda _1z+\mu _1t+\epsilon _1}+k_2e^{\alpha _4x+\beta _4y+\lambda _4z+\mu _4t+\epsilon _4}+ \end{aligned}$$

(7)

$$\begin{aligned}{} & {} e^{\alpha _1x+\beta _1y+\lambda _1z+\mu _1t+\epsilon _1}[m_1\cos (\alpha _2x+\beta _2y+\lambda _2z+\mu _2t+\epsilon _2)+ m_2\sin (\alpha _2x+\beta _2y+\lambda _2z+\mu _2t+\epsilon _2)]+ \\{} & {} e^{\alpha _3x+\beta _3y+\lambda _3z+\mu _3t+\epsilon _3}[m_3\cos (\alpha _4x+\beta _4y+\lambda _4z+\mu _4t+\epsilon _4)+ m_4\sin (\alpha _4x+\beta _4y+\lambda _4z+\mu _4t+\epsilon _4)], \end{aligned}$$

where $\alpha _i, \beta _i, \lambda _i, \mu _i$ and $\epsilon _i(i = 1, 2, 3, 4)$ are constants to be determined later. The assumptions used in the “three-wave method” are special cases of Eq. (7). Substituting Eq. (7) into Eq. (3), a set of algebraic equations about $\alpha _i, \beta _i, \lambda _i, \mu _i$ and $\epsilon _i(i = 1, 2, 3, 4)$ are obtained. With the aid of Mathematica software, we have the following results:

Case (1):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _3=\alpha _4=k_1=k_2=m_1=\mu _3=\mu _4=0, \\ T(x,y,z,t)={ \textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{ 2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{y\beta _{{3}}+z \lambda _{{3}}+\epsilon _{{3}}}} \left( m_{{3}}\cos \left( y\beta _{{4}} +z\lambda _{{4}}+\epsilon _{{4}} \right) +m_{{4}}\sin \left( y\beta _{{4 }}+z\lambda _{{4}}+\epsilon _{{4}} \right) \right) , \\ u(x,y,z,t)=2\,{\frac{{\frac{\partial ^{2}}{\partial {x}^{2}}}T \left( x,y,z,t \right) }{T \left( x,y,z,t \right) }}-2\,{\frac{ \left( {\frac{ \partial }{\partial x}}T \left( x,y,z,t \right) \right) ^{2}}{ \left( T \left( x,y,z,t \right) \right) ^{2}}},\\ T_x(x,y,z,t)=\alpha _{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{ {1}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y \beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{t\mu _{{1 }}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}m_{{2}} \cos \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+ \epsilon _{{2}} \right) \alpha _{{2}},\\ T_{xx}(x,y,z,t)={\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}m_{{2}} ( \sin \left( t\mu _{{2}}+x\alpha _{{2}}+y \beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) {\alpha _{{1}}}^{2}- \\ \sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+ \epsilon _{{2}} \right) {\alpha _{{2}}}^{2}+ 2\,\cos \left( t\mu _{{2}}+x \alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) \alpha _{{1}}\alpha _{{2}} ). \end{array} \right. \end{aligned}$$

(8)

Case (2):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _4=k_1=m_1=\mu _4=0,\ \ \mu _{{3}}=-{\frac{s{\alpha _{{3}}}^{3} \left( \beta _{{4}}+\lambda _{{4} } \right) }{\beta _{{4}}}},\ \delta ={\frac{s{\alpha _{{3}}}^{2}\beta _{{4}}+s{\alpha _{{3}}}^{2} \lambda _{{4}}+s\alpha _{{3}}\beta _{{3}}\lambda _{{4}}-s\alpha _{{3}} \lambda _{{3}}\beta _{{4}}+\beta _{{4}}}{{\alpha _{{3}}}^{2}\beta _{{4}}}}, \\ T(x,y,z,t)=k_{{2}}{\textrm{e}^{y\beta _{{4}}+z\lambda _{{4}}+\epsilon _{{4}}}}+{ \textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{ 2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{-{\frac{ts{ \alpha _{{3}}}^{3} \left( \beta _{{4}}+\lambda _{{4}} \right) }{\beta _{{4 }}}}+x\alpha _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}}}} \left( m_{{3}}\cos \left( y\beta _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) +m_{{4}}\sin \left( y\beta _{{4}}+z\lambda _{{4}}+\epsilon _{{4 }} \right) \right) . \end{array} \right. \end{aligned}$$

(9)

Case (3):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _4=\beta _4=k_1=m_1=0,\ \ \beta _{{3}}=-{\frac{\alpha _{{3}} \left( s{\alpha _{{3}}}^{2}\lambda _{{ 4}}+\mu _{{4}} \right) }{\mu _{{4}}}}, \delta ={\frac{{s}^{2}{\alpha _{{3}}}^{4}\lambda _{{4}}+s{\alpha _{{3}}}^ {2}\mu _{{4}}-s\alpha _{{3}}\lambda _{{3}}\mu _{{4}}+s\alpha _{{3}}\lambda _ {{4}}\mu _{{3}}+\mu _{{4}}}{{\alpha _{{3}}}^{2}\mu _{{4}}}},\\ T(x,y,z,t)=k_{{2}}{\textrm{e}^{t\mu _{{4}}+z\lambda _{{4}}+\epsilon _{{4}}}}+{\textrm{e}^ {t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}} }m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2 }}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{t\mu _{{3}}+x\alpha _{{3}}-{\frac{y\alpha _{{3}} \left( s{\alpha _{{3}}}^{2}\lambda _{{4}}+\mu _{{4}} \right) }{\mu _{{4}}}}+z\lambda _{{3}}+\epsilon _{{3}}}} \left( m_{{3}} \cos \left( t\mu _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) +m_{{4}} \sin \left( t\mu _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(10)

Case (4):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _4=k_2=m_1=\mu _4=0,\ \ \lambda _{{1}}=-{\frac{-s \left( \alpha _{{1}}-\alpha _{{3}} \right) \left( \left( \beta _{{4}}+\lambda _{{4}} \right) \left( \alpha _{{1}} -\alpha _{{3}} \right) + \left( \beta _{{1}}-\beta _{{3}} \right) \lambda _{{4}}+\beta _{{4}}\lambda _{{3}} \right) +\beta _{{4}} \left( -1+ \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{2}\delta \right) }{ \left( \alpha _{{1}}-\alpha _{{3}} \right) s\beta _{{4}}}},\\ \mu _{{1}}=-{\frac{s \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{3} \left( \beta _{{4}}+\lambda _{{4}} \right) -\beta _{{4}}\mu _{{3}}}{\beta _{{4}}}}, \ \ T(x,y,z,t)=k_{{1}}{\textrm{e}^{-{\frac{t \left( s \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{3} \left( \beta _{{4}}+\lambda _{{4}} \right) -\beta _{{4}}\mu _{{3}} \right) }{\beta _{{4}}}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1 }}+\epsilon _{{1}}}}+\\ {\textrm{e}^{-{\frac{t \left( s \left( \alpha _{{1}} -\alpha _{{3}} \right) ^{3} \left( \beta _{{4}}+\lambda _{{4}} \right) - \beta _{{4}}\mu _{{3}} \right) }{\beta _{{4}}}}+x\alpha _{{1}}+y\beta _{{1} }+z\lambda _{{1}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x \alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ { \textrm{e}^{t\mu _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+ \epsilon _{{3}}}} \left( m_{{3}}\cos \left( y\beta _{{4}}+z\lambda _{{4} }+\epsilon _{{4}} \right) +m_{{4}}\sin \left( y\beta _{{4}}+z\lambda _{{ 4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(11)

Case (5):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _4=\beta _4=k_2=m_1=0,\ \ \beta _{{1}}=-{\frac{s\lambda _{{4}} \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{3}+\mu _{{4}} \left( \alpha _{{1}}-\alpha _{{3}}-\beta _{{3}} \right) }{\mu _{{4}}}}, \\ \lambda _{{1}}=-{\frac{-s \left( \alpha _{{1}}-\alpha _{{3}} \right) \left( s\lambda _{{4}} \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{3}+ \mu _{{4}} \left( \alpha _{{1}}-\alpha _{{3}}+\lambda _{{3}} \right) + \lambda _{{4}} \left( \mu _{{1}}-\mu _{{3}} \right) \right) +\mu _{{4}} \left( -1+ \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{2}\delta \right) }{ \left( \alpha _{{1}}-\alpha _{{3}} \right) s\mu _{{4}}}},\\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}-{\frac{y \left( s\lambda _{{ 4}} \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{3}+\mu _{{4}} \left( \alpha _{{1}}-\alpha _{{3}}-\beta _{{3}} \right) \right) }{\mu _{{4}}}}+z \lambda _{{1}}+\epsilon _{{1}}}}+\\ {\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}-{ \frac{y \left( s\lambda _{{4}} \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{3}+\mu _{{4}} \left( \alpha _{{1}}-\alpha _{{3}}-\beta _{{3}} \right) \right) }{\mu _{{4}}}}+z\lambda _{{1}}+\epsilon _{{1}}}}m_{{2} }\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+ \epsilon _{{2}} \right) +\\ {\textrm{e}^{t\mu _{{3}}+x\alpha _{{3}}+y\beta _{{3 }}+z\lambda _{{3}}+\epsilon _{{3}}}} \left( m_{{3}}\cos \left( t\mu _{{4 }}+z\lambda _{{4}}+\epsilon _{{4}} \right) +m_{{4}}\sin \left( t\mu _{{4 }}+z\lambda _{{4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(12)

Case (6):

$$\begin{aligned} \left\{ \begin{array}{ll} k_2=m_1=0,\ \ \delta =-\frac{1}{12}{\frac{4\,s \left( \sqrt{3}\lambda _{{4}}-3\,\alpha _{{1 }}+3\,\alpha _{{3}} \right) \left( \alpha _{{1}}-\alpha _{{3}} \right) + 1}{{\alpha _{{1}}}^{2}-2\,\alpha _{{1}}\alpha _{{3}}+{\alpha _{{3}}}^{2}}}, \\ \mu _{{1}}=-\frac{1}{3}\,{\frac{8\,s \left( \sqrt{3}\lambda _{{4}}-3\,\alpha _{ {1}}+3\,\alpha _{{3}}-3\,\beta _{{1}}+3\,\beta _{{3}}-3\,\lambda _{{1}}+3 \,\lambda _{{3}} \right) \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{3} +8\, \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{2}-3\,\mu _{{3}} \left( \beta _{{1}}-\beta _{{3}}+\alpha _{{1}}-\alpha _{{3}} \right) }{ \beta _{{1}}-\beta _{{3}}+\alpha _{{1}}-\alpha _{{3}}}},\\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}+{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z \lambda _{{1}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{ {2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{t \mu _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}}}} \left( m_{{3}}\cos \left( \frac{4}{3}\,{\frac{t \left( {\alpha _{{1}}}^{2}-2 \,\alpha _{{1}}\alpha _{{3}}+{\alpha _{{3}}}^{2} \right) \sqrt{3}}{\beta _{{1}}-\beta _{{3}}+\alpha _{{1}}-\alpha _{{3}}}}+x\sqrt{3} \left( \alpha _{{1}}-\alpha _{{3}} \right) -y\sqrt{3} \left( \alpha _{{1}}- \alpha _{{3}} \right) +z\lambda _{{4}}+\epsilon _{{4}} \right) +\right. \\ \left. m_{{4}} \sin \left( \frac{4}{3}\,{\frac{t \left( {\alpha _{{1}}}^{2}-2\,\alpha _{{1}} \alpha _{{3}}+{\alpha _{{3}}}^{2} \right) \sqrt{3}}{\beta _{{1}}-\beta _{ {3}}+\alpha _{{1}}-\alpha _{{3}}}}+x\sqrt{3} \left( \alpha _{{1}}-\alpha _{{3}} \right) -y\sqrt{3} \left( \alpha _{{1}}-\alpha _{{3}} \right) +z \lambda _{{4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(13)

Case (7):

$$\begin{aligned} \left\{ \begin{array}{ll} m_1=m_4=0,\ \ \lambda _{{1}}=-{\frac{\delta \, \left( \alpha _{{1}}-\alpha _{{4}} \right) ^{4}+s \left( \alpha _{{1}}-\alpha _{{4}} \right) ^{3} \left( \beta _{{1}}-\beta _{{4}}-\lambda _{{4}} \right) - \left( \alpha _{{1}}- \alpha _{{4}} \right) \left( \alpha _{{1}}-\alpha _{{4}}-\mu _{{1}}+\mu _{ {4}} \right) + \left( \mu _{{1}}-\mu _{{4}} \right) \left( \beta _{{1}}- \beta _{{4}} \right) }{s \left( \alpha _{{1}}-\alpha _{{4}} \right) ^{3}} }, \\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}+k_{{2}}{\textrm{e}^{t\mu _{{4}}+x\alpha _{{4}}+y\beta _{{4 }}+z\lambda _{{4}}+\epsilon _{{4}}}}+\\ {\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}} +y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _ {{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{t\mu _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+z\lambda _{{3 }}+\epsilon _{{3}}}}m_{{3}}\cos \left( t\mu _{{4}}+x\alpha _{{4}}+y\beta _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) . \end{array} \right. \end{aligned}$$

(14)

Case (8):

$$\begin{aligned} \left\{ \begin{array}{ll} k_1=m_1=0,\ \ \delta =-\frac{1}{16}\,{\frac{ \left( \sqrt{3}-3 \right) \left( -8\,s{\alpha _{{4}}}^{3} \left( \beta _{{3}}+\lambda _{{3}} \right) +2\,{\alpha _{{4}} }^{2} \sqrt{3}+3\,\alpha _{{4}}\mu _{{3}} \sqrt{3}+3\, \sqrt{3}\beta _{{3 }}\mu _{{3}}-6\,{\alpha _{{4}}}^{2}+3\,\alpha _{{4}}\mu _{{3}} \right) }{{ \alpha _{{4}}}^{4}}},\\ \lambda _{{4}}=-\frac{1}{16}\,{\frac{8\,s \left( \sqrt{3}\beta _{{3}}+\lambda _ {{3}} \sqrt{3}-2\,\alpha _{{4}}-3\,\beta _{{3}}-3\,\lambda _{{3}} \right) {\alpha _{{4}}}^{3}+4\, \left( 3\, \sqrt{3}-5 \right) {\alpha _ {{4}}}^{2}-3\, \sqrt{3} \left( \sqrt{3}\beta _{{3}}-2\,\alpha _{{4}}-3 \,\beta _{{3}} \right) \mu _{{3}}}{s{\alpha _{{4}}}^{3}}},\\ \alpha _{{3}}=1/3\, \left( 3+ \sqrt{3} \right) \alpha _{{4}},\ \mu _{{4}}=-4/3\,{\frac{ \left( \sqrt{3}-1 \right) {\alpha _{{4}}}^{2} }{ \sqrt{3}\beta _{{3}}-2\,\alpha _{{4}}-3\,\beta _{{3}}}},\\ T(x,y,z,t)=k_{{2}}{\textrm{e}^{-4/3\,{\frac{t \left( \sqrt{3}-1 \right) {\alpha _{{ 4}}}^{2}}{\beta _{{3}}\sqrt{3}-2\,\alpha _{{4}}-3\,\beta _{{3}}}}+x \alpha _{{4}}-y\alpha _{{4}}+z\lambda _{{4}}+\epsilon _{{4}}}}+{\textrm{e}^{ t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}} m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2} }+\epsilon _{{2}} \right) +\\ {\textrm{e}^{t\mu _{{3}}+1/3\,x \left( 3+\sqrt{3} \right) \alpha _{{4}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}}}} \left( m_{{3}}\cos \left( -4/3\,{\frac{t \left( \sqrt{3}-1 \right) {\alpha _{{4}}}^{2}}{\beta _{{3}}\sqrt{3}-2\,\alpha _{{4}}-3\,\beta _{{3} }}}+x\alpha _{{4}}-y\alpha _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) +\right. \\ \left. m_{{4}}\sin \left( -4/3\,{\frac{t \left( \sqrt{3}-1 \right) {\alpha _{{4}}}^{2}}{\beta _{{3}}\sqrt{3}-2\,\alpha _{{4}}-3\, \beta _{{3}}}}+x\alpha _{{4}}-y\alpha _{{4}}+z\lambda _{{4}}+\epsilon _{{4 }} \right) \right) ,\ \ u(x,y,z,t)=2\,(\ln (T(x,y,z,t))_{xx}. \end{array} \right. \end{aligned}$$

(15)

Case (9):

$$\begin{aligned} \left\{ \begin{array}{ll} k_1=m_1=\mu _3=\mu _4=0,\ \ \delta =-\frac{1}{4}\,{\frac{4\,s\alpha _{{4}}\beta _{{4}}+4\,s\alpha _{{4}} \lambda _{{4}}+1}{{\alpha _{{4}}}^{2}}},\ \ \alpha _{{3}}= \left( 1+ \sqrt{3} \right) \alpha _{{4}},\\ \lambda _{{3}}=\frac{1}{2}\,{\frac{ \left( 1+ \sqrt{3} \right) \left( 2\,s \alpha _{{4}}\beta _{{4}}+2\,s\alpha _{{4}}\lambda _{{4}}+1 \right) -2\,s \alpha _{{4}}\beta _{{3}}-1}{s\alpha _{{4}}}}, \\ T(x,y,z,t)=k_{{2}}{\textrm{e}^{x\alpha _{{4}}+y\beta _{{4}}+z\lambda _{{4}}+\epsilon _{ {4}}}}+{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{ 2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{x \left( 1+ \sqrt{3} \right) \alpha _{{4}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{ {3}}}} \left( m_{{3}}\cos \left( x\alpha _{{4}}+y\beta _{{4}}+z\lambda _{ {4}}+\epsilon _{{4}} \right) +m_{{4}}\sin \left( x\alpha _{{4}}+y\beta _ {{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(16)

Case (10):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _3=\alpha _4=k_1=m_1=\mu _3=\mu _4=0,\ \ \lambda _{{3}}={\frac{\beta _{{3}}\lambda _{{4}}}{\beta _{{4}}}},\ \ \mu _{{1}}=-{\frac{s{\alpha _{{1}}}^{3} \left( \beta _{{4}}+\lambda _{{4} } \right) }{\beta _{{4}}}},\ \ \delta ={\frac{{\alpha _{{1}}}^{2}\beta _{{4}}s+{\alpha _{{1}}}^{2}\lambda _{{4}} s+\alpha _{{1}}\beta _{{1}}\lambda _{{4}}s-s\alpha _{{1}}\beta _{{4}} \lambda _{{1}}+\beta _{{4}}}{{\alpha _{{1}}}^{2}\beta _{{4}}}},\\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{-{\frac{ts{\alpha _{{1}}}^{3} \left( \beta _{{4}}+ \lambda _{{4}} \right) }{\beta _{{4}}}}+x\alpha _{{1}}+y\beta _{{1}}+z \lambda _{{1}}+\epsilon _{{1}}}}+k_{{2}}{\textrm{e}^{y\beta _{{4}}+z\lambda _{{4}}+\epsilon _{{4}}}}+\\ {\textrm{e}^{-{\frac{ts{\alpha _{{1}}}^{3} \left( \beta _{{4}}+\lambda _{{4}} \right) }{\beta _{{4}}}}+x\alpha _{{1} }+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{y\beta _{{3}}+{\frac{z\beta _{{3}}\lambda _{{4}}}{ \beta _{{4}}}}+\epsilon _{{3}}}} \left( m_{{3}}\cos \left( y\beta _{{4}} +z\lambda _{{4}}+\epsilon _{{4}} \right) +m_{{4}}\sin \left( y\beta _{{4 }}+z\lambda _{{4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(17)

Case (11):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _4=m_1=\mu _4=0,\ \ \delta ={\frac{{\alpha _{{3}}}^{2}\beta _{{4}}s+{\alpha _{{3}}}^{2} \lambda _{{4}}s+\alpha _{{3}}\beta _{{3}}\lambda _{{4}}s-\alpha _{{3}}\beta _{{4}}\lambda _{{3}}s+\beta _{{4}}}{{\alpha _{{3}}}^{2}\beta _{{4}}}},\ \\ \beta _{{1}}=-\frac{1}{3}\,{\frac{3\,s{\alpha _{{3}}}^{2} \left( \alpha _{{1}}- \alpha _{{3}} \right) ^{2} \left( \alpha _{{1}}-\beta _{{4}} \right) \left( \beta _{{4}}+\lambda _{{4}} \right) +\alpha _{{1}}\beta _{{4}} \left( {\alpha _{{1}}}^{2}-\alpha _{{1}}\alpha _{{3}}+{\alpha _{{3}}}^{2} \right) }{ \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{2} \left( \beta _{{4}}+\lambda _{{4}} \right) s{\alpha _{{3}}}^{2}}},\ \ \lambda _{{1}}=-\frac{1}{3}\,{\frac{3\,s\alpha _{{3}} \left( \alpha _{{1}}- \alpha _{{3}} \right) ^{2} \left( \beta _{{4}}+\lambda _{{4}} \right) M_{ {1}}+\alpha _{{1}}\beta _{{4}}M_{{2}}}{ \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{2} \left( \beta _{{4}}+\lambda _{{4}} \right) s{\alpha _{{3}}} ^{2}\beta _{{4}}}},\\ M_{{1}}=\alpha _{{3}}\lambda _{{4}} \left( \alpha _{{1}}-\beta _{{4}} \right) +\alpha _{{1}} \left( \beta _{{3}}\lambda _{{4}}-\beta _{{4}} \lambda _{{3}} \right) ,\ M_{{2}}={\alpha _{{1}}}^{2} \left( 3\,\beta _{{4}}+4\,\lambda _{{4}} \right) -\alpha _{{1}}\alpha _{{3}} \left( 9\,\beta _{{4}}+10\,\lambda _{ {4}} \right) +{\alpha _{{3}}}^{2} \left( 6\,\beta _{{4}}+7\,\lambda _{{4} } \right) , \\ \mu _{{1}}=-{\frac{s\alpha _{{1}} \left( {\alpha _{{1}}}^{2}\beta _{{4}}+ {\alpha _{{1}}}^{2}\lambda _{{4}}-3\,\alpha _{{1}}\alpha _{{3}}\beta _{{4}} -3\,\alpha _{{1}}\alpha _{{3}}\lambda _{{4}}+3\,{\alpha _{{3}}}^{2}\beta _{ {4}}+3\,{\alpha _{{3}}}^{2}\lambda _{{4}} \right) }{\beta _{{4}}}},\ \ \mu _{{3}}=-{\frac{s{\alpha _{{3}}}^{3} \left( \beta _{{4}}+\lambda _{{4} } \right) }{\beta _{{4}}}}, \\ \ T(x,y,z,t)=k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}+k_{{2}}{\textrm{e}^{y\beta _{{4}}+z\lambda _{{4}}+ \epsilon _{{4}}}}+{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z \lambda _{{1}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{ {2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) \\ +{\textrm{e}^{-{ \frac{ts{\alpha _{{3}}}^{3} \left( \beta _{{4}}+\lambda _{{4}} \right) }{\beta _{{4}}}}+x\alpha _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{ 3}}}} \left( m_{{3}}\cos \left( y\beta _{{4}}+z\lambda _{{4}}+\epsilon _ {{4}} \right) +m_{{4}}\sin \left( y\beta _{{4}}+z\lambda _{{4}}+ \epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(18)

Case (12):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _4=m_1=\mu _4=0,\ \ \delta ={\frac{{\alpha _{{3}}}^{2}\beta _{{4}}s+{\alpha _{{3}}}^{2} \lambda _{{4}}s+\alpha _{{3}}\beta _{{3}}\lambda _{{4}}s-\alpha _{{3}}\beta _{{4}}\lambda _{{3}}s+\beta _{{4}}}{{\alpha _{{3}}}^{2}\beta _{{4}}}},\\ \ \lambda _{{1}}={\frac{\beta _{{1}}\lambda _{{4}}-\beta _{{3}}\lambda _{{4} }+\beta _{{4}}\lambda _{{3}}}{\beta _{{4}}}},\ \mu _{{1}}=-{\frac{s{\alpha _{{3}}}^{3} \left( \beta _{{4}}+\lambda _{{4} } \right) }{\beta _{{4}}}}, \ \mu _{{3}}=-{\frac{s{\alpha _{{3}}}^{3} \left( \beta _{{4}}+\lambda _{{4} } \right) }{\beta _{{4}}}},\\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{-{\frac{ts{\alpha _{{3}}}^{3} \left( \beta _{{4}}+ \lambda _{{4}} \right) }{\beta _{{4}}}}+x\alpha _{{3}}+y\beta _{{1}}+{ \frac{z \left( \beta _{{1}}\lambda _{{4}}-\beta _{{3}}\lambda _{{4}}+ \beta _{{4}}\lambda _{{3}} \right) }{\beta _{{4}}}}+\epsilon _{{1}}}}+k_{ {2}}{\textrm{e}^{y\beta _{{4}}+z\lambda _{{4}}+\epsilon _{{4}}}}+\\ {\textrm{e}^{ -{\frac{ts{\alpha _{{3}}}^{3} \left( \beta _{{4}}+\lambda _{{4}} \right) }{\beta _{{4}}}}+x\alpha _{{3}}+y\beta _{{1}}+{\frac{z \left( \beta _{{1}}\lambda _{{4}}-\beta _{{3}}\lambda _{{4}}+\beta _{{4}}\lambda _{ {3}} \right) }{\beta _{{4}}}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _ {{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{-{\frac{ts{\alpha _{{3}}}^{3} \left( \beta _{{4}}+ \lambda _{{4}} \right) }{\beta _{{4}}}}+x\alpha _{{3}}+y\beta _{{3}}+z \lambda _{{3}}+\epsilon _{{3}}}} \left( m_{{3}}\cos \left( y\beta _{{4}} +z\lambda _{{4}}+\epsilon _{{4}} \right) +m_{{4}}\sin \left( y\beta _{{4 }}+z\lambda _{{4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(19)

Case (13):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _3=\alpha _4=\beta _3=\beta _4=m_1=0,\ \ \delta ={\frac{{\alpha _{{1}}}^{4}\lambda _{{4}}{s}^{2}+{\alpha _{{1}}}^{ 2}\mu _{{4}}s-s\alpha _{{1}}\lambda _{{1}}\mu _{{4}}+\alpha _{{1}}\lambda _{ {4}}\mu _{{1}}s+\mu _{{4}}}{{\alpha _{{1}}}^{2}\mu _{{4}}}}, \ \beta _{{1}}=-{\frac{\alpha _{{1}} \left( {\alpha _{{1}}}^{2}\lambda _{{4 }}s+\mu _{{4}} \right) }{\mu _{{4}}}},\ \lambda _{{3}}={\frac{\lambda _{{4}}\mu _{{3}}}{\mu _{{4}}}},\\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}-{\frac{y\alpha _{{1}} \left( {\alpha _{{1}}}^{2}\lambda _{{4}}s+\mu _{{4}} \right) }{\mu _{{4}} }}+z\lambda _{{1}}+\epsilon _{{1}}}}+k_{{2}}{\textrm{e}^{t\mu _{{4}}+z \lambda _{{4}}+\epsilon _{{4}}}}+\\ {\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}-{ \frac{y\alpha _{{1}} \left( {\alpha _{{1}}}^{2}\lambda _{{4}}s+\mu _{{4}} \right) }{\mu _{{4}}}}+z\lambda _{{1}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{t\mu _{{3}}+{\frac{z\lambda _{{4}}\mu _{{3}}}{ \mu _{{4}}}}+\epsilon _{{3}}}} \left( m_{{3}}\cos \left( t\mu _{{4}}+z \lambda _{{4}}+\epsilon _{{4}} \right) +m_{{4}}\sin \left( t\mu _{{4}}+z \lambda _{{4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(20)

Case (14):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _1=\alpha _4=\beta _1=\beta _4=m_1=0,\ \ \delta ={\frac{{\alpha _{{3}}}^{4}\lambda _{{4}}{s}^{2}+{\alpha _{{3}}}^{ 2}\mu _{{4}}s-\alpha _{{3}}\lambda _{{3}}\mu _{{4}}s+\alpha _{{3}}\lambda _{ {4}}\mu _{{3}}s+\mu _{{4}}}{{\alpha _{{3}}}^{2}\mu _{{4}}}},\ \beta _{{3}}=-{\frac{\alpha _{{3}} \left( {\alpha _{{3}}}^{2}\lambda _{{4 }}s+\mu _{{4}} \right) }{\mu _{{4}}}}, \lambda _{{1}}={\frac{\lambda _{{4}}\mu _{{1}}}{\mu _{{4}}}},\\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{t\mu _{{1}}+{\frac{z\lambda _{{4}}\mu _{{1}}}{\mu _{{4}} }}+\epsilon _{{1}}}}+k_{{2}}{\textrm{e}^{t\mu _{{4}}+z\lambda _{{4}}+ \epsilon _{{4}}}}+{\textrm{e}^{t\mu _{{1}}+{\frac{z\lambda _{{4}}\mu _{{1}} }{\mu _{{4}}}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{ {2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{t \mu _{{3}}+x\alpha _{{3}}-{\frac{y\alpha _{{3}} \left( {\alpha _{{3}}}^{2 }\lambda _{{4}}s+\mu _{{4}} \right) }{\mu _{{4}}}}+z\lambda _{{3}}+ \epsilon _{{3}}}} \left( m_{{3}}\cos \left( t\mu _{{4}}+z\lambda _{{4}}+ \epsilon _{{4}} \right) +m_{{4}}\sin \left( t\mu _{{4}}+z\lambda _{{4}}+ \epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(21)

Case (15):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _4=\beta _4=m_1=0,\\ \delta =\frac{1}{3}\,{\frac{3\,s{\alpha _{{3}}}^{2} \left( \alpha _{{1}}-\alpha _ {{3}} \right) ^{2} \left( s\alpha _{{1}}\lambda _{{4}} \left( {\alpha _{{ 1}}}^{2}-3\,\alpha _{{1}}\alpha _{{3}}+3\,{\alpha _{{3}}}^{2} \right) + \mu _{{4}} \left( \alpha _{{1}}-\lambda _{{1}}+\lambda _{{4}} \right) \right) -\alpha _{{1}}\mu _{{4}} \left( \alpha _{{1}}-2\,\alpha _{{3}} \right) ^{2}}{\alpha _{{1}}{\alpha _{{3}}}^{2}\mu _{{4}} \left( \alpha _{ {1}}-\alpha _{{3}} \right) ^{2}}}, \\ \beta _{{1}}=-{\frac{\alpha _{{1}} \left( s\lambda _{{4}} \left( {\alpha _{{1}}}^{2}-3\,\alpha _{{1}}\alpha _{{3}}+3\,{\alpha _{{3}}}^{2} \right) +\mu _{{4}} \right) }{\mu _{{4}}}},\ \ \beta _{{3}}=-{\frac{\alpha _{{3}} \left( {\alpha _{{3}}}^{2}\lambda _{{4 }}s+\mu _{{4}} \right) }{\mu _{{4}}}},\ \mu _{{1}}=\frac{1}{3}\,{\frac{\mu _{{4}} \left( 3\,{\alpha _{{3}}}^{2}\lambda _{ {4}}s \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{2}-{\alpha _{{1}}}^{3} +{\alpha _{{1}}}^{2}\alpha _{{3}}-\alpha _{{1}}{\alpha _{{3}}}^{2} \right) }{{\alpha _{{3}}}^{2}\lambda _{{4}}s \left( \alpha _{{1}}-\alpha _{{3}} \right) ^{2}}}, \\ \lambda _{{3}}=-\frac{1}{3}\,{\frac{3\,s\alpha _{{3}} \left( \alpha _{{1}}- \alpha _{{3}} \right) ^{2} \left( \alpha _{{1}}\alpha _{{3}}\lambda _{{4}} s \left( \alpha _{{1}}-\alpha _{{3}} \right) \left( \alpha _{{1}}-2\, \alpha _{{3}} \right) -\alpha _{{1}}\lambda _{{4}}\mu _{{3}}-\alpha _{{3}} \mu _{{4}} \left( \lambda _{{1}}-\lambda _{{4}} \right) \right) -\alpha _ {{1}}\mu _{{4}} \left( 4\,{\alpha _{{1}}}^{2}-10\,\alpha _{{1}}\alpha _{{3 }}+7\,{\alpha _{{3}}}^{2} \right) }{\alpha _{{1}} \left( \alpha _{{1}}- \alpha _{{3}} \right) ^{2}s\alpha _{{3}}\mu _{{4}}}}, \\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}+k_{{2}}{\textrm{e}^{t\mu _{{4}}+z\lambda _{{4}}+\epsilon _{{4}}}}+{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1} }+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _ {{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) \\ +{\textrm{e}^{t\mu _{{3}}+x \alpha _{{3}}-{\frac{y\alpha _{{3}} \left( {\alpha _{{3}}}^{2}\lambda _{{ 4}}s+\mu _{{4}} \right) }{\mu _{{4}}}}+z\lambda _{{3}}+\epsilon _{{3}}}} \left( m_{{3}}\cos \left( t\mu _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) +m_{{4}}\sin \left( t\mu _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(22)

Case (16):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _4=\beta _4=m_1=0, \ \delta ={\frac{{\alpha _{{3}}}^{4}\lambda _{{4}}{s}^{2}+{\alpha _{{3}}}^{ 2}\mu _{{4}}s-s\alpha _{{3}}\lambda _{{1}}\mu _{{4}}+\alpha _{{3}}\lambda _{ {4}}\mu _{{1}}s+\mu _{{4}}}{{\alpha _{{3}}}^{2}\mu _{{4}}}}, \\ \beta _{{1}}=-{\frac{\alpha _{{3}} \left( {\alpha _{{3}}}^{2}\lambda _{{4 }}s+\mu _{{4}} \right) }{\mu _{{4}}}},\ \beta _{{3}}=-{\frac{\alpha _{{3}} \left( {\alpha _{{3}}}^{2}\lambda _{{4 }}s+\mu _{{4}} \right) }{\mu _{{4}}}},\lambda _{{3}}={\frac{\lambda _{{1}}\mu _{{4}}-\lambda _{{4}}\mu _{{1}}+ \lambda _{{4}}\mu _{{3}}}{\mu _{{4}}}}, \\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{3}}-{\frac{y\alpha _{{3}} \left( {\alpha _{{3}}}^{2}\lambda _{{4}}s+\mu _{{4}} \right) }{\mu _{{4}} }}+z\lambda _{{1}}+\epsilon _{{1}}}}+k_{{2}}{\textrm{e}^{t\mu _{{4}}+z \lambda _{{4}}+\epsilon _{{4}}}}+\\ {\textrm{e}^{t\mu _{{1}}+x\alpha _{{3}}-{ \frac{y\alpha _{{3}} \left( {\alpha _{{3}}}^{2}\lambda _{{4}}s+\mu _{{4}} \right) }{\mu _{{4}}}}+z\lambda _{{1}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ {\textrm{e}^{t\mu _{{3}}+x\alpha _{{3}}-{\frac{y\alpha _{{3 }} \left( {\alpha _{{3}}}^{2}\lambda _{{4}}s+\mu _{{4}} \right) }{\mu _{{4 }}}}+{\frac{z \left( \lambda _{{1}}\mu _{{4}}-\lambda _{{4}}\mu _{{1}}+ \lambda _{{4}}\mu _{{3}} \right) }{\mu _{{4}}}}+\epsilon _{{3}}}} \left( m_{{3}}\cos \left( t\mu _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) + m_{{4}}\sin \left( t\mu _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(23)

Case (17):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _3 = 1, \alpha _1=\beta _1=\mu _3 =\alpha _4 = \beta _4 = 2, \mu _1=\mu _4 = 3,\ \beta _3=\frac{319}{124},\ \delta =-\frac{1}{2}\,s\lambda _{{4}}-s+\frac{1}{8},\ \\ \lambda _{{3}}=-{\frac{-992\,s\lambda _{{4}}+3120\,s-1704}{1984\,s}},\ \ T(x,y,z,t)=k_{{1}}{\textrm{e}^{z\lambda _{{4}}+3\,t+2\,x+2\,y+\epsilon _{{1}}}}+k_{{2 }}{\textrm{e}^{t\mu _{{4}}+x\alpha _{{4}}+y\beta _{{4}}+z\lambda _{{4}}+ \epsilon _{{4}}}}+\\ {\textrm{e}^{z\lambda _{{4}}+3\,t+2\,x+2\,y+\epsilon _{{ 1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +{\textrm{e}^{t\mu _{{3}}+x\alpha _{{3}}+{ \frac{319\,y}{124}}-{\frac{z \left( -992\,s\lambda _{{4}}+3120\,s- 1704 \right) }{1984\,s}}+\epsilon _{{3}}}}\\ \times \left( m_{{3}}\cos \left( t \mu _{{4}}+x\alpha _{{4}}+y\beta _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) +m_{{4}}\sin \left( t\mu _{{4}}+x\alpha _{{4}}+y\beta _{{4}}+z \lambda _{{4}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(24)

Case (18):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _3 = 1, \alpha _1=\beta _1=\mu _3 =\alpha _4 = \beta _3 = 2, \mu _1=\mu _4 =\beta _1= 3,\ \beta _4=-\frac{406}{225},\ \mu _3=-\frac{27}{2},\ \delta =-\frac{1}{2}\,s\lambda _{{4}}+{\frac{203\,s}{225}}-{\frac{4}{75}},\ \\ \lambda _{{1}}=-{\frac{-450\,s\lambda _{{4}}+2162\,s-3243}{450\,s}},\ \ \lambda _{{3}}=-{\frac{-225\,s\lambda _{{4}}+1306\,s-1779}{450\,s}},\\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{3\,t+2\,x+y\beta _{{1}}-{\frac{z \left( -450\,s \lambda _{{4}}+2162\,s-3243 \right) }{450\,s}}+\epsilon _{{1}}}}+k_{{2} }{\textrm{e}^{t\mu _{{4}}+x\alpha _{{4}}+z\lambda _{{4}}-{\frac{406\,y}{225 }}+\epsilon _{{4}}}}+\\ {\textrm{e}^{3\,t+2\,x+y\beta _{{1}}-{\frac{z \left( -450\,s\lambda _{{4}}+2162\,s-3243 \right) }{450\,s}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z \lambda _{{2}}+\epsilon _{{2}} \right) +{\textrm{e}^{-{\frac{27\,t}{2}}+x \alpha _{{3}}+y\beta _{{3}}-{\frac{z \left( -225\,s\lambda _{{4}}+1306\, s-1779 \right) }{450\,s}}+\epsilon _{{3}}}}\\ \times \left( m_{{3}}\cos \left( t\mu _{{4}}+x\alpha _{{4}}+z\lambda _{{4}}-{\frac{406\,y}{225}}+ \epsilon _{{4}} \right) +m_{{4}}\sin \left( t\mu _{{4}}+x\alpha _{{4}}+z \lambda _{{4}}-{\frac{406\,y}{225}}+\epsilon _{{4}} \right) \right) . \end{array} \right. \end{aligned}$$

(25)

Case (19):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _1 =m_1=0,\ \delta =\frac{1}{4}\,{\frac{4\,s{\alpha _{{4}}}^{2}-4\,s\alpha _{{4}}\lambda _{{4 }}-1}{{\alpha _{{4}}}^{2}}},\ \beta _{{1}}=\frac{1}{24}\,{\frac{M_{{1}}M_{{2}}}{\mu _{{4}} \left( {\alpha _{{3 }}}^{5}+{\alpha _{{3}}}^{4}\alpha _{{4}}-5\,{\alpha _{{3}}}^{3}{\alpha _{{ 4}}}^{2}+7\,{\alpha _{{3}}}^{2}{\alpha _{{4}}}^{3}-2\,{\alpha _{{4}}}^{5} \right) \left( 2\,\alpha _{{3}}-\alpha _{{4}} \right) }}, \\ \beta _{{3}}=\frac{1}{12}\,{\frac{-24\,{\alpha _{{3}}}^{2}\alpha _{{4}}\mu _{{4}} +12\,\alpha _{{3}}{\alpha _{{4}}}^{2}\mu _{{4}}+M_{{1}}}{\alpha _{{4}}\mu _ {{4}} \left( 2\,\alpha _{{3}}-\alpha _{{4}} \right) }},\ \lambda _{{1}}=-\frac{1}{24}\,{\frac{s\alpha _{{4}} \left( 3\,{\alpha _{{3}}}^{2 }-{\alpha _{{4}}}^{2} \right) M_{{2}}M_{{1}}+\mu _{{4}}M_{{3}}}{\alpha _{ {4}}\mu _{{4}} \left( {\alpha _{{3}}}^{5}+{\alpha _{{3}}}^{4}\alpha _{{4}} -5\,{\alpha _{{3}}}^{3}{\alpha _{{4}}}^{2}+7\,{\alpha _{{3}}}^{2}{\alpha _ {{4}}}^{3}-2\,{\alpha _{{4}}}^{5} \right) \left( 2\,\alpha _{{3}}- \alpha _{{4}} \right) \left( 3\,{\alpha _{{3}}}^{2}-{\alpha _{{4}}}^{2} \right) s}},\\ \lambda _{{3}}=-\frac{1}{12}\,{\frac{s\alpha _{{4}} \left( -24\,{\alpha _{{3}}}^ {2}\lambda _{{4}}\mu _{{4}}+12\,\alpha _{{3}}\alpha _{{4}}\lambda _{{4}}\mu _{{4}}+M_{{1}} \right) +\mu _{{4}} \left( 3\,{\alpha _{{3}}}^{2}+12\, \alpha _{{3}}\alpha _{{4}}-13\,{\alpha _{{4}}}^{2} \right) }{s{\alpha _{{4 }}}^{2}\mu _{{4}} \left( 2\,\alpha _{{3}}-\alpha _{{4}} \right) }},\ \mu _{{1}}={\frac{ \left( 3\,{\alpha _{{3}}}^{2}-2\,{\alpha _{{4}}}^{2} \right) \mu _{{4}}}{3\,{\alpha _{{3}}}^{2}-{\alpha _{{4}}}^{2}}}, \\ \mu _{{3}}={\frac{\mu _{{4}} \left( 9\,{\alpha _{{3}}}^{5}+9\,{\alpha _{{ 3}}}^{4}\alpha _{{4}}-79\,{\alpha _{{3}}}^{3}{\alpha _{{4}}}^{2}+60\,{ \alpha _{{3}}}^{2}{\alpha _{{4}}}^{3}+6\,\alpha _{{3}}{\alpha _{{4}}}^{4}- 16\,{\alpha _{{4}}}^{5} \right) }{\alpha _{{4}}M_{{1}}}}, \\ T(x,y,z,t)=k_{{1}}{\textrm{e}^{{\frac{t \left( 3\,{\alpha _{{3}}}^{2}-2\,{\alpha _{{4 }}}^{2} \right) \mu _{{4}}}{3\,{\alpha _{{3}}}^{2}-{\alpha _{{4}}}^{2}}}+ y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}+k_{{2}}{\textrm{e}^{t\mu _{{ 4}}+x\alpha _{{4}}-y\alpha _{{4}}+z\lambda _{{4}}+\epsilon _{{4}}}}+\\ { \textrm{e}^{{\frac{t \left( 3\,{\alpha _{{3}}}^{2}-2\,{\alpha _{{4}}}^{2} \right) \mu _{{4}}}{3\,{\alpha _{{3}}}^{2}-{\alpha _{{4}}}^{2}}}+y\beta _ {{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}m_{{2}}\sin \left( t\mu _{{2}}+x \alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +\\ { \textrm{e}^{t\mu _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+ \epsilon _{{3}}}} \left( m_{{3}}\cos \left( t\mu _{{4}}+x\alpha _{{4}}-y \alpha _{{4}}+z\lambda _{{4}}+\epsilon _{{4}} \right) +m_{{4}}\sin \left( t\mu _{{4}}+x\alpha _{{4}}-y\alpha _{{4}}+z\lambda _{{4}}+ \epsilon _{{4}} \right) \right) ,\\ u(x,y,z,t)=2T_{xx} \left( x,y,z,t \right) /T \left( x,y,z,t \right) -2\left( T_{x} \left( x,y,z,t \right) /T \left( x,y,z,t \right) \right) ^2. \end{array} \right. \end{aligned}$$

(26)

Interpretation of results for double-periodic soliton

In this section, we discuss the dynamic properties by setting some special values for the free parameters in these solutions. For example, substituting

$$\begin{aligned} \alpha _1 = \alpha _3 = \beta _3 = m_2 = \mu _1 = \lambda _3 = \mu _3 = k_1 = \epsilon _1 = \epsilon _3 = 1, \alpha _2 =\beta _1 = \lambda _2 = \epsilon _4 = 1/4, \alpha _4 =\beta _2 =\mu _4 = \epsilon _2 =1/3, \end{aligned}$$

(27)

$$\begin{aligned} \beta _4 =\mu _2 = 1/2, \lambda _4 = 1/5, m_3 =\delta = k_2 = 2, s = 3, \end{aligned}$$

into Eq. (14), we can obtain the following double-periodic soliton solution

$$\begin{aligned} \left\{ \begin{array}{ll} T(x,y,z,t)={\textrm{e}^{t+x+y/4+{\frac{139\,z}{720}}+1}}+2\,{\textrm{e}^{t/3+x/3+y/2+z /5+1/4}}+{\textrm{e}^{t+x+y/4+{\frac{139\,z}{720}}+1}}\sin \left( t/2+x/ 4+y/3+z/4+1/3 \right) +\\ 2\,{\textrm{e}^{t+x+y+z+1}}\cos \left( t/3+x/3+y/2 +z/5+1/4 \right) ,\\ u(x,y,z,t)=2\,{\frac{{\frac{\partial ^{2}}{\partial {x}^{2}}}T \left( x,y,z,t \right) }{T \left( x,y,z,t \right) }}-2\,{\frac{ \left( {\frac{ \partial }{\partial x}}T \left( x,y,z,t \right) \right) ^{2}}{ \left( T \left( x,y,z,t \right) \right) ^{2}}}. \end{array} \right. \end{aligned}$$

(28)

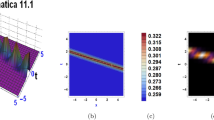
The dynamic properties to Eq. (28) are described in Figs. 1. Figure 1 shows the interaction between two periodic soliton solutions for specified values of $z=t=1, \ \ y=t=1, \ \ x=t=1, \ \ x=y=1, \ \ z=1,y=-1, \ \ x=z=1,\ \ y=-1,z=1,\ \ t=2,z=-2,\ \ x=z=-3$, respectively.

Fig. 1

Double-periodic soliton (28) with different parameters of Case (7) $z=t=1, \ \ y=t=1, \ \ x=t=1, \ \ x=y=1, \ \ z=1,y=-1, \ \ x=z=1,\ \ y=-1,z=1,\ \ t=2,z=-2,\ \ x=z=-3$, respectively.

By substituting below

$$\begin{aligned} \alpha _1 = \beta _3 = \lambda _3 = m_2=m_4 = k_1 = \epsilon _1 = \epsilon _3 = 1, \alpha _2 = \lambda _2 = \epsilon _4 = 1/4, \alpha _4 =\beta _2 =\mu _4 = \epsilon _2 =1/3, \end{aligned}$$

(29)

$$\begin{aligned} \beta _4 =1/2, \lambda _4 = 1/5, \alpha _3=m_3 =\delta = k_2 = 2, s = 3, \end{aligned}$$

into Eq. (18), we can obtain the following double-periodic soliton solution

$$\begin{aligned} \left\{ \begin{array}{ll} T(x,y,z,t)={\textrm{e}^{-{\frac{147\,t}{5}}+x-{\frac{47\,y}{84}}-{\frac{73\,z}{ 420}}+1}}+2\,{\textrm{e}^{y/2+z/5+1/4}}+{\textrm{e}^{-{\frac{147\,t}{5}}+x- {\frac{47\,y}{84}}-{\frac{73\,z}{420}}+1}}\sin \left( 2\,t+x/4+y/3+z /4+1/3 \right) \\ +{\textrm{e}^{-{\frac{168\,t}{5}}+2\,x+y+z+1}} \left( 2\, \cos \left( y/2+z/5+1/4 \right) +\sin \left( y/2+z/5+1/4 \right) \right) ,\\ u(x,y,z,t)=2\,{\frac{{\frac{\partial ^{2}}{\partial {x}^{2}}}T \left( x,y,z,t \right) }{T \left( x,y,z,t \right) }}-2\,{\frac{ \left( {\frac{ \partial }{\partial x}}T \left( x,y,z,t \right) \right) ^{2}}{ \left( T \left( x,y,z,t \right) \right) ^{2}}}. \end{array} \right. \end{aligned}$$

(30)

The dynamic properties to Eq. (30) are described in Fig. 2. Figure 2 shows the interaction between two periodic soliton solutions for specified values of $z=t=1, \ \ y=t=1, \ \ x=t=1, \ \ x=z=1, \ \ x=y=1, \ \ y=z=-2,\ \ x=2,z=-2,\ \ t=2,z=-2,\ \ x=-4,t=1/2$, respectively.

Fig. 2

Double-periodic soliton (30) with different parameters of Case (7) $z=t=1, \ \ y=t=1, \ \ x=t=1, \ \ x=z=1, \ \ x=y=1, \ \ y=z=-2,\ \ x=2,z=-2,\ \ t=2,z=-2,\ \ x=-4,t=1/2$, respectively.

By putting below

$$\begin{aligned} \alpha _3 = \beta _2 = \lambda _2 = m_2= \mu _2=\epsilon _1 = \epsilon _2=\epsilon _3 = \epsilon _4=s=1, \alpha _2 = m_3 = \mu _4 =k_2= 2, \alpha _4 =k_1 =3,\lambda _4 =m_4 =-1, \end{aligned}$$

(31)

into Eq. (26), we can obtain the following double-periodic soliton solution

$$\begin{aligned} \left\{ \begin{array}{ll} T(x,y,z,t)=3\,{\textrm{e}^{5\,t-3/2\,y+{\frac{11\,z}{12}}+1}}+2\,{\textrm{e}^{2\,t+3\, x-3\,y-z+1}}+{\textrm{e}^{5\,t-3/2\,y+{\frac{11\,z}{12}}+1}}\sin \left( t+2\,x+y+z+1 \right) +\\ {\textrm{e}^{-21\,t+x-{\frac{25\,y}{12}}+z/36+1}} \left( 2\,\cos \left( 2\,t+3\,x-3\,y-z+1 \right) -\sin \left( 2\,t+3 \,x-3\,y-z+1 \right) \right) ,\\ u(x,y,z,t)=2\,{\frac{{\frac{\partial ^{2}}{\partial {x}^{2}}}T \left( x,y,z,t \right) }{T \left( x,y,z,t \right) }}-2\,{\frac{ \left( {\frac{ \partial }{\partial x}}T \left( x,y,z,t \right) \right) ^{2}}{ \left( T \left( x,y,z,t \right) \right) ^{2}}}. \end{array} \right. \end{aligned}$$

(32)

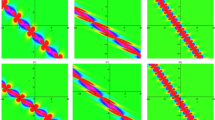
The dynamic properties to Eq. (32) are described in Figs. 3, 4 and 5. Figures 3, 4 and 5 show the interaction between two periodic soliton solutions for specified values of parameters including Fig. 3 the first row $z=t=1$, the second row $y=t=1$ and the third row $x=t=1$ and including Fig. 4 the first row $z=-2,t=2$, the second row $y=-2,t=2$ and the third row $x=-2,t=2$ and also Fig. 5 the first row $y=-1/2, z=1/3$, the second row $x=1/4, z=1/5$ and the third row $x=1/6, y=1/5$.

Fig. 3

Double-periodic soliton (30) with different parameters of (The first row): Case (19) $z=t=1$, (The second row): Case (19) $y=t=1$ and (The third row): Case (19) $x=t=1$.

Fig. 4

Double-periodic soliton (30) with different parameters of (The first row): Case (19) $z=-2, t=2$, (The second row): Case (19) $y=-2, t=2$ and (The third row): Case (19) $x=-2, t=2$.

Fig. 5

Double-periodic soliton (30) with different parameters of (The first row): Case (19) $y=-1/2, z=1/3$, (The second row): Case (19) $x=1/4, z=1/5$ and (The third row): Case (19) $x=1/6, y=1/5$.

Breather wave solutions

According to Three-wave method is used for obtaining the Breather wave solutions by following the steps of this method, T(x, y, z, t) has a solution of the following form

$$\begin{aligned} T(x,y,z,t)=e^{-(\alpha _1x+\beta _1y+\lambda _1z+\mu _1t+\epsilon _1)}+k_1e^{\alpha _1x+\beta _1y+\lambda _1z+\mu _1t+\epsilon _1} \end{aligned}$$

(33)

$$\begin{aligned} + k_2\cos (\alpha _2x+\beta _2y+\lambda _2z+\mu _2t+\epsilon _2)+k_3\sin (\alpha _3x+\beta _3y+\lambda _3z+\mu _3t+\epsilon _3), \end{aligned}$$

where $\alpha _i, \beta _i,\lambda _i,\mu _i$ and $\epsilon _i(i = 1, 2, 3)$ are constants to be determined later. The assumptions used in the “Three-wave method” are special cases of Eq. (33). Substituting Eq. (33) into Eq. (3), a set of algebraic equations about $\alpha _i, \beta _i,\lambda _i,\mu _i$ and $\epsilon _i(i = 1, 2, 3)$ are obtained. With the aid of Mathematica software, we have the following results:

Case (1):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _3=k_2=0,\ \ \beta _{{1}}=\frac{1}{12}\,{\frac{-\beta _{{3}}{k_{{3}}}^{2}\mu _{{3}}+4\,k_{{1} } \left( 3\,{\alpha _{{1}}}^{2}-3\,\alpha _{{1}}\mu _{{1}}+4\,\beta _{{3}} \mu _{{3}} \right) }{k_{{1}}\mu _{{1}}}}, \\ \lambda _{{1}}=-\frac{1}{12}\,{\frac{s{\alpha _{{1}}}^{3} \left( -\beta _{{3}}{k _{{3}}}^{2}\mu _{{3}}+12\,{\alpha _{{1}}}^{2}k_{{1}}-12\,\alpha _{{1}}k_{ {1}}\mu _{{1}}+16\,\beta _{{3}}k_{{1}}\mu _{{3}} \right) +\mu _{{1}} \left( 12\,\delta \,{\alpha _{{1}}}^{4}k_{{1}}-\beta _{{3}}{k_{{3}}}^{2} \mu _{{3}}+4\,\beta _{{3}}k_{{1}}\mu _{{3}} \right) }{k_{{1}}\mu _{{1}}s{ \alpha _{{1}}}^{3}}},\ \\ \lambda _{{3}}=-\frac{1}{12}\,{\frac{12\,s{\alpha _{{1}}}^{3}\beta _{{3}}k_{{1}} \mu _{{1}}-\beta _{{3}}{k_{{3}}}^{2}{\mu _{{3}}}^{2}+12\,{\alpha _{{1}}}^{ 2}k_{{1}}\mu _{{3}}+12\,\beta _{{3}}k_{{1}}{\mu _{{1}}}^{2}+16\,\beta _{{3 }}k_{{1}}{\mu _{{3}}}^{2}}{k_{{1}}\mu _{{1}}s{\alpha _{{1}}}^{3}}}, \\ T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}-z\lambda _{{1}}- \epsilon _{{1}}}}+k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1 }}+z\lambda _{{1}}+\epsilon _{{1}}}}+k_{{3}}\sin \left( t\mu _{{3}}+y \beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) , \\ u(x,y,z,t)=2\,{\frac{{\alpha _{{1}}}^{2}{\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y \beta _{{1}}-z\lambda _{{1}}-\epsilon _{{1}}}}+k_{{1}}{\alpha _{{1}}}^{2} {\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}}{{\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}-z \lambda _{{1}}-\epsilon _{{1}}}}+k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{ 1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}+k_{{3}}\sin \left( t \mu _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) }}-\\ 2\,{ \frac{ \left( -\alpha _{{1}}{\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}-z\lambda _{{1}}-\epsilon _{{1}}}}+k_{{1}}\alpha _{{1}}{\textrm{e}^{t \mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}} \right) ^{2}}{ \left( {\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1} }-z\lambda _{{1}}-\epsilon _{{1}}}}+k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}+k_{{3}}\sin \left( t\mu _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) \right) ^{2}}}. \end{array} \right. \end{aligned}$$

(34)

Case (2):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _3=\mu _3=k_1=k_2=0,\ \ \mu _{{1}}=-{\frac{\gamma \,{\alpha _{{1}}}^{3} \left( \beta _{{3}}+ \lambda _{{3}} \right) }{\beta _{{3}}}}, \ \lambda _{{1}}={\frac{-\delta \,{\alpha _{{1}}}^{2}\beta _{{3}}+\gamma \,{ \alpha _{{1}}}^{2}\beta _{{3}}+\gamma \,{\alpha _{{1}}}^{2}\lambda _{{3}}+ \gamma \,\alpha _{{1}}\beta _{{1}}\lambda _{{3}}+\beta _{{3}}}{\gamma \, \alpha _{{1}}\beta _{{3}}}}, \\ T(x,y,z,t)={\textrm{e}^{{\frac{t\gamma \,{\alpha _{{1}}}^{3} \left( \beta _{{3}}+ \lambda _{{3}} \right) }{\beta _{{3}}}}-x\alpha _{{1}}-y\beta _{{1}}-{ \frac{z \left( -\delta \,{\alpha _{{1}}}^{2}\beta _{{3}}+\gamma \,{\alpha _{{1}}}^{2}\beta _{{3}}+\gamma \,{\alpha _{{1}}}^{2}\lambda _{{3}}+\gamma \,\alpha _{{1}}\beta _{{1}}\lambda _{{3}}+\beta _{{3}} \right) }{\gamma \, \alpha _{{1}}\beta _{{3}}}}-\epsilon _{{1}}}}+k_{{3}}\sin \left( y\beta _ {{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) , \\ u(x,y,z,t)=\frac{2\,{\alpha _{{1}}}^{2}{\textrm{e}^{{\frac{t\gamma \,{\alpha _{{1}}}^{3} \left( \beta _{{3}}+\lambda _{{3}} \right) }{\beta _{{3}}}}-x\alpha _{{1} }-y\beta _{{1}}-{\frac{z \left( -\delta \,{\alpha _{{1}}}^{2}\beta _{{3}} +\gamma \,{\alpha _{{1}}}^{2}\beta _{{3}}+\gamma \,{\alpha _{{1}}}^{2} \lambda _{{3}}+\gamma \,\alpha _{{1}}\beta _{{1}}\lambda _{{3}}+\beta _{{3}} \right) }{\gamma \,\alpha _{{1}}\beta _{{3}}}}-\epsilon _{{1}}}} }{T(x,y,z,t)}-\\ \frac{2\,{\alpha _{{1}}}^{2} \left( {\textrm{e}^{{\frac{t\gamma \,{\alpha _{{1}}} ^{3} \left( \beta _{{3}}+\lambda _{{3}} \right) }{\beta _{{3}}}}-x\alpha _ {{1}}-y\beta _{{1}}-{\frac{z \left( -\delta \,{\alpha _{{1}}}^{2}\beta _{ {3}}+\gamma \,{\alpha _{{1}}}^{2}\beta _{{3}}+\gamma \,{\alpha _{{1}}}^{2} \lambda _{{3}}+\gamma \,\alpha _{{1}}\beta _{{1}}\lambda _{{3}}+\beta _{{3}} \right) }{\gamma \,\alpha _{{1}}\beta _{{3}}}}-\epsilon _{{1}}}} \right) ^{2} }{T^2(x,y,z,t)}. \end{array} \right. \end{aligned}$$

(35)

Case (3):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _1=k_2=\mu _3=0,\ \ \lambda _{{3}}=-{\frac{{\gamma }^{2}{\alpha _{{3}}}^{6}\beta _{{1}}+{ \gamma }^{2}{\alpha _{{3}}}^{6}\lambda _{{1}}+\delta \,{\alpha _{{3}}}^{4} \mu _{{1}}-\gamma \,{\alpha _{{3}}}^{4}\mu _{{1}}+{\alpha _{{3}}}^{2}\mu _{{ 1}}+\beta _{{1}}{\mu _{{1}}}^{2}}{\mu _{{1}}\gamma \,{\alpha _{{3}}}^{3}}}, \\ \beta _{{3}}={\frac{\alpha _{{3}} \left( \gamma \,{\alpha _{{3}}}^{2} \beta _{{1}}+\gamma \,{\alpha _{{3}}}^{2}\lambda _{{1}}-\mu _{{1}} \right) }{\mu _{{1}}}},\ k_{{1}}=\frac{1}{4}\,{\frac{{k_{{3}}}^{2} \left( 3\,{\alpha _{{3}}}^{2}+4\, \beta _{{1}}\mu _{{1}} \right) }{\beta _{{1}}\mu _{{1}}}},\\ T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}-y\beta _{{1}}-z\lambda _{{1}}-\epsilon _{{1}}}}+ \frac{1}{4}\,{\frac{{k_{{3}}}^{2} \left( 3\,{\alpha _{{3}}}^{2}+4\,\beta _{{1}} \mu _{{1}} \right) {\textrm{e}^{t\mu _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}}{\beta _{{1}}\mu _{{1}}}}+k_{{3}}\sin \left( x\alpha _{ {3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) , \\ u(x,y,z,t)=2T_{xx} \left( x,y,z,t \right) /T \left( x,y,z,t \right) -2\left( T_{x} \left( x,y,z,t \right) /T \left( x,y,z,t \right) \right) ^2. \end{array} \right. \end{aligned}$$

(36)

Case (4):

$$\begin{aligned} \left\{ \begin{array}{ll} k_2=\mu _1=\mu _3=0,\ \beta _{{1}}=-{\frac{\delta \,{\alpha _{{1}}}^{3}+\delta \,\alpha _{{1}}{ \alpha _{{3}}}^{2}+\gamma \,{\alpha _{{1}}}^{2}\lambda _{{1}}+\gamma \,{ \alpha _{{3}}}^{2}\lambda _{{1}}-\alpha _{{1}}}{ \left( {\alpha _{{1}}}^{2 }+{\alpha _{{3}}}^{2} \right) \gamma }},\ k_{{1}}=-\frac{1}{4}\,{\frac{{\alpha _{{3}}}^{2}{k_{{3}}}^{2} \left( {\alpha _{ {1}}}^{2}-3\,{\alpha _{{3}}}^{2} \right) }{{\alpha _{{1}}}^{2} \left( 3 \,{\alpha _{{1}}}^{2}-{\alpha _{{3}}}^{2} \right) }}, \\ \lambda _{{3}}=-{\frac{\delta \,{\alpha _{{1}}}^{2}\alpha _{{3}}+\delta \, {\alpha _{{3}}}^{3}+\gamma \,{\alpha _{{1}}}^{2}\beta _{{3}}+\gamma \,{ \alpha _{{3}}}^{2}\beta _{{3}}+\alpha _{{3}}}{ \left( {\alpha _{{1}}}^{2}+ {\alpha _{{3}}}^{2} \right) \gamma }}, \\ T(x,y,z,t)={\textrm{e}^{-x\alpha _{{1}}-y\beta _{{1}}-z\lambda _{{1}}-\epsilon _{{1}}}} -1/4\,{\frac{{\alpha _{{3}}}^{2}{k_{{3}}}^{2} \left( {\alpha _{{1}}}^{2 }-3\,{\alpha _{{3}}}^{2} \right) {\textrm{e}^{x\alpha _{{1}}+y\beta _{{1}}+z \lambda _{{1}}+\epsilon _{{1}}}}}{{\alpha _{{1}}}^{2} \left( 3\,{\alpha _ {{1}}}^{2}-{\alpha _{{3}}}^{2} \right) }}+k_{{3}}\sin \left( x\alpha _{{ 3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) , \\ u(x,y,z,t)=2T_{xx} \left( x,y,z,t \right) /T \left( x,y,z,t \right) -2\left( T_{x} \left( x,y,z,t \right) /T \left( x,y,z,t \right) \right) ^2. \end{array} \right. \end{aligned}$$

(37)

Case (5):

$$\begin{aligned} \left\{ \begin{array}{ll} k_1=k_2=0,\ \beta _{{3}}=\frac{1}{3}\,{\frac{\alpha _{{3}} \left( \alpha _{{1}} \left( { \alpha _{{1}}}^{2}-3\,{\alpha _{{3}}}^{2} \right) ^{2}-3\,\mu _{{1}} \left( {\alpha _{{1}}}^{2}+{\alpha _{{3}}}^{2} \right) ^{2} \right) }{ \mu _{{1}} \left( {\alpha _{{1}}}^{2}+{\alpha _{{3}}}^{2} \right) ^{2}}}, \\ \lambda _{{1}}=-{\frac{\alpha _{{1}} \left( {\alpha _{{1}}}^{2}-3\,{ \alpha _{{3}}}^{2} \right) \left( {\alpha _{{1}}}^{2}+{\alpha _{{3}}}^{2 } \right) \left( \delta \,\alpha _{{1}}+\gamma \,\beta _{{1}} \right) -{ \alpha _{{1}}}^{2} \left( {\alpha _{{1}}}^{2}-3\,{\alpha _{{3}}}^{2} \right) +\mu _{{1}} \left( {\alpha _{{1}}}^{2}+{\alpha _{{3}}}^{2} \right) \left( \alpha _{{1}}+\beta _{{1}} \right) }{\gamma \,\alpha _{{1 }} \left( {\alpha _{{1}}}^{2}-3\,{\alpha _{{3}}}^{2} \right) \left( { \alpha _{{1}}}^{2}+{\alpha _{{3}}}^{2} \right) }}, \\ \lambda _{{3}}=-\frac{1}{3}\,{\frac{ \left( -3\,\mu _{{1}} \left( {\alpha _{{1}} }^{2}+{\alpha _{{3}}}^{2} \right) ^{2} \left( \gamma -\delta \right) + \gamma \,\alpha _{{1}} \left( -{\alpha _{{1}}}^{2}+3\,{\alpha _{{3}}}^{2} \right) ^{2} \right) \alpha _{{3}}}{\gamma \,\mu _{{1}} \left( {\alpha _{ {1}}}^{2}+{\alpha _{{3}}}^{2} \right) ^{2}}},\\ T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}-z\lambda _{{1}}- \epsilon _{{1}}}}+k_{{3}}\sin \left( {\frac{t\alpha _{{3}}\mu _{{1}} \left( 3\,{\alpha _{{1}}}^{2}-{\alpha _{{3}}}^{2} \right) }{\alpha _{{1} } \left( {\alpha _{{1}}}^{2}-3\,{\alpha _{{3}}}^{2} \right) }}+x\alpha _{ {3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) , \\ u(x,y,z,t)=\frac{2\,{\alpha _{{1}}}^{2}{\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}- z\lambda _{{1}}-\epsilon _{{1}}}}-2\,k_{{3}}\sin \left( {\frac{t\alpha _{{3}}\mu _{{1}} \left( 3\,{\alpha _{{1}}}^{2}-{\alpha _{{3}}}^{2} \right) }{\alpha _{{1}} \left( {\alpha _{{1}}}^{2}-3\,{\alpha _{{3}}}^{2 } \right) }}+x\alpha _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) {\alpha _{{3}}}^{2} }{T(x,y,z,t)}+\\ \frac{2\, \left( -\alpha _{{1}}{\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1 }}-z\lambda _{{1}}-\epsilon _{{1}}}}+k_{{3}}\cos \left( {\frac{t\alpha _{{3}}\mu _{{1}} \left( 3\,{\alpha _{{1}}}^{2}-{\alpha _{{3}}}^{2} \right) }{\alpha _{{1}} \left( {\alpha _{{1}}}^{2}-3\,{\alpha _{{3}}}^{2 } \right) }}+x\alpha _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) \alpha _{{3}} \right) ^{2} }{T^2(x,y,z,t)}. \end{array} \right. \end{aligned}$$

(38)

Case (6):

$$\begin{aligned} \left\{ \begin{array}{ll} k_1=k_2=0,\ \alpha _{{1}}={\frac{\alpha _{{3}}}{ \sqrt{3}}},\ M_{{1}}=10\,{\alpha _{{3}}}^{2}+16\,\alpha _{{3}}\beta _{{3}}+9\,{\beta _{ {1}}}^{2}+9\,{\beta _{{3}}}^{2},\ M_{{2}}=2\,{\alpha _{{3}}}^{2}-2\,\alpha _{{3}}\mu _{{3}}+\beta _{{3}}\mu _ {{3}}, \\ \lambda _{{1}}=-\frac{1}{8}\,{\frac{\frac{1}{3}\,\sqrt{3} \left( 8\,\delta \,{\alpha _{ {3}}}^{4} \left( \alpha _{{3}}+\beta _{{3}} \right) -2\,{\alpha _{{3}}}^{ 2} \left( 5\,\alpha _{{3}}+3\,\beta _{{3}} \right) +\mu _{{3}}M_{{1}} \right) +8\,\gamma \,{\alpha _{{3}}}^{3}\beta _{{1}} \left( \alpha _{{3}} +\beta _{{3}} \right) -2\,\beta _{{1}}M_{{2}}}{\gamma \,{\alpha _{{3}}}^{3 } \left( \alpha _{{3}}+\beta _{{3}} \right) }},\\ \lambda _{{3}}=-\frac{1}{4}\,{\frac{4\,\delta \,{\alpha _{{3}}}^{4}+4\,\gamma \,{ \alpha _{{3}}}^{3}\beta _{{3}}+{\alpha _{{3}}}^{2}-\alpha _{{3}}\mu _{{3}}- \beta _{{3}}\mu _{{3}}}{\gamma \,{\alpha _{{3}}}^{3}}},\ \mu _{{1}}=\frac{1}{3}\,{\frac{1}{\alpha _{{3}}+\beta _{{3}}} \left( {\frac{4\, {\alpha _{{3}}}^{2}-\alpha _{{3}}\mu _{{3}}+2\,\beta _{{3}}\mu _{{3}}}{ \sqrt{3}}}-3\,\beta _{{1}}\mu _{{3}} \right) }, \\ T(x,y,z,t)={\textrm{e}^{-1/3\,{\frac{t \left( 1/3\,\sqrt{3} \left( 4\,{\alpha _{{3} }}^{2}-\alpha _{{3}}\mu _{{3}}+2\,\beta _{{3}}\mu _{{3}} \right) -3\,\beta _{{1}}\mu _{{3}} \right) }{\alpha _{{3}}+\beta _{{3}}}}-1/3\,x\sqrt{3} \alpha _{{3}}-y\beta _{{1}}-z\lambda _{{1}}-\epsilon _{{1}}}}+k_{{3}}\sin \left( t\mu _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) , \\ u(x,y,z,t)=\frac{2/3\,{\alpha _{{3}}}^{2}{\textrm{e}^{-1/3\,{\frac{t \left( 1/3\, \sqrt{3} \left( 4\,{\alpha _{{3}}}^{2}-\alpha _{{3}}\mu _{{3}}+2\,\beta _{{3}}\mu _ {{3}} \right) -3\,\beta _{{1}}\mu _{{3}} \right) }{\alpha _{{3}}+\beta _{{ 3}}}}-1/3\,x \sqrt{3}\alpha _{{3}}-y\beta _{{1}}-z\lambda _{{1}}- \epsilon _{{1}}}}-2\,k_{{3}}\sin \left( t\mu _{{3}}+x\alpha _{{3}}+y \beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) {\alpha _{{3}}}^{2} }{T(x,y,z,t)}-\\ \frac{2\, \left( -1/3\, \sqrt{3}\alpha _{{3}}{\textrm{e}^{-1/3\,{\frac{t \left( 1/3\, \sqrt{3} \left( 4\,{\alpha _{{3}}}^{2}-\alpha _{{3}}\mu _{{ 3}}+2\,\beta _{{3}}\mu _{{3}} \right) -3\,\beta _{{1}}\mu _{{3}} \right) }{\alpha _{{3}}+\beta _{{3}}}}-1/3\,x \sqrt{3}\alpha _{{3}}-y\beta _{{1}}- z\lambda _{{1}}-\epsilon _{{1}}}}+k_{{3}}\cos \left( t\mu _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+z\lambda _{{3}}+\epsilon _{{3}} \right) \alpha _{{3} } \right) ^{2} }{T^2(x,y,z,t)}. \end{array} \right. \end{aligned}$$

(39)

Case (7):

$$\begin{aligned} \left\{ \begin{array}{ll} k_1=k_2=0,\ \lambda _{{1}}=-\frac{1}{8}\,{\frac{8\,\delta \,{\alpha _{{1}}}^{4}+8\,\gamma \,{ \alpha _{{1}}}^{3}\beta _{{1}}-2\,{\alpha _{{1}}}^{2}-\alpha _{{1}}\mu _{{1 }}-\beta _{{1}}\mu _{{1}}}{\gamma \,{\alpha _{{1}}}^{3}}},\ \lambda _{{3}}=\frac{1}{12}\,{\frac{ \left( -12\,\delta \,{\alpha _{{1}}}^{2}+12 \,\gamma \,{\alpha _{{1}}}^{2}-1 \right) \sqrt{3}}{\alpha _{{1}}\gamma }},\ \mu _{{3}}=\frac{4}{3}\,{\frac{{\alpha _{{1}}}^{2} \sqrt{3}}{\alpha _{{1}}+\beta _{{1}}}}, \\ T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}-z\lambda _{{1}}- \epsilon _{{1}}}}+k_{{3}}\sin \left( 4/3\,{\frac{t{\alpha _{{1}}}^{2} \sqrt{3}}{\alpha _{{1}}+\beta _{{1}}}}+x\sqrt{3}\alpha _{{1}}-y\sqrt{3 }\alpha _{{1}}+z\lambda _{{3}}+\epsilon _{{3}} \right) ,\\ u(x,y,z,t)=\frac{2\,{\alpha _{{1}}}^{2}{\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}- z\lambda _{{1}}-\epsilon _{{1}}}}-6\,k_{{3}}\sin \left( 4/3\,{\frac{t{ \alpha _{{1}}}^{2} \sqrt{3}}{\alpha _{{1}}+\beta _{{1}}}}+x \sqrt{3} \alpha _{{1}}-y \sqrt{3}\alpha _{{1}}+z\lambda _{{3}}+\epsilon _{{3}} \right) {\alpha _{{1}}}^{2} }{T(x,y,z,t)}-\\ \frac{2\, \left( -\alpha _{{1}}{\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1 }}-z\lambda _{{1}}-\epsilon _{{1}}}}+k_{{3}}\cos \left( 4/3\,{\frac{t{ \alpha _{{1}}}^{2} \sqrt{3}}{\alpha _{{1}}+\beta _{{1}}}}+x \sqrt{3} \alpha _{{1}}-y \sqrt{3}\alpha _{{1}}+z\lambda _{{3}}+\epsilon _{{3}} \right) \sqrt{3}\alpha _{{1}} \right) ^{2} }{T^2(x,y,z,t)}. \end{array} \right. \end{aligned}$$

(40)

Case (8):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _2=k_3=0,\ \ \beta _{{1}}=\frac{1}{12}\,{\frac{-\beta _{{2}}{k_{{2}}}^{2}\mu _{{2}}+4\,k_{{1} } \left( 3\,{\alpha _{{1}}}^{2}-3\,\alpha _{{1}}\mu _{{1}}+4\,\beta _{{2}} \mu _{{2}} \right) }{k_{{1}}\mu _{{1}}}}, \\ \lambda _{{1}}=-\frac{1}{12}\,{\frac{-\gamma \,{\alpha _{{1}}}^{3}\beta _{{2}}{k_ {{2}}}^{2}\mu _{{2}}+12\,\delta \,{\alpha _{{1}}}^{4}k_{{1}}\mu _{{1}}+12 \,\gamma \,{\alpha _{{1}}}^{5}k_{{1}}-12\,\gamma \,{\alpha _{{1}}}^{4}k_{{ 1}}\mu _{{1}}+16\,\gamma \,{\alpha _{{1}}}^{3}\beta _{{2}}k_{{1}}\mu _{{2}} -\beta _{{2}}{k_{{2}}}^{2}\mu _{{1}}\mu _{{2}}+4\,\beta _{{2}}k_{{1}}\mu _{ {1}}\mu _{{2}}}{k_{{1}}\mu _{{1}}\gamma \,{\alpha _{{1}}}^{3}}}, \\ \lambda _{{2}}=-\frac{1}{12}\,{\frac{12\,\gamma \,{\alpha _{{1}}}^{3}\beta _{{2}} k_{{1}}\mu _{{1}}-\beta _{{2}}{k_{{2}}}^{2}{\mu _{{2}}}^{2}+12\,{\alpha _{ {1}}}^{2}k_{{1}}\mu _{{2}}+12\,\beta _{{2}}k_{{1}}{\mu _{{1}}}^{2}+16\, \beta _{{2}}k_{{1}}{\mu _{{2}}}^{2}}{k_{{1}}\mu _{{1}}\gamma \,{\alpha _{{1 }}}^{3}}}, \\ T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}-z\lambda _{{1}}- \epsilon _{{1}}}}+k_{{1}}{\textrm{e}^{t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1 }}+z\lambda _{{1}}+\epsilon _{{1}}}}+k_{{2}}\cos \left( t\mu _{{2}}+y \beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) ,\\ u(x,y,z,t)=\frac{2\,{\alpha _{{1}}}^{2}{\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}- z\lambda _{{1}}-\epsilon _{{1}}}}+2\,k_{{1}}{\alpha _{{1}}}^{2}{\textrm{e}^ {t\mu _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}} } }{T(x,y,z,t)}-\\ \frac{2\, \left( -\alpha _{{1}}{\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1 }}-z\lambda _{{1}}-\epsilon _{{1}}}}+k_{{1}}\alpha _{{1}}{\textrm{e}^{t\mu _ {{1}}+x\alpha _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}} \right) ^{2} }{T^2(x,y,z,t)}. \end{array} \right. \end{aligned}$$

(41)

Case (9):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _1=k_3=\mu _2=0,\ \beta _{{2}}={\frac{\alpha _{{2}} \left( \gamma \,{\alpha _{{2}}}^{2} \beta _{{1}}+\gamma \,{\alpha _{{2}}}^{2}\lambda _{{1}}-\mu _{{1}} \right) }{\mu _{{1}}}},\ k_{{1}}=\frac{1}{4}\,{\frac{{k_{{2}}}^{2} \left( 3\,{\alpha _{{2}}}^{2}+4\, \beta _{{1}}\mu _{{1}} \right) }{\beta _{{1}}\mu _{{1}}}},\\ \lambda _{{2}}=-{\frac{{\gamma }^{2}{\alpha _{{2}}}^{6}\beta _{{1}}+{ \gamma }^{2}{\alpha _{{2}}}^{6}\lambda _{{1}}+\delta \,{\alpha _{{2}}}^{4} \mu _{{1}}-\gamma \,{\alpha _{{2}}}^{4}\mu _{{1}}+{\alpha _{{2}}}^{2}\mu _{{ 1}}+\beta _{{1}}{\mu _{{1}}}^{2}}{\mu _{{1}}\gamma \,{\alpha _{{2}}}^{3}}},\\ T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}-y\beta _{{1}}-z\lambda _{{1}}-\epsilon _{{1}}}}+k_ {{1}}{\textrm{e}^{t\mu _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}} }+k_{{2}}\cos \left( x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+ \epsilon _{{2}} \right) ,\\ u(x,y,z,t)=-2\,{\frac{k_{{2}}\cos \left( x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2 }}+\epsilon _{{2}} \right) {\alpha _{{2}}}^{2}}{{\textrm{e}^{-t\mu _{{1}}-y \beta _{{1}}-z\lambda _{{1}}-\epsilon _{{1}}}}+k_{{1}}{\textrm{e}^{t\mu _{{1 }}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}+k_{{2}}\cos \left( x \alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) }}-\\ 2 \,{\frac{{k_{{2}}}^{2} \left( \sin \left( x\alpha _{{2}}+y\beta _{{2}}+ z\lambda _{{2}}+\epsilon _{{2}} \right) \right) ^{2}{\alpha _{{2}}}^{2} }{ \left( {\textrm{e}^{-t\mu _{{1}}-y\beta _{{1}}-z\lambda _{{1}}-\epsilon _ {{1}}}}+k_{{1}}{\textrm{e}^{t\mu _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}+k_{{2}}\cos \left( x\alpha _{{2}}+y\beta _{{2}}+z \lambda _{{2}}+\epsilon _{{2}} \right) \right) ^{2}}}. \end{array} \right. \end{aligned}$$

(42)

Case (10):

$$\begin{aligned} \left\{ \begin{array}{ll} \mu _2=k_3=0,\ \alpha _1=-\beta _1,\ \beta _{{2}}={\frac{\gamma \, \left( {\alpha _{{2}}}^{2}+{\beta _{{1}}}^{ 2} \right) ^{3} \left( \beta _{{1}}+\lambda _{{1}} \right) -\delta \, \beta _{{1}} \left( {\alpha _{{2}}}^{2}+{\beta _{{1}}}^{2} \right) ^{3}+M _{{1}}}{\alpha _{{2}} \left( {\alpha _{{2}}}^{2}-3\,{\beta _{{1}}}^{2} \right) \mu _{{1}}}},\ \ k_{{1}}=-\frac{1}{4}\,{\frac{{\alpha _{{2}}}^{2}{k_{{2}}}^{2} \left( 3\,{ \alpha _{{2}}}^{2}-{\beta _{{1}}}^{2} \right) }{{\beta _{{1}}}^{2} \left( {\alpha _{{2}}}^{2}-3\,{\beta _{{1}}}^{2} \right) }}, \\ M_{{1}}={\alpha _{{2}}}^{4}\beta _{{1}}-{\alpha _{{2}}}^{4}\mu _{{1}}+2\,{ \alpha _{{2}}}^{2}{\beta _{{1}}}^{3}+3\,{\alpha _{{2}}}^{2}{\beta _{{1}}}^ {2}\mu _{{1}}+{\beta _{{1}}}^{5}, \ M_{{2}}=\delta \,{\alpha _{{2}}}^{4}-6\,\delta \,{\alpha _{{2}}}^{2}{\beta _{{1}}}^{2}+\delta \,{\beta _{{1}}}^{4}+{\alpha _{{2}}}^{2}-{\beta _{{1}}} ^{2}, \\ \lambda _{{2}}=-{\frac{{\gamma }^{2} \left( {\alpha _{{2}}}^{2}+{\beta _{ {1}}}^{2} \right) ^{3} \left( \beta _{{1}}+\lambda _{{1}} \right) - \gamma \,\beta _{{1}}\delta \, \left( {\alpha _{{2}}}^{2}+{\beta _{{1}}}^{2 } \right) ^{3}+\gamma \, \left( M_{{1}}+\beta _{{1}}\mu _{{1}} \left( 3\, {\alpha _{{2}}}^{2}-{\beta _{{1}}}^{2} \right) \left( \beta _{{1}}+ \lambda _{{1}} \right) \right) +\mu _{{1}}M_{{2}}}{\alpha _{{2}} \left( {\alpha _{{2}}}^{2}-3\,{\beta _{{1}}}^{2} \right) \mu _{{1}}\gamma }}, \\ T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}+x\beta _{{1}}-y\beta _{{1}}-z\lambda _{{1}}- \epsilon _{{1}}}}+k_{{1}}{\textrm{e}^{t\mu _{{1}}-x\beta _{{1}}+y\beta _{{1} }+z\lambda _{{1}}+\epsilon _{{1}}}}+k_{{2}}\cos \left( x\alpha _{{2}}+y \beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) ,\\ u(x,y,z,t)=\frac{2\,{\beta _{{1}}}^{2}{\textrm{e}^{-t\mu _{{1}}+x\beta _{{1}}-y\beta _{{1}}-z \lambda _{{1}}-\epsilon _{{1}}}}+2\,k_{{1}}{\beta _{{1}}}^{2}{\textrm{e}^{t \mu _{{1}}-x\beta _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}-2 \,k_{{2}}\cos \left( x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+ \epsilon _{{2}} \right) {\alpha _{{2}}}^{2} }{T(x,y,z,t)}-\\ \frac{2\, \left( \beta _{{1}}{\textrm{e}^{-t\mu _{{1}}+x\beta _{{1}}-y\beta _{{1}}- z\lambda _{{1}}-\epsilon _{{1}}}}-k_{{1}}\beta _{{1}}{\textrm{e}^{t\mu _{{1} }-x\beta _{{1}}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}-k_{{2}} \sin \left( x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) \alpha _{{2}} \right) ^{2} }{T^2(x,y,z,t)}. \end{array} \right. \end{aligned}$$

(43)

Case (11):

$$\begin{aligned} \left\{ \begin{array}{ll} T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}+1/8\,{\frac{z \left( 8\,\delta \,{\alpha _{{1}}}^{4}+8\,\gamma \,{\alpha _{{1}}}^{3} \beta _{{1}}-2\,{\alpha _{{1}}}^{2}-\alpha _{{1}}\mu _{{1}}-\beta _{{1}}\mu _{{1}} \right) }{\gamma \,{\alpha _{{1}}}^{3}}}-\epsilon _{{1}}}}+\\ k_{{2} }\cos \left( \frac{4}{3}\,{\frac{t{\alpha _{{1}}}^{2} \sqrt{3}}{\alpha _{{1}}+ \beta _{{1}}}}+x \sqrt{3}\alpha _{{1}}-y \sqrt{3}\alpha _{{1}}+\frac{1}{12}\,{ \frac{z \left( -12\,\delta \,{\alpha _{{1}}}^{2}+12\,\gamma \,{\alpha _{{ 1}}}^{2}-1 \right) \sqrt{3}}{\gamma \,\alpha _{{1}}}}+\epsilon _{{2}} \right) . \end{array} \right. \end{aligned}$$

(44)

Case (12):

$$\begin{aligned} \left\{ \begin{array}{ll} T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}-{\frac{z\mu _{{1}}}{s\,\alpha _{{3}}\mu _{{3} }}}-\epsilon _{{1}}}}+k_{{2}}\cos \left( t\mu _{{2}}+{\frac{z\mu _{{2}} }{s\,\alpha _{{3}}\mu _{{3}}}}+\epsilon _{{2}} \right) +\\ k_{{3}}\sin \left( t\mu _{{3}}+x\alpha _{{3}}+{\frac{y\alpha _{{3}} \left( \alpha _{ {3}}-\mu _{{3}} \right) }{\mu _{{3}}}}-{\frac{z\alpha _{{3}} \left( \delta \,\mu _{{3}}+s\,\alpha _{{3}}-s\,\mu _{{3}} \right) }{ s\,\mu _{{3}}}}+\epsilon _{{3}} \right) . \end{array} \right. \end{aligned}$$

(45)

Case (13):

$$\begin{aligned} \left\{ \begin{array}{ll} T(x,y,z,t)={\textrm{e}^{-y\beta _{{1}}+{\frac{z\beta _{{1}} \left( s\,{\alpha _{{ 3}}}^{3}-\mu _{{3}} \right) }{s\,{\alpha _{{3}}}^{3}}}-\epsilon _{{ 1}}}}+k_{{2}}\cos \left( y\beta _{{2}}-{\frac{z\beta _{{2}} \left( s\,{\alpha _{{3}}}^{3}-\mu _{{3}} \right) }{s\,{\alpha _{{3}}}^ {3}}}+\epsilon _{{2}} \right) +\\ k_{{3}}\sin \left( t\mu _{{3}}+x\alpha _{ {3}}+{\frac{y\alpha _{{3}} \left( \alpha _{{3}}-\mu _{{3}} \right) }{\mu _{{3}}}}-{\frac{z\alpha _{{3}} \left( \delta \,\mu _{{3}}+s\,\alpha _{{3}}-s\,\mu _{{3}} \right) }{s\,\mu _{{3}}}}+\epsilon _{{3}} \right) . \end{array} \right. \end{aligned}$$

(46)

Case (14):

$$\begin{aligned} \left\{ \begin{array}{ll} T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}-x\alpha _{{1}}-y\beta _{{1}}+{\frac{z \left( \delta \,{\alpha _{{1}}}^{4}+s{\alpha _{{1}}}^{3}\beta _{{1}}-{\alpha _{{1} }}^{2}+\alpha _{{1}}\mu _{{1}}+\beta _{{1}}\mu _{{1}} \right) }{s{\alpha _{ {1}}}^{3}}}-\epsilon _{{1}}}}+\\ k_{{2}}\cos \left( y\beta _{{2}}-{\frac{ z\beta _{{2}} \left( s{\alpha _{{1}}}^{3}+\mu _{{1}} \right) }{s{\alpha _{ {1}}}^{3}}}+\epsilon _{{2}} \right) +k_{{3}}\sin \left( y\beta _{{3}}-{ \frac{z\beta _{{3}} \left( s{\alpha _{{1}}}^{3}+\mu _{{1}} \right) }{s{ \alpha _{{1}}}^{3}}}+\epsilon _{{3}} \right) . \end{array} \right. \end{aligned}$$

(47)

Case (15):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _1=\alpha _3=\beta _1=\beta _3=0,\ \beta _{{2}}={\frac{\alpha _{{2}} \left( \alpha _{{2}}-\mu _{{2}} \right) }{\mu _{{2}}}},\ \lambda _{{1}}={\frac{\mu _{{1}}}{\alpha _{{2}}\mu _{{2}}\gamma }},\ \lambda _{{2}}=-{\frac{\alpha _{{2}} \left( \delta \,\mu _{{2}}+\gamma \, \alpha _{{2}}-\gamma \,\mu _{{2}} \right) }{\gamma \,\mu _{{2}}}},\ \lambda _{{3}}={\frac{\mu _{{3}}}{\alpha _{{2}}\mu _{{2}}\gamma }},\\ T(x,y,z,t)={\textrm{e}^{-t\mu _{{1}}-{\frac{z\mu _{{1}}}{\alpha _{{2}}\mu _{{2}}\gamma } }-\epsilon _{{1}}}}+k_{{1}}{\textrm{e}^{t\mu _{{1}}+{\frac{z\mu _{{1}}}{ \alpha _{{2}}\mu _{{2}}\gamma }}+\epsilon _{{1}}}}+\\ k_{{2}}\cos \left( t \mu _{{2}}+x\alpha _{{2}}+{\frac{y\alpha _{{2}} \left( \alpha _{{2}}-\mu _ {{2}} \right) }{\mu _{{2}}}}-{\frac{z\alpha _{{2}} \left( \delta \,\mu _{ {2}}+\gamma \,\alpha _{{2}}-\gamma \,\mu _{{2}} \right) }{\gamma \,\mu _{{2} }}}+\epsilon _{{2}} \right) +k_{{3}}\sin \left( t\mu _{{3}}+{\frac{z \mu _{{3}}}{\alpha _{{2}}\mu _{{2}}\gamma }}+\epsilon _{{3}} \right) ,\\ \\ u(x,y,z,t)=2T_{xx} \left( x,y,z,t \right) /T \left( x,y,z,t \right) -2\left( T_{x} \left( x,y,z,t \right) /T \left( x,y,z,t \right) \right) ^2. \end{array} \right. \end{aligned}$$

(48)

Case (16):

$$\begin{aligned} \left\{ \begin{array}{ll} T(x,y,z,t)={\textrm{e}^{-y\beta _{{1}}+{\frac{z\beta _{{1}} \left( s{\alpha _{{2}}}^{3 }-\mu _{{2}} \right) }{s{\alpha _{{2}}}^{3}}}-\epsilon _{{1}}}}+k_{{1}}{ \textrm{e}^{y\beta _{{1}}-{\frac{z\beta _{{1}} \left( s{\alpha _{{2}}}^{3}- \mu _{{2}} \right) }{s{\alpha _{{2}}}^{3}}}+\epsilon _{{1}}}}+\\ k_{{2}} \cos \left( t\mu _{{2}}+x\alpha _{{2}}+{\frac{y\alpha _{{2}} \left( \alpha _{{2}}-\mu _{{2}} \right) }{\mu _{{2}}}}-{\frac{z\alpha _{{2}} \left( \delta \,\mu _{{2}}+s\alpha _{{2}}-s\mu _{{2}} \right) }{s\mu _{{2} }}}+\epsilon _{{2}} \right) +k_{{3}}\sin \left( y\beta _{{3}}-{\frac{z \beta _{{3}} \left( s{\alpha _{{2}}}^{3}-\mu _{{2}} \right) }{s{\alpha _{{ 2}}}^{3}}}+\epsilon _{{3}} \right) ,\\ \\ u(x,y,z,t)=2T_{xx} \left( x,y,z,t \right) /T \left( x,y,z,t \right) -2\left( T_{x} \left( x,y,z,t \right) /T \left( x,y,z,t \right) \right) ^2. \end{array} \right. \end{aligned}$$

(49)

Case (17):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _3=\mu _3=0,\ \beta _{{1}}=\frac{1}{3}\,{\frac{{\alpha _{{1}}}^{2}\alpha _{{2}}-3\,{\alpha _{{1 }}}^{2}\mu _{{2}}-2\,{\alpha _{{2}}}^{3}}{\alpha _{{1}}\mu _{{2}}}},\ \beta _{{2}}=1/3\,{\frac{\alpha _{{2}} \left( 2\,{\alpha _{{1}}}^{2} \alpha _{{2}}-3\,{\alpha _{{1}}}^{2}\mu _{{2}}-{\alpha _{{2}}}^{3} \right) }{{\alpha _{{1}}}^{2}\mu _{{2}}}},\\ \lambda _{{1}}=-\frac{1}{3}\,{\frac{3\,\delta \,{\alpha _{{1}}}^{2}{\alpha _{{2}} }^{2}\mu _{{2}}+s{\alpha _{{1}}}^{2}{\alpha _{{2}}}^{3}-3\,s{\alpha _{{1}} }^{2}{\alpha _{{2}}}^{2}\mu _{{2}}-2\,s{\alpha _{{2}}}^{5}-{\alpha _{{1}}} ^{2}\mu _{{2}}-{\alpha _{{2}}}^{2}\mu _{{2}}}{\alpha _{{1}}{\alpha _{{2}}}^ {2}\mu _{{2}}s}},\\ \lambda _{{2}}=-\frac{1}{3}\,{\frac{3\,\delta \,{\alpha _{{1}}}^{2}{\alpha _{{2}} }^{2}\mu _{{2}}+s{\alpha _{{2}}}^{2} \left( 2\,{\alpha _{{1}}}^{2}\alpha _ {{2}}-3\,{\alpha _{{1}}}^{2}\mu _{{2}}-{\alpha _{{2}}}^{3} \right) +{ \alpha _{{1}}}^{2}\mu _{{2}}+{\alpha _{{2}}}^{2}\mu _{{2}}}{s\alpha _{{2}}{ \alpha _{{1}}}^{2}\mu _{{2}}}}, \\ T(x,y,z,t)={\textrm{e}^{{\frac{t{\alpha _{{1}}}^{3}\mu _{{2}}}{{\alpha _{{2}}}^{3}}}-x \alpha _{{1}}-y\beta _{{1}}-z\lambda _{{1}}-\epsilon _{{1}}}}+\frac{1}{4}\,{ \frac{{\alpha _{{2}}}^{4}{k_{{2}}}^{2}}{{\alpha _{{1}}}^{4}}{\textrm{e}^{- {\frac{t{\alpha _{{1}}}^{3}\mu _{{2}}}{{\alpha _{{2}}}^{3}}}+x\alpha _{{1 }}+y\beta _{{1}}+z\lambda _{{1}}+\epsilon _{{1}}}}}+\\ k_{{2}}\cos \left( t \mu _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) +k_{{3}}\sin \left( y\beta _{{3}}-{\frac{z\beta _{{3}} \left( s{\alpha _{{2}}}^{3}-\mu _{{2}} \right) }{s{\alpha _{{2}}}^{3}}}+ \epsilon _{{3}} \right) ,\\ \\ u(x,y,z,t)=2T_{xx} \left( x,y,z,t \right) /T \left( x,y,z,t \right) -2\left( T_{x} \left( x,y,z,t \right) /T \left( x,y,z,t \right) \right) ^2. \end{array} \right. \end{aligned}$$

(50)

Case (18):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _3=0,\ k_3=-3k_2,\ \beta _{{1}}=-1/9\,{\frac{ \left( 2\,\alpha _{{2}}+9\,\mu _{{2}} \right) \alpha _{{2}}}{ \sqrt{2}\mu _{{2}}}},\ \beta _{{2}}=1/9\,{\frac{\alpha _{{2}} \left( 4\,\alpha _{{2}}-9\,\mu _{{ 2}} \right) }{\mu _{{2}}}},\ \lambda _{{3}}=1/9\,{\frac{3\,s{\alpha _{{2}}}^{3}\mu _{{2}}-3\,{\mu _{{2 }}}^{2}+4\,{\mu _{{3}}}^{2}}{\alpha _{{2}}\mu _{{2}}\mu _{{3}}s}}, \\ \lambda _{{1}}=-\frac{1}{9}\,{\frac{9\,\delta \,{\alpha _{{2}}}^{2}\mu _{{2}}-2\, s{\alpha _{{2}}}^{3}-9\,s{\alpha _{{2}}}^{2}\mu _{{2}}-4\,\mu _{{2}}}{ \sqrt{2}\alpha _{{2}}\mu _{{2}}s}},\ \lambda _{{2}}=-\frac{1}{9}\,{\frac{9\,\delta \,{\alpha _{{2}}}^{2}\mu _{{2}}+4\, s{\alpha _{{2}}}^{3}-9\,s{\alpha _{{2}}}^{2}\mu _{{2}}+8\,\mu _{{2}}}{ \alpha _{{2}}\mu _{{2}}s}}, \\ T(x,y,z,t)={\textrm{e}^{1/4\,t\mu _{{2}}\sqrt{2}-1/2\,x\sqrt{2}\alpha _{{2}}-y\beta _ {{1}}-z\lambda _{{1}}-\epsilon _{{1}}}}+k_{{1}}{\textrm{e}^{-1/4\,t\mu _{{2 }}\sqrt{2}+1/2\,x\sqrt{2}\alpha _{{2}}+y\beta _{{1}}+z\lambda _{{1}}+ \epsilon _{{1}}}}+\\ k_{{2}}\cos \left( t\mu _{{2}}+x\alpha _{{2}}+y\beta _{ {2}}+z\lambda _{{2}}+\epsilon _{{2}} \right) -3\,k_{{2}}\sin \left( t \mu _{{3}}-1/3\,{\frac{y{\alpha _{{2}}}^{2}}{\mu _{{3}}}}+z\lambda _{{3}} +\epsilon _{{3}} \right) , \\ u(x,y,z,t)=2T_{xx} \left( x,y,z,t \right) /T \left( x,y,z,t \right) -\left( T_{x} \left( x,y,z,t \right) /T \left( x,y,z,t \right) \right) ^2. \end{array} \right. \end{aligned}$$

(51)

Fig. 6

Breather wave soliton (53) with different parameters of Case (15) $x=t=1, \ \ y=t=1, \ \ z=t=1, \ \ x=y=1, \ \ x=z=1, \ \ y=z=1,\ \ x=-2,t=3,\ \ y=-2,t=3,\ \ z=-2,t=3$, respectively.

Fig. 7

2D plot of Breather wave soliton (53) with different parameters of Case (15) $x=t=1, \ \ y=t=1, \ \ z=t=1, \ \ x=y=1, \ \ x=z=1, \ \ y=z=1,\ \ x=-2,t=3,\ \ y=-2,t=3,\ \ z=-2,t=3$, respectively.

Fig. 8

Breather wave soliton (55) with different parameters of Case (15) $x=t=1, \ \ y=t=1, \ \ z=t=1, \ \ x=y=1, \ \ x=z=1, \ \ y=z=1,\ \ x=-2,t=3,\ \ y=-2,t=3,\ \ z=-2,t=3$, respectively.

Fig. 9

Density plots of Breather wave soliton (57) with different parameters of Case (15) $x=t=1, \ \ y=t=1, \ \ z=t=1, \ \ x=y=1, \ \ x=z=1, \ \ y=z=1,\ \ x=-2,t=3,\ \ y=-2,t=3,\ \ z=-2,t=3$, respectively.

Fig. 10

2D plots of Breather wave soliton (57) with different parameters of Case (15) $x=t=1, \ \ y=t=1, \ \ z=t=1, \ \ x=y=1, \ \ x=z=1, \ \ y=z=1,\ \ x=-2,t=3,\ \ y=-2,t=3,\ \ z=-2,t=3$, respectively.

Fig. 11

The one-order rogue wave (70) at the first row $a_{0, 2} = 2, a_{0, 0} = 2, p = 5, q = 5, b = 1, d = 2, \delta = 2, s = 1$, the second row $a_{0, 2} = 2, a_{0, 0} = 2, p = 0, q = 0, b = 1, d = 2, \delta = 2, s = 1$ and the third row $a_{0, 2} = 2, a_{0, 0} = 2, p = -5, q = -5, b = 1, d = 2, \delta = 2, s = 1$.

Fig. 12

The second form rogue wave (75) at $p = 10, q = 10, b_{2, 0} = 2, c_{2, 0} = 3, b = 3, d = 1, a_{6, 0} = 1, c_{0, 0} = 1, \delta = 2$ (the first row), $p = -3, q = -3, b_{2, 0} = 2, c_{2, 0} = 3, b = 3, d = 1, a_{6, 0} = 1, c_{0, 0} = 1, \delta = 2$ (the second row) and $p = -10, q = -10, b_{2, 0} = 2, c_{2, 0} = 3, b = 3, d = 1, a_{6, 0} = 1, c_{0, 0} = 1, \delta = 2$ (the third row).

Interpretation of results for breather wave

In this section, we discuss the dynamic properties by setting some special values for the free parameters in these solutions. For example, substituting

$$\begin{aligned} \alpha _2 = 1, k_1 = 1, k_2 = 2, k_3 = 2, \mu _1 = 1, \mu _2 = 3, \mu _3 = 2, \epsilon _1=\epsilon _2=\epsilon _3= 1, s = 1, \delta = 2, \end{aligned}$$

(52)

into Eq. (48), we can obtain the following breather wave soliton solution

$$\begin{aligned} \left\{ \begin{array}{ll} u(x,y,z,t)=-4\,{\frac{\cos \left( -3\,t-x+2/3\,y+4/3\,z-1 \right) }{{\textrm{e}^{-t -z/3-1}}+{\textrm{e}^{t+z/3+1}}+2\,\cos \left( -3\,t-x+2/3\,y+4/3\,z-1 \right) +2\,\sin \left( 2\,t+2/3\,z+1 \right) }}-\\ 8\,{\frac{ \left( \sin \left( -3\,t-x+2/3\,y+4/3\,z-1 \right) \right) ^{2}}{ \left( { \textrm{e}^{-t-z/3-1}}+{\textrm{e}^{t+z/3+1}}+2\,\cos \left( -3\,t-x+2/3\,y+ 4/3\,z-1 \right) +2\,\sin \left( 2\,t+2/3\,z+1 \right) \right) ^{2}}}. \end{array} \right. \end{aligned}$$

(53)

The dynamic properties to Eq. (53) are described in Figs. 6 and 7. Figures 6 and 7 show the interaction breather wave soliton solutions for specified values of $x=t=1, \ \ y=t=1, \ \ z=t=1, \ \ x=y=1, \ \ x=z=1, \ \ y=z=1,\ \ x=-2,t=3,\ \ y=-2,t=3,\ \ z=-2,t=3$, respectively. Figure 6 includes density solutions and Fig. 7 presents two dimensional behaviours.

By substituting below

$$\begin{aligned} \alpha _1=2,\alpha _2 = 1, k_2 = 2, k_3 = 2, \beta _3 = 1, \mu _2 = 2, \epsilon _1=\epsilon _2=\epsilon _3= 1, s = 1, \delta = 2, \end{aligned}$$

(54)

into Eq. (50), we can obtain the following breather wave soliton solution

$$\begin{aligned} \left\{ \begin{array}{ll} u(x,y,z,t)=\frac{8\,{\textrm{e}^{16\,t-2\,x+{\frac{11\,y}{6}}+4/3\,z-1}}+1/2\,{\textrm{e}^{- 16\,t+2\,x-{\frac{11\,y}{6}}-4/3\,z+1}}-4\,\cos \left( -2\,t-x+{ \frac{17\,y}{24}}+{\frac{41\,z}{24}}-1 \right) }{{\textrm{e}^{16\,t-2\,x+{\frac{11\,y}{6}}+4/3\,z-1}}+1/16\,{\textrm{e}^{-16 \,t+2\,x-{\frac{11\,y}{6}}-4/3\,z+1}}+2\,\cos \left( -2\,t-x+{\frac{ 17\,y}{24}}+{\frac{41\,z}{24}}-1 \right) +2\,\sin \left( y+z+1 \right) }-\\ \frac{2\, \left( -2\,{\textrm{e}^{16\,t-2\,x+{\frac{11\,y}{6}}+4/3\,z-1}}+1/8 \,{\textrm{e}^{-16\,t+2\,x-{\frac{11\,y}{6}}-4/3\,z+1}}+2\,\sin \left( - 2\,t-x+{\frac{17\,y}{24}}+{\frac{41\,z}{24}}-1 \right) \right) ^{2} }{\left( {\textrm{e}^{16\,t-2\,x+{\frac{11\,y}{6}}+4/3\,z-1}}+1/16\,{ \textrm{e}^{-16\,t+2\,x-{\frac{11\,y}{6}}-4/3\,z+1}}+2\,\cos \left( -2\, t-x+{\frac{17\,y}{24}}+{\frac{41\,z}{24}}-1 \right) +2\,\sin \left( y+z+1 \right) \right) ^{2} }. \end{array} \right. \end{aligned}$$

(55)

The dynamic properties to Eq. (55) are described in Fig. 8. Figure 8 show the interaction breather wave soliton solutions for specified values of $x=t=1, \ \ y=t=1, \ \ z=t=1, \ \ x=y=1, \ \ x=z=1, \ \ y=z=1,\ \ x=-2,t=3,\ \ y=-2,t=3,\ \ z=-2,t=3$, respectively. Figure 8 includes density solutions.

By substituting below

$$\begin{aligned} \alpha _1=2,\alpha _2 = 1, k_2 = 2, k_3 = 2, \beta _3 = 1, \mu _2 = 2, \epsilon _1=\epsilon _2=\epsilon _3= 1, s = 1, \delta = 2, \end{aligned}$$

(56)

into Eq. (51), we can obtain the following breather wave soliton solution

$$\begin{aligned} \left\{ \begin{array}{ll} u(x,y,z,t)=\left[ {\textrm{e}^{1/4\,t \sqrt{2}-1/2\,x \sqrt{2}+{\frac{11\,y \sqrt{2}}{18}} +1/6\,z \sqrt{2}-2}}+2\,{\textrm{e}^{-1/4\,t \sqrt{2}+1/2\,x \sqrt{2}-{ \frac{11\,y \sqrt{2}}{18}}-1/6\,z \sqrt{2}+2}}-\right. \\ \left. 4\,\cos \left( -t-x+5/ 9\,y+7/3\,z-1 \right) \right] /T(x,y,z,t)- 2\, \left( -1/2\, \sqrt{2}{\textrm{e}^{1/4\,t \sqrt{2}-1/2\,x \sqrt{2}+{ \frac{11\,y \sqrt{2}}{18}}+1/6\,z \sqrt{2}-2}}+ \right. \\ \left. \sqrt{2}{\textrm{e}^{-1/ 4\,t \sqrt{2}+1/2\,x \sqrt{2}-{\frac{11\,y \sqrt{2}}{18}}-1/6\,z \sqrt{2}+2}}+2\,\sin \left( -t-x+5/9\,y+7/3\,z-1 \right) \right) ^{2}/T^2(x,y,z,t),\\ T(x,y,z,t)={\textrm{e}^{1/4\,t \sqrt{2}-1/2\,x \sqrt{2}+{\frac{11\,y \sqrt{2}}{18}} +1/6\,z \sqrt{2}-2}}+2\,{\textrm{e}^{-1/4\,t \sqrt{2}+1/2\,x \sqrt{2}-{ \frac{11\,y \sqrt{2}}{18}}-1/6\,z \sqrt{2}+2}}+\\ 2\,\cos \left( -t-x+5/ 9\,y+7/3\,z-1 \right) -6\,\sin \left( 2\,t-y/6+{\frac{8\,z}{9}}+2 \right) . \end{array} \right. \end{aligned}$$

(57)

The dynamic properties to Eq. (57) are described in Figs. 9 and 10. Figures 9 and 10 show the interaction breather wave soliton solutions for specified values of $x=t=1, \ \ y=t=1, \ \ z=t=1, \ \ x=y=1, \ \ x=z=1, \ \ y=z=1,\ \ x=-2,t=3,\ \ y=-2,t=3,\ \ z=-2,t=3$, respectively. Figure 9 includes density solutions and Fig. 10 presents two dimensional behaviours.

Multiple Rogue wave

This part explains a efficient clarification of different Exp-function strategy^85,86 so that it can be encourage connected to the nonlinear PDEs as bellow:

Step 1: Consider NLPDE

$$\begin{aligned} {\mathcal {P}}(x,y,z,t,u, u_x, u_y, u_z, u_t, u_{xx}, u_{xxx},u_{xxy},u_{xxz},...)=0.\hspace{2cm} \end{aligned}$$

(58)

A Painlevé analysis is introduced

$$\begin{aligned} u={\mathfrak {T}}(T), \hspace{2.5cm} \end{aligned}$$

(59)

according to the dependant variable function T. Step 2: By utilizing the relation (59), the nonlinear equation (58) is given as the following Hirota’s bilinear form

$$\begin{aligned} {\mathfrak {G}}(D_{\xi },D_z; T)=0, \hspace{2.5cm} \end{aligned}$$

(60)

where $\xi =x+by-dt$ and b, d are the real values. Moreover, the D-operator is shown as

$$\begin{aligned} \prod _{i=1}^{2}D_{m_i}^{\beta _i}T_1. T_2=\left. \prod _{i=1}^{2}\left( \frac{\partial }{\partial m_i}-\frac{\partial }{\partial m_i'}\right) ^{\beta _i}T_1(m)T_2(m')\right| _{m'=m}, \hspace{6cm} \end{aligned}$$

(61)

where the vectors $m=(m_1,m_2)=(\xi ,z)$, $m'=(m'_1,m'_2)=(\xi ',z')$ and $\beta _1,\beta _2$ are arbitrary nonnegative integers. Step 3: Let⁸⁶

$$\begin{aligned} {\mathfrak {T}}={\mathfrak {T}}(\xi ,z; q,p)=\chi _{n+1}(\xi ,z)+2p z\, p_n(\xi ,z)+2q\xi \, s_n(\xi ,z)+(q^2+p^2)\,\chi _{n-1}(\xi ,z), \hspace{3cm} \end{aligned}$$

(62)

with

$$\begin{aligned} \chi _{n}(\xi ,z)=\sum _{k=0}^{\frac{n(n+1)}{2}}\sum _{i=0}^{k}a_{n(n+1)-2k,2i}z^{2i}\xi ^{n(n+1)-2k}, \hspace{3cm} \end{aligned}$$

(63)

$$\begin{aligned} p_{n}(\xi ,z)=\sum _{k=0}^{\frac{n(n+1)}{2}}\sum _{i=0}^{k}b_{n(n+1)-2k,2i}z^{2i}\xi ^{n(n+1)-2k}, \hspace{3cm} \\ s_{n}(\xi ,z)=\sum _{k=0}^{\frac{n(n+1)}{2}}\sum _{i=0}^{k}c_{n(n+1)-2k,2i}z^{2i}\xi ^{n(n+1)-2k}, \hspace{3cm} \end{aligned}$$

$\chi _0= 1, \chi _1=p_0= s_0= 0$, where $a_{m,l}, b_{m,l}, c_{m,l} (m, l \in \{0, 2, 4,\ldots , n(n+1)\})$ and p, q are real values. The coefficients $a_{m,l}, b_{m,l}, c_{m,l}$ can be found, and special values p, q are utilized to control the wave center. The rest steps were presented in⁸⁵. Based on $\xi =x+by-dt$, Eq. (6) is transformed as bellow form

$$\begin{aligned} {\widetilde{B}}(T)=[(\delta +sb)\,D_\xi ^4-(1+b+bd)D_\xi ^2+s D_\xi ^3D_z]T.T \end{aligned}$$

(64)

$$\begin{aligned} = (\delta +sb)(TT_{\xi \xi \xi \xi }-4T_\xi T_{\xi \xi \xi }+3T_{\xi \xi }^2)-(1+b+bd)(TT_{xx}-T_{x}^2)+ \\ s(T_{\xi \xi \xi z}-T_zT_{\xi \xi \xi }-3T_xT_{\xi \xi z}+3T_{\xi \xi }T_{\xi z})=0. \end{aligned}$$

in which b, d are unfound parameters and Eq. (64) is used using the below bilinear transformation

$$\begin{aligned} u=2(\ln T)_{\xi \xi }.\hspace{6.5cm} \end{aligned}$$

(65)

With considering $n=0$ at (62), then (62) will be as

$$\begin{aligned} {\mathfrak {T}}={\mathfrak {T}}_1(\xi ,z; q,p)=\chi _{1}(\xi ,z)+2p z\, p_0(\xi ,z)+2q\xi \, s_0(\xi ,z)+(q^2+p^2)\chi _{-1}(\xi ,z)=a_{2,0}\xi ^2+a_{0,2}z^2+a_{0,0}, \hspace{0cm} \end{aligned}$$

(66)

without loss of generality, we can choose $a_{2,0}= 1$. Inserting (66) into (65) and setting all the coefficients of the different powers of $z^m\xi ^m$ to zero, the nonlinear algebraic equations are reached as

$$\begin{aligned} -4\,bda_{{0,0}}+24\,bs-4\,da_{{0,0}}+24\,\delta -4\,a_{{0,0}}=0, \end{aligned}$$

(67)

$$\begin{aligned} 4bd+4d+4\ne 0. \ \ \ \end{aligned}$$

Solving Eq. (67), we get

$$\begin{aligned} a_{{0,0}}=6\,{\frac{bs+\delta }{bd+d+1}}, \ \ \ a_{{0,2}}=a_{{0,2}}. \end{aligned}$$

(68)

Therefore, the solution of Eq. (66) is

$$\begin{aligned} {\mathfrak {T}}={\mathfrak {T}}_1(\xi ,z; q,p)=a_{{0,2}} \left( z-p \right) ^{2}+ \left( \xi -q \right) ^{2}+6\,{ \frac{bs+\delta }{bd+d+1}}, \hspace{0cm} \end{aligned}$$

(69)

by supposing $bd+d+1>0$, then the first-order rogue wave solutions of Eq. (1) is given

$$\begin{aligned} u(\xi ,z)=4\, \left( a_{{0,2}} \left( z-p \right) ^{2}+ \left( \xi -q \right) ^{2 }+6\,{\frac{bs+\delta }{bd+d+1}} \right) ^{-1}- \end{aligned}$$

(70)

$$\begin{aligned} 2\,{ \left( 2\,\xi -2\,q \right) ^{2} \left( a_{{0,2}} \left( z-p \right) ^{2}+ \left( \xi -q \right) ^{2}+6\,{\frac{bs+\delta }{bd+d+1}} \right) ^{-2}}. \end{aligned}$$

The above rogue wave has the following features

$$\begin{aligned} \lim _{\xi \longrightarrow \pm \infty }u(\xi ,z)=0,\ \ \ \ \lim _{z\longrightarrow \pm \infty }u(\xi ,z)=0. \hspace{4cm} \end{aligned}$$

(71)

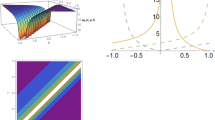
By selecting suitable values of parameters, the graphical representation of periodic wave solution is presented in Fig. 11 including 3D plot, contour plot, and 2D plot when three spaces arise at spaces $z=-1$, $z=0$, and $z=1$. In Fig. 11 (the first row) the rogue wave has one center (5, 5), (the second row) the rogue wave has one center (0, 0), while in Fig. 11 (the third row) the rogue wave has one center $(-5, -5)$. Because of using a simple computation, the lump has two critical points, but we investigate only one point $(\xi _1, z_1) =\left( q, p\right)$. At the point $(\xi _1, z_1)$, the second order derivative and Hessian matrix can be determined in below

$$\begin{aligned} \left\{ \begin{array}{ll} \Theta {1}=\left. \frac{\partial ^2}{\partial \xi ^2}\Psi (\xi ,z)\right| _{(\xi _1,z_1)}= -2/3\,{\frac{ \left( bd+d+1 \right) ^{2}}{ \left( bs+\delta \right) ^ {2}}}, \\ \Delta _1= det\left( \begin{array}{cc} \frac{\partial ^2}{\partial \xi ^2}u(\xi ,z) &{} \frac{\partial ^2}{\partial \xi \partial z}u(\xi ,z) \\ \frac{\partial ^2}{\partial \xi \partial z}u(\xi ,z) &{} \frac{\partial ^2}{\partial z^2}u(\xi ,z) \\ \end{array} \right) _{(\xi _1,z_1)}={\frac{4\, \left( bd+d+1 \right) ^{4}a_{{0,2}}}{27\, \left( bs+\delta \right) ^{4}}}. \end{array} \right. \hspace{5cm} \end{aligned}$$

(72)

If $a_{{0,2}}<0$, then the solution $(\xi _1, z_1)$ is the lump solution is the only local maximum point of function $u(\xi ,z)$, while if $a_{{0,2}}>0$, then the local minimum point of function $u(\xi ,z)$ does not occurs. Based on above analysis, the point $(\xi _1, z_1)$ is a maximum value point with value $u_{max}$ in which is $2/3\,{\frac{bd+d+1}{bs+\delta }}$. Figure 11 (the first row) is presented for first rogue solution with values $a_{0, 2} = 2, a_{0, 0} = 2, p = 5, q = 5, b = 1, d = 2, \delta = 2, s = 1$. Figure 11 (the second row) is shown for first rogue solution with values $a_{0, 2} = 2, a_{0, 0} = 2, p = 0, q = 0, b = 1, d = 2, \delta = 2, s = 1$. Moreover, Fig. 11 (the third row) is presented for first rogue solution with values $a_{0, 2} = 2, a_{0, 0} = 2, p = -5, q = -5, b = 1, d = 2, \delta = 2, s = 1$.

For finding second rogue wave, take $n=1$ at (62), then (62) will be as

$$\begin{aligned} {\mathfrak {T}}={\mathfrak {T}}_2(\xi ,z; q,p)=\chi _{2}(\xi ,z)+2p z\, p_1(\xi ,z)+2q\xi \, s_1(\xi ,z)+(q^2+p^2)\,\chi _{0}(\xi ,z)=\hspace{4cm} \end{aligned}$$

(73)

$$\begin{aligned} {\xi }^{6}+a_{{4,2}}{z}^{2}{\xi }^{4}+a_{{2,4}}{z}^{4}{\xi }^{2}+a_{{0,6} }{z}^{6}+a_{{4,0}}{\xi }^{4}+a_{{2,2}}{z}^{2}{\xi }^{2}+a_{{0,4}}{z}^{4} +a_{{2,0}}{\xi }^{2}+a_{{0,2}}{z}^{2}+a_{{0,0}}+ \\ 2\,p\,z \left( { \xi }^{2}b_{{2,0}}+{z}^{2}b_{{0,2}}+b_{{0,0}} \right) + 2\,q\,\xi \, \left( {\xi }^{2}c_{{2,0}}+{z}^{2}c_{{0,2}}+c_{{0,0}} \right) +{p }^{2}+{q}^{2}, \end{aligned}$$

for simplifying we choose $a_{6,0}= 1$. Inserting (73) into (65) we can get the following results:

$$\begin{aligned} a_{{0,0}}=-1/9\,{\frac{9\,b \left( bd+d+1 \right) \left( -{q}^{2}{c_ {{2,0}}}^{2}+{p}^{2}a_{{6,0}}+{q}^{2}a_{{6,0}} \right) -\delta \,{p}^{2 }{b_{{2,0}}}^{2}}{ba_{{6,0}} \left( bd+d+1 \right) }},\ \ a_{{0,2}}={\frac{a_{{6,0}}{c_{{0,0}}}^{2} \left( bd+d+1 \right) b}{{c _{{2,0}}}^{2}\delta }}, \end{aligned}$$

(74)

$$\begin{aligned} a_{{0,4}}=-2\,{\frac{{b}^{2} \left( bd+d+1 \right) ^{2}a_{{6,0}}c_{{0,0}}}{{\delta }^{2}c_{{2,0}}}}, \ \ a_{{0,6}}={\frac{{b}^{3} \left( bd+d+1 \right) ^{3}a_{{6,0}}}{{\delta }^{3}}},\ a_{{2,0}}={\frac{a_{{6,0}}{c_{{0,0}}}^{2}}{{c_{{2,0}}}^{2}}}, \\ a_{{2,4}}=3\,{\frac{{b}^{2} \left( bd+d+1 \right) ^{2}a_{{6,0}}}{{ \delta }^{2}}},\ a_{{4,0}}=2\,{\frac{a_{{6,0}}c_{{0,0}}}{c_{{2,0}}}},\ a_{{4,2}}=3\,{\frac{ba_{{6,0}} \left( bd+d+1 \right) }{\delta }}, \\ b_{{0,0}}=1/3\,{\frac{b_{{2,0}}c_{{0,0}}}{c_{{2,0}}}}, \ b_{{0,2}}=-1/3\,{\frac{b_{{2,0}} \left( bd+d+1 \right) b}{\delta }}, \ c_{{0,2}}=-3\,{\frac{ \left( bd+d+1 \right) bc_{{2,0}}}{\delta }}, \ a_{{2,2}}=0, \end{aligned}$$

in which $b,d,c_{{0,0}}, b_{{2,0}},a_{{6,0}}$ and $c_{{2,0}}$ are arbitrary values. Thus, the second-order rogue wave solutions of Eq. (1) is given as

$$\begin{aligned} u(\xi ,y)=2(\ln {\mathfrak {T}}_2(\xi ,z; q,p))_{\xi \xi },\hspace{5.5cm} \end{aligned}$$

(75)

where ${\mathfrak {T}}_2(\xi ,y; q,p)$ is given in Eq. (73). We analysis of second order rogue wave solution plots related to (73) with parameters available in (74). Figure 12 (the first row) is presented for second rogue solution with values $p = 10, q = 10, b_{2, 0} = 2, c_{2, 0} = 3, b = 3, d = 1, a_{6, 0} = 1, c_{0, 0} = 1, \delta = 2$. Figure 12 (the second row) is shown for second rogue solution with values $p = -3, q = -3, b_{2, 0} = 2, c_{2, 0} = 3, b = 3, d = 1, a_{6, 0} = 1, c_{0, 0} = 1, \delta = 2$. Moreover, Fig. 12 (the third row) is presented for second rogue solution with values $p = -10, q = -10, b_{2, 0} = 2, c_{2, 0} = 3, b = 3, d = 1, a_{6, 0} = 1, c_{0, 0} = 1, \delta = 2$.

Sets of solutions are listed as:

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathfrak {T}}_{2_1}(\xi ,z; q,p)=a_{{6,0}}{\xi }^{6}+3\,{\frac{a_{{6,0}} \left( bd+d+1 \right) bc_{{2,0 }}{z}^{2}{\xi }^{4}}{bdc_{{0,0}}+dc_{{0,0}}+\delta \,c_{{2,0}}+c_{{0,0}} }}+3\,{\frac{ \left( bd+d+1 \right) ^{2}{b}^{2}{c_{{2,0}}}^{2}a_{{6,0 }}{z}^{4}{\xi }^{2}}{ \left( bdc_{{0,0}}+dc_{{0,0}}+\delta \,c_{{2,0}}+c _{{0,0}} \right) ^{2}}}+{\frac{{b}^{3}{c_{{2,0}}}^{3} \left( bd+d+1 \right) ^{3}a_{{6,0}}{z}^{6}}{ \left( bdc_{{0,0}}+dc_{{0,0}}+\delta \, c_{{2,0}}+c_{{0,0}} \right) ^{3}}}-25\,{\frac{a_{{6,0}}c_{{0,0}}{\xi } ^{4}}{c_{{2,0}}}}\\ -90\,{\frac{a_{{6,0}}c_{{0,0}} \left( bd+d+1 \right) b{z}^{2}{\xi }^{2}}{bdc_{{0,0}}+dc_{{0,0}}+\delta \,c_{{2,0}}+c _{{0,0}}}}-17\,{\frac{{b}^{2} \left( bd+d+1 \right) ^{2}a_{{6,0}}c_{{0,0}}c_{{2,0}}{z}^{4}}{ \left( bdc_{{0,0}}+dc_{{0,0}}+\delta \,c_{{2,0}} +c_{{0,0}} \right) ^{2}}}-125\,{\frac{a_{{6,0}}{c_{{0,0}}}^{2}{\xi }^{ 2}}{{c_{{2,0}}}^{2}}}+475\,{\frac{a_{{6,0}}{c_{{0,0}}}^{2} \left( bd+ d+1 \right) b{z}^{2}}{c_{{2,0}} \left( bdc_{{0,0}}+dc_{{0,0}}+\delta \, c_{{2,0}}+c_{{0,0}} \right) }}\\ - 1/9\,{\frac{9\,b \left( bd+d+1 \right) \left( -{c_{{2,0}}}^{5}{q}^{2}+{p}^{2}a_{{6,0}}{c_{{2,0}}}^{ 3}+{q}^{2}a_{{6,0}}{c_{{2,0}}}^{3}+1875\,{a_{{6,0}}}^{2}{c_{{0,0}}}^{3 } \right) -{p}^{2}{b_{{2,0}}}^{2}{c_{{2,0}}}^{2} \left( bdc_{{0,0}}+dc _{{0,0}}+\delta \,c_{{2,0}}+c_{{0,0}} \right) }{{c_{{2,0}}}^{3}ba_{{6,0 }} \left( bd+d+1 \right) }}+\\ 2\,pz \left( {\xi }^{2}b_{{2,0}}-1/3\,{ \frac{{z}^{2}b_{{2,0}} \left( bd+d+1 \right) bc_{{2,0}}}{bdc_{{0,0}}+ dc_{{0,0}}+\delta \,c_{{2,0}}+c_{{0,0}}}}- 5/3\,{\frac{b_{{2,0}}c_{{0,0 }}}{c_{{2,0}}}} \right) +2\,q\xi \, \left( {\xi }^{2}c_{{2,0}}-3\,{ \frac{{z}^{2} \left( bd+d+1 \right) b{c_{{2,0}}}^{2}}{bdc_{{0,0}}+dc_ {{0,0}}+\delta \,c_{{2,0}}+c_{{0,0}}}}+c_{{0,0}} \right) +{p}^{2}+{q}^{ 2},\\ {\mathfrak {T}}_{2_2}(\xi ,z; q,p)=a_{{6,0}}{\xi }^{6}+3\,{\frac{a_{{6,0}} \left( bd+d+1 \right) b{z}^{2} {\xi }^{4}}{\delta }}+3\,{\frac{ \left( bd+d+1 \right) ^{2}{b}^{2}a_{{6,0}}{z}^{4}{\xi }^{2}}{{\delta }^{2}}}+{\frac{{b}^{3} \left( bd+d+1 \right) ^{3}a_{{6,0}}{z}^{6}}{{\delta }^{3}}}+a_{{4,0}}{\xi }^{4}-{ \frac{{b}^{2} \left( bd+d+1 \right) ^{2}a_{{4,0}}{z}^{4}}{{\delta }^{2 }}}+\\ 1/4\,{\frac{{a_{{4,0}}}^{2}{\xi }^{2}}{a_{{6,0}}}}+1/4\,{\frac{{a _{{4,0}}}^{2} \left( bd+d+1 \right) b{z}^{2}}{\delta \,a_{{6,0}}}},\\ {\mathfrak {T}}_{2_3}(\xi ,z; q,p)=a_{{6,0}}{\xi }^{6}-75\,{\frac{{a_{{6,0}}}^{2} \left( bd+d+1 \right) b {z}^{2}{\xi }^{4}}{bda_{{4,0}}+da_{{4,0}}-25\,\delta \,a_{{6,0}}+a_{{4,0 }}}}+1875\,{\frac{{a_{{6,0}}}^{3} \left( bd+d+1 \right) ^{2}{b}^{2}{z }^{4}{\xi }^{2}}{ \left( bda_{{4,0}}+da_{{4,0}}-25\,\delta \,a_{{6,0}}+a _{{4,0}} \right) ^{2}}}-\\ 15625\,{\frac{{b}^{3}{a_{{6,0}}}^{4} \left( b d+d+1 \right) ^{3}{z}^{6}}{ \left( bda_{{4,0}}+da_{{4,0}}-25\,\delta \, a_{{6,0}}+a_{{4,0}} \right) ^{3}}}+a_{{4,0}}{\xi }^{4}-90\,{\frac{a_{{ 4,0}}a_{{6,0}} \left( bd+d+1 \right) b{z}^{2}{\xi }^{2}}{bda_{{4,0}}+da _{{4,0}}-25\,\delta \,a_{{6,0}}+a_{{4,0}}}}+ 425\,{\frac{{b}^{2}{a_{{6,0 }}}^{2}a_{{4,0}} \left( bd+d+1 \right) ^{2}{z}^{4}}{ \left( bda_{{4,0} }+da_{{4,0}}- 25\,\delta \,a_{{6,0}}+a_{{4,0}} \right) ^{2}}}- 1/5\,{ \frac{{a_{{4,0}}}^{2}{\xi }^{2}}{a_{{6,0}}}}\\ -19\,{\frac{{a_{{4,0}}}^{ 2} \left( bd+d+1 \right) b{z}^{2}}{bda_{{4,0}}+da_{{4,0}}-25\,\delta \, a_{{6,0}}+a_{{4,0}}}}-{\frac{225\,b{a_{{6,0}}}^{2} \left( {p}^{2}+{q} ^{2} \right) \left( bd+d+1 \right) - a_{{4,0}} \left( bd+d+1 \right) \left( -{p}^{2}{b_{{2,0}}}^{2}+27\,b{a_{{4,0}}}^{2} \right) -25\, \delta \,{p}^{2}{b_{{2,0}}}^{2}a_{{6,0}}}{225\,b{a_{{6,0}}}^{2} \left( bd+d+1 \right) }}+\\ 2\,pz \left( {\xi }^{2}b_{{2,0}}+{\frac{25\,{z}^{2}b _{{2,0}}a_{{6,0}} \left( bd+d+1 \right) b}{3\,bda_{{4,0}}+3\,da_{{4,0} }-75\,\delta \,a_{{6,0}}+3\,a_{{4,0}}}}+1/15\,{\frac{b_{{2,0}}a_{{4,0} }}{a_{{6,0}}}} \right) +{p}^{2}+{q}^{2},\\ {\mathfrak {T}}_{2_4}(\xi ,z; q,p){\textbf {=}}a_{{6,0}}{\xi }^{6}+3\,{\frac{a_{{6,0}} \left( d\delta -ds-s \right) {z }^{2}{\xi }^{4}}{{s}^{2}}}+3\,{\frac{a_{{6,0}} \left( d\delta -ds-s \right) ^{2}{z}^{4}{\xi }^{2}}{{s}^{4}}}+{\frac{a_{{6,0}} \left( d \delta -ds-s \right) ^{3}{z}^{6}}{{s}^{6}}}+ a_{{4,0}}{\xi }^{4}-{\frac{ \left( d\delta -ds-s \right) ^{2}a_{{4,0}}{z}^{4}}{{s}^{4}}}+\\ 1/4\,{ \frac{{a_{{4,0}}}^{2}{\xi }^{2}}{a_{{6,0}}}}+ 1/4\,{\frac{{a_{{4,0}}}^ {2} \left( d\delta -ds-s \right) {z}^{2}}{a_{{6,0}}{s}^{2}}}-1/9\,{ \frac{-{p}^{2}{s}^{2}{b_{{2,0}}}^{2}+9\,d\delta \,{p}^{2}a_{{6,0}}+9\, d\delta \,{q}^{2}a_{{6,0}}-9\,d{p}^{2}sa_{{6,0}}-9\,d{q}^{2}sa_{{6,0}}- 9\,{p}^{2}sa_{{6,0}}-9\,{q}^{2}sa_{{6,0}}}{a_{{6,0}} \left( d\delta -ds -s \right) }}+\\ 2\,pz \left( {\xi }^{2}b_{{2,0}}-1/3\,{\frac{{z}^{2}b_{{ 2,0}} \left( d\delta -ds-s \right) }{{s}^{2}}}+1/6\,{\frac{b_{{2,0}}a_ {{4,0}}}{a_{{6,0}}}} \right) +{p}^{2}+{q}^{2}. \end{array} \right. \end{aligned}$$

(76)

Result and discussion

This portion compares the arrangements to a generalized breaking soliton system in (3 + 1)-dimensions arising in wave propagation inferred from the expository wave arrangements in this article and those found within the writing. Numerous analysts have examined to analyze a generalized breaking soliton system arising with diverse procedures. Alternately, the nonlinear differential administrator has been utilized to produce numerous wave arrangements for the specified equation as shown in the related section.

Furthermore, an analysis based on the Hirota bilinear approach is made on arrangements advertised in this original copy as well as we found by wrinkle soliton arrangements. In spite of employing a assortment of strategies, four cases have been effectively completed including periodic form solutions to a generalized breaking soliton system. Among them, cosines function forms also investigated the exact soliton solutions. Also, numerous soliton arrangements for the given demonstrate are found utilizing the hirota bilinear method.

Conclusion

This paper included two methods including the Hirota bilinear technique to resolve the (3 + 1)-dimensional a generalized breaking soliton system. As a resultant, numerous double-periodic solitons and breather waves were created, counting singular wave arrangement, periodic wave solution, asymptotic case of periodic wave solution, and soliton solutions. In addition, the multiple rogue wave solutions were obtained. The affect of wave speed and other free variables on the wave profile was additionally examined. This approach was proven to be effective and applicable to a variety of NLEEs in mathematical physics. The display comes about can be extended indeed encourage when different other sorts of nonlinearities are examined. This can be formidable research in the future.

In the field of nonlinear engineering, the soliton structures found in the literature may be of interest to researchers. It was realized that this strategy is brief, worthwhile, and productive and that considerable number of solutions can be obtained in comparison to previous ways. The accuracy of the results was tested using Maple software by substituting the obtained results into the original equation.