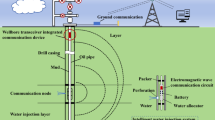
Abstract
Over recent years, as digitalization and intelligence in oil wellbore have increased, so have the stricter requirements for wireless communication technology in terms of distance, accuracy, and portability. As a result, it’s necessary to rely on more advanced and efficient wireless communication technologies to meet the industry’s needs. However, traditional communication technologies such as cables and optical fibers have inherent shortcomings in construction, data interpretation, and cost. ELF electromagnetic waves are an ideal solution for communication in complex wellbore conditions due to long-distance communication and strong penetration capabilities, making it a highly effective option. Based on the theory of network splitting, this paper establishes a polygonal multiple-delays uncertainty coupled complex network model of ELF electromagnetic waves propagating through the casing in layered media and designs a controller, including expressions for the intensity of the magnetic and electric fields in different directions, and the propagation and distribution characteristics in different media. We determined that the optimal transmitting frequency of ELF electromagnetic waves under general conditions is 12.7 Hz. Based on field experiments, we verified that ELF electromagnetic waves can enable wireless wellbore communication within 1500 m without relays. We also analyzed the impact of casing thread deformation on ELF electromagnetic wave propagation due to high-temperature and high-pressure environments. We used simulation experiments to solve the distribution relationship between the electric and magnetic fields of the solenoids through casing and strata, as well as the coupling coefficients between the transmitting and receiving solenoids, and explore how different transmitting frequencies affect the efficiency of signal propagation. Both theories and experiments have verified the correctness of the model, and have also demonstrated the reliability and continuity of using ELF electromagnetic waves to achieve wireless wellbore communication, which provides a theoretical basis and feasibility for subsequent engineering applications.
Similar content being viewed by others
Introduction
Efficient wireless communication transmission in the wellbore has become crucial for achieving precise control of layers and collecting production data, especially with the gradual increase in oilfield production scale. However, the complexity and variability of underground working conditions as well as the varying structure of wellbore tool strings, make traditional communication technologies unable to be directly applied. At present, the mainstream wellbore communication methods mainly include cable communication, pressure wave communication, and acoustic relay communication. Cable communication utilizes steel tubular cable to achieve surface and subsurface communication is currently the most widely used technology. However, cable communication has a certain degree of rapid amplitude attenuation characteristics, and signals will experience significant voltage attenuation and low-pass effects when passing through the cable1. In field applications, the construction process is complex, and the cost is high. Pressure wave communication utilizes changes in pressure to transmit information, using low-frequency continuous wave actions and pulse signals as carriers. The transmission distance is long, but the continuous wave generation device’s structure is complex and the process requires large-scale equipment, such as fracturing trucks for ground operations, which is costly and complex to operate2,3. Acoustic relay communication uses the casing as the transmission channel, acoustic waves as the carrier, and relays are installed on the casing. The technology has the advantages of fast transmission speed and low transmission device cost4. However, it has a short transmission distance, severe attenuation, and low communication efficiency. It often takes several hours to transmit a set of data, and the relay's inter-code interference is significant, making large-scale bidirectional data transmission impossible.
The casing used in underground operations typically consists of metal, predominantly carbon steel. This material exhibits a significant shielding effect against high-frequency electromagnetic waves, rendering transmission in conventional frequency bands unfeasible5. In contrast to traditional communication methods, extremely low-frequency (ELF) communication circumvents issues related to cable load and trafficability. ELF electromagnetic signals demonstrate superior penetration capabilities, allowing them to traverse complex channels comprising thicker oil tubing, metal wellbore walls, oil, gas, water, and strata for data transmission. Signal propagation remains stable and reliable, with minimal susceptibility to interference from other electromagnetic pulses, thereby highlighting its robust anti-interference capability6,7. Hence, the exploration of ELF electromagnetic wave signals for wireless wellbore communication bears considerable engineering significance.
As early as the 1970s, scientists such as Wait and HILL began to study theoretical issues such as the current distribution and signal bandwidth of ELF electromagnetic waves propagating along drill pipes, but they have yet to establish a complete model8,9. The paper by D. A. HILL and Wait gives calculations of the signal from the bottom of the well to the surface and predicts that the optimal transmitting frequency should be between 10 and 100 Hz, with no return below 10 Hz8. DeGauque’s paper evaluates the electromagnetic communication capability and permeability of electromagnetic waves during measurement while drilling and points out that simply lowering the transmitting frequency to a few Hertz or so does not improve communication and there is no noticeable change in the vector field distribution, which is consistent with our simulation results10.
In the 1990s, Xia studied the acceptability of ELF electromagnetic wave signals and the relationship between frequency and stratigraphy during drilling but did not develop a layered model11. Trofimenkoff utilized the current element method for resistive casing modeling during electromagnetic wave transmission, resulting in faster calculations than the conventional EFIE method, yet lacking a complete electromagnetic field analysis12.
In 2012, Lu et al. conducted a study on the effect of casing on electromagnetic wave tomography. However, their assumption of the downhole environment as a three-layer cylindrical medium limits the generalizability of their findings13. In 2013, Y.K Wei examined current distribution in metal casing surrounded by inhomogeneous ground, but without a layered medium and simulation experiments14. Pei et al. conducted field experiments using 6.75 Hz electromagnetic waves to confirm the feasibility of ELF electromagnetic wave wellbore communication, but they did not provide theoretical derivation15. There is no quantitative study of the effect of casing thread deformation on the transmission of ELF electromagnetic waves in the available studies.
The research on complex network models predominantly focuses on unilateral networks. However, the propagation of ELF electromagnetic waves constitutes a multivariate complex network with mutual coupling characteristics. Modeling this process requires consideration of internal topology, dynamic nodes, and other complex issues, so it is necessary to seek a more appropriate solution to the problem, and the establishment of polygonal multiple-delays uncertainty coupled complex network model is a suitable solution to this problem.
As intelligent well systems continue to develop, there is an increasing need for reliable and stable wireless communication between surface and downhole instruments. Utilizing ELF electromagnetic wave transmission along the casing emerges as one of the most promising solutions. Establishing a layered medium model for electromagnetic waves and deriving the relevant transmission characteristics are the key issues in this case. Currently, most studies either do not consider layered medium models or are limited to modeling in the context of measurement while drilling.
Because of this, this article proposes using ELF electromagnetic waves as carriers and oil tubing and casing as transmission channels to achieve efficient data communication between the underground wellbore and the surface. A polygonal multiple-delays uncertainty coupled complex network model of ELF electromagnetic waves in the wellbore is established for various media, and its stability is analyzed. The transmission characteristics of ELF electromagnetic waves are studied, and the optimal transmitting frequency is determined. Simulation and field experiments are conducted to verify the theory’s correctness.
Propagation characteristics of ELF electromagnetic wave
Currently, there is no unified standard for the frequency range and naming of electromagnetic waves, and the naming rules vary from country to country. The International Telecommunication Union (ITU) regulations divide radio frequency bands into super low frequency (SLF) for 30-300 Hz and Extremely Low Frequency (ELF) for frequencies below 30 Hz, as shown in (Table 1).
The skin effect states that the penetration of electromagnetic waves into metals is related to frequency. Extremely low frequency electromagnetic waves have characteristics such as strong penetration ability, long transmission distance, stable propagation, and the strong ability to penetrate attenuation media. They can penetrate rocks and metal tubing walls of a certain thickness16.
The basic oil production wellbore consists of tubing and casing, which can transmit ELF electromagnetic waves.
The results of references5,16,17,18,19,20,21 indicate that when the low-frequency electromagnetic wave emission solenoid is placed coaxially with the tubing line, the radial component of the magnetic induction intensity exhibits a “bimodal symmetry” distribution, while the axial component exhibits a “unimodal symmetry” distribution. The efficiency of transmitting electromagnetic waves depends on parameters such as permeability, conductivity, and permittivity of the wellbore and surrounding strata. The intensity of the extremely low frequency electromagnetic field continues to decay as the wall thickness, diameter, and relative magnetic permeability of the material increase. Tubing with high magnetic permeability transmits weaker magnetic pulse intensity under the same wall thickness. Conductivity also affects the attenuation of electromagnetic waves. However, the wellbore and layered rock structures are complex and variable, resulting in varying conductivity for each layer. Conductivity is not constant even in the same layer and varies due to various factors. At extremely low frequencies, there is a correlation between the conductivity of rock layers and the frequency. The substrate losses and attenuation of electromagnetic waves increase with the permittivity.
According to references22,23, burying metal tubing in seawater results in similar attenuation characteristics for the horizontal electric and magnetic field components, indicating that the polarization mode has little effect on the propagation of ELF electromagnetic waves.
In conductive media, the impedance of ELF electromagnetic waves can be expressed as:
where \(\mu\) is the magnetic permeability of the medium, \(\sigma\) is the electric conductivity, \(\varepsilon\) is the permittivity of dielectric material.
Cagniard apparent resistivity can be used to analyze the resistivity values of various layered media qualitatively and accurately24:
In conductive media, the wavelength and velocity of ELF electromagnetic waves can be expressed as:
If the propagation medium is a good conductor, the conduction current is much greater than the displacement current, that is \(\frac{\lambda }{\omega \varepsilon } \gg 1\), the above expression can be simplified as:
To assess the feasibility and propagation characteristics of ELF electromagnetic waves for underground communication, a pilot experiment was conducted on a well in Dagang Oilfield, China. A signal transmission of 5 Hz ELF electromagnetic waves was used based on engineering experience. This well has a surface casing depth of 150 m, a production casing of 1034 m, and an inner diameter of 124.26 mm.
We place the transmitting solenoid inside the oil tubing and take sealing measures, while the receiving solenoid is placed at the wellhead on the ground, and the power of the transmitting coil is five watts to ensure the penetration of the ELF electromagnetic wave signals and the upward transmission of the signals.
The data demonstrates the correlation between the depth of the well and the voltage of the receiving solenoid, well pressure, and noise value, as illustrated in (Fig. 1).
It is evident that there is no significant or sudden change in the noise value as the depth of the well gradually increases. The value remains around 0.1 mV, and the well pressure changes normally. This indicates that the tubing used in the field experiment, its buried soil, and the surface air medium have good properties, and the impact on ELF electromagnetic waves can be disregarded. The noise can be attributed to thermal and motion-induced noise generated by sensor shaking. This can be eliminated by optimizing the solenoid structure and sensitivity. The voltage value received by the wellhead remained above 1.5 mV up to a depth of approximately 380 m. Subsequently, the casing deformation caused a drop to approximately 0.3 mV at 900 m. This indicates that the ELF electromagnetic wave, with a transmitting frequency of 5 Hz, can successfully achieve communication within 900 m under these well conditions. Strong signals can be received under communication conditions within 400 m.
The results of pilot experiments have proved that the ELF electromagnetic waves have the ability of stable communication in the wellbore and the receiving solenoid can also receive strong signals at a depth of 400 m. On the premise that ELF electromagnetic waves have the feasibility of communication in practical engineering, we established a mathematical model of its transmission and simulated its transmission in layered media.
Polygonal multiple-delays uncertainty coupled complex network model of ELF electromagnetic waves for wellbore communication in layered media
The environment of the downhole is shown in (Fig. 2), It can be approximately assumed that each layer of medium(\(\mathop M\nolimits_{i}\)) is homogeneous, the position of the receiving solenoid is \(P\), the electromagnetic parameters of each layer are \(\mathop \mu \nolimits_{i}\)(magnetic permeability), \(\mathop \sigma \nolimits_{i}\) (electric conductivity), \(\mathop \varepsilon \nolimits_{i}\)(permittivity). The source current of the transmitting solenoid is \(\mathop {\mathop I\nolimits_{0} e}\nolimits^{ - j\omega t}\), \(\omega\) is the angular frequency, in which \(i = 1,2,3\).
In injection and production wellbores, extremely low-frequency electromagnetic fields induce eddy currents in the tubing, casing wall, and bottom layer. These eddy currents create a magnetic field that interacts with the magnetic field produced by the transmitting solenoid, jointly affecting the ground-receiving solenoid. The evolving magnetic field stimulates the eddy current's electric field, which in turn stimulates the eddy current’s magnetic field. This reciprocal stimulation between the alternating electric and magnetic fields creates a sustained electromagnetic oscillation that propagates through space, illustrating the principle of electromagnetic oscillations, as depicted in (Fig. 3).
The vectorial magnetic potential generated by the ampere density \(\mathop J\nolimits_{s}\) in space can be expressed as25:
where \(k = \omega \sqrt {\varepsilon \mu }\).
Based on the relationship between electric field intensity and magnetic field intensity, it can be inferred that:
Based on the above discussion, the mathematical model for the distribution of ELF electromagnetic waves in the wellbore can be established, the solenoids used for the model and its simplification are shown in (Fig. 4).
Electromagnetic waves propagate through either a single path or a mixed path, depending on the conductivity of the propagation area. If there is a significant difference in conductivity within the propagation area of electromagnetic waves, the propagation path can be changed from a single path to a mixed path. Watt A.D. mentioned in his monograph26 that Millington and Wait studied and approximately experimented with the mixed path problem in 1946 and 1956–1957, and found that due to the recovery effect, the mixed path effect is relatively small in ELF electromagnetic waves, Therefore, the problem of wellbore propagation of ELF electromagnetic waves can be considered as a single path propagation.
The Maxwell equations describe the general laws of time-varying electromagnetic fields, with both electrostatic and constant magnetic fields being special cases of time-varying electromagnetic fields. In any medium layer, the electromagnetic field satisfies the Maxwell equation system in differential form:
where \(E\) is the electric field intensity in \(V/m\), \(H\) is the magnetic field intensity in \(A/m\),\(B\) is the magnetic induction intensity in \(T\), \(\rho\) is the charge density in \(C/m^{3}\), \(D\) is the electric displacement vector in \(C/m^{2}\), \(J_{s}\) is the current density of transmitting solenoid in \(A/m^{2}\).
As the current applied is of an extremely low frequency, it generates an ELF electromagnetic wave, with the source current taking a sinusoidal form. The magnetic field intensity and electric field intensity can be expressed as \(\mathop {\mathop {H = H}\nolimits_{0} e}\nolimits^{ - j\omega t}\) and \(\mathop {\mathop {E = E}\nolimits_{0} e}\nolimits^{ - j\omega t}\) respectively; By introducing Eq. (10), the Helmholtz equation for the electric field intensity in the dielectric layer can be obtained.
where \(\mathop k\nolimits^{2} = \mathop \omega \nolimits^{2} \mu \varepsilon + j\omega \mu \varepsilon\).
The electric field intensity and magnetic field intensity in each layer of medium are {\(E_{1} ,E_{2} ,E_{3}\)} and {\(H_{1} ,H_{2} ,H_{3}\)} respectively, and the transmitting solenoid is located in the layer \(\mathop M\nolimits_{1}\), then:
In layered media, there are the following boundary conditions:
(1) when \(x \to \infty ,y \to \infty ,z \to \infty\), \(H \to 0\) and \(E \to 0\); when \(x \to 0,y \to 0,z \to 0\), \(E\) and \(H\) are finite values.
(2) At the interface of each media, the electric field intensity and magnetic field intensity should ensure the continuity of the tangential component at the interface, and the following connection conditions must be met.:
Presented in vector format:
For areas without the transmitting solenoid, it is possible to expand \(\mathop \nabla \nolimits^{2} E + \mathop k\nolimits^{2} E = 0\) in cylindrical coordinates:
The general solution of the Bessel equation obtained by converting Eq. (15) and solving it can be expressed as:
where \(K\) is the magnetic moment of the transmitting solenoid, \(a(k)\) and \(b(k)\) are undetermined coefficients.
For the region where the transmitting solenoid is located, there is also an initial excitation component, the electromagnetic intensity of the source region can be generally solved as:
In cylindrical coordinates, due to the axial symmetry of the media environment, only \(E_{\phi }\) is considered for the electric field intensity, and only \(H_{r}\) and \(H_{z}\) are considered for the magnetic field intensity.
By combining Eqs. (16) and (17) with the boundary conditions, it can be derived that the electric field intensity in each layer satisfies:
From Eq. (9), it can be determined that the magnetic field intensity in each layer satisfies:
In the above equations, \(I_{0} (x_{i} r)\)\(I_{1} (x_{i} r)\)\(l_{0} (x_{i} r)\)\(l_{1} (x_{i} r)\) are all modified Bessel functions, \(\mathop {k_{i} }\nolimits^{2} = \mathop \omega \nolimits^{2} \mu_{i} \varepsilon_{i} + j\omega \mu_{i} \varepsilon_{i}\)\(i = 1,2,3\) and \(K = NIS_{T}\) are the magnetic moment of the transmitting solenoid, \(N\) is the number of turns, and \(S_{T}\) is the cross-sectional area of the transmitting solenoid.
In summary, Eqs. (18) and (19) describe the mathematical model of ELF electromagnetic waves in various media within the wellbore. They reflect the intensity of the electric and magnetic fields and the distribution patterns of ELF electromagnetic waves in different directions.
According to the idea of network splitting27,28, the problem can be split into three different subnetworks based on the different nature of the field, namely: oil tubing subnetwork, casing subnetwork, and strata subnetwork, the fastest network, i.e., the casing subnetwork is counted as the benchmark network, at this time, in the casing subnetwork, the delay is zero, and the delay of the other sub-networks is relative to the benchmark network, and is expressed by the polygonal multiple-delays uncertainty coupled complex network model:
where \(x_{i} (t) = (x_{1} (t),x_{2} (t), \cdots ,x_{in} (t))^{\rm T} \in R^{n}\) and \(u_{i} (t) \in R^{n}\) are the state variables and control variables of node \(i\) at time \(t\). \(f:R^{n} \to R^{n}\) is a continuously differentiable nonlinear function, \(\tau_{k} \ge 0(k = 0,1, \cdots m)\) is an arbitrary but bounded time delay, \(\tau_{0} = 0,A_{k} = (a_{(k)} ij) \in R^{N \times N} (k = 1,2, \cdots m)\) is the coupling matrix reflecting the coupling strength and topological structure, and \(a_{(k)ij} \ge 0,i \ne j\) is defined as \(a_{(k)ij} > 0\) if connected from node \(i\) to node \(j\), otherwise \(a_{(k)ij} = 0(i \ne j,i,j = 1,2, \cdots N)\), and \(\Psi_{l} \in R^{n \times n}\) is a positive definite diagonal matrix representing the individual coupling between nodes \(i\) and \(j\). Due to the presence of many uncertain factors in this complex network, and the weak signal received by electromagnetic field propagation in this problem, a large amount of noise often appears in the channel, corresponding to negative feedback noise in the feedback channel of the model network.
In this problem, due to the divergence of ELF electromagnetic wave transmission, we define the interface with a common coupling channel as the nodes of the network model, which are: the inner wall of the oil tubing, the tubing-casing annulus, the cement annulus, the interface between cement and strata, the layered interface between different strata, and the interface between the ground receiving solenoid and strata; The control variables include the transmitting frequency, well depth, number of threads and material for oil tubing and casing, the number of turns and material of receiving and transmitting solenoids, the position of receiving and transmitting solenoids, the stratum parameters, etc. The subnetwork splitting and node diagram for this problem is shown in (Fig. 5).
Therefore, for the ELF electromagnetic wave transmission problem shown in (Fig. 5), N = 6, M = 2, the delay of the casing subnetwork is 0, the oil tubing subnetwork has a delay \(\tau_{1}\) relative to the casing subnetwork, and the strata subnetwork has a delay \(\tau_{2}\) relative to the casing subnetwork, and the model of this network can be expressed as follows:
Taking the electric and magnetic field intensity in each layer as state variables, i.e., substituting Eqs. (18) and (19) into Eq. (21), the polygonal multiple-delays uncertainty coupled complex network model of the problem can be obtained as follows:
\(\dot{E}(t),\dot{H}(t)\) in the above two Eqs. (22) and (23) reflect the tendency of magnetic and electric field intensity at the next instant.
Adding controllers to all nodes in this model will result in exceedingly high costs and impose a significant burden on the system, leading to slow resolution and potentially rendering it incapable of resolving. To minimize the number of controlled nodes and enhance system stability, we implement controller over the first c (c = N) nodes. The controller is expressed as follows:
where \(\dot{k}_{i} (t)\) is the updating laws of the controller and satisfies \(\dot{k}_{i} (t) = \theta_{i} \left\| {\left. {e_{i} (t)} \right\|} \right.^{2}\) \(\theta_{i}\) is the weight, and \(e_{i} (t)\) is the synchronization error.
To demonstrate the stability of established model, we use the Lorenz system to describe the dynamic equation of a single node:
We set N = 6 and M = 2 to obtain the synchronization error curve as shown in (Fig. 6).
As can be seen from the figures above, the corresponding error variables of all nodes of the whole network model rapidly and smoothly converge to zero over time, indicating that the model we built reaches synchronization at a fast rate, which verifies the correctness and generalizability of the model.
Selection of the optimal transmitting frequency
In decaying media, the magnetic field component of electromagnetic waves satisfies the following equation17:
The electromagnetic attenuation constant and propagation constant are:
where \(\alpha\) is the phase attenuation factor and \(\beta\) is the intensity attenuation factor; Metal tubing and oil gas mixture media, as good conductors, have the characteristic of \(\sigma > \omega \varepsilon\), which can be approximately simplified as:
As the conductivity and transmitting frequency increase, the attenuation factor also increases sharply. According to the skin effect, the penetration depth of electromagnetic waves into a conductor is limited. The depth at which the electromagnetic intensity decays to \(1/e\) of transmitting intensity is called the skin depth, denoted by \(\mathop d\nolimits_{\max }\).
If the electromagnetic field generated by the transmitting solenoid wants to penetrate the oil tubing wall and propagate upwards, it must meet the requirement that the skin depth is greater than the thickness of the metal tubing wall, i.e.\(\mathop d\nolimits_{0} < \mathop d\nolimits_{\max }\), thus obtaining:
The thread at the oil tubing connection can also exacerbate the attenuation of electromagnetic waves. Taking the example of the thickened P105 steel thread, its tensile safety factor under normal working conditions is about 1.5. The axial stress received during injection and production exceeds 550 kN, while the yield strength of the pipe body reaches 1052 kN, with a minimum internal yield pressure of 121.6 MPa.
The electrical conductivity of metals has the following linear relationship with temperature:
where \(\alpha\) is the average resistance temperature coefficient at 0℃ ~ T℃ and \(\rho\) is the metal resistivity.
The relationship between the magnetic permeability, resistivity, and temperature of steel is shown in (Fig. 7):
The permittivity in a constant electric field is directly proportional to the change in temperature, but the magnitude of the change is generally very small. Therefore, the effect of stress and fatigue on the permittivity of tubing can be ignored.
In summary, when stress is applied to the thread, the resulting change in yield strength can cause a temperature change in tubing wall. This, in turn, can cause a sudden change in conductivity and magnetic permeability, which to some extent exacerbates the attenuation of electromagnetic waves. Figures 8 and 9 depict the relationship between the yield strength, tensile strength, and temperature of commonly utilized steel surfaces:
When the thread is subjected to stress and temperature changes, for example at 100 ℃, as an example, according to Eq. (26), the conductivity increases to 0.634 times that of normal conditions, while the magnetic permeability fluctuates slightly.
If the transmitting frequency is higher, the attenuation factor increases, and the skin depth of electromagnetic waves is smaller, resulting in faster attenuation of electromagnetic waves. However, the power of electromagnetic waves is inversely proportional to their wavelength, so the lower the transmitting frequency, the lower the electromagnetic wave intensity and power, the weaker the signal that can be received by the receiving solenoid, and the poorer the anti-interference ability. Therefore, selecting the optimal transmitting frequency reasonably is a crucial parameter for receiving electromagnetic signals on the ground and outputting the maximum voltage.
Media such as soil, rocks, and air all have low electrical conductivity, i.e.\(\sigma < \omega \varepsilon\), Eqs. (21) and (22) can be approximately simplified in this scenario as:
In a time-varying magnetic field, the induced voltage output by the solenoid is:
where \(f\) is the transmitting frequency, \(N\) is the number of turns, \(S_{T}\) is the cross-sectional area of the transmitting solenoid, and \(\theta\) is the angle between the incident direction of the time-varying magnetic field and the axis of the solenoid.
According to Eq. (27), if the induced voltage output by the solenoid is maximized, let \(\frac{{d\mathop V\nolimits_{out} }}{df} = 0\), and the solution that satisfies the condition can be obtained as \(\theta = n\pi\), \(n = 0,1,2, \cdots\). It can be known that when the solenoid is horizontal, the output voltage of the induction solenoid is maximum.
Equation (20) shows that the voltage of the receiving solenoid is directly proportional to the magnetic field intensity and is also proportional to the attenuation constant and propagation constant, i.e. \(U(f)_{out} \propto \omega \gamma B\). In the equation, \(\gamma\) is a function related to \(\alpha\) and \(\beta\) expressed as:
Let \(\frac{{dU(f)_{out} }}{df} = 0\), the transmitting frequency should satisfy the following requirements:
where \(C_{i}\) is the amplifying coefficients, which should be satisfied \(\sum C_{i} = 1\).
As previously stated, positioning the transmitting solenoid horizontally can determine the optimal transmitting frequency based on Eqs. (25) and (29).
On the spot, if metal tubing lines are buried in dry or thin sandy soil and severe dissolution areas at a certain depth, the influence of soil and air on ELF electromagnetic waves can be ignored. If buried in seawater or moist soil without severe dissolution, it is necessary to measure key parameters such as conductivity and magnetic permeability of the environment in order to select the optimum transmitting frequency.
For a general metal wellbore, its relative magnetic permeability is \(\mu = 100\), the conductivity is \(\sigma = 10^{6} S/m\), relative permittivity is \(\varepsilon = 1\), and tubing wall thickness is \(\mathop d\nolimits_{0} = 6cm\); Let the relative magnetic permeability of the soil is \(\mu = 1\), the conductivity is \(\sigma = 10^{ - 5} S/m\), and the relative permittivity is \(\varepsilon = 5\). By calculating the above parameters, the optimal transmitting frequency is 12.7 Hz, which is an extremely low frequency electromagnetic wave. This is consistent with the results of D. A. Hill and Wait’s paper.
After completing the pilot experiment and theoretical derivation, in order to explore the maximum depth of ELF electromagnetic wave wellbore communication, we conducted field experiments with a transmitting frequency of 12.7 Hz in Xinjiang oilfield in China, which has low electromagnetic pollution and an ideal experimental environment. The relationship between well depth and receiving voltage is shown in (Fig. 10).
Overall, the pilot experiment using 5 Hz ELF electromagnetic waves completed communication at a depth of 900 m, while subsequent field experiments achieved stable transmission up to 1500 m. The experimental data aligns with the model's expression, validating our theoretical derivation. Figure 10 illustrates that the signal amplitude received by the ground-receiving solenoid remains above 1.5 mV within 1100 m and consistently above 0.4 mV within 1500 m, confirming the feasibility of wireless communication within a 1500 m range without relays using ELF electromagnetic waves. With appropriate signal reception and noise reduction algorithms, it is possible to achieve wellbore communication over 2000 m without relays, Compared to other wireless communication methods, ELF electromagnetic waves offer significant structural and communication distance advantages while substantially reducing costs compared to cable-based methods, making them a highly promising solution for wellbore communication.
Simulation experiments
The transmission characteristics of the oil tubing can be analyzed by simulating the extremely low frequency electromagnetic waves in the ground wellbore environment. The oil casing, made of annealed carbon steel, has an inner diameter of 76 mm and an outer diameter of 89 mm. The transmitting frequency is 12.7 Hz, with a solenoid current of 1A and voltage of 30 V. The material of the solenoid is copper wire with a ferromagnetic internal part, with the number of 100 turns, and the strata medium is sandstone. The simulation results in the eddy current magnetic field are as follows:
Figures 11 and 12 demonstrate that ELF electromagnetic waves propagate directionally in sandstone formations. The layers exhibit even distribution of magnetic and electric fields, with magnetic vectors being denser and more widely distributed than electric fields. The majority of the ELF field’s magnetic field lines pass through the tubing wall and buried medium, generating eddy currents in both the tubing wall and the formation.
Figures 13 and 14 show that the volume current density distribution on the oil casing is mainly concentrated on the side of the solenoid’s excitation position, mostly above the solenoid, with a slight distribution inside the solenoid and in the strata.
Figures15–17 show that the magnetic and electric fields on the inner wall of the oil casing are denser compared to those on the outer wall. The magnetic field diffuses from the center to the outside, while the electric field is concentrated mainly on the external winding solenoid and less distributed on the inner ferromagnet.
Simulation experiments were conducted on the transmitting and receiving solenoids at distances of 2, 5, 7, and 10 m with 12.7 Hz. The results are presented below:
Figures 18 and 19 show that the distribution of the magnetic field between the two solenoids is more uniform and denser compared to the electric field, although the amplitude is not significant.
The electric field vector is relatively sparse at 2, 5, and 7 m, but returns to normal at 10 m, but returns to normal at 10 m, while the magnetic field vector gradually decreases with the increase of distance. This may be caused by the anisotropy of sandstone or annealed carbon steel materials in the simulation process.
Based on comprehensive analysis, under the wellbore working condition, the electromagnetic field signal received outside the tubing is influenced by various factors, such as the transmitting frequency, geometric dimensions of the tubing wall, buried medium layer, electromagnetic parameters, etc. Both magnetic field and electric field are distributed between the two solenoids. Although the magnetic field distribution is more uniform, at long distances, the electric field should be dominant compared to the magnetic field.
At a distance of 10 m, simulation experiments were carried out at transmitting frequencies of 5HZ, 10 Hz, 100 Hz, 1 MHz, and 1 GHz, and the experimental results are shown in Figs. (20–23):
The coupling coefficients between the transmitting and receiving solenoids at different distances with 12.7 Hz are shown in (Table 2):
From the above figures, the electric field strength between the transmitting and receiving solenoids changes with the increase in transmitting frequency. At 12.7 Hz, the electric field intensity is the highest and exhibits the densest and most uniform distribution. At 5 Hz, it is the second highest. However, when the transmitting frequency is set to 100 Hz or higher, the electric field vectors at the receiving solenoid begin to decrease. At 1 GHz, there are almost no electric field vectors distributed. The magnetic induction intensity and magnetic field intensity show a non-linear relationship with the transmission frequency. As the transmitting frequency increases from 5 Hz, the magnetic induction intensity decreases at 12.7 Hz due to the high electric field intensity generating induced currents that lead to a reverse magnetic field, weakening the original magnetic field. There is no significant change in magnetic induction intensity at other transmitting frequencies, and the magnetic field intensity vector remains almost unchanged at each transmitting frequency. This situation may be due to the weak excitation capability of the electric field to the magnetic field and the weak mutual coupling between the transmitting and receiving solenoids. As shown in Table 2, the coupling coefficients are very small when the distance between the two solenoids is 10 m.
It has been proven that reducing the transmitting frequency simply does not improve the efficiency of signal transmission; instead, it may increase the attenuation of electromagnetic wave transmission, highlighting the importance of optimal transmitting frequency. The electric field's distribution is stronger than that of the magnetic field, and the coupling between them is not significant, but their internal topological relationship is complex, necessitating more accurate analysis methods for subsequent handling. For the transmission of weak signals, effective noise reduction measures are indispensable. The solenoid inductance at different distances with 12.7 Hz is shown in (Fig. 24):
Vectorgraph of solenoid inductance at different distances: (A) Vectorgraph of solenoid inductance at a distance of 2 m; (B) Vectorgraph of solenoid inductance at a distance of 5 m; (C) Vectorgraph of solenoid inductance at a distance of 7 m; (D) Vectorgraph of solenoid inductance at a distance of 10 m.
From Fig. 24 and Table 2, with the distance between the two solenoids increases, the inductance value gradually decreases, and considering that the magnetic vector is also gradually sparse, it indicates that the mutual inductance between the solenoids gradually decreases as the distance increases. This also confirms that the energy transfer between solenoids will gradually weaken during ELF electromagnetic wave transmission. If ultra-long-distance communication is to be achieved, the signal strength of the transmitter must be increased.
The relationship between the intensity of electromagnetic fields in the outer space of the casing and environmental parameters reflects the “shielding effect”, to a certain extent, and verifies the effectiveness of the established model to some extent.
In this simulation model, the average ohmic loss of the two solenoids is calculated to be \(1.13889 \times e^{ - 5}\) ohms with the formula:
\(\Gamma (\Omega ,T)\) is the function of metal resistance and temperature over time, which is also well characterized by Eq. (32) and (Figs. 8 and 9).
The maximum electric field intensity of the simulation experiment was calculated to be 0.1651 V, located at coordinates (0.0074 0, 0.10055, 10.00237) within the range of the receiving solenoid at the wellhead; The maximum magnetic induction intensity is 0.00570 T, located at coordinates (0.046310, −0.05643, 0.28125), which is within the range of the transmitting solenoid. This also reflects the advantage of electrical signals over magnetic signals when receiving solenoid at the wellhead. Radial signal intensity between two solenoids with 12.7 Hz is shown in (Fig. 25):
As shown in the figure above, the signal intensity of the receiving solenoid is weaker than the transmitting solenoid, but it can ensure that within the acceptable range, as the distance increases, there is no large-scale interruption of the signal on the casing. Even if the signal cannot be continuously transmitted due to factors such as high resistance strata or casing deformation, communication can be resumed after passing through the isolated layer, which proves the continuity of wireless communication in the wellbore using ELF electromagnetic waves.
Conclusion
To overcome shortcomings of traditional wellbore communication technology such as short communication distance, poor performance, multiple relays, and high cost, as well as better satisfy the present high requirements of wellbore communication, achieve wireless remote control of the wellbore, this article proposes the use of ELF electromagnetic waves as a new method of wellbore communication.
Firstly, the propagation characteristics of ELF electromagnetic waves in different media were analyzed, and the distribution characteristics of electric field intensity and magnetic field intensity were analyzed. The influence of sensitive parameters such as conductivity, permeability, and permittivity on ELF electromagnetic waves was summarized. The transmission parameters such as wave impedance, Cagniard apparent resistivity, wavelength, and velocity were derived, and a simplified analysis based on good conductors was performed. On this basis, field experiments were conducted, and the experimental results showed that the use of ELF electromagnetic waves as a communication carrier was feasible and had a certain degree of stability. Establish a polygonal multiple-delays uncertainty coupled complex network model for ELF electromagnetic waves in three layers of media inside the underground wellbore and design a controller. We propose that ELF electromagnetic waves should be approximately regarded as a single path for propagation in this environment. We studied the attenuation characteristics of ELF electromagnetic waves and proposed a method for selecting the optimal transmitting frequency in various media. We solved the problem and found that the optimal transmitting frequency in a general wellbore should be 12.7 Hz. We discussed the issue of thread deformation that affects ELF electromagnetic waves wellbore communication and provided a quantitative method. We also determined through field experiments that ELF electromagnetic waves can achieve wireless wellbore communication within 1500 m without relays.
Finally, through simulation experiments, it was determined that under the working conditions of underground wells, the magnetic field and electric field are denser on the inner wall of the oil tubing. Although the magnetic vector is denser and widely distributed on a single solenoid, and the magnetic field distribution is more uniform, the electric field dominates between the transmitting and receiving solenoids at a longer distance compared to the magnetic field. The coupling coefficients between the solenoids are given, and the mutual inductance gradually decreases as the distance increases. This simulation also shows that the transmission efficiency of ELF waves cannot be improved by simply reducing the transmitting frequency. Simulation results have proven the continuity of ELF electromagnetic wave wireless wellbore communication.
ELF electromagnetic waves have feasibility in current wellbore communication due to their long propagation distance, strong penetration ability for metal media, and low cost. It has wide applications in stratified gas injection, oil recovery, and other fields. We will dig into the noise reduction and reception algorithms, and transmitter structure for ELF electromagnetic waves in wellbore communication in the future.
Data availability
All data generated or analyzed during this study are included in this published article and its supplementary information files.
References
Jiantao, J. et al. Application of QAM modulation in mono-cable communication. Well Logging Technol. 42, 577–580 (2018).
Jun, L. Continuous pressure fluctuation prppagation in tubingline and its application in measurement-while-drilling and hanger pressure test. Doctor dissertation, Harbin Institute of Technology, Harbin, Heilongjiang, China. (2015)
Lichen, Z. et al. Vibration wave down hole communication technique. Petrol. Explor. Dev. 44, 295–300 (2017).
Binbin, W. Analysis of the spectrum characteristics of acoustic wave transmission channel for drill string. Ch. Petrol. Mach. 42, 6–9 (2014).
Weihong, L. I. Research on the ELF Communication System inside and Outside the Oil and Gas Tubingline (China University of Petroleum, 2021).
Wait, J. Historical background and introduction to the special issue on extremely low frequency communications (ELF). IEEE Trans. Commun. 22, 353–354 (2003).
Hanjie, D. Design and implementation of bidirectional communication system for smart plug. Ch. Petrol. Mach. 45, 92–99 (2017).
Wait, J. R. & Hill, D. A. Theory of transmission of electromagnetic waves along a drill rod in conducting rock. Geosci. Electron. IEEE Trans. 17, 21–24 (1977).
David, A. H. et al. Coupling between a dipole antenna and an infinite cable over an ideal ground plane. Radio Sci. 12, 231–238 (1977).
Degauque, P. & Grudzinski, R. Propagation of electromagnetic waves along a drillstring of finite conductivity. Spe Drill. Eng. 12, 127–134 (1987).
Xia, M. Y. & Chen, Z. Y. Attenuation predictions at extremely low frequencies for measurement-while-drilling electromagnetic telemetry system. IEEE Trans. Geosci. Remote Sens. 31, 1222–1228 (1993).
Trofimenkoff, F. N. et al. Characterization of EM downhole-to-surface communication links. IEEE Trans. Geosci. Remote SenS. 38, 2539–2548 (2000).
Hong, Lu., Liu, Ju. & Linru, C. Influence of wellbore casing on cross well electromagnetic tomography signal. Chin. J. Radio Sci. 27, 754–759 (2012).
Wei, Y. Propagation of Electromagnetic Signal along a Metal Well in an Inhomogeneous Medium (Norwegian University of Science and Technology, 2013).
Xiaohan, P., et al. Study of EM Communication Technology in the Cased Well. Proceedings of the International Field Exploration and Development Conference 2022. IFEDC 2022. Springer Series in Geomechanics and Geoengineering. Springer, Singapore. https://doi.org/10.1007/978-981-99-1964-2_590.
Pu, G. O. N. G. Research on the ELF Communication Technology Inside and Outside the Oil and Gas Tubingline and its Application (China University of Petroleum, 2019).
Wei, M. S., Tong, M. M., Bin, Z. I., Xia, J. & Yang, L. U. Adaptive localization method based on wireless magnet sensors for tubingline robots. Opt. Precis. Eng. 20, 772–781 (2017).
Jia, Y., Fengxia, L. I., Tao, J. & Wang, P. Transmission characteristics of very low frequency electromagnetic wave of mine-seam wireless through-the-earth communication system. Ind. MIne Autom. 41, 31–33 (2015).
Yufei, Z. Application of low-frequency electromagnetic wireless transmission test technology in the complex fault block reservoirs of abei sag. Oil Drill. Prod. Technol. 43, 328–333 (2018).
Gao, S. W., Sun, X. J. & Yang, L. J. Localization technique of tubingline detecting based on extremely low frequency electromagnetic wave. J. Shenyang Univ. Technol. 31, 266–270 (2009).
Juan, C. Construction of SLF magnetic induction communication system and research on its propagation characteristics. Master dissertation, Huazhong University of Science and Technology, Wuhan, Hubei, China (2020).
Wen Zhang, Q. U., Cheng, X. U., Pu, S. U. N. & Ding Shan, L. I. YAN Jian-feng study on attenuation characteristics of extremely frequency electromagnetic waves in seawater in TE and TM polarization modes. Ship Sci. Technol. 45, 139–142 (2023).
Lichen, Z. Study on Propagation Characteristics of Extremely Low Frequency Electromagnetic Wave in Seawater. Doctor dissertation, Northwestern Polytechnical University, Xian, Shaanxi, China (2016).
Louis, C. Basic theory of the magneto-telluric methond of geophysical prospecting. Geophysics 18, 605–635 (1953).
Mingxian, K. A. N. A numerical simulation for equation of magnetic vector. J. Sich. Univ. 6, 810–818 (2000).
Watt, A. D. Very Low Frequency Radio Engineering (National Defense Industry Press, 1973).
Andree, H. M. A., Lodder, A. W. & Taal, A. Divergence measures based on entropy families: A tool for guiding the growth of neural networks. Netw. Comput. Neural Syst. 7, 533–554 (2009).
Kang, B. et al. Split-match-aggregate (SMA) algorithm: Integrating sidewalk data with transportation network data in GIS. Int. J. Geogr. Inf. Sci. 29, 440–453 (2015).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (52074345) and China National Petroleum Corporation (2021ZG12). All authors have given approval to the final version of the manuscript.
Author information
Authors and Affiliations
Contributions
Z.W., and D.J. conceived the idea and designed the experiments. F.S., Q.C., and S.Z. performed the experiments. The manuscript was written by Z.W., and Q.W. reviewed and revised the manuscript. All authors have approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, Z., Jia, D., Sun, F. et al. Research on extremely low frequency electromagnetic wave model and simulation in wellbore communication. Sci Rep 14, 20093 (2024). https://doi.org/10.1038/s41598-024-71011-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-71011-3