Introduction

The emergence of acoustic artificial materials (including phononic crystals and acoustic metamaterials) has provided new ways to modulate acoustic and elastic waves. By artificially designing different structural units, many special physical properties that natural materials do not possess can be obtained, such as negative equivalent mass1,2,3,4 and negative equivalent modulus5,6. With the gradual deepening of the research on acoustic artificial materials, researchers have attempted to integrate them with various other disciplines. In recent years, the introduction of topological phases in condensed matter physics into acoustic artificial materials has attracted the attention of many scholars.

Zhang and Liu7 first discovered the Dirac cone in the dispersion relation of phonon crystals, which appears at the corner points of the irreducible Brillouin zone, and observed experimentally that the anomalous transport transmission occurs at the Dirac point. Chen8 utilized mode degeneracy to obtain a Dirac cone at \(\Gamma\) point in the Brillouin zone of a two-dimensional phononic crystal. In addition, similar lattices are found to have zero-valued equivalent mass densities and body modulus inverses at the Dirac degeneracy point based on equivalent medium theory studies, which can be used to realize zero-refractive-index acoustic materials9. Xiao10 introduced the concept of Zak phase into acoustic periodic systems and constructed a topological phase transition point in a cylindrical waveguide. Energy band inversion occurs at this point and the Zak phase varies with the structural parameters. Subsequently,11 one-dimensional topology was also introduced into the field of elastic waves. The band reversal can be realized by adjusting the stiffness coefficients of the springs in the one-dimensional spring-vibrator system, and different topological phases can be distinguished by calculating the number of windings, based on which the topology-protecting boundaries and interface states are constructed. These topological boundary protection properties are independent of boundary defects and material impurities. This has led to continuous research on acoustic metamaterials in acoustic topological insulators12,13,14, acoustic topological isolators15,16,17, and topological valley transport18,19,20.

Considering that the materials/structures applied in practical engineering will inevitably be affected by environmental temperature, resulting in changes in material parameters and structural stiffness, which have an undeniable impact on structural dynamics21,22.Li23 and Liu24 investigated the acoustic vibration response characteristics of asymmetric laminates and sandwich panels in thermal environments, respectively. They found that the intrinsic frequency decreased with the rise of temperature, and the peaks of the resonance response curves were shifted to the lower frequencies with the temperature rise. Dai25 designed a topological acoustic system consisting of an array of triangular steel columns embedded in water. It was found that the topological bandgap frequency range is very sensitive to the water temperature, and its topological characteristics can be switched by controlling the water temperature. The effect of thermal environment on the inherent properties and dynamic response of the structure further inspires us that the topological properties of acoustic topological insulators can be regulated by changing the environmental temperature of the insulators through non-contact heating. This also provides a basis for the design of vibration damping and low-frequency noise-reducing materials in thermal environments.

Conventional acoustic topological insulators do not have the adjustable bandgap properties after the structural design is completed, which limits their application range and cannot meet the requirements of different operating environments. In addition, current research has found that the thermal environment can have some influence on the propagation and topological properties of elastic waves, but its research perspective mainly focuses on the influence of the thermal environment on the physical properties of materials. However, the effect of thermal stresses on the band properties of acoustic topological insulators has been relatively rarely investigated and has not yet been investigated with simultaneous consideration of thermal stresses and physical properties of the material.

Therefore, in this paper, two-dimensional two-component honeycomb phononic crystals constructed with tungsten-epoxy are investigated to study the evolution of their band properties when thermal stresses are considered. By adjusting the environmental temperature to open the quadruple Dirac point degeneracy at \(\Gamma\) point, the topological phase transition of phononic crystals can be achieved. Taking advantage of this effect, a temperature-controllable acoustic switch is constructed to regulate its topological frequency range and topological edge states through environmental temperature to realize non-contact active control of the topological state.

The band structure of the acoustic system

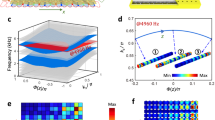
The proposed two-dimensional two-component honeycomb structural unit is shown in Fig. 1a. The structure is a regular hexagonal honeycomb lattice consisting of six metal arms (with side lengths a = 24 mm and side width t), and six additional counterweights (equilateral triangular regions with side lengths w enclosed by the dashed lines in the figure) are located at the vertices of the hexagon, where w = 9.2 mm, lattice constant \(a _{s} =\sqrt{3} a\). The gray area in the figure is epoxy (density \(\rho {_ {{\rm Exp} } } =1180 \, \mathrm {kg/m^{3} }\) , Young’s modulus \(E _{{\rm Exp} } =0.559 \, {\textrm{ GPa} }\) , Poisson’s ratio \(v {_ {{\rm Exp} } } =0.368\) ) and the light blue part is tungsten metal (density \(\rho {_ {{\rm Tun} } } =19,100 \, \mathrm {kg/m^{3} }\), Poisson’s ratio \(v {{_ {\rm Tun}} } =0.35\) ). The Young’s modulus of tungsten is related to temperature (T(\(^{\circ } \textrm{C}\)))26: \(E {_ {{\rm Tun} } } =391.448-1.3160\times 10 {^{-2} } \times \textrm{T} -1.4838\times 10 {^{-5} }\times \mathrm {T^{2} }\) . The solid mechanics module of COMSOL Multiphysics is used to calculate the band structure and displacement field distribution of elastic waves in this phononic crystal. Floquet periodic boundary conditions are imposed at primary cells (supercells) in the calculation of the body (edge) energy band dispersion relation. Figure 1b shows the band structure of acoustic metamaterial I at room temperature (20\(^{\circ } \textrm{C}\)), i.e., temperature difference \(\Delta T=0^{\circ }\textrm{C }\) ), when the hexagonal side width t = 0.328 mm. It can be clearly seen that the band gap closes at 21.96 kHz, forming a quadruple degenerate Dirac point (purple point), which exhibits a double Dirac cone feature in the Brillouin zone.

Figure 1
figure 1

(a) Schematic structure of acoustic metamaterial I and (b) corresponding energy band diagrams.

Full size image

The effect of temperature on the band structure

Figure 2
figure 2

Structural band diagrams of acoustic metamaterial I at different temperatures. (a) \(\triangle T=-70 \,^{\circ }\textrm{ C}\) and (b) \(\triangle T=70\,^{\circ }\textrm{ C}\), (c) the displacement field distribution corresponding to the degenerate eigenstate at \(\Gamma\) point, (d) the thermal stress distribution at \(\triangle T=-70\,^{\circ }\textrm{ C}\) and \(\triangle T=70\,^{\circ }\textrm{ C}\).

Full size image

It is known from previous studies that for acoustic topological metamaterials with fixed structures, the corresponding topological bandgap is not tunable. The topological phase transition can be realized by adjusting the stress to accomplish the regulation of topological edge states27,28,29 which provides a new approach for us to realize the topological phase transition. However, temperature can alter the material properties of a structure, causing thermal deformation and inducing thermal stress, thereby altering the inherent characteristics of the structure. Therefore, changing the temperature can open/close the band gap and achieve band regulation30,31,32. In view of this, thermal effects can be introduced into phononic crystals to generate thermally induced stresses through temperature changes, thus realizing topological phase transitions and the modulation of topological states. The band structure of acoustic metamaterial I at different temperatures \(\triangle T=-70\,^{\circ }\textrm{ C}\) and \(\triangle T=70\,^{\circ }\textrm{ C}\) is given in Fig. 2. It can be clearly seen from the graph that the temperature change causes the quadruple degenerate state at Dirac point to split into twofold degenerate states and form a topological complete bandgap, whose degenerate eigenstates at \(\Gamma\) point are marked by blue and red dots. The corresponding displacement field distributions of these double degenerate states are shown in Fig. 2c. For \(\triangle T=-70\,^{\circ }\textrm{ C}\), the double degenerate state above the bandgap is a pseudo-spin quadrupole mode (d-state), and the one below the bandgap is a pseudo-spin dipole mode (p-state), which behaves as a topologically trivial phase. For \(\triangle T=70\,^{\circ }\textrm{ C}\) , although the bandgap still exists, the energy band positions of the d-state and p-state are reversed, which then behave as topologically nontrivial phases. Figure 2d shows the stress distribution at different temperatures. Thermal stresses behave as tensile stresses at \(\triangle T=-70\,^{\circ }\textrm{ C}\), while thermal stresses are compressive stresses at \(\triangle T=70\,^{\circ }\textrm{ C}\). Therefore, the change in temperature can produce different forms of thermally induced stresses, which can open the band gap and realize the topological phase transition.

In order to further reveal the influence of temperature on the topological properties of acoustic metamaterials, the variation curve of bandgap boundary frequency with temperature is shown in Fig. 3, where the blue and red lines correspond to the d-state and p-state, respectively. It can be observed that the bandgap moves to lower frequencies as the temperature changes from \(\triangle T=-120\,^{\circ }\textrm{ C}\) to \(\triangle T=120\,^{\circ }\textrm{ C}\), and the bandgap undergoes a process from open-closed-open again. The bandgap behaves topologically trivial for \(\triangle T<0\) and becomes topologically nontrivial for \(\triangle T>0\). The topological properties of the energy band change before and after \(\triangle T=0^{\circ }\textrm{ C}\) . Therefore, by regulating the environmental temperature, not only can the energy band be inverted to realize the topological phase change, but also the position and width of the bandgap can be controlled. Therefore, non-contact active modulation of topological states can be realized by manipulating temperature.

Figure 3
figure 3

The p-state (red line) and d-state (blue line) frequencies of acoustic metamaterial I at different temperatures.

Full size image

Temperature regulation of edge states

The interface edge exist only between two materials with different topological properties and a common bandgap. Thus, the energy band evolution of the acoustic metamaterial II (t = 0.16 mm) at different temperatures was also studied. It can be seen from Fig. 4 that the energy bands behave as topologically trivial bands and have the common bandgap with the acoustic metamaterial I. According to the body-boundary correspondence principle, edge states must exist at the boundary between topologically nontrivial phononic crystal and topologically trivial phononic crystal. As shown in Fig. 5a, a supercell composed of acoustic metamaterials I and II has was constructed. Fig. 5b illustrates the variation of the intrinsic frequency of the supercell with temperature. It can be clearly seen that the edge state exists in the common band gap of the system for \(\triangle T>0\) and disappears for \(\triangle T<0\) .Further analysis shows that for \(\triangle T>0\) , the bandgap of acoustic metamaterial I in the supercell is topologically nontrivial, while the bandgap of acoustic metamaterial II is topologically trivial, and hence there are edge states in the supercell. For \(\triangle T<0\) , the bandgaps on both sides of the supercell are topologically trivial, therefore, the edge state will vanish.

Figure 4
figure 4

Evolution of energy bands at different temperatures for acoustic metamaterial structure II (t = 0.16 mm).

Full size image
Figure 5
figure 5

(a) Schematic of the supercell structure and (b) variation of the eigenfrequency with temperature.

Full size image

Figure 6 shows the projected band structure of the supercell along the \(\Gamma\)-K direction at \(\triangle T=10^{\circ }\textrm{ C}\) and \(\triangle T=-10^{\circ }\textrm{ C}\). In Fig. 6a, a pair of edge states appear within the bulk bandgap in the frequency range of 21.68 kHz to 21.86 kHz (labeled with red and blue curves, respectively), while only the bulk bandgap exists in Fig. 6b. The displacement distributions corresponding to the eigenmodes at points A and B are given in Fig. 6c. It is clearly seen that the maximum value of the amplitude at point A is mainly concentrated at the interface between the two phononic crystal structures and decays rapidly to both sides, which indicates that these topological edge states can be well localized at the interface. In contrast, it can be seen from the eigenmodes at point B that the vibrations are no longer concentrated at the interface and they do not have the properties of edge states. Therefore, without changing the structure, the edge state can disappear and appear by changing the temperature, achieving dynamic adjustability.

Figure 6
figure 6

Band structures of topological supercell projections at (a) \(\triangle T=10^{\circ }\textrm{C}\) and (b) \(\triangle T=-10^{\circ }\textrm{C}\). (c) Displacement fields corresponding to points A and B.

Full size image

To further investigate its temperature control effect, a topological acoustic straight waveguide consisting of acoustic metamaterials I and II is constructed. The eigenmode displacement field at \(\triangle T=10^{\circ }\textrm{ C}\) is given in Fig. 7a, and it can be seen that the edge states are well localized near the two-phase interface. Since there are no body propagation modes within the bandgap range, the edge states decay rapidly on both sides vertically to the interface. However, it can be seen from Fig. 7b that the acoustic wave does not propagate when \(\triangle T=-10^{\circ }\textrm{ C}\). As a result, the acoustic straight waveguide exhibits completely different transmission effects when the temperature is different, and this distinct on and off behavior can be viewed as a topological acoustic switch.

Figure 7
figure 7

Acoustic switching transmission at (a) \(\triangle T=10^{\circ }\textrm{ C}\) and (b) \(\triangle T=-10^{\circ }\textrm{ C}\).

Full size image

In order to verify the acoustic switch functionality across different temperatures, we fabricated a sample for acoustic experiments, as shown in Fig. 8a, the orange pentagram is the excitation point and the red line indicates the interface between acoustic metamaterials I and II. The testing process is shown in Fig. 8b, the signal generator generates a pulse signal, which is amplified by the power amplifier and then applied to the piezoelectric sheet to produce excitation on the sample. The laser vibrometer emits detection signal to the sample and collects the reflected signal based on the Doppler effect to measures the vibration response of the sample. The laboratory temperature can be regulated by air conditioning. The measurement line from line1 to line5 is selected and the vibration displacements are measured point by point (point 1–point 9). The normalized velocity is obtained after analyzing and processing the collected data, which can be used to determine the transmission path of the elastic wave by the velocity magnitude.

Figure 8
figure 8

Schematic diagram of (a) sample and (b) experimental test system.

Full size image

Figure 9 shows the experimental results of the waveguide at \(\triangle T=10^{\circ }\textrm{ C}\). From the fitted curves and velocity fields, it can be seen that the elastic waves are mainly concentrated near the interface and decay rapidly to the both sides, showing the transmission characteristics of the topological edge state, which is consistent with the simulation results in Fig. 7a. Figure 10 shows the normalized velocity field at \(\triangle T=-10 \, ^{\circ }\textrm{ C}\). It can be observed that there is no obvious velocity field observed on the measurement lines from line 3 to line 5, which implies that the elastic wave does not propagate. This is consistent with the simulation results in Fig. 7b.

Figure 9
figure 9

The normalized velocity of line 1–line 5 at \(\triangle T=10 \, ^{\circ }\textrm{ C}\).

Full size image
Figure 10
figure 10

The normalized velocity of line 1–line 5 at \(\triangle T=-10 \, ^{\circ }\textrm{ C}\) .

Full size image

Conclusion

In this paper, tunable topological acoustic metamaterials consisting of two-dimensional two-component honeycomb structures are investigated. By adjusting the environmental temperature, the quadruple Dirac point degeneracy at \(\Gamma\) point can be opened, inverting the energy bands and realizing the topological phase transition. Based on the principle of body-boundary correspondence, two-dimensional supercells are constructed using metamaterial structures with different topological properties. Without changing the structure, the dispersion relation of the supercell can be dynamically adjusted only by changing the temperature, and the position of the edge state can be effectively regulated. This effect enables us to design edge state switches at the interface between acoustic metamaterials with both trivial and non trivial bandgaps.