Introduction

As hydraulic systems are characterized by large output force and strong environmental adaptability, they are still the main transmission system of heavy industry, construction machinery etc.1,2,3,4. But they have the disadvantage of low energy efficiency. Therefore, how to improve their energy efficiency have been the hot issue5,6,7,8. Because a large amount of hydraulic energy is lost by throttling, to address this issue, the IMS is proposed. By controlling the two chambers of the cylinder independently, the throttling loss can be reduced, then energy saving is achieved9,10. At the same time, the IMS is a system of multi-input and multi-output, which increases the control flexibility of the system11.

Thanh Ha Nguyen et al. designed a fractional-order PID controller for a new IMS to improve the tracking accuracy12. Chen Li et al. developed a nonlinear flow model of valves for IMS to improve the control performance13. To improve the energy efficiency of the system further, literatures14,15 combines the pump control technology with the independent metering technology to get a higher tracking precision of position and energy-efficiency of the hydraulic system. Although these control methods improve the tracking performance of the cylinder, the forces on the cylinder in these studies are constant, and the tracking performance of the system under varying load conditions are not considered. However, in practice, the magnitude and direction of the load force on the equipment vary with the working conditions16,17,18.

Bing Xu et al. designed different modes for every working quadrant of excavator actuators, and developed a three-layer controller to save energy and improve control performance19. Song Liu et al. designed different operating modes for IMS based on the direction of load and speed of cylinder, and designed a two-stage coordinated control strategy to get a high control accuracy and energy-saving effect20. Thanh Ha Nguyen et al. developed different metering modes for variable load of excavator arm system to obtain high tracking accuracy and maximum energy saving21. In the studies above, different working modes are designed to achieve energy-saving effects for the hydraulic cylinder, but they do not take into account the system oscillations caused by the changes of cylinder working modes.

From the research above, it is obvious that, in order to make the IMS have a better energy saving effect, it is necessary to change the cylinder’s working mode according to the operating conditions of the cylinder. At present, the main working mode switching method is to calculate the force of the cylinder, and then compared with the direction of the desired speed of the cylinder to determine the working quadrant, and then according to the working quadrant to change the working mode of cylinder9,22. However, when the cylinder’s working mode changes, the working modes of valves change too, which will result in oscillations. To solve this problem, Jing Yang developed a new hydraulic system of IMS, and proposed a mode switching method based on the predicted force direction and chamber pressure to reduce the frequency of mode switching23. Ruqi Ding et al.increased the dynamic dwell time in mode switching and designed a bidirectional tracking control method to reduce oscillation, and the results show that this method can effectively reduce the oscillations and instabilities24. Karem Abuowda et al. proposed a micro independent metering control algorithm to detect the operating modes of a hydraulic cylinder so that it can switch between working modes25. Hu shuang et al. presented a mode switching control strategy based on the fuzzy principle to realize the hydraulic cylinder switching between different modes by designing fuzzy rules26. The above studies achieved some good results in the mode switching of cylinder, however, since changes in the valve's operating mode still occur during the control process, the problem of oscillations caused by mode switching is not addressed essentially. CHEN Zheng et al.27 designed a pressure planning and tracking based control strategy to reduce the oscillations due to the change of the valve operating mode in principle, but the study only focuses on the large acceleration and deceleration conditions, however, most of the hydraulic system operates in a quasi-equilibrium state.

In order to make the cylinder of IMS operates smoothly between multiple quadrants and eliminate the oscillations caused by the change of the valve's operating mode in principle, and make the method able to adapt to the quasi-equilibrium state, a novel multiple quadrants displacement tracking control strategy is proposed in this paper. The main contributions of this paper are as follows:

  1. (1)

    It is proposed innovatively that the cylinder return chamber pressure under resistance working condition and the inlet chamber pressure under overrunning working condition are both controlled by the inlet valve. The cylinder displacement is controlled via the outlet valve in both resistance and overrunning conditions. The method enables the cylinder to operate in energy-efficient modes in all working quadrants and to switch smoothly between multiple quadrants without changing the working modes of vales.

  2. (2)

    As the hydraulic system is nonlinear and the characteristics change with the environment28,29,30,31, the controller is designed using the ADRC theory. The controller is simplified by designing a reduced order ADRC displacement controller, and an ADRC pressure controller is designed to realize the control of the two chambers pressure by the same valve.

  3. (3)

    To verify the feasibility of the proposed method, a serious of experiments are done and the results illustrate that the control method can achieve smooth switching of the cylinder between multiple quadrants. Meanwhile, the pressure and displacement controllers have good anti-interference ability and robustness.

The remainder of the paper is organized as follows: in the "Control strategy design", the control strategy of cylinder multiple quadrants switching is introduced; the "Controller design" designs the displacement and pressure controllers; in the "Experimental verification", experimental results and analysis are provided; finally, the conclusions are given in the "Conclusion".

Control strategy design

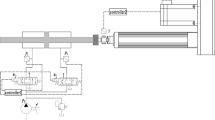
Figure 1 shows the schematic diagram of IMS. The two chambers of the hydraulic cylinder are controlled by two different proportional servo valves, realizing the mechanical decoupling of the spool. The valve 1 is connected to the rodless chamber and the valve 2 is connected to the rod chamber. When the directions of the force and the speed of the hydraulic cylinder are the same, the hydraulic cylinder is in the overrunning quadrant, otherwise, the hydraulic cylinder is in the resistance quadrant.

Fig. 1
figure 1

Schematic diagram of IMS.

Full size image

To reduce the system energy consumption, the main working modes of IMS in the research are as follows:

  1. (1)

    For resistance conditions, the pump drives the cylinder, and the speed of the cylinder is controlled by adjusting the inlet valve. By adjusting the return valve, return chamber pressure is maintained at a low level to prevent cavitation and to reduce the system pressure.

  2. (2)

    For overrunning conditions, the pump acts as the oil source for cylinder to supply the flow required, and the system pressure is set at the lowest. By adjusting the inlet valve, the pressure of inlet chamber is kept at a low level. As the load drives the cylinder, the displacement of the cylinder is controlled by the outlet valve.

The above control methods can reduce the energy consumption effectively. However, the displacement is controlled by the inlet valve for resistance conditions, but for overrunning conditions, it is controlled by the outlet valve. When the working quadrant of the cylinder changes, the switching of the working mode of valve will inevitably cause oscillation. Aiming at this problem, this paper proposes a novel multiple quadrants displacement tracking control method for IMS, whose principle is shown in Fig. 2.

Fig. 2
figure 2

Multiple quadrants displacement tracking control strategy for IMS.

Full size image

Displacement control strategy

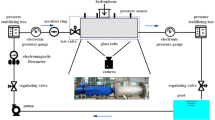
First, the direction of the desired speed \(v\) of the cylinder is determined by the given displacement reference \({x}_{d}\). When the desired speed of the cylinder is positive, i.e. \(v>0\), the cylinder needs to extend, the rodless chamber of the cylinder and the pump is connected by valve 1, and valve 2 makes the hydraulic cylinder and the tank connected, as shown in Fig. 2. Then the command that valve 1 controls the chamber pressure and valve 2 controls the displacement of the cylinder is carried out throughout the extension process of the cylinder. The inputs of the displacement controller are the displacement reference signal \({x}_{d}\) and the actual displacement \({x}_{p}\) of the cylinder, and the output is the control signal \({u}_{2}\) of valve 2. When the desired speed of the cylinder is negative, i.e. \(v<0\), the hydraulic cylinder should retract and the control pattern is reversed.

Pressure control strategy

As the magnitude and direction of the load change during cylinder operation, it is necessary to convert the pressure of the rod or rodless chamber as the pressure control target to reduce the energy consumption of the system. When the cylinder works in the resistance condition, it is necessary to control the return chamber pressure at low level, otherwise the inlet chamber pressure of cylinder need to be adjusted at low level. Figure 2 shows the diagram of the pressure control. \({p}_{d}\) is the set reference pressure of the pressure control, usually between 10 to 20 bar. Compare the rodless chamber pressure \({p}_{1}\) and the rod chamber pressure \({p}_{2}\) of the hydraulic cylinder at the initial moment. If \({p}_{2}\) is bigger, it is considered that the directions of load and the speed of cylinder are the same in the initial state, and the load acts as a driving force. Then control the pressure \({p}_{1}\) at \({p}_{d}\). Otherwise, control the pressure \({p}_{2}\) at \({p}_{d}\).

When the rodless chamber pressure \({p}_{1}\) is the target of pressure control, it is considered that the hydraulic cylinder is working in the overrunning extension quadrant. Then, the inlet chamber pressure is controlled at a low level, and the cylinder is driven by the load force, which enables the hydraulic cylinder to operate in a highly energy-efficient mode. During cylinder operation, if the force changes from the driven force to resistance, at this time the pressure \({p}_{2}\) will gradually decrease. When the pressure \({p}_{2}\) decreases to the threshold pressure \({p}_{th}\), the pressure \({p}_{2}\) is taken as the target to control, i.e., by controlling the valve 1 to control \({p}_{2}\) at \({p}_{d}\). Then, the hydraulic cylinder works in the resistance extension quadrant, the pump drives the hydraulic cylinder. By controlling the return chamber pressure \({p}_{2}\) at \({p}_{d}\), the cavitation of the return chamber can be prevented, and the pressure \({p}_{s}\) can also be reduced to lower the energy consumption. Although the working quadrant of the cylinder changes during extension and the working mode of the cylinder changes, the operating mode of the two valves remains unchanged. The displacement of the hydraulic cylinder is always controlled by valve 2, and the chamber pressure is controlled by valve 1, which eliminates the switch of valve between displacement and pressure control mode. Thus, the oscillations of velocity and pressure during the operation of the hydraulic cylinders are reduced in principle. This control strategy need not to calculate the force of load that on the hydraulic cylinder. It is only necessary to measure the pressure in the two chambers, which is very easy to achieve. Thus, the complexity of the control strategy is greatly simplified.

The pressure threshold \({p}_{th}\) needs to satisfy \({p}_{th}<{p}_{d}\), and in order to improve the driving force of the hydraulic cylinder during the quadrant switching process, the \({p}_{th}\) should be a larger value. When the expected velocity of the hydraulic cylinder is negative, the hydraulic cylinder needs to retract, and the control mode of pressure and displacement is opposite to that of extension.

Controller design

As the load varies during cylinder running, the controller needs to have a good ability of disturbance rejection and strong robustness. The modeling of the controller should not be completely dependent on the mathematical model of the hydraulic system since the accurate mathematical model cannot be established. Taking the hydraulic cylinder extension as an example, the controller is designed as follows.

According to the section above, during the hydraulic cylinder extension, valve 1 controls the chamber pressure, and the displacement of the cylinder is controlled by valve 2.

From Fig. 1, the force balance equation can be estimated as follows:

$${p}_{1}{A}_{1}-{p}_{2}{A}_{2}=m\frac{{d}^{2}{x}_{p}}{d{t}^{2}}+B\frac{d{x}_{p}}{dt}+K{x}_{p}$$
(1)

where \({p}_{1}\) and \({p}_{2}\) are the two chamber pressures, \({A}_{1}\) and \({A}_{2}\) are the effective areas of two chambers, \({x}_{p}\) is the hydraulic cylinder displacement, \(B\) is the coefficient of viscosity, \(K\) is the coefficient of elastic, \(m\) is the mass.

Ignore the external leakage of cylinder, according to the flow continuity equation, the two chambers flow can be written as follows:

$${Q}_{1}={A}_{1}\frac{{dx}_{p}}{dt}+{C}_{ip}\left({p}_{1}-{p}_{2}\right)+\frac{{V}_{1}}{{\beta }_{e}}\frac{{dp}_{1}}{dt}$$
(2)
$${Q}_{2}={A}_{2}\frac{{dx}_{p}}{dt}+{C}_{ip}\left({p}_{1}-{p}_{2}\right)-\frac{{V}_{2}}{{\beta }_{e}}\frac{{dp}_{2}}{dt}$$
(3)

where \({Q}_{1}\) and \({Q}_{2}\) are the flow of the rodless and rod chambers of the cylinder respectively, \({C}_{ip}\) is the internal leakage coefficient of the cylinder, \({\beta }_{e}\) is bulk modulus of oil, \({V}_{1}\) is the total volume of cylinder inlet chamber, and \({V}_{2}\) is the total volume of cylinder outlet chamber.

The flow through the valves can be expressed as:

$${Q}_{1}={C}_{d}w{x}_{v1}\sqrt{\frac{2}{\rho }\Delta {p}_{1}}$$
(4)
$${Q}_{2}={C}_{d}w{x}_{v2}\sqrt{\frac{2}{\rho }\Delta {p}_{2}}$$
(5)

where \({C}_{d}\) is the flow coefficient of valve, \(w\) is the area gradient of valve, \({x}_{vi}\) is the displacement of spool, \(\Delta {p}_{1}={p}_{s}-{p}_{1}\) is the pressure drop of valve 1, \(\Delta {p}_{2}={p}_{2}-{p}_{r}\) is the pressure drop of valve 2, \({p}_{s}\) is the pressure of system, \({p}_{r}\) is the pressure of tank.

The function of the input signal \(u\) and the spool displacement can be simplified as:

$${x}_{v}={k}_{s}u$$
(6)

where \({k}_{s}\) is the gain of valve.

Displacement controller design

Since the velocity of the cylinder is determined by the flow rate through the valve, a reduced order displacement controller can be developed according to Eqs. (3), (5), and (6), as follows:

$${\dot{x}}_{p}=\frac{1}{{A}_{2}}\left({C}_{d}w{k}_{s}{u}_{2}\sqrt{\frac{2}{\rho }\Delta {p}_{2}}-{C}_{ip}\left({p}_{1}-{p}_{2}\right)+\frac{{V}_{2}}{{\beta }_{e}}{\dot{p}}_{2}\right)$$
(7)

For simplicity, let \({k}_{v}={C}_{d}w\sqrt{2/\rho }\), \({R}_{1}=\sqrt{\Delta {p}_{1}}\), \({R}_{2}=\sqrt{\Delta {p}_{2}}\), then the Eq. (7) can be written as:

$${\dot{x}}_{p}=\frac{1}{{A}_{2}}\left({k}_{v}{k}_{s}{R}_{2}{u}_{2}-{C}_{ip}\left({p}_{1}-{p}_{2}\right)+\frac{{V}_{2}}{{\beta }_{e}}{\dot{p}}_{2}\right)$$
(8)

Let \({b}_{d}={k}_{v}{k}_{s}{R}_{2}/{A}_{2}\), \({f}_{d}=\left(-{C}_{ip}\left({p}_{1}-{p}_{2}\right)+\frac{{V}_{2}}{{\beta }_{e}}{\dot{p}}_{2}\right)/{A}_{2}\), then Eq. (8) can be expressed as:

$${\dot{x}}_{p}={b}_{d}{u}_{2}+{f}_{d}$$
(9)

Let \({\varvec{z}}={\left[\begin{array}{cc}{z}_{1}& {z}_{2}\end{array}\right]}^{T}={\left[\begin{array}{cc}{x}_{p}& {f}_{d}\end{array}\right]}^{T}\), then the Eq. (9) can be rewritten as:

$$\left\{\begin{array}{c}{\dot{z}}_{1}={b}_{d}{u}_{2}+{z}_{2}\\ {\dot{z}}_{2}=h\end{array}\right.$$
(10)

where \(h=\dot{{f}_{d}}\).

Let \({\widehat{z}}_{i}\) as the estimation of \({z}_{i}\), the linear extended state observer (ESO) can be designed as32,33,34:

$$\left\{\begin{array}{c}{\dot{\widehat{z}}}_{1}={\widehat{z}}_{2}+2{\omega }_{od}\left({\widehat{z}}_{1}-{z}_{1}\right)+{b}_{d}{u}_{2}\\ {\dot{\widehat{z}}}_{2}=-{\omega }_{od}^{2}\left({\widehat{z}}_{1}-{z}_{1}\right)\end{array}\right.$$
(11)

where, \({\omega }_{od}\) is the bandwidth of ESO, the accuracy of the observer can be improved by increasing the value of \({\omega }_{od}\).

According to the theory of ADRC33, design the linear PD state error feedback (SEF) control law as:

$$\left\{\begin{array}{c}{u}_{02}={k}_{d}\left({x}_{d}-{\widehat{z}}_{1}\right)\\ {u}_{2}=\left({u}_{02}-{\widehat{f}}_{d}\right)/{b}_{d}\end{array}\right.$$
(12)

where, \({k}_{d}\) is the regulated parameters, increasing the value of \({k}_{d}\) the displacement tracking accuracy of the system can be improved.

Pressure controller design

Depending on Eqs. (2), (4) and (6), the equation of rodless chamber pressure \({p}_{1}\) of the cylinder controlled by valve 1 can be obtained as:

$${\dot{p}}_{1}=\frac{{\beta }_{e}{k}_{v}{k}_{s}{R}_{1}}{{V}_{1}}{u}_{1}-\frac{{A}_{1}{\beta }_{e}}{{V}_{1}}{\dot{x}}_{p}-\frac{{C}_{ip}{\beta }_{e}}{{V}_{1}}\left({p}_{1}-{p}_{2}\right)$$
(13)

The derivation of Eq. (1) yields:

$${\dot{p}}_{1}{A}_{1}-{\dot{p}}_{2}{A}_{2}=m{\stackrel{...}{x}}_{p}+{\dot{F}}_{L}$$
(14)

where \({F}_{L}=B\frac{d{x}_{p}}{dt}+K{x}_{p}\).

According to Eqs. (13) and (14), the equation of rod chamber pressure \({p}_{2}\) controlled by valve 1 can be derived as:

$$\begin{array}{l}{\dot{p}}_{2} =\frac{1}{{A}_{2}}\left({\dot{p}}_{1}{A}_{1}-m{\stackrel{...}{x}}_{p}-{\dot{F}}_{L}\right)\\ =\frac{1}{{A}_{2}}\left(\left(\frac{{\beta }_{e}{k}_{v}{k}_{s}{R}_{1}}{{V}_{1}}{u}_{1}-\frac{{A}_{1}{\beta }_{e}}{{V}_{1}}{\dot{x}}_{p}-\frac{{C}_{ip}{\beta }_{e}}{{V}_{1}}\left({p}_{1}-{p}_{2}\right)\right){A}_{1}-m{\stackrel{...}{x}}_{p}-{\dot{F}}_{L}\right)\\ =\frac{{{A}_{1}\beta }_{e}{k}_{v}{k}_{s}{R}_{1}}{{A}_{2}{V}_{1}}{u}_{1}+\frac{1}{{A}_{2}}\left(\left(-\frac{{A}_{1}{\beta }_{e}}{{V}_{1}}{\dot{x}}_{p}-\frac{{C}_{ip}{\beta }_{e}}{{V}_{1}}\left({p}_{1}-{p}_{2}\right)\right){A}_{1}-m{\stackrel{...}{x}}_{p}-{\dot{F}}_{L}\right)\end{array}$$
(15)

From Eqs. (13) and (15), it can be found that the gain ratio of the input signal \({u}_{1}\) for controlling the \({p}_{1}\) and \({p}_{2}\) by valve 1 is \({A}_{1}/{A}_{2}\), which is the ratio of the effective areas of the rodless and rod chambers of the hydraulic cylinder. In the theory of ADRC, the total disturbance includes internal and external disturbances of the system, and it is observed and compensated by an ESO in the controller. Therefore, the gain of the input signal \({u}_{1}\) in the pressure control equations of \({p}_{1}\) and \({p}_{2}\) can be uniformly regarded as a nominal value \({b}_{p}\) for the sake of simplicity of the controller design. In this way, the deviation of the nominal value of the input signal gain from the actual value is treated as an internal disturbance in the system, and it will be compensated by the ESO. Considering all but the term of input signal in Eqs. (13) and (15) as total disturbance, the equations of pressure control for the rodless and rod chambers of the hydraulic cylinder controlled by valve 1 can be written uniformly as:

$${\dot{p}}_{i}={b}_{p}{u}_{1}+{f}_{p} ,i=\text{1,2}$$
(16)

where \({b}_{p}\) is the nominal gain of input signal of valve 1, \({f}_{p}\) is the total disturbance of pressure control system.

Let \({\varvec{\theta}}={\left[\begin{array}{cc}{\theta }_{1}& {\theta }_{2}\end{array}\right]}^{T}={\left[\begin{array}{cc}{p}_{i}& {f}_{p}\end{array}\right]}^{T}\), then the state space equation of the pressure control system is:

$$\left\{\begin{array}{c}{\dot{\theta }}_{1}={b}_{p}{u}_{1}+{\theta }_{2}\\ {\dot{\theta }}_{2}=g\end{array}\right.$$
(17)

where \(g=\dot{{f}_{p}}\).

According to Eq. (17), the linear ESO of the pressure control system is designed as:

$$\left\{\begin{array}{c}{\dot{\widehat{\theta }}}_{1}={\widehat{\theta }}_{2}+2{\omega }_{o\text{p}}\left({\widehat{\theta }}_{1}-{\theta }_{1}\right)+{b}_{p}{u}_{1}\\ {\dot{\widehat{\theta }}}_{2}=-{{\omega }_{o\text{p}}}^{2}\left({\widehat{\theta }}_{1}-{\theta }_{1}\right)\end{array}\right.$$
(18)

where, \({\omega }_{op}\) is the bandwidth, and \({\widehat{\theta }}_{i}\) is the estimation of \({\theta }_{i}\), the accuracy of the observer can be improved by increasing the value of \({\omega }_{op}\).

According to the theory of ADRC, design the linear PD SEF control law as:

$$\left\{\begin{array}{c}{u}_{01}={k}_{p}\left(r-{\widehat{\theta }}_{1}\right)\\ {u}_{1}=\left({u}_{01}-\widehat{d}\right)/{b}_{p}\end{array}\right.$$
(19)

where \({k}_{p}\) is the regulated parameters, increasing the value of \({k}_{p}\) the pressure control accuracy of the system can be improved.

Figure 3 shows the control structure diagram of the proposed control method. The process of regulating the controller parameters has been explained in detail in the authors' previous work32 and will not be repeated in this paper.

Fig. 3
figure 3

Control structure diagram.

Full size image

Experimental verification

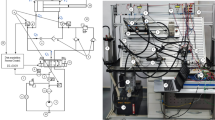
In this section, the proposed control strategy will be verified by experiments. The picture and schematic diagrams of the test bench are shown in Fig. 4. The test bench is mainly composed of IMS hydraulic system, loading system, transducers and controllers. The IMS hydraulic system mainly includes a hydraulic cylinder, two proportional servo valves, a pump and a motor. The loading system consists of the power source, two reducing valves and loading cylinder. Table 1 shows the main components of the test bench. The control program is transferred to dSPACE via the computer, and the dSPACE captures the sensor signals of displacement and pressure and outputs the servo valve control signals. The dSPACE sampling frequency is 1000 Hz. The servo motor and pump form the power source of the system and provide the system with the required hydraulic fluid. The force is loaded by the two reducing valves, two reducing valves apply different pressures to the two chambers of the load cylinder to achieve positive and negative load variations.

Fig. 4
figure 4

Picture and schematic diagram of the test bench.

Full size image
Table 1 Main components of the test bench.
Full size table

First, the experiments of cylinder runs from the working quadrant of resistance extension to overrunning extension (RETOE) are carried out. In the experiments, the parameters \({k}_{d}\), \({\omega }_{od}\), \({k}_{p}\),\( {\omega }_{op}\) of controllers are given as 25, 6, 120 and 60, respectively. The reference pressure \({p}_{d}\) is 15 bar, and the pressure threshold \({p}_{th}\) is 13 bar.

At the beginning, set the maximum pressure of system \({p}_{smax}\) as 75 bar, the minimum pressure \({p}_{smin}\) as 20 bar, and the flow rate of system as 30 L/min. The reference of \({x}_{d}\) is a ramp signal with the slop of 0.1 m/s and the amplitude of 0.4 m. Figure 5 is the results of displacement control of RETOE. During the operation of the cylinder, the force of load changes from positive 19 kN to negative 6.7 kN, thus the hydraulic cylinder operates from the working quadrants of RETOE. As can be seen from the Fig. 5, although the direction and the magnitude of the force are changing during the entire process, the stability tracking errors of displacement are maintained at about 3.5 mm. When the force changes from positive to negative, the displacement tracking is smooth, and the tracking error is basically unchanged, which indicates that the displacement tracking controller has strong robustness and resistance to load disturbances. It illustrates that the control accuracy of the displacement controller is not affected by the change of the working quadrant. And the displacement tracking errors do not oscillate after the change of working quadrant, demonstrating that the hydraulic cylinder can switch smoothly between multiple working quadrants.

Fig. 5
figure 5

Displacement control of RETOE.

Full size image

Figure 6 is the results of pressure control of RETOE. In 0–2.4 s \({p}_{2}\) is controlled at 15 bar and after 2.4 s \({p}_{1}\) is controlled at 15 bar. Pressure controller can automatically change the target of pressure control after the cylinder working quadrant changes, the rod chamber pressure \({p}_{2}\) under resistance conditions, and the rodless chamber pressure \({p}_{1}\) under overrunning condition are controlled both by valve 1. The hydraulic cylinder operates in energy-efficient mode under both resistance and overrunning conditions. The pressure control curve is the same as the expected result of the theoretical pressure control strategy. From Fig. 6, we can see that the pressure is controlled at 15 bar, and the pressure fluctuation is relatively small, which indicates that the control precision is high. When the working quadrant of the cylinder is overrunning extension, as the pump is only used as an oil source to provide the required flow of the cylinder, pressure of the system is set to the minimum 20 bar as shown in the figure.

Fig. 6
figure 6

Pressure control of RETOE.

Full size image

Figure 7 shows the variation of the estimated total disturbance of the displacement and pressure control system of RETOE. From the curve of displacement disturbance \({f}_{d}\), it can be noticed that, after switching from resistance extension to overrunning extension, \({f}_{d}\) becomes larger gradually. It is because the deviation between the actual value and the nominal value \({b}_{d}\) of the input signal gain is larger as the force increases. Since this deviation is considered as an internal disturbance which is observed and compensated by the observer, the displacement tracking error is not affected by the load variation and is able to remain constant in different working quadrants. During the pressure control process, the input signal gain \({b}_{p}\) of pressure control varies due to the shift of working quadrant of the cylinder. Thus, the difference of \({f}_{p}\) in the working quadrant of resistance extension and overrunning extension is relatively large. It is due to the observation and compensation of total disturbances that the controllers have a strong anti-interference capability.

Fig. 7
figure 7

Estimation of total disturbance.

Full size image

Figure 8 shows the input signals of valve 1 and valve 2. In the initial stage, the force of resistance is large, so the value of \({u}_{1}\) is big. With the force reduction during the cylinder running, the rodless chamber pressure \({p}_{1}\) is also reduced. In order to control the rod chamber pressure \({p}_{2}\) at a low constant value, \({u}_{1}\) gradually decreases. When the hydraulic cylinder enters the working quadrant of overrunning extension, the pressure of rodless chamber is controlled by \({u}_{1}\) at a low constant value. As the system pressure gradually decreases to 20 bar in overrunning extension quadrant, \({u}_{1}\) is increasing to control \({p}_{1}\) at a constant value, which can realize the purpose of reducing energy consumption. The displacement of the cylinder is controlled by valve 2. In the beginning, as the displacement tracking error is big, the input signal \({u}_{2}\) is large. When entering the stabilization phase of cylinder operation, the signal \({u}_{2}\) remains basically unchanged. When the cylinder operates in the overrunning extension quadrant, the load acts as the driving force, then \({u}_{2}\) decreases and becomes progressively smaller as the force becomes larger.

Fig. 8
figure 8

Input signals of vales.

Full size image

Figure 9 shows the power and torque of motor. After 2.4 s, both power and torque decrease, which is due to the fact that after the hydraulic cylinder extends from resistance to overrunning condition the cylinder is driven by the force of load. In about 0.5 s, the power is reduced from 3 to 0.9 kW, and the torque is reduced from 48.7 to 17.4 Nm. It is calculated that the system consumes 9.18 kJ to complete the extension process.

Fig. 9
figure 9

Power and torque of motor.

Full size image

Then the experiment of traditional constant pressure valve control (TCPVC) is performed. System pressure set at 75 bar. Design the PID controller with parameters P = 760, I = 25, D = 0, displacement tracking error as shown in Fig. 10. From the figure, it can be found that, as the driving force is provided by the pump, the displacement tracking error becomes larger with the load becomes larger during the resistance extension working quadrant. In the overrunning extension working quadrant, as the cylinder is driven by the load force, the displacement tracking error decreases when the load force is higher. During the operation of the hydraulic cylinder, the displacement tracking error is affected by the magnitude and direction of the load force. It is calculated that 11.92 kJ of energy is consumed during the extension process of TCPVC. Using the control strategy proposed in this paper saves 2.74 kJ of energy and reduces energy consumption by 23%.

Fig. 10
figure 10

TCPVC displacement tracking errors of RETOE.

Full size image

In order to verify the robustness of the controller and the ability of disturbance rejection, experiments are conducted at different maximum system pressures. Figure 11 shows the results of displacement control of cylinder at different system pressures when the velocity of cylinder is 0.1 m/s. From the figure, it’s clear that the tracking errors at different system pressures is basically unchanged, which is about 4 mm. As the disturbance generated by the system pressure change is observed and compensated by the ESO, the system has a strong anti-interference ability, so that the displacement tracking errors of cylinder will not change under different pressure.

Fig. 11
figure 11

Displacement control at different system pressures.

Full size image

Figure 12 is the results of pressure control of cylinder at different system pressures. Although the system pressures are different, the rod chamber pressure \({p}_{2}\) can be controlled at 15 bar during the resistance extension stage, and the rodless chamber pressure \({p}_{1}\) is controlled at 15 bar during the overrunning extension stage. According to Eq. (13), the change of system pressure results in the change of \(\Delta {p}_{2}\),which will and the increase in the deviation of the actual value from the nominal value of the input signal gain of valve 2. This deviation causes a disturbance effect on the system pressure control. However, the disturbance is observed and compensated by the ESO, so that the pressure control accuracy is not affected by changes in system pressure. Figures 11 and 12 illustrate that the controller has good capability of anti- interference and robustness.

Fig. 12
figure 12

Pressure control at different system pressures.

Full size image

Figures 13 and 14 show the estimated total disturbance and input signals of valves at different system pressures respectively. The estimated total disturbance varies when the system pressure changes, which is due to the pressure drop of valves is changed. Then, the input signals of valves change accordingly to counteract the effect of the disturbances on the system.

Fig. 13
figure 13

Estimated total disturbance at different system pressures.

Full size image
Fig. 14
figure 14

Input signals of valves at different system pressures.

Full size image

Figure 15 is the power and torque of motor at different system pressures. The higher the system pressure, the higher the power and torque of the motor under resistance extension condition. In the overrunning stage, the pump pressure is 20 bar, then the power and torque are the same and lower.

Fig. 15
figure 15

Power and torque of motor at different system pressures.

Full size image

Figure 16 shows the energy consumption of the motor at different pressures employing the IMS and the TCPVC. With the increasing of the system pressure, the energy consumption is larger, where the extra energy is converted into heat and dissipated in the orifice of valve. When the system pressures are 90 bar, 100 bar, and 110 bar respectively, the energy consumption can be reduced by 26.0%, 26.5%, and 27.8% respectively by using the proposed control strategy.

Fig. 16
figure 16

Energy consumption of motor at different pressures.

Full size image

Secondly, the experiments of cylinder runs from the working quadrant of overrunning extension to resistance extension (OETRE) are carried out. Figure 17 is the results of displacement control of OETRE. Before 1.5 s the force is less than zero, after 1.5 s the force is greater than zero and gradually increases, then the hydraulic cylinder runs from the overrunning extension to resistance extension. The hydraulic cylinder operates smoothly during extension. When switching from overrun to resistance, the tracking error decreases. This is due to the driving force increases when the operating quadrant is switched. The displacement tracking errors are about 4.5 mm for both resistance and overrunning conditions.

Fig. 17
figure 17

Displacement control of OETRE.

Full size image

Figure 18 shows the results of pressure control of OETRE. It can be seen from the figure, in the quadrant of overrunning extension, the rodless chamber pressure \({p}_{1}\) is controlled to be 15 bar. When the hydraulic cylinder is switched from overrunning to resistance condition, the pressure control target is switched to be the rod chamber pressure \({p}_{2}\). And during the resistance extension, \({p}_{2}\) is controlled at 15 bar. When overrunning condition is changed to resistance condition, the cylinder is able to automatically change the pressure control target and operate in an energy-efficient mode. The system pressure is low at 20 bar during overrunning condition and rises to 75 bar after the cylinder run to the resistance extension quadrant.

Fig. 18
figure 18

Pressure control of OETRE.

Full size image

Figure 19 shows the estimated total disturbances of the displacement and pressure control systems of OETRE. Since the deviation of the actual and nominal values of the valves input signal gains change during the extension of the hydraulic cylinder, the total disturbances change during the extension. Since this disturbance is observed and compensated by the ESO, the control accuracy of displacement and pressure remains unchanged even though the load force on the hydraulic cylinder is constantly changing.

Fig. 19
figure 19

Estimated total disturbances of OETRE.

Full size image

Figure 20 is the input signals of valves. The pressure is controlled by \({u}_{1}\). In the overrunning condition, valve 1 controls the cylinder rodless chamber pressure at 15 bar, and due to the system pressure is only 20 bar, the value of \({u}_{1}\) is large. Because the load force acts as the driving force to extend the hydraulic cylinder in this condition, and the force gradually decreases, the input signal \({u}_{2}\) of valve 2 increases accordingly. In the resistance extension quadrant, to overcome the increasing force, the input signal \({u}_{1}\) of valve 1 becomes progressively larger. As the rod chamber pressure is nearly constant under this condition, the input signal \({u}_{2}\) of valve 2 is smooth when the cylinder extends.

Fig. 20
figure 20

Input signals of valves.

Full size image

Figure 21 shows the power and torque of the motor of ORTER. In the overrunning condition, the power is 1 kW and when the hydraulic cylinder runs to the resistance extension work quadrant, the power increases to 3 kW and the torque becomes 49.5 Nm. The energy consumption is 8.4 kJ during the extension, and the energy consumed by the system of TCPVC 13.1 kJ, which can be reduced by 35.9% by using the control strategy proposed in this paper.

Fig. 21
figure 21

Power and torque of motor.

Full size image

Figure 22 shows the results of TCPVC displacement tracking control of OETRE when the PID controller is used. From the figure, it can be found that the displacement tracking error varies during the hydraulic operation, which is caused by the change in the direction and magnitude of the force on the cylinder. In overrunning extension quadrant, as the load is the driving force, the displacement tracking error becomes larger as the load decreases. And in the resistance extension quadrant, the displacement tracking error decreases with the increasing of force. The displacement tracking error is more affected by load variations easily.

Fig. 22
figure 22

TCPVC displacement tracking errors of OETRE.

Full size image

For different system pressures, when the speed of cylinder is 0.1 m/s and the system flow rate is 30 L/min, the experiment results of OETRE are shown as follows.

Figure 23 shows the displacement tracking errors of the cylinder of OETRE when the system pressures are 90 bar, 100 bar, and 110 bar respectively. Under different system pressures, the displacement tracking accuracy maintains the same in both overrunning and resistance conditions, which indicates that the controller has strong robustness.

Fig. 23
figure 23

Displacement control of OETRE at different pressures.

Full size image

Figure 24 is the results of pressure control of OETRE. At different pressures, it is possible to realize that the valve 1 controls the rodless chamber pressure \({p}_{1}\) at 15 bar in the overrunning and the rod chamber pressure \({p}_{2}\) at 15 bar in the resistance condition. During the process of overrunning to resistance quadrant, the chamber pressures rise. This is because that the driving force is the load in the overrunning condition, but in the resistance condition it is provided by the pump, thus the driving force increases when the cylinder runs from overrunning to resistance conditions.

Fig. 24
figure 24

Pressure control of OETRE at different pressures.

Full size image

Figures 25 and 26 show the estimated total disturbances of the displacement and pressure control systems and the input signals of the valves at different pressures respectively. The Changes of system pressure act as internal disturbance to the system. This internal disturbance is estimated by the ESO, so the observed total disturbance varies at different system pressures. Due to the total disturbance concept of ADRC, the total disturbance is compensated in the control law so that the input signal of the valve is varied to counteract the disturbance. Therefore, the variation of the input signal of the valve is affected by the variation of the total disturbance.

Fig. 25
figure 25

Estimated total disturbances at different pressures.

Full size image
Fig. 26
figure 26

Input signals at different pressures.

Full size image

Figure 27 is the power and torque curves of the motor at different pressures. In the initial stage of the hydraulic cylinder operation, the cylinder is working in the overrunning extension quadrant, at this time the system pressure is small, so the motor power and torque is minor. When the hydraulic cylinder switches to resistance extension, the system pressure starts to increase to overcome the load to drive the cylinder to extend. As the system pressure rises, the power and torque of the motor increases, and the excess pressure is converted into heat and dissipated by throttling.

Fig. 27
figure 27

Motor power and torque at different pressures.

Full size image

Figure 28 shows the comparison of energy consumption of motor at different pressures of TCPVC and the IMS. When the pressure of the system increases, more hydraulic energy is dissipated through throttling losses at the valve ports, resulting in more wasted energy. Therefore, when the pressure of the system increases, the energy saving rate increases. The results show that the energy consumption can be reduced by more than 40% at different pressures.

Fig. 28
figure 28

Motor energy consumption at different pressures.

Full size image

Conclusion

For the cylinder of IMS works at the quasi-equilibrium state between multiple quadrants, a novel multiple quadrants switching displacement tracking control strategy is proposed in this paper. The proposed method is validated by a series of experiments and the following conclusions can be obtained.

  1. (1)

    It is feasible to control both the pressures of the return chamber under resistance condition and the inlet chamber under overrunning condition by inlet valves. It is reasonable to control the displacement of the hydraulic cylinder by the outlet valve in both resistance and overrunning conditions. This method enables hydraulic cylinder to work in an energy-efficient mode all the time and to switch smoothly between multiple quadrants without changing the working mode of valves which avoids system oscillations and instability caused by changes in the valve's working mode in principle.

  2. (2)

    This paper designs a reduced-order ADRC displacement controller and a ADRC pressure controller to achieve high-precision control of the displacement and pressure. The experiments results show that the controller has strong robustness and anti-load interference ability.

  3. (3)

    The control strategy can effectively reduce the energy consumption of the system, the experiments results show that the energy consumption can be reduced by more than 23% compared to the traditional constant pressure valve control system.

In future work, the authors will study the method under more variable working conditions to verify its reliability more comprehensively and apply the method in actual construction machinery. And the authors will design the controller using more advanced control methods such as fractional-order ADRC to further improve the control accuracy and immunity of the system. And apply the method to the existing research system and compare it with the effect of existing control methods.