Introduction

Natural halloysite nanotubes (HNTs) are a type of alumina-silicate clay with the chemical composition Al2Si2O5(OH)4⋅2H2O and feature a tubular structure1,2,3,4. In contrast to carbon nanotubes (CNTs)5,6, HNTs are not entangled, thus they are more readily dispersed in various media compared to CNTs7,8. Additionally, the limited inter-tubular contact area of HNTs obviates the need for an extensive exfoliation process, enabling their dispersion in polymer mediums through shearing9. Previous research has indicated that HNTs can enhance the thermal, mechanical, and anti-flammability properties of polymer composites10,11,12,13. However, despite these experimental findings, few studies have explored models for determining the properties of HNT-based nanocomposites14,15,16. Furthermore, prior research has predominantly focused on the experimental investigation of this system as a novel multifunctional material for advanced technologies.

Numerous studies have identified an interphase zone between polymer mediums and nanofillers17,18,19,20. However, these investigations primarily concentrate on modeling the interphase characteristics due to the limited experimental accessibility caused by the small size and complex structure of the interphase. Various modeling studies have evaluated the effectiveness of systems by examining the properties of the interphase21,22,23,24,25. Generally, a strong interphase is advantageous as it transfers the significant forces from the polymer medium to the nanofiller26,27.

Many models were proposed for the modulus of composites. Hui and Shia28 suggested some equations for tensile modulus of composites with aligned platelets assuming the perfectly bonded interface. Kolarik29 also proposed a three perpendicular plates system for the modulus of particulate composites by filler concentration and the moduli of both matrix and filler. Besides, Halpin and Tsai30 developed a model for tensile modulus of polymer composites by filler concentration, the moduli of both matrix and filler and filler size. Moreover, Paul31 and Takayanagi32 models could estimate the modulus of composites by filler concentration and the moduli of both matrix and filler. However, these conventional models have not assumed the interphase zone in determining the modulus of composites. Instead, they simply correlate the composite’s modulus with the primary properties of the particles. The interphase section has been overlooked in limited models assessing the stiffness of polymer HNT systems. Incorporating an interphase in HNT-based materials is crucial, as it yields new and accurate insights into the reinforcing efficiencies of all components within the system.

This work introduces a two-stage procedure based on Paul and Takayanagi models, aiming to express the reinforcing efficacies of both HNT and the interphase zone in HNT-filled systems below mechanical percolation. Actually, the interphase is a bridge between the polymer matrix and HNT, but the linking of interphase zone to polymer matrix and HNT is perfect and adequate. Hence, we used the interphase properties to examine the interfacial bonding between the HNT and the polymer matrix controlling the stress transferring in the real samples. In the two-stage technique, the dispersed HNTs and surrounding interphase are considered. Initially, the HNTs and adjacent interphase are treated as pseudoparticles, and their modulus is evaluated using the Paul model. In the subsequent stage, the nanocomposite comprising a polymer medium and pseudoparticles is analyzed, and its modulus is predicted using the Takayanagi model. The influences of various factors on the moduli of the samples are justified, and the calculations within this two-step technique are correlated with experimental data from various samples. This novel two-step approach incorporates the meaningful and measurable factors by a reasonable and sensible manner.

Two-step modeling

We use Paul and Takayanagi models in the two-step methodology, because they are simple and user-friendly models. Also, we need the models including the filler modulus to estimate the nanocomposite modulus, because the modulus of pseudoparticles calculated in the first step is applied to estimate the modulus of nanocomposite at the second step.

Paul31 suggested the equation below for calculating the modulus of a composite, based on the assumption of constant stress across the components by the moduli of medium (Em) and filler (Ef) as:

$$ E = E_{m} \frac{{1 + (h - 1)\phi_{f}^{2/3} }}{{1 + (h - 1)(\phi_{f}^{2/3} - \phi_{f}^{{}} )}}, $$
(1)
$$ h = \frac{{E_{f} }}{{E_{m} }}, $$
(2)

where \(\phi_{f}\) is the filler volume share.

Takayanagi32 associated the composite’s modulus with the features of the medium and filler, as follows:

$$ E = E_{m} \bigg[(1 - a) + \frac{b}{{(1 - a) + b\frac{{E_{f} }}{{E_{m} }}}}\bigg]^{ - 1}, $$
(3)
$$ a = b = \sqrt {\phi_{f} }. $$
(4)

However, these equations cannot be used to determine the modulus of nanocomposites since they overlook the interphase. These models are grounded on formulas designed for the moduli of traditional composites; thus, their application to nanocomposites results in inaccurate outcomes. Consequently, enhancing them by integrating interphase characteristics could improve their accuracy in estimating the reinforcement in nanocomposites.

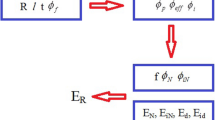
We propose a two-stage procedure that utilizes these models to evaluate the modulus of polymer HNT products by the interphase section. This approach encompasses the reinforcing efficiencies of both HNTs and the interphase within the samples. Figure 1 illustrates a schematic for considering pseudoparticles and nanocomposites in two steps. It presupposes that the HNT and its surrounding interphase produce a pseudoparticle at the nanoscale, and then the nanocomposite consists of a polymer medium and pseudoparticles at macro-scale. We used the Paul model for the calculation of pseudoparticle modulus. Then, the modulus of pseusoparticles is applied to predict the modulus of nanocomposites by Takayanagi model in the second step.

Fig. 1
figure 1

Two-stage methodology assuming HNTs and surrounding interphase as pseudoparticle at the first stage. The nanocomposite comprising the polymer medium and the pseudoparticles is considered at the second stage.

Full size image

In the first step, it is assumed that pseudoparticles are formed, wherein the interphase section encircles the HNTs (Fig. 1). It is further posited that the interphase medium envelops the HNTs. In fact, the interphase is considered as a matrix surrounding the HNT. The modulus of the pseudoparticles is determined using the Paul model. The total volume of the pseudoparticles is considered to be \(\phi_{f} + \phi_{i}\), where \(\phi_{i}\) is interphase volume portion in the nanocomposite. Therefore, the volume proportion of HNTs in the pseudoparticles is estimated as \(\frac{{\phi_{f} }}{{\phi_{f} + \phi_{i} }}\) and the modulus of matrix (Em) in the Paul model is equal to the interphase modulus (Ei).

The modulus of pseudoparticles is estimated by modified Paul model (Eqs. 1, 2) as follows:

$$ E_{p} = E_{i} \frac{{1 + (h - 1)(\frac{{\phi_{f} }}{{\phi_{f} + \phi_{i} }})^{2/3} }}{{1 + (h - 1)\bigg[(\frac{{\phi_{f} }}{{\phi_{f} + \phi_{i} }})^{2/3} - \frac{{\phi_{f} }}{{\phi_{f} + \phi_{i} }}\bigg]}}, $$
(5)
$$ h = \frac{{E_{f}^{{}} }}{{E_{i}^{{}} }}, $$
(6)

where Ei is the interphase modulus.

The volume share of the interphase in products comprising a tubular filler (such as CNTs or HNTs)33 is evaluated from:

$$ \phi_{i} = \phi_{f} \bigg[\bigg(1 + \frac{t}{R}\bigg)^{2} - 1\bigg], $$
(7)

where t is the interphase depth and R is the radius of HNTs. By integrating Eq. (7) into Eq. (5), the modulus of the pseudoparticles is linked to the characteristics of the HNTs and the adjacent interphase section. All parameters are meaningful and measurable. Subsequently, the nanocomposite, comprising the polymer medium and the pseudoparticles (Fig. 1) is examined at the second stage, and the nanocomposite modulus is calculated using the Takayanagi model. The volume proportion of the pseudoparticles in the sample is \(\phi_{f} + \phi_{i}\), since the pseudoparticles contain both HNT and interphase. Also, the pseudoparticles are considered as the dispersed filler in the polymer matrix. Hence, the modulus of pseusoparticles (Ep), which was calculated in the first step, is considered as the modulus of the filler in the second step.

These assumptions develop the Takayanagi model (Eqs. 3, 4) for calculating the modulus of polymer nanocomposites as follows:

$$ E = E_{m} \left[(1 - a) + \frac{b}{{(1 - a) + b\frac{{E_{p} }}{{E_{m} }}}}\right]^{ - 1}, $$
(8)
$$ a = b = \sqrt {\phi_{f} + \phi_{i} }, $$
(9)

which presumes the reinforcing efficiencies of all parts in the sample.

When Ep and \(\phi_{i}\) variables are derived from Eqs. (5) and (7) and applied to Eqs. (8) and (9), Eq. (8) establishes a relationship between the modulus of the system and the characteristics of the polymer matrix, HNTs, and interphase section. All variables in this multi-step technique are significant and measurable, enabling researchers to evaluate the stiffness of a HNT-filled sample using a straightforward and practical approach.

Results and discussion

Investigation of factors

The results of the innovative technique across various ranges of factors are plotted and discussed to elucidate the influences of model parameters on the modulus of HNT-based nanocomposites (summarized as modulus here). Each graph illustrates how the stiffness depends on a single factor, while other factors are kept at constant or standard levels. The standard ranges are presumed as R = 30 nm, \(\phi_{f}\) = 0.02, Ef = 140 GPa34, Em = 2 GPa, Ei = 30 GPa, and t = 10 nm. These plots can guide researchers to control the parameters that affect the modulus.

Figure 2 presents the calculated modulus at various interphase depths utilizing the two-step technique. The absence of an interphase (t = 0) results in a modulus of 2.3 GPa. However, the modulus increases to 2.51 GPa when the interphase depth is at t = 20 nm. This increase suggests that the stiffness of the system improves with a thicker interphase. The modulus of the products rises as the interphase thickens, establishing a direct relationship between the modulus and the interphase depth. Consequently, the modulus escalates incrementally with interphase depth, indicating that a thicker interphase leads to a stiffer composite.

Fig. 2
figure 2

Effect of interphase depth on the E using the present technique.

Full size image

A denser interphase contributes to an increased volume share within the samples, as described by Eq. (7), thereby enhancing the modulus. Generally, a denser interphase expands the reinforcing phase, which in turn raises the modulus. A thicker interphase is indicative of the establishment of strong interfacial bonding between the polymer medium and the HNTs, thereby promoting reinforcement35,36. Consequently, a dense interphase is advantageous for reinforcing nanocomposites. Conversely, a narrower interphase around HNTs reduces their concentration within the system, diminishing the reinforcement effect. Furthermore, a thin interphase signifies the weak interfacial adhesion that may easily fail under load, suggesting that a narrow interphase causes a minimal reinforcing in the system, with only a negligible enhancement in stiffness. This analysis demonstrates that the multi-step technique effectively correlates the modulus to the depth of interphase.

Figure 3 illustrates the variations in the modulus at different levels of interphase modulus, as determined by the current technique. An interphase modulus of 10 GPa yields a modulus of 2.342 GPa, whereas the modulus reaches 2.41 GPa at an interphase modulus of 60 GPa. These findings underscore a direct relationship between the moduli of composites and the interphase section. Smaller interphase moduli (Ei < 40 GPa) significantly enhance the stiffness. However, an excessively stiff interphase results in only a marginal improvement in the modulus.

Fig. 3
figure 3

Connection of modulus to interphase modulus using a multi-step technique.

Full size image

A stronger interphase enhances the reinforcement as the stiffness correlates with the moduli of the components. A more robust interphase can absorb more stress during loading, thereby strengthening the sample. Conversely, a weaker interphase has a reduced capacity to dissipate the load, leading to weaker nanocomposites37,38. A more substantial interphase fosters a stronger connection between the medium and the nanofiller, augmenting reinforcement. On the other hand, a deficient interphase creates a weak bond between the polymer and particles, impairing stress transfer and reinforcement. It is generally recognized that a tougher interphase results in a stronger nanocomposite, since the interphase acts as the third critical component alongside the polymer medium and nanoparticles. Therefore, a direct correlation exists between the modulus and the interphase modulus, validating the predictive capability of the two-step methodology.

Figure 4 illustrates the outcomes of the two-step technique at various interphase volume fractions. A modulus of 2.3 GPa is achieved with \(\phi_{i}\) = 0.005, and the modulus escalates to 2.5 GPa at \(\phi_{i}\) = 0.03. Consequently, more interphase volume fraction results in a tougher nanocomposite. Additionally, there is a straight correlation among the modulus and \(\phi_{i}\). These findings imply that the stiffness linearly correlates with \(\phi_{i}\) and that the modulus is progressively improved by augmenting the interphase volume fraction.

Fig. 4
figure 4

Outputs of modulus by two-step technique at various interphase volume portions.

Full size image

A larger interphase section significantly reinforces the examples, as the modulus of the interphase zone surpasses that of the polymer host39,40,41,42. The interphase acts as a strengthening agent in nanocomposites, and its higher content evidently fortifies the system. Thus, a substantial presence of nanoparticles and their surrounding interphase can considerably reinforce a nanocomposite. In contrast, minimal interphase content offers negligible reinforcement to the examples, given that the amount of interphase is substantially lower than the volume of a weak polymer host. In essence, a small proportion of interphase in the system has a trivial effect on reinforcement. This finding corroborates the predictions made by the two-step technique regarding various interphase volume fractions.

Figure 5 depicts the relationship between stiffness and HNT weight percentage, as determined through the multi-step technique. A HNT concentration of 2 wt% yields a stiffness of 2.21 GPa, which increases to 2.67 GPa at a HNT content of 10 wt%. Accordingly, the modulus is directly linked to the HNT quantity. The modulus rises with HNT concentration, where a greater concentration of HNTs invariably enhances the reinforcement of samples. The notable increase in stiffness with HNT concentration highlights that the HNT amount is a critical factor for modulating the modulus.

Fig. 5
figure 5

Changes of stiffness at several HNT concentrations using the multi-step technique.

Full size image

A high volume of HNT significantly contributes to stiffening, as the modulus of HNT is considerably higher than that of the polymer. The presence of a large number of rigid HNTs undoubtedly enhances the modulus, due to the robustness of HNTs against stress. Within a nanocomposite comprising a polymer medium, HNTs, and an interphase zone, the HNTs play the most significant reinforcing role, possessing the highest modulus (140 GPa)34. Consequently, an increased quantity of rigid HNTs in the samples compromises the effectiveness of a weaker polymer medium and strengthens the system. Conversely, a limited quantity of HNTs has only a minimal impact on reinforcement, given their relatively small volume compared to that of the polymer. It is important to recognize that a small number of HNTs is insufficient to significantly reinforce the large volume of polymer. Hence, the direct correlation between stiffness and the quantity of HNTs is confirmed, supporting the efficacy of the multi-step technique.

Figure 6 demonstrates the relationship determined between the modulus and the HNT radius utilizing the two-step technique. While stiffness increases to 2.45 GPa at the HNT radius (R) of 20 nm, enlarging the HNT radius diminishes the stiffness, which decreases to 2.34 GPa at R = 60 nm. Therefore, a larger HNT radius results in a reduced modulus, whereas narrower HNTs contribute positively to the modulus. The stiffness significantly drops at low HNT radii (R < 45 nm), but higher HNT radii only slightly reduce the modulus. The thinnest HNT, with R = 20 nm, significantly boosts stiffness, marking it as a crucial factor in HNT-based system.

Fig. 6
figure 6

Plot of modulus against HNT radius using the two-step methodology.

Full size image

Thin HNTs prove advantageous by expanding the interphase within composites. Equation (7) illustrates that slimmer HNTs (lower R) extend the interphase section in the samples. Additionally, narrower HNTs enhance the \(\phi_{i}\) in the system, thereby increasing reinforcement. Typically, slim HNTs provide a larger surface area, augmenting the size of the interphase between the HNTs and the polymer host43,44. Furthermore, narrow HNTs boost the reinforcing efficiency of the interphase in the samples. It has been noted that small nanoparticles can produce a nano-effect in samples, enhancing reinforcement45. Conversely, thicker HNTs diminish the interphase and lessen its strengthening impact in the nanocomposites. Moreover, thick HNTs create a weaker interphase section, leading to negligible reinforcement in the samples. This observation confirms the precision of the calculations using the two-step technique for varying HNT radii.

Use of experimented findings

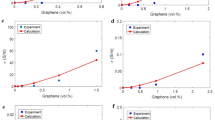
The calculations from the two-step technique are compared with the experimental findings from various examples in published articles. Real sample data are utilized to validate the predictive capabilities of the new methodology. Table 1 lists some products along with the properties of their matrix and HNTs. HNT dimensions and the modulus of polymer matrix were reported form the original references. Also, the HNT modulus is assumed to be 140 GPa34. However, the interphase properties are calculated by fitting of measured moduli of samples to the two-step model. Moreover, HNT concentrations were reported in the original references. By integrating Eq. (7) into Eq. (5), the modulus of the pseudoparticles is linked to the characteristics of the HNTs and the adjacent interphase section. Actually, the modulus of pseudoparticles is obtained by HNT amount, HNT radius, HNT modulus (140 GPa), interphase depth and interphase modulus. Then, the obtained equation for pseudoparticle modulus is substituted into Eq. (8) to estimate the modulus of nanocomposite. Since \(a = b = \sqrt {\phi_{f} + \phi_{i} }\) (Eq. 9), all parameters are meaningful and measurable easing the modulus predictions. Really, the two-step model needs the properties of HNT, polymer matrix and interphase to calculate the modulus of nanocomposites. Figure 7 compares the modulus data derived from experiments and the two-step technique. The results from the two-step technique are matched with the experimental moduli of the nanocomposites, indicating that the experimental moduli of various types of nanocomposites closely correspond with the calculations, thus confirming the accuracy of the two-step methodology.

Table 1 Characteristics of various HNT-reinforced samples.
Full size table
Fig. 7
figure 7

Experimental and theoretical moduli using two-step technique for (a) PA61046, (b) PLA14, (c) PA647, (d) PVA48, (e) cellulose49 and (f) EPDM50 HNT products.

Full size image

The harmonious alignment between the tested and theoretical data allows the two-step technique to estimate the interphase characteristics. When the two-step model is fitted to the experimental data, many values for both t and Ei are calculated. We reported the average and meaningful values for t and Ei in Table 1, since t as interphase thickness cannot be higher than the gyration radius of polymers. Also, Ei as interphase modulus changes between the moduli of matrix and HNT. The calculated values for interphase depth and modulus are documented in Table 1, showcasing interphase depths ranging from 10 to 43 nm for the specimens. Among the examples, the polyamide-6 (PA6)/HNT and cellulose/HNT samples possess the narrowest and densest interphases, respectively. Furthermore, the stiffness of the interphase in these samples varies from 15 to 80 GPa. These findings are logical, considering the interphase modulus is impacted by the moduli of both the matrix and the nanofiller.

The weakest and the strongest interphases are observed in the PA6 and cellulose samples, respectively. The findings suggest that the cellulose/HNT system possesses the deepest and most robust interphase among the evaluated samples, as evidenced by this sample displaying the highest measured modulus at low HNT concentrations (Fig. 7e). Conversely, the PA6/HNT system is characterized by the thinnest and weakest interphase section, with the modulus results indicating that this sample experiences the least improvement in modulus at high HNT concentrations (Fig. 7c). These outcomes validate the predictions made by the two-step technique regarding interphase properties within the samples, as stiffness is directly correlated with the attributes of the interphase section21,39,40. Consequently, the experimental moduli and the determined interphase characteristics corroborate the efficacy of the two-step methodology.

Conclusions

A two-stage technique has been developed for analyzing the stiffness of HNT-filled composites by considering interphase characteristics. The impacts of various factors on the moduli of the samples were thoroughly examined, and the results from the two-stage approach were compared to experimental data from several studies. The stiffness has been observed to increase to 2.51 GPa at an interphase depth (t) of 20 nm, demonstrating how the enhancement of stiffness is influenced by the thickening of the interphase section. Additionally, an interphase modulus (Ei) of 10 GPa results in a stiffness of 2.342 GPa, although the stiffness reaches 2.41 GPa with an interphase modulus of 60 GPa. This establishes a direct correlation between the moduli of the composite and the characteristics of the interphase. Furthermore, very high levels of interphase modulus only yield slight improvements in the modulus of the samples. An interphase volume fraction of 0.03 optimizes the modulus of the composites to 2.5 GPa, indicating that a greater proportion of interphase volume results in a stronger sample. The modulus of the nanocomposite is linearly associated with the interphase volume fraction. A HNT content of 10 wt% enhances the stiffness to 2.67 GPa, and the modulus of the samples progressively increases by HNT concentration. At HNT radius (R) of 20 nm, the stiffness increases to 2.45 GPa; however, an increase in HNT radius reduces the reinforcing effect. Consequently, narrower HNTs are more advantageous for the modulus of the samples. The stiffness significantly decreases at R < 45 nm, though higher HNT radii only marginally reduce the modulus. The results from the two-stage technique precisely align with the experimental moduli of the samples reported in related articles. The moduli obtained for the examples and the predicted interphase characteristics validate the predictive accuracy of the two-stage methodology. It is important to highlight that the two-stage method is adaptable to various HNT lengths and different types of polymer matrices.