After the Industrial Revolution, the greenhouse gas content in the atmosphere increased, the energy balance and material cycling processes in the Earth’s terrestrial and atmospheric cycles changed, and the global temperature continued to rise, which led to a series of extreme weather events1. The IPCC Sixth Assessment Report states that 1970–2020 was the hottest 50-year period in the last 2000 years, with a global average temperature increase of 1.09 °C in 2011–2020 compared with 1850–19902. China is a sensitive area and a significant impact area of global climate change, and the warming rate in China from 1951 to 2020 was as high as 0.26 °C/10a, much higher than the global average (0.15 °C/10a), and the average temperature at the end of the twenty-first century may rise by 4 °C3,4. Warming will lead to an increase in the capacity of the atmospheric boundary layer to hold water vapor and a rise in atmospheric water vapor content, resulting in an increase in the intensity of extreme precipitation5. Extreme rainfall is a typical manifestation of extreme weather, which is sudden, destructive, regional, and prone to inducing geological disasters6 and causing serious impacts on society, economy, and people’s lives. Therefore, clarifying the characteristics of extreme rainfall variability and its response to temperature changes in the context of climate change is crucial for sustainable regional development.

The study of the response of extreme rainfall to climate change has attracted a great deal of scholarly attention, with the Clausius–Clapeyron (C–C) equations being the most controversial. This equation states that the atmospheric water-holding capacity increases by 7% for every 1 °C rise in temperature, assuming constant relative humidity7, and that the change in extreme rainfall intensity with temperature is also controlled by the C–C Eq.8. However, the response of extreme rainfall to temperature is not the same in different regions and peaked, bimodal, and monotonically rising structures have been observed in different regions of China7,9,10. These response structures are constrained by the natural environment, climate, and other factors11, and changes in extreme rainfall intensity are likely to become more pronounced in the context of future climate warming12. Among the natural environmental factors, the structure of the subsurface can significantly influence the formation of regional microclimate and precipitation13, thus affecting the response of extreme rainfall to changes in temperature. Therefore, from a regional perspective, analyzing the characteristics of extreme rainfall and its response to temperature change under different subsurface conditions in historical and future periods can provide a more comprehensive understanding of extreme rainfall. Currently, the Couple Model Inter-comparison Project (CMIP) has become an important tool for climate prediction, and CMIP has now reached its sixth phase (CMIP6)14. The CMIP6 model has a large number of models, huge simulation data, and perfect scientific experiments15, which can better simulate the temperature, and extreme rainfall in the Chinese region16,17,18. Therefore, the CMIP6 model data was selected in this study to analyze the relationship between future extreme rainfall and temperature changes in the region.

Guizhou Province in China is influenced by the southeast monsoon from the Pacific Ocean and the southwest monsoon from the Indian Ocean and receives abundant rainfall. However, the complex structure of its subsurface and the uneven spatial distribution of rainfall make it prone to extreme rainfall, increasing the risk of geologic disasters. Studies have been conducted to analyze the characteristics of the historical period of extreme rainfall in Guizhou19 and to predict future extreme rainfall in Guizhou using the CMIP6 model data20, but studies on the characteristics of the extreme rainfall and its response to temperature change in Guizhou under different subsurface conditions in the past and in the future periods have not been reported. Therefore, this paper will propose to solve the following problems on this basis: (1) the spatiotemporal and recurrence period characteristics of extreme rainfall in Guizhou under different subsurface conditions in the past and future periods; (2) the spatiotemporal characteristics of Guizhou's air temperature in the years of 1990–2020 and 2021–2100; and (3) to explore the response of extreme rainfall to the changes of air temperature in different periods and under different subsurface conditions. The results of the study can provide a solid and scientific decision-making basis for disaster prevention and mitigation in Guizhou Province.

Study area

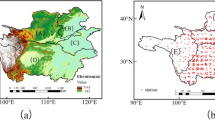
Guizhou Province is located in southwestern China, and its latitude and longitude range is 103°36′–109°35′E, 24°37′–29°13′N (Fig. 1). The province covers an area of 176,000 km2, and the karst landscape is widely distributed, accounting for 73.8% of the area. Guizhou Province has a dense network of rivers, with the Wumeng Mountains-Miao Ling as the watershed, and belongs to the Yangtze River and Pearl River Basin. The climate belongs to the subtropical monsoon climate, with abundant rainfall but uneven spatial and temporal distribution, prone to extreme rainfall21.

Fig. 1
figure 1

Geomorphology of the study area and meteorological stations distribution. Map was created with ArcGIS version 10.8 (https://www.arcgis.com/).

Full size image

Study data and methods

Dataset

Extreme rainfall is calculated using daily rainfall data from 31 stations in Guizhou Province, and the 95th and 99th percentile values are often chosen to characterize extreme rainfall in the international arena, whereas Guizhou Province has special geomorphological types, thin soil layers, and poor water retention capacity, which are highly susceptible to erosion by rainfall, so the study chose the index R95p to characterize extreme rainfall in Guizhou Province. Historical period set to 1990–2020, data from China Meteorological Data Network (CMDN); future period data from 5 GCMs under CMIP6 (see Table 1 for details), time set to 2021–2100. The study selects the scenario data of SSP245, which is an update to scenario RCP4.5, with an additional radiative forcing of 4.5 W/m2 by the year 2100 represents the medium pathway of future greenhouse gas emissions, in order to investigate the characteristics of extreme rainfall and its response to temperature change in Guizhou Province under the medium pathway scenario. Due to the different resolutions of the selected scenario data, resampling was used to unify the spatial resolution to 0.05°. Temperature data and rainfall data at the same source and scale. To analyze the impact of different subsurface structures on extreme rainfall, this paper selects slope, DEM and aspect and explores their grading, the grading criteria refer to Zhang22 and Li23, details are provided in Table 2. The DEM data originates from the geospatial data cloud, the spatial resolution is 30m, and the slope and aspect data are extracted based on the DEM data. Due to the slow change of DEM, the impact of future topographic changes is not considered in this study. The results of the grading results of the subsurface structures of 31 stations are shown in Fig. 2.

Table 1 Spatio-temporal resolution of CMIP6 data and its sources.
Full size table
Table 2 Criteria for structural grading of underlayment.
Full size table
Fig. 2
figure 2

Graph of structural grading results of the subsurface. Map was created with ArcGIS version 10.8 (https://www.arcgis.com/).

Full size image

Methods

Distribution function

In this study, seven distribution functions, namely, Normal distribution, Log-normal distribution, Gamma distribution, Logistic distribution, Extreme value (EV) distribution, Generalized extreme value (GEV) distribution, and Weibull distribution, were chosen to fit the R95p series of Guizhou Province. The specific formula and parameters of each distribution function are shown in Table 3.

Table 3 Distribution function and its parameters.
Full size table

Optimal model selection

Preferred distribution line shape methods mainly include hypothesis testing and certain criterion-based fitting preference, in this paper, we choose the hypothesis testing based Anderson–Darling (A-D)24, Kolmogorov–Smirnov (K–S) test24,25, and criterion-based Akaike Information Criterion (AIC)26, and Bayesian Information Criterion (BIC)26 to prefer distributional line shapes. The specific formulas for the four fitting preference methods are as follows:

The statistic used in the A-D test is generally denoted by A2 and its expression is:

$$A^{2} = - n - \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {2i - 1} \right)\left\{ {\ln F\left( {y_{i} } \right) + \ln \left[ {1 - F\left( {y_{n - i + 1} } \right)} \right]} \right\}}$$
(1)

where \(n\) is the sample size and \(F(y_{i} )\) is the cumulative distribution function (CDF) of the probability distribution under consideration. The A-D test is constructed as follows: \(H_{0}\) for sample data, from the aggregate of a particular distribution; \(H_{1}\) for sample data, not from the aggregate of a particular distribution.

The statistic used in the K-S test is generally denoted by D and its expression is:

$$D = \mathop {\max }\limits_{1 < = i < = n} \left[ {F\left( {y_{i} } \right) - \frac{1 - i}{n},\frac{i}{n} - F\left( {y_{i} } \right)} \right]$$
(2)

where \(n\) is the sample size and \(F(y_{i} )\) is the cumulative distribution function (CDF) of the probability distribution under consideration. The A-D test is constructed as follows: \(H_{0}\) for sample data, from the aggregate of a particular distribution; \(H_{1}\) for sample data, not from the aggregate of a particular distribution.

The AIC criterion takes into account both the fit of the model and the impact of model complexity, the smaller the AIC value, the closer the estimated probability distribution is to the true distribution. The BIC criterion also takes into account the effect of the number of samples, when the number of samples is too large, it can effectively prevent the model complexity caused by the model precision is too high. Assuming that the probability density function \(f(x)\) contains the parameter \(\theta\), if \(\theta\) is a \(k\)-dimensional vector and \(L\) is the likelihood function, the expression of AIC and BIC values is:

$$AIC = 2k - 2\ln (L)$$
(3)
$$BIC = k\ln (n) - 2\ln (L)$$
(4)

Clausius-Clapeyron (C–C) equation

The C–C equation explains to a large extent the response mechanism of extreme rainfall to changes in air temperature, and is now considered by many national and international scholars to be the physical mechanism for the occurrence of extreme rainfall9,27. The equation states that, assuming a constant relative humidity, the atmospheric water-holding capacity increases by 7% for every 1 °C rise in temperature, with an excess of 7%/°C being a super-C–C scale and a decrease of less than 7%/°C being a sub-C–C scale. The C–C equation is expressed as:

$$\frac{{\partial e_{s} }}{\partial T} = \frac{{L_{s} \partial e_{s} }}{{R_{v} T^{2} }}$$
(5)

where \(L_{{^{s} }} = 2.5 \times 10^{6} J/{\text{kg}}\);\(R_{v} = 4.61.5J/kg\); \(T\) is the absolute atmospheric temperature, K; \(e_{s}\) is the saturated water vapor pressure.

Results

Characteristics of extreme rainfall changes in Guizhou Province

CMIP6 data optimization

In order to prefer future model data more suitable for Guizhou Province, the study utilized five GCM model data under CMIP6 and their ensemble averaging (multi-model ensemble, MME) with the observation data to calculate and obtain the rainfall and temperature Taylor diagrams for Guizhou Province under the SSP245 model. As can be seen in Fig. 3, the simulation effect of the five model data on rainfall varies widely and is poor, but MME has a better simulation effect, the correlation coefficient reaches 0.821, the standard deviation and root mean square error of 1.35 and 0.78, respectively, the simulation effect is ideal. Each model data has a better effect on temperature simulation, among which MME also has the best effect, the correlation coefficient is as high as 0.93, the standard deviation (0.97) is close to 1, and the root mean square error is only 0.37. Therefore, whether it is rainfall or temperature, MME has the best effect on climate simulation in Guizhou Province.

Fig. 3
figure 3

Taylor diagram of CMIP6 model data for simulation of rainfall and temperature in Guizhou.

Full size image

Temporal evolution of extreme rainfall characteristics

Guizhou 1990–2020 (historical period) R95p ranged from 203.52 to 508.10 mm (Fig. 4a), with the minimum occurring in 2013, followed by the maximum in 2014, with an extreme difference of 304.58 mm; 2021–2100 (future period) R95p ranged from 150.09 to 566.62 mm, with the maximum and minimum occurring in 2100, 2028, respectively, and the extreme difference (416.52 mm) larger than the historical period. It can be seen that rainfall extremes are stronger in the future period than in the historical period. The difference in R95p between the two periods under different subsurface conditions (Fig. 4b) suggests that the structure of the subsurface affects rainfall extremes to some extent. In both periods, DEM, slope, and R95p were negatively correlated, i.e. , the higher the rank of both, the smaller the R95p. This may be due to the fact that the higher the elevation and steeper the slope, the harder it is for water vapor to climb and the less rainfall there is; Under different slope orientations, R95p was more prominent on the southwest slope in both periods, which may be due to the fact that southwest Guizhou is a windward slope, which is conducive to the transport of water vapor from the Bay of Bengal and the South China Sea northward28. Extreme rainfall, both overall and under different subsurface conditions, is skewed in most of the epochs, indicating that extreme rainfall in Guizhou is not directly characterized by a normal distribution that can be fitted to its characteristics.

Fig. 4
figure 4

Boxplots of R95p as a whole and under different subsurface conditions.

Full size image

The time trend showed a non-significant increase in R95p in the historical period (Fig. 5a), with a rate of increase of 0.77/a (p > 0.1); whereas, R95p showed a significant increase in the future period (2.07/a (p < 0.01)), with a larger rate of increase than in the historical period. Under different subsurface conditions (Fig. 5b), R95p showed a slowing trend in some subsurface conditions during the historical period, such as the western slope, and R95p showed an increasing trend in all subsurface conditions during the future period, and the rate of increase was generally larger than that of the historical period , which was similar to the overall characteristics. R95p as a whole shows a trend of slowly increasing (historical period)—slowing down (early future period)—and rapidly increasing, which is due to the fact that GHG emissions are controlled by anthropogenic factors in the SSP245 scenario, and therefore rainfall extremes are moderated at the beginning of the future period.

Fig. 5
figure 5

Trends of R95p as a whole and under different subsurface conditions.

Full size image

Characterization of the spatial distribution of extreme rainfall

Due to the uniform spatial distribution of meteorological stations in Guizhou Province, the study interpolates and analyzes the meteorological data of Guizhou with the help of the inverse distance weight interpolation method. R95p in Guizhou during the historical period showed a spatial distribution pattern of “high in the south and low in the north, high in the east and low in the west” (Fig. 6), with the center of the low value located in the area of Weining and Bijie in the northwest and the lowest value of 202.02 mm; the high value was mainly concentrated in the vicinity of Duyun in the southeast and in the area of Xingyi in the southwest, with the maximum value of 431.17 mm, and the extreme difference of 229.15 mm. This may be due to the high altitude of the towering Wumeng Mountains in western Guizhou, which makes it difficult for water vapor to enter, while the southeastern and southwestern regions have lower altitudes and slopes and are on windward slopes, with ample water vapor and rainfall28. R95p in the future scenario shows a spatial distribution pattern of high in the southeast and low in the northwest, which is similar to the spatial distribution of extreme rainfall in the historical period. The high value of R95p was located in the eastern-southern region of Guizhou, but the high value was reduced from the historical period to 334.69 mm, and the high-value site did not occur near Xingyi in the southwest. R95p values have increased in the northwest, but remain the main distribution area for low values. This scenario has a larger R95p minimum (253.36 mm) and a smaller extreme difference (81.33 mm) than in the historical period. This indicates that the SSP245 scenario has less regional extreme rainfall variability in Guizhou than in the historical period. The SSP245 scenario assumes that climate protection measures are being taken29, so that the decrease in rainfall extremes may be due to active interference by human activities.

Fig. 6
figure 6

Spatial distribution of R95p in historical and future periods. Map was created with ArcGIS version 10.8 (https://www.arcgis.com/).

Full size image

Characterization of extreme rainfall recurrence

Extreme rainfall in Guizhou can not be directly fitted to its characteristics using normal distribution, in order to get more reasonable extreme rainfall values, the study selected seven distribution functions and four testing methods to fit the optimization of R95p for two periods at 31 meteorological stations in Guizhou, respectively. This process first uses MATLAB to calculate the parameters of the seven distribution functions corresponding to the extreme rainfall at each site, then uses the parameters to find out the results of the optimal test index corresponding to each distribution function, and finally ranks the results of the optimal test to get a comprehensive ranking, then selects the optimal probability distribution model for each site according to the ranking. According to the optimal distribution function summary chart (Fig. 7), Weibull and Gamma functions are the optimal distribution functions for R95p for most sites in the historical and future periods, respectively, with 71% and 81% of the sites in that order, but the EV function did not fit the sites optimally in either period. The distribution of the optimal distribution function in the historical period is more diverse than that of the future scenario, indicating that the characteristics of extreme rainfall in Guizhou in the historical period are more complex and diverse.

Fig. 7
figure 7

Plot of the optimal site distribution function.

Full size image

Under the 5-, 10-, 25-, and 50-year recurrence (Fig. 8), the mean values of R95p in Guizhou were 458.85 mm, 542.11 mm, 636.14 mm, and 699.63 mm for the historical period, and the mean values of R95p were 367.18 mm, 483.18 mm, 527.01 mm, and 568.80 mm for the future period, in that order. Extreme rainfall is more severe in the historical period than in the future period, which may be due to the moderation of climate extremes in the SSP245 scenario, where GHG emissions are controlled by anthropogenic factors. Under each recurrence period, the high values of R95p in the historical period are mainly located in the southwest and southeast regions, and the low values are concentrated in the northwest around Weining, with extreme differences of 271.04 mm, 372.85 mm, 516.12 mm, and 632.49 mm, respectively; the high and low values of R95p in the future period are located in the southeast and northwest, with extreme differences of 105.41 mm, 147.94 mm, 164.13 mm, 179.60 mm, respectively. The spatial distribution of extreme rainfall under each recurrence period is similar to that of the non-recurrence period, indicating that it is also influenced by the structure of the subsurface. In addition, the extreme rainfall extremes were larger in the historical period than in the future period, indicating that rainfall extremes varied widely across Guizhou in the historical period, while regional rainfall extremes were comparable in the future period.

Fig. 8
figure 8

R95p recurrence spatial distribution. Map was created with ArcGIS version 10.8 (https://www.arcgis.com/).

Full size image

Characteristics of temperature change in Guizhou Province

Temporal evolution of temperature characteristics

The average annual temperature of Guizhou in the historical period ranged from 15.23 to 16.57 °C, and the average multi-year temperature was 15.99 °C(Fig. 9); the average annual temperature in the future period ranged from 15.16 to 17.66 °C, and the average multi-year temperature (16.53 °C) was larger than that in the historical period. In terms of time trend, the average annual temperature in Guizhou during the historical period showed a significant upward trend, with an increase rate of 0.02 °C/a (p < 0.01), which is similar to the national average warming rate (0.026 °C/a) and the global average warming rate (0.0202 °C/a)30; Mean annual temperatures also show a significant upward trend in the future period, rising at a rate of 0.03 °C/a (p < 0.01), the average annual temperature in the future period also shows a significant upward trend, with a rate of increase of 0.03 °C/a (p < 0.01), which is faster than the rate of increase in the historical period, and is close to the rate of increase in global temperatures in the SSP245 scenario (0.0322 °C/a)31. Overall, the temperature in Guizhou from 1990 to 2100 shows a trend of slow increase (historical period)-slowdown (early future period)-and rapid increase, which is consistent with the trend of the temporal evolution of extreme rainfall. This may be due to the fact that GHG emissions under the SSP245 scenario are influenced by anthropogenic factors in the context of a warming climate, leading to a slowdown in warming in the early part of the future period, but the overall temperature is still on an upward trend.

Fig. 9
figure 9

Temperature time change trend.

Full size image

Characteristics of the spatial distribution of temperature

Guizhou temperature in the historical period was “high in the south and low in the north, high in the east and low in the west” spatial distribution pattern (Fig. 10), and in the future period, the high value of temperature shifted to the southeast, showing a “high in the southeast and low in the northwest” spatial distribution pattern. The spatial distribution of temperature and the spatial distribution pattern of extreme rainfall are similar in both periods, which suggests that there is a relationship between temperature and extreme rainfall. In addition, the low value of temperature in the historical period is concentrated in the northwest Weining area, with the lowest value of 11.15 °C; the high value of the center of the south Luodian, Wangmo, the highest value of 19.94 °C, the extreme difference of 8.79 °C. The range of high temperatures in the coming period is wider than in the historical period, with the maximum (18.30 °C) occurring in Libo; the range of low values is narrower, still located in the northwestern part of the country near Weining, and the minimum (14.38 °C) is higher than in the historical period, with the extreme difference (3.92 °C) diminishing. It indicates that under the SSP245 scenario, the regional temperature in Guizhou has increased and the temperature difference between locations has decreased.

Fig. 10
figure 10

Spatial distribution of temperature in historical and future periods. Map was created with ArcGIS version 10.8 (https://www.arcgis.com/).

Full size image

Response of extreme rainfall to changes in temperature

In order to explore the response structure of extreme rainfall to temperature change, the average extreme rainfall intensity within the temperature interval of 1 °C in the whole of Guizhou and under different subsurface conditions in the historical and future two periods were counted, and the climate response characteristics of extreme rainfall in Guizhou were derived based on the changes.

Strength of extreme rainfall response to temperature change

Most of the response strengths of extreme rainfall to temperature in Guizhou are greater than 7%/°C on a super-C–C scale (Fig. 11). There are differences in the response strength in different periods and under different subsurface structures. The intensity of the response of extreme rainfall to temperature in the historical period was 7.32%/°C, which was slightly greater than 7%/°C. The intensity of the response of extreme rainfall to temperature in the future period was greater than in the historical period, at 11.85%/°C. This may be due to future warmer temperatures and increased atmospheric water-holding capacity32. Under different DEM levels, the response intensity in the historical period ranged from 8.47 to 11.73%/°C, with an average intensity of 9.62%/°C. The response intensity in the future period ranged from 10.90 to 14.82%/°C, with an average intensity of 13.37%/°C, which was enhanced compared with the historical period. The intensity of the response increased with increasing DEM level in both periods, which implies that the atmospheric water-holding capacity is stronger at higher elevations in Guizhou. Under different slope levels, the response intensity in the historical period ranged from 8.96 to 13.08%/°C with an average intensity of 11.25%/°C, while the response intensity in the future period ranged from 11.31 to 13.39%/°C with an average intensity of 12.20%/°C, which was larger than that in the historical period. The intensity of the response was maximized in both periods when the slope was level, indicating that the atmospheric water-holding capacity was stronger in the region with steeper slopes. Under different aspect conditions, the response intensity in the historical period ranged from 6.70 to 16.66%/°C, with an average intensity of 10.55%/°C, and the response intensity was slightly lower than 7%/°C only in the southeastern slope direction, which was on a sub-C–C scale; and in the future period, the response intensity ranged from 9.30 to 13.38%/°C, and the average intensity (11.41%/°C) was also enhanced compared with that in the historical period.

Fig. 11
figure 11

Summary of the intensity of the response of extreme rainfall to changes in temperature.

Full size image

Structure of extreme rainfall response to temperature change

Extreme rainfall in Guizhou generally shows a Hook response structure: when the temperature is below the peak temperature, extreme rainfall strengthens with increasing temperature; when the temperature is overheated and above the peak temperature, extreme rainfall shows a weakening trend (Fig. 12). However, there are differences in Hook morphology due to different climatic characteristics at different times and different moderating effects of different subsurface structures on climate. Extreme rainfall in Guizhou in the historical period occurs at temperatures ranging from 3 to 25 °C, with a peak point temperature of 22 °C, corresponding to an extreme rainfall intensity of 2.39/mm·d−1; in the future period, it occurs at temperatures ranging from 7 to 27 °C, with the peak point temperature (25 °C) increasing by 3 °C compared with that of the historical period, and the intensity of the extreme rainfall is enhanced compared with that of the historical period, at 2.51/mm·d−1. This suggests that future warming may lead to a rightward shift in the climate response structure and enhance extreme rainfall intensity11. Extreme rainfall in the historical period generally occurred between 2 and 28 °C and extreme rainfall in the future period generally occurred between 5 and 28 °C under different subsurface conditions. Under different DEM levels, the peak temperatures corresponding to level2, level3, and level4 in the historical period are 23 °C, 23 °C, and 20 °C, respectively; and the peak temperatures corresponding to level2, level3, and level4 in the future period are 26 °C, 25 °C, and 24 °C, respectively. Peak point temperatures increased with decreasing DEM class in both periods, and the climate response structure shifted rightward with decreasing DEM class. This may be due to the fact that the lower the elevation and the higher the temperature, the climate response structure moves in the direction of warming. For different slope classes, the peak temperature is 22 °C at level1 in the historical period and 21 °C under the rest of the classes; the peak temperature is 26 °C at level1 in the future period and 25 °C under the rest of the classes. Peak point temperatures ranged from 19 to 23 °C in the historical period and from 24 to 26 °C in the future period under different slope orientation conditions. It can be seen that there is no significant correlation between wind power temperature and slope and direction. In addition, as the climate warms, peak point temperature increase of about 3 °C under different subsurface conditions, with a rightward shift in the response structure, the same as the overall characterization.

Fig. 12
figure 12

Structure of the response of extreme rainfall to temperature change.

Full size image

Discussion

The structure of the subsurface has a significant impact on the formation of regional microclimate and precipitation, which in turn affects the formation of extreme rainfall and its response to changes in air temperature. In this paper, we analyze the characteristics of extreme rainfall in Guizhou Province in the historical and future periods from the regional subsurface structure, and discuss the relationship between the response of extreme rainfall to air temperature in the two periods under different subsurface conditions. The study found MME to be the best for climate simulation in Guizhou Province when preferring CMIP6 model data, after Park33, Swain34 and others have confirmed the credibility of the data features observed by MME. The temporal characteristics of extreme rainfall in Guizhou Province are consistent with the results of Feng20 and Zhang35, et al. and show the trend characteristic of a faster rise in the future period than in the historical period. Spatially, the high values of extreme rainfall in Guizhou mainly occur in the southeastern part of the region, and the low values occur in the northwestern part of the region, which is inextricably related to the structure of the subsurface of Guizhou Province. The western part of Guizhou Province has the high-elevation Wumeng Mountains, which make it difficult for water vapor to enter, while the southeastern part has a lower elevation and belongs to the windward slopes, which have sufficient regional water vapor and are prone to form rainfall. In addition, the center line of the extreme rainfall box plot in Guizhou Province is not located in the middle of the box, showing a skewed distribution. Optimization of the distribution functions of the weather stations also reveals that the optimal distribution functions of most stations are not normally distributed. Therefore, when exploring the characteristics of regional extreme rainfall return periods, it is necessary to seek the optimal distribution functions of meteorological stations to obtain accurate return period values.

It has been shown that extreme rainfall and temperature are controlled by the C–C equation, and in this paper, when exploring the relationship between extreme rainfall and temperature in Guizhou Province with the help of C–C, it is found that most of the response strengths of extreme rainfall to temperature in Guizhou are on the super-C–C scale. This may be due to the fact that Guizhou Province has a monsoon climate and the structure of the subsurface exhibits a low southeast and high northwest, and the windward slope at low elevations, which allows for the smooth transport of the South China Sea water vapor transport, resulting in sufficient regional water vapor. In addition, Gao36 found a super C–C relationship between extreme rainfall and temperature at most stations in mainland China. Similar to the results of Yin37 and Gao38 extreme rainfall in Guizhou Province showed a Hook response structure to temperature changes in both periods, which deviated from the expected results of the C–C equation. This may be caused by the suppression of rainfall amount and rainfall duration as atmospheric moisture content decreases with increasing temperature. Peak point temperatures in the future period were all about 3°C higher than in the historical period for different subsurface conditions, suggesting that higher peak point temperatures, driven by future warming, lead to a shift of the Hook curve in a warmer direction39,40. It is worth noting that DEM level and peak point temperature show a negative correlation, with the climate response structure shifting to the right as DEM level decreases. This may be due to the fact that at lower elevations and higher temperatures, the climate response structure moves closer to the warmer end of the spectrum.

Extreme rainfall has a serious impact on the economic development and environmental protection of Guizhou Province, and this study uses annual-scale indicators to analyze its characteristics, which will weaken the characteristic information to some extent, and the results are not fine enough. In addition, rainfall duration (hourly, daily, and multi-day) also affects the response structure, and to further clarify the mechanism of its occurrence, extreme rainfall at different time scales can be included for a more in-depth and comprehensive discussion.

Conclusion

To investigate the characteristics of extreme rainfall and its response to temperature change, this paper grades the structure of Guizhou's subsurface, based on which it analyzes the characteristics of Guizhou's extreme rainfall in the past and future periods under different subsurface conditions and explores the response mechanism of extreme rainfall to temperature change, and obtains the following conclusions:

  1. 1)

    Extreme rainfall in Guizhou in both the historical and future periods showed an increasing trend under all subsurface conditions, with the rate of increase in the future period being faster than that in the historical period, and the overall trend showing a slow increase (historical period)-a slowdown (early in the future period)-a rapid increase; Spatially, the distribution of extreme rainfall in the historical period was characterized by " high in the south and low in the north, high in the east and low in the west ", while in the future period, the high value of extreme rainfall shifted to the southeast, showing a spatial distribution pattern of " high in the southeast and low in the northwest ".

  2. 2)

    The Weibull, Gamma function is the optimal distribution function for the 71% and 81% site R95p for the historical and future periods, respectively; R95p estimates increase with increasing recurrence period in both periods, but extreme rainfall is more severe in the historical period than in the future period; the pattern of R95p distribution under each recurrence period is consistent with the non-recurrence period.

  3. 3)

    Guizhou shows an increasing trend in temperature in both the historical and future periods, with the future scenario showing a larger rate of increase than the historical period, and the overall trend of slow increase (historical period)-slowdown (early in the future period)-rapid increase; the spatial distribution of temperature in the two periods is similar to the pattern of distribution of extreme rainfall.

  4. 4)

    Hook response structure of extreme rainfall to temperature in different periods and under different subsurface conditions, and in the context of future warming, the peak point temperature increases by about 3 °C, and the climate response structure is shifted rightward; The change in extreme rainfall intensity with increasing temperature is greater than the C–C rate for all conditions except for the southeastern slope direction during the historical period, and the intensity of the response is greater under the future scenario than during the historical period.