Introduction

The northern Guizhou coalfield, the third largest coalfield in Guizhou, boasts abundant coal reserves1,2. The primary mining seam in this area is the No. 9 coal seam. Owing to the proximity of the coal seam roof to the underlying aquifer boundary, which is typically less than 80 m, and the extensive development of karst formations in the region, the karst aquifer exhibits high water yield characteristics3,4,5. During mining operations, there is a risk of connecting with the overlying Changxing Formation aquifer, leading to multiple water inrush incidents. Therefore, understanding the development patterns of water-conducting fracture zones and the mechanisms of water inrush in this region is crucial for ensuring safe mining practices.

Many scholars have researched the characteristics of overlying strata damage and the mechanisms of roof water inrush disasters, achieving beneficial results. The "key stratum"6,7, "cantilever beam"8, and "upper three zones"9 theories have been widely recognized in the field of geotechnical engineering. These theories have guided the prediction of overlying strata movement10,11, stability control of overlying strata12,13,14, and mine pressure prevention and control15 in engineering applications. Similar simulation experiments are a common method used to study the deformation and failure patterns of overlying strata. Liao et al.16 studied the deformation and failure patterns of steep coal seam roofs through similar simulation experiments, dividing the postmining fracture zone from the stable zone. Zhang et al.17 developed a brittle similar simulation material to analyse the movement characteristics of mining strata. Dong et al.18 used similar simulation experiments to study the effects of different rock ratios and joint fractures on overlying strata deformation and failure.

In recent years, with the development of computer technology, numerical simulations have been widely used to simulate and analyse the stress fields, displacement fields, and fracture field evolution characteristics of working faces19,20,21,22. Li et al.23 simulated the effect of the dip angle of a deeply buried ore body on the stress of a mining field, and reported that when the dip angle is 30°, the roof is most susceptible to shear failure. Cao et al.24 studied the effect of fault activation on the development height of water-conducting fracture zones via FLAC3D. Furthermore, in the prediction of the development height of water-conducting fracture zones, scholars have proposed methods such as neural networks25,26,27, grey theory28, and factor analysis29, enriching existing theories.

The core of mine water inrush lies in the water inrush source and water filling intensity. Ji et al.30 studied the mechanism of roof water inrush in Jurassic coalfields and determined the optimal position for mine drainage. Li et al.31 analysed the mechanism of roof water inrush disasters in the Hongliu Coal Mine via a combination of borehole colour TV imaging and numerical simulation. Wang et al.32 studied the dynamic evolution law of roof water hazards under different mining sequences and proposed water prevention and control measures.

These achievements have enhanced theories on the deformation and failure of overlying strata and the mechanisms of water inrush disasters. However, there is a lack of relevant research focused on the thick limestone aquifers beneath the Qianbei coalfield, as well as a quantitative calculation model for the development height of water-conducting fracture zones under these geological conditions. Therefore, this study takes the representative Longfeng Coal Mine in the Qianbei coalfield as the typical research object. Building upon a systematic analysis of overlying strata structural features, a calculation model for the development height of water-conducting fracture zones is established by calculating the stratum stretching rate. Through numerical simulations, the characteristics of overlying strata deformation and failure within the mining area are analysed. By employing similar simulations combined with digital speckle technology, this study investigates the development patterns and spatiotemporal evolution of water-conducting fracture zones under the influence of coal seam roof mining, and analyse the strain evolution characteristics and key stratum instability effects during mining. Additionally, field measurements of water-conducting fracture zones are conducted. Finally, a coal seam roof water inrush disaster model specific to the Qianbei coalfield is proposed. This research provides significant reference value for enhancing water prevention and control measures in mines throughout the region.

Engineering background

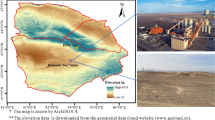
The Longfeng Coal Mine is located in the northern Guizhou Plateau, where karst formations are well developed and heterogeneous. The stratigraphic sequence in the mining area, from oldest to youngest, includes the Maokou Formation, Longtan Formation, Changxing Formation, and Yelang Formation (Shabaowan Member, Yulongshan Member, and Jiujitan Member). The Changxing Formation and Yulongshan Member act as aquifers in the mining area and have good water-bearing properties. Additionally, the Shabaowan Member serves as a relatively thin aquitard, creating complex "aquifer-aquitard-aquifer" sandwich-like hydrogeological conditions, as illustrated by the 3D geological model in Fig. 1. Notably, in the central part of the mining area, the Shabaowan aquitard is missing, resulting in the Changxing Formation being exposed in a banded distribution, which facilitates direct recharge of the aquifer by atmospheric precipitation, reducing the effectiveness of the aquitard.

Fig. 1
figure 1

3d geological model.

Full size image

Moreover, the main mining seam in the current mining area is the No. 9 coal seam, and the overlying Longtan Formation aquitard has a thickness ranging from 29.6 to 52.4 m, with an average thickness of 39 m. During mining, it is easy to connect to the overlying Changxing Formation aquifer and even establish a hydraulic connection with the Yulongshan Member aquifer, causing water inrush into the working face and threatening operational safety33. Therefore, the 120,907 working face, located in an area with a weak aquitard, was selected as the key research area to study the development patterns of the water-conducting fracture zone and the mechanisms of water inrush, which is highly important for ensuring safe mining operations.

Roof overlying strata structure and fracture characteristics

Identification of key stratum positions

The roof overlying strata structure in the Longfeng Coal Mine exhibits interlayer characteristics of soft and hard rocks, with aquicludes mainly composed of sandstone and mudstone. Extensive engineering practices have shown that a relatively thick and hard rock layer above the coal seam roof serves as the main carrier of the overlying strata load, controlling the transfer and movement of loads between different rock layers. This layer is referred to as the key stratum34,35,36. Determining the number and position of key strata is highly important for studying the structure and fracture characteristics of overlying strata. To determine the number and position of key strata, the following steps can be taken:

Assume that there are m layers of rock above the coal seam roof subjected to a uniform load q and that the first layer is a hard rock layer. To determine the load exerted by the overlying n layers on the first hard rock layer, the load for each layer is calculated incrementally. When the load from the (n + 1)-th layer on the first hard rock layer is less than the load from the n-th layer, the (n + 1)-th layer is considered the second hard rock layer. The n layers below it do not need to bear its load. At this point, the deformation from the first layer to the n-th layer is coordinated and can be regarded as a composite beam. The load acting on the first hard rock layer can be expressed as:

$$ (q_{n} )_{1} = \frac{{E_{1} h_{1}^{3} \mathop \sum \limits_{i = 1}^{n} h_{i} \gamma_{i} }}{{\mathop \sum \limits_{i = 1}^{n} E_{i} h_{i}^{3} }} $$
(1)

where, (qn)1 is the load of the n-th rock layer on the first rock layer, MPa; Ei is the Young's modulus of the i-th overlying layer, GPa; hi is the thickness of the i-th layer, m; and hi is the thickness of the i-th layer, kN/m3.

The load from the (n + 1)-th layer on the first hard rock layer is given by:

$$ (q_{{{\text{n}} + 1}} )_{1} = \frac{{{\text{E}}_{1} h_{1}^{3} \mathop \sum \limits_{i = 1}^{n + 1} h_{i} \gamma_{i} }}{{\mathop \sum \limits_{i = 1}^{n + 1} {\text{E}}_{i} h_{i}^{3} }} $$
(2)

If the (n + 1)-th layer is assumed to be the second hard rock layer, then its deformation curvature is less than that of the underlying layers from 1 to n, and it does not require the underlying n layers to bear its load. At this point, the criterion for identifying the second hard rock layer is as follows:

$$ \left( {q_{n + 1} } \right)_{1} < \left( {q_{n} } \right)_{1} $$
(3)

After the second hard rock layer is identified, the same calculation and identification process is applied from this layer onwards to determine the position of the third hard rock layer until all hard rock layers are identified. At this point, all other layers, apart from the hard rock layers, are considered relatively weak layers, whose deformation and failure are controlled by the hard rock layers.

Once the number and positions of the hard rock layers are determined, according to the key stratum principle, the fracture span of the lower hard rock layer should be smaller than that of the upper hard rock layer. If the span of the lower layer exceeds that of the upper layer, the load borne by the upper hard rock layer should be transferred to the lower hard rock layer, and the failure step distance should be recalculated. Notably, when the upper hard rock layer fractures, the lower hard rock layer subsequently fractures. The fracture span of the hard rock layers can be determined via the following formula:

$$ L_{s} = h_{s} \sqrt {\frac{{2R_{s} }}{{(q_{n} )_{s} }}} (s = 1,2, \cdots ,k) $$
(4)

where hs represents the thickness of the s-th layer of hard rock, m; Rs represents the tensile strength of the s-th layer of hard rock, MPa; and (qn)s represents the load imposed on the s-th layer of hard rock by the n-th layer, MPa.

According to the key stratum fracture span discrimination principle, the fracture span of the (s + 1)-th layer of hard rock should be greater than that of the s-th layer of hard rock, as follows:

$$ L_{{\text{s}}} < L_{{{\text{s}} + 1}} $$
(5)

According to the key stratum discrimination steps, taking the 120,907 working face as an example and considering the lithological characteristics of nearby boreholes 401 and 402, the key stratum position of the roof of the No. 9 coal seam is determined. The rock layer parameters are shown in Table 1.

Table 1 Roof lithology characteristics of 120,907 face.
Full size table

After the number and positions of the hard rock layers are calculated separately and their failure step distances are compared, four key strata in the roof overlying the 120,907 working face of the Longfeng Coal Mine are determined, as shown in Table 2.

Table 2 Breaking steps of each hard rock layer.
Full size table

The sub-key stratum 1 with a failure step distance of 5.07 m and key stratum 2 with a failure step distance of 4.48 m have small difference, and their elevation differences is only 6.31 m. During the mining process of the working face, they will break successively. However, the limestone of the Changxing Formation has a greater failure step distance and thicker layer position, making it the primary key stratum of the roof overlying the 120,907 working face. It directly controls the movement of the layers above it to the surface. Since the mining length of the 120,907 working face is 580 m, which is less than the failure step distance of hard rock layer 4, this hard rock layer will not break during the mining process of the 120,907 working face.

Roof overlying strata fracture characteristics

After the characteristics of the roof overlying strata are determined, the top strata of the No. 9 coal seam in the Longfeng Coal Mine can be divided into four stratum groups. The deformation and fracture behaviour of each stratum group are controlled by the key stratum at the bottom of each stratum group. When the coal seam is mined, free space is created directly below the roof, which can be viewed as a beam fixed at both ends. The rock strata are subjected to bending and fracture due to the combined effect of their own weight and overlying load. Compared with the original state (Fig. 2a), the middle region of the rock strata experiences deformation due to layer-to-layer stretching (Fig. 2b). During this process, the tensile force on the rock strata gradually increases. When the tensile strength of the rock strata is exceeded, cracks form (Fig. 2c). As the amount of subsidence increases, the degree of crack penetration continuously increases. When the degree of penetration is significant enough, the cracks become permeable, thus falling into the range of water-conducting fracture zones.

Fig. 2
figure 2

Process of stretching and deformation of rock strata. (a) Embedded solid sorghum. (b) Tensile deformation. (c) Breaking deformation.

Full size image

By establishing the relationships between the stratum stretching rate of rock layers and their position, mining thickness, and lithology, it is possible to determine the fracture law of overlying strata and establish a quantitative formula for determining the development height of water-conducting fractures in roof strata. Assuming the original length of a rock layer before tension is L0 and that the length after tension is L1, the deformation of the rock layer due to loading-induced sinking and tension is illustrated in Fig. 3.

Fig. 3
figure 3

Geometric diagram of rock stratum bending and subsidence.

Full size image

On the basis of the previous analysis, L1 > L0. Here, L1 is not only the length of the rock layer but also the width of the fractures. The tensile strain rate ε can be represented by Eq. (6):

$$ \varepsilon = (L_{1} - L_{0} )/L_{0} $$
(6)

where, L1 represents the length of the intermediate rock layer after stretching, and L0 denotes the length before stretching.

The above figure shows that \(L_{0} = AD + DB\). On the basis of trigonometric functions, we can derive the following:

$$ L_{0} = h(\cot \delta + \cot \psi ) $$
(7)

where, h is the vertical distance from the middle layer of the rock stratum to the coal seam roof; δ is the fully exploited angle; ψ is the boundary angle, approximately equal.

When determining the value of L1, it can be assumed that L1 is composed of two segments of circular arcs with the same radius r and opposite curvature, thus:

$$ CF = 2r,CG = BC + BG = r + BG = r + (r - w_{0} ) $$
(8)
$$ CF^{2} = CG^{2} + L_{0}^{2} = (2r)^{2} = (r + (r - w_{0} ))^{2} + L_{0}^{2} $$
(9)
$$ \beta = arcsin\frac{{L_{0} }}{2r} $$
(10)

By substituting Eq. (7) into Eqs. (9) and (10), the values of r and β can be solved simultaneously as follows:

$$ r = \frac{{w_{0}^{2} + L_{0}^{2} }}{{4w_{0} }} $$
(11)
$$ \beta = \arcsin \frac{{2w_{0} \cdot L_{0} }}{{w_{0}^{2} + L_{0}^{2} }} $$
(12)

where, w0 represents the maximum subsidence of the rock strata.

w0 can be calculated via the following equation:

$$ w_{0} = m \times q $$
(13)

where, m represents the thickness of the coal seam, and q represents the subsidence coefficient of the rock layer.

Assuming that the subsidence coefficient at the surface is q0 and that the coal seam roof is 1, we approximate that the subsidence from the coal seam roof to the surface decreases linearly. Therefore, the subsidence coefficient of the rock layer at height h is given by:

$$ q = 1 - \frac{{h(1 - q_{0} )}}{H} $$
(14)

where h represents the elevation of the rock layer, and H indicates the depth of the coal seam.

The equation \(L_{I} = \frac{2r\beta \pi }{{180}}\), when combined with Eqs. (1) to (10), leads to:

$$ L_{1} = \frac{{\beta \pi {\text{(w}}_{0}^{2} { + }L_{0}^{2} )}}{{360{\text{w}}_{0} }} $$
(15)

The magnitude of the stratum stretching rate is related to factors such as the rock stratum elevation, subsidence coefficient, coal seam depth, full exploited angle, boundary angle, and mining height, as revealed by the combined equations.

The mining depth of the 120,907 working face is 187.79 m, and the overall rock hardness is moderately hard. Referring to the "Specification for Coal Pillar Retention and Coal Mining in Buildings, Water Bodies, Railways and Main Wells and Alley"37, the surface subsidence coefficient under medium-hard strata conditions ranges from 0.55 to 0.84. Considering the actual conditions in the mining area, this paper adopts q0 = 0.75, and cotδ = cotψ = 0.62. According to Table 1, which describes the roof rock characteristics, the calculation yields the roof stratum stretching rate for the key stratum of the 120,907 working face as shown in Table 3.

Table 3 Calculation results of key stratum tensile ratios.
Full size table

The stratum stretching rate decreases gradually with increasing stratum elevation. The stratum stretching rate reaches 50.794% in sub-key stratum 1, indicating severe stratum stretching deformation and significant stratum fracturing and collapse. This stratum can be classified into the collapse zone. The stratum stretching rate in key stratum 2 is 1.657%, indicating that the stratum still experiences fracturing but with relatively good development of fractures at this elevation. For the primary key stratum, the stratum stretching rate is 0.132%. Studies38 have shown that the stratum stretching rate of the water-conducting fracture zone in the weak rock layer is greater than 0.40%. In medium-hard strata, the stratum stretching rate ranges from 0.1 to 0.24%, whereas in hard strata, it is approximately 0.04%. This indicates that the stratum fracturing phenomenon gradually ceases at this elevation, and a water-conducting fracture zone develops within the 38.53 m thick limestone of the primary key stratum. Furthermore, in the upper strata, the stratum stretching rate becomes negative, indicating that these strata will no longer experience stretching and sinking deformation. The stratum stretching rate is effectively 0, indicating that it has exited the water-conducting fracture zone category. The degree of stratum fracturing is positively correlated with the stratum stretching rate.

Owing to the differences in the failure step distance and degree of fracturing between key strata, each controls the deformation and settlement patterns of weak strata differently. This leads to stratum separation during the advancement of the working face, creating storage space for water in the roof strata, which could lead to roof water inrush accidents when the water-conducting fracture zone penetrates the height of separated strata. Therefore, determining the development height of the water-bearing fracture zone is particularly crucial.

Derivation of the theoretical development height of the roof water-conducting fracture zone

From the above, it can be inferred that the water-conducting fracture zone extends into the Changxing Formation limestone. However, the upper boundary of the water-conducting fracture zone remains undetermined. After coal mining, free space exists beneath the roof, which leads to initial fracturing and collapse under the load of the overlying strata. This results in accumulation within the free space, accompanied by subsidence of the overlying strata. As a consequence, water-conducting fractures develop upwards. As the roof rock collapses and settles, filling the entire free space, the overlying strata cease to subside and reach stress equilibrium. Consequently, the water-conducting fracture zone no longer extends upwards. Hence, the development height of the water-conducting fracture zone can be determined by calculating the remaining free space beneath the roof rock.

After rock fracture and fragmentation, there is a phenomenon of volumetric expansion, where the volume of the fractured rock that fills the free space is greater than the volume of the intact rock before fracture. This volumetric expansion capacity of rock is represented by the expansion coefficient, which directly determines the movement and subsidence characteristics of the overlying strata. Taking main roof i as an example, the free space below it can be determined via Eq. (16)39:

$$ {\Delta }S = M - \mathop \sum \limits_{i = 1}^{n} h_{i} (K_{i} - 1) $$
(16)

where M is the mining height of the coal seam, hi is the thickness of layer i, and Ki is the expansion coefficient of layer i.

The expansion coefficient of rock layers is related to the properties of the rock itself and factors such as loading. As the position of the rock layer increases, the blockiness of the fractured rock mass gradually increases, and the expansion coefficient of the rock layer decreases logarithmically. The relationship between the expansion coefficient of the rock layer and the height of the rock layer can be determined via Eq. (17)40:

$$ K_{i} = 1.11 - 0.017InH $$
(17)

where, H represents the height of the rock layer.

Substituting Eq. (17) into Eq. (16), we obtain:

$$ {\Delta }S = M - \mathop \sum \limits_{i = 1}^{n} h_{i} (1.11 - 0.017InH - 1) $$
(18)

The stratum height of the middle layer is used as the value for H, and the amount of free space below each stratum after fracture is calculated according to Eq. (18), as shown in Table 4.

Table 4 Free space filling amount of each rock formation.
Full size table

As the stratum position increases, the expansion coefficient of each stratum gradually decreases. After the complete fracture of the 38.53 m thick limestone layer, the free space below reaches − 0.73 m, indicating that the stratum has not fractured to the top of the Changxing Formation. When the free space below is completely filled, the stratum position is estimated to be 51.37 m. At this point, the overlying strata of the roof are supported from below, ceasing to sink and gradually stabilizing, leading to the cessation of fracture development. Therefore, the theoretical development height of the water-conducting fracture zone in the roof of the 120,907 working face of the Longfeng Coal Mine is 51.37 m, penetrating 56.79% of the thickness of the aquifer in the Changxing Formation and meeting the conditions for roof water inrush.

Development patterns of the roof water-conducting fracture zone

Deformation and failure patterns of the top rock roof

Through detailed modelling of the 120,907 working face, a numerical simulation model was constructed, as illustrated in Fig. 4. The model measures 450 m in length and 300 m in width, comprising 563,251 grid points. The grid density increases closer to the mining area. The model simulates the entire depth to the surface and is influenced solely by self-weight. The No. 9 coal seam is fully extracted in one operation, with a working face length of 180 m. The bottom of the model is defined as a "fixed constraint", restricting deformation in three-dimensional space, meaning that the displacement is zero. The top is set as a free boundary surface. The sides of the model are defined as "roller boundaries", allowing vertical displacement only, with horizontal displacement being zero. Protective coal pillars are left on all sides of the model to eliminate boundary effects. The model is excavated step-by-step until equilibrium is achieved, advancing 10 m each time for a total of 200 m. Monitoring lines are arranged along the excavation direction at the sub-key stratum (immediate roof) and key stratum 2 (main roof) to collect stress and displacement data during the excavation process. Each monitoring line contains 21 measurement points, with intervals matching the excavation step distance.

Fig. 4
figure 4

Numerical simulation model.

Full size image

After coal seam extraction, the original stress equilibrium is disrupted, leading to stress redistribution as depicted in Fig. 5a. Stress concentrations occur at the face of the advancing working face and in the open cut area, causing the stress concentration factor at the immediate roof to increase from 1.17 to 1.44. Post excavation, the pressure at the immediate roof stabilizes approximately 2.7 MPa. As the working face progresses, the peak stress ahead of the face gradually decreases from 5.82 to 5.05 MPa. The peak stress at Sub-Key stratum 2 is lower than that at the immediate roof, exhibiting some lag as shown in Fig. 5b. This is primarily due to the lower vertical stress at this location and the stability of the key stratum structure.

Fig. 5
figure 5

Numerical simulation model. (a) Stress evolution contour map. (b) Vertical stress distribution of working face under different advancing distance.

Full size image

The overall top roof of the goaf area experiences subsidence, whereas the bottom roof experiences uplift, as shown in Fig. 6a. After stabilization of the extraction face, influenced by the original rock stress distribution, the maximum displacement of the roof occurs approximately 50 m into the goaf area and continues to increase, whereas the maximum displacement of the bottom roof decreases as the working face advances. The maximum vertical displacement of the immediate roof is 0.49 m, and that of key stratum 2 is 0.27 m, as depicted in Fig. 6b. The displacement curve of the immediate roof can be divided into a middle subsidence segment and two end bending deformation segments, indicating a pronounced beam constraint effect. The displacement change curve at key stratum 2 is smoother, indicating more stable rock movement in this area, essentially departing from the collapse zone range, with predominant damage in the form of extraction fractures. Additionally, with the advancement of the working face, the increase in subsidence of the top roof gradually decreases, indicating that the deformation and failure of the overlying rock of the mining face are approaching stability.

Fig. 6
figure 6

Numerical simulation model. (a) Displacement evolution contour map. (b) Vertical displacement distribution of working face under different advancing distance.

Full size image

During the initial advancement of the working face, the main failure mode of the top rock roof is shear failure, which gradually transitions to a mixed mode of shear and tensile failure. Overall, the plastic zone of the top roof shows a "stepped" growth characteristic, as illustrated in Fig. 7. Owing to the boundary of the goaf providing support to the overlying rock above the mining area, as the working face advances, this support continuously shifts forwards. This results in reduced support in the central part of the goaf, exacerbating the damage to the overlying rock above it. Consequently, the plastic zone develops upwards, and the subsidence of the roof increases. As the working face advances, the rear part of the goaf area gradually compacts, and under the effect of beam constraints, roof failure primarily occurs in the middle of the goaf area.

Fig. 7
figure 7

Development height evolution of water flowing fractured zone.

Full size image

The evolution of the water-conducting fracture zone development height, using the highest point of the plastic zone, goes through three stages: slow growth, rapid growth, and stable growth. The slow growth stage mainly occurs within the mining interval of 0–30 to 30 m, which is caused primarily by immediate roof collapse, with the collapse zone measuring approximately 9.2 m. The rapid growth stage occurs within the mining interval of 30–110 m. At this point, key stratum 2 reaches its limit of failure step distance, leading to instability, and the overlying soft rock layers experience coordinated settlement deformation, resulting in their rupture and a rapid increase in the development height of the water-conducting fracture zone. When the working face advances to 90 m, the primary key stratum becomes unstable, applying impact loads to the underlying rock layers, which rapidly increases the development height of the water-conducting fracture zone by 36.68%. The water-conducting fracture zone subsequently develops into the primary key stratum and gradually stabilizes, finally determining the development height of the water-conducting fracture zone to be 49.17 m. Since the Changxing Formation is a strong aquifer, water-conducting fractures may serve as long-term water channels, leading to roof water inrush or water accumulation in the goaf area.

Spatiotemporal evolution characteristics of the water-conducting fracture zone

Using a two-dimensional similarity simulation platform, the model size is 1.5 m × 0.25 m × 1.2 m (length × width × height). On the basis of factors such as the overlying rock structure, coal seam height, mining face parameters, and dimensions of the similarity simulation platform, the geometric similarity ratio of the model was determined to be \(C_{l} = 140\), with a simulated cross-sectional height of 168 m, a density similarity ratio of \(C_{r} = 1.7\), and a time similarity ratio of \(C_{{\text{t}}} = 12.65\). A compensating load was applied above the model, the simulation materials included sand as the aggregate and gypsum and lime as binders, and the water mass accounted for 1/9 of the total rock mass. The proportions of similar materials for each rock layer are shown in Table 5, with mica powder used as the interlayer material. After the similarity model was constructed, it was air-dried for 21 days, and digital speckle points were marked on the surface to facilitate analysis of strain evolution during the mining process via an XTDIC digital speckle system. The experimental process is shown in Fig. 8.

Table 5 Ratios of similar materials in different rock layers.
Full size table
Fig. 8
figure 8

Flowchart of similar model construction.

Full size image

Simulated excavation of the No. 9 coal seam was conducted, considering boundary effects by leaving 30 cm coal pillars on both sides of the model. The full-height mining was carried out in one step, and high-definition cameras from the speckle system were used to photograph and record the process. After excavation, the simulation results were analysed for strain.

When the working face advanced to 30 m, as shown in Fig. 9a, the main roof (key stratum 2) exhibited a typical supported beam structure, with slight bending and sinking, approaching the ultimate tensile strength and fracture. At this point, discontinuous fractures appeared above the main roof, indicating uneven bending deformation between rock layers. However, owing to the small extent of the goaf, the suspended distance of the supported beam was not significant, and the soft rock layers above could still bear the load of the overlying strata, which had not yet fully acted on the immediate roof. As depicted in Fig. 9b, strains were observed within the goaf area, with the maximum strain occurring at the entry point of the excavation and the advancing face. Under the stress‒strain effect, the overlying rock continuously collapsed and accumulated into a "trapezoidal" collapse layer.

Fig. 9
figure 9

Development height evolution of water flowing fractured zone. (a) Immediate roof collapse. (b) Strain distribution. (c) Key stratum 2 instability. (d) Strain distribution.

Full size image

When the working face advanced to 60 m, as shown in Fig. 9c, the overall bending and deformation of the overlying weak rock strata occurred due to the fracturing of key stratum 2. At this point, the separation fractures between the weak rock layers gradually closed, generating new separation fractures below the Changxing Formation limestone. Because the Changxing Formation limestone is relatively thick and the similar simulation materials are strong and not easily fractured, a large range of separation fracture spaces is created. Additionally, owing to the instability of key stratum 2, a fracture line appeared on the left wing of the working face, causing the overburden from the main roof to press down. This led to a large-scale collapse of the roof overburden in a trapezoidal distribution, deteriorating the stability of the roof. Vertical fractures became more pronounced on both sides of the working face, but owing to premature detachment of the gypsum surface with speckle points during the experiment (Fig. 9d), the strains near the separation fractures could not be measured. Therefore, the maximum strain point was located mainly at the advancing face of the working face.

When the working face advanced to 80 m, as shown in Fig. 10a, the overlying rock structure became extremely unstable. Vertical fractures predominated in the water-conducting fracture zone, and the space of the separated strata above expanded continuously. At this stage, the primary key stratum begins to bear its own weight and the overlying rock load, leading to bending and sinking, as illustrated in Fig. 10b. The strains generated at the advancing face of the working face caused the weak rock layers in the roof to lose their supporting capacity. Parts of the weak rock layers above the coal seam collapsed successively, and the remaining weak rock layers reached their fracture limit and were nearly fractured.

Fig. 10
figure 10

Development height evolution of water flowing fractured zone. (a) Separated strata continues to increase. (b) Strain distribution. (c) Primary key stratum instability. (d) Strain distribution.

Full size image

When the working face advanced to 90 m, as shown in Fig. 10c, the primary key stratum experienced unstable fracturing. The space of the separated strata below reached its maximum and then rapidly decreased. Owing to the dynamic disturbance caused by the instability of the primary key stratum, the rock layers below it all fractured, leading to further development of the water-conducting fracture zone upwards. The maximum principal strain occurred in the area of newly formed fractures (Fig. 10d). At this point, the development of the water-conducting fracture zone stabilized, with a redistribution of the fracture morphology, primarily consisting of lateral fractures. This may be related to the impact load generated by the instability of the overlying rock layers, which causes sliding and shearing deformation in the underlying rock strata due to dynamic disturbances.

As the working face continues to advance, the collapsed rock layers below undergo fragmentation and deformation, gradually filling the space of separated strata in the mined-out area. The degree of downwards bending deformation of the primary key stratum is restrained, and almost no new strains are generated in the roof of the coal seam or at the mining boundaries. The entire fracture field tends to stabilize, leading to the cessation of water-conducting fracture development in this stratum.

Field validation

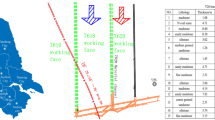
To validate the theoretical calculations and experimental results mentioned above, onsite measurements of the water-conducting fracture zone were conducted via a borehole imaging instrument, which provides images of the borehole wall rock layers, facilitating the analysis of fracture morphology and orientation. The field validation work took place in the main haulage roadway of the 120,907 working face, ensuring that the drill hole penetrated through the protective coal pillars and entered the goaf area beneath the roof. The drill hole was immediately cleaned, and the corresponding tests were conducted to prevent deformation of the drill hole from causing test failure. This approach facilitates the detection of the development of the water-conducting fissure zone within the goaf area beneath the roof. The designed borehole inclination angle was 74°, the borehole diameter was 94 mm, and the final depth reached 61 m. The field measurement results, as shown in Fig. 11, revealed three main types of fracture morphology above the mined-out area. The first type consists of intersecting tension‒shear fractures at lower strata levels, which exhibit strong water conductivity. These fractures are caused by significant stretching deformation in the lower strata layers, resulting in severe rock deformation. Additionally, instability in the overlying key stratum leads to shear displacement between fractured rock layers. The second type includes vertical or horizontal through-type fractures at intermediate strata levels, with moderate water conductivity. These fractures mainly result from fractures in key strata, further developing the water-conducting fracture zone upwards. The third type comprises discrete fractures at higher strata levels, with weak water conductivity. This type is influenced by reduced free space below, resulting in less stretching deformation at this strata level. Overall, the distribution pattern of the water-conducting fracture zone morphology observed in the field aligns with the results obtained from similar simulations.

Fig. 11
figure 11

Borehole imaging of roof overlying rock. (a) 5.8 m. (b) 10.5 m. (c) 18.3 m. (d) 22.7 m. (e) 27.4 m. (f) 42.7 m. (g) 47.5 m. (h) 53.1 m. (i) 55.4 m.

Full size image

Additionally, after coal seam mining, the overlying roof strata exhibit distinct "three-zone" distribution characteristics. This can be observed within the borehole depth range of 5.8–18.3 m, which can be categorized as the caving zone (figures a–c), where the rock layers show severe deformation and fracture, with large fracture apertures. The borehole depth range of 22.7–53.1 m can be classified as the fracture zone (figures d–h), where the fracture apertures gradually decrease with increasing borehole depth, transitioning from extensive rock cracking to localized nonpenetrating small fractures, resulting in reduced water conductivity. Above this zone, no significant fractures are observed, indicating the range of the bending subsidence zone.

Owing to the water-conducting fracture zone stabilizing at a borehole depth of 47.5 m (vertical height of 45.66 m), with the borehole wall becoming gradually smoother, and considering the theoretical calculation value of 51.37 m on the basis of the stratum stretching rate, the comprehensive determination of the actual height of the water-conducting fracture zone is 51 m (borehole depth of 53.1 m). This value closely aligns with the numerical simulation result of 49.17 m.

Mechanism analysis of roof water inrush in coal seams

The development type of separated strata is influenced by the lithology of the roof, the advancing time of the working face, and the amount of roof subsidence. The development and closure of separated strata are controlled by the failure step distance of the key stratum. The daily advancement of the 120,907 working face is 5.4 m/day. On the basis of the failure step distance of each key stratum, the duration of roof separated strata development is determined via Eq. (19), as shown in Table 6.

$$ T = \frac{\Delta L}{\nu } $$
(19)

where T is the duration of interface void development; ΔL is the difference in the failure step distance between adjacent key strata; and v is the advancing speed of the working face.

Table 6 Duration of fracture development under each key stratum.
Full size table

During the mining of the 120,907 working face, the 5.07 m thick siltstone above the coal seam first fractured and collapsed, forming "fracture-type" separation fractures beneath key stratum 2, as shown in Fig. 12. However, the fracture step distance of the 4.48 m thick fine sandstone of key stratum 2 is not significantly different from that of sub-key stratum 1. The separation fractures persist for only 0.59 days, and as the working face advances, these separation fractures are compacted and closed, having minimal impact on the working face.

Fig. 12
figure 12

"Fracture type" separation formation.

Full size image

After key stratum 2 fractured, it controlled the movement of all the rock layers above it down to the bottom of the Changxing Formation. Owing to the thickness of the limestone in the Changxing Formation, discordant deformation and movement of the underlying rock layers occurred, resulting in "cavity-type" separation fractures beneath the Changxing Formation, as shown in Fig. 13. Because the Changxing Formation has good water-bearing properties, water inrush sources collect within separation fractures through dissolution fractures and cavities within the Changxing Formation, serving as water channels. As the working face advances, the separation fractures continuously expand, generating hydrostatic pressure that reduces the effective water-resistant layer thickness. The water-conducting fracture zone continues to develop upwards during this process, leading to a prolonged duration of separation fractures, which is conducive to enriching the water inrush source.

Fig. 13
figure 13

Cavity water collection.

Full size image

When the primary key stratum reaches its ultimate failure step distance, the key stratum undergoes structural instability. Owing to sudden dynamic instability, the limestone in the Changxing Formation rapidly releases enormous amounts of kinetic energy and impacts the water body within the separation fractures, generating instantaneous ultrahigh water pressures that breach the water-resistant layer. This leads to secondary fracturing of the underlying rock layers beneath the separated strata, creating water conduits, as indicated by the aforementioned similar simulation results. The secondary fracturing of the underlying rock layers also redistributes the water-conducting fracture morphology, increasing the drainage area and thus causing separation water damage, as shown in Fig. 14. Therefore, the roof water inrush pattern at the Longfeng Coal Mine can be classified as dynamic water inrush41, characterized by inconspicuous warning signs, a large instantaneous water inrush, and a significant amount of broken rock accompanying the water flow into the working face. An abnormal water inrush event occurred in the adjacent Guiyuan Coal Mine 11901-1 working face, with a water inrush rate of 150 m3/h, which was significantly higher than the normal water inrush rate for the working face.

Fig. 14
figure 14

Dynamic water inrush on the roof.

Full size image

After the primary key stratum fractured, the water-conducting fracture zone developed into the Changxing Formation. Owing to the good water-bearing properties of this layer, sudden water inrush continuously flows into the working face along the water-conducting fracture zone. At this point, the water volume is not large but lasts for a longer duration. For example, at the 5914 working face in the area, a sudden water inrush incident occurred with a maximum instantaneous flow rate of 165 m3/h, gradually decreasing and stabilizing at 5 m3/h after 7 days. Although "cavity-type" separation fractures also formed beneath key stratum 4, owing to the good water-bearing properties of key stratum 4, the water inrush source collected within the separation fractures through dissolution fractures and cavities within the Changxing Formation. However, because the overlying water-resistant layer of the Changxing Formation is relatively thick, there is usually no downwards replenishment of water from the separated strata. Nevertheless, in areas with thinner water-resistant layers, influenced by rainfall, etc., the water pressure within the separated strata continuously increases, reducing the thickness of the effective water-resistant layer below and leading to the penetration of the water-conducting fracture zone into the water-resistant layer, causing hydrostatic pressure water inrush at the working face, as shown in Fig. 15.

Fig. 15
figure 15

Roof hydrostatic water inrush diagram.

Full size image

On the basis of the above analysis, during the mining process at the Longfeng Coal Mine, "cavity-type" separation water formed mainly beneath the Changxing Formation, with the potential to develop into dynamic water inrush, requiring enhanced geophysical exploration and drainage measures. Additionally, during the rainy season, attention should be focused on the separation water beneath key stratum 4 to prevent hydrostatic pressure water inrush. When the water-conducting fracture zone enlarges and penetrates the water-resistant layer due to significant hydrostatic pressure, it can cause hydrostatic pressure water inrush at the working face. For example, in July 2023, there was a mining water inrush incident at the Longfeng Coal Mine due to heavy rain, with a water inrush rate reaching 300 m3/h.

Conclusion

  1. (1)

    The roof strata at the Longfeng Coal Mine exhibit alternating soft and hard rock characteristics. On the basis of key stratum theory, the karst aquifer in the Changxing Formation is identified as the primary key stratum. Calculations of the stratum stretching rate lead to a theoretical development height of 51.37 m for the water-conducting fracture zone, which has penetrated through the bottom boundary of the Changxing Formation aquifer. The water in the Changxing Formation limestone is thus capable of flowing towards the mining face.

  2. (2)

    The deformation and failure characteristics of the overlying rock strata were studied through numerical simulation, and the spatiotemporal evolution of the water-conducting fissure zone was analysed via similar simulations combined with digital speckle technology. The analysis revealed a "step-type" development characteristic of the water-conducting fracture zone during the mining process. Instability in the Changxing Formation aquifer led to a redistribution of the fissure morphology below, increasing the catchment area and the risk of water inrush.

  3. (3)

    The spatiotemporal evolution pattern of the water-conducting fracture zone was analysed via similar simulations combined with digital speckle technology. During the mining process, the water-conducting fracture zone exhibits a "step-type" development characteristic, with strain concentration zones appearing at the boundary of the goaf. Instability in the key stratum may lead to a redistribution of the fracture morphology below.

  4. (4)

    Field tests of the water-conducting fracture zone were conducted via borehole imaging, which revealed that the measured height of the water-conducting fracture zone was 51 m. This value is close to the theoretical calculation (51.37 m) and the numerical simulation (49.17 m) results. The overlying strata postmining were categorized into low-level tensile‒shear fractures, mid-level vertical or transverse throughgoing fractures, and high-level discrete fractures, with their water-conducting capacity decreasing sequentially.

  5. (5)

    The characteristics of "fracture-type" and "cavity-type" interlayer voids occurring during the mining process beneath the karst aquifer were analysed. From the perspective of instantaneous energy release caused by the fracture and instability of the karst key stratum, the disaster mechanisms of dynamic water inrush and hydrostatic pressure water inrush in the roof of the Longfeng Coal Mine were elucidated.