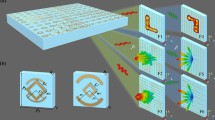
Abstract
Independent control of electromagnetic (EM) waves by metasurfaces for multiple tasks are highly desired and is the recent hot topic of research. In this work we contribute a polarization insensitive frequency multiplexed 2-bit coding metasurface to control the Terahertz (THz) waves in the two operating bands independently. In this regard, as a first step a cascaded meta-atom composed of square rings and/or square metallic patches separated by two polyimide substrates is designed and optimized that provides sixteen independent distinct discrete phases in the reflection geometry. These meta-atoms are then distributed with distinct coding sequences in the two-dimensional spatial plane to realize various bi-functional metasurfaces. As a proof of the concept various full structures are designed and simulated to realize a series of bi-functionalities including anomalous reflection/beam shaping, beam shaping/anomalous reflection, beam deflection/Orbital angular momentum (OAM) beam generation with distinct modes and propagating wave to surface wave (PW–SW) conversion/PW beam manipulation in the lower and higher THz bands, respectively. All the simulation results are in excellent agreement with their theoretical equivalents. We envision that the proposed meta-designs have potential applications for the multi-spectral control of EM waves in THz band. The idea can be further extended to design frequency dependent tri-functional and multi-functional THz meta-devices.
Similar content being viewed by others
Introduction
Metasurfaces (MTSs)1,2,3, allow for the exotic control and manipulation of electromagnetic (EM) waves, which have led to the demonstration of phenomena like flat lenses3, highly efficient and switchable surface plasmon couplers4,5,6, high-resolution three-dimensional (3D) MTS holograms7,8,9, and different functional interfaces10. Technologically, MTSs have bridged the gap between the engineered structures and high technological industry, showing great potential to realize novel operational devices for high resolution imaging, wireless power transfer and modern communication11,12,13,14. The working principle of these MTS based devices is to modulate the phase, amplitude and polarization of an impinging wave in a continuous manner1,2,3,11. From the perspective of circuit theory these designs can be considered as analog circuits15,16. On the contrary, Cui et al.17, introduced a new approach to these engineered structures by designing and defining a new class of MTSs called the digital/coding and programmable MTSs. In this class of MTSs, the degrees of freedom of EM waves (phase, amplitude, and polarization) are mapped upon binary numbers 0, 1, 00, 01 ..., and the meta devices are studied from the perspective of digital circuits, for potential applications in the realm of information sciences17,18,19,20,21,22,23.
In the past decade, variety of digital/coding and programmable MTSs, in distinct frequency regimes from Microwaves (MWs) to Terahertz (THz), have been proposed17,18,19,20,21,22,24,25,26,27,28 to demonstrate various optical functionalities. Among the distinct coding MTSs designs17,18,19,20,21,22,24,25,26,27,28, a digital/coding MTS design of particular interest is the re-configurable/programmable MTSs17,19,20,22,24,29,30 realized in the microwave regimes. In these designs, the functionalities of the digital/coding MTSs are controlled and programmed in real-time by embedding a lumped element such as positive-intrinsic-negative (PIN) diode or varactor diode at each unit cell. Indeed, these re-configurable coding MTSs designs have demonstrated many mature algorithms in the information and imaging theory17,18,29,30,31. Another interesting class of digital/coding MTS is the bi/multi-functional MTS. Such designs, realized in both the MWs and THz regimes of EM spectrum, demonstrate independent and multiple functionalities from a single MTS design26,32,33,34. Operationally, independent bi/multiple functions in the digital/coding MTS designs are encoded on either the polarization of the incident waves34, or frequency of operation32,33, or both25,35. Notably, digital/coding MTS bi-functional designs are advantageous over the analog MTSs working on the principle of continuous modulation phase/amplitude counterpart36,37, with regard to their relatively easier design processes and their ability to perform digital algorithms18,19,20,21,38.
THz radiations, which lie between the MWs and infrared regimes of the EM wave spectrum, have the features of strong penetration power, low photon energy, low attenuation, and wider bandwidth B.W. With these advantages, control and manipulation of the THz radiations possess tremendous potentials in various applications including high speed communication, non-invasive detection and imaging39,40,41 are to mention a few. The conventional THz devices, in this regard are mostly bulky, which hinders their integration to chip scales42,43, consequently, limiting their practical applications. MTSs, however, provided a readily available plateform39 to manipulate the THz waves for various functions. Likewise, distinct digital/coding MTS designs, for THz manipulation has also been proposed21,44,45,46,47,48. At this point, it is worth mentioning that despite the challenges in the availability of tuning elements and mechanisms in this part of EM wave spectrum, there have been attempts to realize THz re-configurable and programmable MTSs45,46,47,48, by utilizing some novel tuneable materials such as Vanadium dioxide (VO2), graphene and liquid crystals, showing the potential of programmable meta-devices at higher frequencies. Similarly, the THz digital/coding meta-devices, demonstrating multiple tasks from the same shared aperture shall enable highly miniaturized and integrated devices21,34,49. In the past few years, some studies have been published to demonstrate bi-functional THz digital/coding MTSs based on either the polarization of the incident waves (polarization multiplexed)34,50 or the frequencies of operation (frequency multiplexed MTSs)33. Meanwhile, these designs have significant limitations, especially in the case of frequency dependent coding MTSs. For example, the frequency multiplexed structures previously reported can operate for a single polarization, have limited phase resolution, narrow band of operation and angularly unstable. Moreover, the dual-band coding MTSs33,51 have been reported so far have limited phase resolution which consequently limits their number of possible functionalities.
In a bid to cover this gap, this work demonstrates a complete 2-bit dual-band polarization insensitive coding MTS for the THz regime. The proposed MTS design with its 2-bit coding resolution in each operating band provides more flexibility in manipulating the reflected waves independently in different frequency bands , much worthier from the previously published frequency dependent THz works, as those were performing limited tasks. Functionalities demonstrated here include independent deflection of the normally incident waves to different anomalously reflected angles and in different directions, Orbital angular momentum (OAM) beam generation with distinct topological charges and deflected to distinct directions, anomalous reflection and beam shaping, conversion and controlling of normally incident propagating waves to surface waves (PW–SW) in the two operating bands independently. Moreover, based on the spatial convolution theorem a compensation scheme has been used with which, regardless of the frequency band and the direction in which the anomalously reflected wave is to be deflected, the angle can be engineered desirably with negligible distortions, mitigating the strong wavelength dependence of such kind of multi-band devices. Furthermore, besides the demonstrated functionalities, all other frequency dependent bi-functionalities can also be achieved by the proper selection and distribution of the designed coding meta-atoms. Some of the dual functionalities of the proposed work are shown in the schematic illustration in Fig. 1.
Schematic illustration. The schematic illustrates different bi-functionalities of the proposed design. Each bi-functionality is achieved with a specific coding sequence ‘\(CS_{n}\)’. MTSs with ‘\(CS_{1}\)’, ‘\(CS_{2}\)’ and ‘\(CS_{3}\)’ illustrates beam shaping/ beam deflection, OAM beam generation with \(l_{1}=m=+1\)/ OAM beam generation with \(l_{2}=m=+{2}\) (deflected to different planes), and PW–SW conversion/PW beam manipulation in lower and higher bands (\(f_{l}/f_{h}\)), respectively.
Design and simulation
Dual-band coding meta-atom design and simulation
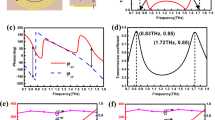
To achieve an independent 2-bit phase response in two different frequency bands, a total of sixteen unit cells are required. Here, a three-metallic-layer structure shown in Fig. 2a is used as the coding meta-atom for a 2-bit dual-band coding MTS. The lattice constant of the proposed meta-atom is \(p = 70\, um\) which in terms of operating wavelength (\(\lambda _{o}\)) of the incident waves in free space is \(p \approx \lambda _{o}/7\) at ‘\(f_{l}\)’ while at ‘\(f_{h}\)’ \(p \approx \lambda _{o}/3.5\). All the metallic layers used are of lossy Aluminum, where a fully metallic bottom layer acting as a ground is separated by a polyimide spacer of thickness \(d_{1} = 20\, um\) from the inner layer. The inner, and outer metallic layers are separated by the same polyimide with thickness \(d_{2} = 10\, um\), and dielectric properties of the polyimide are \(\varepsilon = 3.0\), and loss tangent \(\delta = 0.03\). A square loop-patch structure with parameters \(w_{l}(i,o)\), \(w_{p}(i,o)\), w(i, o), as shown in Fig. 2b and square patch with parameters \(w_{pt}(i,o)\), as shown in Fig. 2c, have been used to load inner and outer metallic layers. Note that the subscripts ‘i and ‘o, here suggests that a coding meta-atom, may either have both layers (inner and outer) loaded with a square loop-patch or a simple square patch, or it can be a combination of both. For design and simulation of the coding meta-atom, the commercially available software computer simulation technology (CST) Microwave studio is used. The unit cell is simulated using the unit cell boundary conditions, in the x–y plane with the same period p along the x and y-axis and Floquet ports are set at a distance of 400um along the z-axis as the excitation source. The surface of the structure is selected as the reference plane, and above that region upto 400um the phases and amplitudes of reflection are extracted. The simulation results obtained are plotted in Fig. 3, where Fig. 3a and Fig. 3b show the amplitude and phase states in the lower band (0.53–0.73 THz), having a B.W \(\approx 0.2\), while Fig. 3c and Fig. 3d show the corresponding phase and amplitude spectra in higher band (1.25–1.45 THz) with a B.W\(\approx\) 0.25. Note that the amplitudes of coding meta-atoms in each working band remain in the rage of 0.7–1 in linear scale, however at central frequencies for each row this difference reduces to \(\approx 0.15\), consequently not causing any significant changes in the overall results of the full structures. Similarly, the phase differences between the consecutive digital phase states also remain approximately to \(90^{\circ }\pm 10^{\circ }\) which fulfills the definition of binary digital phase states of a 2-bit coding meta-atom. Moreover, the separation between the two operating bands is \(\approx 0.5\) THz that is large enough to avoid any cross-talk between the two functions obtained from the same design. Figure 2d provides locations of the 16 optimized coding meta-atoms in the reflection phase diagram, with horizontal and vertical axes representing the reflection phases under the lower and higher frequency, respectively. It is apparent that phase response at a lower frequency in each row remain the same and are independent of the coding states in the higher frequency band (the number before the slash). The similar kind of trend appears when seen from each column, corresponding to independent digital states at higher frequency band (the number after the slash), allowing us to encode dual functionalities using a single MTS.
It is also very important to mention that the phase and amplitude spectra obtained here represent the overall response of the meta atom. Any changes in the dimensions of metallic patches or the substrates sizes can potentially alters this over all response. To further investigate a tolerance analysis on the meta-atom performance is carried out (see Supplementary information, Section S1) to study how the variations in the meta-atom’s parameters affect its behavior.
Full structures design and simulation
After realizing the 2-bit dual-band coding meta-atoms, the next stage is to distribute them with different coding sequences in the x–y spatial plane for designing full structures. In the following text different bi-functional structures are discussed where each structure is encoded with a specific coding sequence to perform distinct tasks independently. In the design process of full structures the idea of super unit cell is adopted, which facilitates to minimize the unwanted inter element coupling between the coding meta-atoms, and to flexibly manipulate the scattered waves. For the simulation purposes of the full structure CST MWS is used but with time domain solver and open add space boundary condition in the ± z direction. Linearly polarized plane waves are impinged to excite the structures. Furthermore, other necessary simulation conditions and requirements are explained for each design in the following text.
Results and discussion
Bi-functional full structures for beam shaping/steering and flexible beam shaping
Beam forming/shaping that includes beam splitting and quad beam generation, can be realized by employing coding MTS with a periodic ‘00/10’ coding sequence, chess board like coding pattern, respectively. Although, it has already been established that beam shaping can be achieved using coding MTSs with 1-bit phase resolution17,21,25, however, joint independent dual-band beam shaping, and beam shaping at one frequency along other tasks at another frequency band have rarely been reported. In the proposed case since independent phase modulation with 2-bit resolution can be performed thus it is feasible to achieve flexible beam shaping in the two operating bands and also beam shaping in one band along another useful functionality such as beam deflection in the other band. For this purpose, firstly we selected the coding meta-atoms from the matrix \(M^{2-bit}\) as shown in Eq. (1), which have digital phase states with 1-bit resolution in the lower and 2-bit resolution in the higher band, i.e., ‘00/00, 01/00, 10/10, 11/10’.
A full structure labeled as \({\textbf {S}}_{1}\) is designed with period of eight coding meta-atoms and overall size of \(x\times y=(70\times 72)\times (70\times 72)\, um^{2}\). Full wave simulations are performed for both lower and higher bands under the normal illumination of x-polarized incident waves to measure the far field patterns. The simulation results are shown in Fig. 4a–d, where Fig. 4a and c shows the 3D far field pattern, while Fig. 4b and d show their 2D equivalents, respectively. The results clearly manifest that a splitted and a deflected beam is achieved at the lower and higher band, respectively. The angle at which each beam is deflected have the numerical values which are almost same as predicted by the Generalized Snell’s law1 described in Eq. (2).
In addition, we designed a coding MTS of the same size labeled as ‘S2’ which can deflect the reflected beam in the lower band and split the reflected beam in to two equal parts in higher band, i.e., opposite function as that of the first structure ‘S1’. This task is accomplished by selecting the coding meta-atoms which have 2-bit phase resolution in the lower and 1-bit in the higher band. The coding sequence that can perform this function is, ‘00/00, 01/00, 10/10, 11/10’. The results obtained for this case are depicted in Fig. 4e–h, where Fig. 4e and Fig. 4g shows the far field patterns while Fig. 4f and Fig. 4h shows their corresponding 2D equivalents. The results clearly shows that beam deflection and beam splitting in the lower and higher band, respectively, has been achieved efficiently. Furthermore, a MTS that can shape the beam in two distinct patterns in the two operating bands is designed. In this case the full structure labeled as ‘S3’ can shape the reflected beam into a quad beam pattern in the lower band and a splitting pattern in the higher band. This task can be achieved by selecting the coding meta-atoms which have 1-bit phase resolution in both bands but a chess board like distribution in the lower band and a periodic distribution in the higher band, i.e., ‘00/00, 10/10, 10/00, 00/10’. The results obtained in this case are depicted in Fig. 4i–l, where Fig. 4i and Fig. 4k shows the 3D far field pattern while Fig. 4j and Fig. 4l shows the corresponding 2D patterns. Here the angle at which each beam in the quad beam pattern is deflected can be calculated using the Eqs. (3) and (4)19,21.
and
The results shown in Fig. 4i–j have very close agreement with the theoretically predicted results of Eqs. (3) and (4).
Beam shaping and deflection. (a–d) 3D and 2D far field pattern of beam splitting and beam deflection in the lower and higher bands,respectively. (e–h) 3D and 2D far field pattern of beam deflection and beam splitting in the lower and higher bands, respectively. (i–l) 3D and 2D far field pattern of quad beam shaping and beam splitting in the lower and higher bands, respectively.
OAM vortex beam generation and control
OAM beams are the conical vortex beams which have the feature of non-diffractiveness and mode orthogonality52,53,54. Each OAM vortex beam has a mode number ‘\(\pm l\)’ which is orthogonal to any other OAM mode. This feature of the OAM vortex beams make them strong agents to use them as independent channels for transferring information. Theoretically, the OAM provides another degree of freedom to EM waves which can enhance the channel capacity26,55,56,57.
The phase profile of an OAM vortex beam is described by ‘\(e^{il\varphi }\)’ where ‘l’ is the topological charge (mode number) and ‘\(\varphi\)’ is the azimuth angle54,55. To realize OAM vortex beam from a MTS composed of \(m\times n\) elements, the required phase distribution at the mnth element should satisfy the following relation with the azimuthal angle
where \(l=0,\pm 1,\pm 2,\pm 3\ldots\) is the OAM mode number and ‘\(\textit{x}\)’, ‘\(\textit{y}\)’ are the Cartesian coordinates in the x–y plane. The relation shown in Eq. (5), is the necessary and sufficient condition to generate an OAM vortex beam of mode ‘\(\pm l\)’. In order to generate OAM beam from the proposed MTS firstly we designed a full structure by selecting the off diagonal elements of the matrix \(M^{2-bit}\) and distributed them with the pattern labeled as ‘S4’ depicted in Fig. 5a. This phase pattern fulfills the relation described in Eq. (5). Moreover the gradient of the phase pattern in lower and higher bands are opposite to each other which adds another feature to the design that is the generation of OAM beam in the two operating bands with mode number opposite to each other, i.e., ‘\(+l\)’ at ‘\(f_{l}\)’ and ‘\(-l\)’ at ‘\(f_{h}\)’. In this regard, a full structure composed of \(40\times 40\) elements is designed and simulated under the normal incidence of y-polarized plane waves.
OAM beam generation with distinct modes. (a) Coding pattern of the MTS to generate OAM with opposite modes ‘\(l=+1\)’ and ‘\(l=-1\)’ in lower nad higher bands, respectively. (b, c) Far-field pattern and the corresponding phase of OAM in lower band. (d, e) Far-field pattern and the corresponding phase of OAM in higher band. (f) Coding pattern of the MTS to generate OAM with distinct modes ‘\(l=+1\)’ and ‘\(l=+2\)’ in lower and higher bands, respectively. (g, h) Far-field pattern and the corresponding phase of OAM in lower band. (i, j) Far-field pattern and the corresponding phase of OAM in higher band.
The simulation results shown in Fig. 5b and Fig. 5d show the 2D far-field pattern in lower and higher bands, respectively, where a donut-like pattern with a null in the center can be observed which satisfies the requirements of an OAM beam. Figure 5c and Fig. 5e show the corresponding OAM phase patterns in the lower and higher bands, respectively. The phase patterns clearly show that the OAM beam generated has mode number ‘\(l=+1\)’ and ‘\(l=-1\)’ in the two operating bands, respectively. Consequently, two independent channels are established using the same design. The idea is further applied to design a full structure to generate OAM beams with two distinct integral values of topological charge l. For this purpose, we selected the coding meta-atoms which has a phase distribution shown in Fig. 5f, i.e., a single repetition of the digital phase state in the lower band and a double repeating pattern of the same digital phases in the higher band. The meta-atoms which fulfill this condition have the digital phase states of ‘00/00, 00/01, 01/10, 01/11, 10/00, 10/01, 11/10, 11/11’, which have decimal equivalents ‘0/0, 0/1, 1/2, 1/3, 2/0, 2/1, 3/2, 3/3’. A full structure labeled as ‘S5’, composed of \(64 \times 64\) coding meta-atoms are distributed with the pattern as shown in Fig. 5f. The simulation results are shown in Fig. 5g–j, where Fig. 5g and Fig. 5i show the 2D far-field patterns in the lower and higher bands, respectively. Figure 4h and j shows that the generated OAM has mode numbers ‘\(l=1\)’ and ‘\(l=2\)’, respectively. Furthermore, the idea is extended to design a full structure that can steer the OAM beams in different directions independently. For this purpose, convolution operation on coding MTSs is employed to accomplish the task. Note that convolution operation on coding MTSs allows us to simply make binary addition of two or more different coding patterns that result in a new useful coding pattern where the resultant pattern can simultaneously perform all the tasks of all the individual coding patterns. For this purpose, we selected the phase states lying on the off-diagonal of the Matrix \(M ^{2-bit}\) and distributed them in the two patterns as shown in Fig. 6a and Fig. 6b, both having the same size of \(64\times 64\) coding meta-atoms. As mentioned earlier the coding pattern shown in Fig. 6a is responsible to generate the OAM beam in the normal direction with mode ‘\(l=+1\)’ and ‘\(l=-1\)’ in the two operating bands, respectively, while the coding pattern shown in Fig. 6b can be employed to deflect the reflected beam to opposite half-planes for the two frequencies of operation. Now performing the binary addition of these two coding patterns we get the new coding pattern as shown in Fig. 6c, which can perform both the tasks of OAM beam generation and deflection, simultaneously. A full structure labeled as ‘S6’ is designed according to this new coding pattern and simulated in both operating bands under the normal illumination of x-polarized plane waves. The simulation results are shown in Fig. 6d–i, where Fig. 6d and Fig. 6g show the 3D far-field patterns of the steered OAM beam, while Fig. 6e and h shows their corresponding 2D far-field patterns in the two operating bands, respectively. The deflection angle has almost the same value as predicted by the Eq. (2), which in other words verify that the simulated results have excellent agreement with theoretical results. Similarly, the phase patterns in the two operating bands for the steered OAM beams are depicted in Fig. 6f and Fig. 6i, respectively, showing that the OAM beam of mode ‘\(l=+1\)’ and ‘\(l=-1\)’ have been generated.
OAM beam generation with steering features. (a) Coding pattern of the MTS to generate OAM in the normal direction with opposite modes ‘\(l=1\)’ and ‘\(l=-1\)’ in lower and higher bands, respectively. (b) Coding pattern of the MTS to steer the reflected beams to opposite half planes. (c) Coding pattern of the MTS to generate and steer the OAM beams to opposite half planes. (d, e) 3D and 2D far field pattern of the generated OAM beam in the lower band, respectively (f) The phase pattern of the generated OAM beam in the lower band. (g, h) 3D and 2D far field pattern of the generated OAM beam in the higher band, respectively. (i) The phase pattern of the generated OAM beam in the higher band.
OAM mode purity
An important feature of OAM beams generated by a MTS is their mode purity, which is desired in most practical scenarios so that information can be transferred without distortion. To analyze the performance of the designed coding MTS in generation of OAM beams with different modes, the purity of different OAM modes can be extracted based on the spectral analysis of Fourier transform58. For this purpose, we analyzed the performance of the structures ‘S4–S6’ that generate OAM beams with ‘\(l=+1\)’,‘\(l=-1\)’ (design S4), ‘\(l=+1\)’,‘\(l = +2\)’(design S5) in the specular direction and ‘\(l=+1\)’,‘\(l=-1\)’ (design S6) deflected in the lower and higher band, respectively. By sampling the fields along a circle with a specific radius, \(\xi (\phi )\), the Fourier relation can be written as
where the amplitude ‘\(a_{n}\)’ can be calculated as
In Eq. (7), ‘\(e^{in\phi }\)’ indicates the spiral harmonics of each mode. Utilizing the above two equations the normalized spectral intensities of different OAM harmonics are calculated and displayed in Fig. 7. In the lower operating band the normalized spectral intensities of the OAM modes ‘\(l=+1\)’ and ‘\(l=-1\)’, are shown in Fig. 7a and b,respectively, while Fig. 7c and d shows the same for modes ‘\(l=+1\)’ and ‘\(l=+2\)’, in the lower and higher band, respectively. It should be noted that compared to lower band the intensities of the unwanted higher order modes in the high frequency band are relatively higher which are due to the increased losses induced in the structures at the higher frequency. Moreover, the OAM mode purity of the deflected beams generated by ‘S6’ are relatively lower as compared to the other two structures which is due to the increased unwanted coupling between the adjacent unit cells resulted from the addition of two different coding sequences. The results in this case for ‘\(l=+1\)’ and ‘\(l=-1\)’, are displayed in Fig. 7e and f, in the lower and higher band, respectively. From these results it can be seen that the proposed designs have generated OAM beams with high purity since the dominant OAM modes carry ‘\(>87\%\)’ of the total energy for all the modes ‘\(l=+1\)’ and ‘\(l=-1\)’ of (S4) ‘\(>85\%\)’ for ‘\(l=+1\)’ and ‘\(l=+2\)’ of (S5) and ‘\(>80\%\)’ of the total energy for all the modes ‘\(l=+1\)’ and ‘\(l=-1\)’ of the structure (S6). The generation of OAM beams with high purity shows their applicability for mode division multiplexing communication meta-devices.
OAM beam mode purity. (a, b) Normalized intensity of the OAM beams with mode ‘\(l=+1\)’ and ‘\(l=-1\)’ in lower and higher band, respectively. (c, d) Normalized intensity of the OAM beams with mode ‘\(l=+1\)’ and ‘\(l=+2\)’ in lower and higher band, respectively. (e, f) Normalized intensity of the deflected OAM beams with mode ‘\(l=+1\)’ and ‘\(l=-1\)’ in lower and higher band, respectively.
PW–SW conversion and PW beam manipulation
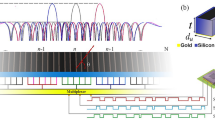
It has been established previously that a gradient MTS and digital/coding MTS as well can convert the PW to SW when it fulfills the required conditions5,59,60. The necessary condition for phase modulated coding MTS to convert the PW–SW is to select a gradient coding sequence that has a period length equal to or less than the operating wavelength, i.e., ‘\(\lambda \ge \Gamma\)’. The proposed design which has the coding meta-atoms with the feature of deep sub-wavelength size, provides the flexibility to convert PW–SW at least at lower band operating frequencies and performs PW beam manipulation in higher band,as illustrated in Fig. 8a. Moreover, the direction of the flow of the SWs can also be controlled by changing the coding sequence of the design. In this regard, various structures are designed to convert the PW–SW in the lower band and perform other useful tasks at the higher band independently. Firstly, the coding meta-atoms which have the digital phase states lie on the off-diagonal of the Matrix \(M^{2-bit}\), i.e., ‘00/11, 01/10, 10/01, 11/00’, with a period of \(\Gamma =4\times 70\,\mu \hbox {m}\), are selected. The length of this period is less than the operating wavelength \((\lambda _{o} > \Gamma )\) in the lower band. The operating wavelength here we consider is the wavelength corresponding to 0.63 THz. A full structure labeled ‘S7’ is designed with an overall size of \(64\times 64\) coding elements and simulated by adjusting the waveguide port with an aperture size of \(3200\times 2800\,\mu \hbox {m}^{2}\), \(1000\,\mu \hbox {m}\) above the design as an excitation source so that the design can receive the plane waves. Both near and far field monitors are set at the selected frequencies in both lower and higher bands to observe the near field distributions and far-field patterns.
Simultaneous manipulation of surface waves and propagating waves. (a) Schematic illustration of PW–SW conversion in lower band and PW beam manipulation in higher band, (b, c) SWs received from PW–SW converter and beam deflection in lower and higher bands, respectively, employing off diagonal elements of the matrix \(M^{2-bit}\). (d, e) SWs received from PW–SW converter and beam deflection in lower and higher band, respectively using diagonal elements of the matrix \(M^{2-bit}\). (f, g) SWs received from PW–SW converter flowing in both \(\pm x\) directions and beam deflection in and lower and higher band, respectively using elements, ‘00/00, 00/01, 10/10, 10/11’. (h, i) SWs received from PW–SW converter and normal reflection in lower and higher band, respectively using first row elements of the matrix \(M^{2-bit}\).
To record the SWs quartz slabs with permittivity, \(\varepsilon = 4.4\) and loss tangent \(\delta = 0.0004\), having a size of \(4480\times 2240 \times 80\,um^{3}\) is placed at each side (‘±x’ and ‘±y’) directions of the PW–SW converter. As it is obvious that the design ‘S7’ has a period length of the coding sequence \((\Gamma <\lambda _{o})\) at the lower band, and \((\Gamma >\lambda _{o})\) at the higher band, consequently, the design should convert the PW–SW at lower band and steer PW beam at higher band. The simulation results displayed in Fig. 8b and Fig. 8c show the above predictions where in the lower band the design has efficiently converted PW–SW which flows to-x direction on the quartz substrate (see Fig. 8b), while in the higher band (Fig. 8c) the structure deflected the beam to (x-z plane) and the angle, ‘\(\theta _{d}\approx 26^{\circ }\)’ has a close agreement with the value calculated by Eq. (2). In the second case, we designed a full structure labeled as ‘S8’ to convert PW–SW in the lower band and scatter the PW reflected beam to the same plane. This function can be achieved using coding elements lying on the diagonal of Matrix \(M^{2-bit}\), i.e., 00/00, 01/01, 10/10, and11/11. The results are shown in Fig. 8d and Fig. 8e which shows SW flowing on the dielectric substrates and PW deflected to an angle ‘\(\theta _{d}\approx -26^{\circ }\)’ at lower and higher band, respectively. To further explore the PW–SW conversion of the proposed MTS. In the third case, we designed a full structure labeled ‘S9’ that can convert the PW–SW in the lower band which flows in both \(\pm x\) direction and steer the propagation waves in the higher band. For this purpose, we designed a full structure that has a beam-splitting coding sequence in the lower band and beam deflection (‘00/00, 00/01, 10/10, 10/11’) in the higher band. Here the period length is \(\Gamma =4\times 70\,um\) and the full structure size again is \(64\times 64\) meta-atoms. The corresponding results are shown in Fig. 8f and Fig. 8g for lower and higher bands, respectively. In the last case, another full structure labeled as ‘S10’ is constructed to scatter the reflected beam in the normal direction and to convert PW–SW in the lower band. The coding sequence for this purpose can be used is any row of the matrix \(M^{2-bit}\), however, for simplicity we selected the first row with phase states, ‘00/00, 01/00, 10/00, 11/00’. Clearly, this sequence has a gradient phase pattern in the lower and a constant phase pattern in the higher band which fulfills the required condition for this case. The simulation results are plotted in Fig. 8h and Fig. 8i for lower and higher bands, respectively, clearly showing the SW propagating to-x direction and PW reflected normally.
To prove the novelty and strength of the proposed design compared to the previous works, a brief comparison has been made that can be seen in Table 1. The comparison clearly shows that the proposed design is superior to previously demonstrated THz works in many aspects, including phase resolution in both operating bands, polarization insensitivity and the number of achievable bi-functionalities.
Efficiency and angular stability analysis
The efficiency of the MTS for a specific functionality at a particular frequency can be calculated as:
In Eq. (8), \(P_{out}\) and \(P_{in}\) shows the scattered output and input power, respectively. For a reflection type MTS the efficiency can be estimated as the ratio of power reflected by MTS to the power reflected by a bare metal of the same size, i.e.,
where \(P_{r}^{MTS}\) is the power reflected in the presence of MTS while \(P_{r}^{Metal}\) the power reflected by the bare metallic structure.
To numerically calculate the efficiency of the proposed design, for simplicity we have simulated the structure shown in Fig. 4a and Fig. 4c which has the functionality of beam splitting and beam deflection in the lower and higher band, respectively, as shown in Supplementary Fig. S4(a) and Fig. S4(c). Next, a bare metallic structure of the same size is also simulated and the reflected power at the same central frequencies are recorded and plotted (see Supplementary Fig. S4b,d), which shows the specular reflection in both bands. Furthermore, to compare the reflected power and calculate the efficiency, the reflected power are plotted in lower and higher band, for both MTS and bare metal case that can be seen in (Supplementary Fig. S1e,f). The comparison of the two plots shows that the proposed design for this functionality has the efficiency \(\eta _{r}=34\%\) in lower band and \(\eta _{r}= 85\%\) in the higher band. The lower efficiency in lower band is due to the fact that the energy is distributed into two equal parts.
Furthermore for angular stability analysis of the proposed work, we designed a full structure composed of the off diagonal elements ‘00/11, 01/10, 10/01, 11/00’ of the Matrix \(M^{2-bit}\) and simulated it for plane waves incidence with different oblique angles. The structure at the normal incidence ‘\(\theta _{inc}=0^{\circ }\)’, deflects the reflected beam to the opposite half planes as shown in (Supplementary Fig. S5a,b). The same structure is further simulated for two distinct incidence angles including ‘\(\theta _{inc}=15^{\circ }\)’ and ‘\(\theta _{inc}=30^{\circ }\)’, as shown (Supplementary Fig. S5c–f) which shows the reflected E-field pattern in the lower and higher band for ‘\(\theta _{inc}=15^{\circ }\)’ and ‘\(\theta _{inc}=30^{\circ }\)’, respectively, confirming that the proposed design still works efficiently for oblique incidence, especially from the functionality point of view. Increasing the oblique incidence further the performance of the MTS degraded, due to the growing unwanted coupling between the meta-atoms and also possibly due to the in destructive interference between the incidence and reflected waves.
Conclusion
In summary, we have presented a bi-functional polarization insensitive dual-band digital/coding MTS to flexibly manipulate the reflected THz waves independently in the two operating bands. Various full structures are designed and encoded with different coding sequences to perform two independent tasks from the same shared aperture. A series of two independent tasks reported here from the proposed frequency-dependent meta-devices, including beam shaping and beam deflection, beam deflection to opposite half-planes, high mode purity OAM beam generation and deflecting to different directions with distinct mode numbers and lastly PW–SW conversion at the lower band and PW beam manipulation at the higher frequency band. All the simulated trends match well with their theoretical predictions. The proposed design is superior compared to the previously frequency dependent MTSs as many other bi-functionalities could also be achieved by the proper distribution of the designed meta-atoms. We believe that the proposed idea has the potential to design polarization-insensitive multi-spectral multipurpose meta-devices in the THz regime, which could find application in multi-color holography and frequency beam manipulators for the spatial separation of signals modulated with different frequencies.
Data availability
All the authors agreed that they have no competing interests. The authors declare that the data supporting the findings of this study are available within the paper. Any other simulation data sets are available from the corresponding author on a reasonable request.
References
Yu, N. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011).
Yu, N. et al. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 12, 6328–6333 (2012).
Aieta, F. et al. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett. 12, 4932–4936 (2012).
Grady, N. K. et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 340, 1304–1307 (2013).
Sun, S. et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 11, 426–431 (2012).
Lin, J. et al. Polarization-controlled tunable directional coupling of surface plasmon polaritons. Science 340, 331–334 (2013).
Huang, L. et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 4, 2808 (2013).
Chen, W. T. et al. High-efficiency broadband meta-hologram with polarization-controlled dual images. Nano Lett. 14, 225–230 (2014).
Ni, X., Kildishev, A. V. & Shalaev, V. M. Metasurface holograms for visible light. Nat. Commun. 4, 2807 (2013).
Farmahini-Farahani, M., Cheng, J. & Mosallaei, H. Metasurfaces nanoantennas for light processing. JOSA B 30, 2365–2370 (2013).
Chen, H.-T., Taylor, A. J. & Yu, N. A review of metasurfaces: physics and applications. Rep. Prog. Phys. 79, 076401 (2016).
Song, M. et al. Smart table based on a metasurface for wireless power transfer. Phys. Rev. Appl. 11, 054046 (2019).
Lee, D., Gwak, J., Badloe, T., Palomba, S. & Rho, J. Metasurfaces-based imaging and applications: From miniaturized optical components to functional imaging platforms. Nanoscale Adv. 2, 605–625 (2020).
Huang, C. X., Zhang, J., Cheng, Q. & Cui, T. J. Polarization modulation for wireless communications based on metasurfaces. Adv. Funct. Mater. 31, 2103379 (2021).
Chen, H., Ran, L., Huangfu, J., Grzegorczyk, T. M. & Kong, J. A. Equivalent circuit model for left-handed metamaterials. J. Appl. Phys. 100, 024915 (2006).
Bilotti, F. et al. Equivalent-circuit models for the design of metamaterials based on artificial magnetic inclusions. IEEE Trans. Microw. Theory Tech. 55, 2865–2873 (2007).
Cui, T. J., Qi, M. Q., Wan, X., Zhao, J. & Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light: Sci. Appl. 3, e218–e218 (2014).
Ma, Q. & Cui, T. J. Information metamaterials: Bridging the physical world and digital world. PhotoniX 1, 1–32 (2020).
Liu, S. & Cui, T. J. Concepts, working principles, and applications of coding and programmable metamaterials. Adv. Opt. Mater. 5, 1700624 (2017).
Bao, L. & Cui, T. J. Tunable, reconfigurable, and programmable metamaterials. Microw. Opt. Technol. Lett. 62, 9–32 (2020).
Liu, S. et al. Convolution operations on coding metasurface to reach flexible and continuous controls of terahertz beams. Adv. Sci. 3, 1600156 (2016).
Cui, T.-J., Liu, S. & Li, L.-L. Information entropy of coding metasurface. Light: Sci. Appl. 5, e16172–e16172 (2016).
Iqbal, S. et al. Dual-band and dual-polarization coding metasurface for independent controls of phases and amplitudes with cross-polarized transmissions in two bands. Results Phys. 58, 107452 (2024).
Liu, C. et al. A programmable diffractive deep neural network based on a digital-coding metasurface array. Nat. Electron. 5, 113–122 (2022).
Iqbal, S. et al. Polarization-selective dual-band digital coding metasurface for controls of transmitted waves. J. Phys. D Appl. Phys. 51, 285103 (2018).
Iqbal, S., Madni, H. A., Liu, S., Zhang, L. & Cui, T. J. Full controls of OAM vortex beam and realization of retro and negative reflections at oblique incidence using dual-band 2-bit coding metasurface. Mater. Res. Express 6, 125804 (2019).
Iqbal, S. et al. Power modulation of vortex beams using phase/amplitude adjustable transmissive coding metasurfaces. J. Phys. D Appl. Phys. 54, 035305 (2020).
Zhang, K. et al. Phase-engineered metalenses to generate converging and non-diffractive vortex beam carrying orbital angular momentum in microwave region. Opt. Express 26, 1351–1360 (2018).
Zhang, L. et al. Space-time-coding digital metasurfaces. Nat. Commun. 9, 4334 (2018).
Li, L. et al. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 8, 197 (2017).
Ma, Q. et al. Smart metasurface with self-adaptively reprogrammable functions. Light: Sci. App. 8, 98 (2019).
Iqbal, S. et al. Dual-band 2-bit coding metasurface for multifunctional control of both spatial waves and surface waves. JOSA B 36, 293–299 (2019).
Liu, S. et al. Frequency-dependent dual-functional coding metasurfaces at terahertz frequencies. Adv. Opt. Mater. 4, 1965–1973 (2016).
Liu, S. et al. Anisotropic coding metamaterials and their powerful manipulation of differently polarized terahertz waves. Light: Sci. Appl. 5, e16076–e16076 (2016).
Wu, L. W. et al. Multitask bidirectional digital coding metasurface for independent controls of multiband and full-space electromagnetic waves. Nanophotonics 11, 2977–2987 (2022).
Xu, H.-X. et al. Chirality-assisted high-efficiency metasurfaces with independent control of phase, amplitude, and polarization. Adv. Opt. Mater. 7, 1801479 (2019).
Liu, L. et al. Broadband metasurfaces with simultaneous control of phase and amplitude. Adv. Mater. 26, 5031–5036 (2014).
Wu, R. Y., Shi, C. B., Liu, S., Wu, W. & Cui, T. J. Addition theorem for digital coding metamaterials. Adv. Opt. Mater. 6, 1701236 (2018).
He, J., Dong, T., Chi, B. & Zhang, Y. Metasurfaces for terahertz wavefront modulation: A review. J. Infrared Millim. Terahertz Waves 41, 607–631 (2020).
Tian, H. W. et al. Terahertz metasurfaces: Toward multifunctional and programmable wave manipulation. Front. Phys. 8, 584077 (2020).
Al-Naib, I. & Withayachumnankul, W. Recent progress in terahertz metasurfaces. J. Infrared Millim. Terahertz Waves 38, 1067–1084 (2017).
Scherger, B. et al. Compression molded terahertz transmission blaze-grating. IEEE Trans. Terahertz Sci. Technol. 2, 556–561 (2012).
Gospodaric, J. et al. 3D-printed phase waveplates for THZ beam shaping. Appl. Phys. Lett. 112, 221104 (2018).
Liu, S. et al. Anomalous refraction and nondiffractive Bessel-beam generation of terahertz waves through transmission-type coding metasurfaces. ACS Photonics 3, 1968–1977 (2016).
Rouhi, K., Rajabalipanah, H. & Abdolali, A. Multi-bit graphene-based bias-encoded metasurfaces for real-time terahertz wavefront shaping: From controllable orbital angular momentum generation toward arbitrary beam tailoring. Carbon 149, 125–138 (2019).
Xu, J., Liu, W. & Song, Z. Terahertz dynamic beam steering based on graphene coding metasurfaces. IEEE Photonics J. 13, 1–9 (2021).
Manjappa, M. et al. Reconfigurable mems fano metasurfaces with multiple-input–output states for logic operations at terahertz frequencies. Nat. Commun. 9, 4056 (2018).
Cong, L., Pitchappa, P., Wang, N. & Singh, R. Electrically programmable terahertz diatomic metamolecules for chiral optical control. Research (2019).
Fu, X., Yang, F., Liu, C., Wu, X. & Cui, T. J. Terahertz beam steering technologies: from phased arrays to field-programmable metasurfaces. Adv. Opt. Mater. 8, 1900628 (2020).
Yang, W. et al. Full-space dual-helicity decoupled metasurface for a high-efficiency multi-folded reflective antenna. Opt. Express 30, 33613–33626 (2022).
Li, S.-H. & Li, J.-S. Frequency coding metasurface for multiple directions manipulation of terahertz energy radiation. AIP Adv. 9, 035146 (2019).
Allen, L., Padgett, M. & Babiker, M. IV the orbital angular momentum of light. Prog. Opt. 39, 291–372 (1999).
Iqbal, S. et al. Controls of transmitted electromagnetic waves for diverse functionalities using polarization-selective dual-band 2 bit coding metasurface. J. Opt. 22, 015104. https://doi.org/10.1088/2040-8986/ab5e18 (2019).
Yao, A. & Padgett, M. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 3(2), 161–204 (2011).
He, J. et al. Generation and evolution of the terahertz vortex beam. Opt. Express 21, 20230–20239 (2013).
Tang, S. et al. High-efficiency broadband vortex beam generator based on transmissive metasurface. Opt. Express 27, 4281–4291 (2019).
Iqbal, S. et al. Broadband and high-efficiency manipulation of transmitted vortex beams via ultra-thin multi-bit transmission type coding metasurfaces. IEEE Access 8, 197982–197991 (2020).
Shi, Y. & Zhang, Y. Generation of wideband tunable orbital angular momentum vortex waves using graphene metamaterial reflectarray. IEEE Access 6, 5341–5347 (2017).
Liu, S. et al. Full-state controls of terahertz waves using tensor coding metasurfaces. ACS Appl. Mater. Interfaces 9, 21503–21514 (2017).
Liu, S. et al. Negative reflection and negative surface wave conversion from obliquely incident electromagnetic waves. Light: Sci. Appl. 7, 18008–18008 (2018).
Chen Xi, Liu et al. Programmable manipulations of terahertz beams by transmissive digital coding metasurfaces based on liquid crystals. Adv. Opt. Mater. 9, 2100932 (2021).
Yunping, Qi. et al. Efficient manipulation of terahertz waves by multi-bit coding metasurfaces and further applications of such metasurfaces. Chin. Phys. B 30, 024211 (2021).
Jiu-sheng, Li. & Jian quan, Yao. Manipulation of terahertz wave using coding Pancharatnam–Berry phase metasurface. IEEE Photonics J. 10, 1–12 (2018).
Funding
This work is partly supported by, National Natural Science Foundation of China under grant number. 62171289 and partly supported by, State Key Laboratory of Radio Frequency Heterogeneous Integration, Shenzhen university, Shenzhen China (Independent Scientific Research Program number. 2024012).
Author information
Authors and Affiliations
Contributions
S.I.: Writing—review and editing, writing—original draft, visualization, validation, software, project administration, investigation, formal analysis, data curation, conceptualization. A.N.: Writing review and editing, software, formal analysis, data curation. N.U.: Writing—review and editing, methodology, formal analysis, data curation. Y.S.: Writing—review and editing, methodology, formal analysis, data curation. S.A.: Writing—review and editing, formal analysis, data curation. M.S.N.: Writing—review and editing, formal analysis, data curation. S.-W.W.: Writing—review and editing, supervision, project administration, methodology, funding acquisition, formal analysis, data curation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Iqbal, S., Noor, A., Ullah, N. et al. Polarization insensitive non-interleaved frequency multiplexed dual-band Terahertz coding metasurface for independent control of reflected waves. Sci Rep 14, 21199 (2024). https://doi.org/10.1038/s41598-024-71910-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-71910-5