Introduction

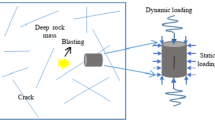
After experiencing the long-term geological activity, buried field rock masses generally contain myriads of cross fissures, which significantly influence the mechanical response of rock masses when suffering exterior dynamic loads1. For instance, as shown in Fig. 1, buried field rock masses with cross fissures under static tectonic stress can be influenced by the external dynamic disturbance from excavation, and the propagation of cross fissures affects the mechanical properties and fragment size distribution of rock masses2. In this case, static tectonic stress corresponding with static energy accumulation within the rock can be regarded as the intrinsic cause of rock failure after dynamic disturbance. So technically speaking, both the static pre-stress and dynamic disturbance influences the failure of deep rock masses3,4,5. Thus, it is necessary to investigate the effect of dynamic strain rate on the mechanical properties and fragment characteristics of rocks with cross discontinuities under static pre-stress.

Fig. 1
figure 1

Schematic diagram of the field rock masses with cross fissures under static tectonic stress and external dynamic disturbance from excavation.

Full size image

For the study of cross-fissured rocks, existing literatures mainly focus on static loading situations6. Liu et al.7,8 studied the mechanical behaviors of molded gypsum specimens with one set of cross fissures under uniaxial compression and biaxial compression, and they concluded nine crack types. Zhang et al. and Zhou et al.9,10,11,12 further conducted a series of uniaxial compression tests on rock-like materials containing one or two sets of cross fissures with different fissure configurations and they analyzed the mechanical response and crack coalescence behaviors. The preexisting cross fissure can significantly weaken the strength of rock-like materials, and the cross-fissure geometry influences the rock bridge coalescence patterns13. Zhou et al.14 systematically investigated the difference between two-dimensional and three-dimensional cracking behaviors of PMMA specimens with cross‑embedded fissures, involving crack growth, coalescence and wrapping. In addition, Cao et al.15 experimentally and numerically studied the mechanical behaviors of rock-like materials with multiple cross fissures, including the uniaxial compressive strength and failure patterns of the specimens (stepped path failure pattern, planar failure pattern, and two other shear type failure patterns). Existing literatures on the cross-fissured rock specimens under static loading are summarized in Table 1. However, the research for cross-fissured specimens under dynamic loads is rare compared to static loading conditions. Feng et al.16 studied the effects of individual dynamic strain rates on the mechanical behaviors of sandstones with symmetrical and asymmetrical cross fissures based on the Split Hopkinson Pressure Bar (SHPB) loading system.

Table 1 The summary of existing literatures on the cross-fissured specimens under individual static loading.
Full size table

Under a dynamic loading case, the load increases at a higher rate, and the deformation and fracture propagation occurs in a limited time. Thus, the fissured rock might exhibit more complicated mechanical response and fracture behaviors under dynamic loading than static loading17. Due to more energy absorption, rock materials under dynamic strain rate are generally broken into irregular-distributed fragments in a certain scale range18,19. Essentially, the formation of rock fragments experiences a complex process, which is related to the exterior loading condition and inherent constitutive behavior20,21. After suffering dynamic impact, the recovered rock fragments can be regarded as following a statistical distribution, such as Rosin–Rammler distribution22, Gate-Gaudin-Schuhmann distribution23, Weibull distribution24, and generalized extreme value (GEV) distribution25. Moreover, the fragments with fractal-based structures generally exhibit a self-similarity characteristic, where the structures show a similar pattern with different fragment scales. The fragment size can be described by the fractal behavior, and the distribution of fragment sizes can be quantitatively characterized using the fractal dimension26, a higher fractal dimension generally corresponds with more fragments with smaller volumes and higher crush degrees27.

So far, research focused on the dynamic fragmentation characteristics of fissured rocks is limited, especially for rock specimens under coupled static-dynamic loads. In this study, we systematically investigate the dynamic mechanical behaviors of cross-fissured sandstones under static pre-compression based on the SHPB dynamic loading system. In addition, the fragments of the fractured specimens are carefully collected, and a series of sieving tests are performed to reveal the fragment characteristics of broken rocks based on the fractal theory and statistical principle.

Specimen preparation and experimental equipment

A relatively homogeneous sandstone material from Neijiang, Sichuan province of China, is selected for specimen preparation in this experimental campaign. The sandstone is composed of feldspar (43%), quartz (35%), rock fragments (20%) and clay minerals (2%). All the rock specimens are prismatic in appearance, and their geometric dimensions (width × thickness × height) are 35 mm × 35 mm × 45 mm, as shown in Fig. 2a. To avoid the influence of potential anisotropy on experimental results, all the rock specimens are processed to have consistent loading directions relative to the virgin sandstone block. The preparation process of the fissured specimens is as follows: (a) place the relatively homogeneous sandstone block on a rock-cutting machine, and cut it according to the preset size to obtain the intact specimen; (b) use a high-strength alloy to process a micro-hole with 1.5 mm diameter at the geometric center of the surface where the width and height are located; (c) employ a 1-mm-thick diamond wire saw to cut the fissures with 7 mm length and desired inclination angles; and (d) polish the specimen surfaces to control their roughness to be within 0.02 mm. Three specimens are prepared for each set of experimental parameters. In this manuscript, fissure represents the preexisting through-going fractures of the specimen, and flaw stands for the generated cracks within specimens during dynamic loading process. The configuration of asymmetrical cross fissures can be defined via three geometrical parameters: fissure length (b = 7 mm), fissure inclination angle I (α = 45°) and fissure inclination angle II (β = 75°). Fissure inclination angle of zero parallel the orientation of applied dynamic load. F1 and F2 represent the tips of the preexisting fissure with inclination angle of 45°, while the F3 and F4 stand for the tips of the preexisting fissure with inclination angle of 75°, respectively (Fig. 2a). Static mechanical parameters of the cross-fissured sandstone acquired through laboratory tests include the uniaxial compressive strength of 51.2 MPa and the elastic modulus of 5.18 GPa. In addition, each rock specimen is notated as R-Dn, where R represents the ratio of static pre-stress to static uniaxial compressive strength of the fissured specimen, and Dn denotes the number of the dynamic strain rate. For example, 0.5-D3 represents the cross-fissured sandstone subjected to the static pre-stress of 0.5 times uniaxial compression strength and the dynamic strain rate numbered 3.

Fig. 2
figure 2

(a) Geometrical characteristics of the asymmetrical cross-fissured specimen and (b) schematic diagram of the SHPB rock dynamic loading system.

Full size image

A series of coupled static-dynamic compressive loading tests are conducted on the SHPB dynamic loading system, which consists of a striker system, a bar system, a data-acquiring system, and a high-speed camera system, as shown in Fig. 2b. Before loading, cross-fissured sandstones coated with Vaseline are clamped between the incident bar and the transmitted bar. Then, the specimen is axially compressed to the designated stress level in a quasi-static manner. The pre-applied static stress is assumed to be constant throughout the dynamic loading phase of the experiment and added to the dynamic stress history derived from the SHPB system. During the dynamic loading process, a compressive wave (incident wave) is generated from the striker and propagates through the incident bar28. Once reaching the incident bar-specimen interface, the incident wave can be transferred into two parts: one is the transmitted stress wave through the fissured specimen and then enter the transmitted bar, and the other one is the reflected stress wave reflected into the incident bar. The three pulse signals can be recorded via the strain gauges, which are mounted on the surfaces of incident and transmitted bars at the prescribed position and connect to the data acquiring system29,30. Figure 2b shows a typical equal arm bridge, where RG and R0 are the resistance of the strain gauge and the precise standard resistance; ΔU and U0 represent the output voltage and the input voltage of the bridge. If the RG is increased with the value of ΔR, the corresponding strain ε(t) measured via the strain gauge and the voltage signal ΔU(t) can be expressed as follows19:

$$\varepsilon \left( t \right){ = }\frac{{2\Delta U\left( {\text{t}} \right)}}{K1K2U0}$$
(1)

here, K1 and K2 stand for the sensitivity coefficient and the amplification factor of the corresponding strain gauge.

Based on the three recorded pulse signals including the incident wave signal (εi), reflected wave signal (εr) and transmitted wave signal (εt), the strain rate \(\dot{\varepsilon }\left( t \right)\), the strain ε(t), and the dynamic stress σ(t) of the cross-fissured rocks can be acquired31,32:

$$\begin{aligned} \dot{\varepsilon }\left( t \right) & = \frac{C}{{L_{{}} }}\left[ {\varepsilon_{i} - \varepsilon_{r} - \varepsilon_{tr} } \right] = \frac{{\sqrt {E/\rho } }}{{L_{{}} }}\left[ {\varepsilon_{i} - \varepsilon_{r} - \varepsilon_{tr} } \right] \hfill \\ \varepsilon \left( t \right) & = \int\limits_{0}^{t} {\dot{\varepsilon }\left( t \right)} dt = \frac{C}{L}\int\limits_{0}^{t} {\left[ {\varepsilon_{i} - \varepsilon_{r} - \varepsilon_{tr} } \right]} dt \hfill \\ \sigma \left( t \right) & = \frac{AE}{{2A_{s} }}\left[ {\varepsilon_{i} + \varepsilon_{r} + \varepsilon_{tr} } \right] \hfill \\ \end{aligned}$$
(2)

In the formula, C, A, ρ, and E represent the longitudinal wave velocity, cross-sectional area, density, and the elastic modulus of the elastic SHPB, respectively. As and L stand for the cross-sectional area and length of the cross-fissured rock specimen.

Note that the deformation of cross-fissured sandstones occurs in a very limited time during dynamic loading process. The high-speed camera is thus employed herein to capture the fracture and deformation process on the surface of cross-fissured specimens. The recorded pictures are recorded with resolution of 256 × 256 pixel at a frame rate of 180,000 frames per second (fps). Subsequently, the digital image correlation (DIC) technique is utilized to measure the full-field strain fields of rock specimens after covering speckles based on the captured photos.

Methodology

Sieving tests

A series of sieving tests are conducted after collecting the fragments of broken sandstone in the SHPB loading tests. In this manuscript, the sieve with bore diameters of 0.075, 0.25, 0.5, 1, 2, 5, 10, 20 and 40 mm is utilized. Based on the sieving results, the mean fragment size (\(\overline{M}\)) is utilized to represent the damage degree of the fissured rocks, which can be expressed as follows27:

$$\overline{M} = \sum\limits_{i = 1}^{n} {midi/Mt}$$
(3)

Here, Mt stands for the total mass of the cross-fissured rock specimen; n is the gradient value of the sieves; mi represents the mass of the fragment size between two adjacent sieves, in which the average diameter of the two sieves is represented by di.

In addition, for the statistical perspective, an exponential-like function, generalized extreme value (GEV) distribution is adopted herein to describe the fragment distribution of rock specimens, which can be expressed as follows33,34:

$$F\left( {d;\xi ,\mu ,\lambda } \right) = \exp \left\{ { - \left[ {1 + \xi \left( {\frac{d - \mu }{\lambda }} \right)} \right]^{ - 1/\xi } } \right\}$$
(4)

where represents the shape parameter; μ is the location parameter, indicating the average size of the rock fragments; λ stands for the scale parameter, describing the range of the fragment size distribution of recovered specimens. The deep analysis on the parameters μ and λ can provide rich information on the fragment size distribution and help to illuminate the strain rate effects on the distribution of rock fragmentation.

Additionally, as an effective tool to reflect the broken degree of rock fragmentation, fractal theory originally defined by Mandelbrot is employed to quantify the irregular characteristics and self-similarity of fragment size distribution35,36,37. The fractal dimension D can be calculated based on the mass and equivalent size of the broken fragments with the following formula38:

$$D = 3 - k = 3 - \left[ {\frac{{\Delta \lg (M\left( {r < r_{i} } \right)/Mt)}}{{\Delta \lg (r_{i} /r_{\max } )}}} \right]$$
(5)

where \(M\left( {r < r_{i} } \right)\) represents the cumulative fragment mass with the associated fragment size less than or equal to ri; k is the slope of the fitting line of \(\ln \left( {M\left( {r < r_{i} } \right)/M_{0} } \right)\) and \(\ln \left( {r_{i} /r_{\max } } \right)\).

Digital image correlation technique

Based on the captured images of rock specimen during dynamic loading process, the digital image correlation (DIC) technique is employed here to calculate the deformation of cross-fissured rock specimen via tracing the difference of each point in the referenced and deformed images, as shown in Fig. 3. The deformation of the point q’ (x’, y’) can be calculated as follows39:

$$\left\{ \begin{aligned} x^{\prime} & = x + u + \frac{\partial u}{{\partial x}}\Delta x + \frac{\partial u}{{\partial y}}\Delta y \hfill \\ y^{\prime} & = y + v + \frac{\partial v}{{\partial x}}\Delta x + \frac{\partial v}{{\partial y}}\Delta y \hfill \\ \end{aligned} \right.$$
(6)
Fig. 3
figure 3

Schematic diagram of the calculation principle of DIC algorithm.

Full size image

In this formula, u, v, \(\frac{\partial u}{{\partial x}}\), \(\frac{\partial u}{{\partial y}}\), \(\frac{\partial v}{{\partial x}}\) and \(\frac{\partial v}{{\partial y}}\) stand for the six deformation parameters. u and v represent x- and y- displacement components; \(\frac{\partial u}{{\partial x}}\), \(\frac{\partial u}{{\partial y}}\), \(\frac{\partial v}{{\partial x}}\) and \(\frac{\partial v}{{\partial y}}\) stand for the first-order displacement gradients of the reference subset. The displacement gradient tensor \(\nabla u\) can be expressed in the form of matrix as40:

$$\nabla u = \left[ {\begin{array}{ll} {\frac{\partial u}{{\partial x}}} & {\frac{\partial u}{{\partial y}}} \\ {\frac{\partial v}{{\partial x}}} & {\frac{\partial v}{{\partial y}}} \\ \end{array} } \right]$$
(7)

The strain tensor ε can be described as follows:

$$\varepsilon = \left[ {\begin{array}{ll} {\frac{\partial u}{{\partial x}}} & \quad {\frac{1}{2}\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)} \\ {\frac{1}{2}\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)} & \quad {\frac{\partial v}{{\partial y}}} \\ \end{array} } \right]$$
(8)

Note that the arbitrary orientation of the generated cracks during dynamic loading process. Based on the coordinate transformation, the displacement gradients and strain tensor in any direction can thus be acquired as follows:

$$\left\{ \begin{aligned} & \nabla u^{\prime} = \left[ {\begin{array}{*{20}c} {\frac{\partial u^{\prime}}{{\partial x^{\prime}}}} & {\frac{\partial u^{\prime}}{{\partial y^{\prime}}}} \\ {\frac{\partial v^{\prime}}{{\partial x^{\prime}}}} & {\frac{\partial v^{\prime}}{{\partial y^{\prime}}}} \\ \end{array} } \right] = T^{T} \cdot \nabla u \cdot T,\varepsilon ^{\prime} = T^{T} \cdot \varepsilon \cdot T \hfill \\ & T = \left[ {\begin{array}{*{20}c} {\cos \alpha } & {\sin \alpha } \\ { - \sin \alpha } & {\cos \alpha } \\ \end{array} } \right] \hfill \\ \end{aligned} \right.$$
(9)

Here, T represents the coordinate transformation matrix, α is the angle between transformed and original axis.

Results and discussion

Mechanical response

In the coupled static-dynamic loading test for cross-fissured rock specimen, the stress equilibrium of the two ends of specimen before failure should be guaranteed to avoid premature failure prior to reaching peak stress in the rock specimen33. The momentum trap is an important consideration in SHPB experiments, which was not employed in the present study. In this study, a shaper made via copper sheet with dimension of Φ10*10 mm is utilized to generated a slowly rising half sine wave to promote the stress equilibrium of the specimen during dynamic loading process. Figure 4 compares the incident stress, reflected stress, transmitted stress, and the sum of the incident stress and reflected stress of the two typical fissured specimens (Nos. 0.2-D1 and 0.8-D4) during loading process. The transmitted stress approach a favorable agreement with the sum of the incident stress and reflected stress, indicating that the valid stress equilibrium condition is achieved and maintained for the cross-fissured sandstones in the present coupled static-dynamic loading tests. Figure 5 depicts the stress–strain curves of the cross-fissured rock specimens subjected to varied coupled static-dynamic loads. All the dynamic stress–strain curves exhibit the elastic–plastic deformation characteristics before reaching the peak stress, which can be concluded into two stages. The one is the linear deformation stage, where the stress increases linearly with the increase of strain. The other one is the nonlinear deformation stage, corresponding with the unstable crack initiation and propagation. After peak stress, the stress–strain curves feature an immediate decrease, associated with the macro failure of the fissured specimen. Figure 6 shows the effects of static and dynamic strain rate on the coupled strength of the cross-fissured rock specimens under varied coupled static-dynamic loads; the details are listed in Table 2. In this study, the direct dynamic strength can be acquired from the peak values of dynamic stress–strain curves. The coupled strength is the sum of the static pre-stress and direct dynamic strength. Under the same static pre-stress, the cross-fissured specimens with higher dynamic strain rate can be characterized via the greater coupled strength, featuring evidently loading-rate dependence. However, for a given dynamic strain rate, the static pre-stress shows dual effects on the coupled strength of the fissured sandstones. The data from tests at 0.2, 0.4, and 0.6 UCS converge on a similar trend line, while the 0.8 UCS shows failure at lower dynamic stresses. When the lower static pre-stress applied on the fissured specimen, a part of preexisting micro discontinues are compressed, and the propagation of stress wave within rock specimen can be enhanced, which greatly inhibits the deterioration of rock material and induce the higher coupled strength. The greater static pre-stress can strengthen the enhancing effect of stress wave propagation, corresponding with the higher coupled strength. However, once the axial static pre-stress exceeds the limitation of elastic deformation of the rock materials, the closed micro discontinues open again, and more cracks generate within rock specimen, which provides abundant reflected surfaces for the stress wave, resulting in the decrease of the coupled strength. The 0.2, 0.4, and 0.6 UCS test are effectively testing the undeformed rock while some amount of inelastic deformation has accrued during the application of the 0.8 UCS which has weakened the rock. This complexity partly might results from the inherently strain hardening nature of microcrack growth under compressive loads before cracks reach a critical length41,42. In other words, the lower UCS tests did not achieve the critical crack length while the higher 0.8 UCS did. Similar behavior was noted in Aben et al.43 and in Braunagel and Griffith44 wherein a certain threshold of pre-existing damage was required in a sample in order to achieve a significant decline in dynamic compressive strength. Therefore, under a given dynamic strain rate, the coupled strength increases with increasing static pre-stress first and then decreases, where the maximum value occurs under the static pre-stress of 60% UCS; the similar results were also observed in the intact rock specimen and rock specimen containing combined fissures and rectangular holes5.

Fig. 4
figure 4

Dynamic stress equilibrium check for the typical cross-fissured specimens (a) (No.0.2- D1) and (b) (No. 0.8- D4).

Full size image
Fig. 5
figure 5

Three dimensional stress–strain curves of the cross-fissured rock specimens under coupled static-dynamic loading tests with different pre-stress of (a) 0.2 UCS, (b) 0.4 UCS, (c) 0.6 UCS, and (d) 0.8 UCS.

Full size image
Fig. 6
figure 6

(a) Determination of the dynamic strength and coupled dynamic strength; (b) the coupled strengths of the cross-fissured rock specimens under varied coupled static-dynamic load in three-dimensional perspective; (c) and (d) show the effects of dynamic strain rate and static pre-stress on the coupled strength and total strength of the fissured specimens.

Full size image
Table 2 Coupled strength of the fissured specimens under varied coupled static-dynamic strain rates.
Full size table

Failure mechanism

The typical failure modes of the fissured sandstones under coupled static-dynamic loads are concluded in two categories, i.e., the similar dynamic strain rate (Fig. 7a–c) and the same static pre-stress (Fig. 7d–f). It can be observed that the failure mode is mainly influenced via the dynamic strain rate ignoring the static pre-stress in this investigation. In addition, based on the DIC technology, the full-field strain and displacement field of the fissured rock specimen are analyzed to further the failure mechanism. In this study, referenced from the categories of displacement fields proposed by Zhang and Wong45, two displacement field types (DF_I and DF_II) are observed, as shown in Fig. 8a. In the region of two displacement trend lines, DF_I corresponds with relative tensile displacement, while DF_II is associated with both a relative tensile displacement and a shear displacement. In addition, in terms of macroscopic view, four cracks are observed on the specimen surface during loading process, as shown in Fig. 8b. Wing crack initiates from the fissure tips and grows along the axial loading direction, while the anti-wing crack propagates opposite to the wing crack. The shear crack generally extends coplanar or oblique with the preexisting fissure. The mixed tensile-shear cracks can be regarded as the connection of tensile and shear cracks.

Fig. 7
figure 7

Failure modes of the cross-fissured specimens under different coupled static-dynamic loads.

Full size image
Fig. 8
figure 8

(a) Two microscopic displacement field types and (b) macro crack types observed in this study.

Full size image

According to the calculated results of DIC technology, all the failure modes can be categorized into two groups including the mixed tensile-shear failure mode and the shear failure mode, shown in Figs. 9 and 10, respectively. Field rocks generally contains myriads of micro discontinues with irregular distribution due to the geotechnical activities. When the rock specimen is experienced the low dynamic strain rate with insufficient incident energy, the generated cracks generally extend and propagate along or oblique to the axial loading direction, featuring the mixed tensile-shear failure mode. In this loading case, the fissured rock specimen generally broken into large fragments. When the dynamic strain rate increases, the compressed stress wave fleetly propagates to the fissure tips, and the cross-fissured rocks absorb more energy in a short time, resulting in the initiation of more shear cracks for releasing exterior input energy and appearing in the shear failure mode. As the dynamic strain rate increases, the number of broken fragments and the evolution of shear cracks gradually increase, while the fragment size gradually decreases. Generally, a specimen with low aspect ratio may bear more confinement, due to the end friction effect on the surfaces between the specimen end and the bar46,47.

Fig. 9
figure 9

Progressive failure process of the cross-fissured specimens with mixed tensile-shear failure subjected to dynamic load.

Full size image
Fig. 10
figure 10

Progressive failure process of the cross-fissured specimens with shear failure subjected to dynamic load.

Full size image

Figure 9a–f shows the evolution of full-field strain and displacement field of the fissured rock specimen 0.6-D1 with mixed tensile-shear failure subjected to coupled static-dynamic load; Fig. 9g show the corresponding displacement field of the ultimate failure and the recovered fragments. At the initial loading stage, the main stress concentration occurs around the tips of the fissure with inclination angle of 75°, inferred from some scattered tiny high strain zones around the fissure tips F3 and F4, as shown in Fig. 9b. Then, two anti-wing cracks (A1 and A2) coalescence with the two fissure tips at the same side, forming a pair of tensile band with butterfly shape, as shown in Fig. 9c. In addition, a shear crack (S1) initiates from the fissure tip F3 and propagate to the transmitted bar-specimen surface, and two shear cracks (S2 and S3) emerge from fissure tips F1 and F2, and grow oblique to the fissure plane, as shown in Fig. 9d and e. After that, another tensile cracks (T1) initiates from the fissure tip F4, and extends to the incident bar-specimen surface, as shown in Fig. 9e. Eventually, the development of these generated cracks forms an X-shaped fracture networks, as shown in Fig. 9f.

The typically progressive failure process of the cross-fissured specimen 0.6-D4 with shear failure subjected to coupled static-dynamic load is shown in Fig. 10a–f, and the Fig. 10g show the corresponding displacement field of the ultimate failure and the recovered fragments. At the initial loading stage, similar to the specimen 0.6-D1, the relative high strain zone also distributes around the preexisting fissure with inclination angle of 75°. However, new cracks begin to initiate under the action of greater stress concentration. With further loading, strain localizations at the fissure tip propagate further, a visible fracture appears at the right side wall of the opening. During dynamic loading stage, micro cracks initiate from the tip of two pre-existing fissures and extend perpendicularly to the inclination angle; they are in the fashion of anti-wing cracks (A1 and A2). At 165.0 μs, four typical shear cracks (S1, S2, S3 and S4) initiate respectively from the fissure tips are formed as V-shaped. Then, all the cracks propagates towards the loading end and penetrate the whole specimen, gradually losing the integrity of the specimen.

Fragmentation characteristics

During coupled static-dynamic loading process, numerous fractures can be generated and propagate within the fissured rocks, resulting in broken fragments with different size distributions, accompanied with energy dissipation. Thus, the fragment size distribution of the broken specimens can reflect the deformation degree and the fracture behaviors of fissured rocks. The dynamic fragmentation characteristics of the fissured sandstone are affected by the static pre-stress and dynamic strain rate. Under low dynamic strain rate, large fragments play a dominated role in the broken specimen, and feature with columns or lamellar structures. When the fissured sandstone subjected to high dynamic impacting, the specimens are broken into small fragment with homogenous size distribution, and the relatively great cone-shape fragment can be frequently encountered in this loading condition. All the fragment size distributions of the fissured specimens after suffering coupled static-dynamic loads are shown in Fig. 11, which plots the cumulative mass percentage of rock fragment in each interval, as well as the mean fragment size for each specimen. It can be observed that the main fragment size ranges from 10 to 40 mm, and the increasing dynamic strain rate decrease the proportion of large fragments under a given static pre-stress, resulting in the smaller mean fragment size. Under a given dynamic strain rate, the smaller mean fragment size of fissured sandstone can be characterized via the higher static pre-stress.

Fig. 11
figure 11

(a) Fragment size distribution and (b) mean fragment size of the cross-fissured rock specimens under different coupled static-dynamic loads.

Full size image

Figure 12 depicts the influence of static pre-compression and dynamic strain rate on the μ and λ of the fragment size distribution with GEV fitting; the details are tabled in Table 3. The fragment size distributions of fissured sandstone after coupled static-dynamic loading can be well characterized by the GEV distribution. In this manuscript, the location parameter μ and the scale parameter λ are employed to describe the mean fragment size of broken specimen and the range of the fragment size distribution, respectively. Higher dynamic strain rate and the greater static pre-stress can induce the smaller location parameter μ, associated with smaller fragments size distribution. On the whole, the effect of static pre-stress and dynamic strain rate on the scale parameter λ is not significant. Figure 13 depicts the influence of dynamic strain rate and static pre-stress ratio on the fractal dimension of the fissured specimens under coupled static-dynamic loads in three-dimensional and two-dimensional views. In this investigation, the fractal dimension varies from 2.26 to 2.49, with relative deviation of 10.2%. Fractal dimension supplies a different viewpoint from traditional Euclidian geometry, where the dimensions of plane and body are represented via two and three48. The cross-fissured specimen under higher static pre-stress and greater dynamic strain rate can be characterized via the greater fractal dimension, corresponding with the smaller fragment size with more homogeneous distribution.

Fig. 12
figure 12

(a) and (b) depict the location parameter μ of the fragment size distribution of the cross-fissured specimens with GEV fitting in three-dimensional and two-dimensional perspective; (c) and (d) show the scale parameter λ of the fragment size distribution of the cross-fissured specimens with GEV fitting in three-dimensional and two-dimensional perspective.

Full size image
Table 3 GEV of rock specimens under different coupled static-dynamic loads.
Full size table
Fig. 13
figure 13

Influence of dynamic strain rate and static pre-stress ratio on the fractal dimension of the fissured specimens under coupled static-dynamic loads in three-dimensional and two-dimensional perspective.

Full size image

Conclusions

Field rock masses containing preexisting cross fissures at great deep generally experience both the static pre-stress and dynamic disturbances simultaneously. Understanding the mechanical behaviors of these cross-fissured rock specimens is benefit for improving the efficacy of rock breaking. This study systematically investigated the mechanical response and fragment characteristics of cross-fissured sandstones under coupled static-dynamic loads. Based on the experimental and numerical results, the following conclusions can be drawn.

  1. 1.

    Under the same static pre-load, the coupled strength of cross-fissured sandstones shows evident loading-rate dependence with the increase of dynamic strain rate. Whereas, the coupled strength of fissured specimens increases first and then decreases with increasing static pre-stress under a given dynamic strain rate. The highest coupled strength is observed under the static pre-stress of 60% UCS.

  2. 2.

    According to the calculated results of DIC technology, the failure mode is mainly influenced via the dynamic strain rate ignoring the static pre-stress in this investigation. In this investigation, all the failure modes can be categorized into two groups including the mixed tensile-shear failure mode under low dynamic strain rate and the shear failure mode under high dynamic strain rate. Regardless of the loading condition, the main stress concentration occurs around the tips of the fissure with greater inclination angle.

  3. 3.

    The dynamic fragmentation characteristics of the fissured sandstone are affected by the static pre-stress and dynamic strain rate. The higher static pre-stress and greater dynamic strain rate can induce the smaller mean fragment size, the smaller location parameter μ in GEV fitting, and the greater fractal dimension of fissured sandstones, corresponding with smaller fragment size with more homogeneous distribution. Whereas, the effect of static pre-stress and dynamic strain rate on the scale parameter λ is not significant.