Introduction

Understanding the mechanisms underlying the long-term maintenance of biodiversity is essential for improving conservation efforts and preventing further biodiversity loss1,2. Ecological communities change over time and through space as a function of numerous internal and external processes3. In this continuous assembly process some species persist while others disappear (species losses) and (re)appear (species gains) over time4,5 while maintaining local diversity. Various internal and external factors shape community assembly, therefore observing compositional changes over time might shed light on what factors drive assembly processes as well as how biodiversity is maintained in the face of environmental change5.

The combination of two major mechanisms can lead to continuous community assembly; dispersal-assembly, whereby stochastic processes such as dispersal, random birth and death events dominate6, and selection- or niche-based assembly7, whereby species interactions drive community assembly. Ecological communities are on the spectrum between niche-based and dispersal-based regimes, where their relative positions according to analytic arguments depend on population sizes and the variability of the environment8. Under highly stochastic environmental conditions, such as in river ecosystems driven by cycles of flood and drought disturbances, community assembly is often assumed to be dominated by external factors such as hydrologic variability that override biotic control of communities9,10. However, empirical evidence suggests that species interactions in stream communities, such as competition, predation and herbivory, exert important effects on population and community dynamics11,12,13. Species traits such as average body size, voltinism and feeding habits (e.g. predation) have been extensively shown to influence the dynamics of benthic communities14. In particular, benthic predators often influence the evolution of prey trait distributions. Predatory effects include increase in prey body size and change in body shape, increase in movement speed15,16, or change in voltinism such that prey species grow more slowly in the presence of predators17.

In order to empirically detect the driving force of ecological communities, we investigate the temporal relationship between species (re)appearances (gains) and disappearances (losses) in the community. Community assembly driven primarily by stochastic processes should render species gains and losses independent, uncorrelated events. However, it is possible that the same external factors drive local population disappearances or (re)appearances, potentially leading to correlated gain-loss processes—also known as the confounding effect18. By contrast, niche-based assembly theory asserts that species diversity arises from ecological selection (i.e. partially or non-overlapping niches). Species fitness differences and interactions are the main drivers of assembly that hypothetically might lead to not only correlated but causally-related species gain-loss events19. To test this cause-effect relationship, we use time-series data of benthic invertebrate communities from 66 locations across New Zealand recorded between 1990 and 2019 (Fig 1a). River flow regimes are a dominant external force in regulating stream biodiversity20,21,22. Therefore, we couple these community data with continuously monitored river flow data and species traits to generate causal linkages. Due to its maritime climate, New Zealand running waters are highly unpredictable and aseasonal relative to continental systems23,24. First, we establish our causal hypothesis for how species gains and losses are related and how external processes, in the form of highly dynamic river flow regimes, regulate this connection. To discover these causal hypotheses, we employed a nonparametric causal discovery approach based on conditional independence testing18,25. Since observational data are often confounded, they fail to establish cause-effect relationships. In this line, causal inference tools have been developed that allow us to infer causation from observational data18,25. Then, based on the discovered causal links we use a stochastic dynamic model combined with scaling theory26 to theoretically investigate what processes can potentially generate the observed cause-effect relationship between species gains and losses.

Results

Empirical results and causal hypothesis

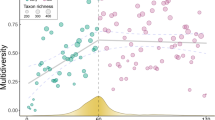
Despite the highly unpredictable river flow regimes observed in these systems, we found clear evidence of deterministic forces structuring the benthic macroinvertebrate communities. The signal-to-noise ratio of river flow indicates that macroinvertebrate communities experience a highly stochastic environment in most rivers (Fig 1b,c). However, benthic communities showed relatively stable biodiversity patterns over time (Fig 2a–c)—we found that relative species richness increased only slightly, while species evenness and species turnover remained constant during the entire time period.

Species gains and losses—defined as the relative number of species gained and lost from one time period to the next27,28—showed strong negative associations and high mutual dependence in all locations (Fig 2d, e). However, to gain cause-effect knowledge about the relationship between species gains and losses that could potentially point towards the importance of species interactions, a context must first be established. Specifically, we assume that this context incorporates stochastic processes such as environmental noise and dispersal along with other species traits that potentially affect species gains and losses in relation to assembly processes. Because species traits are naturally not independent of each other, but rather inter-related, graphical models are needed to establish causal relationships and accurately estimate effect sizes. This graphical model—also called as a causal hypothesis—can be constructed using expert knowledge or intuition or by means of causal discovery algorithms18. Here we applied a causal discovery algorithm29 on concatenated time series of each variable from all sampling sites in order to obtain a reliable average estimate of each causal link. Environmental noise was calculated from river flow data30 and species traits were measured as the community weighted mean (CWM) of body size, voltinism, dispersal, and predation (for details see Methods). The direct structural causal effects between two variables were quantified as partial Spearman’s correlation coefficients18. The causal analysis indicated that species gains and losses are causally related, describing a fluctuating behavior (Fig. 3), which was partly driven by predation. The removal of predation from the causal analysis disconnects gains and losses from the rest of the graph, which indicates that predation is the only community trait directly connected to gain-loss cycles. Body size was strongly connected to all other species traits with similar effect sizes confirming its importance of body size in structuring communities. As expected, predation and dispersal affected body size distributions in opposite directions; predation led to larger average body sizes, while better dispersal abilities caused smaller average body sizes in the community. In turn, larger-bodied communities resulted in longer average generation time. Surprisingly, environmental noise from river flow was not directly related to species gains and losses, but slightly increased the average generation time in the community. We also tested the role of environmental noise in a causal model including species turnover (the sum of species gains and losses) to complement our analysis. The analysis showed no causal link between environmental noise and any other variable (Supporting Information Fig S6).

Theoretical results

Based on the findings of the causal inference analysis, we can now establish a simple theoretical investigation in order to determine how the observed patterns between species gains and losses were generated given the relative strength of biotic interactions and stochastic processes. We generated synthetic communities combining a stochastic dynamic model with metabolic scaling theory26,31. Specifically, we defined stochastic population dynamics as a birth-death process, where new individuals are gained by \(B(n_i) = q_i + n_i \cdot \lambda _i \cdot (1 - n_i / K_i)\), where \(q_i\) is density-independent immigration rate and \(\lambda _i\) is the intrinsic growth rate. Species lose individuals as \(D(n_i) = d_i \cdot n_i + n_i \cdot \Sigma (a_{ij} \cdot n_j / K_i)\), where \(d_i\) is death rate, \(K_i\) is the carrying capacity and \(a_{ij}\) is the interaction coefficient including competitive and predator-prey interactions (see Methods for details). First, we randomly generated interaction matrices, where predation and competition coefficients were determined based on body size scaling32,33. Second, dispersal processes were mimicked by the immigration rate (\(q_i\)), which was set according to the discovered relationship between body size and dispersal in the causal analysis. The intrinsic growth rates (\(\lambda _i = G_i^{-1}\), G generation time) were also set according to the discovered relationship between size and voltinism. Based on our empirical analysis, environmental noise affected only voltinism, which was incorporated as external noise (\(\sigma _i\)) added to the intrinsic growth rates (\(\lambda _i\)) at each time step. All other parameters including immigration rate, death rate, carrying capacity and interaction coefficients were kept constant in the model (see Methods and Fig S5). Then, each community was sampled over 30 times by equal intervals under different levels of average interaction strengths, \(\mu = \{0, 0.1, 0.5, 1, 1.5\}\), defined as the mean value of all interspecific interaction coefficients. Note that interaction matrices contain both positive and negative coefficients and pairwise interactions are asymmetric. The carrying capacity (\(K_i\)) was also scaled with body size and we assumed the same death rate (\(d_i\)) for each species stemming from external sources such as flooding. All community started from a regional species pool with 55 species that is median value of empirical observations (Fig S4). The theoretical analysis confirmed that the observed empirical patterns are driven by strong species interactions. When the average interaction strengths are higher, the relationship between species gain and losses are stronger compared to very low level of interspecific interactions (Fig 4a, b). Relative richness, evenness and turnover approached the observed values when interactions were stronger (Fig 4c, d). Stochasticity alone, i.e. where the average interactions strength is zero, leads to the correlation between species gains and losses approaching zero as well as to high relative richness, highly-even species distributions with low species turnover. As expected, imposing stronger interactions reduces local species richness and species evenness and increases species turnover moving all metrics closer to the observed values.

Discussion

Both empirical and theoretical findings suggest that species gains and losses are causally-related driven by strong biotic interactions in these stochastic environments. Species gains and losses empirically showed negative association, similarly to previous observations28,34. The relationship between species gains and losses is the product of the combination of interaction structure and stochastic processes, whereby a small fraction of species persisted over time, another fraction of species had an intermediate temporal presence and the remainder species rarely appeared potentially resulting from stochastic processes and weak competitive abilities. Our theoretical predictions based on body size scaling relationships also supported that biotic interactions are needed to reconstruct the observed fluctuating relationship between species gains and losses. The role of biotic interactions in the dynamics of river ecosystems have been long debated because of the strong external forcing from cycles of floods and droughts9,10 and are therefore deemed to be highly-context dependent14. For instance, while previous work found that flow variability breaks down competitive hierarchies11 and predator–prey interactions35, benthic predators have been suggested to have cascading effects on altering prey abundance, size or age structure, behavior, and morphology14. Our causal inference analysis identified predatory effects to be partly responsible for the observed continuous community assembly reflected by species gains and losses. Second, the synthetic analysis strongly supported the role of predator-prey and competitive interactions shaping community dynamics closely matching the empirical observations.

We showed that environmental stochasticity affects the number of generations per year (voltinism), i.e. communities under higher environmental noise comprised more species with longer generation time. However, more precise information on changes in voltinism in low and high environmental noise requires further investigation with measured species trait distributions. We observed a limited effect of environmental noise on the communities in these dynamic rivers. This weak influence is expected in living systems due to species adapting to the fluctuation structure of their environment (e.g. variances and correlations) given that it remains constant over evolutionary timescales36. In our case, the highly autocorrelated noise with relatively small or in some cases nonexistent characteristic signal present in stream flow measurements (Fig. 1b) suggests that species will have developed adaptive strategies such as bet hedging37. For instance, most predatory species in our analysis were also generalists suggesting an adaptive feeding behavior to a constantly-changing environment. Due to its maritime climate and unpredictable flow regimes, New Zealand stream communities are a case in point of such adaptation, being highly generalist and opportunistic23.

Our synthetic analysis generated predictions tightly coupled to the observed metrics. As expected, increasing internal constraints reduced the number of species present from the regional pool and reduced evenness due to stronger predation and competitive exclusion within the communities. The presence of internal structure led some species to persist and some species to disappear and reappear according to stochastic events, which creates the observed fluctuations of species gains and losses. When species weakly interact, more species were included in the local communities from the regional species pool leading to highly even species distributions and low species turnover, which rendered species disappearances and (re)appearances independent events confirming previous expectations19. The synthetic analysis also revealed that the discovered causal relationships among species traits in stochastic model communities can be utilized to closely reproduce observed biodiversity patterns, without directly inferring species interactions coefficients from empirical data. In our theoretical investigation, we assumed that biological rates and interactions vary as a function of species body sizes. Body size, as a master trait, is known to scale with other species traits such as dispersal ability38, predation39, and voltinism40. Here we empirically demonstrated that body size not only correlates with, but is causally-related to other species traits and biological processes in stream communities. Predation and dispersal changed body size distribution in benthic communities corroborating previous observations15,38. The increase in average body sizes can be explained by size-selective predation of smaller-bodied prey species. Therefore, we assumed that macroinvertebrate communities are size-structured and likely governed primarily by predator-prey and competitive interactions, however, other interactions types such as facilitation might have an important role in macroinvertebrate communities41. For instance, aggregation, a form of facilitation, reduces the individual risk of predation and can benefit individuals by recycling each other’s byproducts42. Nevertheless, the causal association between predators and gains and losses, and the lack of any other direct association, indicates a dominant role of antagonistic interactions in structuring these communities.

In this work, we showed that species occurrence information allow the detection of mechanisms driving community dynamics by combining causal inference analysis with theoretical models. Following a causal discovery approach, we identified causal links between species traits, environmental noise and internal processes. Then, we used the information obtained from causal discovery to calibrate and parameterize a stochastic trait-based dynamical model. Given the high match between the theoretical results and observations, we believe that our work provides a future avenue towards a data-driven general framework to investigate continuous community assembly.

Methods

Data

Overall, we analyzed 1795 communities from 66 geographical sites (Fig. 1) across New Zealand comprising population abundance data from more than 114 macroinvertebrate taxa sampled from 1990 to 2019. These surveys were conducted for New Zealand’s National River Water Quality Network (NRWQN)43. Samples were collected following standardized protocols43 and under baseflow conditions. Seven Surber samples (\(0.1\hbox {m}^2\) and 250 \(\mu \)m mesh net) were collected on all sampling occasions during which macroinvertebrates were removed from a 0.1 \(m^2\) area in the sampler down to a depth of ca. 10 cm and from as many substrate types as possible. Individuals were later identified in the laboratory, to the lowest practicable taxonomic level44. The information on functional traits related to morphology, life-history, dispersal strategies and resource acquisition methods was obtained from the New Zealand freshwater macroinvertebrate trait database prepared by NIWA, which has been explicitly developed for New Zealand’s standardised freshwater macroinvertebrate sampling protocols45. Functional traits were fuzzy-coded from 0 to 346 and converted to a single value for each taxon using weighted averages. Daily average river discharge data (l/s) at each sampling location collected from NIWA database. The time series of environmental noise was obtained as the root mean squared noise, or amplitude of all noncharacteristic frequencies of the daily average time series of each year using FFT (Fast Fourier Transform). Flow data were log10-transformed and normalised by the average discharge across the entire period at each site30.

Species gains and losses were calculated as the number of species gained and lost from previous to next year divided by the total number of species observed in both years27,28. Furthermore, we used traditional biodiversity metrics that capture important structural aspects of communities such as number of species at given time compared to the number of species occurred in that given location over the studied period (relative richness), species abundance distribution (evenness) and species identity change over time (species turnover). Species evenness (J) is a description of the distribution of species abundances within a community and is defined as the Shannon information entropy divided by the maximum entropy of relative species abundances: \(J = - \Sigma _{i=1}^{S} P_i log[P_i] / logS \), where \(P_i\) is the relative abundance of species i. Species turnover—defined as the relative number of species gained and lost from one time period to the next — describes local compositional changes over time27,28. The relationship between species gain-loss time-series were quantified by Spearman’s correlation coefficient and normalised mutual information. Mutual information is a nonparametric and non-monotonic similarity metric between two random variables and calculated as \(MI_{XY} = H(X) + H(Y) - H(X,Y)\), where H denotes the Shannon entropy. The \(MI_{XY}\) was then normalised by the maximum mutual information : \(NMI_{XY} = MI_{XY} / MI^{max}_{XY}\), where \(MI^{max}_{XY} = min(H(X),H(Y))\).

Causal discovery and causal effects

In order to infer causal relationships from observational time series, a first step involves the construction a graphical causal model, i.e. DAG (directed acyclic graph), among the variables in question referred to as causal discovery18. Causal discovery algorithms based on conditional independence testing (or constraint-based approaches) have four major steps: first, we start with a full undirected graph on n nodes (variables), with edges between all nodes. Second, we test each pair of variables X and Y, and each set of other variables S. If X and Y variables are independent given S (\(X \perp \!\!\! \perp Y |S\)), the edge between X and Y should be removed. Third, we search for colliders (i.e. nodes that receive edges from at least two other nodes) by checking for conditional dependencies between independent variables where \(X \perp \!\!\! \perp Y\), but \(X \not \!\perp \!\!\!\perp Y |S\) . Lastly, we orient the remaining undirected edges (if possible) by consistency with already-oriented edges. We applied the PC (Peter-Clark) algorithm for time series data29,47. In order to obtain a general picture of the causal relationships among our variables and to gain statistical confidence, we combined each variable of all 66 sites into a single concatenated time series48. All variables V were shifted with a time lag of \(\tau = 1\) (variables were first shifted then concatenated). The time lag corresponds to the average generation time of the macroinvertebrate species, where most species are uni- or plurivoltine (Fig S4). We did not include the time lagged version of the environmental noise in the causal model due to its high temporal autocorrelation (Fig. S1). Since, all variables were continuous random variables but from different distributions, nonparametric Spearman’s partial correlation test have been applied to test for conditional independence49,50. The threshold for conditional independence tests were set to \(\alpha = 5 \cdot 10^{-4}\) based on Structural Hamming Distance (SHD) analysis51,52. The SHD analysis counts the number of edge insertions, deletions and flips between two completed partially directed cyclic graphs (CPDAG)52, the PC algorithm generates a stable skeleton, but edge orientation can be dependent on the ordinality of the variables added to the algorithm49. Therefore, we measured the SHD between two CPDAGs with randomly ordering the variables. This was repeated 5000 times in order to obtain the threshold (\(\alpha \)) for the analysis that gives the most stable CPDAGs (with the smaller SHD) regardless of the order of variables (see Fig. S2). The window causal graph (Fig. S3), which covered all variables (\(V_t\) and \(V_{t+1}\)), showed time consistency. The summary causal graphs (Fig. 3) which was deduced from the window causal graph and directly relate variables without time, gives an overview of the relationships47. The effect sizes were calculated as partial correlation coefficients applying the corresponding adjustment sets based on the window causal graph.

Theoretical analysis

We defined the population dynamics as a birth-death process8,53. The population birth B(n) and death D(n) rates are expressed as \(B(n_i) = q_i + n_i \cdot \lambda _i \cdot (1 - n_i / K_i) \) and \(D(n_i) = d_i \cdot n_i + n_i \cdot \Sigma (a_{ij} \cdot n_j / K_i) \). We consider that a community of species is characterized by an interaction matrix (A), whose elements (\(a_{ij}\)) define the direct per-capita effect of a species j on the per-capita growth rate of a species i. Note that \(a_{ij}\) and \(a_{ji}\) are not the same. Interaction matrices were generated using scaling relationships based on species body masses: \(M_i = M_0 \cdot 10^{k_i}\) with \(k_i \sim N(1,0.3)\) and \(M_0 = 1\). Competitive and predator-prey interaction coefficients were estimated as \(a_{ij} = a_0 M_i^{s_i} M_j^{s_j}\) with \(s_i=2/3\) and \(s_j=11/12\)32 or \(s_i=-3/4\) and \(s_j=3/4\)33, respectively. The interaction matrices with a certain average interaction strength (excluding the diagonal elements) were generated via one-dimensional optimisation process. The immigration rate (\(q_i\)) scaled with body sizes \(n_0 \cdot M_i^{-1/4 + \epsilon _i}\) with added Gaussian noise N(0, 0.1) to the exponent, where \(n_0 = 10\), which represent the noise resulting from dispersal processes (see Supporting Information). The amount of noise added were set to simulate the observed values obtained from causal inference analysis. Note that dispersal abilities generally positively scale with body mass, however in our empirical analysis smaller macroinvertebrate species have better dispersal abilities. We added external noise (representing environmental fluctuations) by varying the intrinsic growth rates (\(\lambda _i\)) of all species at each time step54. The intrinsic growth rates were scaled with body masses as \(\lambda _i^{-1/4 + \sigma _i}\) adding noise (\(\sigma _i\)) drawn from normal distribution N(0, 0.1) to the exponent. The intrinsic growth rates represent the inverse generation time, i.e. species with longer generation time have lower birth rates. The amount of noise added was set to simulate the observed values obtained from the causal inference analysis (see Supporting Information). Carrying capacities were calculated based on body size scaling as \(K_i = K_0 \cdot M_i^{-3/4 + \gamma _i}\), where \(\gamma _i\) is drawn from N(0, 0.1) and \(K_0 = 10^3\). Death rates were uniformly set to 0.5 across all species. In each case, the fraction of predator species were set to 40% similar to observations (see Supporting Information). The state of the system can be characterized by the probability P of having n individuals at time t. The time evolution of the probability distribution is described by a differential equation called a master equation: \( \frac{dP(n,t)}{dt} = \sum \limits _{i} \{ (D(n_i+1) \cdot P(n_i+1,t) + B(n_i-1) \cdot P(n_i-1,t) ) - (B(n_i) \cdot P(n_i, t) + D(n_i) \cdot P(n_i,t) ) \} \). Communities were simulated using Gillespie’s algorithm55. Simulations were run starting with 55 species representing the regional species pool across different levels of average interaction strengths, \(\mu = \{0.01, 0.1, 0.5, 1, 1.5\}\), each interaction strength was replicated 100 times. Each stochastic simulation process was sampled over 30 times by equal time intervals. At each sampling event species identities and abundances were recorded.

Fig 1
figure 1

Sampling locations and river discharge in New Zealand. (a) Macroinvertebrate communities sampled annually across New Zealand rivers over 30 years at 66 sampling sites. (b) The signal-to-noise ratio (SNR) of river discharge time series indicate that New Zealand have rivers ranging from (c) aseasonal (left) to highly seasonal (right) discharge patterns.

Full size image
Fig 2
figure 2

Community metrics. Macroinvertebrate communities were sampled annually across New Zealand rivers over 30 years at 66 sampling sites. (a) Communities show overall a slight increase in richness through time. (b) Species evenness was also unchanged through time. (c) Species identity changes in communities were steady over time with relatively high turnover rates. (d) Species gains and losses were negatively correlated in each community (measured as the Spearman’s correlation) (e) with various levels of mutual dependence (dashed orange lines indicate the average value).

Full size image
Fig 3
figure 3

Causal graph. Causal relationships between species gains and losses, environmental noise (measured as the noise component of Fourier transform of river discharge) and community weighted mean (CWM) traits. Using causal discovery (PC algorithm) for time series data, results show that predation is the only variable that is directly linked to species gains and losses. Species gains and losses have a negative bidirectional relationship indicating the presence of cycles. Higher environmental noise slightly increases the mean generation time (voltinism) in the community. Higher predation leads to larger average body sizes and higher dispersal tend to lead to smaller body sizes. Larger average body sizes increases the average generation time.

Full size image
Fig 4
figure 4

Synthetic analysis of continuous community assembly. Communities assuming stochastic birth-death processes were generated with different levels of interaction strengths over 30 sampling events repeated 100 times for each parameter level. Interaction strengths refer to the average value of the non-diagonal elements of the interaction matrix. The purple dashed line indicates the empirical values. Panel (a) shows the Spearman’s correlation coefficient and panel (b) depicts the mutual information between species gains and losses time series. Stronger species interactions caused a more stronger negative association between gains and losses time series and higher mutual information. (c) Species richness is the highest when species do not interact and decreased with interaction strength. Similarly, interaction strength decreased (d) species evenness and increased (e) species turnover.

Full size image