Decoupling and predicting natural gas deviation factor using machine learning methods

Abstract

Accurately predicting the deviation factor (Z-factor) of natural gas is crucial for the estimation of natural gas reserves, evaluation of gas reservoir recovery, and assessment of natural gas transport in pipelines. Traditional machine learning algorithms, such as Support Vector Machine (SVM), Extreme Gradient Boosting (XGBoost), Light Gradient Boosting Machine (LightGBM), Artificial Neural Network (ANN) and Bidirectional Long Short-Term Memory Neural Networks (BiLSTM), often lack accuracy and robustness in various situations due to their inability to generalize across different gas components and temperature-pressure conditions. To address this limitation, we propose a novel and efficient machine learning framework for predicting natural gas Z-factor. Our approach first utilizes a signal decomposition algorithm like Variational Mode Decomposition (VMD), Empirical Fourier Decomposition (EFD) and Ensemble Empirical Mode Decomposition (EEMD) to decouple the Z-factor into multiple components. Subsequently, traditional machine learning algorithms is employed to predict each decomposed Z-factor component, where combination of SVM and VMD achieved the best performance. Decoupling the Z-factors firstly and then predicting the decoupled components can significantly improve prediction accuracy of all traditional machine learning algorithms. We thoroughly evaluate the impact of the decoupling method and the number of decomposed components on the model’s performance. Compared to traditional machine learning models without decomposition, our framework achieves an average correlation coefficient exceeding 0.99 and an average mean absolute percentage error below 0.83% on 10 datasets with different natural gas components, high temperatures, and pressures. These results indicate that hybrid model effectively learns the patterns of Z-factor variations and can be applied to the prediction of natural gas Z-factors under various conditions. This study significantly advances methodologies for predicting natural gas properties, offering a unified and robust solution for precise estimations, thereby benefiting the natural gas industry in resource estimation and reservoir management.

Introduction

The deviation factor stands out as one of the most critical thermodynamic properties of natural gas, serving as the foundation for computing various other properties such as natural gas density, volume coefficient, and heat capacity¹. Essentially, the natural gas Z-factor quantifies the ratio of the real natural gas volume to its theoretical volume. This parameter plays a pivotal role in correcting measurements of gas volume, as it encapsulates the non-ideality of natural gases. Its significance reverberates throughout the entire natural gas process, spanning from extraction to transportation². Accurately predicting the Z-factor of natural gas is paramount for ensuring the precision and consistency of gas measurement and metering. This level of accuracy carries significant implications across multiple domains, including the estimation of gas in place, determination of gas reservoir recovery, assessment of pipeline transport capacity, and comprehension of fluid dynamics behavior within pipelines^3,4,5.

The value of the Z-factor depends on factors such as the components, temperature, and pressure of natural gas. Generally, there are two methods to obtain the Z-factor. One involves experimental studies through constant volume depletion (CVD) tests, and the other relies on empirical or semi-empirical mathematical correlations for estimation^6,7. CVD experiments are considered the most accurate means of obtaining the Z-factor, requiring fluid samples from gas well to simulate reservoir behavior at different pressure depletion stages⁸. Despite laboratory tests being theoretically more accurate than mathematical relationships in estimating the Z-factor, there are two significant drawbacks. Firstly, it requires obtaining well stream for experiments, which is impractical throughout the entire life cycle of natural gas production for CVD experiments. Additionally, for a gas reservoir, the impact of the natural gas accumulation process results in significant variations in gas components at different locations⁹. Sampling and testing for each well, especially in gas fields with potentially hundreds of wells, is impractical. Secondly, experimental acquisition of the Z-factor requires expensive laboratory facilities and complex experimental procedures, making it challenging to estimate the cost and time investment for non-specialists¹⁰. Consequently, laboratory testing is not suitable for routine industry analysis.

The second commonly used method to obtain the Z-factor is through empirical or semi-empirical mathematical approaches. Mathematical approaches are typically developed based on a large dataset of Z-factors to establish correlations applicable under specific conditions¹¹. Each Z-factor correlations developed in previous research has its own advantages and limitations in estimating the accuracy of the Z-factor. The applicability of these correlations largely depends on the gas components, including the content of non-hydrocarbons such as nitrogen, carbon dioxide, and heavy hydrocarbons¹². The content of these components varies based on region, pressure, and temperature range. None of these correlations can guarantee universal applicability across all components and under any temperature and pressure conditions¹³. Especially when the content of $\hbox {CO}_2$ and $\hbox {H}_2$S is high, most correlations failed to estimate Z-factors, leading to significant errors in predicting the Z-factor^14,15. Therefore, determining the optimal Z-factor correlation for different gas reservoirs in various regions remains a challenging task. Additionally, developing a suitable correlation is quite difficult. The mentioned developed Z-factor correlations typically involve over 10 undetermined parameters. The complexity of correlations is staggering, making the development of an accurate correlation challenging for engineers. Moreover, correlations based on the equation of state are often implicit, requiring expensive iterative computational costs¹⁶.

The rapid development of data-driven methods in recent years has provided a straightforward and swift path for the development of Z-factor prediction models. The correlation of natural gas Z-factors, and even other properties such as viscosity and density, is essentially a nonlinear function with pressure and temperature. Machine learning models demonstrate powerful capabilities in regression and prediction of nonlinear functions^17,18,19. Nevertheless, conventional machine learning algorithms like SVM, XGBoost and LightGBM have poor generalization ability in predicting Z-factor and are less commonly used. Therefore, researchers have developed numerous improved models based on ANNs to characterize the properties of natural gas²⁰. Chamkalani et al. introduced particle swarm optimization and genetic algorithms to optimize neural networks, thus developing an ANN model for predicting the Z-factor²¹. Tariq & Mahmoud utilized ANNs to linearly present an improved Z-factor empirical correlation, addressing the issue of correlations inaccurately predicting the Z-factor at high gas reservoir pressures¹⁶. Tariq et al. developed a data-driven model to estimate the natural gas density²². Orodu et al. compared conventional methods and machine learning methods in predicting the natural gas density at high temperatures and pressures²³. Faraji et al. used ANN to develop a model predicting the Z-factor of two-phase condensate gas⁹. Numerous ANN based models have been developed to address the issue of conventional correlations failing to accurately predict Z-factors under abnormal conditions^24,25. On the other hand, unlike conventional machine learning algorithms, the architecture of ANNs is arbitrary, and its design varies significantly across different datasets²⁶. ANNs do not have a unified architecture to predict the Z-factor under various conditions. Thus, researchers have selected a large number of other algorithms to predict the Z-factors under specific conditions. Gaganis et al. developed a hybrid model based on Truncated Regularized Kernel Ridge Regression algorithm in conjunction with a simple linear-quadratic interpolation scheme to estimate the Z-factor in the presence of impurities²⁷. Maalouf et al. applied the kernel ridge regression in the form of the recently developed truncated regularized kernel ridge regression algorithm to estimate Z-factor²⁸. Abdolhossein et al. proposed a second-order polynomial method based on the group method of data handling²⁹. However, due to the complexity of the Z-factor itself, these improved models are only applicable under specific conditions. The previously proposed algorithms including SVM, XGBoost, LightGBM ANNs and other algorithms mentioned above cannot be generalized to different gas components, temperature and pressure conditions, and therefore often lack accuracy and robustness in various prediction situations.

This paper aims to develop a straightforward and efficient machine learning framework capable of swiftly predicting Z-factors under diverse temperature and pressure conditions, as well as complex natural gas compositions. Given that natural gas comprises a mixture of various gas components, each exerting a collective influence on its thermodynamic properties, the Z-factor serves as a comprehensive representation of their combined impact. Drawing inspiration from this concept, we employ a signal decomposition algorithm to decoupled the Z-factor into several components. Subsequently, utilizing pseudo pressure, pseudo temperature, temperature, and pressure as independent variables, we apply conventional machine learning methods to predict these decoupled variables separately, before reassembling and summing the Z-factor. Remarkably, this model achieves exceptionally high accuracy without relying on complex network structures or intricate parameter tuning, rendering it easily accessible to engineers for practical applications in gas reservoir development and production.

Methodology

Basic dataset

The foundational Z-factor data for developing the machine learning models were sourced from gas wells of the Jurassic Shaximiao Formation gas reservoir in the Sichuan Basin, China. The Shaximiao Formation is a thick red formation developed in the Middle Jurassic of the Sichuan Basin, with a thickness ranging from 1000 to 2000 m. It primarily consists of dark purple-red mudstone, interspersed with multiple sets of sandstone. The reservoir pressure ranges from 19.1 to 26.5 MPa, and the pressure coefficient varies between 0.845 and 1.155. The reservoir temperature ranges from 323.86 to 356.75 K with an average of 338.23K. Natural gas migrates from the underlying source rocks Xujiahe Formation through large faults³⁰. Influenced by the gas accumulation, trapping conditions and gas migration, there are significant differences in the components of natural gas at different locations. Among the sampled gas wells, 88% contain wet gas, while 12% contain condensate gas. We collected a total of 6914 sets of Z-factors with different components at different temperature and pressure. All Z-factors were obtained through CVD experiments.

The statistical summary of natural gas components and properties in the dataset is presented in Table 1 and Fig. 1. The hydrocarbon composition of natural gas is predominantly methane, with methane content ranging from 73.391 to 93.728%. Ethane content varies from 4.512 to 10.4%. The dryness coefficient ranges from 0.858 to 0.944, indicating predominantly wet gas³⁰. Additionally, the natural gas contains around 1% nitrogen, approximately 0.08% carbon dioxide, and around 0.3% C₇⁺ components.

Figure 1

Boxplot of components and properties of natural gas.

Table 1 The mole fraction and gas properties of natural gases used for modelling.

Machine learning models

In this section, we briefly introduced the main principles of machine learning algorithms used in this study. This article primarily employs five regression algorithms: SVM, XGBoost, LightGBM, ANN and BiLSTM. The solutions and implementations of the models can be found in most machine learning library such as Pytorch, Keras, TensorFlow, and MATLAB³¹. However, all the models in this paper are implemented under the MATLAB 2023a library (https://www.mathworks.com)³².

SVM

SVM is a supervised learning algorithm that includes Support Vector Regression (SVR) for regression. It demonstrates good robustness and adaptability in addressing non-linear regression problems. In regression problems, the goal is to fit the data and find a function that minimizes the error between predicted values and actual values. The loss is zero only when the actual value f(x) and the predicted value y are exactly the same. In the case of SVR used for regression problems, the objective is to find a hyperplane that minimizes the distance between the training data points and this hyperplane within a certain tolerance $\epsilon$. In other words, the loss is only calculated when $|f(x)-y|>\epsilon$. It is equivalent to constructing a band with a width of $2\epsilon$ centered around $f(x)=\omega \cdot x+b$, as illustrated in Fig. 2a. If the training samples fall within the interior of this band, the prediction is considered correct, resulting in no loss³³.

SVR finds the optimal hyperplane by minimizing a loss function with a tolerance threshold and regularization term. Its optimization objective can be formulated as a minimization problem with a penalty term. Typically, a loss function with L1 or L2 regularization is employed to control the model’s complexity³⁴. The minimized objective function can be expressed as:

$$\begin{aligned} SVM_{-}Loss=\min _{\omega , b} \frac{1}{2}\Vert \omega \Vert ^{2}+C \sum _{i=1}^{n} L_{\varepsilon }\left( y_{i}, \omega \cdot x_{i}+b\right) \end{aligned}$$

(1)

where $\omega$ is the normal vector of the hyperplane; i is the data index; n is the number of training samples; C is the regularization parameter; $L_\epsilon$ is the loss function; $y_i$ is the true label; b is the margin of the “band”, which serves as the penalty term and is typically a penalty for model complexity.

XGBoost

XGBoost is an ensemble learning method based on the gradient boosting framework. Its fundamental learner is a decision tree, and by combining multiple base learners, each iteration iteratively corrects the errors of the previous round’s model, thus constructing a robust model. The difference between XGBoost and random forest lies in how the models are trained. In each step, XGBoost adds a tree based on the previous step, and the newly added tree is designed to address the deficiencies of the preceding one. Its basic structure is illustrated in Fig. 2b. Due to XGBoost incorporating the complexity of tree models into the regularization term, it excels in preventing overfitting and enhancing generalization performance as well³⁵.

XGBoost trains the model by minimizing the sum of weighted residuals. The loss function includes terms for prediction errors and regularization. The objective function of XGBoost is to minimize the loss function, and its general form is typically expressed as:

$$\begin{aligned} XGBoost_{-} L o s s=\sum _{i=1}^{n} L\left( y_{i}, \hat{y}_{i}\right) +\sum _{k=1}^{K} \Omega \left( f_{k}\right) \end{aligned}$$

(2)

where n is the number of training samples; $\hat{y}_{i}$ is the predicted value; $L\left( y_{i}, \hat{y}_{i}\right)$ is typically the Mean Squared Error (MSE) loss function; $\omega (f_k)$ is the regularization term for decision tree $f_k$, used to control model complexity and prevent overfitting.

LightGBM

LightGBM is similar to XGBoost, both being machine learning models based on the gradient boosting mechanism, as illustrated in Fig. 2. While XGBoost can precisely find split points, it incurs significant computation and memory overhead and is prone to overfitting. LightGBM utilizes a learning method optimized with histograms, adopts a leaf-wise growth strategy, and supports feature parallelism, reducing the number of candidate split points and memory usage, enhancing computational speed, and effectively preventing overfitting³⁶.

During the training process, the LightGBM algorithm differs from traditional Gradient Boosting Decision Trees (GBDT) algorithms by not requiring multiple passes through the entire dataset. Instead, it utilizes residuals, using the previous round of training as the input for the subsequent round. LightGBM primarily splits decision trees through histograms, employing an intelligent leaf-wise growth strategy based on depth constraints to compute, dividing feature values into discrete intervals and then constructing histograms. LightGBM employs a leaf-wise growth strategy with depth limitations, replacing the level-wise growth strategy typically used in GBDT algorithms. In comparison to XGBoost level-wise growth strategy, LightGBM leaf-wise growth strategy reduces the computational cost of finding the optimal split points, lowering the overall computational burden. This efficiency makes LightGBM more memory-efficient and mitigates the risk of overfitting³⁷.

Feature parallelism can effectively handle high-dimensional data, with each processing unit focusing on only a subset of features. LightGBM follows a parallel computing strategy, dividing the dataset into several nodes, where different nodes process features in parallel, and then model parameters are updated by merging the results from each node. Additionally, LightGBM supports cross-validation to evaluate model performance and provides early stopping functionality, which halts training when the performance on the validation set no longer improves to prevent overfitting. In practical use, LightGBM iteratively optimizes the tree structure and requires careful adjustment of hyperparameters based on the dataset and learning objectives to achieve optimal performance.

ANN

ANNs are suitable for handling complex nonlinear regression problems and can be adapted to specific tasks by adjusting the network structure and parameters. An artificial neural network consists of three main parts: the input layer, the hidden layers, and the output layer⁵. Each layer’s neurons are connected by weights. The neurons in the input layer are used to receive input data from external sources. The hidden layers, located between the input and output layers, can consist of one or more layers. Each hidden layer is composed of multiple neurons, which are connected by weights. The main role of the hidden layers is to extract features. The output layer is the final layer of the network and is used to produce the final output variable in regression tasks. ANNs utilize multiple hidden layers and activation functions to capture the nonlinear relationships in the data, and they prevent overfitting through standardization and validation sets. This study employs a neural network with three hidden layers: the first layer has 12 neurons, the second layer has 10 neurons, and the third layer has 8 neurons, as shown in Fig. 2d. All hidden layers use the ReLU activation function, which is very effective in handling nonlinear problems and can help mitigate the vanishing gradient problem. The ReLU activation function is defined as follows:

$$\begin{aligned} ReLU(x)=max(0,x) \end{aligned}$$

(3)

BiLSTM

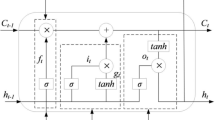
LSTM and BiLSTM are effective in capturing long-term dependencies in sequential data. Originally designed for time series prediction problems, both are frequently utilized in regression problems due to their powerful feature extraction capabilities. Derived from recurrent neural networks (RNNs), LSTM introduces improvements to the structure of the hidden layer on the traditional RNN architecture of input, hidden, and output layers. It achieves this by introducing gating mechanisms to control the information flow, selectively retaining or discarding information through these gates. This ultimately alleviates the issues of gradient vanishing or exploding caused by the derivative multiplication, effectively enhancing the memory capacity of deep learning networks³⁸. The basic architecture of an LSTM single hidden layer includes forget gate, input gate, and output gate, as described in Fig. 2e.

BiLSTM is an improvement of LSTM, and its hidden layer is composed of both forward LSTM and backward LSTM, considering both past and future information of the data. Its structure is shown in Fig. 2f, and the BiLSTM memory network has two-directional transmission layers. The forward layer follows the forward training time series, the backward layer follows the backward training time series, and both the forward and backward layers are connected to the output layer³⁹.

LSTM controls the selection or forgetting of data information through the forget gate, deciding which effective information in the training data is used for training. The amount of information to be stored in the memory unit is determined by the input gate. The input gate is used to control the amount of current input data $x_t$ flowing into the memory unit. The output gate controls the influence of the memory unit $c_t$ on the current output value $h_t$⁴⁰. Their formulas are:

$$\begin{aligned}{}&f_{m}=\sigma \left( \varvec{W}_{m}\left[ h_{t-1}, x_{t}\right] +b_{m}\right) \end{aligned}$$

(4)

$$\begin{aligned}{}&i_{t}=\sigma \left( \varvec{W}_{i}\left[ h_{t-1}, x_{t}\right] +b_{i}\right) \end{aligned}$$

(5)

$$\begin{aligned}{}&o_{t}=\sigma \left( \varvec{W}_{o}\left[ h_{t-1}, x_{t}\right] +b_{o}\right) \end{aligned}$$

(6)

$$\begin{aligned}{}&h_{t}=o_{t} \tanh \left( c_{t}\right) \end{aligned}$$

(7)

where $f_m$ is the state of the forget gate, the closer its value is to 0, the more forgotten information; $\sigma$ is the Sigmoid function; $\varvec{W}$ and b are the weight matrix and bias term of the forget gate, input gate, and output gate; $h_{t-1}$ is the result of the previous output; $x_t$ is the information input at the current time t; $i_t$ is the state of the input gate, the higher its value, the higher the importance of new information, and unimportant information will be deleted. $o_t$ is the state of the output gate, the closer its value is to 0, the more external state $h_t$ can obtain more information from the memory unit $c_t$.

BiLSTM consists of two LSTM networks in different directions. Input information is passed to the two-directional LSTM networks, and the input sample signal is output from the forward LSTM layer as $h_t$ and from the backward LSTM layer as $h_t$. The output $y_t$ is jointly determined by the outputs of the LSTM from both directions, and its update formula is as follows,

$$\begin{aligned} \left\{ \begin{array}{l} \overrightarrow{h}_t={\text {LSTM}}\left( x_t, \overrightarrow{h}_{t-1}\right) \\ \overleftarrow{h}_t={\text {LSTM}}\left( x_t, \overleftarrow{h}_{t-1}\right) \end{array}\right. \end{aligned}$$

(8)

$$\begin{aligned} y_t=\overrightarrow{\varvec{W}} \overrightarrow{h}_t+\overleftarrow{\varvec{W}} \overleftarrow{h}_t+b_y \end{aligned}$$

(9)

where $\overrightarrow{\varvec{W}}$ and $\overleftarrow{\varvec{W}}$ are the weight matrix from the forward and backward LSTM layer to the output layer, respectively; $b_y$ represents the bias matrix of the output layer.

Figure 2

Structure of models used in this study.

Decoupling methods

The method of decoupling Z-factors mainly employs signal decomposition algorithms. The primary purpose of signal decomposition algorithms is to decompose complex signals into different components for a better understanding of the structure, nature, and characteristics of the data. Utilizing signal decomposition algorithms to decouple Z-factors helps extract useful information from the Z-factors, remove noise, reveal patterns hidden in the data, and provide a foundation for further analysis and processing. In the process of decoupling Z-factors, we mainly use three signal decomposition methods: VMD⁴¹, EFD⁴², and EEMD⁴³. In subsequent studies, we compared the performance of the three hybrid models VMD+SVM, EFD+SVM and EEMD+SVM on the testing set, VMD was selected due to its best performance. Therefore, the usage process and principle of VMD is mainly introduced. The other two algorithms with poor performance are used for comparison, which will not be described in detail. The workflows of other signal decomposition methods are similar, and more detailed explanations about all decomposition methods can be found in the references cited above.

The specific implementation steps of using VMD to decouple Z-factors are as follows: (1) Establish a variational model. Hilbert transform is used to decompose the original data f(t) into K components. Each component has a finite bandwidth around the center frequency. Then, data is shifted to baseband and mix the center frequency to estimate the signal bandwidth, ensuring that the sum of the estimated bandwidths of each mode is minimized, and the sum of all components is equal to the original signal. The constructed variational function model is as follows:

$$\begin{aligned} \left\{ \begin{array}{c} \min _{\left\{ u_{k}\right\} \left\{ \omega _{k}\right\} }\left\{ \sum _{i=1}^{K}\left\| \partial _{t}\left[ \left( \delta (t)+\frac{j}{\pi t}\right) * u_{k}(t)\right] e^{-j \omega _{k} t}\right\| _{2}^{2}\right\} \\ \text{ s.t. } \sum _{i=1}^{K} u_{k}=f(t) \end{array}\right. \end{aligned}$$

(10)

where $u_k$ and $\omega _k$ are, the i-th modal component and central frequency after decomposition, respectively; $\partial _t$ is the partial derivative with respect to time t; $\delta (t)$ is the Dirac function; j is the imaginary unit; $u_k (t)$ is the modal function.

(2) Solve the optimal solution of the variational model. Lagrangian multiplier operator $\lambda (t)$, Lagrangian parameter $\lambda$, and quadratic penalty parameter $\alpha$ are introduced for solving. Equation (11) is transformed into the augmented Lagrangian function:

$$\begin{aligned} \begin{array}{l} L\left( \left\{ u_{k}\right\} ,\left\{ \omega _{k}\right\} , \lambda \right) =\alpha \sum _{i=1}^{K}\left\| \partial _{t}\left[ \left( \delta (t)+\frac{j}{\pi t}\right) * u_{k}(t)\right] e^{-j \omega _{k} t}\right\| _{2}^{2} +\left\| f(x)-\sum _{i=1}^{K} u_{k}(t)\right\| _{2}^{2} +\left\langle \lambda (t), f(t)-\sum _{i=1}^{K} u_{k}(t)\right\rangle \\ \end{array} \end{aligned}$$

(11)

where $\alpha$ is the penalty parameter; $\lambda (t)$ is the Lagrange multiplier.

(3) Alternate direction method of multipliers is used to solve $u_k^{n+1}$, $\omega _k^{n+1}$ and $\lambda ^{n+1}$:

$$\begin{aligned}{}&u_k^{n+1}(\omega )=\frac{f(\omega )-\sum _{i \ne k} u_i(\omega )+\frac{\lambda (\omega )}{2}}{1+2 \alpha \left( \omega -\omega _k\right) ^2} \end{aligned}$$

(12)

$$\begin{aligned}{}&\omega _k^{n+1}=\frac{\int _0^{\infty } \omega \left| u_k(\omega )\right| ^2 d \omega }{\int _0^{\infty }\left| u_k(\omega )\right| ^2 d \omega }\end{aligned}$$

(13)

$$\begin{aligned}{}&\lambda ^{n+1}(\omega )=\lambda ^n(\omega )+\tau \left( f(\omega )-\sum _k u_k^{n+1}(\omega )\right) \end{aligned}$$

(14)

where n is the iterations; $\tau$ is the time step of the dual ascent.

(4) Repeat procedure in step (3) until solution satisfies the convergence condition. Then K components with limited bandwidth are obtained,

$$\begin{aligned} \sum _i^K\left( \left\| u_k^{(n+1)}-u_k^n\right\| _2^2\right) /\left\| u_k^n\right\| ^2<\varepsilon \end{aligned}$$

(15)

where $\varepsilon$ is the convergence condition.

For the Z-factor with K modal components, the original Z-factor is obtained by summing up each component.

Snow ablation optimizer

When decoupling the Z-factor into multiple components using signal decomposition algorithms, it is necessary to set an appropriate number of decompositions K. At the same time, influenced by the decomposition algorithm, a large value of $\alpha$ may cause the loss of frequency band information, while a small value may lead to information redundancy. Therefore, it is necessary to determine the optimal parameter combination [K,$\alpha$]. There are two methods to determine the number of Z-factor decompositions. One is the manual parameter tuning method, where different K values are tried from small to large. This method is random and time-consuming^44,45. Another method is to use metaheuristic optimization algorithms for automatic optimization. The optimal values of the [K,$\alpha$] combination were selected metaheuristics in this study. In the outer layer of the entire machine learning model, metaheuristic optimization algorithms, such as genetic algorithms, particle swarm optimization algorithms, etc., can be used as model parameter optimization algorithms⁴⁶. Here, we use the Snow Ablation Optimizer (SAO) as the method for optimizing model parameters. The SAO algorithm is a heuristic optimization algorithm that simulates the process of snow melting to solve optimization problems. This algorithm achieves the search process by adaptively adjusting temperature and melting speed and gradually finding the optimal solution through iterative optimization. The advantages of the SAO algorithm over other optimization algorithms lie in its unique dual-population mechanism, efficient exploration and exploitation strategies, and flexible position update equations. These features make it exhibit better balance, search efficiency, and adaptability when dealing with complex optimization problems, especially in the case of multi-peak and high-dimensional problems⁴⁷. The performance of the hybrid model in this study is mainly affected by the number of decompositions K, and each K corresponds to an $\alpha$. $\alpha$ has a little impact on the model performance and is therefore ignored during the optimization process. The goal of SAO optimization is to find K with the smallest RMSE within a defined iteration. The SAO optimization process takes K as the main optimization variable, and its search range is [1,20]. The results section below discusses the impact of the decompositions number on model performance. Finally, it is found that when the number of decompositions reaches 11, the performance of all models hardly increases, so the K value is 11 in this study.

Evaluation metrics

Root Mean Square Error (RMSE) and the adjusted coefficient of determination ($R^2$) are primarily employed to evaluate the model performance in this paper. A smaller RMSE indicates more accurate predictions of Z-factors by the model. A higher $R^2$ signifies better model performance⁴⁸. Their formulas are as follows:

$$\begin{aligned}{}&RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^{N}(Z_i-Z_{pred})^2} \end{aligned}$$

(16)

$$\begin{aligned}{}&r^2 = 1-\frac{\sum _{i=1}^{N}(Z_i-Z_{pred})^2}{\sum _{i=1}^{N}(Z_i-\bar{Z}_{pred})^2}\end{aligned}$$

(17)

$$\begin{aligned}{}&R^2 = 1-\frac{(1-r^2)(N-1)}{N-m-1} \end{aligned}$$

(18)

where N represents the number of Z-factor samples, $Z_i$ represents the true Z-factor, $Z_{pred}$ represents the predicted Z-factor,$\bar{Z}$ represents the sample mean Z-factor, and m represents the number of features influencing the Z-factor.

Additionally, some models also use Mean Absolute Percentage Error (MAPE) for evaluation, where a lower MAPE indicates a more perfect model. The formula is expressed as follows:

$$\begin{aligned} MAPE=\frac{100 \%}{N} \sum _{i=1}^{N}\left| \frac{Z_{pred}-Z_{i}}{Z_{i}}\right| \end{aligned}$$

(19)

The hybrid model

Figure 3

Proposed hybrid model for decoupling and predicting natural gas Z-factors.

The conventional Z-factor correlation predicts the Z-factor by establishing a mathematical expression between the Z-factor and the pseudoreduced pressure and temperature of natural gas. Pseudoreduced pressure and temperature are defined as:

$$\begin{aligned}{}&P_{pr}=\frac{p}{P_{pc}}\end{aligned}$$

(20)

$$\begin{aligned}{}&T_{pr}=\frac{T}{T_{pc}} \end{aligned}$$

(21)

where $P_{pc}$ and $T_{pc}$ are pseudocritical pressure and temperature of natural gas, respectively.

This approach simplifies the difficulty of obtaining the Z-factor correlation to some extent. However, it has certain drawbacks, namely, the $P_{pr}$ and $T_{pr}$ for different natural gases with different components may be equal at different pressures and temperatures. Yet, their Z-factors may not be equal. Therefore, the Z-factor correlation obtained in this way is only applicable to constant component natural gas. When the component of natural gas changes, a new correlation needs to be established to predict the Z-factor. Machine learning models, to some extent, overcome this difficulty. They can establish a connection between multiple factors and the Z-factor by inputting parameters that include the composition of natural gas, temperature, pressure, and all other factors influencing the Z-factor⁹. Previous machine learning models also used $P_{pr}$ and $T_{pr}$ as input variables to establish Z-factor prediction models^7,22. This approach also faces the problem of data overlap. Considering the difficulty of obtaining the gas composition for all wells, and $P_{pc}$ and $T_{pc}$ of natural gas already partially contains information about different gas components. Therefore, in this paper, we employ $P_{pc}$, $T_{pc}$, P, and T as input variables to predict the Z-factor. The overall architecture of the proposed Z-factor prediction model is shown in Fig. 3. The workflow of predicting the Z-factor has four main steps:

Setp 1: Decoupling the Z-factor into several components using decomposition algorithm. For the original undecoupled data set:

$$\begin{aligned} D_{\text{ original } }=\{\left[ p_r, T_r, p, T\right] _{Input},[Z]_{Output}\} \end{aligned}$$

(22)

After the Z-factor is decomposed by the VMD, EFD or EEMD algorithms, k Z-factor components are obtained. The decoupled components are combined with the original data to form k data sequences, which can be expressed as:

$$\begin{aligned} \left\{ \begin{array}{l} D_1=\{\left[ p_r, T_r, p, T\right] _{Input},[Z_1]_{Output}\} \\ D_2=\{\left[ p_r, T_r, p, T\right] _{Input},[Z_2]_{Output}\} \\ \cdots \\ D_k=\{\left[ p_r, T_r, p, T\right] _{Input},[Z_k]_{Output}\} \end{array}\right. \end{aligned}$$

(23)

Step 2: Training the hybrid model. Dividing the k data sequences into training sets and testing sets, machine learning algorithms (SVM, XGBoost, LightGBM, ANN and BiLSTM) are employed to train the models. For k data sequences, k models are trained respectively:

$$\begin{aligned} {\text {Mdl}}[i]={\text {train}}\left( \left[ p_r, T_r, p, T\right] _{Input}, [Z_i]_{Output}\right) , i=1,2, \ldots k \end{aligned}$$

(24)

Step 3: Evaluating the performance of hybrid models using Eqs. (16) and (18). In this step, the hybrid model with the best performance and the optimal number of decompositions k are selected. When k changes, repeat steps 1 and 2 until the hybrid model reaches the optimal RMSE and $R^2$ within the defined iterations. Therefore, decompositions number k can be adjusted manually by user or automatically by SAO to achieve the optimal RMSE at this step.

Step 4: Predicting the Z-factor under various conditions using the well-trained hybrid model. After all the model is well-trained and achieves satisfactory performance in the testing set, the k well-trained models are used to predict k decoupled Z-factors:

$$\begin{aligned} Z[i]={\text {predict}}\left( {\text {Mdl}}[i],\left[ p_r, T_r, p, T\right] _{Input\ for\ Prediction}\right) \end{aligned}$$

(25)

The final predicted Z-factor is obtained by adding k decoupled Z-factors:

$$\begin{aligned} Z=\sum _{i=1}^k Z[i] \end{aligned}$$

(26)

The above statement briefly describes the entire prediction framework. It is easier to understand the prediction workflow by combining it with the codes. The source code of this study is available at https://github.com/gengshaoyang/Decoupling-and-predicting-Z-factor.git.

Results

Comparison with correlations

Initially, we compared the predictive performance of Z-factor correlations with the developed machine learning model using the base dataset. Three commonly employed correlations were selected, among which the correlation proposed by Papay can be directly calculated through $T_{pr}$ and $P_{pr}$, while the DAK and Hall-Yarborough correlations necessitate iterative solutions^49,50. For machine learning, we utilized the SVM+VMD combination for prediction because this hybrid model performed best. The final results are illustrated in Fig. 4. Remarkably, the predictive accuracy of the machine learning model substantially surpassed that of correlations, yielding a correlation coefficient of 0.9982 and a MAPE of merely 0.2077%. This discrepancy arises because correlation coefficients are derived by fitting the Z-factor chart of Standing and Katz⁵¹, which is solely applicable to natural gas devoid of non-hydrocarbon components such as $\hbox {N}_2$ and $\hbox {CO}_2$⁵². However, the natural gas in our study predominantly comprises wet gas, partly containing condensate gas, and features varying levels of $\hbox {N}_2$ and $\hbox {CO}_2$. Numerous studies have attested that correlations become obsolete for Z-factor prediction when significant changes in gas composition occur⁹. Moreover, the greater the disparity in gas composition, the larger the error in Z-factor prediction.

Figure 4

Prediction results comparison between traditional Z factor correlations and SVM+VMD machine learning model.

Figure 5

Prediction results comparison between different machine learning models.

Performance on different machine learning models

Next, we conducted a comparison of the predictive performance of different machine learning models, divided into two parts: comparing different regression algorithms and evaluating the impact of utilizing the decomposition algorithm. Figure 5 displays scatter plots between predicted Z-factors and true Z-factors, as well as RMSE and $R^2$ values of the models. Initially, without utilizing the decomposition algorithm, ANN exhibited the best performance, while SVM showed the poorest performance. This explains why ANNs dominate the previous Z-factor prediction framework. However, upon introducing the VMD algorithm to decouple the Z-factor, the performance of all models significantly improved. Notably, after implementing VMD, the SVM model’s performance notably enhanced, with MAPE decreasing from 0.65 to 0.24% and RMSE decreasing from 0.01195 to 0.002532, positioning it as the top-performing model in Z-factor prediction. This indicates the effectiveness of VMD in extracting relevant features or patterns from Z-factors that original machine learning models may not adequately capture. Integrating advanced machine learning models with VMD technology can substantially enhance the predictive performance of natural gas Z-factors. Additionally, upon scrutinizing the predictive results without Z-factor decoupling, it is evident that Z-factor predictions are generally accurate across most temperature and pressure levels, albeit with some deviations from true values. Upon investigation, it was found that these deviations primarily occurred in condensate gas data points. Since our dataset predominantly comprises wet gas (88%) and only a small portion of condensate gas (12%), the model predominantly learned about the variation patterns of wet gas Z-factors during training. Consequently, the model’s generalization ability in predicting condensate gas Z-factors needs improvement. However, post-VMD implementation to decouple Z-factors, all models can more accurately capture variations in both wet gas and condensate gas Z-factors, significantly enhancing their generalization ability.

Uncovering the essence of decoupling

Figure 6

Correlations between gas components and decoupled decompositions. (a) Components of natural gas. (b) Compositions of Z-factor. (c) At different wells. (d) At different temperatures and pressures.

In the previous section, we observed a substantial enhancement in the performance of all models upon decoupling the Z-factors using VMD. The underlying mechanism driving this improvement is of significant interest. Understanding how decoupling Z-factors enhances model capability is crucial for improving model generalization, enhancing predictive performance, and extending the model’s applicability to predicting Z-factors under diverse temperature, pressure, and gas component conditions.Given that natural gas consists of a mixture of several different gases, and the VMD algorithm decouples the Z-factors into multiple sub-components, it prompts the question of whether there exists a correlation between the decoupled Z-factor components and the natural gas components. To investigate this relationship, we sorted the natural gas components in ascending order based on their mole fractions and concurrently sorted the decoupled Z-factors from small to large (utilizing the example of decoupling the Z-factors into 11 components), as depicted in Fig. 6a and b. In the distribution of natural gas components, $\hbox {C}_1$ occupies the majority, while other hydrocarbons and non-hydrocarbon components constitute a smaller portion. Similarly, the decoupled Z-factors exhibit a comparable pattern, with 10 components representing a very small proportion, while the last one dominates the majority.

Following the application of the VMD algorithm to decouple the Z-factors and subsequent removal of maximum values from both the decoupled Z-factor components and the mole fractions of natural gas, we conducted regression analysis between these decoupled Z-factors and the mole fractions of natural gas, as depicted in Fig. 6c and d. Remarkably, we observed a highly positive correlation between the decoupled Z-factor components and the mole fractions of natural gas. This relationship is well-fitted with a logarithmic function, yielding correlation coefficients exceeding 0.8 for all cases. This observation substantiates the existence of an unknown relationship between the decoupled variables and the mole fractions of natural gas. We posit that the decoupled Z-factor components signify the contribution of individual natural gas components to the overall Z-factors. The decomposition algorithm effectively segregates the influence of different gases on the Z-factors, with a higher molar fraction of a gas corresponding to a greater impact on the Z-factors. Moreover, certain decoupled variables exhibit negative values, indicative of $\hbox {CO}_2$ and heavy hydrocarbons exerting a negative influence on the Z-factors. Numerous studies have corroborated that as the content of $\hbox {CO}_2$ and heavy hydrocarbons increases, the Z-factors of natural gas tend to decrease^14,53,54. Following the decoupling of Z-factors, machine learning algorithms can more readily discern the variation patterns of Z-factors, thereby enhancing the performance of prediction models. In a word, the relationship between the decoupled Z-factor and gas composition underscores how the decomposition algorithm renders the initially chaotic Z-factor more orderly and predictable.

Effect of decomposition methods

We have demonstrated that using decomposition algorithms can significantly improve the ability of machine learning models to predict Z-factors. However, does this hold true for all decomposition algorithms? We compared the performance of three decomposition algorithms-EFD, EEMD, and VMD-as well as the performance without using any decomposition algorithm. All decomposition algorithms were used to decompose the Z-factors into 11 components. The scatter plots of different models on the training set and testing set are shown in Fig. 7. From the perspective of the prediction performance on the testing set, not all algorithms can effectively decouple Z-factors. Although all decomposition algorithms can eliminate the prediction anomalies, the EFD decomposition algorithm actually reduces the prediction results of Z-factors, which should have been predicted accurately. However, overall, using decomposition algorithms to decouple Z-factors first and then using machine learning algorithms ensures that the model has a relatively high lower limit of model performance, and the upper limit of model performance depends on the choice of the decoupling algorithm.

Figure 7

Prediction results comparison between different decomposition algorithms.

To explore the performance differences brought about by algorithms, we compared the differences of each component after decoupling Z-factors using three algorithms. We plotted the components of the 800 samples after decomposition along with their corresponding Z-factors into a heatmap, as shown in Fig. 8. The major decomposition components in the figure refer to the components with the highest content in Fig. 6a, which are relatively close to the Z-factors and are plotted together at the bottom of the figure. The remaining 10 minor decomposition components, which are relatively close in size, are plotted at the top of the figure. It is evident from the heatmap that the results obtained by the three decomposition algorithms are quite different. The minor components decomposed by EFD are different from each other, but for Z-factors at similar pressures, most components cannot completely separate them. In our tests, the model performance decreases with an increase of EFD decompositions number. The Z-factor components are complex, and the decoupling effect of EFD is relatively poor⁵⁵. The components obtained by EMD decomposition exhibit mode mixing, i.e., in different component components, there are signals with similar scales (such as components 2/3 and 4, where the differences are hardly noticeable). VMD, with its adaptive update of the optimal center frequency and bandwidth for each component, can overcome the frequency mixing issues in EMD. For similar Z-factors, even for very small components, VMD can decompose them into several non-overlapping values (such as components 1/2 and 3), without the occurrence of frequency mixing⁵⁶.

Figure 8

Heat map of the major components and minor components for different decomposition algorithms.

To further compare the ability of different algorithms on decoupling Z-factors, we decomposed the Z-factors at different pressures at the same temperature and the same natural gas components, as shown in Fig. 9. The figure more accurately reflects the ability of different algorithms to decouple Z-factors. The VMD algorithm can accurately decouple Z-factors into components of different sizes at different pressures. Although EEMD and EFD can decouple Z-factors, the components decoupled by EEMD have extremely poor correlation with natural gas components. The components decoupled by EFD have a strong correlation with natural gas components but cannot distinguish Z-factors at different pressures.

Figure 9

Decomposition components comparison for different decomposition algorithms under different pressures.

Effect of decomposition number

Since natural gas is a mixture of various gases, the Z-factor is most affected by the gas components. The performance of decomposition algorithms is also influenced by the number of decomposition. Therefore, it is essential to study the impact of different decomposition numbers on the performance of the hybrid model. Based on the VMD decomposition algorithm, we trained machine learning models with decomposition numbers ranging from 0 to 14. Figure 10 depicts the heat maps of the major and minor decomposed components when the decomposition number changes from 6 to 11. When the decomposition number changes, the main decomposed components do not change much, and the overall trend of decomposition is consistent. With the increase in the decomposition number, the additional components in the minor decomposed components are mostly small in value, and the overall trend of the other components remains unchanged, with only slight changes in numerical values. This indicates that regardless of how the decomposition algorithm changes, the main features of the Z-factors extracted by the decoupling algorithm remain unchanged, and with the increase in the decomposition number, more features are extracted by the decoupling algorithm.

Figure 10

Heat map for the major components and minor components for different decomposition numbers.

We trained four regression algorithms under different decomposition numbers. Figure 11 shows the RMSE and $R^2$ of different models under various decomposition numbers. All models perform poorly when the decomposition number is small, especially when only one variable is decomposed, the model performance is even worse than not decomposing. When the decomposition number exceeds 6, the performance of the models generally improves significantly. When the decomposition number is 12, the model performance reaches its maximum, indicating that the decomposition algorithm has extracted all the features of the Z-factors. After that, increasing the decomposition number does not further improve the model performance. Among all the models, decoupling the Z-factors has the greatest impact on improving the performance of the SVM model.

Figure 11

The effect of decomposition number on models performance.

Discussion

At this point, we have comprehended the reasons behind the performance improvement due to decoupling Z-factors and extensively discussed the impact of different decoupling methods and number on model performance. To demonstrate the superior performance of the proposed model, we employ multiple Z-factor datasets to validate our model. These datasets include Z-factors under different gas components and high temperature and pressure. Some of them involve natural gas components with higher contents of $\hbox {CO}_2$ or $\hbox {H}_2$S^53,57, some are related to condensate gas, and others are associated with Z-factors under high temperature and pressure⁵⁸. Some data are provided in the literature, while others are obtained by digitizing images of Z-factors recorded in the literature using OriginLab (a commercial plotting software). Furthermore, some literature only records $T_{pr}$ and $P_{pr}$, and we predict Z-factors based on $T_{pr}$ and $P_{pr}$. For data that provides natural gas components but lacks information on the $T_{pc}$ and $P_{pc}$ of natural gas, we calculate the $T_{pc}$ and $P_{pc}$ using the following formula⁵⁹:

$$\begin{aligned}{}&T_{pc}=\sum _{i=1}y_iT_{ci}\end{aligned}$$

(27)

$$\begin{aligned}{}&P_{pc}=\sum _{i=1}y_iP_{ci} \end{aligned}$$

(28)

Table 2 Performance comparison of the proposed model on different datasets.

For datasets with sizes smaller than 100 and containing similar natural gas components, we amalgamate them into corresponding datasets. Initially, all datasets are divided into an 8:2 ratio for separate training and prediction purposes. Subsequently, all data are merged for comprehensive evaluation. The final model evaluation results on the test sets of each dataset are presented in Table 2. The $R^2$ for all 10 datasets exceed 0.97, averaging 0.9918. Additionally, MAPE for all datasets generally remains below 2%, with an average of 0.83%. Datasets exhibiting lower model prediction accuracy are primarily attributed to the limited number of trainable sample points. Upon consolidating all data for training, the model achieves an impressive prediction accuracy of 0.9993, accompanied by an MAPE of merely 0.21%. The proposed model demonstrates satisfactory performance both on individual datasets and when trained on the entire dataset. Consequently, the model proposed in this paper is deemed applicable for predicting Z-factors in complex natural gas components under high pressure and high temperature conditions. Notably, on smaller datasets, the model’s training and prediction time is less than one minute, while on datasets comprising more than 7,000 data points, the model requires less than 3 minutes. This indicates the model’s remarkable accuracy and efficiency across varied dataset sizes.

Conclusion

In this study, we developed an innovative machine learning framework to predict the deviation factor (Z-factor) of natural gas with high accuracy. Using Z-factor data from 6914 wet gas samples from the Shaximiao Formation gas reservoir, our approach integrates signal decomposition algorithms with traditional machine learning algorithms (SVM, XGBoost, LightGBM, ANN, BiLSTM), resulting in significant performance improvements under complex natural gas compositions, high-pressure, and high-temperature conditions. Key findings include:

• 1. Machine learning models surpass traditional correlations like DAK and Hall-Yarborough in predictive accuracy and ease of development for engineers.

• 2. The decoupled Z-factor components correlate strongly with natural gas components, enhancing predictive accuracy. VMD outperforms other decomposition methods in feature extraction.

• 3. Using the Variational Mode Decomposition algorithm to decouple Z-factors significantly improves performance of traditional machine learning algorithms, reducing the MAPE from 0.65% to 0.24% and the RMSE from 0.01195 to 0.002532.

• 4. The number of decoupled Z factors affects the prediction performance. When the number of decoupled Z factors is 11, the hybrid model of VMD and SVM achieves the best performance.