Introduction

The optical coherence phenomenon in which a light beam of linearly polarized light undergoes a deviation or lateral shift from its predicted optical path is called Goos-Hänchen shift/ effect. This effect was named after the two scientists Goos and Hänchen who reported it experimentally in 1947. Owing to a vast potential applications of GH-shift, a great deal of interest in the various fields of science has been emerged, for example in photonics1,2, atomic optics3,4, plasmonics5,6,7, nonlinear optics8,9, spintronics10,11, neutronics12,13 and graphene14,15. Moreover, due to fundamental nature of the GH-shift, interesting uses for it exist in optical sensors to measure beam angle, film thickness and refractive index. In positive GH shift, the reflected/transmitted ray shifts in the forward direction while in negative GH-shift, the reflected/transmitted ray shifts in the backward direction. The GH-shifts in the reflection and transmission have been controlled via kerr nonlinearity, Doppler broadening, subluminity and superluminity. On the basis of the above applications, researchers studied GH-shifts theoretically and experimentally using different techniques and mechanisms.

Zia et al.16 measured both positive and negative GH shifts in the reflection and transmission of birefringent beams under subluminal and superluminal effects. Iqbal et al.17studied and examined theoretically GH-shift in a four levels tripodtype configuration of cold and hot atoms via kerr nonlinearity and Doppler broadening. Akhlaq et al.18 controlled and modified the GH-shift in the reflection and transmission using Kerr nonlinearity, Compton scattering and Doppler broadening effects. The GH-shift has a crucial role in the designing of optical sensors19 and switches20. Aniqa et al.21 investigated the temperature dependent GH-shift which helps in controlling the temperature to a desire value. The results of temperature dpendendent GH-shift open the door to make temperature sensors22,23. Recently extensive research has been conducted on the photon spin splitting. The vortex beams possess the capability to modulate the symmetry of the spin splitting. Zhen et al.24 controlled the symmetry of the photon spin Hall effect using vortex beams. The combined effect of longitudinal photon spin splitting and GH-shifts was investigated by Zhen et al.25. The Drude’s model26 based on KMT of gases27 is used to the measure the complex conductivity. The real part of complex conductivity shows forward current while the imaginary part shows backward current. The conducting media exhibits the property of complex conductivity which are either pure metal, semiconductors or graphene. This class of materials has numerous applications in Physics, Chemistry, Biology and material science. Zakir et al.28 investigated the lateral GH-shift in a conductive medium using complex conductivity condition. The optically active medium which rotates the plane of polarization and exhibits the phenomenon of birefringence is called chiral medium. The birefringence plays a crucial role in chemistry29, medicines30, and optics31,32. The circular birefringence occurs as a result of slightly difference in the refractive indices \(\Delta n\) = \(n^{(R)}_r - n^{(L)}_r\) of the medium, where \(n^{(R)}_r\) is the refractive index of RCP and \(n^{(L)}_r\) is the refractive index of LCP respectively. The birefringence has numerous applications in cloacking devices33, telecommunication34, artificial magnetism35 and illusion optics36. Sajid et al.37 reported a contrast behavior for the GH-shifts in the reflection and transmission beams at resonance condition. They measured significant birefringent positive GH-shift in the reflection while significant negative GH-shift in the transmission at resonance using a four levels chiral medium. Ijaz et al.38 reported a maximum group velocities of c/ 40000 for LCP beam with a time delay of 0.1 s while -c/40000 for LCP beam with a time advance of -0.1 s using chiral atomic medium. Humayun et al.39 studied the birefringence in a chiral medium and created a time gap of 47 nanoseconds for temporal cloacking. They noticed 24 ns time delay for RCP beam while -23 ns time advancement for LCP beam. The event cloacking in the birefringent spectra of reflection, transmission and absorption has been noticed in a four levels chiral medium40. Shihao et al.41measured giant positive and negative GH-shifts about thirty times the incident wavelength in photonic crystal. Waqar et al.39 investigated the dependence of complex conductivity on the RCP and LCP beams for the creation of temporal cloacking in a chiral medium. They created a time gap to \(8\upmu\)s between RCP and LCP beams with forward current while \(5\upmu\)s with backward current.

Subject to the above literature review, the GH-shift has been controlled and modified in different media using different techniques but has not yet been controlled in a chiral conductive medium. We will study the birefringent GH-shift with the changing of real and imaginary parts of complex conductivity. The modified results show potential applications in biophotonic, optical and plasmonic devices for the processing of optical signals. The results also have significant role in the designing of waveguide switches, conductive sensor and optical sensors.

Model and its dynamics

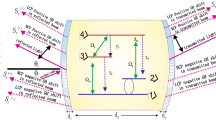
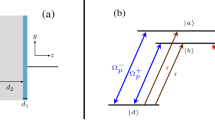
The model consists a cavity within a conductive chiral medium of length \(d_2\) is placed. The conductivity dependent permittivity function of this medium is \(\epsilon (\sigma )\). The charge particles or electrons are at motion due to same external potential. The atomic system of conductive medium is a bulk four levels configuration, where phonon contribution is ignored. The four level conductive medium is surrounded by a polystyrene of permittivity \(\epsilon _1\) and thickness \(d_1\). The conductive medium is connected with a source of potential V due which current is produced and the backward current is also generated as a back Emf. The four levels atomic configuration is shown in Fig. 1. The electric probe field \(E_p\) of Rabi frequency \(\Omega _p\) is coupled with the states \(\left| 2\right\rangle\) and state \(\left| 4\right\rangle\). The magnetic field of Rabi frequency \(\Omega _m\) is coupled with the state \(\left| 1\right\rangle\) and state \(\left| 3\right\rangle\), while the resonance electric control field \(E_c\) of Rabi frequency \(\Omega _c\) is coupled with the level \(\left| 3\right\rangle\) and level \(\left| 4\right\rangle\).

Figure 1
figure 1

Diagram of four levels chiral conductive system.

Full size image

The self Hamiltonian for the four level chiral conductive medium is written bellow:

$$\begin{aligned} H_0=\sum ^{4}_{j=1}\hbar \omega _j \left| j\right\rangle \left\langle j\right| \end{aligned}$$
(1)

The interaction picture’s Hamiltonian for the four level chiral conductive medium is written as:

$$\begin{aligned} H_I= & \sum ^4_{j=1}\hbar \left| j\right\rangle \left\langle j\right| -\frac{\hbar }{2}[\Omega _pe^{-i\omega _p t}\left| 4\right\rangle \left\langle 2\right| \nonumber \\ & +\Omega _ce^{-i\omega _ct}\left| 4\right\rangle \left\langle 3\right| +\Omega _me^{-i\omega _mt}\left| 3\right\rangle \left\langle 1\right| \nonumber \\ & +H.C] \end{aligned}$$
(2)

where

\(\Omega _m=\mu _{31}e^{i\varphi _m}B_0/\hbar\), in which \(\varphi _m\) represents the phase of magnetic field, while \(\mu _{31}\) the magnetic dipole moment between the states \(\left| 1\right\rangle\) and \(\left| 3\right\rangle\) related to atomic decays as \(\mu _{31}=\sqrt{3c^2\hbar \lambda ^3\gamma _b/8\pi ^2}\). The probe Rabi frequency is \(\Omega _p=\varrho _{42}e^{i\varphi _e}E_0/\hbar\), while \(\varphi _e\) represents the phase of electric field and \(\varrho _{42}\) is the electric dipole moment between the states \(\left| 2\right\rangle\) and \(\left| 4\right\rangle\) related to the atomic decays as \(\varrho _{42}=\sqrt{3\hbar \lambda ^3\gamma _e/8\pi ^2}\). To evaluates the dynamic of the system the following density matrix equation’s is used:

$$\begin{aligned} \dot{\rho }=-\frac{i}{\hbar }[H_i,\rho ]-\sum \frac{1}{2}\gamma _{ij}(b^\dagger b \rho + \rho b^\dagger b-2b \rho b^\dagger ) \end{aligned}$$
(3)

where, \(b^\dagger\) and b are rising( creation) and lowering ( annihilation ) operators, while \(\gamma _{ij}\) is the decay rate between the states \(\left| i\right\rangle\) and \(\left| j\right\rangle\), where i,j=1,2,3,4. The coupling equations are obtained by using the master density matrix eq.3. After straight forward algebraical manipulation the following two magnetic coherence \(\overset{\cdot }{\overset{\sim }{\rho }}_{31},\overset{\cdot }{\overset{\sim }{\rho }}_{41}\) and two electric coherence \(\overset{\cdot }{\overset{\sim }{\rho }}_{42},\overset{\cdot }{\overset{\sim }{\rho }}_{32}\) coupled rates equation are calculated.

$$\begin{aligned} \overset{\cdot }{\overset{\sim }{\rho }}_{31}= & (\Delta _p-\frac{1}{2}\gamma _b)\widetilde{\rho }_{31} +\frac{i}{2}\Omega _m(\widetilde{\rho }_{33}-\widetilde{\rho }_{11})\nonumber \\ & -\frac{i}{2}\Omega ^*_c\widetilde{\rho }_{41}. \end{aligned}$$
(4)
$$\begin{aligned} \overset{\cdot }{\overset{\sim }{\rho }}_{41}= & [i\Delta _p-(\frac{1}{2} \gamma _e+\gamma _1)]\widetilde{\rho }_{41} -\frac{i}{2}\Omega _p\widetilde{\rho }_{21}\nonumber \\ & -\frac{i}{2}\Omega _c\widetilde{\rho }_{31}+\frac{i}{2}\Omega _m\widetilde{\rho }_{43} \end{aligned}$$
(5)
$$\begin{aligned} \overset{\cdot }{\overset{\sim }{\rho }}_{42}= & [\Delta _p-\frac{i}{2}( \gamma _1+\gamma _e)]\widetilde{\rho }_{42} +\frac{i}{2}\Omega _p(\widetilde{\rho }_{44}-\widetilde{\rho }_{22})\nonumber \\ & -\frac{i}{2}\Omega _c\widetilde{\rho }_{32} \end{aligned}$$
(6)
$$\begin{aligned} \overset{\cdot }{\overset{\sim }{\rho }}_{32}= & (i\Delta _p-\frac{1}{2}\gamma _b)\widetilde{\rho }_{32} -\frac{i}{2}\Omega ^*_m\widetilde{\rho }_{12}\nonumber \\ & -\frac{i}{2}\Omega _c\widetilde{\rho }_{42} \end{aligned}$$
(7)

Taken the first order perturbation condition and superposition condition \(\left| \psi \right\rangle =\sqrt{1-x}e^{i\varphi }\left| 1\right\rangle +\sqrt{x}\left| 2\right\rangle\) for zeroth order \(\widetilde{\rho }_{ij}^{(0)}\), the following density coherences for electric and magnetic probes are calculated.

$$\begin{aligned} \widetilde{\rho }_{31}^{(1)}= \frac{\Omega _p}{4W_1}\frac{\Omega ^*_c}{(\Delta _p-i(\gamma _1+\gamma _e)/2)}\widetilde{\rho }_{21}^{(0)}+&\frac{\Omega _m}{2W_1}\widetilde{\rho }_{11}^{(0)}\ \end{aligned}$$
(8)
$$\begin{aligned} \widetilde{\rho }_{42}^{(1)}&= \frac{\Omega _m}{4W_2}\frac{\Omega _c}{(\Delta _p-i\gamma _b/2)}\widetilde{\rho }_{12}^{(0)}+&\frac{\Omega _p}{2W_2}\widetilde{\rho }_{22}^{(0)}\ \end{aligned}$$
(9)
$$\begin{aligned} W_1= & \Delta _p-\frac{|\Omega _c|^2}{4(\Delta _P-i\frac{(\gamma _1+\gamma _e)}{2})}-\frac{i\gamma _b}{2} \end{aligned}$$
(10)
$$\begin{aligned} W_2= & \Delta _p-\frac{|\Omega _c|^2}{4(\Delta _p-i\frac{\gamma _b}{2})}-\frac{i(\gamma _e+\gamma _1)}{2} \end{aligned}$$
(11)

where \(\widetilde{\rho }_{11}^{(0)}=1-x\), \(\widetilde{\rho } ^{(0)}=x\), \(\widetilde{\rho }_{12}^{(0)}=\sqrt{x(1-x)}\exp (-i\varphi )\) and \(\widetilde{\rho }_{21}^{(0)}=\sqrt{x(1-x)}\exp (i\varphi )\)

The electric polarization (P) and magnetization (M) in a chiral medium are calculated from coherences terms are written bellow:

$$\begin{aligned} P=N\varrho _{24}\widetilde{\rho }^{(1)}_{42} \end{aligned}$$
(12)

and

$$\begin{aligned} M=N\mu _{13}\widetilde{\rho }^{(1)}_{31} \end{aligned}$$
(13)

From the equations (8-9), inserting the values of \(\widetilde{\rho }^{(1)}_{31}\) and \(\widetilde{\rho }^{(1)}_{42}\) in equations ( 12-13), the polarization and magnetization are modified to the form of:

$$\begin{aligned} P=\alpha _{EE}E_0+\alpha _{EB}B_0 \end{aligned}$$
(14)

and

$$\begin{aligned} M=\alpha _{BE}E_0+\alpha _{BB}B_0 \end{aligned}$$
(15)

The terms \(\alpha _{EE}\), \(\alpha _{EB}\), \(\alpha _{BE}\) and \(\alpha _{BB}\) are written bellow:

$$\begin{aligned} \alpha _{EE}=\frac{N\varrho ^2_{42}\widetilde{\rho }^{(0)}_{22}}{\hbar W_2} \end{aligned}$$
(16)
$$\begin{aligned} \alpha _{BB}=\frac{N\mu ^2_{31}\widetilde{\rho }^{(0)}_{11}}{\hbar W_1} \end{aligned}$$
(17)
$$\begin{aligned} \alpha _{BE}=\frac{N\mu _{31}\varrho _{42}|\Omega _c|e^{i(\varphi _m-\varphi _e)}\rho ^{(0)}_{21}e^{-i(\varphi _c+\varphi )}}{2\hbar W_1[\Delta _p-\frac{i(\gamma _1+\gamma _e)}{2}]} \end{aligned}$$
(18)
$$\begin{aligned} \alpha _{EB}=\frac{N\mu _{31}\varrho _{42}|\Omega _c|e^{i(\varphi _e-\varphi _m)}\rho ^{(0)}_{21}e^{i(\varphi _c+\varphi )}}{2\hbar W_1[\Delta _p-\frac{i(\gamma _1+\gamma _e)}{2}]} \end{aligned}$$
(19)

The another form of magnetization and electric polarization in the term of electric/magnetic susceptibilities as well as chiral coefficients are in the literature as:

$$\begin{aligned} M=\chi ^{(1)}_mH+\frac{\xi _{HE}H}{\mu _0c}E \end{aligned}$$
(20)

and

$$\begin{aligned} P_e=\epsilon _0\chi ^{(1)}_eE+\frac{\xi _{EH}H}{c} \end{aligned}$$
(21)

Comparing the equation.14 and equation.21 of polarization and equation.15 and equation.20 of magnetization the following electric and magnetic susceptibilities and chiral coefficients are calculated:

$$\begin{aligned} \chi _e=\frac{\alpha _{EE}+\mu _0(\alpha _{BE}\alpha _{EB}-\alpha _{EE}\alpha _{BB})}{\epsilon _0(1-\mu _0\alpha _{BB})} \end{aligned}$$
(22)
$$\begin{aligned} \chi _m=\frac{\beta _{BB}\mu _0}{1-\beta _{BB}\mu _0} \end{aligned}$$
(23)
$$\begin{aligned} \xi _{EH}=\frac{(\mu _0\beta _{EB})c }{1-\mu _0\beta _{BB}} \end{aligned}$$
(24)
$$\begin{aligned} \xi _{HE}=-\frac{(\mu _0\beta _{BE})c}{1-\mu _0\beta _{BB}} \end{aligned}$$
(25)

A light ray incident on the chiral medium becomes birefringent. \(n^{(R)}_r\) and \(n^{(L)}_r\) are the refractive indices correspond to the right and left circular polarization of the birefringent beams. The refractive index of one (\(n^{(R)}_r\)) slightly increases, while that of the other (\(n^{(L)}_r\)) is slightly decreases. The difference of chiral coefficients contributes to complex refractive index. The expression for complex refractive index for RCP and LCP are written as:

$$\begin{aligned} n^{(R)}_r= & \sqrt{(1+\chi _m)(1+\chi _e)-\frac{(\xi _{HE}+\xi _{EH})^2}{4}}\nonumber \\ & - i\frac{(\xi _{HE}-\xi _{EH})}{2} \end{aligned}$$
(26)
$$\begin{aligned} n^{(L)}_r= & \sqrt{(1+\chi _m)(1+\chi _e)-\frac{(\xi _{HE}+\xi _{EH})^2}{4}}\nonumber \\ & + i\frac{(\xi _{HE}-\xi _{EH})}{2} \end{aligned}$$
(27)
Figure 2
figure 2

Reflection and transmission of RCP and LCP light beam through chiral atomic medium versus \(\sigma _r\) and \(\sigma _i\) such that \(\gamma _1=2\gamma\), \(\gamma _b=0.2\gamma\), \(\gamma _e=2\gamma\),\(\varphi =0\), \(\varphi _{e,m,c}=\pi /2\), \(\Omega _c=5\gamma\),\(\Delta _p=0.5\gamma\), \(\sigma _r=2000\) S/m, \(\sigma _i=200\) S/m.

Full size image
Figure 3
figure 3

The GH-shifts in reflection and transmission RCP and LCP beams versus \(\sigma _r\) and \(\sigma _i\) such that \(\gamma _1=2\gamma\), \(\gamma _b=0.2\gamma\), \(\gamma _e=2\gamma\),\(\varphi =0\), \(\varphi _{e,m,c}=\pi /2\), \(\Omega _c=5\gamma\),\(\Delta _p=0.5\gamma\), \(\sigma _r=2000\) S/m, \(\sigma _i=200\) S/m.

Full size image
Figure 4
figure 4

Reflection and transmission of RCP and LCP light beam through chiral atomic medium versus versus \(\sigma _r\) and \(\Delta _p/\gamma\) such that \(\gamma _1=2\gamma\), \(\gamma _b=0.2\gamma\), \(\gamma _e=2\gamma\), \(\varphi =0\), \(\varphi _{e,m,c}=\pi /2\), \(\Omega _c=5\gamma\), \(\sigma _i=200S/m\), \(\sigma _r=20000\) S/m, \(\Delta _p=30\gamma\).

Full size image
Figure 5
figure 5

The GH-shifts in reflection and transmission RCP and LCP beams versus \(\sigma _r\) and \(\Delta _p/\gamma\) such that \(\gamma _1=2\gamma\), \(\gamma _b=0.2\gamma\), \(\gamma _e=2\gamma\), \(\varphi =0\), \(\varphi _{e,m,c}=\pi /2\), \(\Omega _c=5\gamma\), \(\sigma _i=200S/m\), \(\sigma _r=20000\) S/m, \(\Delta _p=30\gamma\).

Full size image
Figure 6
figure 6

Reflection and transmission of RCP and LCP light beam through chiral atomic medium versus versus \(\sigma _i\) and \(\Omega _c/\gamma\) such that\(\gamma _1=2\gamma\), \(\gamma _b=0.2\gamma\), \(\gamma _e=2\gamma\), \(\varphi =0\), \(\varphi _{e,m,c}=\pi /2\), \(\Delta _p=0.2\gamma\), \(\sigma _r=200S/m\), \(\sigma _i=200S/m\), \(\Omega _c=20\gamma\).

Full size image
Figure 7
figure 7

The GH-shifts in reflection and transmission RCP and LCP beams versus \(\sigma _i\) and \(\Omega _c/\gamma\) such that \(\gamma _1=2\gamma\), \(\gamma _b=0.2\gamma\), \(\gamma _e=2\gamma\), \(\varphi =0\), \(\varphi _{e,m,c}=\pi /2\), \(\Delta _p=0.2\gamma\), \(\sigma _r=200S/m\), \(\sigma _i=200S/m\), \(\Omega _c=20\gamma\).

Full size image

For the calculation of conductivity dependent dielectric function of right and left circularly polarized beams in conductive chiral medium \(\varepsilon ^{(R,L)}(\sigma )\), the following maxwell’s equation are used:

$$\begin{aligned} \nabla ^2 E=\mu \epsilon \frac{\partial ^2 E}{\partial t^2}+\mu \sigma \frac{\partial E}{\partial t}, \end{aligned}$$
(28)
$$\begin{aligned} \nabla ^2 B=\mu \epsilon \frac{\partial ^2 B}{\partial t^2}+\mu \sigma \frac{\partial B}{\partial t}. \end{aligned}$$
(29)

We are looking for the solutions of Equations. (28), (29) in the form of:

$$\begin{aligned} E(r,t)=E_m\exp -i(\omega t-\textbf{k}.\textbf{r}), \end{aligned}$$
(30)
$$\begin{aligned} B(r,t)=B_m\exp -i(\omega t-\textbf{k}.\textbf{r}), \end{aligned}$$
(31)

where \(E_m\) and \(B_m\) are the amplitudes of the electric field and magnetic field. Plugging Eqs. (30) and (31) in Eq. (28) and (29), the square of wave vector of chiral conductive medium is calculated in the form of complex conductivity and permittivity as:

$$\begin{aligned} \tilde{k}_m^2=\mu \tilde{\epsilon }\omega ^2+i\mu \tilde{\sigma }\omega , \end{aligned}$$
(32)

where the relations for the complex quantities are

$$\begin{aligned} \tilde{k}=k_{m1}+i k_{m2},\,\epsilon ^{c}=\epsilon ^{c}_r+i\epsilon ^{c}_i,\,\tilde{\sigma }=\sigma _r+i\sigma _i. \end{aligned}$$
(33)

Plugging the complex quantities’ values from Eq. (33) into the relation (32), a simple algebraic manipulation leads to

$$\begin{aligned} & \tilde{k}_m^2=(\mu \epsilon ^{c}_r \omega ^2-\mu \sigma _i\omega )+i(\mu \epsilon ^{c}_i \omega ^2+\mu \sigma _r\omega ),\end{aligned}$$
(34)
$$\begin{aligned} & k^2_{m1}-k^2_{m2}=(\mu \epsilon ^{c}_r \omega ^2-\mu \sigma _i\omega ),\end{aligned}$$
(35)
$$\begin{aligned} & 2k_{m1} k_{m2} =(\mu \epsilon ^{c}_i \omega ^2+\mu \sigma _r\omega ). \end{aligned}$$
(36)

Exploiting the standard relations \(\displaystyle \mu _0\epsilon _0={1}/{c^2}\) and \(\displaystyle k_0={\omega }/{c}\), the real and imaginary parts of permittivity is expressed in terms are related to complex refractive indices as \(\epsilon ^{c}_r=\epsilon _0 Re(n^{(R,L)}_r)^2\) and \(\epsilon ^{c}_i=\epsilon _0Im(n^{(R,L)}_r)^2\). Plugging these terms in \(k_m\) and supposing supposing \(\gamma\) and \(\beta\) we obtain \(k^2_{m1}-k^2_{m2}\) and \(2k_{m1} k_{m2}\) as:

$$\begin{aligned} k^2_{m1}-k^2_{m2}=\mu \epsilon _0 \omega ^2(Re(n^{(R,L)}_r)^2-\frac{\sigma _i}{\epsilon ^{c}_0\omega })=k^2_0(Re(n^{(R,L)}_r)^2-\frac{\sigma _i}{\epsilon _0\omega })=\beta ^2, \end{aligned}$$
(37)
$$\begin{aligned} 2k_{m1} k_{m2}=\mu \epsilon _0 \omega ^2(Im(n^{(R,L)}_r)^2-\frac{\sigma _r}{\epsilon _0\omega })=k^2_0(Im(n^{(R,L)}_r)^2-\frac{\sigma _r}{\epsilon _0\omega })=\gamma ^2. \end{aligned}$$
(38)

The real and imaginary parts of \(k_{m1}\) and \(k_{m2}\) of wavector is calculated from eq.(37-38):

$$\begin{aligned} k_{m1}=\pm \frac{\beta }{\sqrt{2}}\sqrt{1\pm \sqrt{1+\left( \frac{\gamma }{\beta }\right) ^4}}, \end{aligned}$$
(39)
$$\begin{aligned} k_{m2}=\pm \frac{\beta }{\sqrt{2}}\sqrt{-1\pm \sqrt{1+\left( \frac{\gamma }{\beta }\right) ^4}}. \end{aligned}$$
(40)

From \(k_{m1}\) and \(k_{m2}\) the wavevector \(k_m\) is calculated. The wavevectors of left and right circularly polarized is related refractive indices \(k^{R,L}_m=k_0n^{(R,L)}_r(\sigma ))\). The conductivity dependent dielectric is calculated from \(n^{(R,L)}_r(\sigma ))=\sqrt{\varepsilon ^{(R,L)}(\sigma )}\) as:

$$\begin{aligned} \varepsilon ^{(R,L)}(\sigma )= & \bigg [\pm \sqrt{\frac{{\sqrt{Re(n^{(R,L)}_r)^2}-\frac{\sigma _i}{\epsilon _0\omega }}}{\sqrt{2}}}\bigg \{i\sqrt{-1\pm \sqrt{1+\frac{[\sigma _r+ \omega \epsilon _0Im(n^{(R,L)}_r)^2 ]^2}{(\sigma _i -\omega \epsilon _0 Re(n^{(R,L)}_r)^2)^2}}}\nonumber \\ & +\sqrt{1\pm \sqrt{1+\frac{[\sigma _r+\omega \epsilon _0Im(n^{(R,L)}_r)^2]^2}{[\sigma _i -\omega \epsilon _0Re(n^{(R,L)}_r)^2]^2}}}\bigg \}\bigg ]^2. \end{aligned}$$
(41)

The probe beam of left and right circularly polarized beams propagating through chiral conductive medium are transmitted and reflected back. The coefficients of reflection and transmission are calculated bellow from \(\varepsilon ^{(R,L)}(\sigma )\) as:

$$\begin{aligned} R^{(R,L)}=\frac{\cos [\alpha ^{(R,L)}](k^2_0-k^2_1)k_1k_2^{(R,L)}\sin [2\alpha _1]+H_3\sin [\alpha ^{(R,L)}]}{k_1k_2^{(R,L)} H_1\cos [\alpha ^{(R,L)}]+H_2\sin [\alpha ^{(R,L)}]} \end{aligned}$$
(42)
$$\begin{aligned} T^{(R,L)}=\frac{2ik_0k_2^{(R,L)}k^2_1}{k_1k_2^{(R,L)}H_1\cos [\alpha ^{(R,L)}]+H_2\sin [\alpha ^{(R,L)}]} \end{aligned}$$
(43)

where \(\alpha _{1}\), \(\alpha ^{(R,L)}\) and \(k_{0,1}\) are written in results and discussion section. The GH- shifts in the reflection and transmission probe are written in explicit form as:

$$\begin{aligned} S^{R,L}_{(r)}= & -\frac{\lambda }{2\pi |R^{R,L}|^2}[Re(R^{R,L})\frac{\partial }{\partial \theta }(Im(R^{R,L}))-Im(R^{R,L}) \frac{\partial }{\partial \theta }Re(R^{R,L})] \end{aligned}$$
(44)
$$\begin{aligned} S^{R,L}_{(t)}= & -\frac{\lambda }{2\pi |T^{R,L}|^2}[Re(T^{R,L})\frac{\partial }{\partial \theta }(Im(T^{R,L}))-Im(R^{R,L}) \frac{\partial }{\partial \theta }Re(T^{R,L})] \end{aligned}$$
(45)

where \(k_2^{(R,L)}\) and \(H_{1-3}\) are written bellow:

$$\begin{aligned} H_1= & 2ik_0k_1\cos [2\alpha _1]+(k^2_0+k^2_1)\sin [2\alpha _1] \\ H_2= & k^2_1(k^2_0+(k_2^{(R,L)})^2)\cos ^2[\alpha _1]-(k^4_1+k^2_0(k_2^{(R,L)})^2)\sin ^2[\alpha _1]\nonumber \\ & -ik_0k_1(k^2_1+(k_2^{(R,L)})^2)\sin [2\alpha _1] \\ H_3= & k^2_1(k^2_0-(k_2^{(R,L)})^2)\cos ^2[\alpha _1]+(k^4_1-k^2_0(k_2^{(R,L)})^2)\sin ^2[\alpha _1] \\ k_2^{(R,L)}=\sqrt{\varepsilon ^{(R,L)}(\sigma )-\sin ^2[\theta ]} \end{aligned}$$

Results and discussions

The results are presented for the reflection/ transmission coefficients of left circularly polarized (LCP) and right circularly polarized (RCP) beams and their corresponding GH-shifts in reflection/transmission through a chiral conductive medium. All the parameters are taken in the atomic units. The decay rate “\(\gamma\)” having value 36.1 GHz is regarded as unit for the comparison of other frequency parameters to be measured. The other parameters are \(\epsilon _1=3.22\) (dielectric constant of polystyrene), \(d_{1}=1.5\lambda\), \(d_{2}=20.5\lambda\), \(x=0.5\), \(L=2d_1+d_2\) and \(k=2\pi /\lambda\). The pulse width in space time domain is taken as \(w=10\lambda _p, \tau _0=1.5\mu s\), where \(k_z=\frac{2\pi }{\lambda _p}\cos [\theta ]\), \(w_y=w\sec [\theta ]\), \(k_{0,1}=\sqrt{\epsilon _{0,1}-\sin ^2[\theta ]}\), \(\alpha ^{(R,L)}=\frac{2\pi }{\lambda _p}d_{2}k_2^{(R,L)}\) and \(\alpha _{1}=\frac{2\pi }{\lambda _p}d_{1}\sqrt{\epsilon _{1}-\sin ^2[\theta ]}\), \(\lambda _p=698.6nm\) and \(\omega =1000\gamma\).

In Fig. 2, The plots are traced for reflection and transmission of light of right circularly polarized beam (RCP) and left circularly polarized beam(LCP) versus forward current \(\sigma _r\) and backward current \(\sigma _i\). The RCP and LCP beams of reflection and transmission are oscillated with forward and backward currents \(\sigma _r\) and \(\sigma _i\). The RCP and LCP beams of the reflection and transmission obey the normalization condition \(|R^{(R)}|+|T^{(R)}|+|A^{(R)}|=1\) and \(|R^{(L)}|+|T^{(L)}|+|A^{(L)}|=1\). The absorption in right and left circularly polarized beams is control to zero such as \(|A^{(R,L)}|\simeq 0\). At the point \((\sigma _r, \sigma _i)\)=(1500S/m, 50S/m), the RCP beam in reflection has value \(|R^{(R)}|\simeq 0.2\) and the transmission coefficients has the value \(|T^{(R)}|\simeq 0.8\), while absorption coefficient \(|A^{(R)}|\simeq 0\) as shown in Fig. 2a,c. Also at the points \((\sigma _r, \sigma _i)\)=\((1000 \mathrm{S/m}, 50 \mathrm{S/m})\), the LCP beam in reflection and transmission has values of \(|R^{(L)}|\simeq 0.2\) and \(|T^{(L)}|\simeq 0.8\), while \(|A^{(L)}|\simeq 0\) as shown in Fig. 2b,d.

In Fig. 3, The plots are traced for the GH-shifts of RCP and LCP beams in the reflection and transmission versus \(\sigma _r\) and \(\sigma _i\). The GH-Shifts in reflection and transmission of right circularly polarized (RCP) beam and left circuital polarized (LCP) beam are strong oscillating function of forward and backward currents (\(\sigma _r, \sigma _i\)). The noisy rapid fluctuation in the GH-shift in reflection and transmission is due to the disturbance in polarization and magnetization produced by relative motion of charge particles fields. The dielectric function and refractive index are directly related to reflection and transmission as well as corresponding GH-shifts. Therefore the noisy fluctuation is more dominant with forward and backward currents. Reflections of both RCP and LCP beams show negative GH-shifts. The value of the shifts in this case are enhanced to \(-10\lambda\). Such as \(S^{(R)}_{r}/\lambda =-10\), So \(S^{(R)}_{r}=-10\lambda\). Similarly \(S^{(L)}_{r}/\lambda =-10\), So \(S^{(L)}_{r}=-10\lambda\) as shown in Fig. 3a,b. Transmission of both RCP and LCP beams show positive GH-shifts. The value of the shifts in this case are enhanced to \(10\lambda\). Such as \(S^{(R)}_{t}/\lambda =10\), So \(S^{(R)}_{t}=10\lambda\). Similarly \(S^{(L)}_{t}/\lambda =10\), So \(S^{(L)}_{t}=10\lambda\) as shown in Fig. 3c,d.

In Fig. 4, the plots are traced for RCP and LCP beams reflection and transmission coefficients versus forward current \(\sigma _r\) and probe field detuning \(\Delta _p/\gamma\). The RCP and LCP beams in reflection and transmission are oscillated with probe field detuning and forward current and obey the normalization condition. The absorption in RCP and LCP beams is again controlled to zero such as \(|A^{(R,L)}|\simeq 0\). The RCP beam in reflection and transmission has values of \(|R^{(R)}|=0.6\) and \(|T^{(R)}|=0.4\) at the points (\(\sigma _r,\Delta _p)=(7500 s/m, -20\gamma )\) as shown in the Fig. 4a,c. Similarly the LCP beam in reflection and transmission has values of \(|R^{(L)}|= 1\) and \(|T^{(L)}|= 0\) at points (\(\sigma _r\), \(\Delta _p/\gamma\))=(200 s/m, -20\(\gamma\)) as shown in Fig. 4b, d.

In Fig. 5, the plots are traced for GH-shifts of RCP and LCP beams in the reflection and transmission versus forward current \(\sigma _r\) and probe field detuning \(\Delta _p/\gamma\). The GH-shifts in reflection and transmission of RCP beams \(S^{(R)}_{r}\) and \(S^{(R)}_{t}\) show contrast behaviors with variation of \(\sigma _r\) and \(\Delta _p/\gamma\). Similarly the GH-shifts in reflection and transmission of LCP beams \(S^{(L)}_{r}\) and \(S^{(L)}_{t}\) show contrast behaviors with variation of \(\sigma _r\) and \(\Delta _p/\gamma\). The GH-shifts in reflection and transmission of RCP and LCP beams are fluctuated slowly with the forward current and probe field detuning. Both positive and negative GH-shifts for RCP and LCP beams in reflection are reported in the range of \(-10\lambda \le S^{(R,L)}_{r} \le 20\lambda\) with forward current and probe detuning as shown in Fig. 5a,b. Also both positive and negative GH-shifts for RCP and LCP beams in transmission are reported in the range of \(-20\lambda \le S^{(R,L)}_{t} \le 10\lambda\) with forward current and probe detuning as shown in Fig. 5c, d.

In Fig. 6, the plots are traced for RCP and LCP beams in reflection and transmission versus backward current \(\sigma _i\) and control field Rabi frequency \(\Omega _c/\gamma\). The RCP and LCP beams in reflection and transmission are oscillated with backward current and control field Rabi frequency and obey the normalization condition, where absorption coefficients are controlled to zero values as as \(|A^{(R,L)}|\simeq 0\). The RCP beam in reflection has maximum value of \(|R^{(R)}|\simeq 1\), while in transmission has minimum value of \(|T^{(R)}|\simeq 0\) at the points (\(\sigma _i\), \(\Omega _c\))=(\(5 S/m, 2.5\gamma\)) as shown in Fig. 6a, c. The same values are true for \(|R^{(R)}|\) and \(|T^{(R)}|\) at the points \(\sigma _i=200 s/m, 0.5\gamma\). Also the LCP beam in reflection has maximum value of \(|R^{(L)}|\simeq 1\), while in transmission has minimum value of \(|T^{(L)}|\simeq 0\) at the points (\(\sigma _i\), \(\Omega _c\))=(\(5 S/m, 2.5\gamma\)) as shown in Fig. 6b, d.

In Fig. 7, the plots are traced for GH-shifts of RCP and LCP beams in the reflection and transmission versus backward current \(\sigma _i\) and control field Rabi frequency \(\Omega _c/\gamma\). The GH-shifts of RCP and LCP beams in reflection and transmission are fluctuated weakly with backward current \(\sigma _i\) and controlled field Rabi frequency \(\Omega _c/\gamma\). Both Positive and negative GH-shifts in RCP beam in the reflection and transmission are investigated. The maximum value of GH-shift for RCP beam in reflection and transmission are calculated to \(\pm 10\lambda\) as shown in Fig. 7a, c. Similarly, both Positive and negative GH-shifts for LCP beam in reflection and transmission are reported. The maximum value of GH-shift for LCP beam in reflection and transmission are calculated to \(\pm 40\) as shown in Fig. 7b, d.

Conclusion

In conclusion a cavity within a conductive chiral medium of length \(d_2\) is placed. The atomic system of conductive medium is a bulk of four levels configuration, where phonon contribution is ignored. The four level conductive medium is surrounded by a thin layer of polystyrene of permittivity \(\epsilon _1\) and thickness \(d_1\). The permittivity function of the conductive medium is \(\epsilon (\sigma )\). The charge particles or electrons are set to move by an external potential V. The backward current is also generated by the induced back Emf. The complex conductivity dependent birefringent of reflection, transmission and corresponding GH-shifts were investigated at the interface of chiral conductive medium and polystyrene. Complex conductivity dependent coefficients for reflection, transmission as well as GH-shifts for the conductive chiral medium were calculated using Maxwell’s equations and density matrix formalism. The birefringence of reflection and transmission as well as their corresponding Goos Hanchen shifts were investigated with variation of complex conductivity and driving fields parameters. The RCP and LCP beams obeyed the normalization condition \(|R^{(R,L)}|+|T^{(R,L)}|=1\) with forward and backward currents as well as coupled driving fields parameters at the interface of a lossy chiral medium of \(|A^{(R,L)}|\simeq 0\) and polystyrene. Negative GH-shifts were reported for birefringent reflection and positive GH-shifts were measured for birefringent transmission. The maximum GH-shifts in reflections of RCP and LCP beams was measured to \(S^{(R,L)}_{r}=-10\lambda\) and transmission was measured \(S^{(R,L)}_{t}=10\lambda\) with complex conductivity. Further GH-shift in the transmission of RCP and LCP beams were reported in the range of \(-20\lambda \le S^{(R,L)}_{t} \le 10\lambda\) and reflection were investigated in the range of \(-10\lambda \le S^{(R,L)}_{r} \le 20\lambda\) with forward current and probe detuning. The maximum value of GH-shifts for LCP in reflection and transmission beams were calculated to \(\pm 40\lambda\) and for RCP beams were calculated to \(\pm 10\lambda\) with control field and backward current variation. The results have significant role in the designing of conductive sensors and optical sensors.