Introduction

Beam deflection devices are employed to change the direction of propagation of a light beam in space and are widely employed in fields such as LIDAR, micro-nano-processing, 3D displays and optical communications1. The relentless advancement in autonomous driving technology demands robust solid-state LIDAR systems2, while the production of micro-optoelectronic devices leans on advanced laser manufacturing techniques3,4,5,6,7. Furthermore, the unyielding demand for high-resolution display technologies in the extensive optical display market continues to surge. These requirements foster the ongoing enhancement of laser deflection technology, which traditionally encompasses macro-mechanical, micro-mechanical and modulation deflection systems. The macro-mechanical systems, however, often suffer from mechanical vulnerabilities, instability and substantial size, leading research to pivot towards more reliable micro-mechanical deflection technologies like MEMS galvanometers8 and digital micromirror devices (DMD)9,10, as well as modulation techniques such as liquid crystal spatial light modulators(LC-SLM)11,12,13 and optical phased arrays14. Among these, DMD exemplifies the successful integration of microelectromechanical systems, large-scale integrated circuits and micro-optical technology. It comprises millions of micro-mirrors fabricated through micro-machining processes, and arrayed in a 2D configuration of aluminum reflective units15,16. It offers advantages such as high contrast, rapid response speed and high luminance compared to modulation deflection technology devices17. Nevertheless, due to limitations imposed by the micro-mirror torsion, the beam deflection angle of DMD is constrained to a narrow range and its spatial resolution is limited. These limitations undoubtedly impact the optimization of DMD performance in practical applications. On the other hand, liquid crystal on silicon (LCOS) spatial light modulators, belonging to modulated deflection technology, manipulate the amplitude, phase and polarization state of reflected light by controlling the pointing vector distribution of LC molecules on independent electrodes18,19. LCOS offers advantages such as high spatial resolution, high refresh rate, low power consumption and flexible independent addressing capability. Consequently, LCOS finds widespread use in scenarios requiring phase modulation. However, due to the polarization-dependent behavior of nematic LC, LCOS can only modulate a single polarization state. This limitation results in high complexity, high cost and low efficiency of existing LCOS devices.

In recent years, metasurfaces have emerged as a focal point of research and represent a highly promising category of devices for manipulating electromagnetic waves within the field of nanophotonics. It’s composed of subwavelength structures arranged in 2D plane20, enabling precise and flexible control over various parameters of incident electromagnetic waves, including phase21,22,23, amplitude24,25,26 and polarization27,28,29. Metasurfaces offer superior control capabilities over electromagnetic wave parameters compared to traditional optical elements. They also have advantages such as ultrathin profiles, low losses, ease of integration and simplified fabrication processes30,31. Over the past decade, metasurfaces have blossomed into a vibrant area of research and various designs of metasurfaces have been applied in applications such as beam steering32, polarization conversion33, chromatic aberration correction lenses34 and full-color holography35. Although metasurfaces can only be subjected to static beam modulation at the completion of preparation, advancements in processing technology and materials science are leading to the emergence of active beam modulation designs for metasurfaces. Current dynamic metasurface designs can be categorized based on their modulation mechanisms, including mechanical actuation, chemical approaches, phase-change materials and opto/electro-responsive control36. These methods facilitate the dynamic modulation of metasurface functionalities to achieve specific beam deflection characteristics. When considering the resonant tuning characteristics of metasurfaces, integrating an external material layer that can stimulate the metasurface structure is an attractive option37. LC, known for their sensitivity to temperature, applied electric and magnetic fields and with well-established preparation processes, emerge as the ideal material to complement static metasurfaces38,39,40,41. Nonetheless, the birefringent nature of LC materials can lead to devices encountering the same polarization-dependent issues as LCOS devices, which is still insufficient compared to polarization-insensitive DMD devices. Some polarization-insensitive LC device designs that exist today, such as those using blue-phase LC materials42 or a special light-controlled azimuth angle (LCAA) process43, suffer from high drive voltage, high liquid crystal thickness, and low efficiency.

In this paper, we propose the design of optical components that leverage both metasurface and LC to achieve large-angle beam deflection capabilities and polarization-independent properties. On one hand, the device can realize dynamic beam deflection with an extensive field of view of approximately ± 27.1° through voltage modulation of LC. On the other hand, the integration of the designed metasurface with the LC enables the device to achieve polarization-independent beam modulation. The benefits of being ultra-light, ultra-thin and offering large-angle beam deflection and polarization insensitivity make metasurface devices well-suited to compensate for the current limitations of DMD chips. They also circumvent the polarization dependence issues of LCOS devices. As a result, metasurface devices are anticipated to replace DMD chips to meet the increasing demand for optical control.

Result and discussions

Design and Simulation

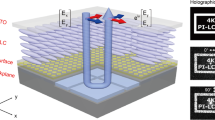
Fig. 1a depicts a polarization-independent dynamic beam modulation metasurface, which combines nematic LC with a reflective metasurface. The device primarily consists of a dynamic modulation layer. This layer includes a metal metasurface in the lower section, stacked with a dielectric grating in the upper section. High birefringent fluorinated phenyl-tolane isothiocyanate LC compounds (\(\:{n}_{e}=1.92\), \(\:{n}_{o}=1.5\) @ 950 nm, 25 °C) are infused within this dynamic modulation layer to facilitate dynamic modulation. An orientation layer of polyimide (PI) is applied to a quartz cover plate coated with indium tin oxide (ITO), which then serves as the top electrode of the device, enabling effective control and modulation of the beam characteristics. The upper and lower layers of the device are structurally distinct yet functionally integrated, collectively achieving the dynamic beam deflection function that remains effective irrespective of the external voltage applied. The lower layer of the metasurface consists of a gold nanorod unit cell enclosed within hydrogen silsesquioxane (HSQ), a silicon dioxide (SiO2) spacer layer and a gold reflective substrate. This configuration forms a metal-insulator-metal (MIM) structure with gold-silicon dioxide-gold layers. The gold structure is coated with HSQ to reduce direct contact between the structure and the LC, providing a protective layer and minimizing interactions between the metasurface and LC. The lower layer of the metasurface is primarily utilized to achieve polarization-independent phase modulation. The designed rectangular metallic structures exploit both geometric phase and plasmonic resonance phase to achieve precise phase responses. By employing the generalized Snell’s law20, an appropriate phase gradient is engineered to achieve beam deflection functionality. Plasmonic resonance refers to the modulation of electromagnetic waves using surface artificial metallic structure units to generate surface plasmon resonance modes44; geometric phase, on the other hand, is a method of controlling the wavefront phase through the rotation angle of anisotropic nanoscale antennas45. By changing the rotation angle of the nanoscale antennas, it is possible to achieve a phase discontinuity in the outgoing beam. The combination of these two wavefront modulation methods enables artificial control of phase gradients or distributions. This simplifies the design and fabrication of metasurface structures, making it possible to achieve phase gradient distributions from 0 to 2π with ease. Concurrently, enhancements in processing accuracy not only improve the precision of experimental outcomes but also enhance the efficiency of beam deflection. Moreover, the integration of an LC dielectric grating with the metasurface enables the modification of the phase gradient, thereby facilitating changes in the beam deflection angle. This advanced capability underscores the metasurface’s potential in sophisticated optical applications, offering precise control over beam steering mechanisms.

In contrast to Digital Micromirror Devices (DMD), we introduce a novel metasurface chip concept, as depicted in Fig. 1b. This chip comprises pixels with varying periods, built on a silicon circuit backplane that incorporates Complementary Metal-Oxide Semiconductor (CMOS) technology. An LC layer is integrated into this backplane, forming an LCOS device. This setup minimizes crosstalk among the LC molecules, thereby enabling a broad spectrum of beam deflection effects. After providing the chip with 2D addressable bias signals in a specific order, each pixel unit can deflect the incident beam to different angles. The dynamic beam deflection effect of the device is achieved through the refractive index variation of the vertically aligned LC, which offers higher stability, a smaller size, and a faster scanning speed compared to traditional DMD devices. Additionally, the device created with pixelated metasurfaces offers the benefits of LCOS, allowing for extremely high pixel resolutions such as 4 K or even 8 K, as well as high efficiency in spatial light modulation. This technology has significant potential for use in a variety of fields, including optical displays, optical communications, laser processing and LIDAR.

Fig. 1
figure 1

(a) Schematic diagram of a polarization-independent dynamic beam deflector. Each unit consists of four group structures enclosed within HSQ, responsible for phase modulation from 0 to 2π with an increment of π/2. The PMMA dielectric grating filled with LC is aligned and etched on the metasurface. The molecular orientation of the LC varies with the applied voltage. \({\theta}_{LC}\) is the pointing angle of the LC molecule pointing vector, which varies with the applied voltage. (b) The pixelated metasurface chip consists of metasurface pixel blocks placed on a CMOS circuit backplane. Each pixel’s state is meticulously controlled by external voltage signals, which directly dictate the deflection angle of the outgoing beam. This precise control mechanism allows for dynamic adjustment of the beam direction.

Full size image

The upper section of the device consists of polymethyl methacrylate (PMMA) gratings interleaved with liquid crystals impregnated with gratings. This PMMA grating is designed to correspond with the underlying metasurface metal structure. When the applied voltage is altered, the orientation of the LC molecules shifts, leading to a corresponding change in the material’s refractive index. Unlike the PMMA material, whose refractive index remains constant, the LC contributes an additional phase shift within the grating layer. \({\theta}_{LC}\) is the rotation angle of the LC molecule pointing vector. In the process of LC molecule change, it is necessary to consider the refractive index in the two states of \({\theta}_{LC}\), 0° and 90°. The formula for the refractive \(n\) of the LC is provided as follows:

$$\frac{1}{{{n^2}\left( {{\theta _{LC}}} \right)}}=\frac{{{{\cos }^2}{\theta _{LC}}}}{{{n_e}^{2}}}+\frac{{{{\sin }^2}{\theta _{LC}}}}{{{n_o}^{2}}}$$
(1)

Here, \({n}_{e}\)and \({n}_{o}\) represent the extraordinary refractive index and ordinary refractive index of the LC (\({n}_{e}=1.92, {n}_{o}=1.5 \) @ 950 nm, 25 °C) respectively. The thickness \(d\)of the dielectric grating on the metasurface can be adjusted to control the phase difference \(\varphi\),

$$\phi =\frac{{2\pi ({n_e} - {n_o})d}}{\lambda }$$
(2)

During the design of the metasurface device, a key objective was to achieve a phase difference of \(\pi\) in the optical path at a wavelength of 950 nm. This was accomplished by integrating a dielectric grating with a height of 1130 nm into the device structure. The specific height of the grating is critical as it directly influences the phase response of the device, ensuring that the optical path length corresponds precisely to the desired phase shift. This addition results in the desired phase response. The phase modulation principle of the device is illustrated in Fig. 2a. When \({\theta}_{LC}\) changes to 90° due to an applied voltage, the refractive index of LC (\({n}_{0}=1.5\)) matches that of PMMA. \({\theta}_{LC}\) does not impact the phase gradient across the dielectric grating on the metasurface. In this scenario, the phase response distribution of the incident light is primarily controlled by the gold nanoantenna, yielding a phase pattern illustrated as \(0,\pi/2,\pi,3\pi/2\) (red dashed line). Conversely, in the absence of voltage, \({\theta}_{LC}\) defaults to 0° due to the influence of the grating grooves and alignment layers. This alters the LC’s refractive index to its extraordinary index (\({n}_{e}=1.92\)), which is distinct from that of PMMA. Consequently, the phase modulation of the incident light becomes a collaborative effect of the gold nanorods and the dielectric grating. Assigning a phase difference of \(\pi\) to each adjacent period of the grating results in a phase response distribution depicted as \(0,-\pi/2,\pi,\pi/2\) (green dashed line). Through periodic calculations, the phase distribution can be expanded as \(0,-\pi/2,-\pi,-3\pi/2\)(blue dashed line). The phase distribution obtained through FDTD simulation of the designed structure (red and blue dots) closely matches the theoretical expectations. The reverse variation of phase difference in the phase gradient of the metasurface can generate beam steering angles in two opposite directions, according to the generalized Snell’s law. This phenomenon enables the formation of a larger-angle dynamic beam deflection effect.

It is worth noting that due to the anisotropy of LC, the refractive index of differently polarized light varies in LC. This is an unavoidable problem in LC-integrated dynamic metasurfaces and many LC-integrated metasurface devices suffer from the problem that only a single line-polarized light source is applicable. In this paper, the polarization insensitivity effect is achieved by the cooperation of LC dielectric grating and gold nanopillars in the upper part of the device, as shown in Fig. 2b. According to Eq. 2, the transmission matrix of the LC modulation layer can be described as:

$${T_{LC}}=\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{\exp (i\phi )} \end{array}} \right)$$
(3)

Grounded in the principles of electromagnetic wave polarization, a pair of orthogonal linear polarizations are used to replace the modulation of arbitrary polarization states of the incident beam by the device under different alignment conditions. In order to attain polarization insensitivity amidst discrepancies in refractive index, the design of the gold nanorod mirrors that of a half-wave plate, positioned at a 45° angle relative to the grating direction. The transmittance matrix of the metasurface can be described as follows:

$${T_M}={T_{LC}}{T_{Structure}}{T_{LC}}=\left( {\begin{array}{*{20}{c}} 0&{\exp (i\phi )} \\ {\exp (i\phi )}&0 \end{array}} \right)$$
(4)

Here, \({T_{structure}}\) is the transmission matrix of the 45° aligned gold nanorods, \({T_{structure}}=R(45^\circ )\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{\exp (i\pi )} \end{array}} \right)R( - 45^\circ )=\left( {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right)\), \(R(\theta )=\left( {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta } \\ {\sin \theta }&{\cos \theta } \end{array}} \right)\).

In Eq. 4, the rotation angle \({\theta}_{LC}\) of the LC molecules is decoupled from \({T}_{M}\)to achieve the polarization-independent properties of the device. In the overall design, when \({\theta}_{LC}=90^\circ\), for any polarized light incident on the LC, the refractive index remains the same. For a pair of orthogonal linearly polarized light entering the device, both the incident and outgoing light experience the same refractive index in the LC and PMMA layers. During the beam’s incidence and emergence, they acquire an additional phase shift \(\:{\varphi}_{o}\) (blue). When \({\theta}_{LC}=0^\circ\), the incident orthogonal linearly polarized light undergoes a phase difference after passing through the LC layer, depending on whether it is parallel or perpendicular to the long axis of the LC molecules. They are respectively assigned phases \({\varphi}_{o}\) (blue) and \({\varphi}_{e}\) (purple). After passing through the gold nanorods, the orthogonal linear polarization directions are interconverted. The polarized light, upon re-entry through the LC layer, undergoes an additional phasing akin to that at the time of incidence, resulting in the outgoing orthogonal polarizations acquiring phases \({\varphi}_{o}+{\varphi}_{e}\) (green). Thus, through the clever combination of the metasurface and the LC layer, we can achieve polarization-independent characteristics of the device.

To achieve substantial beam deflection over a wide angle and ensure polarization independence, the architectural design of the metasurface structure is pivotal. The gold nanorod structure must secure a significant phase difference via plasmonic resonance while sustaining a high polarization conversion ratio (PCR). This work primarily uses FDTD Solutions software for scanning simulations. The simulations produced the optimal parameters for the metamaterial surface, with a period of 280 nm and a height of 50 nm for the gold nanorods (refer to Supplementary Information Fig. S1). From this database, two sets of structural parameters (W1 = 100 nm, L1 = 310 nm; W2 = 70 nm, L2 = 130 nm) were selected to construct the metasurface. Fig. 2c shows the far-field diffraction patterns and normalized intensity of the metasurface under two different LC states. The beam exhibits significant deflection, coupled with a pronounced alternating variation in the intensities of the ± 1 diffraction orders at ± 25.5° consequent to the switching of the LC states. We have similarly simulated the beam deflection effect for circular polarizations incident device, as shown in Supplementary Information Fig. S2a, and the results are consistent with those for linear polarization, demonstrating that the beam deflection function is independent of the incident polarization state. Furthermore, the diffraction intensity distributions of orthogonal linearly polarized beams are similar, indicating that the beam deflection functionality is independent of the incident polarization state. Additionally, we validated the polarization-insensitive characteristics of the device by simulating the diffraction patterns when linearly polarized beams with different tilt angles were incident on the device, as shown in Fig. 2d. Under both states of the LC, the diffraction efficiencies of each linear polarization for each diffraction order are consistent, with a variation rate of less than 9.8%, indicating high stability.

Fig. 2
figure 2

(a) Principle and simulation of phase modulation for dynamic beam deflection. (b) Schematic diagram of the polarization-insensitive metasurface. (c) Far-field diffraction patterns and normalized intensity patterns (using the same arbitrary units scale) for orthogonal linear polarization under different LC states. (d) Diffraction efficiency of the ± 1 diffraction order for the device under different tilt angles of linear polarization when the angle \({\theta}_{LC}\)of the LC molecule is 0° or 90°.

Full size image

Multi steering angle simulation

Following the optimization and simulation of the single-period metasurface structure, this investigation delved into analyzing metasurface unit cells across varying periods to fully harness the capabilities of the beam deflector device. Six different periods were considered: 260 nm, 280 nm, 300 nm, 320 nm, 340 nm and 360 nm. These periods enable multi-level switching of beam deflection angles ranging from approximately ± 19.2° to ± 27.1°. The design parameters were selected for each period unit from the gold nanorods database. Fig. 3a shows the far-field diffraction patterns of the metasurfaces with different periods, under different LC states and polarizations. The diffraction efficiencies of each target diffraction order are presented in Fig. 3b. The metasurfaces with different periods exhibit significant beam deflection effects in different LC states. The maximum diffraction efficiency for the target diffraction order (+ 1 order) is 89.1%, while for the target diffraction order (-1 order) it is 68.4%. The diffraction distributions are consistent for all periods under orthogonal linear polarization, demonstrating the device’s polarization-independent characteristics. However, the diffraction efficiency of the target diffraction order decreases when the period of the metasurface unit increases or decreases due to the interference of the dielectric grating. Therefore, selecting an appropriate unit cell period is crucial for future device fabrication.

Fig. 3
figure 3

(a) The far-field diffraction patterns of unit structures with six different periods: 260 nm, 280 nm, 300 nm, 320 nm, 340 nm and 360 nm, where the X polarization is perpendicular to the PMMA grating and the Y polarization is parallel to the grating. (b) Displays the diffraction efficiency of the ± 1 diffraction order for the metasurfaces with different period unit cells under different states.

Full size image

Optimization of grating offset

The simulation results aforementioned reveal that while the device exhibits comparable outcomes across various polarizations, a discernible reduction in the diffraction efficiency of the target diffraction order (-1 order) is observed, especially in comparison to the target diffraction order (+ 1 order) at \({\theta}_{LC}=0^\circ\). This decrease is particularly significant under the Y-polarized beam. This decrease is also significant at different PMMA grating heights as well as at different \({\theta}_{LC}\), as shown in Supplementary Information Fig. S2b and Fig. S2c. We believe that this phenomenon is caused by the different modulation sequences of orthogonal polarized light inside the device. As shown in Fig. 4a, when Y-polarized beam enters the device, it is perpendicular to the long axis of the LC molecules and therefore, the grating layer does not add a phase difference to it. The grating only imparts a phase difference to the Y-polarized beam after it is converted by the metasurface upon exiting. However, due to the abnormal reflection caused by the polarization conversion of the metasurface for Y-polarized beam, the beam does not exit perpendicularly. The grating layer phase-modulates the light, allowing it to be deflected only in the intended polarization direction. This is supported by the electric field plots obtained through FDTD simulations, as depicted in Fig. 4b. The abnormal reflection at the exit of the beam causes deviation in the modulation of the grating layer, resulting in an insufficient phase modulation and significantly affecting the final beam deflection performance of the device. In response to this phenomenon, we propose an optimization design scheme for the grating offset, as shown in Fig. 4c. By adjusting the position of the upper grating layer relative to the metasurface, the exiting beam can be more precisely modulated by the grating despite the presence of abnormal reflection, thus enhancing the beam deflection performance. This scheme can improve the diffraction efficiency of the target diffraction order under Y-polarized beam, as shown in Fig. 4d, where the diffraction efficiency is proportional to the distance D of grating offset. However, this offset also induces misalignment in the grating modulation for beams incident normally under X-polarization, leading to a decrease in diffraction efficiency as the offset distance enlarges. Consequently, meticulous control of the grating offset distance is crucial during both fabrication and practical application of the device to tailor its performance to meet specific operational demands.

Fig. 4
figure 4

(a) Schematic diagram illustrating the modulation of Y-polarized beam by the metasurface upon incidence. (b) Electric field plot showing the modulation of Y-polarized beam by the metasurface. (c) Schematic diagram of grating offset. (d) Variation of the diffraction efficiency of the target diffraction order for orthogonal linear polarizations at different distances of grating offset.

Full size image

Conclusion

In summary, this paper focuses on designing a polarization-insensitive dynamic beam deflection metasurface device to replace DMD. The device comprises a dielectric grating and a metasurface structure. The dielectric grating, made of PMMA and LC, is responsible for achieving the device’s dynamic tunability. The metasurface is composed of gold nano-pillars and a gold reflective substrate. It utilizes phase gradient construction to achieve beam deflection. The combination of these two components enables polarization-insensitive effects. We simulate the beam deflection performance of the device across multiple cycles, observing that the device achieves multi-level dynamic beam deflection ranging from ± 19.2° to ± 27.1° at a 950 nm wavelength, independent of the polarization state of the incident light. Meanwhile, all the design parameters of the device satisfy the processing conditions, for which we designed a potential processing flow for the metasurface device, as shown in Supplementary Information Fig. S3. Building on this, we propose the integration of multiple metasurface devices on a single chip, with control over the chip to facilitate the beam scanning effect through the input of external signals. We aim to combine nanofabrication processes, LC packaging techniques and mature CMOS processes to realize the fabrication of pixelated chips. This device holds the potential to contribute to various fields such as optical displays, optical communications and LIDAR.

Methods

The FDTD Solutions was used to design, optimize and simulate the metasurface device. The device was simulated with a silicon substrate, which included a 150 nm gold reflective layer and a 50 nm silicon dioxide layer. To achieve a high-performance polarization-insensitive beam deflector, it is necessary to rigorously design various parameters of the gold nanostructures, HSQ cladding layer and dielectric grating. This will ensure high reflectivity, PCR, diffraction efficiency, and polarization insensitivity.

To simulate a single unit, we set periodic boundary conditions in the x and y directions and a perfectly matched layer in the z direction. We placed monitors and analysis groups on the x-y plane to observe and analyze the simulation results. The metasurface was optimized through parameter design and simulated to investigate the beam deflection for different polarizations and refractive indices of the LC. This validates the device’s performance characteristics. FDTD Solutions were used for the design, optimization and simulation to gain a better understanding of the device’s behavior and to make parameter adjustments to achieve the desired performance. This simulation approach can guide the fabrication and optimization of practical devices, expediting the development process of metasurface devices for real-world applications.