Analysis of shield tunnel response to bilateral pit excavation with a focus on perimeter pressure and deformation mechanisms

Abstract

This study aims to investigate the responses of shield tunnel structures subjected to disturbances caused by bilateral pit excavation, and it systematically reveals for the first time the impact mechanism of bilateral pit excavation on the distribution of perimeter pressure and deformation patterns of shield tunnels. Using a bilateral pit excavation project in Nanjing as a case study, this research establishes methods for calculating longitudinal displacement and circumferential pressure of tunnels under bilateral pit excavation conditions, employing the image source method for analysis. A refined three-ring segment model is developed, and the load structure method is used to analyze the impact of deep foundation excavation on the tunnel located between the two excavation sites. The results indicate that, compared to unilateral excavation, bilateral excavation significantly increases the perimeter pressure at the top and bottom of the tunnel, with a smaller increase in pressure at the arch waist. The deformation pattern is characterized by contraction at the top and bottom and expansion at the waist, forming a transverse elliptical deformation. The maximum vertical convergence values of the middle segment ring are 25.00 mm at the top and 25.88 mm at the bottom, with a vertical absolute convergence value of 44.5 mm and a convergence ratio (ΔD_t/D_t) of 0.72%. As the foundation coefficient increases, the perimeter pressure at the top and bottom of the tunnel also increases. When the tunnel is closer to the foundation pits (S_p decreases), the perimeter pressure at the bottom of the tunnel increases. Conversely, as the distance between the two foundation pits (S) increases, the impact of excavation on the tunnel shifts from the upper part to the lower part, resulting in decreased upper perimeter pressure and increased lower perimeter pressure. The research findings provide important references for similar engineering projects.

Introduction

Rapid urban development has led to increasingly congested underground spaces in cities. For example, in Qianhai, Shenzhen, China, the density of underground rail traffic reaches 3.2 km/km². With the accelerated construction of urban rail transit and the increasing exploitation of underground space resources, more and more pit projects appear beside existing shield tunnels. The increasing complexity of the current engineering environment often necessitates bilateral pit excavation. This process inevitably displaces the surrounding soil, and if this displacement exceeds safety limits, it can deform or even destroy shield tunnels, posing serious threats to urban transportation safety and stability. Shield tunnels are subject to stringent deformation criteria: the relative bending must not exceed 1/2500, and the maximum absolute displacement of the structure must not exceed 20 mm¹. Given the specific conditions of bilateral excavation, assessing the impact on shield tunnels is crucial for controlling tunnel structure displacement, making relevant research imperative. This study fills a critical gap in the existing literature by systematically analyzing the impact mechanisms of bilateral pit excavation on shield tunnels, which has not been extensively explored before.

Today’s engineering environments are varied and complex, with bilateral pit excavation being increasingly common. Zeng² analyzed two adjacent pits excavated simultaneously in Shanghai, focusing on the deflection of the enclosure structure and ground settlement. Li³ studied the unloading deformation mechanism and deformation control of soft soil foundation pits with bilateral excavation. Unlike unilateral excavation, bilateral pit excavation significantly alters the soil displacement field and introduces additional influencing factors. Consequently, the tunnel response to bilateral excavation differs markedly.

Current research on tunnel response to bilateral pit excavation primarily utilizes numerical simulation and measured analysis^{4,5,6,7,8,9,10,11,12,13,14}, with most studies focusing on engineering cases in soft soil areas. Theoretical research by Zhang et al.¹⁵ and Feng¹⁶ provided preliminary analyses of longitudinal tunnel displacement under bilateral excavation but did not address transverse deformation laws. Subsequently, Wei et al.¹⁷ proposed a method for calculating the additional lateral external load on shield tunnels induced by side pit excavation. Chen et al.¹⁸ also developed a theoretical calculation method for the lateral force on shield tunnels, accounting for the deformation of the enclosing structure. However, these methods apply to tunnels impacted by single side pit excavation.

In summary, while significant progress has been made in understanding shield tunnel deformation due to unilateral pit excavation, research on bilateral pit excavation’s impact remains incomplete. Unlike previous studies that predominantly focus on the effects of unilateral pit excavation, this research pioneers the investigation of shield tunnel responses under bilateral pit excavation conditions, offering a novel approach to understanding the associated displacement and pressure changes.

Theoretical calculation methods

Analytical modeling

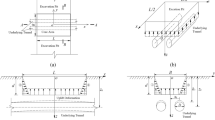
Normal consolidated soil is in a state of static earth pressure at all points before excavation. As shown in Fig. 1, after the excavation of the foundation pit, the unloading of the soil disrupts the original stress equilibrium state of the soil in the sidewalls, generating an unloading stress increment. This disruption causes displacement of the surrounding soil and the supporting structure. Consequently, this additional stress induces a certain displacement of the adjacent tunnel towards the foundation pit.

Fig. 1

Schematic diagram of side tunnel deformation caused by pit excavation.

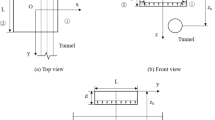
Figure 2 illustrates the theoretical calculation model used in this study, where the shield tunnel is situated on the right side of the side pit. The parameters of the pit are defined as follows: the excavation depth is denoted as d_i, the depth of burial of the enclosure structure as d_0i, and the width as B_i. The external diameter of the shield tunnel is D_t, the radius is R, the segment thickness is d_t, the ring width is b_t, the burial depth of the center axis is h_t, and the horizontal clear distance from the pit is s_i. Here, i denotes the pit number, with i = 1 representing the right side of pit I and i = 2 representing the left side of pit II. The theoretical calculations were implemented using MATLAB version 9.10 R2021a (available at: https://www.mathworks.com/products/matlab.html).

Fig. 2

Model of theoretical calculation in this paper.

Initial tunnel pressure

Before the excavation of the side pit, the existing tunnel is in a stable state. Koyama (2003) mentioned two initial perimeter pressure calculation models in Japan for this stable condition. Lee considered that the initial tunnel perimeter pressure includes (as shown in Fig. 3): P₁, the overlying soil and water pressure; P₂, the reaction force at the tunnel base; P₃, the horizontal soil and water pressure at the top of the arch; P₄, the additional horizontal soil and water pressure at the bottom of the arch; P_G, the self-weight of the lining; and P_e, the ground resistance. Gong et al.¹⁹ built upon the initial load distribution diagram proposed by Lee²⁰.

Fig. 3

Initial load distribution in the tunnel²⁰.

$${P_1}={\gamma _1}{z_1}+{\gamma _2}{z_2}$$

(1)

$${P_2}={\gamma _1}{z_1}+{\gamma _2}{z_2}+\pi {D_t}{\gamma _T}$$

(2)

$${P_3}={q_1}{\tan ^2}\left( {45^\circ - \frac{\varphi }{2}} \right) - 2c\tan \left( {45^\circ - \frac{\varphi }{2}} \right)$$

(3)

$${P_4}=2{\gamma _3}R{\tan ^2}\left( {\frac{\pi }{4} - \frac{\varphi }{2}} \right)$$

(4)

$${P_G}={\gamma _T}{D_t}$$

(5)

$${P_e}={k_s}{\Delta _e}$$

(6)

Where: γ₁ represents the average weight of the soil layer overlying the arch, γ₂ denotes the average weight of the soil layer on the arch shoulder, γ₃ signifies the average weight of the soil layer on the arch waist, and γ_T is the weight of the tube sheet. Additionally, z₁ is the thickness of the soil layer overlying the arch, z₂ is the thickness of the soil layer on the arch shoulder, and φ is the average internal friction angle in the arch waist range. The initial displacement of the new tunnel is denoted as ${\Delta _e}$. The ground resistance coefficient, k_s, can be determined using the modified Vesic²⁷ formula or selected based on empirical values provided in Table 1.

Table 1 Stratigraphic resistance coefficients k_s table.

Free-field calculation of soil displacement in bilateral pit excavation

Sagaseta²¹ introduced an analytical method for calculating displacement at any point within a semi-infinite elastic space resulting from strata loss. This method employs the principle of image source method, which estimates free-field strata displacement by analyzing the deformation of the enclosure structure. It is based on the assumption that the volume change in the enclosure structure due to pit excavation equals the volume change in the strata after excavation. Building upon this theory, our study proposes a method to superimpose the displacement fields for bilateral excavation. This approach assumes that the displacement fields generated by the enclosure structures on both sides, due to their respective volume changes, can be combined. The calculation expression is as follows:

$${S_{xij}}= - \int_{{{H_i}}}^{0} {\frac{{{a^2}}}{2}} \left( {\frac{{{x_{ij}}}}{{{r_{i1}}^{2}}} - \frac{{{x_{ij}}}}{{{r_{i2}}^{2}}}+\frac{{2{x_{ij}}}}{{{r_{i2}}^{2}}}\left[ {1 - \frac{{2{h_t}\left( {{h_t}+{z_i}} \right)}}{{{r_{i2}}^{2}}}} \right]} \right)d{z_i}$$

(7)

$${S_{zij}}= - \int_{{{H_i}}}^{0} {\frac{{{a^2}}}{2}} \left( {\frac{{{h_t} - {z_i}}}{{{r_{i1}}^{2}}} - \frac{{{h_t}+{z_i}}}{{{r_{i2}}^{2}}} - \frac{{2{h_t}}}{{{r_{i2}}^{2}}}\left[ {1 - \frac{{2{x_{ij}}^{2}}}{{{r_{i2}}^{2}}}} \right]} \right)d{z_i}$$

(8)

$$a=\sqrt {\frac{2}{\pi }w({z_i})}$$

(9)

$${r_{i1}}=\sqrt {{x_{ij}}^{2}+{{\left( {{h_t} - {z_i}} \right)}^2}}$$

(10)

$${r_{i2}}=\sqrt {{x_{ij}}^{2}+{{\left( {{h_t}+{z_i}} \right)}^2}}$$

(11)

To accurately establish the soil displacement field, it is crucial to define the boundary soil displacement conditions. This study assumes that within the enclosure structure, the soil displacement is zero from the ground surface (0) to a depth of H_i. Additionally, the influence range of the ground structure is considered to extend below the enclosure structure by a factor of a_x. These boundary conditions are essential for accurately modeling the soil displacement behavior under bilateral pit excavation conditions. It is important to note that the provided formula specifically calculates the soil displacement at the tunnel point (x_ij, h_t). To determine the soil displacement at any arbitrary location (x, y), the variables (x_ij, h_t) in the formula should be appropriately substituted with (x, y).

Where: j = 1, 2 (where j = 1 represents the pit-induced soil displacement around the near side of the tunnel, and j = 2 represents the far side); S_xij denotes the horizontal soil displacement around the tunnel caused by the near pit. $w({z_i})$ represents the displacement curve of the enclosure structure under bilateral excavation conditions, typically exhibiting a composite and concave shape. In this study, $w({z_i})={\delta _{i\hbox{max} }} \cdot {e^{ - 1.5{{\left( {\frac{{{z_i} - {H_i}}}{{{H_i}}}} \right)}^2}}}$ denotes the fitted curve of the enclosure structure displacement, while ${\delta _{i\hbox{max} }}$ represents the cumulative maximum deformation of the enclosure structure.

Calculation of perimeter pressure under displacement field

Calculation of perimeter pressure of additional soil

In unilateral excavation scenarios, Zhang et al.^22,23 identified three stages of perimeter pressure redistribution for tunnels under additional pit excavation loads. The F₁ stage corresponds to the near-side additional load on the tunnel lining generated by unilateral pit excavation. The F₂ stage involves circumferential shear loading between adjacent tube sheets after tunnel displacement. The F₃ stage represents perimeter pressure unloading on the far-side of the tunnel after overall tunnel movement (as shown in Fig. 4(a)). However, unlike unilateral excavation, the process of peripheral pressure redistribution in bilateral excavation environments remains debated, making it challenging to determine the far-side unloading effects of pit excavation.

Chen et al.¹⁸ utilized the image source method to establish the soil displacement field for unilateral pit excavation while also accounting for the inter-ring shear forces induced by misalignment. However, the circumferential pressure distribution function they adopted¹⁹ still requires further refinement.

This study draws on the calculation method for perimeter pressure under unilateral unloading proposed by Chen¹⁸ (as shown in Fig. 4(b)). Initially, the soil displacement field of bilateral pit excavation is established without considering the presence of the tunnel, determining the soil displacement around the tunnel structure. Subsequently, the tunnel’s transverse structure is treated as rigid, enabling the calculation of absolute displacements at the four key points (top, bottom, left, and right) based on the displacement at the tunnel’s axis. For the longitudinal structure, the internal forces acting between the tunnel rings are also considered. Finally, this paper calculates tunnel perimeter pressures based on the additional peripheral pressure distribution function derived from these considerations (as shown in Fig. 4(c)).

Fig. 4

Calculation model of additional peripheral pressure.

For analytical convenience, this paper assumes the vertical additional load follows a rectangular distribution, while the horizontal additional load is simplified as a parabolic distribution.

$$\left\{ {\begin{array}{*{20}{c}} {{p_{zt}}={p_{z21}}+{p_{z11}}} \\ {{p_{zb}}={p_{z22}}+{p_{z12}}} \end{array}} \right.$$

(12)

$$\left\{ {\begin{array}{*{20}{c}} {{p_{zt}}={k_s}\Delta {v_z}_{t}\left| {\cos \theta } \right|\begin{array}{*{20}{c}} {}&{\left( {\begin{array}{*{20}{c}} {0 \leqslant \theta <\pi /2}&,&{3/2\pi \leqslant \theta \leqslant 2\pi } \end{array}} \right)} \end{array}} \\ {{p_{zt}}={k_s}\Delta {v_z}_{t}\left| {\cos \theta } \right|\begin{array}{*{20}{c}} {}&{\left( {\pi /2 \leqslant \theta <3/2\pi } \right)} \end{array}} \end{array}} \right.$$

(13)

Where $\Delta {v_z}_{t}$ represents the difference in ${w_t}$ displacement between the upper part of the tunnel and the tunnel axis, while $\Delta {v_z}_{b}$ represents the difference in displacement between the lower part of the tunnel and the tunnel axis.

When calculating the additional pressure at the arch waist, Gong¹⁹ adopted a parabolic function that only considers cases from π/4 to 3π/4, thus neglecting the pressure distribution generated by horizontal displacement at the arch shoulder. Therefore, this paper adjusts by using a full range “∞” distribution function:

$$\left\{ {\begin{array}{*{20}{c}} {{p_{xr}}=0.5\Delta {v_x}_{r}\left( {{{\cos }^2}(\theta - \frac{\pi }{2})+{{\cos }^2}(\theta - \frac{{3\pi }}{2})} \right)\left| {\sin \theta } \right|\left( {0 \leqslant \theta <\pi } \right)} \\ {{p_{xl}}=0.5\Delta {v_x}_{l}\left( {{{\cos }^2}(\theta - \frac{\pi }{2})+{{\cos }^2}(\theta - \frac{{3\pi }}{2})} \right)\left| {\sin \theta } \right|\left( {\pi \leqslant \theta <2\pi } \right)} \end{array}} \right.$$

(14)

Where $\Delta {v_z}_{r}$ is the displacement difference between the right part of the tunnel and the tunnel axis, and $\Delta {v_z}_{l}$ is the displacement difference between the left part of the tunnel and the tunnel axis.

The distribution function for the circumferential pressure of the inter-ring internal forces Q_x and Q_z is as follows:

$$\left\{ {\begin{array}{*{20}{c}} {{p_{{Q_x}}}={Q_x}/\left( {{D_t}\cdot {b_t}} \right)\begin{array}{*{20}{c}} {}&{(0 \leqslant \theta \leqslant 2\pi )} \end{array}} \\ {{p_{{Q_z}}}={Q_z}/\left( {{D_t}\cdot {b_t}} \right)\begin{array}{*{20}{c}} {}&{(0 \leqslant \theta \leqslant 2\pi )} \end{array}} \end{array}} \right.$$

(15)

Calculation of circumferential pressure transfer between rings

Numerous scholars have extensively researched the prediction of longitudinal displacement of tunnels adjacent to pits. Among them, Feng¹⁵ used an analytical solution (based on the Mindlin solution to calculate the stresses at the tunnel axis and considering the tunnel as a two-parameter Pasternak model) to accurately analyze the vertical deformation of subway tunnels induced by symmetric excavation of deep foundation pits on both sides in soft soil areas. This study demonstrated the feasibility of using analytical solutions to analyze tunnel displacements under two-sided excavation. Feng et al.^28,29 idealized the existing tunnel as an infinite beam based on the three-parameter Kerr model, adapting the model according to the three-parameter relationship improved by Avramidis³⁰. In this paper, the longitudinal displacements and inter-ring internal forces of the tunnel are calculated based on this model.

Fig. 5

Schematic representation of the Kerr model.

The existing tunnel is idealized as an infinite beam based on the three-parameter Kerr model (illustrated in Fig. 5). The following assumptions are made: (1) The existing tunnel is idealized as an Euler-Bernoulli beam, and the soil-tunnel interaction is simulated using a three-parameter Kerr model; (2) The existing tunnel deforms uniformly with the surrounding soil, without local separation; (3) The study ignores the effects of groundwater and changes in soil properties:

$$w(y)={w_1}(y)+{w_2}(y)$$

(16)

where w(x) is the tunnel displacement and w₁(x) and w₂(x) are the ground displacements of 1 and 2 springs, respectively.

Assuming that p₁(x) and p₂(x) are denoted as the stresses on the springs of layer 1 and layer 2, respectively:

$$\left\{ {\begin{array}{*{20}{c}} {{p_1}\left( y \right)={k_1}{w_1}\left( y \right)} \\ {{p_2}\left( y \right)={k_2}{w_2}\left( y \right)} \end{array}} \right.$$

(17)

where k₁ and k₂ are the stiffnesses of the 1st and 2nd layer springs, respectively.

Considering the force acting on the 2nd layer spring, p₁(x) is:

$${p_1}(y)= - G\frac{{{d^2}{w_2}(y)}}{{d{y^2}}}+{k_2}{w_2}(y)$$

(18)

Combine the last two styles:

$$w(y)=(1+\frac{{{k_2}}}{{{k_1}}}){w_2}(y) - \frac{G}{{{k_1}}}\frac{{{d^2}{w_2}(y)}}{{d{y^2}}}$$

(19)

According to Euler-Bernoulli beam theory:

$$\frac{{{d^2}{w_2}(y)}}{{d{y^2}}}= - \frac{M}{{EI}}$$

(20)

where M and EI are the bending moment and bending stiffness of the tunnel, respectively.

Considering the deformation of the tunnel unit as shown in Fig. 5, the vertical force equilibrium equation of the unit is obtained as:

$$\left\{ {\begin{array}{*{20}{c}} {Q+dQ+{p_1}(y)Ddx=Q+q(y){D_t}dy} \\ {M+dM+(Q+dQ)dy+{p_1}(y){D_t}\frac{{{{(dy)}^2}}}{2}=q(y){D_t}\frac{{{{(dy)}^2}}}{2}+M} \end{array}} \right.$$

(21)

At the same time, the shear layer moment M_s satisfies:

$$\frac{{{d^2}{w_2}}}{{d{y^2}}}= - \frac{{{M_s}}}{{EI}}$$

(22)

Combined with (17) to (20) above:

$$\frac{{{d^6}{w_2}}}{{d{y^6}}} - \frac{{{k_1}+{k_2}}}{G}\frac{{{d^4}{w_2}}}{{d{y^4}}}+\frac{{{k_1}}}{{EI}}\frac{{{d^2}{w_2}}}{{d{y^2}}} - \frac{{{k_1}{k_2}}}{{EIG}}{w_2}= - \frac{{{k_1}}}{{EIG}}q$$

(23)

To solve Eq. (22), the finite difference method is chosen. Figure 6 shows that the tunnel is divided into lengths l = L₁/n, where L₁ is the length of the tunnel. Here, the elements of the tunnel are labeled as 0, 1, …, n-1, n in order from left to right. Also, there are six free end virtual displacements at the end of the tunnel labeled as n + 1, n + 2, n + 3, -3, -2, -1.

Fig. 6

Tunnel differential model.

Then Eq. (22) can be rewritten as:

$$\begin{gathered} \frac{{{{({w_2})}_{i+3}} - 6{{({w_2})}_{i+2}}+15{{({w_2})}_{i+1}} - 20{{({w_2})}_i}+15{{({w_2})}_{i+1}}+{{({w_2})}_{i - 3}}}}{{{l^6}}} \hfill \\ - \frac{{{k_1}+{k_2}}}{G}\frac{{{{({w_2})}_{i+2}} - 4{{({w_2})}_{i+1}}+6{{({w_2})}_i} - 4{{({w_2})}_{i - 1}}+{{({w_2})}_{i - 2}}}}{{{l^4}}} \hfill \\ +\frac{{{k_1}}}{{EI}}\frac{{{{({w_2})}_{i+1}} - 2{{({w_2})}_i}+{{({w_2})}_{i - 1}}}}{{{l^2}}} - \frac{{{k_1}{k_2}}}{{EIG}}{({w_2})_i}= - \frac{{{k_1}}}{{EIG}}{q_i} \hfill \\ \end{gathered}$$

(24)

where i = 0, 1,…, n-1, n. (w₂)_i is the deformation of layer 2. q_i is the differential unloading stress as shown in Eq. (10). The ends of the tunnel can be idealized as i = 0, 1,…, n-1, n. Due to the assumption of tunnel infinity, the ends of the tunnel are considered constraint free.

$$\left\{ {{w_2}} \right\}={\left[ K \right]^{ - 1}}\cdot \left\{ {{Q_s}} \right\}$$

(25)

Its {w₂} and {Q_s} are the column vectors of w₂ and q, respectively. k is the stiffness matrix of the tunnel. w₂ and Q_s can be expressed as:

$$\left\{ {\begin{array}{*{20}{c}} {{w_2}={{\left[ {{{({w_2})}_0},{{({w_2})}_1},\ldots,{{({w_2})}_{n - 1}},{{({w_2})}_n}} \right]}^T}} \\ {{Q_s}=\frac{{{k_1}}}{{EIG}}{{\left[ {{q_0},{q_1},{q_2},\ldots,{q_{n - 2}},{q_{n - 1}},{q_n}} \right]}^T}} \end{array}} \right.$$

(26)

K can be expressed as:

$$[K]=\left[ {\begin{array}{*{20}{l}} {{\kappa _4}+2{\kappa _3}+4{\kappa _2}+8{\kappa _1}}&{ - 4{\kappa _2} - 10{\kappa _1}}&{2{\kappa _2}+2{\kappa _1}}&{2{\kappa _1}}&{}&{}&{}&{}&{}&{} \\ {{\kappa _3}+2{\kappa _2}+2{\kappa _1}}&{{\kappa _4} - {\kappa _2}}&{{\kappa _3} - {\kappa _1}}&{{\kappa _2}}&{{\kappa _1}}&{}&{}&{}&{}&{} \\ {{\kappa _2}+2{\kappa _1}}&{{\kappa _3} - {\kappa _1}}&{{\kappa _4}}&{{\kappa _3}}&{{B_i}}&{{\kappa _1}}&{}&{}&{}&{} \\ {{\kappa _1}}&{{\kappa _2}}&{{\kappa _3}}&{{\kappa _4}}&{{\kappa _3}}&{{\kappa _2}}&{{\kappa _1}}&{}&{}&{} \\ {}& \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots &{}&{} \\ {}&{}&{}&{{\kappa _1}}&{{\kappa _2}}&{{\kappa _3}}&{{\kappa _4}}&{{\kappa _3}}&{{\kappa _2}}&{{\kappa _1}} \\ {}&{}&{}&{}&{{\kappa _1}}&{{\kappa _2}}&{{\kappa _3}}&{{\kappa _4}}&{{\kappa _3} - {\kappa _1}}&{{\kappa _2}+2{\kappa _1}} \\ {}&{}&{}&{}&{}&{{\kappa _1}}&{{\kappa _2}}&{{\kappa _3} - {\kappa _1}}&{{\kappa _4} - {\kappa _2}}&{{\kappa _3}+2{\kappa _2}+2{\kappa _1}} \\ {}&{}&{}&{}&{}&{}&{2{\kappa _1}}&{2{\kappa _2}+2{\kappa _1}}&{ - 4{\kappa _2} - 10{\kappa _1}}&{{\kappa _4}+2{\kappa _3}+4{\kappa _2}+8{\kappa _1}} \end{array}} \right]$$

(27)

Where:

$$\left( \begin{gathered} {\kappa _1} \hfill \\ {\kappa _2} \hfill \\ {\kappa _3} \hfill \\ {\kappa _4} \hfill \\ \end{gathered} \right)=\left( {\begin{array}{*{20}{l}} 1&0&0&0 \\ { - 6}&{ - 1}&0&0 \\ {15}&4&1&0 \\ { - 20}&{ - 6}&{ - 2}&{ - 1} \end{array}} \right)\cdot \left( {\begin{array}{*{20}{c}} {1/{l^6}} \\ {({k_1}+{k_2})/G{l^4}} \\ {{k_1}/EI{l^2}} \\ {{k_1}{k_2}/EIG} \end{array}} \right)$$

(28)

From this, the deformation of the 2nd layer spring w₂ is obtained. The tunnel displacement can be calculated by the following equation. 

$$\begin{gathered} {w_i}=(1+{k_2}/{k_1}){({w_2})_i} - \frac{G}{{{k_1}}}\frac{{d{{({w_2})}_i}}}{{d{x^2}}} \hfill \\ \qquad = - \frac{{2G}}{{{k_1}{l^2}}}{({w_2})_{i - 1}}+(\frac{{{k_1}+{k_2}}}{{{k_1}}}+\frac{{2G}}{{{k_1}{l^2}}}){({w_2})_i} - \frac{G}{{{k_1}{l^2}}}{({w_2})_{i+1}} \hfill \\ \end{gathered}$$

(29)

The inter-ring shear is:

$$\begin{gathered} {Q_i}={\left. {\frac{{dM}}{{dx}}} \right|_i}= - EI{\left[ {(1+\frac{{{k_2}}}{{{k_1}}})\frac{{{d^3}{w_2}}}{{d{x^3}}} - \frac{G}{{{k_1}}}\frac{{{d^5}{w_2}}}{{d{x^5}}}} \right]_i} \hfill \\ \qquad = - EI{\left[ \begin{gathered} - \frac{G}{{2{k_1}{l^5}}}{({w_2})_{i+3}}+(1+\frac{{{k_2}}}{{{k_1}}}+\frac{{5G}}{{{k_1}{l^2}}})\frac{1}{{2{l^3}}}{({w_2})_{i+2}} - (1+\frac{{{k_2}}}{{{k_1}}}+\frac{{7G}}{{2{k_1}{l^2}}})\frac{1}{{{l^3}}}{({w_2})_{i+1}} \hfill \\ +(1+\frac{{{k_2}}}{{{k_1}}}+\frac{{7G}}{{2{k_1}{l^2}}})\frac{1}{{{l^3}}}{({w_2})_{i - 1}} - (1+\frac{{{k_2}}}{{{k_1}}}+\frac{{5G}}{{{k_1}{l^2}}})\frac{1}{{2{l^3}}}{({w_2})_{i - 2}}+\frac{G}{{2{k_1}{l^5}}}{({w_2})_{i - 3}} \hfill \\ \end{gathered} \right]_i} \hfill \\ \end{gathered}$$

(30)

Where ${k_1}=7{k_2},{k_2}=4Es/3{h_t},G=2Es{h_t}/9(1+v)$, E_s is the foundation compression modulus.

Engineering case studies

Cases

Project Overview, Case^5,6 involves a twin tunnel that commenced operations in 2010. Two years later, during the construction of 10 high-rise towers, which collectively encompassed a basement area of approximately 90,000 m², extensive excavation took place near the tunnel. The excavation site was divided into four zones, with zones I and III, adjacent to the tunnels, identified as the primary contributors to excessive deformation.

Table 2 Case 1 parameters.

Parameter simplified model as shown in Table 2, the overall depth of the tunnel is located in the range of clay layer, according to the actual soil model this paper k_s selected parameters for 5000 kN/m³.

Perimeter pressure analysis

Figure 7 shows the horizontal and vertical displacements of the left-line tunnel under bilateral excavation calculated using the elastic foundation beam model. Positive values indicate the horizontal displacement of the tunnel moving towards excavation zone I and the vertical displacement moving downward. The maximum horizontal displacement of the tunnel is 21.22 mm at y = 168 m, corresponding to the center of excavation zone (I) The horizontal displacement decreases to both sides, approaching zero at the edge of the excavation zone. The maximum vertical displacement of the tunnel is 44.17 mm at y = 222 m. Similar to the horizontal displacement, the vertical displacement decreases from its maximum value to zero at the edge of the excavation zone. Due to horizontal stresses, excavation zone I does not generate as large an effect as excavation zone (II) The superposition of stresses from excavation zone II offsets part of the unloading stress in excavation zone I, while the superposition of vertical displacements increases the overall downward unloading stress. Additionally, the 50 m distance between the centers of excavation zones I and II affects the locations of the maximum horizontal and vertical displacements, causing the displacement curve of the tunnel to lose its left-right symmetry.

Fig. 7

Soil displacement field under bilateral pit excavation.

The soil displacement field under bilateral excavation, calculated using the image source method, is depicted in Fig. 8. The red line represents the zero-value line of soil displacement. Figure 8(a) illustrates the vertical displacement field, where within the height range of the enclosure structure, overall soil settlement exceeds 30 mm. An arc-shaped bulge area appears within a 5 m range at the bottom of both left and right enclosure structures (indicated by the red line denoting zero settlement). The lateral displacement field is significantly influenced by disparities in enclosure structure displacement. The maximum displacement at the left enclosure structure is 1.2 times that at the right enclosure structure, causing the zero-value line of soil displacement to skew towards the right side, forming an arc shape around the right enclosure structure. Unlike unilateral pit excavation, the settlement value in the vertical soil displacement field under bilateral excavation is considerably larger than that in the lateral soil displacement field. This disparity primarily stems from the symmetric vertical impacts of pit excavation on both sides, which are opposite in the lateral direction. This phenomenon results from the superposition of vertical soil displacement and the counteracting effect of lateral soil displacement.

Fig. 8

Soil displacement field under bilateral pit excavation.

Papers^5,6 primarily focus on the deformation of the left tunnel’s 580th tube sheet. For comparative analysis, this study also examines the deformation of the left tunnel’s 580th tube sheet. The theoretical calculation places the 580th ring tube sheet at a longitudinal coordinate of 240 m, with a horizontal displacement of 13.67 mm and a vertical displacement of 43.01 mm. Figure 7 illustrates the distribution of peripheral pressure calculated in this study under bilateral tunnel excavation conditions. Initially, due to a higher lateral earth pressure coefficient calculated by the Rankine earth pressure theory, the longitudinal deformation of the tunnel exhibits an initial surrounding pressure resembling a “fat gourd” shape. Following the completion of double-sided excavation, the circumferential pressure at the top and bottom of the tunnel increases, while the pressure at the waist decreases. Specifically, the maximum circumferential pressure at the left waist decreases to 74.91 kN, and at the right waist decreases to 18.91 kN.

Analysis of numerical modeling results

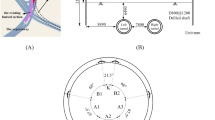
MIDAS GTS NX version 2022 (available at: https://www.midasgeotech.com/products/gtsnx) finite element analysis software is used to refine the simulation of the three-ring staggered-seam assembled pipe sheet. The pipe sheet model, as shown in Fig. 9, has an outer diameter of 6.2 m, an inner diameter of 5.5 m, a ring width of 1.2 m, and a pipe thickness of 0.35 m. There are 6 splicing blocks in the whole ring of the pipe sheet lining ring, among which 1 block of capping block (F block) has a circumcentric angle of 20 °, the circumcentric angles of the 2 neighboring blocks (L1 and L2) are 68.75 °, and the circumcentric angles of the 3 standard blocks (B1, B2 and B3) are 67.5 °, and there is an oblique angle of 5 ° between the capping block of the pipe sheet and the neighboring blocks. There exists a 5° oblique angle. The pipe sheet material is C50 concrete, the pipe sheet splicing blocks are connected by 12 M30 bolts with strength of 8.8 grade, and the pipe sheet rings are connected by 16 M30 bolts with strength of 8.8 grade, and the three rings of pipe sheets are staggered by 180° for splicing. Specific material parameters, as shown in Table 3.

Fig. 9

Tube sheet model.

Table 3 Table of model material parameters.

Figure 10 depicts the schematic diagram of the tunnel lining under bilateral excavation. As shown, the response in the lateral direction of the tunnel’s perimeter pressure exhibits a more pronounced variation in the vertical direction compared to the soil displacement field and longitudinal tunnel displacement caused by bilateral excavation. Specifically, the magnitude of change in perimeter pressure at the top and bottom of the lining structure is greater than that at the waist perimeter pressure. In contrast, perimeter pressure resulting from unilateral pit excavation primarily causes a decrease at the tunnel waist, with slight increases observed at the top of the lining²³.

Fig. 10

Schematic diagram of enclosing pressure.

Figure 11 illustrates the displacement cloud of the tunnel lining structure. The tunnel lining exhibits a collective “transverse ellipse” deformation, with the long axis of the ellipse aligning approximately horizontally. At maximum displacement, the long axis points towards the left and right sides of the enclosure structure, consistent with findings from Paper⁶. Similar to unilateral pit excavation³¹, the tunnel structure undergoes compression into a “transverse ellipse” shape, with maximum displacement occurring at the enclosure structure. However, under bilateral excavation, the convergence values at the top and bottom parts of the tunnel are more pronounced.

Fig. 11

General convergence diagram.

The increase in top pressure is attributed to the tunnel being situated in a settlement-prone soil displacement field. The overburden settlement exceeds that of the tunnel, creating a “thrust” effect. Increased bottom pressure results from the gradient of the soil displacement field, where substantial settlement reduction occurs over a small range, particularly within the tunnel’s diameter of 6.2 m. Consequently, bottom tunnel displacement exceeds soil displacement, leading to passive compression of the soil underneath and an increase in surrounding pressure.

Horizontally, the tunnel resides in a soil displacement field shifted leftward, causing leftward displacement. Soil displacement at the left waist exceeds tunnel displacement, resulting in decreased perimeter pressure on the left side. Conversely, the decrease in perimeter pressure at the right waist is less pronounced due to similar levels of soil and tunnel displacement at that location. The maximum concrete displacement of 28.22 mm occurs at approximately 260°.

Figure 12 displays the lateral convergence cloud diagram of the tunnel lining structure. Lateral convergence deformation is prominently observed between 60° to 120° and 240° to 300°. The maximum horizontal convergence occurs at the left side of the intermediate tube sheet ring, measuring 28 mm, and at the right side, measuring 17.47 mm, resulting in an absolute horizontal convergence of 41.4 mm. This corresponds to a convergence ratio of ΔD_t/D_t of 0.67%.

Fig. 12

Horizontal convergence plot.

Figure 13 depicts the vertical convergence cloud diagram of the tunnel lining structure. Vertical convergence deformation is notable between 0° to 30°, 150° to 210°, and 330° to 360°. The maximum vertical convergence is 25.00 mm at the top of the intermediate tube sheet ring and 25.88 mm at the bottom, yielding an absolute vertical convergence of 44.5 mm. The convergence ratio ΔDt/Dt is 0.72%.

Fig. 13

Vertical convergence plot.

All convergence values at top and bottom positions derived from the calculations in this paper meet the tunnel safety standards under normal operating conditions¹, falling within the range of 0.13–0.77% compared to actual measurements.

The research in this paper focuses on the three-ring pipe sheet model, allowing for a clearer analysis of misalignment deformation between pipe sheets. According to Fig. 14, it can be seen that the middle ring of the pipe sheet deformation volume presents an inward convergence deformation state as a whole, the two sides of the waist of the pipe sheet are warped outward, the top and bottom of the two parts of the pipe sheet are deflected inward, and there is a danger of the upper capping block falling out. The outermost two rings of the tube sheets, due to the model setup, are relatively less affected, which is related to the outer constraints of the tube sheet model.

Fig. 14

Pipe sheet misalignment deformation.

Single factor analysis

Influence of foundation factor and spring stiffness

In this paper, the subgrade reaction coefficient k_s is differentiated from the spring stiffness coefficients k₁ and k₂. The coefficient k_s pertains to the macroscopic longitudinal response, while k₁ and k₂ relate to the microscopic lateral response of the subgrade. However, under specific conditions, these parameters can be equivalent, and thus they are treated as having a proportional relationship. It is assumed that, under identical excavation conditions, variations in the three parameters k_s, k₁, and k₂ do not significantly affect the soil displacement field induced by bilateral excavation. To investigate the combined effects of these parameter variations on the tunnel’s longitudinal displacement and lateral deformation, we define a spring matrix [k_s, k₁, k₂] with a baseline coefficient of 1. The changes in coefficients are then compared at 0.6[k_s, k₁, k₂], 0.8[k_s, k₁, k₂], 1.2[k_s, k₁, k₂], and 1.4[k_s, k₁, k₂].

Figures 15 and 16 present the comparison of horizontal and vertical tunnel displacements under varying spring matrix coefficients. As depicted, decreasing the stiffness coefficient of the spring matrix results in an overall increase in both horizontal and vertical tunnel displacements within the foundation pit range. This increase accelerates as the stiffness coefficient decreases. Notably, the maximum displacement values remain consistently near y = 240 m. Figure 17 illustrates the comparison of tube sheet pressures at the location of y = 240 m across different coefficients starting from 0.6. Initially, the pressure at the top of the tube sheet ring is minimal. As the coefficient increases, pressures on the top and right waist of the tube sheet increase, while pressures on the bottom and left waist decrease gradually. This trend reflects the adjustments between the tube sheet ring displacement and the surrounding soil displacement field. Notably, there exists a critical range between 0.8 and 1.2 where the overall rate of change in tube sheet perimeter pressure converges to zero, aligning the tube sheet ring displacement closely with the soil displacement field.

Fig. 15

Comparison of horizontal displacements of tunnels with different spring matrix coefficients.

Fig. 16

Comparison of vertical displacements of tunnels with different spring matrix coefficients.

Fig. 17

Comparison of tunnel circumferential pressure with different spring matrix factors.

Figure 18 compares tube sheet displacements under different spring matrix coefficients, where lateral tunnel deformation is represented by ΔD/D. As observed in the figure, the overall shape of the tunnel changes with increasing spring coefficient. Initially, the tunnel exhibits an oblique ellipse at the upper right position, transitioning to a flatter ellipse in the middle, and further evolving into an oblique ellipse at the lower left position. This evolution correlates closely with changes in peripheral pressure. It is evident that the lateral deformation pattern of the tunnel is significantly influenced by the spring matrix coefficient, with the long axis of the ellipse generally aligning towards the bottom of the near-side pit.

Fig. 18

Comparison of tunnel lateral displacement with different spring matrix factors.

Influence of horizontal tunnel position

Exploring the horizontal position of the tunnel is mainly concerned in the tunnel and the left and right pits of the distance s₁, s₂ change, defined parameters for S_p = 2s₁ / (s₁ + D_t + s₂). S_p = 0.4, 0.6, 0.8, 1, 1.2 when the tunnel displacement and tube sheet enclosure pressure change.

Figures 19 and 20 illustrate the excavated sections on both sides of the foundation pit, showing that horizontal and vertical displacements decrease as the tunnel position approaches the center between the two foundation pits. Conversely, both horizontal and vertical displacements increase significantly as the tunnel nears the left side of the foundation pit. It’s noted that the vertical displacement of the tunnel at 0.4 exceeds the reasonable prediction range and is therefore not applicable within the scope of this study. Combining Figs. 21 and 22 reveals the evolution of lateral deformation patterns of the tunnel. When the spring matrix coefficient (S_p) equals 1, indicating the tunnel is roughly centered, the tunnel exhibits a compressed transverse ellipse shape at its bottom. As the tunnel moves towards the sides, the top gradually spreads upward while the bottom converges inward. Specifically, when S_p is reduced to 0.6, the tunnel adopts a transverse ellipse shape positioned higher up.

Fig. 19

Horizontal tunnel displacements with different S_p factors.

Fig. 20

Vertical tunnel displacements with different S_p factors.

Fig. 21

Comparison of tunnel envelope pressure with different S_p factors.

Fig. 22

Comparison of tunnel envelope pressure with different S_p factors.

Influence of pit spacing

Li Hang³ investigated the ground displacement field resulting from synchronized excavation at varying pit spacings and concluded that beyond a distance of 4 times the excavation depth, the effects of pit spacing do not superimpose. In this study, the tunnel’s position is fixed centrally between two pits, examining how the tunnel responds under pit spacings (S) of 1, 2, 3, 4, and 5 times the excavation depth.

As depicted in Figs. 23 and 24, the horizontal and vertical displacements decrease as the distance between the two pits increases. Notably, larger displacements are observed when the pit spacing is only double the excavation depth, which falls outside the applicability range of this study’s method. Our calculations reveal that vertical displacements exceed horizontal displacements when S > 4, indicating significant displacement values persist. Hence, even beyond 4 times the excavation depth, the two side pits still exhibit a superposition effect due to their extensive excavation areas.

Fig. 23

Horizontal tunnel displacements with different S-factors.

Fig. 24

Vertical tunnel displacements with different S-factors.

Figures 25 and 26 collectively illustrate changes in the tunnel’s lateral deformation state. Unlike other S values, where peripheral pressures are more uniform, S = 2 shows a distinct pattern: the top of the tunnel experiences significant outward deformation while pressures at the waist are minimal. As S transitions from 2 to 3, there is a critical value marking the tunnel’s shift from top-outward to bottom-convergent deformation. For S ≥ 3, the tunnel generally exhibits slight convergence at the bottom. Regardless of pit spacing variations, the tunnel located precisely between two pits consistently assumes a transversely elliptical shape.

Fig. 25

Comparison of tunnel circumferential pressure with different S-factors.

Fig. 26

Comparison of tunnel circumferential pressure with different S-factors.

Conclusions

This study is relevant to similar engineering scenarios involving bilateral excavation pits adjacent to shield tunnels in soft soil regions. It systematically reveals, for the first time, the mechanisms by which bilateral pit excavation affects the distribution of surrounding pressure and deformation patterns in shield tunnels. Additionally, it introduces a novel method for calculating longitudinal displacement and circumferential pressure under these conditions. The findings enhance the theoretical understanding of this issue and provide valuable insights for similar engineering projects, demonstrating significant practical application.

• 1. In practical engineering, it is advisable to increase the distance between the two foundation pits and adjust the excavation location so that the tunnel is positioned centrally between the pits. Additionally, if tunnel defects occur, it is crucial to focus on grouting the external sides of the tunnel at the arch waist and reinforcing the upper and lower sections within the tunnel.

• 2. There is a difference in the response of the tunnel under bilateral and unilateral pit excavation, which is mainly reflected in that the change of the top and bottom perimeter pressure of the bilateral pit is larger, while the change of the waist perimeter pressure is smaller, and the vertical displacement of the tunnel in the longitudinal direction is much larger than that in the horizontal displacement. At the same time, under the influence of bilateral excavation, the maximum longitudinal displacement of the tunnel mainly corresponds to the center position of the pit excavation, due to the different lengths of the two pits excavation, the maximum horizontal displacement and the maximum vertical displacement will be staggered at different positions.

• 3. Under the influence of bilateral excavation, the tunnel lining exhibits a deformation pattern characterized by contraction at both the top and bottom, and expansion at the waist, resulting in inward convergence. The maximum vertical convergence values for the mid-segment ring are 25.00 mm at the top and 25.88 mm at the bottom, yielding an absolute vertical convergence of 44.5 mm and a convergence ratio (ΔD_t/D_t) of 0.72%. The segments on either side of the waist bulge outward, while the top and bottom segments exhibit inward deflection. This deformation pattern poses a risk of block detachment in the upper part of the lining.

• 4. Based on the actual case, the three influencing factors of foundation coefficient, horizontal position of tunnel and pit spacing are analyzed, and the longitudinal displacement of tunnel is summarized in the state of transverse deformation. With the increase of foundation coefficient, the top and bottom peripheral pressure will also increase, the decrease of Sp makes the bottom of the tunnel peripheral pressure increase, with the increase of S, the impact of excavation on the tunnel will be gradually changed from the upper part to the lower part, i.e., the upper part of the peripheral pressure decreases and the lower part of the peripheral pressure increases.

In addition, this paper simplifies the overall structure of the pit, the assumption of foundation soil, as well as precipitation, construction measures and other factors, and there is a certain deviation from the actual engineering, more factors need to be taken into account for further research.