Introduction

In high altitude and cold areas, the phenomenon of frost heave in fractured rock masses is common due to the influence of freeze–thaw cycles throughout the year. The frost heave deformation of rocks has a significant impact on rock engineering and civil construction, which restricts the development of transportation and economy in high-altitude cold regions1. Many cold region infrastructures have been constructed in northeastern and northwestern China, Japan, Europe, Norway, and Russia2. The cause of local cracking of engineering rock mass is fatigue damage caused by stress concentration at the crack end3,4,5, this is particularly significant in high and cold regions. 104 of 302 highway tunnels had serious frost damage in Hokkaido6. Almost all tunnel projects had a wide range of leakage and freezing in Nordic countries such as Norway, Switzerland, and Sweden7. In the cold region of China, due to the impact of frost damage, some tunnels cannot be used for up to 8–9 months a year, such as Wushaoling Tunnel, Kuixiandaban Tunnel, Guanjiao Tunnel, and the Qiaoliang Tunnel8. Even the Yuxi Molegai Tunnel in No. 217 National Highway was abandoned after several years of operation due to frost damage in Xinjiang. Draebing et al.9 and Wu et al.10 analyzed that engineering disasters in high-altitude cold regions and high latitude areas were mainly caused by the expansion of primary cracks or joints induced by freeze–thaw and load coupling. Through comparative studies, Tharp11 and Zhou12 found that different degrees of frost heave damage would produce different fracture morphology. At the same time, the internal development of cracks will also react to the generation and development of frost heave force. With the deepening of the research, scholars gradually found that the mechanical properties of rock mass after freezing and thawing showed significant deterioration. It can be seen that the frost heave deformation of rocks has a significant impact on rock engineering and civil engineering construction, which restricts the development of transportation and economy in high-altitude cold regions. It is necessary to conduct in-depth research on the deformation and failure laws of frozen rocks, in order to provide theoretical references for the design, construction, and anti-freezing research of engineering in cold regions.

In terms of weakening rock mechanics parameters through freeze–thaw, Peng et al.13 found through experiments that freezing and thawing will intensify the weathering of rocks, thus reducing the mechanical parameters of rocks. Liu et al.14 conducted several freeze–thaw cycle tests on sandstone samples and found that the internal damage of rock mass is a gradual process of freeze–thaw fatigue damage accumulation, and freeze–thaw will lead to an increase in the compaction stage of stress-strain curve. Xiong et al.15 have demonstrated that the dynamic tensile strength of saturated water sandstone gradually decreases with an increase in the number of freeze–thaw cycles, while that of frozen sandstone gradually increases. In terms of crack propagation, Feng et al.16 conducted numerical modeling based on rock mechanics tests and found that with the increase of freeze–thaw cycles, the bearing capacity of sandstone decreases and tensile fractures mainly occur. Wang et al.17 analyzed the crack initiation stress and damage stress based on the evolution law of microcracks in sandstone from the Qinghai-Xizang Plateau, and expounded the crack initiation mechanism. Yahaghi et al.‘s experiment18 shows that with the increase of the number of freeze–thaw cycles, the main failure mode of sandstone changes from axial splitting to single-plane shear, and the crack trend shows a significant zigzag pattern. Abdolghanizadeh et al.19 and Lan et al.20 found that the freeze–thaw cycle caused the formation and expansion of fractures by studying the number of freeze–thaw cycles and the influence of freezing temperature on sandstone. The damage factors of rock samples increased with the increase of the number of freeze–thaw cycles.

The above research mainly discusses the weakening law of the mechanical properties of freeze–thaw rocks. The internal reasons for its weakening include the increase in porosity inside sandstone and the effect of frost heave force inside pores21. Scholars have pointed out that analyzing the compaction stage helps to study the rock damage mechanism under freeze–thaw cycles22. Because the evolution characteristics of the compaction stage can better reflect the changes in porosity. Establishing a constitutive model is a good way to analyze the effect of freeze–thaw cycles on porosity. At present, most constitutive models for freeze–thaw damage of sandstone materials are overall degradation models23, which cannot characterize the deformation law during the compaction stage. Researchers have begun to introduce damage coefficient to construct constitutive models of freeze–thaw rocks, in order to better fit the deformation laws of rocks. MA et al.24 analyzed the law of rock freeze–thaw degradation based on dynamic freeze–thaw damage coefficient and found a negative linear correlation between dynamic uniaxial compressive strength and damage variables. QU et al.25 introduced a damage correction coefficient to correct the total damage of chemical freeze–thaw sandstone under load, and established a damage evolution equation of freeze–thaw sandstone under load, based on statistical strength theory and damage mechanics principles. In fact, from the point of view of damage, the freeze–thaw cycle increases the porosity of rock and softens the rock skeleton, and the internal pores and fissures gradually develop, which can be regarded as the damage field distributed inside the rock26,27. The progressive failure of rock can be said to be the process of damage accumulation. With the deterioration of the meso-structure, the rock will appear obvious nonlinear compaction section in the process of compression. The existing models usually use straight line processing to deal with the curve compaction section, which makes it difficult to accurately describe the deformation and failure process of damaged rock. Therefore, when establishing the freeze–thaw damage constitutive model, it is necessary to consider the compaction deformation stage of rock. Through the direction provided by the essential characteristics of rock damage mechanics, a segmented freeze–thaw damage model can be established by introducing a freeze–thaw damage coefficient.

In view of this, this study intends to conduct freeze–thaw test research on sandstone materials collected from Yulong mining area on the Qinghai-Xizang Plateau. Uniaxial compression tests were carried out on conventional sandstone materials, constant temperature and water saturated sandstone materials and multiple freeze–thaw sandstone materials. The stress-strain curve characteristics, elastic modulus evolution law, peak stress change law and energy change law were analyzed, and the freeze–thaw damage constitutive model of sandstone materials considering compaction stage was constructed.

Engineering background and test methodology

Engineering background

A large number of engineering practices have shown that the instability of almost all tunnel surrounding rocks is not caused by loading, but by the release of in-situ stress in certain directions during excavation unloading, resulting in large-scale unloading effects, increasing rock deformation and joint connectivity, leading to the redistribution of the surrounding rock stress field. After excavation of the tunnel, a new structural failure phenomenon of alternating distribution of fractured and unbroken areas occurred on both sides and in front of the working face, Causing a decrease in rock mass quality and deterioration of mechanical properties, leading to local plastic failure and overall instability of the surrounding rock28. However, the problems faced by tunnels in cold regions are not only limited to this, but also require attention to the instability of tunnel structures caused by frost damage, and the non-uniform frost heave of surrounding rocks is the main cause of frost damage29. During the construction and operation of high-altitude tunnels, cold air enters the tunnel to form air convection. The surrounding rock undergoes freeze–thaw cycles under the influence of external temperature, resulting in problems such as ice accumulation, frost heave, cracking, cracking, and spalling of the surrounding rock30,31. This makes the control of tunnel excavation on the stability of the surrounding rock and the evolution of elastic-plastic damage of the surrounding rock under unloading state more complex. Table 1 records the temperature at different locations in some high-altitude tunnels. It can be seen from the table that the environmental temperature varies at different locations of the tunnel. The temperature at the entrance is the lowest, which is basically consistent with the surrounding environment temperature. As the tunnel is excavated, the temperature gradually increases, and some tunnels can even reach temperatures above 0 °C. Considering the temperature difference between day and night and seasonal changes, it is planned to conduct different freeze–thaw tests on sandstone materials to analyze their failure characteristics and influencing factors. The rock samples used in this experiment were taken from the Yulong mining area on the Qinghai-Xizang Plateau. The mining area has an altitude of 4569–5118 m, and the average daily minimum temperature in the coldest month is -20 ° C. The freezing period within a year is more than 7 months. The Yulong Copper Mine Belt extends north-south for up to 400 km, with an east-west width of 30–70 km. The tectonic framework was mainly formed by the Yanshan Movement, with the direction of the tectonic lines gradually changing from northwest to southeast to north-south, spreading in the north and converging in the south. The main part of the Yulong copper belt is located in the Xizang Autonomous Region, extending northward to Qinghai Province, and may disappear southward in the border area between Yunnan and Xizang. The sampling location for this time is mainly in the exposed strata of Segongnong. The formation is mainly composed of the Upper Triassic Bolila Formation (T2g) and the Upper Triassic Jiapila Formation (T3g), with sampling depths ranging from 18.18 m to 27.87 m. The obtained rock samples are mainly green sandstone, with a uniform green gray surface, few natural joints, small internal pores, and good compactness. According to the ISRM standard, the rock sample is processed into a cylindrical shape with the aspect ratio of 2:1 and a diameter of 50 mm. The unevenness and non-verticality of the end face are both less than 0.02 mm. After the preparation of the rock sample is completed, its quality, height, and ultrasonic longitudinal wave velocity are tested to eliminate rock samples with abnormal data and ensure the integrity and uniformity of the rock sample to the greatest extent possible.

Table 1 Temperature statistics for some high Cold tunnels.
Full size table

Table 2 shows the freeze–thaw experimental plan for the statistical part. In the literature, there is no consensus on the number of freeze–thaw cycles and temperature, with a tendency towards 25 cycles, and the specific basis is not clearly provided. From the commonly used ISRM, ASTM, and UNE-EN test specifications regarding rock freeze–thaw test methods, there are significant differences in freeze–thaw temperature and duration. Based on the statistical analysis, there is currently no unified standard for the description and regulations of the freeze–thaw cycle test plan. Therefore, this study mainly considers the criteria for dividing cold regions in China. According to the classification standards for cold regions in China, the coldest month with an average temperature below − 3 °C and exceeding 10 °C for less than 5 months is considered a cold region. Choosing − 20 °C as the freezing temperature can cover various low temperature conditions in China’s cold regions. Using the traditional indoor room temperature environment (20 °C ± 2 °C) as the melting temperature.

Table 2 Summary of rock freeze–thaw cycle test plan.
Full size table

The rock sample was analyzed by XRD diffraction, and its main mineral components and average content are shown in Table 3. The Initial physical parameters of sandstone rock samples are shown in Table 4.

Table 3 Main mineral composition and content of sandstones.
Full size table
Table 4 Initial physical parameters of sandstone.
Full size table

Experimental equipment and methods

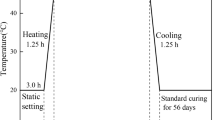
Referring to the ISRM specifications and freeze–thaw test operating standards, and based on the actual working conditions of the mining area with a large temperature difference between day and night, as well as the experience of other scholars in setting parameters for freeze–thaw cycle tests51, the freeze–thaw parameters for this experiment are designed: the freezing temperature is -20 °C, and the dissolution temperature is 20 °C. A complete freeze–thaw cycle is 10 h, with a freezing time of 5 h and a melting time of 5 h, and the freezing and melting rates are both 8 °C/h. (as shown in Fig. 1). This experiment includes 1 set of conventional rock samples and 5 sets of freeze–thaw cycling experiments. The freeze–thaw cycle test was conducted for 0, 20, 40, 60, and 80 freeze–thaw cycles, respectively (as shown in Fig. 2a). Conventional rock samples do not participate in saturation and freeze–thaw.

Fig. 1
figure 1

Temperature curve for freeze–thaw cycle.

Full size image
Fig. 2
figure 2

Experimental procedures and equipment. (a) Rock specimens, (b) Vacuum oven, (c) Vacuum saturation device, (d) BPHJ-120 C freeze–thaw cycle test chamber, (e) MesoMR12-060 H-I nuclear magnetic resonance analysis system, (f) MTS816 Rock Mechanics Testing System.

Full size image

The specific test steps are:

  1. (1)

    Dry the sandstone rock sample in an oven and bake it at a constant temperature of 105 °C for 24 h to obtain a dry rock sample, as shown in Fig. 2b. Number it, as shown in Table 5.

  2. (2)

    Prepare saturated rock samples through vacuum saturation device, as shown in Fig. 2c. All rock samples were subjected to simultaneous saturation treatment at room temperature (20°C), vacuum saturation for 48 h, and atmospheric pressure immersion for 72 h.

  3. (3)

    Perform freeze–thaw cycle test on the rock sample using BPHJ-120 C freeze–thaw cycle test chamber, as shown in Fig. 2d. The temperature change curve of the freeze–thaw cycle is shown in Fig. 1. After unified processing, the integrity of the rock sample can be approximately considered consistent, and its impact on the test results can be ignored.

  4. (4)

    Measure the porosity of rock samples at different freeze–thaw cycles using the MesoMR12-060 H-I nuclear magnetic resonance analysis system, as shown in Fig. 2e.

  5. (5)

    The MTS816 Rock Mechanics Testing System was used to conduct static compression tests on saturated rock samples and conventional rock samples that reached freeze–thaw cycles. The constant loading rate of the rock samples was 1 mm/min, as shown in Fig. 2f. The rock sample after the test is shown in Fig. 3.

    Fig. 3
    figure 3

    Rock samples after uniaxial compression test.

    Full size image

Porosity analysis

Measure the porosity of rock samples at different freeze–thaw cycles using the MesoMR12-060 H-I nuclear magnetic resonance analysis system. The porosity and its variation of saturated sandstone before and after freeze–thaw were statistically analyzed, and the results are shown in Table 5. The relationship between the change in porosity of saturated sandstone and the number of freeze–thaw cycles is shown in Fig. 4.

Fig. 4
figure 4

The relationship curve of sandstone porosity variation with the number of freeze–thaw cycles.

Full size image
Table 5 Porosity test results.
Full size table

Due to the fact that the mineral particles and cementitious matrix inside the rock sample do not generate nuclear magnetic signals, Nuclear Magnetic Resonance Spectroscopy (NMR) can collect the nuclear magnetic signals of pore fluids inside the rock sample, obtain pore volume signals, and invert porosity. The freeze–thaw cycle can cause damage to the interior of the rock, specifically manifested as an increase in the porosity of the rock sample. The change in porosity ΔP can be expressed by the following equation:

$$\Delta P=P\left( {\text{n}} \right) - {P_0}$$
(1)

where, P(n) is the porosity of saturated sandstone after n freeze–thaw cycles; P0 is the porosity of saturated sandstone at 0 freeze–thaw cycles.

Based on Fig. 4; Table 5, it can be seen that as the number of freeze–thaw cycles increases, the porosity of sandstone continuously increases, and the amount of porosity change also increases. After 80 freeze–thaw cycles, the average change in porosity increased by 1.28%. Under the action of freeze–thaw, the pore water inside the rock sample is affected by the phase change of ice and water, resulting in freeze–thaw force, which promotes the expansion of the inner wall of the pores and the initiation of new cracks. When melted, the pore water migrates towards the newly formed micropores, thereby affecting the changes in the pores of the rock sample. The more freeze–thaw cycles there are, the higher the porosity.

Analysis of experimental results

Analysis of the degradation law of mechanical properties

Figure 3 shows the failure mode of freeze–thaw sandstone under uniaxial compression. The typical failure modes in Fig. 3 are summarized in Table 6. According to Fig. 3; Table 6, the macroscopic main cracks of conventional rock samples, rock samples with 0 freezing-thawing cycles, and rock samples with 40 freezing-thawing cycles all show single slope shear failure, and the tensile failure is not obvious. The macroscopic main crack of the rock sample with 20 freeze–thaw cycles shows X-shaped conjugate inclined plane shear failure. The macroscopical main cracks of 60 freezing-thawing cycles and the 80 freezing-thawing cycles have both the form of splitting failure and shear failure. It can be inferred from this that, as the number of freeze–thaw cycles increases, the rock sample gradually transitions from single shear failure to tensile shear composite failure. This means that the severity of sandstone damage gradually increases, resulting in a gradual increase in the number of cracks. This also shows that the freeze–thaw cycle increases the plasticity of the sandstone, promotes the development of cracks in the process of sandstone failure, and makes the sandstone undergo significant ductile failure.

Table 6 Rock sample failure mode.
Full size table

Figure 5 shows the stress-strain curves of sandstone under different freeze–thaw cycles. From Fig. 5, it can be seen that the stress-strain changes of sandstone with different freeze–thaw cycles are similar, including four stages: compaction stage, elastic stage, yield stage, and failure stage. Among them, the elastic modulus is calculated using Eq. (2) 52, and the variation pattern of the elastic modulus is shown in Table 7. It is worth noting that after 80 cycles of thawing, the stress-strain curve of sandstone exhibits a multi peak phenomenon (as shown in Fig. 5f), indicating that the freeze–thaw cycle weakens the ability of sandstone to resist damage. This is mainly because the repeated freeze–thaw force weakens the bonding force between sandstone mineral particles, increases the number of dissolved pores in the cement, and causes the initiation, development, and expansion of new fractures, Ultimately, the ability of sandstone specimens to resist failure is correspondingly degraded.

$${E_n}=\frac{{{\sigma _{60\% }} - {\sigma _{40\% }}}}{{{\varepsilon _{60\% }} - {\varepsilon _{40\% }}}}$$
(2)

where En is the elastic modulus of sandstone after n freeze–thaw cycles, GPa; σ60% and σ40% is the stress at 60% and 40% of the peak stress, MPa; ε60% and ε40% represents the strain corresponding to the peak stress of 60% and 40%, respectively.

Fig. 5
figure 5

Stress-strain curve under different freeze–thaw cycles.

Full size image

From Table 7, it can be seen that with the increase of the number of freeze–thaw cycles, the peak strain of sandstone gradually increases, which is consistent with the previous research results53. The peak strain of rock under different freeze–thaw cycles is 0.753, 0.769, 0.774, 0.783, 0.833, respectively. Compared with the samples with 0 freeze–thaw cycles, the peak strain increased by 0%, 2.13%, 2.79%, 3.99%, 10.62%, respectively.

Extract the data from Table 7 and plot the variation of elastic modulus and peak stress with freeze–thaw cycles as shown in Figs. 6 and 7. From Figs. 6 and 7, it can be seen that as the number of freeze–thaw cycles increases, the compressive strength and elastic modulus of the sample gradually decrease, and the mechanical degradation characteristics caused by freeze–thaw become more obvious. This is mainly because during the freeze–thaw cycle, with the freezing and expansion of pore water, the frost heave stress leads to the gradual loosening of the internal structure of the rock. With the increase of the number of freeze–thaw cycles, the pore structure inside the rock deteriorates, and the small pores are continuously transformed into large pores, resulting in an increase in porosity. As the degree of deterioration of the pore structure continues to increase, the rock ‘s ability to resist deformation gradually decreases, and the compressive strength and elastic modulus of the rock sample gradually decrease.

Fig. 6
figure 6

Elastic modulus under different freeze–thaw cycles.

Full size image
Fig. 7
figure 7

Peak stress under different freeze–thaw cycles.

Full size image
Table 7 Rock mechanics parameters under different freeze–thaw cycles.
Full size table

Analysis on the energy evolution law of freeze–thaw cycle

The process of rock failure involves the evolution of elastic energy and dissipative energy from an energy perspective. Meanwhile, energy is also related to force and deformation. Therefore, from the perspective of energy, the failure law of rocks can also be analyzed. Assuming that the loading of rocks is carried out in a closed space without heat exchange with the external space, according to the laws of energy conservation and thermodynamics, the work done by the testing machine on the rocks is the total strain energy absorbed by the rocks, which can be obtained by integrating the stress-strain curve, as shown in Eq. (3). The elastic strain energy of rocks can be calculated using Eq. (4). By substituting the obtained elastic strain energy into Eq. (3), the dissipated energy during rock failure can be obtained. Thus, the dissipated energy, elastic strain energy, and total strain energy were plotted into curves. Since the stress-strain curves of each group of specimens were basically consistent, one curve was selected for each group to study, as shown in Fig. 8.

$$U={U^d}+{U^e}=\int {{\sigma _i}} d{\varepsilon _i}$$
(3)
$${U^e}=\frac{1}{2}\varepsilon _{i}^{e}{\sigma _i}=\frac{{{\sigma _i}^{2}}}{{2{E_u}}}$$
(4)

where U represents the total absorbed energy during the process of rock failure under load, MJ m− 3; Ud is the energy dissipated during the process of rock failure under load, MJ m− 3; Ue is the elastic energy during rock failure process, MJ m− 3; εei is the elastic strain; σI is the stress at any point on the stress-strain curve during the loading process; Eu is the unloading elastic modulus, usually taken as the elastic modulus, GPa.

As shown in Fig. 8, the total absorbed energy of sandstone with different freeze–thaw cycles shows a gradually increasing trend with increasing strain; Both elastic energy and stress show a trend of first increasing and then decreasing with increasing strain. The dissipation energy is mainly related to the development and closure of cracks, and the evolution law of dissipation energy can reflect the stage of rock fracture development. Before the peak stress, the dissipated energy undergoes four stages: slow increase, basic stability, slow decrease, and rapid increase. Considering the stages after the peak stress, the dissipation energy change curve can be divided into 5 stages, which can be used to benchmark the 5 stages of the rock’s complete stress-strain curve, namely the compaction stage, elastic stage, stage of development of cracks, unstable development stage of cracks, and post fracture stage.

Fig. 8
figure 8

Energy evolution curves of sandstone samples treated with different freeze–thaw cycles. A- Compaction stage; B- Elastic stage; C- Stable development stage of cracks; D- Unstable development stage of cracks; E- Post rupture stage.

Full size image

In the early stage of loading, the sandstone is in the compaction section of crack closure, and the microcracks on the surface of the specimen will close under the action of axial force. Since the pressure sealing of micro cracks requires energy consumption, the dissipated strain energy shows an increasing trend, which will be slightly greater than the elastic strain energy. Therefore, the dissipation energy shows an increasing trend, such as the A interval in Fig. 8. The rock enters the elastic stage after the compaction stage, during which the sandstone has almost no crack development or closure. Therefore, the variation of dissipated energy is gentle, as shown in the B interval in Fig. 8. At this point, the total energy absorbed by sandstone is mainly stored in the form of elastic properties inside the rock. The boundary point between interval A and interval B is the compaction point of sandstone. As the number of freeze–thaw cycles increases, the strain value of the compaction point gradually increases. This also indicates that the ductility of sandstone increases with the number of freeze–thaw cycles, as shown in Fig. 8. After the elastic stage, the rock enters the stable development stage of cracks, and new microcracks begin to appear inside the rock. At this time, the dissipated energy slowly decreases. After the rock enters the unstable development stage of cracks from the stable development stage of cracks, significant through cracks appear inside the rock, some of which are visible to the naked eye. At this time, the dissipation energy suddenly increases.

Figure 9 shows the energy corresponding to the peak stress of sandstone under different freeze–thaw cycles. According to Fig. 9, as the number of freeze–thaw cycles increases, the total energy and elastic energy all show a trend of “first decreasing, then increasing, and then decreasing”. Before the 20 freeze–thaw cycles, the total energy and elastic energy all showed a decreasing trend; Before the 20 to 60 freeze–thaw cycles, the total energy and elastic energy all showed an upward trend; After 60 freeze–thaw cycles, the total energy and elastic energy decreased again. The evolution trend of dissipated energy differs from the total energy and elastic energy. Before 40 freeze–thaw cycles, the dissipated energy showed a slow decreasing trend. After 40 freeze–thaw cycles, the dissipated energy shows a slow upward trend. After undergoing freeze–thaw cycles, although the strength of sandstone decreases, its deformation ability improves. Energy is the product of strength and deformation, and after freeze–thaw cycles, it shows a trend of increasing energy, which is similar to previous research results53. However, when the number of freeze–thaw cycles reaches a certain value, its energy will also decrease, which may be caused by excessive freeze–thaw damage to the bonding force between particles inside the rock. Therefore, the energy change under freeze–thaw cycles depends on the strength and deformation of the rock.

Fig. 9
figure 9

Energy density changes at peak stress with different freeze–thaw cycles.

Full size image

The compaction strain values at the conclusion of the compaction stage under varying freeze–thaw conditions are illustrated in Fig. 10. It is evident from Fig. 10 that an increase in the number of freeze–thaw cycles leads to a gradual rise in strain value during the compaction stage, indicating a corresponding increase in porosity within the rock sample. The observed variations in strain values effectively demonstrate the erosive impact of freeze–thaw cycles on rocks.

Fig. 10
figure 10

Relationship between number of freeze–thaw cycles and compression-density strain.

Full size image

The freeze–thaw damage constitutive model considering the compaction stage

The freeze–thaw damage constitutive model

In the study of damage mechanics, the degree of damage in materials can be reflected by damage variables. Therefore, selecting appropriate damage variables is the foundation of the entire study. Currently, damage variables defined based on continuum damage mechanics include macroscopic and microscopic levels, where the macroscopic level includes elastic modulus, yield stress, density, wave velocity, etc., and the microscopic level includes microcrack length, number, area, etc54. In this study, elastic modulus is selected as the main research object, therefore, the freezing and thawing damage factor of sandstone can be calculated by Eq. (5)55,56.

$$D=\frac{{E - E^{\prime}}}{E}$$
(5)

where D is the damage variable; E is the elastic modulus of conventional sandstone; E′ is the elastic modulus of freeze–thaw sandstone.

In this study, the damage caused by rock freeze–thaw is considered as the first damage state, and the damage under load is defined as the second damage state. Due to the Lemaitre damage model considering the initial damage state and considering that the strain generated by the nominal stress on the damaged material under external loads is equivalent to the strain caused by the effective stress on the non-destructive material57,58. Therefore, this study aims to further describe the freeze–thaw damage characteristics of rocks. Lemaitre derived a stress-strain equation considering damage for brittle materials:

$$\sigma =E\varepsilon \left[ {1 - {{\left( {\frac{\varepsilon }{{{\varepsilon _R}}}} \right)}^{S+1}}} \right]$$
(6)

where ε, ε0, and S are material constants. εR is the fracture strain,\({\varepsilon _R}={\left[ {\left( {S+1} \right){\varepsilon _0}^{{S+1}}} \right]^{{{\left( {S+1} \right)}^{ - 1}}}}\).

Based on the Lemaitre strain equivalence principle, the damage constitutive relationship of rocks can be expressed as follows57:

$$\left[ \sigma \right]=\left[ {{\sigma ^ * }} \right]\left( {1 - \left[ D \right]} \right)=\left[ E \right]\left[ \varepsilon \right]\left( {1 - \left[ D \right]} \right)$$
(7)

where [σ] is the nominal stress tensor; [σ*] is the effective stress tensor; \(\left[ E \right]\) is the elastic modulus matrix; [ε]is a strain tensor; [D] is the damage matrix.

The macroscopic failure of materials is the result of the accumulation of a large number of microelements, so the damage variable of rocks under load is defined as the ratio of the number of damaged microelements to the total number of microelements. Assuming that the damage statistical distribution density function of rock microelements satisfies the following relationship with the damage variable59:

$$d{D_c}=P\left( F \right)dF$$
(8)

where Dc is the rock damage variable under load; P (F) is the density function of the strength distribution of microelements; F is the strength parameter of the microelement.

The probability density function of rock microelement strength based on Weibull distribution can be written as P (F)60,61:

$$P\left( F \right)=\frac{{{S_0}}}{F}{\left( {\frac{F}{{{F_0}}}} \right)^{{S_0} - 1}}\exp \left[ { - {{\left( {\frac{F}{{{F_0}}}} \right)}^{{S_0}}}} \right]$$
(9)

where S0 and F0 are the Weibull distribution parameters of the rock material.

By substituting Eq. (9) into Eq. (8), it can be concluded that:

$${D_c}={\int_{0}^{F} {\frac{{S{}_{0}}}{F}\left( {\frac{F}{{{F_0}}}} \right)} ^{{S_0} - 1}}\exp \left[ { - {{\left( {\frac{F}{{{F_0}}}} \right)}^{{S_0}}}} \right]dF=1 - \exp \left[ { - {{\left( {\frac{F}{{{F_0}}}} \right)}^{{S_0}}}} \right]$$
(10)

According to the research content, Eq. (5) was modified to obtain:

$${D_n}=1 - \frac{{{E_n}}}{E}$$
(11)

where Dn is the damage factor after n freeze–thaw cycles; En is the elastic modulus after n freeze–thaw cycles.

According to Lemaitre’s hypothesis of strain effects, the damage factor under the combined action of freeze–thaw and loading can be obtained62:

$$1 - D=\left( {1 - {D_c}} \right)\left( {1 - {D_n}} \right)$$
(12)

Equation (12) can be rewritten as:

$$D={D_c}+{D_n} - {D_c}{D_n}$$
(13)

By substituting Eqs. (10) and (11) into Eq. (13), it can be concluded that:

$$D=1 - \frac{{{E_n}}}{E}\exp \left[ { - {{\left( {\frac{F}{{{F_0}}}} \right)}^{{S_0}}}} \right]$$
(14)

The Drucker-Prager strength criterion is introduced as the basis for micro element failure of sandstone under freeze–thaw load, and the expression of F can be obtained as follows63:

$$\left\{ \begin{gathered} F=\alpha I_{1}^{ * }+\sqrt {J_{2}^{ * }} \hfill \\ \alpha =\frac{{2\sin \varphi }}{{\sqrt 3 \left( {3 - \sin \varphi } \right)}} \hfill \\ I_{1}^{ * }=\sigma _{1}^{ * }+\sigma _{2}^{ * }+\sigma _{3}^{ * } \hfill \\ J_{2}^{ * }=\frac{1}{6}\left[ {{{\left( {\sigma _{1}^{ * } - \sigma _{2}^{ * }} \right)}^2}+{{\left( {\sigma _{2}^{ * } - \sigma _{3}^{ * }} \right)}^2}+\left( {\sigma _{1}^{ * } - \sigma _{3}^{ * }} \right)} \right] \hfill \\ \end{gathered} \right.$$
(15)

where φ is the internal friction angle, °; I*1is the first invariant of the effective stress tensor; J*2 is the second invariant of the effective stress tensor; σ*1, σ*2, and σ*3are effective stresses, corresponding to nominal stresses of σ1, σ2, and σ3.

Since this study mainly focuses on uniaxial compression tests, σ2 = σ3 = 0. So, the expression.

for F can also be written as:

$$F=\frac{{E\varepsilon \left( {1+\sqrt 3 \alpha } \right)}}{{\sqrt 3 }}$$
(16)

By substituting Eq. (16) into Eq. (14), it can be concluded that:

$$D=1 - \frac{{{E_n}}}{E}\exp \left[ { - {{\left( {\frac{{E\varepsilon \left( {1+\sqrt 3 \alpha } \right)}}{{\sqrt 3 {F_0}}}} \right)}^{{S_0}}}} \right]$$
(17)

Substituting the damage evolution Eq. (17) into Eq. (7) yields the rock damage constitutive equation based on Weibull distribution under freeze–thaw cycles:

$$\sigma =\varepsilon {E_n}\exp \left[ { - {{\left( {\frac{{E\varepsilon \left( {1+\sqrt 3 \alpha } \right)}}{{\sqrt 3 {F_0}}}} \right)}^{{S_0}}}} \right]$$
(18)

The experimental results show that the stress-strain curve of the sample after freeze–thaw treatment shows a concave characteristic during the compaction stage, and as the number of freeze–thaw cycles increases, the compaction stage becomes more obvious and the strain also increases. In view of this, it is necessary to modify Eq. (18). In order to simplify the calculation, the average secant modulus Ec of the compaction section is used in the analysis to describe the stress-strain curve of the compaction stage. Firstly, define the ratio of the average secant modulus of the rock compaction section to the elastic modulus of the complete curve as β, Ec = βEn, 0 < β ≤ 1. End point stress of compaction section σc and peak stress The ratio of is γ, namely σc = γσ, 0 < γ ≤ 1. The corresponding strain of the compaction section is εc. Substituting the above parameters into Eq. (18) yields a segmented expression of the rock damage constitutive Eq. 

$$\sigma =\left\{ {\begin{array}{*{20}{l}} {\beta \varepsilon {E_n}\exp \left[ { - {{\left( {\frac{{E\varepsilon \left( {1+\sqrt 3 \alpha } \right)}}{{\sqrt 3 {F_0}}}} \right)}^{{S_0}}}} \right],}&{\varepsilon \leqslant {\varepsilon _c}} \\ {\beta \left( {\varepsilon - {\varepsilon _c}} \right){E_n}\exp \left[ { - {{\left( {\frac{{E\varepsilon \left( {1+\sqrt 3 \alpha } \right)}}{{\sqrt 3 {F_0}}}} \right)}^{{S_0}}}} \right]+{\sigma _c}}&{\varepsilon >{\varepsilon _c}} \end{array}} \right.$$
(19)

According to Eq. (19), it can be inferred that the constitutive equation derived in this study contains two unknown parameters, S0 and F0. According to the stress-strain partition characteristics, the stress shows a significant decrease after the peak point64,65,66. Therefore, the model parameters S0 and F0 can be solved by the method of solving the parameters by using the extremum of the multivariate function, and the following boundary conditions can be obtained62,67:

Void compression stage: When ε = εc, then σ = σc. Where σc and εc represent stress and strain values at the end of the compression stage, respectively.

Yield stage: When ε = εe, then \(\frac{{\partial \sigma }}{{\partial \varepsilon }}=0\). Where σe and εe represent the stress and strain values at peak stress, respectively.

By substituting the above boundary conditions into Eq. (18) and solving them together with Eqs. (14) and (16), it can be concluded that:

$$\left\{ \begin{gathered} {S_0}=\frac{1}{{\ln \left[ {{E_n}\frac{{{\varepsilon _{1e}}}}{{{\sigma _{1e}}}}} \right]}}\begin{array}{*{20}{c}} {}&{Void{\text{ }}compression{\text{ }}stage} \end{array} \hfill \\ {S_0}=\frac{1}{{\ln \left[ {{E_n}\frac{{{\varepsilon _{1e}} - {\varepsilon _c}}}{{{\sigma _{1e}} - {\sigma _c}}}} \right]}}\begin{array}{*{20}{c}} {}&{Yield{\text{ }}stage} \end{array} \hfill \\ {F_0}={S_0}^{{\frac{1}{{{S_0}}}}}\frac{{{\sigma _{1c}}{E_n}{\varepsilon _{1c}}\left( {1+\sqrt 3 } \right)}}{{\sqrt 3 {\sigma _1}}} \hfill \\ \end{gathered} \right.$$
(20)

where, σ1e and ε1e represent stress and strain values at any point on yield stage, respectively. σ1c and ε1c represent stress and strain values at any point on void compression stage, respectively.

Additionally, it should be noted that in the five stages of stress strain curves (void compression (OA), approximate linear deformation (AB), non-linear deformation (BC), yield (CD), and post peak failure and strain softening (DE)), it is difficult to distinguish between the approximate linear deformation stage, non-linear deformation stage, and yield stage, so they should be analyzed as a whole.

Verification and analysis of constitutive models

Based on the elastic modulus of sandstone obtained in this experiment (Table 7), the relationship between the freeze–thaw damage factor of sandstone and the number of freeze–thaw cycles can be obtained through Eq. (5), as shown in Fig. 11. From Fig. 11, it can be seen that the freezing and thawing damage factor increases approximately exponentially with the increase of the number of freezing and thawing cycles. The correlation coefficient between the damage factors of various parameters of sandstone and the number of freezing and thawing cycles is above 0.8 (R2 = 0.97641), showing good correlation. Comparing Eq. (17) with the damage law fitting equation obtained in this experiment (Fig. 11), both the experimental and theoretical derivation results show that the rock damage law under freeze–thaw load coupling shows exponential growth. Thus, it can be seen that the theoretical derivation results can reflect the experimental rules in this study.

Fig. 11
figure 11

The relationship between damage variable and the number of freeze–thaw cycles.

Full size image

To verify the applicability of the freeze–thaw load rock damage constitutive model derived in this article, combined with freeze–thaw cycle tests and referring to the value taking methods in previous studies68, the above parameters are substituted into Eq. (19) to obtain the uniaxial compression stress-strain theoretical curve of sandstone considering the impact of the compression section under freeze–thaw load, as shown in Fig. 12. In order to further verify the reliability of the constitutive model, it is proposed to compare and analyze the results of uniaxial compression tests in previous literature based on this constitutive model, as shown in Fig. 13. The three stress-strain curves in Fig. 13 are derived from uniaxial compression tests based on freeze–thaw cycles conducted by Ke et al.69, Zhou et al.27, and Feng et al.70.

From Figs. 12 and 13, it can be seen that the theoretical curve can basically reflect the trend of changes in the experimental curve. Meanwhile, the segmented study of stress-strain curves can intuitively reflect the impact of freeze–thaw cycles on the stress-strain curves of rock samples at various stages. It can be inferred that the initial stage of the stress sequence curve can partially reflect the changes in sandstone pore structure under freeze–thaw cycles. To a certain extent, it can well reflect the closure of internal microcracks/fissures in rocks under loading conditions. This will contribute to in-depth research on the instability phenomenon of high cold engineering rock masses under freeze–thaw in the future.

Fig. 12
figure 12

Comparison of theoretical and experimental curves of stress-strain curves.

Full size image
Fig. 13
figure 13

Comparison of stress-strain curves between theoretical models and experimental data from other researchers26,69,70.

Full size image

Conclusions

In this investigation, the standards and references have been summarized for freeze–thaw cycle tests, and analyzed the similarities and differences in experimental methods. And combined with the seasonal changes of frozen rocks in the Qinghai-Xizang Plateau, preprocessed the rock samples using a freeze–thaw interval of 20 °C ~ -20 °C. Uniaxial compression tests were conducted using the MTS816 Rock Mechanics Testing System. A freeze–thaw damage constitutive model considering the compaction stage under the coupling effect of freeze–thaw load was derived based on Lemaitre equivalent strain theory. The conclusions reached in this study were as follows:

  1. (1)

    The porosity test results show that as the number of freeze–thaw cycles increases, the porosity of sandstone continues to increase, and the amount of change in porosity also increases accordingly. During the freezing process, the pore water inside the rock sample is affected by the phase change of water-ice, resulting in frost heave force, which further promotes the expansion of the pore walls and the initiation of new cracks. When melted, pore water migrates towards newly formed micropores, thereby affecting the changes in the pores of rock samples.

  2. (2)

    As the number of freeze–thaw cycles increases, the strength and elastic modulus of the rock sample show a significant decrease, while the damage variable gradually increases. Comparing the frozen and thawed rock samples, conventional rock samples, and saturated rock samples (0 freeze–thaw cycles), it can be concluded that the main reason for the mechanical deterioration of frozen and thawed rock masses is not only due to low-temperature freeze–thaw, but also the erosion effect of water. Therefore, rock sample’s freeze–thaw damage can be considered as fatigue damage resulting from interactions between ice-rock and water-rock interfaces.

  3. (3)

    From the variation pattern of strain values at the end of the compaction stage, it can be seen that the porosity inside the rock sample increases with the increase of freeze–thaw cycles. It can be inferred that the initial stage (the compaction stage) of the stress-strain curve can partially reflect the changes in sandstone pore structure under freeze–thaw cycles.

  4. (4)

    A freeze–thaw damage constitutive model considering the compaction stage under the coupling effect of freeze–thaw load was derived based on Lemaitre equivalent strain theory. The proposed model can well fit the experimental results involved in this study, as well as the experimental results obtained by other researchers. The proposed model can basically reflect the trend of changes in relevant experimental curves. At the same time, segmented research on stress-strain curves can intuitively reflect the influence of freeze–thaw cycles on stress-strain curves of rock samples at different stages. To a certain extent, it can well reflect the closure of microcracks/fissures inside rocks under loading conditions.

  5. (5)

    This study is based on the seasonal freeze–thaw phenomenon in the natural environment of high-altitude cold regions, combined with previous research experience, and conducted indoor freeze–thaw experiments. There is a certain gap between the experimental methods involved in this study and the actual seasonal freeze–thaw cycles, which is also our future research focus. The stress conditions reflected by basic uniaxial compression tests are relatively single, and in the future, rock mechanics tests under complex stress conditions will also be carried out. We hope that our research can provide a theoretical basis for engineering construction in high-altitude cold regions and better promote regional economic development.