Introduction

The most challenging point in tunnel construction is usually at the entrance section, where the tunnel is buried shallowly, the surrounding rock is weathered and broken. It is severely eroded by rainwater, making it prone to collapse and instability. This multifaceted rock structure and the uneven distribution of materials make the geotechnical parameters of the tunnel opening section structural, variable and random1,2, and the stability of the tunnel structure is greatly affected by the geotechnical parameters and design control parameters.

The method commonly used to assess the overall safety of tunnels is the limit state-based safety factor method. Still, because of safety considerations, this method takes a significant value for the safety factor, which usually results in a significant economic waste3. Therefore, many experts and scholars use the reliability theory4,5,6 to evaluate the safety of tunnel construction. In 1984, Whitman7 suggested that reliability analysis could be relied upon to establish implementation plans and design criteria for geotechnical engineering. In 1994, Christian8 described how to obtain the probability characteristic values of soil parameters from field and experimental data and apply them to slope stability analysis. He also pointed out that the safety factor design value in reliability analysis can represent the consistent risk for different types of faults. Kroetz9 et al. established the limit state functional function of the lining structure and calculated the reliability index of the lining structure by combining the relevant statistical characteristics of the physical parameters of the surrounding rock, the primary reliability method, and the Monte Carlo method. At present, the overall reliability analysis of tunnel projects is mainly explored from two aspects of support structure reliability9,10,11 and surrounding rock reliability12,14, which usually have their mechanical equations and limit state functions established under relatively ideal conditions, but still have a high degree of non-linearity and are more complex to compute and study.

When the tunnel passes through weak surrounding rock, the physical and mechanical properties of rock and soil mass are constantly updated in the construction process, and the spatial variability of rock and soil mass caused by excavation disturbance will cause significant deformation of tunnel surrounding rock. Zhao15,16 et al. summarized the mechanical response during tunnel construction and explored the construction mechanical laws of super large cross-section tunnels. Through the analysis of numerical simulation and field monitoring, it is found that the stability of tunnel surrounding rock is improved to a great extent by using support measures such as umbrella arch. Elachachi et al.17 developed a soil spatial variability model within a structure-induced framework. They found that the magnitude of soil structure-induced effects mainly depends on four factors: soil variability, soil structure stiffness ratio, structure connection stiffness ratio (relative flexibility), and soil structure length ratio. Nguyen18 et al. studied the effect of random fields of shear strength parameters on slope failure caused by rainfall through probability stability analysis and found that probability analysis can effectively determine different locations of failure surfaces caused by spatial variation of soil shear strength. Nguyen19,20 et al.evaluated the impact of spatial variability of rock and soil parameters on the statistical characteristics of safety factor and failure probability through random field theory and found that the random field of effective friction angle is the most critical parameter for probabilistic stability analysis. Luo et al.21 proposed a simplified method for analyzing the reliability of foundation pit bottom heave considering the spatial variability of soil parameters, replacing the traditional random field model (RFM), and the results obtained were comparable to those obtained by conventional RFM methods. Nguyen22 et al. used the random field theory and Monte Carlo method to simulate the two-dimensional spatial variability of the undrained shear strength of the foundation clay layer in Bangkok, and found that the spatial variability had a greater impact on the sidewall movement and surface settlement. Nguyen23,24 et al. used copula method to carry out finite element limit analysis (FELA) with adaptive mesh generation to evaluate the reliability of geotechnical engineering problems. Subsequently, the research found that the non-Gaussian copulas provided simulated data that more accurately reflected observed field data, highlighting the importance of copula selection when characterizing soil parameter random fields. The geotechnical parameters usually have significant spatial variability, and they affect the deformation of tunnel surrounding rock. Considering the spatial variability of soil parameters is crucial for evaluating the stability of tunnel engineering.

In the reliability calculation methods, the stochastic finite element method25,26 was initially used to solve the reliability index of geotechnical engineering. Still, the method has high dispersion, and the deviation of calculation accuracy is difficult to control. Then, the stochastic response surface method27,28 was used to analyze the reliability of geotechnical engineering, and the near explicit limit state function was constructed. This method guaranteed calculation accuracy, which was less efficient to calculate29,30,31. In order to solve the above problems and improve the calculation efficiency, Li Dianqing32 proposed the non-invasive stochastic finite element method for the first time and successfully applied it to the reliability analysis of underground chambers. Tanapalungkorn33 et al. used the random adaptive finite element limit analysis and Monte Carlo to study the influence of soil strength variability under different parameters and conducted probability analysis on the stability of supporting excavations. Nguyen34 et al. used stochastic finite element limit analysis to study and found that considering the large cross-correlation coefficients of soil parameters, the failure probability of passive trapdoors in soil is lower. Nguyen35 et al. employed the random adaptive finite element limit analysis method, which incorporating rotated anisotropic random fields, to predict collapse loads and probabilities of design failure for dual circular tunnels constructed in anisotropic rock masses. Wen Ming36 et al. combined with finite splitting method, non-invasive stochastic analysis, and Monte Carlo method to summarize typical engineering models suitable for railway tunnel surrounding rock. Sheng Jianlong and Zhai Mingyang37 investigated the accuracy of fitting Hermite polynomials to rocky slope reliability indicators under different sampling methods and the probability of failure based on the random response surface method and the finite element slip surface stress method. Pan Jiaming38 constructed a surrogate model for calculating the reliability index of shield tunnels using Hermite polynomials based on the finite difference method and non-invasive stochastic analysis. Wang Jian’e39 et al. were redeveloping the MSC.Mar subroutine of finite element software and analyzed the reliability of rockfill dams using Cholesky decomposition and non-invasive stochastic finite element method. The results show that to improve the calculation accuracy, it is necessary to consider the spatial variability of geotechnical parameters. Zhang Fuyou40 et al. used Python programming language to secondary develop the Abaqus software and combined the Cholesky decomposition method with the non-invasive stochastic finite element method to find that considering the spatial variability of the parameters could better enhance the safety of the dam foundation containment wall. Ji Yun41 et al. derived a formula for structural sensitivity analysis based on the non-invasive introductory stochastic finite element method and geometric method and verified the method’s feasibility by example. Shan Xun42 developed a second finite element software based on the Monte Carlo stochastic finite element method, calculating the overturning stability and deformation reliability of deep foundation pits in bulk. In tunnel engineering, to achieve the purpose of risk quantitative analysis, the non-invasive stochastic finite element method is used, and the programming software is used to couple the stochastic analysis and deterministic analysis. This method uses reliability theory to evaluate the safety of tunnel construction stage.It uses reliability method to take the variability and uncertainty of rock and soil mass of tunnel engineering into account, which is a more comprehensive and accurate research method. The non-invasive stochastic finite element method greatly improves the accuracy and efficiency of reliability calculation in geotechnical engineering.It lays a foundation for the reliability analysis of tunnel portal engineering in complex geology.

Therefore, this paper takes the Wenbishan Tunnel in Puyan, Fujian, as a background project and uses ABAQUS v6.1443 for the mechanical analysis of tunnel excavation and parameter sensitivity impact analysis by introducing a non-invasive stochastic finite element method. The software interface program is developed based on Python language, and the explicit limit state equation of the key mechanical indexes of the tunnel is output. Based on this, an efficient calculation method for quantifying the failure probability of tunnel excavation is established to effectively reduce the construction risk of shallow tunnel portal section under unsymmetrical pressure.

Non-invasive stochastic finite element

Construction of functional function models

The random response surface method usually uses polynomials to construct a functional relationship between input parameters and output response quantities, thereby improving the calculation efficiency of reliability indicators for complex geotechnical engineering. The random response surface method adopts a near display state function, namely Hermite random polynomial, which can simplify the workload while ensuring accuracy. It also considers the influence of cross-phase between variables and accurately presents the variation process of the output response of the entire structural space. The Hermite function model suits underground engineering with complex geological exploration and high spatial variability. In practical engineering, it can be used with survey data for auxiliary simulation to ensure engineering safety further. Hermite random polynomial expansion expression is given in Eq. (1):

$${F_p}(\zeta )={a_0}{\Gamma _0}+\sum\limits_{{{i_1}=1}}^{n} {{a_{{i_1}}}{\Gamma _1}({\zeta _{{i_1}}})} +\sum\limits_{{{i_1}=1}}^{n} {\sum\limits_{{{i_2}=1}}^{n} {{a_{{i_1},{i_2}}}{\Gamma _2}({\zeta _{{i_1}}},{\zeta _{{i_2}}})} } + \cdots +\sum\limits_{{{i_1}=1}}^{n} {\sum\limits_{{{i_2}=1}}^{{{i_1}}} {\sum\limits_{{{i_3}=1}}^{{{i_2}}} { \cdots \sum\limits_{{{i_n}=1}}^{{{i_{n - 1}}}} {{a_{{i_1},{i_2}, \cdots ,{i_n}}}{\Gamma _n}({\zeta _{{i_1}}},{\zeta _{{i_2}}}, \cdots ,{\zeta _{{i_n}}})} } } }$$
(1)

Where: \({F_p}(\zeta )\), Output response volume; a, undetermined coefficient; number of undetermined coefficients44\(N=\frac{{(n+p)!}}{{n!p!}}\); \(\zeta\), random variable; \({\Gamma _n}\), p-order Hermite polynomial; n, Random variable extraction quantity.

Iman and Conover45 first proposed Latin hypercube sampling, aiming to increase the sample size and make the samples evenly distributed. When we need a large number of samples, this method ensures that the samples are evenly stratified while distributing a specific distribution of random variables in the head and tail intervals, thus providing the validity of the reliability calculation results. The first step is determining the number N of matching points for the random parameters while dividing them uniformly into N segments within the interval (0, 1). Within each segment, a value is randomly selected, and the collocation points of each random parameter are transformed into independent standard normal distributions according to the Nataf transform46,47 to finally obtain the desired original array. The matching points extracted by this method are independent of the constant linearity of the Hermite stochastic polynomial expansion coefficient matrix. So it is suitable for use in stochastic response surface reliability calculations based on Hermite stochastic polynomial expansion. Therefore, this paper adopts the above method to randomly select input variables to ensure a linear relationship between input variables and output response quantities, to accurately obtain the undetermined coefficient of the function function function.

Abaqus secondary development interface implementation

Using the random response surface method for Abaqus model calculation, including establishing a parameterized finite element model, determining the characteristics of the random distribution, fitting the function of the near display state using the response surface method, normalizing the equivalent of the random distribution parameters, transforming the standard normal space, and other steps, can reduce errors, improve the reliability and sensitivity of engineering structures. This paper uses Python to establish the secondary development program interface of corresponding functions instead of manual sampling, and combines ABAQUS finite element numerical simulation with reliability analysis. This program interface can mainly complete batch modification of parameters and generation of modeling text in model pre-processing, and extract data required for model calculation result file during post-processing. At the same time, the program interface allows the Abaqus software to be called directly in the background as a “dark box”. The specific steps are as follows:

  1. (1)

    Extract the mean, standard deviation, and coefficient of variation of the random input parameters in the geological exploration data. The random variables are normally distributed. Use Latin hypercube sampling to extract samples and obtain the original parameter set through Nataf transformation.

  2. (2)

    Create a finite element numerical model from the project data and save it as a calculation source file in the format “inp”.

  3. (3)

    Use Python for secondary development and write corresponding program interfaces that can be used in Abaqus. Batch replacement of the original set of parameters with the relevant parameters on the base file using the programmatic interface to generate a calculation text in the format “inp”.

  4. (4)

    Based on the developed program interface, the generated inp format file group is traversed to produce a bat format file, which can be used to call the Abaqus software directly in the background as a “dark box”. Perform batch cyclic operation on inp format file group, and monitor the operation result. If it does not converge, it can report an error and skip the calculation of the following file.

  5. (5)

    Similarly, the program interface extracts the required data from all odb format files generated by the calculation to obtain the output response volume.

Reliability analysis of road tunnels

The introduction of the concept of structural reliability48 in road tunnel engineering will give limit state values for the stability of the tunnel to construct a limit state function describing the working state of the road tunnel, i.e., a functional function. In practical project engineering, the functional function is affected by many conditions, such as geotechnical parameters, so when there are n random variables affecting the reliability of a tunnel, the functional function is shown in Eq. (2):

$$Z={\text{g}}\left( {{X_1},{X_2}, \ldots ,{X_{\text{n}}}} \right)=\left\{ {\begin{array}{*{20}{c}} {<0} \\ {=0} \\ {>0} \end{array}} \right.$$
(2)

Where: X, random variable; Z, Limit state function; when Z > 0, the stable is reliable; when Z < 0, the state is unstable; when Z = 0, the state is limited.

The tunnel failure mode is considered a tandem system around the effect of tunnel deformation on the stability of the surrounding rock. In this paper, seven monitoring characteristic parameters are selected to construct deformation limit state functions, expressed as different tunnel envelope failure modes, calculated as follows:

$${H_i}\left( {\text{x}} \right)=U_{i}^{{\hbox{max} }} - U_{i}^{D}$$
(3)

Where: i = 1–7, \(U_{1}^{{\hbox{max} }}\), the permissible limit of vault settlement; \(U_{2}^{{\hbox{max} }}\), the permissible limit of horizontal convergence of left guide pit; \(U_{3}^{{\hbox{max} }}\), the permissible limit of horizontal convergence of right guide pit; \(U_{4}^{{\hbox{max} }}\), the permissible limit of settlement of the left arch shoulder; \(U_{5}^{{\hbox{max} }}\), the permissible limit of settlement of the right arch shoulder; \(U_{6}^{{\hbox{max} }}\), the permissible limits of surface settlement; \(U_{7}^{{\hbox{max} }}\), the permissible limit of the arch base bulge; \(U_{1}^{D}\), vault settlement; \(U_{2}^{D}\), horizontal convergence value of left guide pit; \(U_{3}^{D}\), horizontal convergence value of right guide pit; \(U_{4}^{D}\), the settlement value of left arch shoulder; \(U_{5}^{D}\), the settlement value of right arch shoulder; \(U_{6}^{D}\), surface settlement value; \(U_{7}^{D}\), arch base bulge value. According to the “Technical Specifications for Construction of Highway Tunnel” (JTG/T3660-2020) and the “Code for Design of Road Tunnel” (JTG D70-2004), as well as the monitoring and measurement plan for Puyan Expressway, it can be concluded that the deformation control value for settlement at the top of the arch is 35 mm. The deformation control value for settlement at the bottom of the arch is 35 mm, and the deformation control value for horizontal convergence is 25 mm. If the actual value exceeds the deformation control value, the surrounding rock will be judged to be unstable.

Based on on-site measured data, the correctness of the numerical model is verified. The non-invasive stochastic finite element method is used to analyze the parameter sensitivity, and the Latin hypercube sampling is used to obtain the parameter group for finite element analysis. Hermite polynomials are fitted as a proxy model according to the calculation results, and combined with Monte Carlo method to finally calculate the failure probability of each monitoring index and the system failure probability. The specific flowchart is shown in Fig. 1.

Fig. 1
figure 1

Specific flowchart of non-invasive stochastic finite element method.

Full size image

Application examples

Finite element numerical analysis

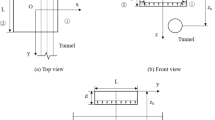
The subject of this study is the right line cavern entry section K218 + 585 ~ K218 + 620 in Wenpengshan Tunnel No.1 Youxi section, 35 m long, all in the range of class V soft and weak surrounding rocks. It is a shallowly buried partial pressure section with poor exposure of bedrock on the hillside, and the geology within the construction area of this section is mainly sandy clayey soil layers and fully weathered mixed granite layers. The sandy clay layer is in the upper part of the lot, at 15 m, and resides in the upper part of the excavated tunnel, as shown in the geological longitudinal section in Fig. 2. The depth of the tunnel is 10 m, the height is 11.7 m, the width is 17.2 m, and the slope of the deviated side is 1:1.5. Therefore, this paper proposes to use the circular stay core method, the single sidewall guide trench method and the double sidewall guide trench method to study the reliability of the tunnel entrance and analyze the influence of different excavation methods on the reliability of the tunnel.

Fig. 2
figure 2

Geological profile diagram.

Full size image

Based on the Mohr-Coulomb constitutive model, this paper establishes the tunnel numerical model according to the site engineering situation and Saint-Venant principle. The tunnel depth is set at 10 m, the hole height at 11.7 m, the hole width at 17.2 m, and the slope on the deviated side at 1:1.5. The bottom of the tunnel arch is three times the height of the tunnel, 35.1 m, and the total width of the model is five times the width of the tunnel, 86 m. The tunnel involves two soil layers: 15 m of sandy clay in the upper layer and 41.8 m of complete weathering migmatitic granite in the lower layer. Taking the double sidewall guide pit method as an example, the model soil and initial support use solid cells, and the temporary support uses shell cells. According to the principle of multi-scale grid division, the crucial areas are refined, and 49,287 grid cells are divided.

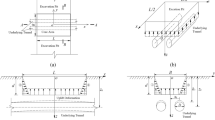
The model boundary is controlled by applying constraints, with Z-direction constraints applied to the front and back, X-direction constraints applied to the left and right surfaces, Y-direction constraints applied to the bottom surface, and the top surface accessible. To avoid displacement caused by dislocation between parts in the process of simulated excavation, resulting in non convergence of calculation, corresponding constraints are also added between parts. The initial support and rock and soil, the initial support and secondary lining, the initial support and temporary support, and the temporary support and soil are all constrained by binding, and the pipe shed and anchor rod are constrained by the form of built-in areas. The excavation section of the tunnel is shown in Fig. 3 (Zones 1, 2, 3, 4, and 5 represent the sequence of tunnel excavation), and the specific excavation model is shown in Fig. 4.

Fig. 3
figure 3

Tunnel excavation section and support drawing.

Full size image
Fig. 4
figure 4

Excavation model of double-side heading method.

Full size image

Excavation mechanical properties of shallowly biased tunnel portal section

According to the calculated displacement cloud (Fig. 5), the maximum vertical displacement of the tunnel surrounding rock occurs at the top and bottom of the arch, 25.76 and 17.53 mm, respectively. The maximum horizontal displacement occurs at the lower left arch waist and the upper right arch waist, 3.84 mm and 7.17 mm, respectively, showing prominent asymmetric characteristics. The reason for this phenomenon is that the section is a tunnel entrance project, with a shallow depth of burial and a weak overburden, which makes it easy for settlement to occur at the top of the vault, and although the bottom of the vault is raised as necessary by the tunnel excavation, the deformation value is always less than at the top of the vault; According to the actual project, the overburden on the left side of the tunnel is more than the right side, and the horizontal displacement on the right side is more significant than that on the left side due to the bias effect. Therefore, the construction should strengthen monitor settlement at the top of the arch and the monitoring of the horizontal convergence of the right arch waist and take corresponding measures to enhance it if necessary.

Fig. 5
figure 5

Displacement nephogram measured by double-side heading method.

Full size image

To further verify the correctness of the numerical model, the monitoring data and numerical results are compared and analyzed. Taking surface subsidence as an example, as shown in Fig. 6, the specific deformation value results are compared in Fig. 7. After adjusting the model parameters many times, the final numerical simulation results are consistent with the actual monitoring values in terms of trend, and the calculation results are in good agreement with the actual situation. Therefore, the model can be used to simulate the actual situation in this paper, which has a specific guiding significance for the actual engineering.

Fig. 6
figure 6

Horizontal displacement nephogram changing with excavation step.

Full size image
Fig. 7
figure 7

Data Comparison Chart.

Full size image

Sensitivity analysis of random variable distributions

There is usually variability and uncertainty in road tunnel excavation geotechnical bodies, but there are more geotechnical parameters. Table 1 shows the specific parameters of the geotechnical bodies. The model used in this article mainly involves geotechnical parameters such as elastic modulus, cohesion, friction angle, and Poisson’s ratio. Due to the significant variability of geotechnical weight density, it has an important impact on the convergence of tunnel calculation, so it also needs to be taken into account. If all numerical simulations are carried out as random variables, it will lead to inefficient work and little practical significance, so sensitivity analysis is carried out on geotechnical parameters49. Select parameters that have a significant impact on the stability of the project, and treat the remaining parameters as constants. The specific formulas are shown in Eqs. (4) and (5). Due to the minor dispersion of soil Poisson’s ratio, sensitivity analysis is conducted on the soil layer cohesion, friction angle, weight, and elastic modulus as random variables to obtain parameters with high sensitivity as random parameters. The sensitivity indicators of soil layer random variables are shown in Table 2. As shown in Table 2, the relative sensitivity indicators and sensitivity rates of the friction angle of the two soil layers are both 0. Therefore, this article selects the elastic modulus, weight, and cohesion of the rock and soil parameters as random variables.

$${\eta _{SR{\text{,i}}}}=\left| {\frac{{\left[ {{F_S}\left( {{\mu _i}+2{\sigma _i}} \right) - {F_S}\left( {{\mu _i} - 2{\sigma _i}} \right)} \right]/{F_S}\left( {{\mu _i}} \right)}}{{\left[ {\left( {{\mu _i}+2{\sigma _i}} \right) - \left( {{\mu _i} - 2{\sigma _i}} \right)} \right]/{\mu _i}}}} \right|$$
(4)
$$\alpha \left( {{X_{\text{i}}}} \right)=\frac{{{\eta _{SR,{\text{i}}}}}}{{\sum\nolimits_{{{\text{i}}=1}}^{{\text{n}}} {{\eta _{SR,{\text{i}}}}} }}$$
(5)

Where, \({\mu _{\text{i}}}\), mean value of parameters; \({\sigma _{\text{i}}}\), standard deviation; \({F_S}=\left( {{\mu _{\text{i}}}} \right)\), is the output response to the mean value of the input; \({F_S}=\left( {{\mu _{\text{i}}}+2{\sigma _{\text{i}}}} \right)\), is the output response to the \({\mu _{\text{i}}}+2{\sigma _{\text{i}}}\); \({F_S}=\left( {{\mu _{\text{i}}} - 2{\sigma _{\text{i}}}} \right)\), is the output response to the \({\mu _{\text{i}}} - 2{\sigma _{\text{i}}}\); n, number of random variables.

Table 1 Statistical characteristics of geotechnical parameters.
Full size table
Table 2 Sensitivity analysis of stochastic parameters of soil layers.
Full size table

Reliability analysis of tunnel deformation

According to the sensitivity analysis of random variables in the previous section, it can be seen that the relative sensitivity indicators and sensitivity rates of elastic modulus, weight density, and cohesion in the rock and soil parameters are relatively high. Therefore, these six random variables are used as input parameters for the tunnel reliability calculations in this paper. Considering the influence of Hermite polynomial order on deformation reliability, the second, third and fourth order polynomials are selected to fit the six random variables of the strata. The output response volumes extracted using the secondary development program interface are shown in Table 3, and the 3D scatter plot of each stratigraphic parameter is shown in Fig. 8.

Table 3 Model output response values(m).
Full size table
Fig. 8
figure 8

3D scatter plot of stratigraphic parameters.

Full size image

This method uses the independent standard regular distribution group obtained from the original parameter group extracted from the Latin hypercube after Nataf transformation as the input for Hermite polynomial fitting, and the output response of the finite element is used as another part of the input for Hermite polynomial fitting. At the same, to avoid problems such as under-fitting or local over-constraint due to the number of matching points, the number of sample points is chosen to be equal to their pending coefficients, and finally, the relationship equation between the input variables and the output response quantities is determined. This section fits the 4th-order Hermite polynomial and obtains its correlation coefficients, as shown in Table 4. Taking the arch settlement as an example, the prediction model is shown in Eq. (6):

$$\begin{aligned} & {F_p}(\zeta )= - 3.15 \times {10^{ - 2}}{\Gamma _0} - \sum\limits_{{{i_1}=1}}^{n} {3.14 \times {{10}^{ - 3}}{\Gamma _1}({\zeta _{{i_1}}})} - \sum\limits_{{{i_1}=1}}^{n} {\sum\limits_{{{i_2}=1}}^{n} {7.7 \times {{10}^{ - 7}}{\Gamma _2}({\zeta _{{i_1}}},{\zeta _{{i_2}}})} } \\ & + \cdots +\sum\limits_{{{i_1}=1}}^{n} {\sum\limits_{{{i_2}=1}}^{{{i_1}}} {\sum\limits_{{{i_3}=1}}^{{{i_2}}} { \cdots - \sum\limits_{{{i_n}=1}}^{{{i_{{\text{n-}}1}}}} {1.01 \times {{10}^{ - 5}}{\Gamma _n}({\zeta _{{i_1}}},{\zeta _{{i_2}}}, \cdots ,{\zeta _{{i_n}}})} } } } \\ \end{aligned}$$
(6)
Table 4 4th order Hermite polynomial coefficients for different monitoring characteristic parameters.
Full size table

To improve the accuracy of non-invasive stochastic finite element method for tunnel reliability calculation, the sampling times were analyzed. As shown in Fig. 9, taking the vault settlement as an example, when the sampling times are more significant than 105, the failure probability of the tunnel surrounding rock fluctuates very little. Therefore, to ensure the sampling accuracy, the sampling times selected in this paper are 106. This paper verifies the accuracy of the non-invasive random response surface method using the Monte Carlo method (MCS)50. Table 5 gives the computational results obtained using Hermite polynomials to calculate a sample of 1 million groups versus those obtained by direct Monte Carlo sampling substitution into the model. The results of both calculations can be found to be closer with less error. Still, the direct Monte Carlo method takes several times as long to calculate with far fewer arrays than with Hermite polynomials. The higher the order of the Hermite polynomial, the greater the goodness of fit R2 and the better the fit, demonstrating the feasibility and accuracy of this method. Moreover, the number of arrays calculated by the Hermite polynomial is vast, which can fully consider the parameter variability of rock and soil, making it more suitable for the actual construction conditions. Thus, compared with the traditional Monte Carlo method, the non-invasive stochastic finite element method based on secondary development can significantly improve computational efficiency and simplify computational steps while ensuring computational accuracy, further demonstrating the accuracy and effectiveness of this method.

Table 5 Reliability of deformation monitoring indicators.
Full size table
Fig. 9
figure 9

Convergence verification of sampling time.

Full size image

The probability density function of the output response is shown in Fig. 10. Taking Fig. 10a as an example, the deviation of the simulation results of Hermite polynomial at order 2, 3, and 4 is tiny, and the trend of the probability density function curve is the same. The height of order 3 and 4 curves coincide, and the failure probability of arch crown is 20.94%, 20.16%, and 20.02%, respectively. The most unfavorable deformation is 70.2 mm, 81.8 mm, and 92.8 mm, respectively. It can be seen that the failure probability of vault settlement is large, and the failure probability decreases with the increase of polynomial order, but the value of extreme cases increases. Therefore, it is necessary to strengthen the monitoring of the vault during construction and to support it in time to avoid collapse.

As can be seen from the above calculation analysis, compared with the direct Monte Carlo method, the Hermite polynomial surrogate model obtained through non-invasive stochastic finite element method fitting not only ensures calculation accuracy but also greatly improves calculation efficiency in solving tunnel deformation reliability. The non-invasive stochastic finite element method achieves the decoupling effect between stochastic finite element analysis and reliability analysis, which can effectively solve the problem of soil parameter variability and uncertainty in geotechnical engineering and provide an effective way to solve the reliability of geotechnical engineering. This article simplifies the establishment of excavation tunnel models to explore the feasibility and efficiency of the method. However, in practical engineering, the construction geological conditions are complex and variable. In the future, more detailed and highly simulated excavation models can be established for specific tunnel engineering to obtain more realistic and accurate results.

Fig. 10
figure 10

Probability density function of the maximum value of the deformation displacement.

Full size image

Impact of excavation methods on tunnel reliability

To study the influence of the tunnel excavation method on the reliability of the tunnel, a three-dimensional numerical model with different excavation methods was developed for calculation and analysis. Based on the above double wall heading method, the ring retaining core soil method and the single wall heading method are selected to establish the tunnel excavation model. Except for the excavation method, the other parameters are the same. In order to further study the influence of different excavation methods on tunnel reliability, the non-invasive finite element method was used to calculate the failure probability of each index. The tunnel excavation displacement clouds are shown in Figs. 11 and 12. The deformation monitoring indexes obtained by the annular retained core soil method, the single sidewall guide pit method, and the double sidewall guide pit method are summarized in Table 6; The corresponding failure probability of each index is shown in Table 7.

From the analysis in Table 6, it can be seen that the comprehensive horizontal displacement, due to the bias of the portal project, has a significant deformation of the left spandrel. According to the deformation monitoring data under different excavation methods, the double wall heading method has the best effect on deformation control, and the maximum horizontal displacement is 20.5 mm. Based on the horizontal convergence under different excavation methods, it can be seen that the annular retained core soil method can better control the horizontal convergence. In terms of maximum deformation vault settlement, the double sidewall guide pit method (25.3 mm) < the single sidewall guide pit method (30.2 mm) < the annular retained core soil method (33.6 mm). By analyzing the failure probability of indexes under different excavation methods (Table 7), the failure probability of vault, left arch shoulder and ground surface of the double sidewall guide pit method is the lowest, which is 20.02%, 4.66%, and 0.15%. The likelihood of horizontal convergence failure for the annular retained core soil method is 0%. Through analysis: (1) The single sidewall pit guide method and the double sidewall pit guide method are set up with temporary support, which bears a large part of the surrounding rock pressure during construction and produces large deformation, so the horizontal convergence of the left and right guide pits are larger. (2) The tunnel surrounding rock deformation is disturbed by the excavation; the double sidewall guide pit method of excavation support makes the tunnel structure less vertically deformed and has better stability. Therefore, in the actual construction, when the surrounding rock of the tunnel is weak and has the geological characteristics of shallow buried bias, the double side heading method with a better control effect can be selected for construction to ensure the overall safety of the tunnel.

Fig. 11
figure 11

Circular core retention soil method.

Full size image
Fig. 12
figure 12

Single sidewall pit guide method.

Full size image
Table 6 Displacement of key points of deformation monitoring indicators under different excavation methods.
Full size table
Table 7 Failure probability of deformation monitoring index under different excavation methods.
Full size table

Influence of stratigraphic parameters on tunnel reliability

Considering that the strata through which the tunnel passes have prominent upper soft and lower complex characteristics, and as shown from the parameter sensitivity analysis above, the parameter sensitivity of the sandy clay layer is higher. In comparison, the parameter sensitivity of the complete weathered migmatitic granite layer is lower. To further explore the impact of different geological parameters on the probability of tunnel engineering failure, this paper sets the six parameters of the two strata as random variables, and only addes the three geotechnical parameters of the sandy clay strata as random variables for comparative analysis to calculate the reliability of each single failure mode and the reliability of the tunnel system. A non-invasive stochastic finite element analysis is carried out for each of these two cases, and the probability of failure is calculated using the fitted polynomial agent model. In this section, only the 4th-order agent model is chosen to simplify the calculation. The failure probabilities are shown in Table 7, where the failure probability of the functional function is selected as the result of the calculation under the log-normal distribution51, and the failure probability of the tunnel system is chosen as the result of the probabilistic network estimation counting method52.

Table 8 Tunnel function failure probability and system failure probability.
Full size table

Based on the results of the calculations in Table 8, the probability of failure of the monitoring indicators and the probability of failure of the tunnel system when the random variable is six geotechnical parameters and when the random variable is three geotechnical parameters are compared, both of which vary less. Most of the deformation monitoring indexes in the function are concentrated in the sandy clay layer, so the deformation law is mainly affected by the spatial variability of rock and soil parameters in the sandy clay layer. The geotechnical parameters of the complete weathering mixed granite meet the strength requirements of tunnel construction better than those of the sandy clay layer, and the geotechnical spatial variability within a specific range does not cause large changes in the deformation of the tunnel envelope during the construction process. Therefore, the reliability of such road tunnels with soft upper and hard lower strata is mainly determined by the geotechnical parameters of the upper soft strata. The influence of the spatial variability of the geotechnical parameters of the lower hard strata on the reliability of the tunnels may be left out of the study to reduce the volume of calculations.

Conclusion

In this paper, a non-invasive stochastic finite element method is used to quantitatively assess the probability of failure of excavation in the cavity section of a shallow buried biased tunnel using the Wenbishan Tunnel in Puyan, Fujian as a background project, with the following main findings:

  1. 1.

    ABAQUS finite element software was used for model deterministic analysis and parameter sensitivity impact analysis, and it was found that the error between the simulated numerical simulation results and monitoring data is within the allowable range, which can be applied to practical engineering. Subsequently, the secondary development is based on Python, and the corresponding interface program is created to obtain the output response. By fitting Hermite polynomials to the explicit limit state equation, and an efficient calculation method for quantifying the failure probability of tunnel excavation is established, which realizes the non-invasive stochastic finite element analysis of highway tunnel engineering deformation.

  2. 2.

    Hermite polynomials of different orders were used to calculate the reliability of road tunnel deformation and compared with the results obtained by the direct Monte Carlo method (MCS). It is found that the fourth-order Hermite polynomial is the closest to the MCS method and is the optimal method. The choice of order can, of course, be calculated and analyzed according to the specific project. At the same time, this method was used to reveal the influence of tunnel parameter distribution types and combinations, as well as tunnel design control parameters on tunnel reliability.

  3. 3.

    When the annular retained core soil method, single sidewall guide pit method, and double sidewall guide pit method are used, respectively, the maximum displacement monitoring points at the entrance section of the Wenbishan tunnel are all vault settlement. Their displacements are 33.6 mm, 30.2 mm, and 25.3 mm respectively, and the failure probability is 36.11%, 28.03%, and 20.02% respectively. Thus, from the point of view of the stability of the surrounding rock, the double sidewall guide pit method is the most effective in controlling the deformation of the surrounding rock and is more suitable for shallow buried biased tunnels under soft surrounding rock.