Inversion of the temperature dependence of thermal conductivity of hcp iron under high pressure

Abstract

Investigating how the thermal transport properties of iron change under extremely high pressure and temperature conditions, such as those found in the Earth’s core, is a major experimental challenge. Over the past decade, there has been a great deal of discussion and debate surrounding the thermal conductivity of the iron-based Earth’s core and its thermal evolution. One reason for this may be the variability in the experimentally obtained thermal conductivity of iron at high pressures and temperatures. In this study, we present the experimental results of measuring the thermal conductivity of hexagonal-closed-pack (hcp) iron over a wide pressure-temperature range up to 176 GPa and 2900 K using the pulsed light heating thermoreflectance technique in a laser-heated diamond anvil cell. Our findings indicate that the temperature derivative of the thermal conductivity of hcp iron undergoes a change from negative to positive above 74 GPa, potentially making hcp iron highly conductive at conditions similar to those observed in the Earth’s core. This observation represents a notable example of a phenomenon where pressure appears to influence the sign of the temperature derivative of the thermal conductivity of an isostructural metal.

Introduction

Highly compressed iron (Fe) is a major component of the metallic core of terrestrial bodies such as the Earth. Hexagonal-closed-pack (hcp) Fe stabilizes above 13 GPa and is thought to be a major component of the Earth’s inner core¹. In addition, hcp Fe is the solid phase just below the melting point of Fe under the outer core conditions^2,3. Therefore, the high pressure (P)-temperature (T) thermophysics of hcp Fe is of great importance for understanding the thermal evolution and dynamics occurring in the Earth’s core. A recent argument for the high thermal conductivity of the Earth’s core, which first arose from ab initio studies^4,5, requires experimental data revealing the P–T dependence of the thermal conductivity of Fe.

Thermal conductivity is a thermophysical property for which many in-situ high-P measurement techniques have been developed⁶. However, direct measurement of the thermal conductivity of Fe under high-P–T conditions is still rare and limited to experiments using a laser-heated diamond anvil cell (DAC)^{7,8,9,10,11,12}. Alternatively, after determining the electrical conductivity (σ) (the reciprocal of the electrical resistivity) of Fe by various high-pressure experiments, the Wiedemann-Franz law is widely used to obtain the electronic thermal conductivity (κ_el):

$${\kappa}_{\text{el}}=\sigma\,LT,$$

(1)

where L is the Lorenz number. However, it is debatable whether this empirical law is applicable in extreme conditions such as the Earth’s core (e.g., refs.^13,14). In fact, the value of L obtained from ab initio calculations of the electrical and thermal conductivity of hcp Fe does not agree with the ideal value (i.e., Sommerfeld value, L₀) of 2.45 × 10⁻⁸ WΩ/K², and temperature and pressure dependence have also been reported^{15,16,17,18,19}.

One method for determining the thermal conductivity of Fe at high P and T is numerical modeling of the temperature structure generated by steady-state heating of Fe in a laser-heated DAC^7,10,12. In 2016, Konôpková et al.¹¹ used an advanced method of rapid thermal radiation detection from the Fe sample in a laser-heated DAC with rapid heating using a pulsed laser and estimated its thermal conductivity in combination with finite element modeling (FEM). Although the thermal conductivity of Fe has been measured under high P–T conditions using these methods, they have the disadvantages of large uncertainty in the measurement temperature conditions and the inability to determine the thermal conductivity near room temperature. Therefore, these methods cannot accurately determine the temperature dependence of the thermal conductivity of Fe.

A thermoreflectance (TR) technique has also been applied to Fe in a DAC to constrain its thermal conductivity at high pressures^8,9. A combination of the TR and the laser-heated DAC techniques has made it possible to determine the thermal conductivity of materials from 300 K to high temperatures relevant to Earth’s core conditions²⁰. In this study, we have determined the high P–T thermal diffusivity (and thermal conductivity) of hcp Fe using a combined technique of the pulsed light heating transient TR and the laser-heated DAC^8,20, which allowed us to determine the thermal conductivity of hcp Fe up to the Mbar pressure regime (up to 176 GPa) from 300 K to several thousand K with about 10% temperature uncertainty (Fig. 1; Table 1).

Fig. 1

P–T conditions of thermal conductivity measurements of Fe. Circles and downward triangles show the conditions. Upward triangles show our previous data⁸. Stars, squares are the pressure points where thermal conductivity of hcp Fe at 300 K were measured by time-domain TR method⁹. Red bars indicate P–T conditions where the pulsed heating method¹¹. Phase boundaries are from the literature^2,52.

Table 1 Experimental pressure (P), temperature (T), heat diffusion time (τ), sample thickness after correction (d), thermal diffusivity (D), density (ρ), isobaric heat capacity (C_P), and thermal conductivity (κ) of Fe.

Methods

Materials and high-pressure generation

The sample was Fe foil (99.999% purity), the same as that used in our previous studies^8,13,21,22. We used symmetrical-type DACs with 90, 120, 200, and 300-µm culet diamond anvils (Fig. 2). Al₂O₃, KCl, and NaCl were used as pressure media and thermal insulators of the Fe sample (Table 1). Pre-indented rhenium (Re) was used as gasket material, the initial thickness of which was 20 ~ 50 μm depending on the culet size. Using a UV laser, a hole 30 ~ 100 μm in diameter (~ 1/3 of the culet size) was drilled in the center of the gasket to serve as the sample chamber. The iron foil sample was cut with a razor to a size slightly smaller than the diameter of the sample chamber and loaded in the sample chamber along with the pressure medium.

Fig. 2

Schematic drawing of the sample configuration for the high P–T thermoreflectance measurement in a DAC. P.M. indicates pressure medium, which also serves as thermal insulator against diamond anvils.

The pulsed light heating thermoreflectance technique in an LHDAC

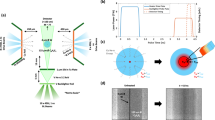
The in-situ high P–T transient TR method provides the thermal diffusion time (τ) through the Fe sample along the thickness direction (Fig. 2). We generate a steady state temperature by using high power continuous wave (CW) laser beams irradiated both sides of the sample in an LHDAC. During operation of the LHDAC system, a pulsed laser beam (pump laser) irradiated the sample to make a temperature gradient inside the sample. To detect the transient temperature, caused by heat diffusion from the heated surface to the opposite, we irradiate the opposite side of the sample with a CW laser (probe laser) beam to observe reflectivity changes due to the temperature change in the sample (i.e., thermoreflectance). The high-power CW laser beams are focused by the objective lens with a diameter of approximately 25 ~ 30 μm. The laser spot sizes of the pump and probe lasers are 25 ~ 30 μm and < 5 μm, respectively. The alignment of the pump and the probe lasers was roughly aligned in the transparent part of the sample chamber (pressure medium only) and then fine-tuned to maximize the TR signal intensity. The reflected light intensity of the CW probe laser is detected by a photodiode and its time variation is recorded by an oscilloscope to obtain a time-resolved TR signal. The other details of the optical system can be found in our previous study⁸. The temperature of the Fe sample during CW infrared laser heating was determined from the thermal radiation spectrum between 640 nm and 740 nm to fit Planck’s law. The thermal radiation spectra from the heated sample were collected from single side. The losses from the optical system for each wavelength are calibrated using a halogen lamp. The timing of the temperature measurement is a few seconds after changing the power of the CW infrared laser irradiating the LHDAC. Exposure time for the thermal radiation collection is 0.5 ~ 5 s, depending on temperature (i.e., the intensity of thermal radiation). A few seconds later, the TR signal was recorded. During the temperature measurement, both the TR pump and probe lasers irradiate the sample. We focused our measurements on a single point where the sample was most shiny during a separate run.

To determine τ through the sample, the obtained transient temperature (i.e., intensity of the reflected probe laser) curves were fitted by a theoretical curve based on the one-dimensional (1D) heat conduction equation for the Fe thickness direction by a pulse heating²³ (Fig. 3):

$$I\left(t\right)=\overline{I}\sqrt{\frac{\tau}{\pi\,t}}\sum\limits_{n=0}^{\infty}{\gamma}^{2n}\text{exp}\left[-\frac{{\left(2n+1\right)}^{2}}{4}\frac{\tau}{t}\right],$$

(2)

where I(t) is the intensity of the reflected probe laser which is lineally proportional to temperature, $\overline{I}$ is a constant, t is time, and γ is a fitting parameter describing the heat effusion to the pressure medium. After the peak time of the transient TR signal, three-dimensional (3D) temperature dissipation from the sample to the surroundings is dominant, so the fitting range of the 1D model is limited to a time slightly past the peak time. The variation of τ with temperature is a direct indication of the temperature dependence of the thermal diffusivity (D), which can be expressed as follows:

$$D = d^{2} /\tau ,$$

(3)

where d is the thickness of the sample at high pressure. The thermal conductivity is a function of D, the density (ρ), and the isobaric heat capacity (C_P):

$$\kappa = D \rho C_{P} .$$

(4)

Fig. 3

The transient TR curves obtained in (a) Run #2 at 85 GPa and 3320 K, (b) Run #3 at 129 GPa and 300 K and at 146 GPa and 2960 K. The black lines are raw data. Yellow and blue curves indicate 1D and 3D thermal diffusion analysis models, respectively. Solid and broken lines are theoretical transient TR curves in the cases of the sample thermal conductivity of 95 W/m/K and 132 W/m/K, respectively. The red lines are the fitting results via Eq. (2).

To validate the 1D heat conduction equation (Eq. 2) used in the data analysis of our TR results, we also performed a finite difference temperature response simulation in a quasi-3D cylindrical coordinate system that accounts for the axial heat flow in the sample chamber of an LHDAC (see Supplementary Information for details). We tested whether a similar transient TR curve could be obtained using the thermal diffusion time (i.e., thermal conductivity) inside the Fe sample obtained using Eq. 2. Based on the more complex quasi-3D thermal diffusion simulations, the 1D thermal diffusion model (Eq. 2) used in previous studies^{8,20,23,24,25,26,27,28,29,30,31} is also able to represent the region of the transient TR signal increase corresponding to heat diffusion in the sample (Fig. 3a). However, since the heat after passing through the sample diffuses toward more external materials such as the pressure medium, gasket, and anvils, the 3D model can more accurately represent the transient TR signal decrease. Therefore, the transient TR curve is more sensitive to the thermal conductivity of the sample than the choice of 1D or 3D model. In other words, factors not considered in the 1D model, such as radial thermal diffusion in the sample chamber configuration in this study, do not affect the thermal diffusion time analysis.

We performed the synchrotron X-ray diffraction (XRD) measurements on the Fe samples before and after the TR experiments at BL10XU, SPring-8 (Fig. 4a). The ρ was determined from the lattice volume of hcp Fe obtained from these measurements, and the P and C_Pwere determined from its equation of state³² and the Debye approximation. The geometry and chemistry of the Fe samples were checked after recovery to ambient conditions (Fig. 4b). The thermal pressure generated by a CW laser heating during high P–T thermal conductivity measurements was reported as 5%/1000 K^33,34.

Fig. 4

(a) XRD patterns of Fe sample at Run #3 at in-situ high pressure before and after TR measurement. (b) A region of the recovered Fe sample performed the TR measurements shown as a SEM image (upper) and an EDS elemental map (lower).

Determination of high P–T thermal conductivity

In the three runs at 40, 85, and 146 GPa, the sample thickness was determined from the recovered samples. A cross section of the pump and probe laser-focused portion of a sample, parallel to a compression axis, was obtained by milling with a focused Ga ion beam (FIB), and we measured the thickness of the recovered sample under a scanning electron microscope (SEM) (Fig. 4b). The thickness of the sample was determined from the measured sample thickness with pressure correction, assuming elastic deformation during decompression based on the equation of state (EOS) of Fe³². We examined the elemental distributions (Fe, Cl, and C) in the cross section with the energy dispersive spectroscopy system, and confirmed the absence of chemical contamination and laser thinning in the Fe sample (Fig. 4b). In the other three runs at 149, 151, and 176 GPa, we could not recover the samples due to severe deformation of the Fe sample during decompression, which was confirmed under an optical microscope. Therefore, we determined the high P–T thermal conductivity from the high-P/room-T thermal conductivity (Fig. 5) and the rate of τ at 300 K and τ at high T (⊿τ), taking into account the temperature effect on density and C_P:

$$\kappa\left(P,T\right)=\frac{\kappa(P,300\,K)\varDelta\rho\varDelta{C}_{P}}{\varDelta\tau}.$$

(5)

Thus, although not a direct estimate of the absolute value of the thermal conductivity of the hcp Fe samples in these three runs, the temperature dependence is directly observed from the TR method.

Fig. 5

Thermal conductivity of Fe at 300 K as a function of pressure. Circles show the present results. Triangle shows our previous datum⁸. Diamond indicates the thermal conductivity of Fe at ambient conditions³⁷. Squares and stars show the thermal conductivity of Fe obtained by means of the time-domain thermoreflectance technique in a DAC at 300 K⁹. Red line is the fitting curve of our data via Eq. (9).

The thermal conductivity (κ) is associated with the heat diffusion time (τ), the thickness (d), the density (ρ), and the isobaric heat capacity (C_P) of the sample. Therefore, the uncertainties (u) of each value propagate to that of the thermal conductivity as follows:

$${u}_{\kappa}=\sqrt{{\left(2{u}_{d}\right)}^{2}+{u}_{\tau}^{2}+{u}_{\rho}^{2}+{u}_{C_{P}}^{2}}.$$

(6)

The largest uncertainty factor in this study is the thickness of the sample. The standard deviation of the thickness around the measured point determined from the SEM image is approximately 10%. The uncertainty of the heat diffusion time u_τ was estimated from a fitting error of the transient temperature signals by Eq. (2). The error primarily arose from noise and distortion of the signal, but it did not exceed 5%. The uncertainty of the density u_ρ was calculated from the error of lattice parameter obtained by the XRD measurements, which was negligibly small. The values of the heat capacity were derived from the Debye approximation, the validity of which is difficult to examine. Therefore, we did not consider u_Cp here. The uncertainty of the values for each measurement is noted in Table 1.

Estimating the temperature uncertainty in the sample chamber

There are two main sources of uncertainty in this measurement. The first is related to the thermal radiation measurement u_rad, and the second is related to the heterogeneity of the sample temperature u_ΔT. This is caused by the Gaussian shape of the laser energy distribution and the heat dissipation from the sample to the surrounding materials. We estimated that the combined standard uncertainty u_T of the above factors may be approximately 10%, according to the following relationship:

$${u}_{T}=\sqrt{{u}_{\text{rad}}^{2}+{u}_{\varDelta\,T}^{2}}.$$

(7)

It was decided that the 10% u_T should be applied to all the data presented in this study. In order to determine the u_rad, we first derived the standard deviation of the residuals between the measured radiation spectrum and the best-fit curve, as illustrated in Fig. 6a. We considered the maximum distribution of the Planck’s law fit curve within the standard deviation to be u_rad, which was typically 5% for the measured temperatures.

Fig. 6

Temperature structure in the sample chamber of an LHDAC. (a) Representative thermal radiation spectrum from CW laser heated sample. Red curve shows Planck function at 2960 K. (b) Temperature distribution of sample during a CW laser heating based on FEM. Graph of the distribution in (c) the Z direction of the heating center and (d) surface of the sample. Solid green line represents the diameter of the TR probe laser (< 5 μm). Broken one is twice as wide as it considering mis-alignment of lasers.

We used a finite element method (FEM, COMSOL Multiphysics) to simulate a typical temperature distribution for the Fe sample and solve the steady-state heat equation to estimate the heterogeneity of the sample temperature u_ΔT during CW laser heating. Figure 6b shows the sample structure and the boundary conditions used for the FEM. The diameter and thickness of the Fe disk were 30 μm and 3.4 μm, respectively. The Fe disk was surrounded by KCl with a diameter and thickness of 40 μm and 5 μm, respectively. We fixed the temperature of the KCl/diamond interfaces at 300 K. In contrast, we set the interfaces at the KCl/Re gasket as an adiabatic condition. A heat source with a Gaussian distribution was applied to the central axis of the Fe disk from both sides. The 1/e radius of the Gaussian heat source was precisely 20 μm. Based on our measurement result at 146 GPa, we assumed a thermal conductivity of 180 W/m/K for Fe. For KCl, we assumed 5.5 W/m/K for the B2 phase in the FEM calculation. We used the EOS and its first and second derivatives for the B2 KCl³⁵ and the Leibfried-Schlomann theory to estimate the following:

$$\kappa={\kappa}_{0}{\left(\frac{\rho}{{\rho}_{0}}\right)}^{g}{\left(\frac{{T}_{0}}{T}\right)}^{m},$$

(8)

where κ₀ = 13.7 W/m/K at 19 GPa and 300 K, g = 3.75 according to McGuire et al.³⁶ and m = 1.

Figure 6c shows the simulated temperature distribution inside the Fe-disk along with the z-axis (i.e., the compression axis). The temperature difference between the surface and the center is precisely 30 K, which is 1% of the highest temperature. Figure 6d shows the surface temperature of the Fe-disk along the radial direction. We estimate that the effect of the temperature gradient in the radial direction is about 8% of the measured temperature. This is based on the assumption that the misalignment of the TR probe laser is twice its diameter.

Results

Figure 5 shows the thermal conductivity of Fe at high P and 300 K determined in this study and in previous experiments^8,9,37. Note that there is no theoretically determined thermal conductivity of Fe at high pressures and 300 K. The thermal conductivity of body-centered cubic (bcc) Fe (α-Fe) at ambient conditions is about 80 W/m/K (e.g., ref.³⁷). The thermal conductivity of Fe increases with pressure, but decreases dramatically at about 13 GPa due to the structural transition from the bcc to the hcp phase. After complete transformation to the hcp phase, the thermal conductivity increases again with pressure. Such a pressure response of the thermal conductivity of Fe has also been observed in electrical resistivity (resistance) measurements (e.g., ref²¹). Although our results and those of Hsieh et al.⁹, both using the TR method, are not in perfect agreement, they are within the margin of error. Since information about the sample thickness at high pressure is important in determining the thermal conductivity using the TR method, the effect of non-isotropic sample deformation during compression/decompression of the sample in the DAC, as claimed by Lobanov and Geballe³⁸, may be responsible for the difference in thermal conductivity at high pressures and 300 K shown in Fig. 5. A model of the pressure derivative of the thermal conductivity (κ) is proposed as follows^39,40:

$$\frac{1}{\kappa}\frac{\partial\kappa}{\partial\,P}=\frac{2\gamma-1/3}{{K}_{T}},$$

(9)

where γ is the Grüneisen parameter and ${K}_{T}$is the isothermal bulk modulus. Using these parameters for hcp Fe from its EOS³² and our thermal conductivity value of 129 GPa as an anchor point, the rest of our data is in good agreement with the proposed model (red curve in Fig. 5).

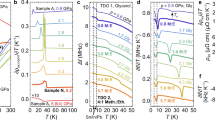
Figure 7 shows the thermal conductivities obtained for hcp Fe at high P–T conditions, which are compared with previous studies^{7,8,9,10,11,12,15,18,19}. At 1 bar, Fe undergoes a series of structural and magnetic transitions with temperature. The mobility of the free electrons should be influenced by the density, the coordination number of the Fe atoms, and a magnetic state. Above room temperature, the thermal conductivity of bcc Fe has a negative temperature dependence, while that of face-centered cubic (fcc) Fe and liquid Fe has a positive temperature dependence (Fig. 7a). Many previous studies have predicted that the thermal conductivity of hcp Fe, like that of bcc Fe, has a negative temperature dependence^7,10,11,12. Indeed, our experimental results (this study and ref⁸). measured around 45 GPa confirm this (Fig. 7b). In contrast to the previous studies using the steady-state heating method including radial T-gradient analyses^7,10,11,12, our TR method provided a clear characterization of the temperature dependence of the thermal conductivity of hcp Fe at high pressures, since the thermal conductivity can be measured over a wide temperature range from 300 K onwards.

Fig. 7

Temperature dependence of the thermal conductivity of Fe at quasi-isobaric conditions of (a) 0 GPa, (b) 37 ~ 53 GPa, (c) 74 ~ 85 GPa, and (d)129 ~ 146 GPa. Plus symbol, solid Fe at 1 bar³⁷; cross, liquid Fe at 1 bar⁵³; circle, this study; triangle, hcp Fe (TR)⁸; smaller pink circle, solid Fe (steady-state heating)¹²; black pentagon, solid Fe (steady-state heating)¹⁰; grey area, solid Fe (radial T gradient)⁷; gray hexagon, solid Fe (flash-heating)¹¹; asterisk, hcp Fe (DFT calc.)¹⁸; purple heptagon, hcp Fe (FT-DFT-MD calc.)¹⁵; right-pointed triangle, hcp Fe considering electron–phonon scattering (the density functional perturbation theory + dynamical mean field theory (DFPT + DMFT) simulation)¹⁹; left-pointed triangle, hcp Fe considering electron–phonon and electron–electron scattering (DFPT + DMFT calc.)¹⁹. Vertical dotted lines in (a) indicate the phase boundaries of bcc (α Fe)-fcc (γ Fe) and bcc’ (δ Fe)-liquid. Color curves are best fitting of Eq. (10) to the present results, and the width of the band is 1σ.

Above 74 GPa, we observed the inversion of the temperature dependence of the thermal conductivity of hcp Fe: the thermal conductivity of hcp Fe increases with increasing temperature (Figs. 7c and d and 8). It should be emphasized that although there is uncertainty in the absolute value of the thermal conductivity due to the lack of sample thickness measurements in experiments above 137 GPa, its temperature dependence is direct information obtained from our TR measurements. To date, no such pressure-induced reversal of the sign of the temperature dependence of thermal conductivity has been observed for any metal. The present results show higher thermal conductivity than previous ones using the steady-state^7,10,12and flash¹¹heating techniques in a laser-heated DAC, but are in good agreement with recent ab initio calculations^15,18. These previous experimental studies may underestimate the thermal conductivity of Fe due to the partial melting and/or impurity scattering by carbon contamination from diamond anvils during laser heating. On the other hand, we provide pieces of evidence for the absence of phase change and impurity contamination in the hcp Fe samples using XRD, SEM, and EDS analyses (Fig. 4). We fit our data up to 176 GPa with the following empirical function derived from the temperature dependent electrical conductivity and the Wiedemann-Franz law (Eq. 1) with a constant Lorenz number (colored lines in Figs. 7b–d and 8):

$$\kappa=\text{A}{T}^{1-{\upalpha}},$$

(10)

where A and α are constant (Table 2). Even allowing for errors in the value of α obtained from the fitting, it has been shown that the temperature dependence of the thermal conductivity is positive in experiments above 85 GPa. As a result of the fitting, we determined κ_{hcp Fe} at 146 GPa and 3700 K, similar to the conditions in the outermost core of the Earth, to be 184 ± 29 W/m/K (Fig. 7d). The uncertainty of the extrapolation is 1σ between the measured values and the best fit. The high P–T TR method used here provided the total thermal conductivity of hcp Fe, including electron-phonon, electron-electron, and phonon–phonon correlations. Our results are in agreement with theoretical calculations considering only electron-phonon scattering, rather than a combination of electron-phonon and electron–electron correlations¹⁹, indicating that the effect of electron correlations on the thermal conductivity of Fe under core conditions is small due to an increased thermal disorder in the Fe lattice, as proposed by Pourouvskii et al.¹⁶ (Fig. 7c, d).

Fig. 8

Temperature dependence of the thermal conductivity of Fe at quasi-isobaric conditions of (a) 137 ~ 151 GPa, (b)156 ~ 176 GPa (Run 4 ~ 7). Magenta heptagon symbols indicate the thermal conductivity of hcp Fe determined by FT-DFT-MD calculation¹⁵.

Table 2 Fitting parameters of Eq. (10).

Discussion

The key finding of this study is that the thermal conductivity of hcp Fe changes to a positive temperature dependence above 74 GPa (Figs. 7, 8 and 9), which has not been observed in the previous experimental and theoretical studies^{7,8,10,11,15,17,18,19}. Furthermore, this behavior has never been confirmed for any pure isostructural metal. Pure metals that exhibit a positive temperature dependence of the thermal conductivity even at 1 bar are rare (platinum, palladium, and several rare earth elements)³⁷. Platinum (a paramagnetic, closed-packed structure) is expected to have similar conduction properties to hcp Fe due to its similar electronic structure⁴¹. Only platinum has been confirmed by experiments and theoretical calculations to exhibit a positive temperature dependence of thermal conductivity at high pressures above 100 GPa^8,20,42,43. The Wiedemann–Franz law (Eq. 1) predicts the positive linear temperature dependence of the electronic thermal conductivity when the electrical conductivity and the Lorenz number are independent of temperature. Under the experimental conditions of this study, the electrical conductivity of hcp Fe was found to decrease with temperature, but the rate of decrease of the electrical conductivity with temperature decreases with pressure^13,44. On the other hand, ab initio calculations indicated that the Lorenz number has a positive temperature dependence^15,17,18. Therefore, according to the Wiedemann–Franz law, the thermal conductivity of hcp Fe is expected to increase with temperature. This is similar to the behavior of its analog, platinum^{8,20,41,42,43}.

Fig. 9

(κ_{hcp Fe} (P, T))/(κ_{hcp Fe} (P, 300 K)) at each experimental pressure. Solid lines indicate Runs in which we determined κ_{hcp Fe} (P,T) directly from the thickness of our samples via Eqs. (2) and (3) (Fig. 5). Broken lines show Runs in which we determined κ_{hcp Fe} (P,T) using the reference value of κ_{hcp Fe} (P,300 K) via Eq. (10).

Then why does the thermal conductivity of hcp Fe decrease with temperature below 74 GPa (Fig. 7b)? Although bcc Fe loses ferromagnetism during the phase transition to hcp Fe, it has been reported that hcp Fe retains a local magnetic moment without long-range order (the so-called “spin smectic state”) up to about 70 GPa⁴⁵, and this residual local magnetic moment may act in addition to electron-phonon scattering to reduce the thermal conductivity with increasing temperature. We consider the elimination of the “spin smectic state” of hcp Fe proposed by Lebert et al.⁴⁵ to be the reason for the sign reversal of the temperature dependence of the thermal conductivity of hcp Fe above 74 GPa. Pozzo et al.¹⁷ performed density functional theory (DFT) calculations with the Kubo–Greenwood formulation to determine the thermal conductivity of hcp Fe under the conditions of the Earth’s inner core (329 ~ 365 GPa, 5500 ~ 6350 K) and showed a positive P–T dependence that is harmonic to the one found in this study above 74 GPa. Recently, Kleinschmidt et al.¹⁵ have also computed the thermal conductivity of hcp Fe using a finite-temperature DFT combined with molecular dynamics (FT-DFT-MD) simulation. They report a positive temperature dependence of the thermal conductivity of hcp Fe from ~ 20 GPa to ~ 350 GPa. However, in these ab initio studies^15,17 only the spin-degenerate version of DFT was used. In other words, the effects of magnetism are not taken into account.

Based on the present results, we determined the thermal conductivity of hcp Fe under the conditions of the top of the Earth’s outer core to be 184 ± 29 W/m/K (Fig. 7d). On the other hand, Ohta et al.¹³ experimentally determined the electrical resistivity of hcp Fe under the same conditions to be 40.4 (+ 6.5/-9.7) µΩcm. These values give a Lorenz number of 2.01(± 0.70)×10⁻⁸ WΩ/K². Note that we do not consider the effect of phonon–phonon conduction here, as it is expected to be much smaller than that of electron–phonon conduction (e.g., ref¹⁸). In addition, as mentioned above, the effects of electron–electron scattering are negligible at these temperature and pressure conditions. The L₀ of 2.45 × 10⁻⁸ WΩ/K²that is based on the Fermi gas model is within the uncertainty of our estimate. Such an uncertainty of about 35% in the Lorenz number is mainly due to the thickness uncertainty of the Fe sample at high pressures in both thermal conductivity and electrical resistivity measurements (this study and refs^13,21). In-situ thickness measurements are therefore crucial for the accurate determination of Fe conductivities and hence the Lorenz number based on the Wiedemann–Franz law under the Earth’s core conditions. However, the thermal conductivity of hcp Fe above 150 W/m/K under the conditions of the Earth’s core shown in this study is certainly much higher than the results of previous experimental studies^11,12, even taking into account errors (Fig. 7d). The Earth’s inner core is less dense than pure hcp Fe, indicating that it is alloyed with some lighter elements (e.g., refs^46,47). The addition of light element impurities is expected to reduce the electrical and thermal conductivities. However, since the solid solution of light elements tends to weaken the temperature dependence of the electrical resistivity of Fe (e.g., ref⁴⁸), it would not change the trend of the positive P–T dependence of the thermal conductivity of Fe as shown in this study when considered according to the Wiedemann–Franz law. Therefore, we argue that the thermal conductivity of Fe-light element alloys under Earth’s inner core conditions is as high as about 300 W/m/K as suggested by Pozzo et al.¹⁷. At such a high inner core thermal conductivity, the interior of the inner core is expected to be close to isothermal, and thus not in the thermal convection regime^17,49. The observed seismically anisotropic structure of the inner core would be produced by the azimuthal Lorentz force resulting from the Earth’s magnetic field^50,51.

In summary, we have determined the thermal conductivity of hcp Fe up to 176 GPa and 2860 K using the TR with a laser-heated DAC technique, which provides a new insight into the inversion of the temperature coefficient of the thermal conductivity above about 70 GPa. We believe that the temperature dependence of the thermal conductivity of hcp Fe becomes positive as a result of the increase in the Lorenz number with increasing temperature and the disappearance of the local magnetic moment in hcp Fe with increasing pressure⁴⁵. This is the first demonstration of a phenomenon where pressure changes the sign of the temperature derivative of the thermal conductivity of an isostructural metal. In addition, our measurements provide clear evidence for the high thermal conductivity of Fe in the conditions of the Earth’s core, confirming decade-old predictions^4,5,17,21.