A hybrid model of ARIMA and MLP with a Grasshopper optimization algorithm for time series forecasting of water quality

Abstract

Water quality monitoring of rivers is necessary in order to properly manage their basins so that steps can be taken to control the amount of pollutants and bring them to the allowable level. The ARIMA (autoregressive integrated moving average) model does not consider nonlinear patterns in modeling water quality components. Also, in modeling using the MLP (Multilayer Perceptrons) model, both linear and nonlinear pattern are not controlled equally. Therefore, in the present study, linear time series models (ARIMA), MLP model, and a hybrid model of MLP and ARIMA optimized by a Grasshopper optimization algorithm are used to predict water quality components in the statistical period of 2011–2019. In the proposed hybrid method, the ability of the ARIMA and the MLP model are exploited. Observational water quality data for forecasting time series in the hybrid method include dissolved oxygen, water temperature, and boron over 108 months. Since, the hybrid model is capable of realizing the nonlinear essence of complicated time series, it makes more reliable forecasts. In the hybrid model, the correlation coefficients between the observational data and the predicted values are 0.9 for dissolved oxygen, 0.91 for water temperature, and 0.91 for boron. To compare the three ARIMA, MLP, and hybrid models, the accuracy indices of each model are calculated. The results show that the hybrid model’s higher accuracy compared with the other two models.

Introduction

Predicting river water quality in order to properly manage the basin and better manage water resources is essential. By predicting the water quality of the river, the amount of pollutants can be controlled and brought to the allowable level to prevent a decrease in water quality in the future. Given that if water quality is poor, it has many negative effects, including on aquatic life and the surrounding ecosystem, so serious management is essential in this situation. Modeling and analyzing river water quality is also essential for water-related ecological decisions. Water quality forecasting is an important part of environmental monitoring. The methods utilized to forecast water quality are founded on a shallow model, so they cannot demonstrate much dependence throughout history, and the rate of false and negative notices in the use of water monitoring is probable to rise. Also, due to the linear and nonlinear features of time series data, the usage of linear time series models such as ARIMA can not be suitable for forecasting water quality data alone. The MLP model also can not control the linear and nonlinear features of the model alone. Therefore, in the current study, an ARIMA and MLP hybrid method with a Grasshopper optimization algorithm is presented.

Given that traditional forecasting methods cannot show the instability and nonlinearity of water quality well. Chen et al.¹ Performed the analysis of water quality prediction based on artificial neural network (ANNs) from three aspects. These three aspects are feedforward, recurrent, and hybrid architectures. They collected water quality variables by a sensor, followed by specialized experimental equipment. And then they used five different output strategies. The result shows the ability of models ANN in different modeling in lakes, rivers, wastewater treatment plants (WWTPs), reservoirs, streams and ponds.

Muhammad Shah et al.² To develop models used in accurate water quality forecasting that require high input parameters and incompatible datasets, provide a method that can be used to pre-process datasets and optimize inputs. They used an integrated neural fuzzy inference system to model EC and TDS in the Upper Indus River. According to the input optimization results, ${\text{Ca}}^{2+}$, ${\text{Na}}^{+}$, and ${\text{Cl}}^{-}$ are the most related inputs to be utilized for EC. Also for modeling TDS level ${\text{Mg}}^{2+}$, ${\text{SO}}_{4}^{2-}$, and ${\text{HCO}}_{3}^{-}$ were chosen. The optimum ANFIS models for the TDS and EC data exhibited R amounts of 0.92 and 0.91, and the RMSE (root mean square error) results of 30.6 µS/cm and 16.7 ppm. Aghel et al.³ studied the correlation between water quality components for instance TSS (total soluble solids), temperature, total hardness, EC, and alkalinity with water pH component, in the water reservoir of Kermanshah province. The required data were collected in 2015. Overall mean (training and experiment) relative error percentage, MAE, RMSE, correlation coefficient, and t-statistic acquired by the ANFIS model and model-proposed PSO less than 3.50, 11.60, 18.90, 0.95, and 0.38. The outcomes supply a useful process to estimating water quality parameters.

Kilinc et al.⁴ conducted an extensive examination of river flow data in the Meriç basin of Turkey, utilizing long-term daily records from 2001 to 2011. For the purpose of forecasting daily river flows, 80% of the dataset was allocated for the training phase, while the remaining 20% was reserved for testing. The findings indicate that the hybrid model yielded accurate and dependable predictions for daily river flow assessments in the Meriç basin. Hai et al.⁵ developed a distinctive hybrid model that integrates multivariate variational mode decomposition with locally weighted linear regression, presenting a novel approach for predicting biochemical oxygen demand in the Klang River, Malaysia. Further, the Hybrid Gradient Boosting Model was implemented in the Sakarya Basin, an area characterized by semi-arid climatic conditions in Turkey⁶. The newly developed hybrid model demonstrated superior performance compared to the benchmark models. The findings indicated that the model is effective for forecasting river flow.

Katimon et al.⁷ to predict the water quality of rivers and hydrological parameters utilizing the transfer function modeling processes, they created a dynamic relationship between the variables. The model used was an ARIMA containing AR (auto regression), I (integrated) and MA (moving average). The outcomes indicate that, rainfall variables and ${\text{Fe}}^{2+}$, ${\text{Al}}^{3+}$, ${\text{NH}}_{4}^{+}$ are the non-linear variables and the rest of the variables are linear. The autocorrelations of whole the examples were encountered within the 95% certainty intervals and the model remainders were encountered to follow a normal probability distribution, which demonstrates the usefulness of the models in prognostication hydrological variables and water quality. Lu and Ma⁸ to accurately forecast water quality in a short period of time, used two new hybrid DT- based machine learning models. These models are random forest (RF) and intense gradient technique (XGBoost). They used 1875 hourly data from May 1, 2019 to July 20, 2019 in the Tulatin River Basin. The performance evaluation was based on six error criteria that the results of the two models used were compared with the other four models. The results show the high performance of CEEMDAN-RF (used for experimental state analysis) to predict specific conductivity, temperature and dissolved oxygen, with average absolute error rates of 0.9%, 0.27% and 1.05%, respectively. CEEMDAN-XGBoost has a high performance in predicting turbidity, pH, and fluorescent organic matter, with average absolute error rates of 14.94%, 0.27%, and 1.59%, respectively. In general, the performance of CEEMDAN-RF and CEEMMDAN-XGBoost in high prediction and their average error rates are 3.90% and 3.91%.

Area of study

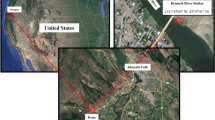
The Huai River is a large flow in China that runs from west to east and is located midway between the Yangtze and Yellow Rivers. The Huai River is 1110 km long with a drainage area of 270,000 ${\text{km}}^{2}$ The Huai River arises from Tongbai Mountain in the Henan region and it Flows into Lake Hongze. The river has long been the center of an extensive network of tributaries and tributaries and was used to irrigate the surrounding farmland. The average annual rainfall is 920 mm, rather than 60% of which happens from June to September, and the Average annual temperature 11–16 °C. There are many water projects in the Huai Basin, and the storage valence of vents and dams accounts for 51% of the annual runoff. China’s most densely populated area is the Huai River Basin, with a people of about 615 people per square kilometer⁹. The majority of the land of the Huai River Basin is agricultural areas, which includes paddy fields and highland fields, which make up 17.85 and 53.43% of the basin area, respectively¹⁰. The source of impurity in the Huai River is agricultural, industrial, and municipal wastes. The major impurities in the this River Basin are COD (39.1 tons) and NH₃-N (2.85 tons), which the whole rate is further than the standard. The declining quality of the Huai River has devastating effects on aquatic and fish life. Figure 1 shows the location of the study of three parameters of water quality, which are Boron (Br), water temperature and dissolved oxygen (DO). These parameters were monitored during 9 years (2012–2020) and their amount was measured by the General Directorate of Power Resources, the State Hydraulic Company, the Office of Research and Development and the General Directorate of Rural Affairs. The data of these parameters are accessible on a monthly basis for a period of 9 years from 2012 to 2020 for analysis. In this study, water quality data model for DO, WT and boron for the first 74 months were utilized for training the model, and the rest of the 34 months’ data were employed to confirm the model results. Table 1 presents the statistical features of water quality time series data. The variability of a water quality parameter can be described by mean, minimum, maximum, skewness, and standard deviation (SD).

Fig. 1

Location of the Huaihe River watershed in China and location of the study site within the middle Huaihe River watershed.

Table 1 Statistical properties of the water quality parameters.

According to Table 1, the low skewness coefficients are related to water temperature and $PH$. The coefficient of skewness related to dissolved oxygen is high, so the difference between the mean and average amounts of DO is extensive.

Methods

In this section, the neural network method and Grasshopper optimization algorithm are briefly reviewed.

ARIMA modeling approach

The model is explained in the state of ARIMA $(p, d, q){(\text{P},\text{ D},\text{ Q})}_{s}$ where $p$ indicates the non-seasonal numeral of lag observations contained in the model or AR rank, $d$ indicates the degree of non-seasonal difference or I, and $q$ indicates the non-seasonal size of the moving average window or MA rank. As the same way, $P, D, Q$ represent the order of seasonal autoregression, the degree of seasonal difference, and the order of seasonal MA. $s$ indicates is the duration of the season (periodicity). The model of ARIMA $(p, d, q){(\text{P},\text{ D},\text{ Q})}_{s}$ is presented below:

$${\varphi }_{p}\left(B\right){\Phi }_{P}\left({B}^{s}\right){\nabla }^{d}{\Delta }_{s}^{D}{z}_{t}={\theta }_{q}(B){\Theta }_{Q}({B}^{s}){a}_{t}$$

(1)

where $\varphi$ signifies the AR operator of order $p$, $\Phi$ signifies the seasonal AR variable of order $P$, ${\nabla }^{d}$ indicates the difference operator, ${z}_{t}$ indicates the observed amount at time $t$, ${\nabla }_{s}^{D}$ indicates the seasonal difference operator, $\Theta$ indicates the seasonal MA variable of order Q, $\theta$ indicates the MA operator of order q, and ${a}_{t}$ indicates the component of the noise of the stochastic model is supposed to be NID($0, {\sigma }^{2}$). In ARIMA modeling, three phases are performed, which are: model identification, variable calculation, and diagnostic review. These three phases are as follows:

In the first step, to determine whether the data is fixed or not, the autocorrelation function (ACF) and the PACF (partial autocorrelation function) are checked. ACF is utilized to measure the relationship between the previous values in the series and the next values. The value of the correlation between a parameter and a lag of itself is obtained by PACF. Regarding the PACF and ACF diagrams of the water quality concentration series, several ARIMA models are recognized for model choice. The best model is selected according to AIC (Akaike Information Criterion). The mathematical equation of the AIC is explained as:

$$AIC=n(\text{ln}\left(\frac{2\pi RSS}{n}\right)+1)+2m$$

(2)

where $m=(p+q+P+Q)$ is the numeral of terms evaluated in the model and RSS signifies the residual sum of squares.

Following the determination of the functions of the ARIMA model, the variable of these functions must be calculated. When a suitable model is specified and its variables are calculated, the process of Box–Jenkins needs to investigate the residues of the model for verifying that the model is a satisfactory one for the series. For specifying whether water quality time series are autonomous or not, the RACF function of the series is investigated. There are numerous helpful trials associated with RACF. In the first test, the remaining ACF function is plotted against the log number to show the correlations. The ARIMA model is appropriate, the evaluated autocorrelations of the residues are unconnected and dispersed around usually around 0. The next test is Ljung–Box–Pierce statistics. For trialing the adequacy of the model, the test statistic is computed for various whole numerals of successive lagged autocorrelations utilizing the Ljung–Box–Pierce statistics ($Q(r)$ trial).

MLP neural network

The biological nervous system inspires nonparametric and intelligent mathematical models such as artificial NNs. Many advances have been made in the use of NNs in the fields of regression, pattern recognition, classification, and prediction problems over the past 30 years¹¹. The use of artificial neural networks significantly depends on the learning process. One type of monitored artificial NNs is feedforward neural networks (FFNNs). Feedforward neural networks constitute a group of processing components named neurons. Neurons are spread on several stacked layers in which each layer is totally correlated with the subsequent one. In MLP architecture, the input layer is the first layer that feeds the network with input parameters. The middle and final layers are called the hidden layers and the output layer, respectively¹². one of the most generally practical FFNNs is multilayer perceptron neural network, where neurons connected in a one-directional and one-way manner. interconnections between neurons are illustrated by weights that are the real amounts placed between -1, 11. The MLP architecture is presented in Fig. 2. Also, the equation for each layer in the neural network is according to Eq. (1).

$${O}_{i}^{(l)}=\varnothing \left({u}_{i}^{\left(l\right)}\right)=\varnothing \left(\sum_{j=1}^{{n}_{l}}{O}_{j}^{\left(l-1\right)}{w}_{j,i}^{\left(l\right)}+{w}_{o,i}^{\left(l\right)}\right), 1\le l\le L$$

(3)

In the above equation, the activation function of the layer is indicated by $\varnothing ()$, This function is generally a nonlinear tangential hyperbolic function for the middle layers and is referred to as the hidden layers. The layer activation function also creates a linear function for the output layer results. The identification of the actual layer in a network of $L$ non-input layers is done by the $l$ index, the numeral of $l$ layer neurons is denoted by ${n}_{l}$, the output of neuron $i$ in the actual layer $l$ is represented by ${O}_{i}^{l}$, ${w}_{j,i}^{\left(l\right)}$ is the weight described to the interconnections of neuron $i$ of layer $l$ with the neurons of the before layer $l-1$, and the bias of neuron $i$ of the actual layer is indicated by ${w}_{o,i}^{\left(l\right)}$. The output vector of layer $l=0$ of length ${n}_{0}$ overlaps with the input specifications vector, which is, ${O}^{(0)}=x$. moreover, the output vector of the last layer $l=L$ of length ${n}_{L}$, that is the output layer of the network, overlaps with the network outcome, which is, ${O}^{(L)}=y$.

Fig. 2

MLP neural network architecture.

Grasshopper optimization algorithm

Grasshoppers are insects known as plant pests. Grasshoppers are often found alone, but if they are in groups, they can number in the millions, which can be very dangerous to pastures, grains and crops¹³. The swarm of grasshopper in nature is the inspiration for the Grasshopper optimization algorithm that has been introduced in recent years¹⁴. In the suggested algorithm, a group of candidate solutions is haphazardly created to produce the initial artificial swarm. Therefore, any candidate factors are calculated according to the fitness amounts and the finest search factor in the current swarm is regarded as the target or leader. As the leader grasshopper starts to absorb others, the grasshoppers in the leader’s neighborhood move toward it. In adulthood, swarming conduct can be seen in grasshopper¹⁵. The low motion and little steps of grasshopper in the larval phase are the major characteristics of swarming. On the opposite, in adulthood, sudden motion and long steps is the basic element of the swarm. Another significant characteristic of the grasshopper batch is the search for food sources. The search process in nature-inspired algorithms is divided into two parts: exploration and exploitation. In the exploration phase, exploration factors are urged to motion abruptly. But in the exploitation phase, the agents tend to motion locally. It should be noted that the targeting simulation and the two stages of exploration and exploitation of the algorithm are based on the behavior of grasshoppers in nature. The following Eq expresses the grasshopper swarm behavior mathematically:

$${X}_{i}={A}_{i}+{S}_{i}+{G}_{i}$$

(4)

where, the location of $ith$ grasshopper is indicated by ${X}_{i}$, ${A}_{i}$ signifies the wind advection, ${S}_{i}$ indicates social relations, ${G}_{i}$ denotes the gravity force on the $ith$ grasshopper. To apply random behavior in the above equation, three random numbers (${r}_{1},{r}_{2},{r}_{3})$ between 0 and 1 can be applied to it, in which case the above equation becomes ${X}_{i}={r}_{1}{A}_{i}+{r}_{2}{S}_{i}+{r}_{3}{G}_{i}$.

$${A}_{i}=u*\widehat{{e}_{w}}$$

(5)

where, $\widehat{{e}_{w}}$ indicates a unit vector in the wind orientation and $u$ defines a steady drift. As the grasshopper has no wings during the nymph period, its movement is extremely related to the direction of the wind. Figure 3 represents the abstract model of the convenience area and both of the attraction and repulsion forces among grasshoppers.

Fig. 3

Elementary correctional model between individuals in a grasshoppers’ swarm.

$${S}_{i}=\sum_{\begin{array}{c}j=1\\ j\ne 1\end{array}}^{N}S({d}_{ij})\widehat{{d}_{ij}}$$

(6)

The span between $jth$ and $ith$ grasshopper is represented by ${d}_{ij}$, which is obtained as ${d}_{ij}=\left|{x}_{j}-{x}_{i}\right|$, $\widehat{{d}_{ij}}$ indicates a unit vector from $ith$ to $jth$ grasshopper and it is equal to $\frac{{x}_{j}-{x}_{i}}{{d}_{ij}}$, $S$ indicates a function for specifying the power of social forces and it is computed as Eq. (5):

$$S\left(r\right)={fe}^{\frac{-r}{l}}-{e}^{-r}$$

(7)

where, the power of attraction is indicated by $f$, and the scale of attractive measurement is specified by $l$. The social behavior of artificial grasshopper is affected by the energy of gravity and repulsion, which is fully explained by Saremi et al.¹⁶. Based on many experiments completed on the behavior of grasshoppers with several amounts of $f$ and $l$ by them, it was concluded that if the Space between the grasshoppers is 0 to 2.079, repulsion happens between them. Otherwise, it can be stated that it enters the convenience area.

$$G=-g*\widehat{{e}_{g}}$$

(8)

In which, the gravitation constant is indicated by $g$, the unity vector towards the earth center is represented by $\widehat{{e}_{g}}$. Determining the new location of the ${i}^{th}$ grasshopper is done according to the location of the food (target) and the location of the other grasshoppers. The relevant equation is presented below.

$${X}_{i}^{d}={C}_{1}\left(\sum_{j=1}^{N}{C}_{2}\frac{{ub}_{d}-{ul}_{d}}{2}s\left(\left|{x}_{j}^{d}-{x}_{i}^{d}\right|\right)\frac{{x}_{j}-{x}_{i}}{{d}_{ij}}\right)$$

(9)

In which, ${ul}_{d}$ and ${ub}_{d}$ indicate the lower and the upper ranges in the $Dth$. The amount of the $Dth$ dimention for the aim grasshopper in expressed by $\widehat{{T}_{d}}$, The formula also uses a reduction factor of C to reduce repulsion and gravity zones and convenience areas. In the above equation, the gravity factor G has been regarded equal to 0, and the orientation of wind $A$ is unto the aim grasshopper $\widehat{{T}_{d}}$.

Closing the food source and eating it is done by slowing down the grasshopper, which is simulated by parameter $C$. To decline the search coverage to the objective grasshopper, the number of epochs is increased and the outer ${C}_{1}$ is used. the inner ${C}_{2}$ has also been utilized to alleviate the effects of gravity and excretion among grasshoppers relative to the numeral of epochs. In the proposed algorithm (GOA), the parameter C must be reduced pro rate to the performed epochs number and this process is done to control the grade exploration and exploitation in the algorithm. Implement this procedure, increases the exploitation grade as the epoch count increases. The following equation can be used to obtain parameter $C$:

$$C={C}_{Max}-z\frac{{C}_{Max}-{C}_{Min}}{Z}$$

(10)

In which, the maximum and minimum amounts of parameter $C$ are indicated by ${C}_{Max}$ and ${C}_{Min}$ are the epoch number is expressed by $z$ and the maximum epoch number is specified by $Z$. The amount of ${C}_{Max}$ and ${C}_{Min}$ are regarded equal to 1 and 0.00001¹⁶. In the grasshopper optimization algorithm, first, the initial solutions (grasshopper population) are formed randomly and then the fitness for each of the solutions is specified. The location of the grasshoppers is updated according to Eq. (7). The finest grasshopper location (objective) acquired so far is updated in all epochs. Normalized spacing between grasshoppers is in the interval 1 and 4, and the parameter $C$ is specified founded on Eq. (8) in all epochs. When the stop criterion is reached, the grasshopper location update is stopped and ultimately, the finest grasshopper (objective) is yielded which illustrates the finest access to the global optimum.

Development algorithm

In this segment the CTM (chaotic tent map) is presented (Xiaolin Wu et al.¹⁷, Congxu Zhu et al.¹⁸, Xun Yi et al.¹⁹). Just like other chaotic maps, the CTM has its own unique features. These characteristics include non-repetition, ergodicity and inherent randomness. Due to the characteristics of CTM, it can be employed to improve and develop meta-heuristic algorithms for finding global solutions. The compound of meta-heuristic algorithms and the CTM is used for many applications including classification, image segmentation, clustering, and feature selection. The following equation relates to CTM:

$${x}_{i+1}=\left\{\begin{array}{l}\frac{{x}_{i}}{0.7} {x}_{i}<0.7\\ \\ \frac{10(1-{x}_{i})}{3} {x}_{i}\ge 0.7\end{array}\right.$$

(11)

To predict the price, three methods including MLP NN, grasshopper optimization algorithm, and CTM were described. Using the GOA algorithm in solving optimization problems can have satisfactory results by adjusting the exploration and exploitation processes and escaping from the local optimization. This algorithm is a new method founded on its adaptive and flexible searching mechanisms. To facilitate the major problem, GOA divides it into several smaller problems, thus avoiding early convergence problems and local optimum. Also, the chaotic map procedure is employed to enhance the efficiency of GOA for specifying the weights of the neural network.

Hybrid model

Water quality data has different specifications such as heteroskedasticity and seasonality. Hence, independent models are not able for forecasting WQ (water quality) data. Also, the ARIMA model alone is not employed to solve nonlinear problems. In modeling and receiving linear problems, artificial neural networks can provide good performance. However, using this model for each kind of data does not make sense²⁰. A model that can predict water quality data well is a hybrid model that can deal with linear and nonlinear problems. It is possible to describe various aspects of the basic patterns by merging several models. A time series of water quality can consist of a linear correlation structure and a nonlinear constituent²¹. The mathematical expression of this concept is as follows:

$${y}_{t}={L}_{t}+{S}_{t}$$

(12)

where ${S}_{t}$ defines the nonlinear component and ${L}_{t}$ defines the linear component. These parameters are obtained using time series data. In the first step, the linear component was obtained using the ARIMA model. The residues from the linear model will include a nonlinear association. The formul is provided below describes the residues ${e}_{t}$ at time $t$ from the linear model:

$${e}_{dxzzt}={y}_{t}-\widehat{{L}_{t}}$$

(13)

where, $\widehat{{L}_{t}}$ indicates the predicted amount of the ARIMA model at time $t$. To determine the sufficiency of ARIMA models, a diagnostic examination of the remainder is necessary. Despite the linear correlation structures in the residues, the ARIMA model alone is not sufficient. Also, nonlinear patterns in time series data can not be detected by examining the residual diagnostic test. After confirming the sufficiency of the model by diagnostic examination of the residues, the model is insufficient due to the fact that nonlinear relationships are not modeled properly. Hence, artificial neural networks are used to model the residues and thus obtain nonlinear relationships. The MLPModel with N input node will be as follows:

$${e}_{t}=f\left({e}_{t-1}, {e}_{t-2},\dots , {e}_{t-N}\right)+{\varepsilon }_{t}$$

(14)

$f$ indicates a nonlinear function specified by the NN and ${\varepsilon }_{t}$ represents the random error. Ultimately the united forecast will be as follows:

$$\widehat{{y}_{t}}=\widehat{{L}_{t}}+\widehat{{S}_{t}}$$

(15)

The forecast from Eq. (12) is indicated by $\widehat{{S}_{t}}$.

Validation of models and measurement procedures

By three various prediction compatibility criteria, a measurement was made between the performance of the MLP and ARIMA. These three criteria include the (MAPE) mean absolute percentage of error, the (RMSE), and the Nash–Sutcliffe coefficient of efficiency (NSC).

$$MAPE=\frac{1}{n}\sum_{i=1}^{n}\left|\frac{{P}_{i}-{O}_{i}}{{P}_{i}}\right|100$$

(16)

where ${O}_{i}$ and ${P}_{i}$ describe the observed and predicted water temperatures on a weekly basis. The number of data is indicated by $n$. The RMSE is specified as:

$$RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{({P}_{i}-{O}_{i})}^{2}}$$

(17)

And the third criterion is as follows, which is less than one, and if it is equal to one, it means $P=0$.

$$NSC=1-\frac{\sum_{i=1}^{n}{({P}_{i}-{O}_{i})}^{2}}{\sum_{i=1}^{n}{(\overline{O }-{O}_{i})}^{2}}$$

(18)

where, $\overline{O }$ represents the mean of observed water quality parameters on a monthly basis. In order to be able to compare the observed and predicted amounts, time series diagrams and scatter plots are provided. NSC amounts of 0, 1 and negative display that the observed average is as acceptable a forecaster as the model, a complete fit, and a finer forecaster than the model, respectively²². Using the results obtained from the predicted and measured parameters, the accuracy of MLP model in predicting the model can be obtained and also significant decisions can be made based on the use of data.

• Rationale for model selection and advantages of the hybrid approach

The selection of the ARIMA, MLP, and the hybrid ARIMA-MLP model in this study was driven by the need to address both linear and nonlinear patterns present in water quality time series data. ARIMA is a well-known statistical model that excels at capturing linear relationships in time series, making it a natural choice for modeling water quality components that exhibit linear trends over time. However, ARIMA has a notable limitation in that it cannot effectively handle nonlinear relationships, which are common in real-world environmental datasets. On the other hand, the MLP is an artificial neural network that is highly effective at modeling both linear and nonlinear patterns. MLP’s flexibility allows it to capture complex dynamics in the data, which is essential when dealing with water quality variables that are influenced by a variety of nonlinear factors. However, relying solely on MLP might lead to suboptimal results in datasets where linear trends also play an important role, as MLP may overfit to complex patterns and overlook simpler linear dependencies.

The hybrid ARIMA-MLP model was chosen because it combines the strengths of both ARIMA and MLP, offering a more comprehensive approach to time series forecasting. In the hybrid approach, ARIMA is first applied to model the linear components of the data, and the residuals (which contain the nonlinear patterns) are then modeled using MLP. This division of tasks enables the hybrid model to capture both types of patterns more effectively than either model could do on its own. By addressing the limitations of both ARIMA and MLP, the hybrid model improves overall prediction accuracy, especially for water quality components like dissolved oxygen, water temperature, and boron.

An additional advantage of the hybrid approach is its balance between simplicity and complexity. While standalone models like ARIMA or MLP may either be too simplistic or too complex for certain datasets, the hybrid model optimally divides the task of modeling linear and nonlinear components. This ensures that the model remains robust while avoiding the risk of overfitting to the data. Furthermore, by optimizing the hybrid model using the Grasshopper Optimization Algorithm (GOA), the model’s efficiency is further enhanced, leading to improved prediction accuracy. What sets the hybrid ARIMA-MLP model apart from other hybrid models is its ability to handle both linear and nonlinear aspects of the data in a structured manner. The ARIMA component focuses on modeling linear relationships, while the MLP component takes on the task of handling the nonlinear residuals. This sequential approach leads to better performance, as demonstrated by the results of the study, where the hybrid model consistently outperforms the individual ARIMA and MLP models.

In conclusion, the hybrid ARIMA-MLP model was selected for its ability to combine the strengths of both ARIMA and MLP, making it more effective at handling the complexity of water quality data. Its versatility in capturing both linear and nonlinear patterns, combined with the optimization provided by the Grasshopper algorithm, makes it a powerful tool for forecasting water quality variables. The results of this study clearly demonstrate the advantages of the hybrid approach over the standalone ARIMA and MLP models, particularly in terms of prediction accuracy and consistency.

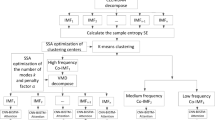
Figure 4 depicts the flow diagram of the model. This diagram illustrates the entire process of the hybrid ARIMA-MLP model optimized by the Grasshopper optimization algorithm. It outlines the integration of the ARIMA model for capturing linear patterns, followed by the application of the MLP model to handle the nonlinear residuals of the ARIMA output, optimized using the Grasshopper algorithm.

Fig. 4

The flow diagram of the model.

Results and discussion

Modeling of ARIMA

Numerous experiments have been designed to obtain the optimal variables for the ARIMA model. Arima prediction model variables were selected to identify the remaining statistics. The period from 2011 to 2019 was considered in the ARIMA models for the purpose of forecasting the time series of monthly water quality. The water quality information for the epoch of 2011 to 2016 were utilized for calibration of modela and to attain the finest model fit for any water quality variable. Periodic information in 2017 to 2019 were also considered to compare the obtained forecasts and model verification. A range between 0 and 1 was regarded, to normalize each variable related to the input and output water quality information set in the ARIMA modeling.

The three-step method including model recognition, computation of model variables, and evaluation of the composed variables was utilized to fit the ARIMA model with the exsisting water quality time series information. In the recognition phase, to specify the probable persistence forecasting in the time series data, the PCF and the ACF were employed. Among the different competing models, the good-fitted models were found utilizing AIC. According to the results presented in Table 2, the seasonal parameters (P, D, Q) of the finest fit the ARIMA models are (0, 1, 1) for boron, (0, 0, 1) for water temperature, and (1, 0, 0) for DO. The non-seasonal parameters (p, d, q) are (1, 0, 1) for boron, (1, 1, 1) for water temperature, and (1, 1, 0) for dissolved oxygen. The finest fit of the statistical variables of the ARIMA model is calculated at the phase of estimating the model variables. The Box-Jenkins method is used to estimate the model variables²³. ARIMA modeling hypotheses including constant variance, independence, and residual normality were examined, and then the finest fit model was chosen. The Ljung–Box–Pierce statistics, RACF, and cumulative periodogram were utilized to examine the independence of the residues. The amounts of RACF were nicely established within confidence limits. Only a very small number of individual correlations seem large. No meaningful relationship was concluded between the residues of any water quality variable. The amounts of Ljung–Box–Pierce Q(r) statistic is represented in Table 2. The amounts of Q(r) were verified to a critical trial amount (${X}^{2}$) distribution with individual degree of freedom at a 5% meaningful level. It became clear that the calculated amounts were smaller than the real (${X}^{2}$) amounts, and this represents the white noise of the remnants of the finest models (Table 2). Based on cumulative periodograms, it can be said that there is no meaningful periodicity in the remaining series at the 95% confidence level. Residual normality diagrams and histograms were examined to confirm the normality of rabies residues. Also, a graph of residues against fitted values was analyzed to investigate the homoscedasticity of the residues. The graphs displayed a random dispersal around 0. As is clear, the models were sufficient because the residues were equally distributed surrounding the mean.

Table 2 Overview of the statistical variables of the finest-fitted multiplicative ARIMA models to WQ (water quality) variables.

Therefore, utilizing the water quality data collection the fitted ARIMA model was tried for a period of 36 months. Figure 5 indicates that the predictions of the ARIMA model are not completely satisfactory due to the fact that it differs from the range of most water quality data.

Fig. 5

Measurement of ARIMA model for any water quality variable.

The correlation coefficient amounts between observed data and model forecasted amounts for DO, boron, and WT are 0.51, 0.49, and 0.75, correspondingly. That is represented in Fig. 6. The ARIMA models could not predict the monthly amounts of water quality well but can indicate the max and min cycle amounts of water quality in a year. This restriction was because primarily of the restrictions of the linear modeling algorithm in the ARIMA model, the efficiency of which was not entirely acceptable in identifying and producing the nonlinear time series of WQ data.

Fig. 6

ARIMA predicted data versus observed data for each water quality variable.

Modeling of MLP neural network

For predicting water quality components including DO, boron, and water temperature, a 3-layer feed-forward neural network model was created using an optimal training algorithm. In the current paper, the Grasshopper optimization algorithm was chosen as the optimized training procedure. In the subsequent section, MLP efficiency validation is expressed in the flow forecast on a monthly basis. Available data for modeling objectives were from 2011 to 2019. DO, WT, and boron time series data were separated into 2 autonomous data categories. The initial collection of data was utilized to teach the model and the next collection of data was utilized to confirm the model. In the MLP modeling approach, the input and output water quality data collections for any variable were normalized in the interval (0,1). The performance of the MLP model in the training for any water quality variable is presented in Fig. 7. As shown in Fig. 7a, the predetermined training purpose of 0.001 for the boron time series data is achieved after 100 iterations. Similarly, the number of iterations required to achieve the training purpose of 0.001 for dissolved oxygen time series data is 30 iterations which is represented in Fig. 7b. Calibration of the model weight was performed by analogizing observational and forecast data. According to Fig. 7c, water temperature data reach the training purpose of 0.001 after 100 iterations. The diagrams in Fig. 7 show that the MLP Model can be trained to set the weight of the model so that the observed data correspond to the predicted water quality variables of the model.

Fig. 7

Training efficiency of MLP model for any water quality variable.

In the verification stage of the model, the network that is trained was utilized to forecast the water quality component on a monthly basis. A comparison between observational data and model predictions for water quality variables is illustrated in Fig. 8. Based on the verification step, there is an acceptable match between the observed and predicted data.

Fig. 8

The verification of the MLP model for any water quality variable.

The correlation coefficient obtained between the observed and forecasted data of the model is satisfactory, which is equal to 0.88 for dissolved oxygen, 0.89 for boron, and 0.9 for water temperature. Figure 9 shows the correlation coefficient diagram. Based on the obtained results, it can be said that the MLP model for predicting water quality data on a monthly basis provides acceptable patterns for the desired stream.

Fig. 9

MLP predicted data versus observed data for any water quality variable.

Hybrid modeling

In the offered hybrid design, two phases were performed, which included modeling the linear sector of the problem with the ARIMA model and utilizing an MLP to model the remains of the ARIMA model. In other words, the nonlinear framework of water quality time series data is modeled by the MLP model. In the hybrid system, the features and capabilities of both neural network and ARIMA models have been used to obtain different patterns. Hence, in order to enhance the modeling efficiency, it is better to model the linear and nonlinear forms individually. In the proposed modeling, the input and output data for any of the water quality components were normalized in the range of 0 and 1. Finally, model adjustment was performed by hybrid model training to obtain a good match between the forecasted water quality components and the observed data. Figure 10 shows the results obtained in the hybrid model prediction and observational data of water quality variables. As it turns out, there is a logical match between the observed data and the predicted data.

Fig. 10

The verification of Hybrid model for any water quality variable.

The graph of the correlation coefficient between the observational data and the forecasted data of the hybrid model is presented in Fig. 11, which is equal to 0.9 for dissolved oxygen, 0.91 for boron, and 0.91 for water temperature. These values indicate that the hybrid model is satisfactory.

Fig. 11

Hybrid model forecasted data versus observed data for any water quality variable.

Enhanced Evaluation of Model Performance

In order to provide a more thorough evaluation of the hybrid ARIMA-MLP model, we have included additional visualizations, namely the violin plot, box plot, and Taylor diagram. These visual aids complement the initial performance metrics by offering deeper insights into the distribution, variability, and correlation of the prediction errors when compared to the observed data.

• 1. Violin Plot (Fig. 12a): The violin plot offers a visual representation of the distribution of prediction errors for each model—ARIMA, MLP, and the hybrid model. It combines elements of a box plot with a kernel density estimation, allowing us to see both the central tendencies (median and quartiles) and the error density. The violin plot highlights that the hybrid model’s error distribution is more concentrated around zero, indicating a reduced variance in prediction errors. This reduced spread suggests that the hybrid model produces more accurate and consistent predictions compared to the individual ARIMA and MLP models, particularly for dissolved oxygen, water temperature, and boron levels.

• 2. Box Plot (Fig. 12b): The box plot provides another layer of insight by visualizing the interquartile range (IQR), median, and outliers of the prediction errors. The narrower IQR of the hybrid model in comparison to ARIMA and MLP models indicates fewer extreme errors and greater consistency. Moreover, the hybrid model produces fewer outliers, which implies that it has a more stable predictive performance with fewer large deviations from the actual values. This stability is crucial for reliable forecasting in water quality management, as extreme deviations can lead to inaccurate decisions regarding pollutant levels and management strategies.

• 3. Taylor Diagram (Fig. 12c): The Taylor diagram offers a comprehensive summary of the model performance by comparing the standard deviation, correlation coefficient, and centered RMSE (Root Mean Square Error) of each model relative to the observed data. In this diagram, the hybrid model shows a higher correlation with the observed data, indicating that it captures the relationship between the input variables and the water quality components more effectively. Additionally, the hybrid model’s standard deviation is closer to that of the observed data, and its RMSE is lower compared to the ARIMA and MLP models. This suggests that the hybrid model is better at capturing both the linear and nonlinear aspects of the time series, leading to more accurate predictions.

Fig. 12

Enhanced evaluation of model performance results: (a) Violin plot, (b) Box Plot, and (c) Taylor diagram.

The combination of these plots allows for a more robust and detailed assessment of the hybrid model’s predictive performance. The violin and box plots illustrate how the hybrid model reduces prediction variability and outliers, while the Taylor diagram demonstrates its ability to closely match the observed data in terms of correlation and error distribution. These results confirm that the hybrid ARIMA-MLP model, optimized by the Grasshopper algorithm, offers significant improvements over the individual models, making it an effective tool for forecasting water quality in rivers.

Comparison of the performances of model

The MAPE, NSC, and RMSE accuracy indices for MLP, ARIMA, and hybrid models were obtained to compare the observed and forecasted data over a period of 36 months and thus the best model was specified. The MLP model and the hybrid system supplied acceptable accuracy for all components of water quality. ARIMA model in forecasting water quality components did not have a proper match with observational data. Table 3 shows the measured indicators for the three various methods utilized to forecast water quality components. In the ARIMA model, the RMSE value between the forecasted and observed data is 0.166 for boron, 0.114 ${\text{mgl}}^{-1}$ for dissolved oxygen, and 0.103 $^\circ{\rm C}$ for water temperature. Similarly, in the MLP model, this value is 0.075 for boron, 0.062 ${\text{mgl}}^{-1}$ for dissolved oxygen, and 0.049 $^\circ{\rm C}$ for water temperature. Using the hybrid system, the RMSE amount was reduced by 16.4%, 14.8%, and 18.8% compared to the MLP model for each of the components of dissolved oxygen, boron, and water temperature, respectively. Likewise, the MAPE amounts between the forecasted and observed data for each of the water quality components in the MLP model seem to be slightly smaller. In the MLP model, the error forecast statistics created MAPE amounts of 30% for dissolved oxygen, 22% for water temperature, and 37% for boron. In the hybrid model the MAPE amount reduced by 8.9%, 13.42% and 8.7% compared to the MLP model for each of the components of dissolved oxygen, water temperature, and boron. In the ARIMA model, lesser NSC amounts are obtained compared to the MLP model. These amounts for the ARIMA model were 0.54 for boron, 0.69 for dissolved oxygen, and 0.72 for water temperature. Nevertheless, the NSC amounts for the MLP model were 0.90 for boron, 0.92 for dissolved oxygen and 0.94 for water temperature. Using the hybrid system, the NSC amount was reduced by 13.5%, 12.4%, and 15.1% compared to the MLP model for each of the components of boron, DO, and WT. These outcomes demonstrated that the hybrid model has the best efficiency in the prognostication of water quality components including boron, DO, and WT.

Table 3 Numerical measurement of predicted and observed data from the hybrid, ARIMA, and MLP modeling strategies.

It can be concluded that the accuracy of water temperature simulation in the hybrid model is one degree compared to the two models MLP and ARIMA. In the case of the Huai River, the hybrid model was also able to simulate well the patterns and the amount of dissolved oxygen concentration observed. Similarly, the improved hybrid model was capable to forecast monthly changes in boron content well by identifying the pattern of input data on boron. The hybrid model generally offers better forecasts of boron, dissolved oxygen time series, and water temperature in the Huai stream compared to the MLP and ARIMA models.

• Visual comparison of model predictions

In addition to the numerical evaluation provided in Table 3, we have included a plot (Fig. 13) that visually compares the predicted values from the ARIMA, MLP, and hybrid models against the actual observed data for an example period. This graphical representation enables a clearer comparison of each model’s ability to forecast water quality components. The solid black line represents the true values, showing the actual measurements of the water quality component over the selected period. These observed values serve as the benchmark for assessing the performance of the models. The ARIMA predictions, depicted by the red dashed line, capture some of the linear trends in the data but show considerable deviation from the true values, particularly in periods where nonlinear patterns dominate. This illustrates ARIMA’s limitations in accurately modeling complex and nonlinear relationships present in the water quality time series.

Fig. 13

Visual comparison of model predictions.

The MLP predictions, shown as the blue dash-dot line, demonstrate a better fit compared to ARIMA, as the MLP model is more adept at capturing nonlinear patterns. However, some deviations from the true values remain, indicating that while MLP improves upon ARIMA, it still struggles to optimally forecast certain trends in the data. The green dotted line represents the predictions from the hybrid ARIMA-MLP model. This model successfully combines the strengths of both ARIMA and MLP, enabling it to account for both linear and nonlinear aspects of the data. As the plot shows, the hybrid model consistently aligns more closely with the true values compared to the ARIMA and MLP models, with significantly reduced deviations. This visual evidence corroborates the numerical results in Table 3, where the hybrid model achieves the highest accuracy, lowest error, and strongest correlation with the observed data.

Limitations of the hybrid approach

While the proposed hybrid ARIMA-MLP model has demonstrated significant improvements in predictive accuracy compared to the individual ARIMA and MLP models, it is important to acknowledge several limitations associated with this approach.

First, the hybrid model requires more computational time and resources. The integration of both ARIMA and MLP, along with the use of the Grasshopper Optimization Algorithm, leads to a more time-consuming training process. This makes the hybrid method computationally intensive, especially for large datasets or real-time applications. In contrast, standalone models such as MLP may be faster and easier to implement in situations where rapid predictions are necessary. Additionally, the hybrid approach introduces greater complexity in analysis and implementation. The need to combine two different modeling frameworks (ARIMA for linear trends and MLP for nonlinear patterns) and optimize their performance using an advanced algorithm requires more effort and expertise. This added complexity might not always be justified in every situation, especially if the dataset predominantly contains nonlinear patterns that could be sufficiently modeled by MLP alone.

It should also be noted that while the hybrid model typically outperforms both ARIMA and MLP, this may not always be the case. There are instances where the results from the MLP model alone may closely match or even surpass those of the hybrid model, particularly in datasets where nonlinear features dominate. Therefore, the necessity of a hybrid approach should be carefully evaluated based on the nature of the data being analyzed. In summary, the hybrid ARIMA-MLP model offers improved accuracy but comes with trade-offs in terms of computational complexity, time, and potential overfitting in certain scenarios. These limitations must be considered when selecting the appropriate modeling approach for a given dataset.

Conclusions

In this study, a hybrid system for modeling water quality time series was presented. In this system, the advantages of MLP and conventional procedures can be used. The efficiency of the hybrid model in forecasting water quality components was compared and assessed with ARIMA and MLP models. The obtained data from the ARIMA model were entered into the hybrid model and the MLP model was used to analyze the remainder of the Arima model which includes the nonlinear features of the time series data. The efficiency of the hybrid model in forecasting river water quality was evaluated on a monthly basis. The results obtained from the ARIMA model simulate the pattern of water quality data for water temperature acceptably, but poor results were obtained for dissolved oxygen and boron. The use of the MLP model was able to provide accurate results in predicting water quality components. In the presented hybrid system, the linear sector analysis of the problem was performed through the ARIMA model, and then the MLP model was utilized for modeling the remains of the ARIMA model. More reasonable results for boron, dissolved oxygen and water temperature time series data were obtained as a result of the hybrid model. The forecasts obtained in the hybrid model were compared with forecasts acquired from the ARIMA and MLP time series procedures. The hybrid model can detect nonlinear features and predict time-series patterns. Also, by obtaining accuracy indicators that included MAPE, NSC, and RMSE, we can say that the hybrid model offers much more accuracy in predicting water quality than the ARIMA and MLP models. Therefore, in the Huai River and other hydrometerologically identical rivers, the suggested hybrid algorithm can be used to forecast water quality data on a monthly basis to determine the intensity of water quality according to boron, dissolved oxygen and water temperature in the futurity. The proposed hybrid model can also be utilized to plan emergency water quality management in the Huai River to guarantee sustainable management of water resources in the basin.

The model’s performance depends heavily on the data quality and quantity. In our study, we used a dataset covering 108 months, which may not capture long-term trends or seasonal variations that could occur in a more extensive dataset. The scope of this study was limited to three water quality parameters: dissolved oxygen, water temperature, and boron. Although the hybrid model performed well for these parameters, its effectiveness on other water quality indicators remains unexplored. The use of the Grasshopper Optimization Algorithm, while effective in this study, could lead to increased computational complexity, especially when applied to larger datasets or in real-time scenarios.

For future work, we propose expanding the hybrid model to include more water quality parameters such as pH, nitrate concentration, and biochemical oxygen demand (BOD) to evaluate its broader applicability. Testing the model on larger datasets from different regions and timeframes will also enhance its generalizability. Additionally, exploring alternative optimization algorithms, such as Particle Swarm Optimization (PSO) or Genetic Algorithms (GA), may improve computational efficiency and further enhance model accuracy.