Exploring N-soliton solutions, multiple rogue wave and the linear superposition principle to the generalized hirota satsuma-ito equation

Abstract

In this work, numerous rogue wave solution strategy (MRWSS) agreeing to the Hirota bilinear hypothesis is utilized. The said strategy to build different soliton wave solutions for the generalized Hirota-Satsuma-Ito (GHSI) condition is considered. These numerous soliton wave solutions incorporate first-order, second-order, third-order, and fourth-order waves solutions and so on, which are all depending on the starting theory of chosen capacities. For the lump solution with one most extreme or least esteem, the properties of the Hessian lattice are examined. Besides, the arrangements are contained the lump-two kink arrangements, cross-kink wave arrangements, periodic wave arrangements, and periodic-kink wave arrangements. The various classes of arrangements are gotten. We make utilize of the direct superposition procedure to find out N-soliton wave arrangements to the said condition. The appropriateness and viability of the obtained arrangements is detailed through the reenactment comes about within the shape of 3-D, density, and 2-D charts. The gotten comes about in this work are anticipated to open modern viewpoints for the traveling wave theory.

Introduction

The (1+1)-dimensional Hirota-Satsuma shallow water wave (HSSWW) equation firstly introduced by Hirota and Satsuma as a demonstrate condition portraying the unidirectional engendering of shallow water waves¹ as follows

$$\begin{aligned} \Psi _{t}-\Psi _{xxt}-3\Psi \Psi _t+3\Psi _{x}\int _{x}^{\infty }\Psi _t dx+\Psi _x=0,\hspace{4.5cm} \end{aligned}$$

(1)

by employing the below bilinear transformation is arisen as

$$\begin{aligned} \Psi =2(\ln f)_{xx}. \end{aligned}$$

(2)

Then, Eq. (1) converted to the bilinear frame as follows:

$$\begin{aligned} \left( D_xD_t-D_x^3 D_t+D_x^2\right) \mathfrak {f}. \mathfrak {f}=0.\hspace{7.cm} \end{aligned}$$

(3)

Also, the (2+1)-dimensional HSSWW equation is presented² as

$$\begin{aligned} \Psi _{xxxt}+3(\Psi _x\Psi _t)_x+\Psi _{yt}+\Psi _{xx}=0,\hspace{6.1cm} \end{aligned}$$

(4)

by help of the following bilinear operation

$$\begin{aligned} \Psi =2(\ln f)_{x},\hspace{9.5cm} \end{aligned}$$

(5)

Eq. (5) changed to the bilinear model can be seen as follows

$$\begin{aligned} \left( D_x^3 D_t+D_yD_t+D_x^2\right) \mathfrak {f}. \mathfrak {f}=0.\hspace{6.9cm} \end{aligned}$$

(6)

Moreover, the (2+1)-dimensional generalized Hirota-Satsuma-Ito shallow water wave (GHSISWW) equation will be read³ as

$$\begin{aligned} \Psi _{xxxt}+3(\Psi _x\Psi _t)_x+\delta _1\Psi _{yt}+\delta _2\Psi _{xx}+ \delta _3\Psi _{xy}+\delta _4\Psi _{xt}+\delta _5\Psi _{yy}=0,\hspace{1cm} \end{aligned}$$

(7)

by exploiting the following bilinear relation

$$\begin{aligned} \Psi =2(\ln f)_{x},\hspace{9.5cm} \end{aligned}$$

(8)

also, Eq. (7) changed to the bilinear model including

$$\begin{aligned} \left( D_x^3 D_t+\delta _1D_yD_t+\delta _2D_x^2+\delta _3D_xD_y+\delta _4D_xD_t+\delta _5D_y^2\right) \mathfrak {f}. \mathfrak {f}=0.\hspace{1.9cm} \end{aligned}$$

(9)

A few later investigates moreover illustrate the strikingly high abundance of lump arrangements to nonlinear partial differential conditions (see, e.g., multi-kink waves⁴, the elastic interaction solution between a line soliton and a periodic soliton⁵and inelastic interactions among the multi-front kink waves⁶). A new class of Hirota-Satsuma-Ito type equations involving general second-order derivative terms was conducted to require having lump solutions by Ma⁷. The Lie symmetry technique has been applied to obtain certain analytic invariant solutions for the generalized Hirota-Satsuma-Ito equations⁸.

For the case of spatially nonlinear frameworks, bounty of known explanatory arrangements exist. On the other hand, these basic frameworks are frequently considered to create and test unused numerical strategies by mathematicians. Be that as it may, in numerous viable issues, the properties of the materials such as the diffusivity and the thickness can broadly shift within the framework, hence we accept that modern comes about for these frameworks are important. On the other hand, there are a huge number of numerical strategies to illuminate the nonlinear models of equation, including trigonometric quadrature rules⁹, the (2+1) dimensional Chaffee-Infante equation¹⁰, wave structures to the modified Schrödinger’s equation¹¹, conventional soliton and bound-state soliton¹², and generalization of regularized long-wave equation¹³. Nonlinear models appear in a range of fields, starting from classical hydrodynamics to advanced gravitational waves, including soliton molecules¹⁴, bistable origami flexible gripper¹⁵, the neural networks method¹⁶, and several other systems due to their interesting propagation as well as works in^17,18.

The foremost broadly known ones have a place to the family of the numerical or explanatory plans counting the multimodal learning paradigm method¹⁹, multimodal hybrid parallel method²⁰, the neural architecture scheme²¹, the accurate automated extraction method²², and improved BPNN technique²³. Apart the solitons arise a unique balance between dispersive and nonlinear effects in a given medium is primarily described by integrable partial differential equations including the homotopy analysis technique²⁴, the homotopy perturbation scheme²⁵, the $tan(\phi /2)$-expansion scheme^26,27, the Hirota’s bilinear scheme^28,29,30,31, the generalized G-expansion method³², the modulation instability analysis³³, the cubic-quintic nonlinear Helmholtz equation³⁴,  the finite difference method³⁵ and the real-time subsurface scattering technique³⁶. Further, the exploration of dynamics of nonlinear waves has attracted renowned interest in diverse physical contexts, which imparts various phenomena associated with characteristics of solitons^{37,38,39,40,41}. The soliton solutions were investigated in Refs^42,43,44. Recent research endeavors have concentrated on uncovering equations and problems for the nonlinear models, which extends to the cases involving network traffic detection, generalized matrix completion, nonlinear descriptor systems, quasi-Z-source inverter, and fuzzy logic^{45,46,47,48,49}.

Also, in continuation we will study the multiple rogue waves for determining the multiple soliton solutions in which refer to valuable work in Ref⁵⁰. In 2011, Ma and Fan introduced linear superposition principle to get multiple wave solutions of the Hirota bilinear equations⁵¹ and it has been applied to solve NLEEs including a combined equation with three types of nonlinear terms⁵², (2+1)-dimensional Hirota-Satsuma-Ito equations⁵³ in recent.

Also, the Hirota bilinear method is used to obtain multiple soliton interaction for nonlinear Schrödinger equation with dispersion and self phase modulation⁵⁴. Ma in two valuable researches investigated and analyzed N-soliton solutions and the Hirota conditions in (1+1)-dimensions⁵⁵, and the B-type Kadomtsev-Petviashvili equation under general dispersion relations⁵⁶.

The bilinear forms and two families of the N-soliton solutions were constructed to a generalized Whitham-Broer-Kaup-Boussinesq-Kupershmidt system⁵⁷. The hetero-Backlund transformations has been applied to an extended coupled (2+1)-dimensional Burgers system⁵⁸. The auto-Bäcklund transformation via a noncharacteristic movable singular manifold, certain families of the solitonic solutions has been used to variable-coefficient generalized forced-perturbed Korteweg-de Vries (KdV)-Burgers equation⁵⁹. Multi-pole solitons in an inhomogeneous multi-component nonlinear optical medium have been applied⁶⁰. The (3+1)-dimensional KdV-Calogero-Bogoyavlenskii-Schif equation in a fluid was investigated using the truncated Painlevé expansion⁶¹.

Solving nonlinear evolution equations analytically can be challenging due to the presence of nonlinear terms, which makes the equations difficult to solve exactly including the classical a-Weyl theorem⁶²,  the iterated function system⁶³, a hydroxyethyl group⁶⁴, the tangential force effects on the vibration⁶⁵ and excellent microwave absorption method⁶⁶. Nevertheless, there are several methods that can be used to obtain analytical solutions for some types of nonlinear evolution equations such as the sacrifice of mechanical strength or thermal stability⁶⁷, controlling the reaction temperature⁶⁸, a robust observer method⁴⁷ an improved transient sub-domain analytical model⁶⁹ and molecular dynamic computations⁷⁰.

We expressed clearly that others’ published papers do not cover our work and results available in the paper is really new.

The rest of this paper is structured as follows: the multiple rouge waves technique is summarized in Section 2. In Section 3, the MRWSM is applied to construct the multiple wave solutions to the generalized Hirota-Satsuma-Ito equation. In Section 4, the interaction one soliton with another types are presented to verify and obtaining the analytic solutions. In sections 5 and 6, N-soliton and multiple wave solutions of the GHSISWW equation are concluded using the Hirota bilinear scheme and linear superposition technique, and also, the linear superposition technique is established when $f=\sum _{i=1}^{N}\phi _if_i$ with each exponential wave $f_i$ satisfies the corresponding nonlinear dispersion relation. Finally, we give the conclusion in Section 7.

Multiple rouge-wave solution method

To think about the gHSI condition (7) and by applying the numerous arrangements by utilizing the Hirota operator, the taking after steps will be explored as:

Step 1. Let a nonlinear PDE with the following format

$$\begin{aligned} \mathcal {W}(\Psi _x, \Psi _y, \Psi _t, \Psi _{xx}, \Psi _{xy}, \Psi _{tt},...)=0.\hspace{6cm} \end{aligned}$$

(10)

With a simple transformation we get to below relation as

$$\begin{aligned} \Psi =\mathfrak {Z}(f), \hspace{2.5cm} \end{aligned}$$

(11)

in which f is a function of some variables.

Step 2. Extracting the relation (11), one becomes

$$\begin{aligned} \mathfrak {H}(D_{\xi },D_y; f)=0, \hspace{2.5cm} \end{aligned}$$

(12)

where $\xi =x-ct$ and c is the free value. Thereby, the D-operator is mentioned in the below shape

$$\begin{aligned} \prod _{i=1}^{2}D_{\varsigma _i}^{\beta _i}f. g=\left. \prod _{i=1}^{2}\left( \frac{\partial }{\partial \varsigma _i}-\frac{\partial }{\partial \varsigma '_i}\right) ^{\beta _i}f(\varsigma )g(\varsigma ')\right| _{\varsigma '=\varsigma }, \hspace{6cm} \end{aligned}$$

(13)

where the vectors $\varsigma =(\varsigma _1,\varsigma _2)=(\xi ,y)$, $\varsigma '=(\varsigma '_1,\varsigma '_2)=(\xi ',y')$ and $\beta _1,\beta _2$ are specified values.

Step 3. Assume

$$\begin{aligned} f=f(\xi ,y; \theta ,\delta )=\chi _{n+1}(\xi ,y)+2\delta y p_n(\xi ,y)+2\delta \xi s_n(\xi ,y)+(\theta ^2+\delta ^2)\chi _{n-1}(\xi ,y), \hspace{3cm} \end{aligned}$$

(14)

with

$$\begin{aligned} & \chi _{\tau }(\xi ,y)=\sum _{k=0}^{\frac{\tau (\tau +1)}{2}}\sum _{l=0}^{k}a_{\tau (\tau +1)-2k,2l}y^{2l}\xi ^{\tau (\tau +1)-2k}, \nonumber \\ & p_{\tau }(\xi ,y)=\sum _{k=0}^{\frac{\tau (\tau +1)}{2}}\sum _{l=0}^{k}b_{\tau (\tau +1)-2k,2l}y^{2l}\xi ^{\tau (\tau +1)-2k}, \nonumber \\ & s_{\tau }(\xi ,y)=\sum _{k=0}^{\frac{\tau (\tau +1)}{2}}\sum _{l=0}^{k}c_{\tau (\tau +1)-2k,2l}y^{2l}\xi ^{\tau (\tau +1)-2k}, \end{aligned}$$

(15)

$\chi _0= 1, \chi _1=p_0= s_0= 0$, where $a_{r,l}, b_{r,l}, c_{r,l} (r, l \in \{0, 2, 4, . . . ,\tau (\tau +1)\})$ and $\theta , \delta$ are the real parameters. The coefficients $a_{r,l}, b_{r,l}, c_{r,l}$ can be obtained, and the articular values $\theta , \delta$ are employed to search the wave center.

Step 4. Substituting (15) into (14) and after simple algebraic computations get to value $a_{r,l}, b_{r,l}, c_{r,l}$.

Step 5. Joining the parameters of $a_{r,l}, b_{r,l}, c_{r,l}$ into (13) reach the solutions to the gHSI equation (7), which are retrieved to find rogue wave (RW) solutions.

Rogue wave solutions of a generalized HSI equation

Choice I: First-order RW

The one-wave function according to $\xi =x-ct$ for Eq. (7) will be converted in the following:

$$\begin{aligned} -c\Psi _{\xi \xi \xi \xi }-3c(\Psi _\xi ^2)_\xi +(\delta _2-c\delta _4)\Psi _{\xi \xi }+(\delta _3-c\delta _1)\Psi _{y\xi }+\delta _5\Psi _{yy}=0, \end{aligned}$$

(16)

in which c is unarticulated value and through inserting the below bilinear relation as

$$\begin{aligned} \Psi =2\frac{d \ln f(y,\xi )}{d \xi },\hspace{8.5cm} \end{aligned}$$

(17)

Eq. (16) mentioned to the bilinear model as follows

$$\begin{aligned} \left( D_\xi ^4+(\delta _3-c\delta _1)D_\xi D_y+(\delta _2-c\delta _4)D_\xi ^2+\delta _5 D_y^2\right) \mathfrak {f}. \mathfrak {f}=0,\hspace{4.5cm} \end{aligned}$$

(18)

with

$$\begin{aligned} D_\xi ^4 \mathfrak {f}. \mathfrak {f}=2(\mathfrak {f}\mathfrak {f}_{4\xi }-4\mathfrak {f}_\xi \mathfrak {f}_{3\xi }+3\mathfrak {f}_{\xi \xi }^2),\ \ \ \ D_\xi ^2 \mathfrak {f}. \mathfrak {f}=2(\mathfrak {f}\mathfrak {f}_{2\xi }-\mathfrak {f}_{\xi }^2), \ \ \ \ D_y^2 \mathfrak {f}. \mathfrak {f}=2(\mathfrak {f}\mathfrak {f}_{2y}-\mathfrak {f}_{y}^2). \end{aligned}$$

By selecting $n=0$ at (14), thereinafter (14) will be presented as

$$\begin{aligned} \mathfrak {f}=\mathfrak {f}_1(\xi ,y; \theta ,\delta )=\chi _{1}(\xi ,y)+2\delta y p_0(\xi ,y)+2\delta \xi s_0(\xi ,y)+(\theta ^2+\delta ^2)\chi _{-1}(\xi ,y)=a_{2,0}\xi ^2+a_{0,2}y^2+a_{0,0}. \end{aligned}$$

(19)

For simplicity select $a_{2,0}= 1$. Putting (19) into (18), the nonlinear algebraic structure will be reached as

$$\begin{aligned} & -4\,ca_{{0,0}}\delta _{{4}}+4\,a_{{0,0}}a_{{0,2}}\delta _{{5}}+4\,a_{{0,0 }}\delta _{{2}}-24\,c =0, \ \ \ \ -4\,ca_{{0,2}}\delta _{{4}}-4\,{a_{{0,2}}}^{2}\delta _{{5}}+4\,a_{{0,2}} \delta _{{2}} =0. \ \ \ \nonumber \\ & 8\,ca_{{0,2}}\delta _{{1}}-8\,a_{{0,2}}\delta _{{3}}=0,\ \ \ \ 4\,c\delta _{{4}}+4\,a_{{0,2}}\delta _{{5}}-4\,\delta _{{2}}=0. \end{aligned}$$

(20)

Solving Eq. (20), one get

$$\begin{aligned} c={\frac{\delta _{{3}}}{\delta _{{1}}}}, \ \ \ \ a_{{0,0}}={\frac{3\delta _{{3}}}{\delta _{{1}}\delta _{{2}}-\delta _{{3 }}\delta _{{4}}}},\ \ \ \ a_{{0,2}}={\frac{\delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}}}{ \delta _{{1}}\delta _{{5}}}}. \end{aligned}$$

(21)

Eq. (19) will be shown as

$$\begin{aligned} \mathfrak {f}=\mathfrak {f}_1(\xi ,y; \theta ,\delta )=(\xi -\theta )^2+{\frac{\delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}}}{ \delta _{{1}}\delta _{{5}}}}(y-\delta )^2+{\frac{3\delta _{{3}}}{\delta _{{1}}\delta _{{2}}-\delta _{{3 }}\delta _{{4}}}}, \hspace{0cm} \end{aligned}$$

(22)

by supposing $\delta _1\delta _5\ne 0,$ and $\delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}}\ne 0$, the first solution of Eq. (7) is determined as

$$\begin{aligned} \Psi (\xi ,y)=\Psi _{{0}}+2\,{(2\,\xi -2\,\theta ) \left( {\frac{ \left( \delta _{{1}}\delta _{{2}} -\delta _{{3}}\delta _{{4}} \right) \left( y-\delta \right) ^{2}}{ \delta _{{1}}\delta _{{5}}}}+ \left( \xi -\theta \right) ^{2}+3\,{\frac{ \delta _{{3}}}{\delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}}}} \right) ^{-1}}. \hspace{0cm} \end{aligned}$$

(23)

The following limit properties is available here as

$$\begin{aligned} \lim _{\xi \longrightarrow \pm \infty }\Psi (\xi ,y)=\Psi _0,\ \ \ \ \lim _{y\longrightarrow \pm \infty }\Psi (\xi ,y)=\Psi _0. \hspace{4cm} \end{aligned}$$

(24)

By selecting the convenient values, Fig. 1 and Fig. 2 are designed. With a straightforward computation can get it that the lump has two basic focuses, but we quest as it were one point $(\xi _1, y_1) =\left( {\frac{\theta \, \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{ 4}} \right) + \sqrt{3\,\delta _{{3}} \left( \delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}} \right) }}{\delta _{{1}}\delta _{{2}}-\delta _{{ 3}}\delta _{{4}}}} , \delta \right)$. At the point $(\xi _1, y_1)$, the second order derivative can be found⁷¹ within the taking after

$$\begin{aligned} \left\{ \begin{array}{ll} \Theta {1}=\left. \frac{\partial ^2}{\partial \xi ^2}\Psi (\xi ,y)\right| _{(\xi _1,y_1)}= -\frac{2}{9}{\frac{ \sqrt{\delta _{{3}} \left( \delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}} \right) } \sqrt{3} \left( \delta _{{1}}\delta _ {{2}}-\delta _{{3}}\delta _{{4}} \right) }{{\delta _{{3}}}^{2}}} , \\ \Delta _1= det\left( \begin{array}{cc} \frac{\partial ^2}{\partial \xi ^2}\Psi (\xi ,y) & \frac{\partial ^2}{\partial \xi \partial y}\Psi (\xi ,y) \\ \frac{\partial ^2}{\partial \xi \partial y}\Psi (\xi ,y) & \frac{\partial ^2}{\partial y^2}\Psi (\xi ,y) \\ \end{array} \right) _{(\xi _1,y_1)}={\frac{4\, \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{4}}{27\,{\delta _{{3}}}^{3}\delta _{{1}}\delta _{{5}}}} . \end{array} \right. \hspace{5cm} \end{aligned}$$

(25)

If $\delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}}>0, \delta _3>0$, and $\Delta _1>0$, then the point $(\xi _1, y_1)$ is extreme point. According to above treatment, the point $(\xi _1, y_1)$ is a maximum point at which $\Psi _{max}$. By utilizing diverse $\delta _1,\delta _2,\delta _3$ and $\delta _4$ values, the lump solution $\Psi (\xi ,y)$ has one maximum value including $\Psi _{\max }=\frac{1}{3}{\frac{2\, \sqrt{3} \sqrt{\delta _{{3}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) }+3\,\delta _{{3}}\Psi _{{0}}}{ \delta _{{3}}}}$.

Figure 1

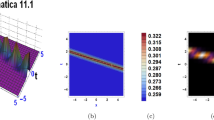
Outlook of the lump wave solution (23) in $\delta =\theta =2,\alpha =1.2, \delta _1=2,\delta _2=3, \delta _3=1,\delta _4=2, \delta _5=1, \Psi _0= 1$.

Figure 2

Outlook of the lump wave solution (23) in $\delta =\theta =-2,\alpha =1.2, \delta _1=2,\delta _2=3, \delta _3=1,\delta _4=2, \delta _5=1, \Psi _0= 1$.

Choice II: The second-order RW

The two-wave form concurring to $xi=x-ct$ and with catching $n=1$ at (refe4), at that point Eq. (7) will be changed over as the taking after shape

$$\begin{aligned} & \mathfrak {f}=\mathfrak {f}_2(\xi ,y; \theta ,\delta )=\chi _{2}(\xi ,y)+2\delta y p_1(\xi ,y)+2\delta \xi s_1(\xi ,y)+(\theta ^2+\delta ^2)\chi _{0}(\xi ,y)\hspace{4cm} \nonumber \\ & = {\xi }^{6}+a_{{4,2}}{y}^{2}{\xi }^{4}+a_{{2,4}}{y}^{4}{\xi }^{2}+a_{{0,6} }{y}^{6}+a_{{4,0}}{\xi }^{4}+a_{{2,2}}{y}^{2}{\xi }^{2}+a_{{0,4}}{y}^{4} +a_{{2,0}}{\xi }^{2}+a_{{0,2}}{y}^{2}+a_{{0,0}}\nonumber \\ & + 2\,\delta \,y \left( { \xi }^{2}b_{{2,0}}+{y}^{2}b_{{0,2}}+b_{{0,0}} \right) + 2\,\theta \,\xi \, \left( {\xi }^{2}c_{{2,0}}+{y}^{2}c_{{0,2}}+c_{{0,0}} \right) +{\delta }^{2}+{\theta }^{2}. \end{aligned}$$

(26)

For simplicity we put $a_{6,0}= 1$. After plugging (26) into (18) and solve the related system one obtain the following findings:

$$\begin{aligned} & a_{{0,0}}=\frac{1}{9}{\frac{{\delta }^{2} \left( \delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}} \right) ^{2} \left( {b_{{2,0}}}^{2}\delta _{{1 }}\delta _{{5}}-9\,\delta _{{1}}\delta _{{2}}+9\,\delta _{{3}}\delta _{{4}} \right) +9\,{\theta }^{2} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}} \right) ^{3} \left( {c_{{2,0}}}^{2}-1 \right) +16875\,{ \delta _{{3}}}^{3}}{ \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{3}}}, \nonumber \\ & a_{{0,2}}={\frac{475{\delta _{{3}}}^{2}}{\delta _{{5}}\delta _{{1}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) }} ,\ \ a_{{0,4}}={\frac{17\delta _{{3}} \left( \delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}} \right) }{{\delta _{{1}}}^{2}{\delta _{{5}}}^{2 }}} ,\ \ a_{{0,6}}={\frac{ \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _ {{4}} \right) ^{3}}{{\delta _{{1}}}^{3}{\delta _{{5}}}^{3}}},\ \ a_{{2,0}}=-{\frac{125{\delta _{{3}}}^{2}}{ \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{2}}}, \nonumber \\ & a_{{2,2}}={\frac{90\delta _{{3}}}{\delta _{{1}}\delta _{{5}}}},\ \ a_{{2,4}}={\frac{3 \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}} \right) ^{2}}{{\delta _{{1}}}^{2}{\delta _{{5}}}^{2}}},\ \ a_{{4,0}}={\frac{25\delta _{{3}}}{\delta _{{1}}\delta _{{2}}-\delta _{{ 3}}\delta _{{4}}}},\ \ a_{{4,2}}={\frac{3\delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} }{\delta _{{1}}\delta _{{5}}}},\ \ b_{{0,0}}=5/3\,{\frac{b_{{2,0}}\delta _{{3}}}{\delta _{{1}}\delta _{{2}} -\delta _{{3}}\delta _{{4}}}}, \nonumber \\ & b_{{0,2}}=-\frac{1}{3}{\frac{b_{{2,0}} \left( \delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}} \right) }{\delta _{{1}}\delta _{{5}}}},\ \ b_{{2,0}}=b_{{2,0}},\ \ c_{{0,0}}=-{\frac{c_{{2,0}}\delta _{{3}}}{\delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}}}},\ \ c_{{0,2}}=-{\frac{3c_{{2,0}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) }{\delta _{{1}}\delta _{{5}}}},\ \ c_{{2,0}}=c_{{2,0}}, \end{aligned}$$

(27)

in which $b_{{2,0}}$ and $c_{{2,0}}$ are the undesignated values. Hence, the second-order RW solutions of Eq. (7) can be mentioned as

$$\begin{aligned} \Psi (\xi ,y)=2(\ln \mathfrak {f}_2(\xi ,y; \theta ,\delta ))_{\xi },\hspace{5.5cm} \end{aligned}$$

(28)

in which $\mathfrak {f}_2(\xi ,y; \theta ,\delta )$ is determined in Eq. (26). The following limit properties is available here as

$$\begin{aligned} \lim _{\xi \longrightarrow \pm \infty }\Psi (\xi ,y)=\Psi _0,\ \ \ \ \lim _{y\longrightarrow \pm \infty }\Psi (\xi ,y)=\Psi _0. \hspace{4cm} \end{aligned}$$

(29)

By choice the convenient values, Fig. 3 and Fig. 4 are designed. In Fig. 3 the rogue wave has one center $(\delta ,\theta )=(1, 5)$, while in Fig. 4 the rogue wave has one center $(\delta ,\theta )=(-2, -3)$.

Figure 3

Outlook of the two lump wave solution (28) in $\delta =1, \theta =5,c_{2,0}= -2, b_{2,0}= 3, \delta _1=2,\delta _2=3, \delta _3=1,\delta _4=2, \delta _5=1, \Psi _0= 1$.

Figure 4

Outlook of the two lump wave solution (28) in $\delta =-2, \theta =-3, c_{2,0}= -2, b_{2,0}= 3, \delta _1=2,\delta _2=3, \delta _3=1,\delta _4=2, \delta _5=1, \Psi _0= 1$.

Choice III: The third-order RW

The three-wave form according to $\xi =x-dt$ and with considering $n=2$ at (14), at the same time Eq. (7) will be reached in the following form

$$\begin{aligned} & \mathfrak {f}=\mathfrak {f}_3(\xi ,y; \theta ,\delta )=\chi _{3}(\xi ,y)+2\delta y p_2(\xi ,y)+2\delta \xi s_2(\xi ,y)+(\theta ^2+\delta ^2)\chi _{1}(\xi ,y) \nonumber \\ &= a_{{0,0}}+{\xi }^{12}+2\,\theta \,\xi \, \left( {\xi }^{6}c_{{6,0}}+{\xi }^ {4}{y}^{2}c_{{4,2}}+{\xi }^{2}{y}^{4}c_{{2,4}}+{y}^{6}c_{{0,6}}+{\xi }^{ 4}c_{{4,0}}+{\xi }^{2}{y}^{2}c_{{2,2}}+{y}^{4}c_{{0,4}}+{\xi }^{2}c_{{2,0 }}+{y}^{2}c_{{0,2}}+c_{{0,0}} \right) \hspace{4cm}\nonumber \\ &+ a_{{0,6}}{y}^{6}+a_{{4,0}}{\xi } ^{4}+a_{{0,4}}{y}^{4}+a_{{2,0}}{\xi }^{2}+a_{{0,2}}{y}^{2}+a_{{8,2}}{y} ^{2}{\xi }^{8}+a_{{6,4}}{y}^{4}{\xi }^{6}+a_{{8,4}}{y}^{4}{\xi }^{8}+a_{{ 10,2}}{y}^{2}{\xi }^{10}+a_{{4,8}}{y}^{8}{\xi }^{4}+a_{{6,2}}{y}^{2}{\xi }^{6}\nonumber \\ & + a_{{6,6}}{y}^{6}{\xi }^{6}+a_{{4,4}}{y}^{4}{\xi }^{4}+a_{{4,6}}{y} ^{6}{\xi }^{4}+a_{{2,8}}{y}^{8}{\xi }^{2}+a_{{2,6}}{y}^{6}{\xi }^{2}+a_{{ 2,10}}{y}^{10}{\xi }^{2}+2\,\delta \,y ( {\xi }^{6}b_{{6,0}}+{\xi }^{ 4}{y}^{2}b_{{4,2}}+{\xi }^{2}{y}^{4}b_{{2,4}}\nonumber \\ & + {y}^{6}b_{{0,6}}+{\xi }^{4 }b_{{4,0}}+{\xi }^{2}{y}^{2}b_{{2,2}}+{y}^{4}b_{{0,4}}+{\xi }^{2}b_{{2,0 }}+{y}^{2}b_{{0,2}}+b_{{0,0}}) +a_{{0,8}}{y}^{8}+a_{{0,10}}{y}^ {10}+a_{{0,12}}{y}^{12}+ \left( {\delta }^{2}+{\theta }^{2} \right) \chi _1(\xi ,y), \end{aligned}$$

(30)

where $\chi _1(\xi ,y)=(\xi -\theta )^2+{\frac{\delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}}}{ \delta _{{1}}\delta _{{5}}}}(y-\delta )^2+{\frac{3\delta _{{3}}}{\delta _{{1}}\delta _{{2}}-\delta _{{3 }}\delta _{{4}}}}$. For simplicity we choice $a_{12,0}= 1$. Substituting (30) into (18) and solve the related framework one get the underneath comes about:

$$\begin{aligned} & a_{{0,0}}={\frac{\delta _{{3}} \left( 27\,{\delta }^{2}{b_{{6,0}}}^{2} \delta _{{1}}\delta _{{5}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}} \right) ^{4}-675\, \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{5} \left( -{\theta }^{2}{c_{{6,0}}}^{2}+{ \delta }^{2}+{\theta }^{2} \right) +21970650625\,{\delta _{{3}}}^{5} \right) }{225\, \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{ 4}} \right) ^{6}}} , \nonumber \\ & a_{{0,2}}={\frac{3\,{\delta }^{2}{b_{{6,0}}}^{2}\delta _{{1}}\delta _{{5 }} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{ 4}-75\, \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{5} \left( -{\theta }^{2}{c_{{6,0}}}^{2}+{\delta }^{2}+{\theta }^{2} \right) +7522418750\,{\delta _{{3}}}^{5}}{75\,\delta _{{5}}\delta _ {{1}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{4}}}, \nonumber \\ & a_{{0,4}}={\frac{16391725\,{\delta _{{3}}}^{4}}{3\,{\delta _{{5}}}^{2}{ \delta _{{1}}}^{2} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{ {4}} \right) ^{2}}} ,\ \ a_{{0,6}}={\frac{798980\,{\delta _{{3}}}^{3}}{3\,{\delta _{{5}}}^{3}{ \delta _{{1}}}^{3}}},\ \ a_{{0,8}}={\frac{4335{\delta _{{3}}}^{2} \left( \delta _{{1}}\delta _{ {2}}-\delta _{{3}}\delta _{{4}} \right) ^{2}}{{\delta _{{5}}}^{4}{\delta _ {{1}}}^{4}}},\ \ a_{{0,10}}={\frac{58\delta _{{3}} \left( \delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}} \right) ^{4}}{{\delta _{{5}}}^{5}{\delta _{{1}} }^{5}}},\ \ \nonumber \\ & a_{{0,12}}={\frac{ \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{6}}{{\delta _{{1}}}^{6}{\delta _{{5}}}^{6}}},\ \ a_{{0,2}}={\frac{3\,{\delta }^{2}{b_{{6,0}}}^{2}\delta _{{1}}\delta _{{5 }} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{ 4}-75\, \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{5} \left( -{\theta }^{2}{c_{{6,0}}}^{2}+{\delta }^{2}+{\theta }^{2} \right) +3994663750\,{\delta _{{3}}}^{5}}{75\,\delta _{{5}}\delta _ {{1}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{4}}}, \nonumber \\ & a_{{2,2}}={\frac{565950{\delta _{{3}}}^{4}}{\delta _{{5}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{3}\delta _{ {1}}}},\ \ a_{{2,4}}=-{\frac{14700{\delta _{{3}}}^{3}}{{\delta _{{5}}}^{2}{ \delta _{{1}}}^{2} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{ {4}} \right) }},\ \ a_{{2,6}}={\frac{ 35420\left( \delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}} \right) {\delta _{{3}}}^{2}}{{\delta _{{5}}}^{3}{\delta _{{1 }}}^{3}}},\ \ a_{{2,8}}={\frac{570\delta _{{3}} \left( \delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}} \right) ^{3}}{{\delta _{{5}}}^{4}{\delta _{{1}} }^{4}}}, \nonumber \\ & a_{{2,10}}=6\,{\frac{ \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}} \right) ^{5}}{{\delta _{{5}}}^{5}{\delta _{{1}}}^{5}}},\ \ a_{{4,0}}=-{\frac{5187875\,{\delta _{{3}}}^{4}}{3\, \left( \delta _{{1} }\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{4}}},\ \ a_{{4,2}}={\frac{220500{\delta _{{3}}}^{3}}{\delta _{{5}}\delta _{{1}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{2} }},\ \ a_{{4,4}}={\frac{37450{\delta _{{3}}}^{2}}{{\delta _{{5}}}^{2}{\delta _{{1}}}^{2}}},\ \ \nonumber \\ & a_{{4,6}}={\frac{1460\left( \delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}} \right) ^{2}\delta _{{3}}}{{\delta _{{5}}}^{3}{\delta _{{1}} }^{3}}}, \ \ a_{{4,8}}=15\,{\frac{ \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}} \right) ^{4}}{{\delta _{{5}}}^{4}{\delta _{{1}}}^{4}}},\ \ a_{{6,0}}={\frac{75460\,{\delta _{{3}}}^{3}}{3\, \left( \delta _{{1}} \delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{3}}} ,\ \ a_{{6,2}}={\frac{18620{\delta _{{3}}}^{2}}{\delta _{{5}}\delta _{{1}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) }}, \nonumber \\ & a_{{6,4}}={\frac{ 1540\left( \delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}} \right) \delta _{{3}}}{{\delta _{{5}}}^{2}{\delta _{{1}}}^{2 }}} ,\ \ a_{{6,6}}={\frac{ 20\left( \delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}} \right) ^{3}}{{\delta _{{5}}}^{3}{\delta _{{1}}}^{3}}} ,\ \ a_{{8,0}}={\frac{735{\delta _{{3}}}^{2}}{ \left( \delta _{{1}}\delta _ {{2}}-\delta _{{3}}\delta _{{4}} \right) ^{2}}}, \ \ a_{{8,2}}={\frac{690\delta _{{3}}}{\delta _{{1}}\delta _{{5}}}},\ \ a_{{8,4}}=15\,{\frac{ \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}} \right) ^{2}}{{\delta _{{5}}}^{2}{\delta _{{1}}}^{2}}}, \nonumber \\ & a_{{10,0}}=98\,{\frac{\delta _{{3}}}{\delta _{{1}}\delta _{{2}}-\delta _{ {3}}\delta _{{4}}}} ,\ \ a_{{10,2}}=6\,{\frac{\delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4} }}{\delta _{{1}}\delta _{{5}}}},\ \ b_{{0,0}}={\frac{3773\,b_{{6,0}}{\delta _{{3}}}^{3}}{3\, \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{3}}},\ \ b_{{0,2}}=-49\,{\frac{{\delta _{{3}}}^{2}b_{{6,0}}}{\delta _{{5}}\delta _{{1}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) }},\ \ \nonumber \\ & b_{{0,4}}=-\frac{7}{5}{\frac{\delta _{{3}}b_{{6,0}} \left( \delta _{{1}} \delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) }{{\delta _{{5}}}^{2}{ \delta _{{1}}}^{2}}},\ \ b_{{0,6}}=1/5\,{\frac{b_{{6,0}} \left( \delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}} \right) ^{3}}{{\delta _{{5}}}^{3}{\delta _{{1}} }^{3}}},\ \ b_{{2,0}}=-133\,{\frac{{\delta _{{3}}}^{2}b_{{6,0}}}{ \left( \delta _{{ 1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{2}}},\ \ b_{{2,2}}=-38\,{\frac{\delta _{{3}}b_{{6,0}}}{\delta _{{5}}\delta _{{1}} }}, \nonumber \\ & b_{{2,4}}=-\frac{9}{5}{\frac{b_{{6,0}} \left( \delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}} \right) ^{2}}{{\delta _{{5}}}^{2}{\delta _{{1}} }^{2}}} ,\ \ b_{{4,0}}=21\,{\frac{\delta _{{3}}b_{{6,0}}}{\delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}}}},\ \ b_{{4,2}}=-{\frac{b_{{6,0}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{ 3}}\delta _{{4}} \right) }{\delta _{{5}}\delta _{{1}}}},\ \ b_{{6,0}}=b_{{6,0}},\ \ c_{{0,0}}={\frac{12005\,c_{{6,0}}{\delta _{{3}}}^{3}}{3\, \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{3}}}, \nonumber \\ & c_{{0,2}}=535\,{\frac{{\delta _{{3}}}^{2}c_{{6,0}}}{\delta _{{1}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) \delta _{{5}}}} ,\ \ c_{{0,4}}=45\,{\frac{\delta _{{3}}c_{{6,0}} \left( \delta _{{1}}\delta _ {{2}}-\delta _{{3}}\delta _{{4}} \right) }{{\delta _{{5}}}^{2}{\delta _{{1 }}}^{2}}},\ \ c_{{0,6}}=5\,{\frac{c_{{6,0}} \left( \delta _{{1}}\delta _{{2}}-\delta _ {{3}}\delta _{{4}} \right) ^{3}}{{\delta _{{5}}}^{3}{\delta _{{1}}}^{3}}}, \ \ c_{{2,0}}=-245\,{\frac{{\delta _{{3}}}^{2}c_{{6,0}}}{ \left( \delta _{{ 1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{2}}}, \nonumber \\ & c_{{2,2}}=-230\,{\frac{\delta _{{3}}c_{{6,0}}}{\delta _{{5}}\delta _{{1} }}},\ \ c_{{2,4}}=-5\,{\frac{c_{{6,0}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{2}}{{\delta _{{5}}}^{2}{\delta _{{1}}}^{2}} },\ \ c_{{4,0}}=13\,{\frac{\delta _{{3}}c_{{6,0}}}{\delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}}}},\ \ c_{{4,2}}=-9\,{\frac{c_{{6,0}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) }{\delta _{{5}}\delta _{{1}}}},\ \ c_{{6,0}}=c_{{6,0}}, \end{aligned}$$

(31)

in which $b_{{4,2}}$ and $c_{{4,2}}$ are unfound values. And so, the three-order RW arrangements of Eq. (7) can be spoken to as

$$\begin{aligned} \Psi (\xi ,y)=2(\ln \mathfrak {f}_3(\xi ,y; \theta ,\delta ))_{\xi },\hspace{5.5cm} \end{aligned}$$

(32)

where $\mathfrak {f}_3(\xi ,y; \theta ,\delta )$ is defined in Eq. (26). The following limit properties is available here as

$$\begin{aligned} \lim _{\xi \longrightarrow \pm \infty }\Psi (\xi ,y)=\Psi _0,\ \ \ \ \lim _{y\longrightarrow \pm \infty }\Psi (\xi ,y)=\Psi _0. \hspace{4cm} \end{aligned}$$

(33)

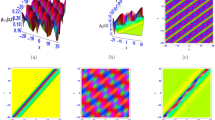
By choice the right amounts of parameters, the realistic representation of three-lump soliton wave arrangements are advertised in Fig. 5, Fig. 6 and Fig. 7 counting 3D graph, form graph, density graph, and 2D graph when three spaces get up at cases ($y=-2,-1.5,-1.2$), ($y=1.3,1.5,2$), and ($y=-1,-0.2,0.5$), respectively. In Fig. 5 the rogue wave has one center $(\delta ,\theta )=(-1, 5)$ and in Fig. 6 the rogue wave has one center $(\delta ,\theta )=(1, 5)$, while in Fig. 7 the rogue wave has one center $(\delta ,\theta )=(0, 0)$.

Figure 5

Outlook of the three lump wave solution (32) in $\delta =-1, \theta =-15, c_{6,0}= -2, b_{6,0}= 3, \delta _1=2,\delta _2=3, \delta _3=1,\delta _4=2, \delta _5=1, \Psi _0= 1$.

Figure 6

Outlook of the three lump wave solution (32) in $\delta =1, \theta =5, c_{6,0}= -2, b_{6,0}= 3, \delta _1=2,\delta _2=3, \delta _3=1,\delta _4=2, \delta _5=1, \Psi _0= 1$.

Figure 7

Outlook of the three lump wave solution (32) in $\delta =0, \theta =0, c_{6,0}= -2, b_{6,0}= 3, \delta _1=2,\delta _2=3, \delta _3=1,\delta _4=2, \delta _5=1, \Psi _0= 1$.

Set IV: The fourth-order RW

The fourth-wave frame according to $\xi =x-ct$ and with considering $n=3$ at (14), next Eq. (7) will be converted in the following form

$$\begin{aligned} & \mathfrak {f}=\mathfrak {f}_4(\xi ,y; \theta ,\delta )=\chi _{4}(\xi ,y)+2\delta y p_3(\xi ,y)+2\delta \xi s_3(\xi ,y)+(\theta ^2+\delta ^2)\chi _{2}(\xi ,y)={\xi }^{20}+a_{{8,0}}{\xi }^{8}+ \left( {\delta }^{2}+{\theta }^{2} \right) \chi _2(\xi ,y)\nonumber \\ & +a_{{0,8}}{y}^{8}+a_{{0,10}}{y}^{10}+a_{{0,12}}{y}^{12}+a_{ {0,14}}{y}^{14}+a_{{0,16}}{y}^{16}+a_{{0,18}}{y}^{18}+a_{{0,20}}{y}^{ 20}+2\,\delta \,y ( b_{{0,0}}+b_{{4,8}}{y}^{8}{\xi }^{4}+b_{{10,2}} {y}^{2}{\xi }^{10}+b_{{6,4}}{y}^{4}{\xi }^{6}+b_{{8,2}}{y}^{2}{\xi }^{8}\nonumber \\ & + b_{{4,6}}{y}^{6}{\xi }^{4}+b_{{6,6}}{y}^{6}{\xi }^{6}+b_{{2,8}}{y}^{8}{ \xi }^{2}+b_{{2,4}}{y}^{4}{\xi }^{2}+b_{{6,2}}{y}^{2}{\xi }^{6}+b_{{4,4}} {y}^{4}{\xi }^{4}+b_{{2,10}}{y}^{10}{\xi }^{2}+b_{{2,6}}{y}^{6}{\xi }^{2} +b_{{8,4}}{y}^{4}{\xi }^{8}+b_{{4,2}}{y}^{2}{\xi }^{4}+b_{{2,2}}{y}^{2}{ \xi }^{2}\nonumber \\ & + b_{{0,2}}{y}^{2}+b_{{0,4}}{y}^{4}+b_{{0,6}}{y}^{6}+b_{{0,8}}{ y}^{8}+b_{{0,10}}{y}^{10}+b_{{0,12}}{y}^{12}+{\xi }^{2}b_{{2,0}}+b_{{10 ,0}}{\xi }^{10}+b_{{8,0}}{\xi }^{8}+b_{{6,0}}{\xi }^{6}+b_{{4,0}}{\xi }^{4 }+b_{{12,0}}{\xi }^{12} ) +a_{{18,0}}{\xi }^{18}+a_{{16,0}}{\xi }^{ 16}\nonumber \\ & + a_{{14,0}}{\xi }^{14}+a_{{12,0}}{\xi }^{12}+a_{{10,0}}{\xi }^{10}+2\, \theta \,\xi \, ( c_{{0,0}}+c_{{2,4}}{y}^{4}{\xi }^{2}+c_{{2,10}}{y} ^{10}{\xi }^{2}+c_{{6,2}}{y}^{2}{\xi }^{6}+c_{{6,6}}{y}^{6}{\xi }^{6}+c_{ {10,2}}{y}^{2}{\xi }^{10}+c_{{2,6}}{y}^{6}{\xi }^{2}+c_{{2,8}}{y}^{8}{ \xi }^{2}\nonumber \\ & + c_{{8,2}}{y}^{2}{\xi }^{8}+c_{{4,4}}{y}^{4}{\xi }^{4}+c_{{4,6}} {y}^{6}{\xi }^{4}+c_{{6,4}}{y}^{4}{\xi }^{6}+c_{{8,4}}{y}^{4}{\xi }^{8}+c _{{4,8}}{y}^{8}{\xi }^{4}+c_{{2,2}}{y}^{2}{\xi }^{2}+c_{{4,2}}{y}^{2}{ \xi }^{4}+c_{{0,2}}{y}^{2}+c_{{0,4}}{y}^{4}+c_{{0,6}}{y}^{6}+c_{{0,8}}{ y}^{8}\nonumber \\ & + c_{{0,10}}{y}^{10}+c_{{0,12}}{y}^{12}+c_{{12,0}}{\xi }^{12}+c_{{ 10,0}}{\xi }^{10}+c_{{8,0}}{\xi }^{8}+c_{{6,0}}{\xi }^{6}+c_{{4,0}}{\xi }^ {4}+{\xi }^{2}c_{{2,0}} ) +a_{{2,18}}{y}^{18}{\xi }^{2}+a_{{0,0}}+ a_{{8,8}}{y}^{8}{\xi }^{8}+a_{{2,16}}{y}^{16}{\xi }^{2}+a_{{2,14}}{y}^{ 14}{\xi }^{2}\nonumber \\ & + a_{{2,12}}{y}^{12}{\xi }^{2}+a_{{2,6}}{y}^{6}{\xi }^{2}+a_{ {8,6}}{y}^{6}{\xi }^{8}+a_{{8,12}}{y}^{12}{\xi }^{8}+a_{{6,6}}{y}^{6}{ \xi }^{6}+a_{{6,2}}{y}^{2}{\xi }^{6}+a_{{6,4}}{y}^{4}{\xi }^{6}+a_{{10,4} }{y}^{4}{\xi }^{10}+a_{{10,6}}{y}^{6}{\xi }^{10}+a_{{8,10}}{y}^{10}{\xi } ^{8}\nonumber \\ & + a_{{10,10}}{y}^{10}{\xi }^{10}+a_{{8,2}}{y}^{2}{\xi }^{8}+a_{{4,14} }{y}^{14}{\xi }^{4}+a_{{4,10}}{y}^{10}{\xi }^{4}+a_{{6,8}}{y}^{8}{\xi }^{ 6}+a_{{6,10}}{y}^{10}{\xi }^{6}+a_{{6,14}}{y}^{14}{\xi }^{6}+a_{{6,12}}{ y}^{12}{\xi }^{6}+a_{{4,8}}{y}^{8}{\xi }^{4}+a_{{12,6}}{y}^{6}{\xi }^{12} \nonumber \\ & + a_{{12,8}}{y}^{8}{\xi }^{12}+a_{{10,8}}{y}^{8}{\xi }^{10}+a_{{8,4}}{y}^ {4}{\xi }^{8}+a_{{10,2}}{y}^{2}{\xi }^{10}+{\xi }^{2}{y}^{2}a_{{2,2}}+a_{ {12,2}}{y}^{2}{\xi }^{12}+a_{{14,6}}{y}^{6}{\xi }^{14}+a_{{14,4}}{y}^{4} {\xi }^{14}+a_{{18,2}}{y}^{2}{\xi }^{18}+{\xi }^{4}{y}^{2}a_{{4,2}}\nonumber \\ & + a_{{ 16,2}}{y}^{2}{\xi }^{16}+a_{{12,4}}{y}^{4}{\xi }^{12}+a_{{14,2}}{y}^{2}{ \xi }^{14}+a_{{16,4}}{y}^{4}{\xi }^{16}+{\xi }^{2}{y}^{4}a_{{2,4}}+a_{{4, 6}}{y}^{6}{\xi }^{4}+a_{{4,4}}{y}^{4}{\xi }^{4}+{\xi }^{6}a_{{6,0}}+{y}^{ 6}a_{{0,6}}+{\xi }^{4}a_{{4,0}}+{y}^{4}a_{{0,4}}+{\xi }^{2}a_{{2,0}}\nonumber \\ & + {y} ^{2}a_{{0,2}}+a_{{2,8}}{y}^{8}{\xi }^{2}+a_{{4,16}}{y}^{16}{\xi }^{4}+a_ {{4,12}}{y}^{12}{\xi }^{4}+a_{{2,10}}{y}^{10}{\xi }^{2}, \end{aligned}$$

(34)

with

$$\begin{aligned} & \chi _2(\xi ,y)= \left( \xi -\theta \right) ^{6}+3\,{\frac{ \left( \delta _{{1}}\delta _ {{2}}-\delta _{{3}}\delta _{{4}} \right) \left( y-\delta \right) ^{2} \left( \xi -\theta \right) ^{4}}{\delta _{{5}}\delta _{{1}}}}+3\,{\frac{ \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{2 } \left( y-\delta \right) ^{4} \left( \xi -\theta \right) ^{2}}{{\delta _{{1}}}^{2}{\delta _{{5}}}^{2}}}+{\frac{ \left( \delta _{{1}}\delta _{{2 }}-\delta _{{3}}\delta _{{4}} \right) ^{3} \left( y-\delta \right) ^{6} }{{\delta _{{1}}}^{3}{\delta _{{5}}}^{3}}}\\ & + 25\,{\frac{\delta _{{3}} \left( \xi -\theta \right) ^{4}}{\delta _{{1}}\delta _{{2}}-\delta _{{3}} \delta _{{4}}}}+90\,{\frac{\delta _{{3}} \left( y-\delta \right) ^{2} \left( \xi -\theta \right) ^{2}}{\delta _{{5}}\delta _{{1}}}}+17\,{ \frac{\delta _{{3}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) \left( y-\delta \right) ^{4}}{{\delta _{{1}}}^{2}{ \delta _{{5}}}^{2}}}-125\,{\frac{{\delta _{{3}}}^{2} \left( \xi -\theta \right) ^{2}}{ \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4 }} \right) ^{2}}}+475\,{\frac{{\delta _{{3}}}^{2} \left( y-\delta \right) ^{2}}{\delta _{{5}}\delta _{{1}} \left( \delta _{{1}}\delta _{{2} }-\delta _{{3}}\delta _{{4}} \right) }}\\ & + \frac{1}{9}{\frac{{\delta }^{2}{b_{{2,0 }}}^{2}\delta _{{1}}\delta _{{5}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{2}-9\, \left( \delta _{{1}}\delta _{{2}}- \delta _{{3}}\delta _{{4}} \right) ^{3} \left( -{\theta }^{2}{c_{{2,0}}}^ {2}+{\delta }^{2}+{\theta }^{2} \right) +16875\,{\delta _{{3}}}^{3}}{ \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) ^{3} }}\\ & + 2\,\delta \, \left( y-\delta \right) \left( \left( \xi -\theta \right) ^{2}b_{{2,0}}-\frac{1}{3}{\frac{ \left( y-\delta \right) ^{2}b_{{2 ,0}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) }{\delta _{{5}}\delta _{{1}}}}+\frac{5}{3}{\frac{b_{{2,0}}\delta _{{3}}}{ \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}}}} \right) \\ & + 2\,\theta \, \left( \xi -\theta \right) \left( \left( \xi -\theta \right) ^{2}c_ {{2,0}}-3\,{\frac{ \left( y-\delta \right) ^{2}c_{{2,0}} \left( \delta _{{1}}\delta _{{2}}-\delta _{{3}}\delta _{{4}} \right) }{\delta _{{5 }}\delta _{{1}}}}-{\frac{c_{{2,0}}\delta _{{3}}}{\delta _{{1}}\delta _{{2 }}-\delta _{{3}}\delta _{{4}}}} \right) +{\delta }^{2}+{\theta }^{2}. \end{aligned}$$

For simplicity we put $a_{20,0}= 1$. Plugging (34) into (18) and solve the mentioned system one become the following results:

$$\begin{aligned} & a_{{0,0}}={\frac{392759613589451185441\,{a_{{18,0}}}^{17}+ 4376759565260494368360000000000000\,{\theta }^{2}{c_{{2,0}}}^{2}}{ 136657746435196794212496000000\,{a_{{18,0}}}^{7} \left( {\delta }^{2}+{ \theta }^{2}+1 \right) }} , \nonumber \\ & a_{{0,2}}={\frac{c_{{2,10}} \left( 115308451900230145739\,{a_{{18,0}} }^{17}+554389544932995953325600000000000\,{\theta }^{2}{c_{{2,0}}}^{2} \right) }{6496400007448323875098560000\,{a_{{18,0}}}^{7}c_{{2,0}}{R_{ {1}}}^{4} \left( {\delta }^{2}+{\theta }^{2}+1 \right) }} , \nonumber \end{aligned}$$

(35)

$$\begin{aligned} & a_{{0,4}}={\frac{c_{{2,10}} \left( 23143464233783035597\,{a_{{18,0}}} ^{17}+39682620058361815606464000000000\,{\theta }^{2}{c_{{2,0}}}^{2} \right) }{481214815366542509266560000\,{a_{{18,0}}}^{7}c_{{2,0}}{R_{{ 1}}}^{3} \left( {\delta }^{2}+{\theta }^{2}+1 \right) }} , \nonumber \\ & a_{{0,6}}={\frac{c_{{2,10}} \left( 597357697607735519\,{a_{{18,0}}}^{ 17}+486306618362277152040000000000\,{\theta }^{2}{c_{{2,0}}}^{2} \right) }{3713077279062828003600000\,{R_{{1}}}^{2}{a_{{18,0}}}^{7}c_{ {2,0}} \left( {\delta }^{2}+{\theta }^{2}+1 \right) }} , \nonumber \end{aligned}$$

$$\begin{aligned} & a_{{0,8}}={\frac{177908423\,{a_{{18,0}}}^{10}{R_{{1}}}^{4}}{ 573956280000000}} ,\ \ a_{{0,10}}={\frac{200709983929\,{a_{{18,0}}}^{10}c_{{2,10}}}{ 3389154437772000000\,c_{{2,0}}}},\ \ a_{{0,12}}={\frac{6637859137\,R_{{1}}{a_{{18,0}}}^{10}c_{{2,10}}}{ 251048476872000000\,c_{{2,0}}}}, \nonumber \\ & a_{{0,14}}={\frac{41899301171\,{a_{{18,0}}}^{10}{c_{{2,10}}}^{2}}{ 16471290567571920000\,{R_{{1}}}^{3}{c_{{2,0}}}^{2}}},\ \ a_{{0,16}}={\frac{1302924259\,{a_{{18,0}}}^{10}{c_{{2,10}}}^{2}}{ 2711323550217600000\,{R_{{1}}}^{2}{c_{{2,0}}}^{2}}},\ \ a_{{0,18}}={\frac{8281\,{a_{{18,0}}}^{10}{R_{{1}}}^{4}c_{{2,10}}}{ 38263752000000\,c_{{2,0}}}},\ \ \nonumber \end{aligned}$$

$$\begin{aligned} & a_{{0,20}}={\frac{68574961\,{a_{{18,0}}}^{10}{c_{{2,10}}}^{2}}{ 4518872583696000000\,{c_{{2,0}}}^{2}}},\ \ a_{{2,0}}=-{\frac{23103506681732422673\,{a_{{18,0}}}^{17}+ 145891985508683145612\times 10^{12}\,{\theta }^{2}{c_{{2,0}}}^{2}}{ 253069900805919989282400000\,{a_{{18,0}}}^{8} \left( {\delta }^{2}+{ \theta }^{2}+1 \right) }}, \nonumber \\ & a_{{2,2}}={\frac{c_{{2,10}} \left( 28883995444263292333\,{a_{{18,0}}} ^{17}+105042229566251864840640000000000\,{\theta }^{2}{c_{{2,0}}}^{2} \right) }{24060740768327125463328000\,{a_{{18,0}}}^{8}c_{{2,0}}{R_{{1 }}}^{4} \left( {\delta }^{2}+{\theta }^{2}+1 \right) }} , \nonumber \end{aligned}$$

$$\begin{aligned} & a_{{2,4}}={\frac{c_{{2,10}} \left( 754157056565293927\,{a_{{18,0}}}^{ 17}+875351913052098873672000000000\,{\theta }^{2}{c_{{2,0}}}^{2} \right) }{222784636743769680216000\,{R_{{1}}}^{3}{a_{{18,0}}}^{8}c_{{ 2,0}} \left( {\delta }^{2}+{\theta }^{2}+1 \right) }} ,\ \ a_{{2,6}}={\frac{73409791\,{a_{{18,0}}}^{9}{R_{{1}}}^{3}}{ 14348907000000}}, \nonumber \\ & a_{{2,8}}={\frac{2331679\,{a_{{18,0}}}^{9}{R_{{1}}}^{4}}{ 1062882000000}} ,\ \ a_{{2,10}}={\frac{6178644563\,{a_{{18,0}}}^{9}c_{{2,10}}}{ 12552423843600000\,c_{{2,0}}}},\ \ a_{{2,12}}={\frac{54662881\,{a_{{18,0}}}^{9}c_{{2,10}}R_{{1}}}{ 77484097800000\,c_{{2,0}}}},\ \ \nonumber \end{aligned}$$

$$\begin{aligned} & a_{{2,14}}={\frac{13509267317\,{a_{{18,0}}}^{9}{c_{{2,10}}}^{2}}{ 183014339639688000\,{R_{{1}}}^{3}{c_{{2,0}}}^{2}}} ,\ \ a_{{2,16}}={\frac{604513\,{a_{{18,0}}}^{9}{R_{{1}}}^{3}c_{{2,10}}}{ 19131876000000\,c_{{2,0}}}},\ \ a_{{2,18}}={\frac{8281\,{a_{{18,0}}}^{9}{R_{{1}}}^{4}c_{{2,10}}}{ 2125764000000\,c_{{2,0}}}}, \nonumber \\ & a_{{4,0}}={\frac{12649431260134041373\,{a_{{18,0}}}^{17}+ 58356794203473258244800000000000\,{\theta }^{2}{c_{{2,0}}}^{2}}{ 1874591857821629550240000\,{a_{{18,0}}}^{9} \left( {\delta }^{2}+{ \theta }^{2}+1 \right) }} , \nonumber \end{aligned}$$

$$\begin{aligned} & a_{{4,2}}={\frac{c_{{2,10}} \left( 11046760559953573\,{a_{{18,0}}}^{ 17}+35014076522083954946880000000\,{\theta }^{2}{c_{{2,0}}}^{2} \right) }{891138546975078720864\,c_{{2,0}}{R_{{1}}}^{4}{a_{{18,0}}}^{ 9} \left( {\delta }^{2}+{\theta }^{2}+1 \right) }} ,\ \ a_{{4,4}}=-{\frac{6012643\,{a_{{18,0}}}^{8}{R_{{1}}}^{2}}{ 573956280000}}, \nonumber \\ & a_{{4,6}}={\frac{1675457\,{R_{{1}}}^{3}{a_{{18,0}}}^{8}}{53144100000} } ,\ \ a_{{4,8}}={\frac{79037\,{a_{{18,0}}}^{8}{R_{{1}}}^{4}}{1574640000}},\ \ a_{{4,10}}={\frac{145091401\,{a_{{18,0}}}^{8}c_{{2,10}}}{ 7748409780000\,c_{{2,0}}}}, \ \ a_{{4,12}}={\frac{14897519\,{a_{{18,0}}}^{8}c_{{2,10}}R_{{1}}}{ 1721868840000\,c_{{2,0}}}}, \nonumber \end{aligned}$$

$$\begin{aligned} & a_{{4,14}}={\frac{157339\,{a_{{18,0}}}^{8}{R_{{1}}}^{2}c_{{2,10}}}{ 95659380000\,c_{{2,0}}}} ,\ \ a_{{4,16}}={\frac{8281\,{R_{{1}}}^{3}{a_{{18,0}}}^{8}c_{{2,10}}}{ 47239200000\,c_{{2,0}}}},\nonumber \\ & a_{{6,0}}={\frac{289024438126543483\,{a_{{18,0}}}^{17}+ 1458919855086831456120000000000\,{\theta }^{2}{c_{{2,0}}}^{2}}{ 4339333004216735070000\,{a_{{18,0}}}^{10} \left( {\delta }^{2}+{\theta } ^{2}+1 \right) }},\ \ a_{{6,2}}=-{\frac{19319573\,{a_{{18,0}}}^{7}R_{{1}}}{143489070000}}, \nonumber \end{aligned}$$

$$\begin{aligned} & a_{{6,4}}={\frac{23569\,{a_{{18,0}}}^{7}{R_{{1}}}^{2}}{5314410000}},\ \ a_{{6,6}}={\frac{141659\,{a_{{18,0}}}^{7}{R_{{1}}}^{3}}{196830000}},\ \ a_{{6,8}}={\frac{28007\,{a_{{18,0}}}^{7}{R_{{1}}}^{4}}{36450000}},\ \ a_{{6,10}}={\frac{82834843\,{a_{{18,0}}}^{7}c_{{2,10}}}{430467210000 \,c_{{2,0}}}}, \nonumber \\ & a_{{6,12}}={\frac{2144779\,{a_{{18,0}}}^{7}c_{{2,10}}R_{{1}}}{ 47829690000\,c_{{2,0}}}} ,\ \ a_{{6,14}}={\frac{8281\,{a_{{18,0}}}^{7}{R_{{1}}}^{2}c_{{2,10}}}{ 1771470000\,c_{{2,0}}}},\ \ a_{{8,0}}=-{\frac{26384449\,{a_{{18,0}}}^{6}}{57395628000}},\ \ a_{{8,2}}={\frac{72163\,{a_{{18,0}}}^{6}R_{{1}}}{212576400}}, \nonumber \end{aligned}$$

$$\begin{aligned} & a_{{8,4}}={\frac{158809\,{a_{{18,0}}}^{6}{R_{{1}}}^{2}}{78732000}},\ \ a_{{8,6}}={\frac{8351\,{a_{{18,0}}}^{6}{R_{{1}}}^{3}}{1215000}},\ \ a_{{8,8}}={\frac{10031\,{R_{{1}}}^{4}{a_{{18,0}}}^{6}}{1620000}},\ \ a_{{8,10}}={\frac{7014007\,{a_{{18,0}}}^{6}c_{{2,10}}}{9565938000\,c_ {{2,0}}}}, \nonumber \\ & a_{{8,12}}={\frac{57967\,{a_{{18,0}}}^{6}c_{{2,10}}R_{{1}}}{708588000 \,c_{{2,0}}}} ,\ \ a_{{10,0}}={\frac{2326961\,{a_{{18,0}}}^{5}}{1594323000}},\ \ a_{{10,2}}={\frac{119483\,{a_{{18,0}}}^{5}R_{{1}}}{59049000}},\ \ a_{{10,4}}={\frac{3493\,{a_{{18,0}}}^{5}{R_{{1}}}^{2}}{121500}}, \nonumber \end{aligned}$$

$$\begin{aligned} & a_{{10,6}}={\frac{9191\,{a_{{18,0}}}^{5}{R_{{1}}}^{3}}{202500}},\ \ a_{{10,8}}={\frac{7\,{a_{{18,0}}}^{5}{R_{{1}}}^{4}}{360}}, \ \ a_{{10,10}}={\frac{57967\,{a_{{18,0}}}^{5}c_{{2,10}}}{59049000\,c_{{2 ,0}}}},\ \ a_{{12,0}}=-{\frac{41951\,{a_{{18,0}}}^{4}}{11809800}},\ \ a_{{12,2}}={\frac{1967\,{a_{{18,0}}}^{4}R_{{1}}}{36450}}, \nonumber \\ & a_{{12,4}}={\frac{1519\,{a_{{18,0}}}^{4}{R_{{1}}}^{2}}{8100}},\ \ a_{{12,6}}={\frac{287\,{a_{{18,0}}}^{4}{R_{{1}}}^{3}}{2250}},\ \ a_{{12,8}}={\frac{21\,{R_{{1}}}^{4}{a_{{18,0}}}^{4}}{1000}}, \ \ a_{{14,0}}={\frac{13\,{a_{{18,0}}}^{3}}{729}},\ \ a_{{14,2}}={\frac{17\,{a_{{18,0}}}^{3}R_{{1}}}{45}}, \nonumber \end{aligned}$$

$$\begin{aligned} & a_{{14,4}}={\frac{23\,{a_{{18,0}}}^{3}{R_{{1}}}^{2}}{45}},\ \ a_{{14,6}}={\frac{3\,{R_{{1}}}^{3}{a_{{18,0}}}^{3}}{25}}, \ \ a_{{16,0}}={\frac{41\,{a_{{18,0}}}^{2}}{180}},\ \ a_{{16,2}}={\frac{101\,{a_{{18,0}}}^{2}R_{{1}}}{90}}, \nonumber \\ & a_{{16,4}}={\frac{9\,{R_{{1}}}^{2}{a_{{18,0}}}^{2}}{20}},\ \ a_{{18,0}}=a_{{18,0}},\ \ a_{{18,2}}=R_{{1}}a_{{18,0}},\ \ b_{{0,0}}=b_{{0,2}}=b_{{0,4}}=b_{{0,6}}=b_{{0,8}}=b_{{0,10}}=b_{{0,12}}=0, \nonumber \end{aligned}$$

$$\begin{aligned} & b_{{2,0}}=b_{{2,2}}=b_{{2,4}}=b_{{2,6}}=b_{{2,8}}=b_{{2,10}}=b_{{4,0}}= b_{{4,2}}=b_{{4,4}}=b_{{4,6}}=b_{{4,8}}=b_{{6,0}}=b_{{6,2}}=b_{{6,4}}=b_{{6,6}}=0,\ \nonumber \\ & b_{{8,0}}=b_{{8,2}}=b_{{8,4}}=b_{{10,0}}=b_{{10,2}}=b_{{12,0}}=0,\ \ c_{{0,0}}=-{\frac{169\,a_{{18,0}}c_{{2,0}}}{79380}},\ \ c_{{0,2}}=-{\frac{627145\,a_{{18,0}}c_{{2,10}}}{3188646\,{R_{{1}}}^{4 }}},\ \ c_{{0,4}}=-{\frac{60235\,a_{{18,0}}c_{{2,10}}}{236196\,{R_{{1}}}^{3}} }, \nonumber \end{aligned}$$

$$\begin{aligned} & c_{{0,6}}=-{\frac{55\,a_{{18,0}}c_{{2,10}}}{243\,{R_{{1}}}^{2}}},\ \ c_{{0,8}}=-{\frac{145\,a_{{18,0}}c_{{2,10}}}{972\,R_{{1}}}}, \ \ c_{{0,10}}=-{\frac{7\,a_{{18,0}}c_{{2,10}}}{90}},\ \ c_{{0,12}}=-\frac{1}{20}c_{{2,10}}R_{{1}}a_{{18,0}},\ \ c_{{2,2}}={\frac{134125\,c_{{2,10}}}{59049\,{R_{{1}}}^{4}}} \nonumber \\ & c_{{2,4}}={\frac{1150\,c_{{2,10}}}{243\,{R_{{1}}}^{3}}}, \ \ c_{{2,6}}={\frac{3550\,c_{{2,10}}}{243\,{R_{{1}}}^{2}}},\ \ c_{{2,8}}=5\,{\frac{c_{{2,10}}}{R_{{1}}}},\ \ c_{{4,0}}=-{\frac{63675\,c_{{2,0}}}{8281\,a_{{18,0}}}},\ \ c_{{4,2}}=-{\frac{26500\,c_{{2,10}}}{2187\,a_{{18,0}}{R_{{1}}}^{4}}},\ \ c_{{4,4}}=-{\frac{1750\,c_{{2,10}}}{243\,a_{{18,0}}{R_{{1}}}^{3}}}, \nonumber \end{aligned}$$

$$\begin{aligned} & c_{{4,6}}={\frac{1300\,c_{{2,10}}}{9\,a_{{18,0}}{R_{{1}}}^{2}}},\ \ c_{{4,8}}=45\,{\frac{c_{{2,10}}}{R_{{1}}a_{{18,0}}}},\ \ c_{{6,0}}={\frac{2284200\,c_{{2,0}}}{57967\,{a_{{18,0}}}^{2}}},\ \ c_{{6,2}}=-{\frac{443000\,c_{{2,10}}}{1701\,{a_{{18,0}}}^{2}{R_{{1}}} ^{4}}},\ \ c_{{6,4}}=-{\frac{29000\,c_{{2,10}}}{63\,{R_{{1}}}^{3}{a_{{18,0}}}^{2 }}}, \nonumber \\ & c_{{6,6}}={\frac{1800\,c_{{2,10}}}{7\,{R_{{1}}}^{2}{a_{{18,0}}}^{2}}},\ \ c_{{8,0}}=-{\frac{12028500\,c_{{2,0}}}{57967\,{a_{{18,0}}}^{3}}},\ \ c_{{8,2}}=-{\frac{935000\,c_{{2,10}}}{189\,{R_{{1}}}^{4}{a_{{18,0}}}^ {3}}},\ \ c_{{8,4}}=-{\frac{12500\,c_{{2,10}}}{7\,{R_{{1}}}^{3}{a_{{18,0}}}^{3} }},\ \ c_{{10,0}}={\frac{291308400\,c_{{2,0}}}{57967\,{a_{{18,0}}}^{4}}}, \nonumber \end{aligned}$$

$$\begin{aligned} & c_{{10,2}}=-{\frac{90000\,c_{{2,10}}}{7\,{R_{{1}}}^{4}{a_{{18,0}}}^{4 }}} ,\ \ c_{{12,0}}={\frac{1062882000\,c_{{2,0}}}{57967\,{a_{{18,0}}}^{5}}},\ \ \delta _{{2}}={\frac{R_{{1}}a_{{18,0}}\delta _{{5}} \left( a_{{18,0}} \delta _{{4}}+270 \right) }{2700}},\ \ \delta _{{3}}={\frac{{a_{{18,0}}}^{2}R_{{1}}\delta _{{1}}\delta _{{5}}}{ 2700}}, \end{aligned}$$

in which $R_1$ solves the relation $531441\,{R_{{1}}}^{5}c_{{2,0}}-207025\,c_{{2,10}}=0$ and $a_{{18,0}}, b_{{0,12}}, c_{{2,0}}, c_{{2,10}}$ are arbitrary values. So, the fourth-order rogue wave solutions of Eq. (7) can be reached by employing Eq. (17) as follows

$$\begin{aligned} \Psi (\xi ,y)=2(\ln \mathfrak {f}_4(\xi ,y; \theta ,\delta ))_{\xi },\hspace{5.5cm} \end{aligned}$$

(36)

where $\mathfrak {f}_4(\xi ,y; \theta ,\delta )$ is given in Eq. (34). The following limit properties is available here as

$$\begin{aligned} \lim _{\xi \longrightarrow \pm \infty }\Psi (\xi ,y)=\Psi _0,\ \ \ \ \lim _{y\longrightarrow \pm \infty }\Psi (\xi ,y)=\Psi _0. \hspace{4cm} \end{aligned}$$

(37)

By choice the suitable values, Fig. 8, Fig. 9 and Fig. 10 are designed. In Fig. 8 the RW has one center $(\delta ,\theta )=(1, 7)$, provided in Fig. 9 the RW has as $(\delta ,\theta )=(-3, -3)$ and eventually in Fig. 10 the RW has as $(\delta ,\theta )=(0, 0)$.

Figure 8

Outlook of the four lump wave solution (36) in $\delta =1, \theta =7, c_{2,0}= 1, c_{2,10}= 1, \delta _4=2, \delta _5=2, \Psi _0= 1$.

Figure 9

Outlook of the four lump wave solution (36) in $\delta =-3, \theta =-3, c_{2,0}= 1, c_{2,10}= 1, \delta _4=2, \delta _5=2, \Psi _0= 1$.

Figure 10

Outlook of the four lump wave solution (36) in $\delta =0, \theta =0, c_{2,0}= 1, c_{2,10}= 1, \delta _4=2, \delta _5=2, \Psi _0= 1$.

Interaction one soliton wave with another types

Lump-two kink wave solutions

In the present section, the lump with two kink wave solution involving compound of three functions for the (2+1)-dimensional generalized HSI model via applying the bilinear technique is presented in the following shape:

$$\begin{aligned} f=\tau _1^2+\tau _2^2+e^{\tau _3}+e^{\tau _4}+\epsilon _5, \ \ \ \tau _l=\alpha _l x+\beta _l y+\varepsilon _l t+\epsilon _l, \ \ l=1,2,3,4. \end{aligned}$$

(38)

The amounts $\alpha _l, \beta _l, \varepsilon _l, \epsilon _l (l=1,...,4)$ are real values to be computed. Via putting (38) into (8) a system involving thirty one nonlinear equations has been concluded. Via solving the nonlinear system the determined coefficients will be got as below issues:

Option I:

$$\begin{aligned} \alpha _1=\alpha _2=\alpha _4=\beta _1=\beta _2=\beta _4=0,\ \ \alpha _3={\frac{ \sqrt{2} \sqrt{\delta _{{5}} \left( \delta _{{1}}\delta _{{ 3}}-2\delta _{{4}}\delta _{{5}}\pm \sqrt{-4\,{\delta _{{1}}}^{2}\delta _{{ 2}}\delta _{{5}}+{\delta _{{1}}}^{2}{\delta _{{3}}}^{2}} \right) }}{2 \delta _{{5}}}},\ \ \beta _{{3}}=-{\frac{\alpha _{{3}} \left( {\alpha _{{3}}}^{2}+\delta _{{4 }} \right) }{\delta _{{1}}}}. \end{aligned}$$

(39)

The solution is given as follows:

$$\begin{aligned} \Psi _1={\frac{2\,\alpha _{{3}}\,{\textrm{e}^{t\epsilon _{{3}}+x\alpha _{{3}}+y\beta _ {{3}}+\epsilon _{{3}}}}}{f}} ,\ \ \ \ f=(t\varepsilon _1+\epsilon _1)^2+(t\varepsilon _2+\epsilon _2)^2+e^{t\epsilon _{{3}}+x\alpha _{{3}}-{\frac{\alpha _{{3}} \left( {\alpha _{{3}}}^{2}+\delta _{{4 }} \right) }{\delta _{{1}}}}y+\epsilon _3}+e^{t\varepsilon _4+\epsilon _4}+\epsilon _5. \end{aligned}$$

(40)

By taking $\Psi _1$ in solution (40) as an instance, with the hypothesis that x, y are values and $\theta <0$ in $e^{\alpha _l x+\beta _l y+\theta t+\epsilon _l}, l=3,4$. And so, if $\tau _1^2+\tau _2^2+e^{\tau _3}+e^{\tau _4}+\epsilon _5\rightarrow \infty$, the lump and 2-kink kind solutions $u\rightarrow 0$, when $t\rightarrow -\infty$, in this case the exponential expression $e^{\tau _3}+e^{\tau _4}$ is the dominant one and deprive the existence of lump frame. Insomuch the function $\tau _1^2+\tau _2^2+\epsilon _5$ is the dominant expression and $\Psi \rightarrow \frac{2\tau _2\beta _2}{\tau _1^2+\tau _2^2+\epsilon _5}$ until $t\rightarrow +\infty$. To the extent that as time approaches zero $t\rightarrow 0$, the lump frame trends to emerge and prosper. Figure. 11 presents the 3-D graph and density graph of $\Psi$ with determined amounts in Eq. (40).

Figure 11

The plot of lump-2 kink (40) at $\delta _1= 2, \delta _2= 3, \delta _3= 1, \delta _4= 1, \delta _5= 3, \varepsilon _1= 1.5, \varepsilon _2= 2, \varepsilon _3= 1, \varepsilon _4= 2, \epsilon _1= 1, \epsilon _2= 1.5, \epsilon _3= 3, \epsilon _4= 1, \epsilon _5= 1, y = 1$.

Option II:

$$\begin{aligned} & \alpha _1=\alpha _2=\beta _1=\beta _2=0,\ \ \alpha _3=-{\frac{ \sqrt{2} \sqrt{\delta _{{5}} \left( \delta _{{1}}\delta _{{ 3}}-2\delta _{{4}}\delta _{{5}}\pm \sqrt{-4\,{\delta _{{1}}}^{2}\delta _{{ 2}}\delta _{{5}}+{\delta _{{1}}}^{2}{\delta _{{3}}}^{2}} \right) }}{2 \delta _{{5}}}},\ \ \alpha _4=-\alpha _3,\ \ \nonumber \\ & \beta _{{3}}={\frac{\alpha _{{3}} \left( {\alpha _{{3}}}^{2}+\delta _{{4 }} \right) }{\delta _{{1}}}},\ \ \beta _{{4}}=-{\frac{\alpha _{{3}} \left( {\alpha _{{3}}}^{2}+\delta _{{4 }} \right) }{\delta _{{1}}}}. \end{aligned}$$

(41)

The solution is given as follows:

$$\begin{aligned} & \Psi _2={\frac{2\,\alpha _{{3}}{\textrm{e}^{t\epsilon _{{3}}+x\alpha _{{3}}+y\beta _ {{3}}+\epsilon _{{3}}}}+2\,\alpha _{{4}}{\textrm{e}^{t\epsilon _{{4}}+x \alpha _{{4}}+y\beta _{{4}}+\epsilon _{{4}}}}}{g}} ,\ \ \ \ \nonumber \\ & g=(t\varepsilon _1+\epsilon _1)^2+(t\varepsilon _2+\epsilon _2)^2+e^{t\epsilon _{{3}}+x\alpha _{{3}}+{\frac{\alpha _{{3}} \left( {\alpha _{{3}}}^{2}+\delta _{{4 }} \right) }{\delta _{{1}}}}y+\epsilon _3}+e^{t\epsilon _{{4}}-x\alpha _{{3}}-{\frac{\alpha _{{3}} \left( {\alpha _{{3}}}^{2}+\delta _{{4 }} \right) }{\delta _{{1}}}}y+\epsilon _4}+\epsilon _5. \end{aligned}$$

(42)

Cross-kink wave solutions

Hither, the cross-kink wave solution involving compound of three functions for the (2+1)-dimensional generalized HSI equation by employing the bilinear technique is presented in the following model:

$$\begin{aligned} f=\sinh (\tau _1)+\sin (\tau _2)+\epsilon _3, \ \ \ \tau _j=\alpha _j x+\beta _j y+\varepsilon _j t+\epsilon _j, \ \ j=1,2. \end{aligned}$$

(43)

The amounts $\alpha _i, \beta _i, \varepsilon _i, \epsilon _i (i=1,2)$ are real values to be computed. By substituting (43) into (8) a system involving five nonlinear equations has been concluded. Via solving the nonlinear system the determined coefficients will be got as below issues:

Choice I:

$$\begin{aligned} & \delta _{{2}}=-{\frac{-2\delta _{{4}} \left( \beta _{{1}}\epsilon _{{2}}-\beta _{{2}}\epsilon _{{1}} \right) \left( \alpha _{{1}}\beta _{{2 }}-\alpha _{{2}}\beta _{{1}} \right) +\epsilon _{{1}}A_{{1}}-\epsilon _{{2 }}A_{{2}}}{ 2\left( \alpha _{{1}}\beta _{{2}}-\alpha _{{2}}\beta _{{1}} \right) ^{2}}},\ \ \delta _{{3}}={\frac{\epsilon _{{1}}B_{{1}}-\epsilon _{{2}}B_{{2}}}{ \left( \alpha _{{1}}\beta _{{2}}-\alpha _{{2}}\beta _{{1}} \right) ^{2}}} -{\frac{\delta _{{4}} \left( \alpha _{{1}}\epsilon _{{2}}-\alpha _{{2}} \epsilon _{{1}} \right) -\delta _{{1}} \left( \beta _{{1}}\epsilon _{{2}}- \beta _{{2}}\epsilon _{{1}} \right) }{\alpha _{{1}}\beta _{{2}}-\alpha _{{2 }}\beta _{{1}}}} , \nonumber \\ & A_{{1}}=3{\alpha _{{1}}}^{3}{\beta _{{1}}}^{2}+5{\alpha _{{1}}}^{3}{ \beta _{{2}}}^{2}-6{\alpha _{{1}}}^{2}\alpha _{{2}}\beta _{{1}}\beta _{{2 }}+3\alpha _{{1}}{\alpha _{{2}}}^{2}{\beta _{{1}}}^{2}-3\alpha _{{1}}{ \alpha _{{2}}}^{2}{\beta _{{2}}}^{2}+2{\alpha _{{2}}}^{3}\beta _{{1}} \beta _{{2}},\ \ B_{{1}}=3{\alpha _{{1}}}^{4}\beta _{{1}}+2{\alpha _{{1}}}^{3}\alpha _{ {2}}\beta _{{2}}-2\alpha _{{1}}{\alpha _{{2}}}^{3}\beta _{{2}}+{\alpha _{ {2}}}^{4}\beta _{{1}}, \nonumber \\ & A_{{2}}=2{\alpha _{{1}}}^{3}\beta _{{1}}\beta _{{2}}-3{\alpha _{{1}}}^ {2}\alpha _{{2}}{\beta _{{1}}}^{2}+3\,{\alpha _{{1}}}^{2}\alpha _{{2}}{ \beta _{{2}}}^{2}-6\alpha _{{1}}{\alpha _{{2}}}^{2}\beta _{{1}}\beta _{{2 }}+5{\alpha _{{2}}}^{3}{\beta _{{1}}}^{2}+3{\alpha _{{2}}}^{3}{\beta _ {{2}}}^{2},\ \ B_{{2}}={\alpha _{{1}}}^{4}\beta _{{2}}-2{\alpha _{{1}}}^{3}\alpha _{{2} }\beta _{{1}}+2\alpha _{{1}}{\alpha _{{2}}}^{3}\beta _{{1}}+3{\alpha _{ {2}}}^{4}\beta _{{2}}, \nonumber \\ & \delta _{{5}}=-\frac{1}{2}\,{\frac{2\,\delta _{{1}} \left( \alpha _{{1}}\epsilon _{{2}}-\alpha _{{2}}\epsilon _{{1}} \right) \left( \alpha _{{1}}\beta _{{ 2}}-\alpha _{{2}}\beta _{{1}} \right) + \left( {\alpha _{{1}}}^{2}+{ \alpha _{{2}}}^{2} \right) \left( 3\,{\alpha _{{1}}}^{3}\epsilon _{{1}}+ {\alpha _{{1}}}^{2}\alpha _{{2}}\epsilon _{{2}}-\alpha _{{1}}{\alpha _{{2}} }^{2}\epsilon _{{1}}-3\,{\alpha _{{2}}}^{3}\epsilon _{{2}} \right) }{ \left( \alpha _{{1}}\beta _{{2}}-\alpha _{{2}}\beta _{{1}} \right) ^{2}}},\ \ \epsilon _3=0. \end{aligned}$$

(44)

The solution is given as follows:

$$\begin{aligned} \Psi _1=2\,{\frac{\cosh \left( t\epsilon _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+ \epsilon _{{1}} \right) \alpha _{{1}}+\cos \left( t\epsilon _{{2}}+x \alpha _{{2}}+y\beta _{{2}}+\epsilon _{{2}} \right) \alpha _{{2}}}{\sinh \left( t\epsilon _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+\epsilon _{{1} } \right) +\sin \left( t\epsilon _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+ \epsilon _{{2}} \right) }}. \end{aligned}$$

(45)

By taking $\Psi _1$ in solution (45), if $\sinh (\tau _1)+\sin (\tau _2)\rightarrow \infty$, the cross-kink type solutions $\Psi \rightarrow 2\alpha _1$, at the time of $t\rightarrow \pm \infty$, in this case the exponential term $\sinh (\tau _1)$ is the dominant one and deprive the existence of periodic property. Figure 12 shows the 3-D graph and density graph of $\Psi$ with determined amounts in Eq. (45).

Figure 12

The plot of cross-kink (45) at $\delta _1= 2, \delta _4= 1, \alpha _1=\beta _1=2, \alpha _2=\beta _2=1, \varepsilon _1= 1.5, \varepsilon _2= 2, \epsilon _1= 1, \epsilon _2= 1.5, y = 1$.

Choice II:

$$\begin{aligned} & \alpha _2=\epsilon _3=0,\ \ \delta _{{2}}={\frac{\epsilon _{{2}} \left( 3\,{\alpha _{{1}}}^{5} \beta _{{1}}+3\,{\alpha _{{1}}}^{3}\beta _{{1}}\delta _{{4}}+3\,{\alpha _{{ 1}}}^{2}{\beta _{{1}}}^{2}\delta _{{1}}+5\,{\beta _{{2}}}^{2}{\alpha _{{1} }}^{2}\delta _{{1}}+2\,{\beta _{{2}}}^{2}\delta _{{1}}\delta _{{4}} \right) +\beta _{{2}}\delta _{{5}} \left( 3\,{\alpha _{{1}}}^{2}{\beta _{ {1}}}^{2}+5\,{\beta _{{2}}}^{2}{\alpha _{{1}}}^{2}+2\,{\beta _{{2}}}^{2} \delta _{{4}} \right) }{3{\alpha _{{1}}}^{4}\beta _{{2}}}} , \nonumber \\ & \delta _{{3}}=-{\frac{\epsilon _{{2}} \left( 3\,{\alpha _{{1}}}^{6} +3\,{\alpha _{{1}}}^{4}\delta _{{4}}+3\,{\alpha _{{1}}}^{3}\beta _{{1}} \delta _{{1}}-2\,{\beta _{{2}}}^{2}{\delta _{{1}}}^{2} \right) +2\,\beta _ {{2}}\delta _{{5}} \left( 3\,{\alpha _{{1}}}^{3}\beta _{{1}}-{\beta _{{2}} }^{2}\delta _{{1}} \right) }{3{\alpha _{{1}}}^{4}\beta _{{2}}}},\ \ \epsilon _{{1}}=-\frac{2}{3}\,{\frac{\beta _{{2}} \left( \beta _{{2}}\delta _{{5} }+\delta _{{1}}\epsilon _{{2}} \right) }{{\alpha _{{1}}}^{3}}}. \end{aligned}$$

(46)

The solution is given as follows:

$$\begin{aligned} \Psi _2=\frac{2\,\cosh \left( \frac{2}{3}\,{\frac{t\beta _{{2}} \left( \beta _{{2}}\delta _{{5 }}+\delta _{{1}}\epsilon _{{2}} \right) }{{\alpha _{{1}}}^{3}}}-x\alpha _{ {1}}-y\beta _{{1}}-\epsilon _{{1}} \right) \alpha _{{1}} }{-\sinh \left( \frac{2}{3}\,{\frac{t\beta _{{2}} \left( \beta _{{2}}\delta _{{5}} +\delta _{{1}}\epsilon _{{2}} \right) }{{\alpha _{{1}}}^{3}}}-x\alpha _{{1 }}-y\beta _{{1}}-\epsilon _{{1}} \right) +\sin \left( t\epsilon _{{2}}+y \beta _{{2}}+\epsilon _{{2}} \right) }. \end{aligned}$$

(47)

Choice III:

$$\begin{aligned} & \alpha _1=\epsilon _3=0,\ \ \delta _{{2}}=-{\frac{\epsilon _{{1}} \left( 3\,{\alpha _{{2}}}^{5} \beta _{{2}}-3\,{\alpha _{{2}}}^{3}\beta _{{2}}\delta _{{4}}-5\,{\beta _{{1 }}}^{2}\delta _{{1}}{\alpha _{{2}}}^{2}-3\,{\alpha _{{2}}}^{2}{\beta _{{2} }}^{2}\delta _{{1}}+2\,{\beta _{{1}}}^{2}\delta _{{1}}\delta _{{4}} \right) -\beta _{{1}}\delta _{{5}} \left( 5\,{\alpha _{{2}}}^{2}{\beta _{ {1}}}^{2}+3\,{\alpha _{{2}}}^{2}{\beta _{{2}}}^{2}-2\,{\beta _{{1}}}^{2} \delta _{{4}} \right) }{3{\alpha _{{2}}}^{4}\beta _{{1}}}} , \nonumber \\ & \delta _{{3}}={\frac{\epsilon _{{1}} \left( 3\,{\alpha _{{2}}}^{6}- 3\,{\alpha _{{2}}}^{4}\delta _{{4}}-3\,{\alpha _{{2}}}^{3}\beta _{{2}} \delta _{{1}}-2\,{\beta _{{1}}}^{2}{\delta _{{1}}}^{2} \right) -2\,\beta _ {{1}}\delta _{{5}} \left( 3\,{\alpha _{{2}}}^{3}\beta _{{2}}+{\beta _{{1}} }^{2}\delta _{{1}} \right) }{3{\alpha _{{2}}}^{4}\beta _{{1}}}},\ \ \epsilon _{{2}}=\frac{2}{3}\,{\frac{\beta _{{1}} \left( \beta _{{1}}\delta _{{5}} +\delta _{{1}}\epsilon _{{1}} \right) }{{\alpha _{{2}}}^{3}}} . \end{aligned}$$

(48)

The solution is given as follows:

$$\begin{aligned} \Psi _3=\frac{2\,\cos \left( \frac{2}{3}\,{\frac{t\beta _{{1}} \left( \beta _{{1}}\delta _{{5} }+\delta _{{1}}\epsilon _{{1}} \right) }{{\alpha _{{2}}}^{3}}}+x\alpha _{{ 2}}+y\beta _{{2}}+\epsilon _{{2}} \right) \alpha _{{2}} }{-\sinh \left( \frac{2}{3}\,{\frac{t\beta _{{2}} \left( \beta _{{2}}\delta _{{5}} +\delta _{{1}}\epsilon _{{2}} \right) }{{\alpha _{{1}}}^{3}}}-x\alpha _{{1 }}-y\beta _{{1}}-\epsilon _{{1}} \right) +\sin \left( t\epsilon _{{2}}+y \beta _{{2}}+\epsilon _{{2}} \right) }. \end{aligned}$$

(49)

Choice IV:

$$\begin{aligned} & \beta _{{i}}=-{\frac{\alpha _{{i}} \left( 3\,{\alpha _{{1}}}^{4}-2 \,{\alpha _{{1}}}^{2}{\alpha _{{2}}}^{2}+3\,{\alpha _{{2}}}^{4}+3\,{ \alpha _{{1}}}^{2}\delta _{{4}}-3\,{\alpha _{{2}}}^{2}\delta _{{4}} \right) }{3 \left( {\alpha _{{1}}}^{2}-{\alpha _{{2}}}^{2} \right) \delta _{{1}}}},\ \ i=1,2,\ \ \epsilon _3=0, \nonumber \\ & \delta _{{2}}=-{\frac{\sum _{i=1}^{4}A_{{i}}}{ 9\left( 3\,{\alpha _ {{1}}}^{2}-{\alpha _{{2}}}^{2} \right) \left( {\alpha _{{1}}}^{2}-{ \alpha _{{2}}}^{2} \right) ^{2}{\delta _{{1}}}^{2}}},\ \ A_{{1}}=-9\,\delta _{{4}} \left( 3\,{\alpha _{{1}}}^{2}-{\alpha _{{2}}}^{ 2} \right) \left( {\alpha _{{1}}}^{2}-{\alpha _{{2}}}^{2} \right) ^{2} \left( \delta _{{1}}\delta _{{3}}-\delta _{{4}}\delta _{{5}} \right) ,\ \nonumber \\ & A_{{2}}=-6\,\alpha _{{2}}{\delta _{{1}}}^{2}\epsilon _{{2}} \left( 9\,{ \alpha _{{1}}}^{4}-14\,{\alpha _{{1}}}^{2}{\alpha _{{2}}}^{2}+9\,{\alpha _ {{2}}}^{4} \right) \left( {\alpha _{{1}}}^{2}-{\alpha _{{2}}}^{2} \right) ,\ \ A_{{3}}=\delta _{{5}} \left( 3\,{\alpha _{{1}}}^{2}-{\alpha _{{2}}}^{2} \right) \left( 3\,{\alpha _{{1}}}^{4}-2\,{\alpha _{{1}}}^{2}{\alpha _{{ 2}}}^{2}+3\,{\alpha _{{2}}}^{4} \right) ^{2}, \nonumber \\ & A_{{4}}=-3\, \left( 3\,{\alpha _{{1}}}^{2}-{\alpha _{{2}}}^{2} \right) \left( 3\,{\alpha _{{1}}}^{4}-2\,{\alpha _{{1}}}^{2}{\alpha _{{2}}}^{2}+ 3\,{\alpha _{{2}}}^{4} \right) \left( {\alpha _{{1}}}^{2}-{\alpha _{{2}} }^{2} \right) \left( \delta _{{1}}\delta _{{3}}-2\,\delta _{{4}}\delta _{ {5}} \right) , \ \ \epsilon _{{1}}=-{\frac{\alpha _{{2}}\epsilon _{{2}} \left( {\alpha _{{1} }}^{2}-3\,{\alpha _{{2}}}^{2} \right) }{\alpha _{{1}} \left( 3\,{\alpha _ {{1}}}^{2}-{\alpha _{{2}}}^{2} \right) }}. \end{aligned}$$

(50)

The solution is given as follows:

$$\begin{aligned} \Psi _4=\frac{2\,\cosh \left( {\frac{t\alpha _{{2}}\epsilon _{{2}} \left( {\alpha _{{1 }}}^{2}-3\,{\alpha _{{2}}}^{2} \right) }{\alpha _{{1}} \left( 3\,{\alpha _{{1}}}^{2}-{\alpha _{{2}}}^{2} \right) }}-x\alpha _{{1}}-y\beta _{{1}}- \epsilon _{{1}} \right) \alpha _{{1}}+2\,\cos \left( t\epsilon _{{2}}+x \alpha _{{2}}+y\beta _{{2}}+\epsilon _{{2}} \right) \alpha _{{2}} }{-\sinh \left( {\frac{t\alpha _{{2}}\epsilon _{{2}} \left( {\alpha _{{1}} }^{2}-3\,{\alpha _{{2}}}^{2} \right) }{\alpha _{{1}} \left( 3\,{\alpha _{ {1}}}^{2}-{\alpha _{{2}}}^{2} \right) }}-x\alpha _{{1}}-y\beta _{{1}}- \epsilon _{{1}} \right) +\sin \left( t\epsilon _{{2}}+x\alpha _{{2}}+y \beta _{{2}}+\epsilon _{{2}} \right) }. \end{aligned}$$

(51)

Option V:

$$\begin{aligned} & \alpha _{{1}}={\frac{\alpha _{{2}}}{ \sqrt{3}}},\ \ \beta _{{1}}={\frac{\alpha _{{2}} \left( 4\,{\alpha _{{2}}}^{2}-3\, \delta _{{4}} \right) }{ 3\sqrt{3}\delta _{{1}}}},\ \ \beta _{{2}}={\frac{\alpha _{{2}} \left( 4\,{\alpha _{{2}}}^{2}-3\, \delta _{{4}} \right) }{3\delta _{{1}}}} ,\ \ \nonumber \\ & \delta _{{2}}=-{\frac{16\,{\alpha _{{2}}}^{4}\delta _{{5}}+12\,{ \alpha _{{2}}}^{2}\delta _{{1}}\delta _{{3}}-24\,{\alpha _{{2}}}^{2}\delta _{{4}}\delta _{{5}}+6\, \sqrt{3}\alpha _{{2}}\epsilon _{{1}}{\delta _{{1}} }^{2}-9\,\delta _{{1}}\delta _{{3}}\delta _{{4}}+9\,{\delta _{{4}}}^{2} \delta _{{5}}}{9{\delta _{{1}}}^{2}}}, \ \ \varepsilon _2=\epsilon _3=0. \end{aligned}$$

(52)

The solution is given as follows:

$$\begin{aligned} \Psi _5=\frac{\frac{2}{3}\,\cosh \left( t\epsilon _{{1}}+\frac{1}{3}\,x\alpha _{{2}} \sqrt{3}+\frac{1}{9}\,{ \frac{y\alpha _{{2}} \left( 4\,{\alpha _{{2}}}^{2}-3\,\delta _{{4}} \right) \sqrt{3}}{\delta _{{1}}}}+\epsilon _{{1}} \right) \alpha _{{2} } \sqrt{3}+2\,\cos \left( x\alpha _{{2}}+\frac{1}{3}\,{\frac{y\alpha _{{2}} \left( 4\,{\alpha _{{2}}}^{2}-3\,\delta _{{4}} \right) }{\delta _{{1}}}} +\epsilon _{{2}} \right) \alpha _{{2}} }{\sinh \left( t\epsilon _{{1}}+\frac{1}{3}\,x\alpha _{{2}} \sqrt{3}+\frac{1}{9}\,{\frac{ y\alpha _{{2}} \left( 4\,{\alpha _{{2}}}^{2}-3\,\delta _{{4}} \right) \sqrt{3}}{\delta _{{1}}}}+\epsilon _{{1}} \right) +\sin \left( x\alpha _{{2}}+\frac{1}{3}\,{\frac{y\alpha _{{2}} \left( 4\,{\alpha _{{2}}}^{2}-3\, \delta _{{4}} \right) }{\delta _{{1}}}}+\epsilon _{{2}} \right) }. \end{aligned}$$

(53)

By taking into consideration $\Psi _5$ in solution (53), if $\sinh (\tau _1)+\sin (\tau _2)\rightarrow \infty$, the cross-kink type solutions $\Psi \rightarrow \frac{2\sqrt{3}\alpha _2}{3}$, at the time of $t\rightarrow \pm \infty$, in this case the exponential term $\sinh (\tau _1)$ is the dominant one and deprive the existence of periodic property. Figure. 13 shows the 3-D plot and density plot of $\Psi$ with determined amounts in Eq. (53).

Figure 13

The plot of cross-kink (53) at $\delta _1= 2, \delta _4= 1, \alpha _2=1, \varepsilon _1= 2, \epsilon _1= 1, \epsilon _2= 2, y = 1$.

Periodic-kink wave solutions

Hither, the periodic-kink wave solution involving compound of three functions for the (2+1)-dimensional generalized HSI equation by handling the bilinear technique is presented as below model:

$$\begin{aligned} f=\cosh (\tau _1)+\cos (\tau _2)+\epsilon _3, \ \ \ \tau _l=\alpha _l x+\beta _l y+\varepsilon _l t+\epsilon _l, \ \ l=1,2. \end{aligned}$$

(54)

The amounts $\alpha _i, \beta _i, \varepsilon _i, \epsilon _i (i=1,2)$ are real values to be computed. By appending (54) into (8) a system containing five nonlinear equations has been reached. Through solving the nonlinear system the determined coefficients will be got as below issues:

Choice I:

$$\begin{aligned} & \delta _{{2}}={\frac{\alpha _{{1}}\delta _{{5}} \left( {\beta _{{1}}}^{2} +{\beta _{{2}}}^{2} \right) \left( \alpha _{{1}}\beta _{{2}}-\alpha _{{2} }\beta _{{1}} \right) +\epsilon _{{2}} \left( {\alpha _{{1}}}^{2}+{\alpha _{{2}}}^{2} \right) A_{{1}}}{\alpha _{{1}} \left( {\alpha _{{1}}}^{2}+{ \alpha _{{2}}}^{2} \right) \left( \alpha _{{1}}\beta _{{2}}-\alpha _{{2}} \beta _{{1}} \right) }} ,\ \ \delta _{{3}}=-{\frac{2\,\alpha _{{1}}\delta _{{5}} \left( \alpha _{{1}} \beta _{{1}}+\alpha _{{2}}\beta _{{2}} \right) \left( \alpha _{{1}}\beta _ {{2}}-\alpha _{{2}}\beta _{{1}} \right) +\epsilon _{{2}} \left( {\alpha _{ {1}}}^{2}+{\alpha _{{2}}}^{2} \right) A_{{2}}}{\alpha _{{1}} \left( { \alpha _{{1}}}^{2}+{\alpha _{{2}}}^{2} \right) \left( \alpha _{{1}}\beta _{{2}}-\alpha _{{2}}\beta _{{1}} \right) }} , \nonumber \\ & A_{{1}}={\alpha _{{1}}}^{3}\beta _{{1}}+3\,{\alpha _{{1}}}^{2}\alpha _{{2} }\beta _{{2}}-3\,\alpha _{{1}}{\alpha _{{2}}}^{2}\beta _{{1}}-{\alpha _{{2} }}^{3}\beta _{{2}}+\alpha _{{1}}\beta _{{1}}\delta _{{4}}+\alpha _{{2}} \beta _{{2}}\delta _{{4}}+{\beta _{{1}}}^{2}\delta _{{1}}+{\beta _{{2}}}^{2 }\delta _{{1}}, \nonumber \\ & A_{{2}}={\alpha _{{1}}}^{4}-{\alpha _{{2}}}^{4}+{\alpha _{{1}}}^{2}\delta _{{4}}+\alpha _{{1}}\beta _{{1}}\delta _{{1}}+{\alpha _{{2}}}^{2}\delta _{{ 4}}+\alpha _{{2}}\beta _{{2}}\delta _{{1}} ,\ \ \varepsilon _{{1}}=-{\frac{\alpha _{{2}}\varepsilon _{{2}}}{\alpha _{{1}}}},\ \ \epsilon _3=0. \end{aligned}$$

(55)

The solution is given as follows:

$$\begin{aligned} \Psi _1=2\,{\frac{\sinh \left( t\epsilon _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+ \epsilon _{{1}} \right) \alpha _{{1}}-\sin \left( t\epsilon _{{2}}+x \alpha _{{2}}+y\beta _{{2}}+\epsilon _{{2}} \right) \alpha _{{2}}}{\cosh \left( t\epsilon _{{1}}+x\alpha _{{1}}+y\beta _{{1}}+\epsilon _{{1}} \right) +\cos \left( t\epsilon _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+ \epsilon _{{2}} \right) }} . \end{aligned}$$

(56)

By taking into consideration $\Psi _1$ in solution (56), if $\cosh (\tau _1)+\cos (\tau _2)\rightarrow \infty$, the periodic-kink type solutions $\Psi \rightarrow 2\alpha _1$, at the time of $t\rightarrow \pm \infty$, in this form the exponential expression $\cosh (\tau _1)$ is the dominant one and deprive the existence of periodic property. Figure 14 presents the three-D graph and density graph of $\Psi$ with determined parameter settings in Eq. (56).

Figure 14

The plot of periodic-kink (56) at $\delta _1= 2, \delta _4= 1, \alpha _1=\beta _1=2, \alpha _2=\beta _2=1, \varepsilon _1= 1.5, \varepsilon _2= 2, \epsilon _1= 1, \epsilon _2= 1.5, y = 1$.

Choice II:

$$\begin{aligned} & \epsilon _3=0,\ \ \beta _{{i}}=-{\frac{\alpha _{{i}} \left( {\alpha _{{1}}}^{2}-{\alpha _{{ 2}}}^{2}+\delta _{{4}} \right) }{\delta _{{1}}}} ,\ \ i=1,2,\ \ \nonumber \\ & \delta _{{2}}=-{\frac{\delta _{{5}} \left( {\alpha _{{1}}}^{2}-{\alpha _{ {2}}}^{2} \right) ^{2}- \left( \delta _{{1}}\delta _{{3}}-2\,\delta _{{4} }\delta _{{5}} \right) \left( {\alpha _{{1}}}^{2}-{\alpha _{{2}}}^{2} \right) -\delta _{{4}} \left( \delta _{{1}}\delta _{{3}}-\delta _{{4}} \delta _{{5}} \right) -2\,\alpha _{{2}}{\delta _{{1}}}^{2}\epsilon _{{2}} }{{\delta _{{1}}}^{2}}} ,\ \ \varepsilon _{{1}}=-{\frac{\alpha _{{2}}\varepsilon _{{2}}}{\alpha _{{1}}}}. \end{aligned}$$

(57)

The solution is given as follows:

$$\begin{aligned} \Psi _2=\frac{-2\,\sinh \left( {\frac{t\alpha _{{2}}\epsilon _{{2}}}{\alpha _{{1}}}}-x \alpha _{{1}}+{\frac{y\alpha _{{1}} \left( {\alpha _{{1}}}^{2}-{\alpha _{ {2}}}^{2}+\delta _{{4}} \right) }{\delta _{{1}}}}-\epsilon _{{1}} \right) \alpha _{{1}}-2\,\sin \left( t\epsilon _{{2}}+x\alpha _{{2}}-{ \frac{y \left( {\alpha _{{1}}}^{2}-{\alpha _{{2}}}^{2}+\delta _{{4}} \right) \alpha _{{2}}}{\delta _{{1}}}}+\epsilon _{{2}} \right) \alpha _{ {2}} }{\cosh \left( {\frac{t\alpha _{{2}}\epsilon _{{2}}}{\alpha _{{1}}}}-x \alpha _{{1}}+{\frac{y\alpha _{{1}} \left( {\alpha _{{1}}}^{2}-{\alpha _{ {2}}}^{2}+\delta _{{4}} \right) }{\delta _{{1}}}}-\epsilon _{{1}} \right) +\cos \left( t\epsilon _{{2}}+x\alpha _{{2}}-{\frac{y \left( { \alpha _{{1}}}^{2}-{\alpha _{{2}}}^{2}+\delta _{{4}} \right) \alpha _{{2}} }{\delta _{{1}}}}+\epsilon _{{2}} \right) }. \end{aligned}$$

(58)

Choice III:

$$\begin{aligned} \beta _{{1}}={\frac{\alpha _{{1}}\beta _{{2}}}{\alpha _{{2}}}},\ \ \delta _{{2}}=-{\frac{\beta _{{2}} \left( \alpha _{{2}}\delta _{{3}}+ \beta _{{2}}\delta _{{5}} \right) }{{\alpha _{{2}}}^{2}}},\ \ \varepsilon _1=\varepsilon _2=\epsilon _3=0. \end{aligned}$$

(59)

The solution is given as follows:

$$\begin{aligned} \Psi _3=\frac{2\,\sinh \left( x\alpha _{{1}}+{\frac{y\alpha _{{1}}\beta _{{2}}}{\alpha _{{2}}}}+\epsilon _{{1}} \right) \alpha _{{1}}-2\,\sin \left( x\alpha _{ {2}}+y\beta _{{2}}+\epsilon _{{2}} \right) \alpha _{{2}} }{\cosh \left( x\alpha _{{1}}+{\frac{y\alpha _{{1}}\beta _{{2}}}{\alpha _{{ 2}}}}+\epsilon _{{1}} \right) +\cos \left( x\alpha _{{2}}+y\beta _{{2}}+ \epsilon _{{2}} \right) }. \end{aligned}$$

(60)

Option IV:

$$\begin{aligned} & \delta _{{1}}=\frac{1}{2}\,{\frac{2\,{\alpha _{{1}}}^{3}\epsilon _{{2}}+\delta _{ {5}} \left( \beta _{{1}}-\beta _{{2}} \right) ^{2}}{\epsilon _{{2}} \left( \beta _{{1}}-\beta _{{2}} \right) }} ,\ \ \delta _{{2}}={\frac{\epsilon _{{2}} \left( {\alpha _{{1}}}^{2} \left( { \beta _{{1}}}^{2}-4\,\beta _{{1}}\beta _{{2}}+{\beta _{{2}}}^{2} \right) - \delta _{{4}} \left( {\beta _{{1}}}^{2}-{\beta _{{2}}}^{2} \right) \right) }{\alpha _{{1}} \left( \beta _{{1}}-\beta _{{2}} \right) ^{2}}}, \nonumber \\ & \delta _{{3}}=\frac{1}{2}\,{\frac{2\,\alpha _{{1}}\epsilon _{{2}} \left( {\alpha _{{1}}}^{2}\beta _{{1}}+{\alpha _{{1}}}^{2}\beta _{{2}}+2\,\beta _{{1}} \delta _{{4}}-2\,\beta _{{2}}\delta _{{4}} \right) -\delta _{{5}} \left( { \beta _{{1}}}^{2}-{\beta _{{2}}}^{2} \right) ^{2}}{\alpha _{{1}} \left( \beta _{{1}}-\beta _{{2}} \right) ^{2}}},\ \ \varepsilon _1=-\varepsilon _2. \end{aligned}$$

(61)

The solution is given as follows:

$$\begin{aligned} \Psi _4=2\,{\frac{-\sinh \left( t\epsilon _{{2}}-x\alpha _{{1}}-y\beta _{{1}}- \epsilon _{{1}} \right) \alpha _{{1}}-\sin \left( t\epsilon _{{2}}+x \alpha _{{1}}+y\beta _{{2}}+\epsilon _{{2}} \right) \alpha _{{1}}}{\cosh \left( t\epsilon _{{2}}-x\alpha _{{1}}-y\beta _{{1}}-\epsilon _{{1}} \right) +\cos \left( t\epsilon _{{2}}+x\alpha _{{1}}+y\beta _{{2}}+ \epsilon _{{2}} \right) +\epsilon _{{3}}}} . \end{aligned}$$

(62)

Option V:

$$\begin{aligned} & \alpha _{{2}}=-\alpha _1,\ \ \delta _{{1}}=\frac{1}{2}\,{\frac{2\,{\alpha _{{1}}}^{3}\epsilon _{{2}}-\delta _{ {5}} \left( \beta _{{1}}+\beta _{{2}} \right) ^{2}}{\epsilon _{{2}} \left( \beta _{{1}}+\beta _{{2}} \right) }},\ \ \delta _{{2}}=-{\frac{\epsilon _{{2}} \left( {\alpha _{{1}}}^{2}{\beta _{ {1}}}^{2}+4\,{\alpha _{{1}}}^{2}\beta _{{1}}\beta _{{2}}+{\beta _{{2}}}^{2 }{\alpha _{{1}}}^{2}-{\beta _{{1}}}^{2}\delta _{{4}}+{\beta _{{2}}}^{2} \delta _{{4}} \right) }{\alpha _{{1}} \left( \beta _{{1}}+\beta _{{2}} \right) ^{2}}}, \nonumber \\ & \delta _{{3}}=-\frac{1}{2}\,{\frac{2\,\alpha _{{1}}\epsilon _{{2}} \left( { \alpha _{{1}}}^{2}\beta _{{1}}-{\alpha _{{1}}}^{2}\beta _{{2}}+2\,\beta _{{ 1}}\delta _{{4}}+2\,\beta _{{2}}\delta _{{4}} \right) +\delta _{{5}} \left( \beta _{{1}}-\beta _{{2}} \right) \left( \beta _{{1}}+\beta _{{2} } \right) ^{2}}{\alpha _{{1}} \left( \beta _{{1}}+\beta _{{2}} \right) ^{ 2}}} , \ \ \varepsilon _1=\varepsilon _2. \end{aligned}$$

(63)

The solution is given as follows:

$$\begin{aligned} \Psi _5=2\,{\frac{\sinh \left( t\epsilon _{{2}}+x\alpha _{{1}}+y\beta _{{1}}+ \epsilon _{{1}} \right) \alpha _{{1}}+\sin \left( t\epsilon _{{2}}-x \alpha _{{1}}+y\beta _{{2}}+\epsilon _{{2}} \right) \alpha _{{1}}}{\cosh \left( t\epsilon _{{2}}+x\alpha _{{1}}+y\beta _{{1}}+\epsilon _{{1}} \right) +\cos \left( t\epsilon _{{2}}-x\alpha _{{1}}+y\beta _{{2}}+ \epsilon _{{2}} \right) +\epsilon _{{3}}}} . \end{aligned}$$

(64)

By considering $\Psi _5$ in solution (64), if $\cosh (\tau _1)+\cos (\tau _2)\rightarrow \infty$, the cross-kink type solutions $\Psi \rightarrow -2\alpha _1$, at the time of $t\rightarrow \pm \infty$, in this form the exponential expression $\cosh (\tau _1)$ is the dominant one and deprive the existence of periodic property. Figure 15 shows the three-D graph and density graph of $\Psi$ with determined parameter settings in Eq. (64).

Figure 15

The plot of periodic-kink (64) at $\alpha _1=\frac{2}{3}, \beta _1=1, \beta _2=-2, \varepsilon _1= 2, \varepsilon _2=1, \epsilon _1= 1, \epsilon _2= 2,\epsilon _3=2, y = 1$.

Kink-dark wave solutions

Here, the kink-dark wave solution involving compound of three functions for the (2+1)-dimensional generalized HSI equation because of applying the bilinear technique is presented as below case:

$$\begin{aligned} f=\exp (\tau _1)+\exp (-\tau _1)+\tanh (\tau _2)+\tan (\tau _3)+\epsilon _4, \ \ \ \tau _l=\alpha _l x+\beta _l y+\varepsilon _l t+\epsilon _l, \ \ l=1,2,3. \end{aligned}$$

(65)

The amounts $\alpha _i, \beta _i, \varepsilon _i, \epsilon _i (i=1,2,3)$ are real values to be computed. After plugging (65) into (8) a system involving forty four nonlinear equations the regarding solutions has been represented. Through solving the nonlinear system the determined coefficients will be received as below issues:

Choice I:

$$\begin{aligned} \alpha _2=\alpha _3=\delta _1=\delta _5=\varepsilon _1=0,\ \ \delta _{{2}}={\frac{\beta _{{1}}\epsilon _{{3}} \left( {\alpha _{{1}}}^{ 2}+\delta _{{4}} \right) }{\alpha _{{1}}\beta _{{3}}}},\ \ \delta _{{3}}=-{\frac{\epsilon _{{3}} \left( {\alpha _{{1}}}^{2}+\delta _ {{4}} \right) }{\beta _{{3}}}},\ \ \varepsilon _{{2}}={\frac{\beta _{{2}}\varepsilon _{{3}}}{\beta _{{3}}}}. \end{aligned}$$

(66)

The solution is given as follows:

$$\begin{aligned} \Psi _1=2\,{\frac{\alpha _{{1}}{\textrm{e}^{x\alpha _{{1}}+y\beta _{{1}}+\epsilon _ {{1}}}}-\alpha _{{1}}{\textrm{e}^{-x\alpha _{{1}}-y\beta _{{1}}-\epsilon _{{ 1}}}}}{{\textrm{e}^{x\alpha _{{1}}+y\beta _{{1}}+\epsilon _{{1}}}}+{\textrm{e} ^{-x\alpha _{{1}}-y\beta _{{1}}-\epsilon _{{1}}}}+\tanh \left( t\epsilon _{{2}}+x\alpha _{{2}}+y\beta _{{2}}+\epsilon _{{2}} \right) +\tan \left( t\epsilon _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+\epsilon _{{3}} \right) +\epsilon _{{4}}}}. \end{aligned}$$

(67)

Option II:

$$\begin{aligned} \alpha _2=\alpha _3=\varepsilon _1=0,\ \ \delta _{{2}}={\frac{\beta _{{1}}\epsilon _{{2}} \left( {\alpha _{{1}}}^{ 2}+\delta _{{4}} \right) }{\alpha _{{1}}\beta _{{2}}}},\ \ \delta _{{3}}=-{\frac{\epsilon _{{2}} \left( {\alpha _{{1}}}^{3}+\alpha _ {{1}}\delta _{{4}}-\beta _{{1}}\delta _{{1}} \right) }{\alpha _{{1}}\beta _ {{2}}}} ,\ \ \delta _{{5}}=-{\frac{\delta _{{1}}\varepsilon _{{2}}}{\beta _{{2}}}},\ \ \varepsilon _{{3}}={\frac{\beta _{{3}}\varepsilon _{{2}}}{\beta _{{2}}}}. \end{aligned}$$

(68)

The solution is given as follows:

$$\begin{aligned} \Psi _2=\frac{2\,\alpha _{{1}}{\textrm{e}^{x\alpha _{{1}}+y\beta _{{1}}+\epsilon _{{1}}}}- 2\,\alpha _{{1}}{\textrm{e}^{-x\alpha _{{1}}-y\beta _{{1}}-\epsilon _{{1}}}} }{{\textrm{e}^{x\alpha _{{1}}+y\beta _{{1}}+\epsilon _{{1}}}}+{\textrm{e}^{-x \alpha _{{1}}-y\beta _{{1}}-\epsilon _{{1}}}}+\tanh \left( t\epsilon _{{2 }}+y\beta _{{2}}+\epsilon _{{2}} \right) +\tan \left( {\frac{t\beta _{{ 3}}\epsilon _{{2}}}{\beta _{{2}}}}+y\beta _{{3}}+\epsilon _{{3}} \right) +\epsilon _{{4}} }. \end{aligned}$$

(69)

By taking into consideration $\Psi _2$ in solution (69), if $\exp (\tau _1)+\exp (-\tau _1)+\tanh (\tau _2)+\tan (\tau _3)+\epsilon _4\rightarrow \infty$, the kink-dark type solutions $\Psi \rightarrow 0$, at the time of $t\rightarrow \pm \infty$, in this form the exponential expression $\tanh (\tau _2)$ is the dominant one and deprive the existence of $\tan (\tau _3)$ property. Figure 16 reveals the three-D graph and density graph of $\Psi$ with determined values in Eq. (69).

Figure 16

The plot of kink-dark (69) at $\delta _1= 2, \delta _4= 1, \alpha _1=\frac{2}{3}, \beta _1=1,\beta _2=2, \beta _3=3, \varepsilon _1= 2, \varepsilon _2= 1, \epsilon _1= 1, \epsilon _2= 2,\epsilon _3=3,\epsilon _4=4, x = 1$.

N-soliton treatment

Through the solution f of bilinear model (9) with respect to $\phi$ we have,

$$\begin{aligned} f=1+f^{(1)}\phi +f^{(2)}\phi ^2+...+f^{(h)}\phi ^h+..._-. \hspace{4cm} \end{aligned}$$

(70)

Next, by appending expression (70) into bilinear equation (9) and decollating at the second power of $\phi$, one becomes

$$\begin{aligned} f^{(1)}_{xxxt}+\delta _1f^{(1)}_{yt}+\delta _2f^{(1)}_{xx}+\delta _3f^{(1)}_{xy}+\delta _4f^{(1)}_{xt}+\delta _5f^{(1)}_{yy} =0, \hspace{6cm} \end{aligned}$$

(71)

and

$$\begin{aligned} & -\left( D_x^3 D_t+\delta _1D_yD_t+\delta _2D_x^2+\delta _3D_xD_y+\delta _4D_xD_t+\delta _5D_y^2\right) (f^{(1)}. f^{(1)})= \hspace{4cm} \nonumber \\ & =2\left[ f^{(2)}_{xxxt}+\delta _1f^{(2)}_{yt}+\delta _2f^{(2)}_{xx}+ \delta _3f^{(2)}_{xy}+\delta _4f^{(2)}_{xt}+\delta _5f^{(2)}_{yy}\right] . \end{aligned}$$

(72)

Based on equation (71), the solution with below form is extracted

$$\begin{aligned} f^{(1)}=\exp (\eta _a) \end{aligned}$$

where $\eta _i=k_a(x+m_ay+\omega _at)+\eta _{i0}, k_a,m_a,\omega _a, (1\le a\le N)$ are nonzero values and $\eta _{i0}$ is optional amount. Appending $f^{(1)}=\exp (\eta _a)$ into equation (71), we acquire $\omega _a=-{\frac{\delta _{{5}}{m_{{a}}}^{2}+\delta _{{3}}m_{{a}}+\delta _{{2}}}{ \delta _{{1}}m_{{a}}+{k_{{a}}}^{2}+\delta _{{4}}}}$. Afterwards, based on the superposition technique of findings of linear equations, $f^{(1)}=\exp (\eta _a)+\exp (\eta _b)$ where $\eta _b=k_b(x+m_by+\omega _bt)+\eta _{b0}, (1\le a\le b\le N)$ is also the solution of equation (71) in order that $f^{(2)}=\exp (\eta _a+\eta _b+\Omega _{ab})$ is the result of equation (72). Imposing $f^{(1)}=\exp (\eta _a)+\exp (\eta _b)$ and $f^{(2)}=\exp (\eta _a+\eta _b+\Omega _{ab})$ into equation (72) where $\exp (\Omega _{ab})$ is nonzero value and exploiting the characters of the Hirota bilinear scheme to exponential functions, one arises

$$\begin{aligned} \exp (\Omega _{ab})=-\frac{\left( k_{{a}}-k_{{b}} \right) ^{3} \left( \omega _{{a}}-\omega _{{b}} \right) +\delta _{{1}} \left( m_{{a}}-m_{{b}} \right) \left( \omega _{ {a}}-\omega _{{b}} \right) +\delta _{{2}} \left( k_{{a}}-k_{{b}} \right) ^{2}+\delta _{{3}} \left( k_{{a}}-k_{{b}} \right) \left( m_{{ a}}-m_{{b}} \right) +H }{\left( k_{{a}}+k_{{b}} \right) ^{3} \left( \omega _{{a}}+\omega _{{b}} \right) +\delta _{{1}} \left( m_{{a}}+m_{{b}} \right) \left( \omega _{ {a}}+\omega _{{b}} \right) +\delta _{{2}} \left( k_{{a}}+k_{{b}} \right) ^{2}+\delta _{{3}} \left( k_{{a}}+k_{{b}} \right) \left( m_{{ a}}+m_{{b}} \right) +G },\hspace{0cm} \end{aligned}$$

(73)

where $H=\delta _{{4}} \left( k_{{a}}-k_{{b}} \right) \left( \omega _{{a}}-\omega _{{b}} \right) +\delta _{{5}} \left( m_{{a}} -m_{{b}} \right) ^{2}, G=\delta _{{4}} \left( k_{{a}}+k_{{b}} \right) \left( \omega _{{a}}+\omega _{{b}} \right) +\delta _{{5}} \left( m_{{a}} +m_{{b}} \right) ^{2}$ and g(t) is function of t and $\lambda , k_a, m_a, \omega _a, (1\le a\le b\le N)$ are nonzero constants. The N-soliton form of bilinear equation (9), can be expressed in the following shape

$$\begin{aligned} f=f_N=\sum _{\mu =0,1}exp\left( \sum _{a=1}^{N}\mu _a\eta _a +\sum _{a<b}^{N}\mu _a\mu _b\Omega _{ab}\right) , \ \ \ \ 1\le a\le b\le N, \end{aligned}$$

(74)

where $\eta _a=k_a\left( x+m_ay-{\frac{\delta _{{5}}{m_{{a}}}^{2}+\delta _{{3}}m_{{a}}+\delta _{{2}}}{ \delta _{{1}}m_{{a}}+{k_{{a}}}^{2}+\delta _{{4}}}} t\right) +\eta _{a0}, (1\le a\le b\le N)$.

Handeling the linear superposition technique

According to the⁵¹ and by utilizing $u=2(\ln f)_{x}$, the bilinear form of Eq. (7) will be concluded as:

$$\begin{aligned} & \left( D_x^3 D_t+\delta _1D_yD_t+\delta _2D_x^2+\delta _3D_xD_y +\delta _4D_xD_t+\delta _5D_y^2\right) \mathfrak {f}. \mathfrak {f}= \hspace{4cm} \nonumber \\ & =2\left[ ff_{xxxt}-3f_{xxx}f_{t}+3f_{xx}f_{xt}-f_xf_{xxt}+\delta _1(ff_{yt}- f_yf_t)+\delta _2(ff_{xx}-f_x^2)+\right. \nonumber \\ & \left. \delta _3(ff_{xy}-f_xf_y)+\delta _4(ff_{xt}-f_xf_t) +\delta _5(ff_{yy}-f_{y}^2)\right] =0. \end{aligned}$$

(75)

In order to find N-wave solution, let

$$\begin{aligned} f=\exp (\vartheta _i),\,\,\,\, \vartheta _i=k_ix+m_iy+\omega _it, \,\,\,\ i=1,2,...,N. \hspace{4cm} \end{aligned}$$

(76)

After plugging f (76) into bilinear equation (75), which represents the regarding solution of below equation

$$\begin{aligned} & {k_{{i}}}^{3}\omega _{{i}}-{k_{{i}}}^{3}\omega _{{j}}-3\,{k_{{i}}}^{2}k_ {{j}}\omega _{{i}}+3\,{k_{{i}}}^{2}k_{{j}}\omega _{{j}}+3\,k_{{i}}{k_{{j }}}^{2}\omega _{{i}}-3\,k_{{i}}{k_{{j}}}^{2}\omega _{{j}}-{k_{{j}}}^{3} \omega _{{i}}+{k_{{j}}}^{3}\omega _{{j}}+\delta _{{1}}m_{{i}}\omega _{{i}} -\delta _{{1}}m_{{i}}\omega _{{j}}- \nonumber \\ & \delta _{{1}}m_{{j}}\omega _{{i}}+ \delta _{{1}}m_{{j}}\omega _{{j}}+\delta _{{2}}{k_{{i}}}^{2}-2\,\delta _{{ 2}}k_{{i}}k_{{j}}+\delta _{{2}}{k_{{j}}}^{2}+\delta _{{3}}k_{{i}}m_{{i}} -\delta _{{3}}k_{{i}}m_{{j}}-\delta _{{3}}k_{{j}}m_{{i}}+\delta _{{3}}k_{ {j}}m_{{j}}+\delta _{{4}}k_{{i}}\omega _{{i}}- \nonumber \\ & \delta _{{4}}k_{{i}}\omega _ {{j}}-\delta _{{4}}k_{{j}}\omega _{{i}}+\delta _{{4}}k_{{j}}\omega _{{j}}+ \delta _{{5}}{m_{{i}}}^{2}-2\,\delta _{{5}}m_{{i}}m_{{j}}+\delta _{{5}}{m _{{j}}}^{2}=0,\ \ \ (1\le i\le j\le N). \end{aligned}$$

(77)

Consequently the comparing arrangements are extricated, working in much the same line:

Case I:

$$\begin{aligned} k_i=k_i,\,\,\,\ m_i=\rho k_i,\,\,\,\ \omega _i=-{\frac{ \left( {\rho }^{2}\delta _{{5}}+\rho \,\delta _{{3}}+\delta _{{2} } \right) k_{{i}}}{\rho \,\delta _{{1}}+{k_{{i}}}^{2}+\delta _{{4}}}} ,\,\,\,\ i=1,2,...,N. \end{aligned}$$

(78)

Case II:

$$\begin{aligned} k_i=k_i,\,\,\,\ m_i=\rho k_i^2,\,\,\,\ \omega _i=-{\frac{ \left( {\rho }^{2}\delta _{{5}}{k_{{i}}}^{2}+\rho \,\delta _{{3} }k_{{i}}+\delta _{{2}} \right) k_{{i}}}{\rho \,\delta _{{1}}k_{{i}}+{k_{{ i}}}^{2}+\delta _{{4}}}} ,\,\,\,\ i=1,2,...,N. \end{aligned}$$

(79)

Case III:

$$\begin{aligned} k_i=k_i,\,\,\,\ m_i=\tau \,{k_{{i}}}^{2}+\rho \,k_{{i}},\,\,\,\ \omega _i=-{\frac{k_{{i}} \left( {\tau }^{2}\delta _{{5}}{k_{{i}}}^{2}+\tau \,k_{{ i}} \left( 2\,\rho \,\delta _{{5}}+\delta _{{3}} \right) +{\rho }^{2} \delta _{{5}}+\rho \,\delta _{{3}}+\delta _{{2}} \right) }{\tau \,\delta _{{ 1}}k_{{i}}+\rho \,\delta _{{1}}+{k_{{i}}}^{2}+\delta _{{4}}}} ,\,\,\,\ i=1,2,...,N, \end{aligned}$$

(80)

where $\rho$ and $\tau$are the free amounts. Accordingly by the linear superposition technique expressed in^42,43, the generalized Hirota-Satsuma-Ito equation (7) has the following N-wave solutions, respectively, as:

$$\begin{aligned} & u_{Case\ I}=2\frac{\partial }{\partial x}\left( \ln \sum _{i=1}^{N}\phi _ie^{k_ix+\rho k_iy-{\frac{ \left( {\rho }^{2}\delta _{{5}}+\rho \,\delta _{{3}}+\delta _{{2} } \right) k_{{i}}}{\rho \,\delta _{{1}}+{k_{{i}}}^{2}+\delta _{{4}}}} t}\right) , \end{aligned}$$

(81)

$$\begin{aligned} & u_{Case\ II}=2\frac{\partial }{\partial x}\left( \ln \sum _{i=1}^{N}\phi _ie^{k_ix+\rho k_i^2y-{\frac{ \left( {\rho }^{2}\delta _{{5}}{k_{{i}}}^{2}+\rho \,\delta _{{3} }k_{{i}}+\delta _{{2}} \right) k_{{i}}}{\rho \,\delta _{{1}}k_{{i}}+{k_{{ i}}}^{2}+\delta _{{4}}}} t}\right) , \end{aligned}$$

(82)

$$\begin{aligned} & u_{Case\ III}=2\frac{\partial }{\partial x}\left( \ln \sum _{i=1}^{N}\phi _ie^{k_ix+(\tau \,{k_{{i}}}^{2}+\rho \,k_{{i}})y-{\frac{k_{{i}} \left( {\tau }^{2}\delta _{{5}}{k_{{i}}}^{2}+\tau \,k_{{ i}} \left( 2\,\rho \,\delta _{{5}}+\delta _{{3}} \right) +{\rho }^{2} \delta _{{5}}+\rho \,\delta _{{3}}+\delta _{{2}} \right) }{\tau \,\delta _{{ 1}}k_{{i}}+\rho \,\delta _{{1}}+{k_{{i}}}^{2}+\delta _{{4}}}} t}\right) , \end{aligned}$$

(83)

where $\phi _i$ is a free value.

Multiple wave solution

According to linear superposition technique (^52,53), the corresponding polynomial of (9) expresses,

$$\begin{aligned} P(x,y,t)=x^3t+\delta _1yt+\delta _2x^2+\delta _3xy+\delta _4xt+\delta _5y^2. \end{aligned}$$

(84)

Introducing N-wave function

$$\begin{aligned} f=\sum _{i=1}^{N}\phi _i\widehat{f_i}=\phi _1\widehat{f_1}+\phi _2\widehat{f_2}+...+\phi _N\widehat{f_N}= \phi _1\exp (\vartheta _1)+\phi _2\exp (\vartheta _2)+...+\phi _N\exp (\vartheta _N), \end{aligned}$$

(85)

where $\widehat{f_i}=\exp (\vartheta _i)=\exp (k_ix+m_iy+\omega _it), \ 1\le i\le N$, and $k_i,m_i,\omega _i$ are nonzero constants. Inserting $f=\sum _{i=1}^{N}\phi _i\widehat{f_i}$ into bilinear equation (9), we obtain

$$\begin{aligned} & \left( D_x^3 D_t+\delta _1D_yD_t+\delta _2D_x^2+\delta _3D_xD_y+\delta _4D_xD_t+\delta _5D_y^2\right) (f. f)= \hspace{6cm} \nonumber \\ & =2\sum _{1\le i<j\le N}\phi _i\phi _jP(k_i-k_j,m_i-m_j,\omega _i-\omega _j)e^{\vartheta _i+\vartheta _j}=0. \end{aligned}$$

(86)

Therefore, f solves the bilinear model (9) if and only if $P(k_i-k_j,m_i-m_j,\omega _i-\omega _j)=0$ in order that the N-wave solutions condition can be acquired

$$\begin{aligned} & (k_i-k_j)^3 ( \omega _i-\omega _j) +\delta _1(m_i-m_j) ( \omega _i-\omega _j) +\delta _2(k_i-k_j)^{2}+\delta _3(k_i-k_j) (m_i-m_j) + \nonumber \\ & \delta _4(k_i-k_j) ( \omega _i-\omega _j) +\delta _5 (m_i-m_j)^{2} =0. \end{aligned}$$

(87)

By comparing the power of $k_i,k_j,m_i,m_j,\omega _i,\omega _j$ we have (I) $m_i=\rho k_i,\,\ \omega _i=-{\frac{ \left( {\rho }^{2}\delta _{{5}}+\rho \,\delta _{{3}}+\delta _{{2} } \right) k_{{i}}}{\rho \,\delta _{{1}}+{k_{{i}}}^{2}+\delta _{{4}}}},$$m_j=\rho k_j,\,\ \omega _j=-{\frac{ \left( {\rho }^{2}\delta _{{5}}+\rho \,\delta _{{3}}+\delta _{{2} } \right) k_{{j}}}{\rho \,\delta _{{1}}+{k_{{j}}}^{2}+\delta _{{4}}}}$, (II) $m_i=\rho k_i^2,\,\ \omega _i=-{\frac{ \left( {\rho }^{2}\delta _{{5}}{k_{{i}}}^{2}+\rho \,\delta _{{3} }k_{{i}}+\delta _{{2}} \right) k_{{i}}}{\rho \,\delta _{{1}}k_{{i}}+{k_{{ i}}}^{2}+\delta _{{4}}}}$, $m_j=\rho k_j^2,\,\ \omega _j=-{\frac{ \left( {\rho }^{2}\delta _{{5}}{k_{{j}}}^{2}+\rho \,\delta _{{3} }k_{{j}}+\delta _{{2}} \right) k_{{j}}}{\rho \,\delta _{{1}}k_{{j}}+{k_{{j}}}^{2}+\delta _{{4}}}}$ and (III) $m_i=\tau \,{k_{{i}}}^{2}+\rho \,k_{{i}},\,\ \omega _i=-{\frac{k_{{i}} \left( {\tau }^{2}\delta _{{5}}{k_{{i}}}^{2}+\tau \,k_{{ i}} \left( 2\,\rho \,\delta _{{5}}+\delta _{{3}} \right) +{\rho }^{2} \delta _{{5}}+\rho \,\delta _{{3}}+\delta _{{2}} \right) }{\tau \,\delta _{{ 1}}k_{{i}}+\rho \,\delta _{{1}}+{k_{{i}}}^{2}+\delta _{{4}}}}$, $m_j=\tau \,{k_{{j}}}^{2}+\rho \,k_{{j}},\,\,\,\ \omega _j=-{\frac{k_{{j}} \left( {\tau }^{2}\delta _{{5}}{k_{{j}}}^{2}+\tau \,k_{{j}} \left( 2\,\rho \,\delta _{{5}}+\delta _{{3}} \right) +{\rho }^{2} \delta _{{5}}+\rho \,\delta _{{3}}+\delta _{{2}} \right) }{\tau \,\delta _{{ 1}}k_{{j}}+\rho \,\delta _{{1}}+{k_{{j}}}^{2}+\delta _{{4}}}}$. Accordingly, after plugging it into equation (87) the N-wave solutions condition, one becomes

$$\begin{aligned} \alpha _1={\rho }^{2}\delta _{{5}}+\rho \,\delta _{{3}}+\delta _{{2}},\,\ \alpha _2=\rho \,\delta _{{1}}+\delta _{{4}}. \end{aligned}$$

Also, the N-wave solutions can be expressed in the below issues:

$$\begin{aligned} & f_I=\sum _{i=1}^{N}\phi _i\widehat{f_i}=\phi _1\widehat{f_1}+\phi _2\widehat{f_2}+...+\phi _N\widehat{f_N}= \sum _{i=1}^{N}\phi _i\exp \left( k_ix+\rho k_iy-{\frac{\alpha _{{1}}k_{{i}}}{{k_{{i}}}^{2}+\alpha _{{2}}}}t\right) , \end{aligned}$$

(88)

$$\begin{aligned} & f_{II}=\sum _{i=1}^{N}\phi _i\widehat{f_i}=\phi _1\widehat{f_1}+\phi _2\widehat{f_2}+...+\phi _N\widehat{f_N}= \sum _{i=1}^{N}\phi _i\exp \left( k_ix+\rho k_i^2y-{\frac{ \left( {\rho }^{2}\delta _{{5}}{k_{{i}}}^{2}+\rho \,\delta _{{3} }k_{{i}}+\delta _{{2}} \right) k_{{i}}}{\rho \,\delta _{{1}}k_{{i}}+{k_{{ i}}}^{2}+\delta _{{4}}}} t\right) , \end{aligned}$$

(89)

$$\begin{aligned} & f_{III}=\sum _{i=1}^{N}\phi _i\widehat{f_i}=\phi _1\widehat{f_1}+\phi _2\widehat{f_2}+...+\phi _N\widehat{f_N}= \sum _{i=1}^{N}\phi _i\exp \left( k_ix+(\tau k_i^2+\rho k_i)y-{\frac{k_{{i}} \left( {\tau }^{2}\delta _{{5}}{k_{{i}}}^{2}+\tau \,k_{{ i}} \left( 2\,\rho \,\delta _{{5}}+\delta _{{3}} \right) +\alpha _{{1}} \right) }{\tau \,\delta _{{1}}k_{{i}}+{k_{{i}}}^{2}+\alpha _{{2}}}} t\right) . \end{aligned}$$

(90)

Remark 1

We used the multiple rogue wave solution method based on the Hirota bilinear theory and also constructed the abundant multiple soliton wave solutions for the generalised Hirota-Satsuma-Ito equation. The solutions obtained are applicable to ocean waves, so that they can be used in more widely applicable nonlinear models. In addition, the multiple soliton waves can be applied to particular ocean waves in this study, and some nonlinear models that will be which will be studied in the near future. The applicability and effectiveness of the solutions obtained are demonstrated by the numerical numerical results in the form of 3-D, density and 2-D plots. Finally, the obtained results show that the proposed multiple rogue wave solution method is simple, straightforward, and effective, which is expected to bring a light to the investigate the ocean wave theory. This work in comparison with already published papers have applicable to constructive findings in nonlinear sciences as particular in the ocean area. A soliton is a nonlinear solitary wave with the additional property that the wave retains its permanent structure, even after interacting with another soliton. Solitons are solitary waves that maintain their shape and speed while propagating with constant velocity.

Conclusion

In this paper, we investigate the (2+1)-dimensional generalized Hirota-Satsuma-Ito equation, and obtain its abundant multiple wave solutions in the form of lump, two and three lump soliton wave, kinky dark, periodic-dark, bright-dark, solitary wave solutions, periodic wave solution, etc by applying the Hirota operator. The applicability and effectiveness of the found solutions are shown by the numerical results in the form of 3-D, density, and 2-D graphs. And so, the N-soliton and multiple wave solutions of model (7) by linear superposition technique to the bilinear model were earned. Various types of new analytic solutions in the form of first-, second-, third-, fourth-order rogue wave functions are obtained. We can conclude that the Hirota bilinear and linear superposition techniques are more powerful and efficient approaches in finding rational lump wave solutions for large classes of nonlinear problems and can be applied to many other nonlinear partial differential equations arising in mathematical physics. In addition, the obtained results show that the proposed MRWSM is simple, straightforward and productive, which is expected to bring a light to the study of the traveling wave theory. Moreover, with the help of Maple computer program, we put out the direction of the gotten arrangements for visualizing the accomplished dynamical properties. The strength of the described equation that it is predictable, trustworthy, and computationally appealing. We are certain that the indicated methodologies will play a vital role in future research.