Introduction

Underground mining activities can lead to mountain subsidence deformation, landslides, and other disasters, posing significant threats to the geological environment, to buildings and inhabitants1,2,4. The southwest region of Guizhou, China, is rich in coal resources and is predominantly mountainous, characterized by steep slopes. These slopes, with their considerable height differences and steep gradients, present complex multilayer coal seam mining conditions. Consequently, some slopes have experienced large-scale geological disasters, notably including the Manling landslide in 20045, the Madaling landslide in 20066, and the Pusa landslide in 20177,8. The Pusa landslide, which was triggered by coal mining, resulted in 26 fatalities and 9 individuals missing. In the realm of mine geological disaster prevention and control, a critical research area has emerged around the insufficient understanding of the deformation evolution mechanism of high-steep mining slopes. This particular focus is on the deformation and failure laws of slopes under complex mining conditions and with concealed overburden deformation.

Within mining slopes, voids left by mining (goafs) lead to the deformation of the overlying rock, which in turn causes changes to the slope surface. The extent and visible characteristics of slope deformation are influenced by varying conditions of the goaf. Previous research has explored this issue through numerical and physical simulations, examining factors such as mining sequence9, mining depth10, multilayer mining11, mining thickness12 and the relationship between the goaf and slope height13. While these studies have revealed the effects of these factors, the impact of other significant variables on the movement mechanism of mining slopes remains largely uncertain. Notably, the location of the goaf within high-steep mining slopes has demonstrated a more significant impact. Variations in gob locations lead to the formation of diverse slope structures, which in turn induce distinct deformation evolution processes14,15. Research has confirmed that large-scale landslides are likely to occur when a goaf is situated beneath a steep slope shoulder or slope toe16. However, the specific effects of different goaf positions, including those at the slope shoulder and slope toe, on the deformation of overburden and slope require further investigation.

Physical model testing is recognized as an effective approach for validating the failure modes and characteristics of mining slopes17. This method allows for the investigation of the deformation and fracture evolution laws of overlying strata resulting from mining activities18,19,20. Model tests elucidate the impact of ultra-thick coal seam mining on the deformation characteristics of overburden, aiding in analyzing the movement, deformation, failure, and pressure variations across different mining stages12. By constructing a physical model under true triaxial stress conditions, researchers can examine the stress, deformation, and fracture fields during coal and rock mining21. Additionally, centrifuge tests enable the replication of complex mining slope structures and the observation of their deformation and failure processes, including the failure mechanisms of slopes with unique structures6. The use of a multimethod monitoring approach involving terrestrial laser scanning (TLS) and digital image correlation (DIC) allows for precise monitoring of subsidence deformation in models under multiple mining scenarios, aiding in the refinement of settlement prediction methods22,23. In these physical simulation test models, acoustic emission (AE) and infrared radiation thermography (IRT) techniques are employed to monitor the testing process, facilitating the detection of changes in the overlying strata following coal seam mining24. The extent of damage to overlying rock and the pattern of fracture expansion can be assessed through statistical analysis of the quantity, length, and area of fractures in a physical model19,20,21. Physical model testing provides a more direct and significant observation of deformation and failure characteristics when considering a single variable, thereby elucidating the underlying mechanisms and influences.

In this study, we focus on the typical mining slopes found in southwest Guizhou Province, abstracting a general geological conceptual model based on shared characteristics for physical model testing. We established three distinct models to examine various scenarios: (1) a goaf situated at the base of the slope shoulder; (2) a goaf located directly beneath the slope shoulder; and (3) a goaf positioned within the slope itself. An innovative mining simulation technique that combines the use of a pumping rod and melting wax was employed for the experiments. The outcomes of these physical model tests were analysed in terms of model deformation indicators, displacement features, and fracture statistics. From these analyses, we revealed the deformation and failure mechanisms, as well as the distribution and laws of overburden fractures in high-steep mining slopes with gently inclined internal siltstone, under the influence of three different goaf positions. The findings from this research have laid a foundation for optimizing premining plans and for preventing and controlling postmining geological disasters in such mining environments.

Modelling

Geological model

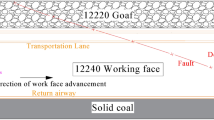
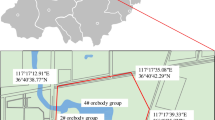
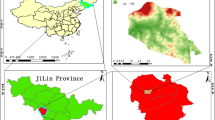
After extensive investigations, it was discovered that the primary lithology of the high steep slopes in southwestern Guizhou, China, predominantly consists of hard siltstone and limestone, interbedded with mudstone and argillaceous siltstone, which all form in a gently sloping rock formation. Within the study area, where high-steep slopes and sand-mudstone formations are prevalent, five significant geological hazard points associated with high-steep slope mines were identified. These include the Pusa landslide in Nayong County, the Jianshanying deformation-body in Shuicheng County, the Dayantou deformation-body in Dafang County, the Dajingjiao deformation-body in Liupanshui County, and the Yingshanhongshan deformation-body in Xingren County, as illustrated in Figs. 1 and 2.

Fig. 1
figure 1

Study area and 5 typical high-steep slope mine geological disaster points. (Drawn by ArcGIS, version 10.7.0.10450, http://www.esri.com. Digital elevation data from https://www.gscloud.cn.)

Full size image
Fig. 2
figure 2

The overall situation and profile of five typical cases (1 Limestone; 2 Siltstone; 3 Argillaceous siltstone; 4 Gravelly soil; 5 Coal seam; 6 Goaf; 7 Fractures; 8 Stratigraphic boundary; 9 Fault; 10 Upper member of the Lower Triassic Yelang Formation; 11 Lower Triassic Yelang Formation lower member; 12 Lower Triassic Jialingjiang Formation; 13 Lower Triassic Yongningzhen Formation; 14 Lower Triassic Feixianguan Formation; 15 Upper Permian Changxing-Dalong Formation; 16 Upper Permian Longtan Formation; 17 Section direction; 18 Rock occurrence).

Full size image

Table 1 presents the fundamental geological conditions, characteristics of the slope structure, and features of coal seam extraction for the aforementioned five typical high-steep mining slopes. The upper portions of these slopes are notably steep, contrasting with the gentler lower sections. The slopes are primarily composed of limestone, siltstone, and argillaceous siltstone. The orientation of the strata is toward the slope, with a dip angle that is commonly less than 15 degrees. The coal seams undergo multilayer mining involving two or more strata. Typically, the width of goaf is approximately 200 m.

Table 1 Structural characteristics of typical high-steep mining slopes.
Full size table
Table 2 Model size.
Full size table

Among the five cases examined, the Dayantou deformation-body is in a relatively stable state, providing an excellent and safe environment for investigation. Significant deformation phenomena have been observed at the front, foot, shoulder, and top of the slope, accompanied by minor collapses within the slope body. The positions on the slopes corresponding to the deformation indicators depicted in Fig. 3 are marked in Fig. 2c. It is important to note that the cracks displayed represent only a portion of those identified; extensive cracking is found throughout the middle and upper sections of the slope during field investigations. Consequently, this study will focus on the deformations at Dayantou as the primary subject of study, using this deformation-body as a foundation to integrate other typical geological hazards associated with mining, with the aim of developing a conceptual geological model.

Fig. 3
figure 3

Dayantou Deformation Features with Partial Deformation. (a) Slope upper part collapse, (b) Fractures in the lower part of the collapsed rock mass, (c) Ground fractures behind the slope, (d) Ground fractures below the slope shoulder, (e) and (f) Mid-slope fractures and steep scarp.

Full size image

Model generalization

Reflecting on the development traits of typical mining slopes, characteristics such as the lithology of the formation, the topography of the slope, and the distribution of coal seams are summarized individually. The composition of the mining slope predominantly encompasses four lithological types: limestone, siltstone, argillaceous siltstone, and coal. Notably, the limestone located at the slope summit exhibits distinct mechanical properties compared to those of other rock masses. The primary lithology for the middle and lower segments of the slope is predominantly siltstone, making it the most characteristic. Hence, the generalized model primarily accounts for three types of lithology: limestone at the slope’s peak, siltstone constituting the main body, and the coal seam present in the subsurface mined-out areas (goaf).

The limestone layers are represented by the Yongningzhen Formation, Jialingjiang Formation, and Liangshan Formation, with thicknesses ranging from 15 to 300 m. In the most representative examples of steep, high mining slopes, limestone is prominently exposed at the slope’s summit. Based on the attributes of three typical cases within the model, the conceptual model assigns a thickness of 43 m to the limestone layer, and the slope is positioned at an angle of 80 degrees.

Beneath the limestone layer, the strata typically transition into the Feixianguan Formation, which is characterized predominantly by sandstone and mudstone. This formation is extensively exposed across the study area, boasting considerable thickness ranging from 100 to 400 m. Based on the thickness and slope characteristics of siltstone in typical examples, the model sets the siltstone strata’s slope above the slope toe at 55 degrees, with a thickness of 135 m.

In the southwestern region of Guizhou, the strata containing coal primarily consist of the Longtan Formation, Xuanwei Formation, and Wangjiazhai Formation, among others, where it is common to find multiple layers of coal seams. In the area under study, the number of coal seam layers mined ranges from 2 to 6, with the majority being 2 layers, and the average coal seam thickness is 2.67 m. Consequently, the model incorporates two coal layers, with a set thickness of 2.5 m for each layer and a spacing of 15 m between the coal seams. The coal-bearing strata are typically of a softer lithology with the surrounding terrain being relatively flat, leading to the lower slope part being set at an angle of 6 degrees.

In the study area, the rock layer of the slope is generally minimally influenced by structural factors, predominantly exhibiting a flat structure, with the rock layer maintaining a consistent orientation. Consequently, the generalized model is designed with an inclination toward the slope, featuring an inclination angle of 8 degrees. Considering these characteristics, an ideal geological conceptual model has been developed for a high-steep mining slope composed of gently inclined siltstone (Fig. 4).

Fig. 4
figure 4

Geological conceptual model of a typical mining slope.

Full size image

Physical model tests

Physical model

  1. 1.

    Model geometry.

    Drawing from the geological generalized model described earlier, a physical test model was constructed adhering to the principles of similarity5,8. The idealized model spans approximately 750 m in length and 370 m in height. According to the actual test conditions, the geometric similarity ratio \(\:{\text{C}}_{\text{L}}\) of the model is set to 400. Because the horizontal stress in southwestern Guizhou is small, it is mainly the vertical stress of the self-weight. Therefore, the three factors of the cohesion similarity ratio \(\:{\text{C}}_{c}\), internal friction angle similarity ratio \(\:{\text{C}}_{\phi\:}\) and bulk density similarity ratio \(\:{\text{C}}_{r}\) are considered:

    $$\:{\text{C}}_{\text{c}}\text{\:}\text{=}{\text{\:}\text{C}}_{\text{r}}\text{*}\text{\:}{\text{C}}_{\text{L}}\text{\:}\text{=}\text{\:}\text{400}$$
    (1)
    $$\:{\text{C}}_{r}\text{\:}\text{=}\text{\:}{\text{C}}_{\text{φ}}\text{\:}\text{=}\text{\:}\text{1}$$
    (2)

    The dimensions of the physical model, derived through the application of the similarity principle, are presented in Table 2 and illustrated in Fig. 5. The model’s dimensions are 182 cm in length, 25 cm in width, and each unit plate is 2 cm thick. After applying the similarity ratio, the coal seam thickness is approximately 0.625 cm, which is not conducive to observing overburden deformation and slope surface displacement in the scaled model. In previous studies, the coal seam or the mining thickness in the models has also been magnified to observe the deformation and fracturing of the overlying strata, with good results obtained6,8,25. Consequently, for practicality and to meet the objectives of the experimental research, the coal seam thickness was standardized to 2 cm with two layers, aligning with the geological generalization model. The experiment primarily focused on observing the deformation of the overlying rock; therefore, the space between the two coal layers was eliminated, creating a goaf with a thickness of 4 cm.

    Fig. 5
    figure 5

    Physical simulation test model.

    Full size image

    A physical simulation test model has been developed based on a geological conceptual model. The properties of materials simulating coal are suboptimal, as shown in Table 3, making them prone to settlement compression deformation due to the model’s self-weight. Additionally, previous studies have used the lithology of adjacent strata to represent the coal seam in their models6,8; therefore, in this physical simulation test model, coal material is not used, and only a goaf is included. The model is composed of two similar materials, siltstone and limestone. As depicted in Fig. 5, the coal outside the goaf in the test model is substituted with siltstone.

    Table 3 Physical simulation test of the original rock parameters and target parameters(\(\:{\text{C}}_{\text{L}}\)=400).
    Full size table

    The physical simulation test uses three models to study the slope deformation characteristics under different conditions of the relationship between the goaf boundary and the position of slope shoulder and slope foot. The configurations of the three goaf arrangements are detailed in Figs. 5 and 6.

    Fig. 6
    figure 6

    Range and sequence of model mining (a) The corresponding mining range of the three models, (b) The mining sequence of the models, (c) Paraffin and the round stick wrapped with resistance wire.

    Full size image

    Model 1 positions both the slope shoulder and slope toe directly above the goaf, with a goaf width of H = 50 cm and two mining layers (N = 2), resulting in the goaf’s outer boundary intersecting the slope toe and placing both the slope shoulder and toe within the goaf. Model 2, maintaining the same goaf width and number of mining layers, situates only the slope shoulder above the goaf, thereby incorporating only the slope shoulder within the goaf boundary. Conversely, Model 3 encapsulates the goaf entirely within the slope, with the goaf still measuring H = 50 cm in width and comprising two mining layers (N = 2), which distances the goaf from both the slope’s shoulder and toe, presenting a distinct arrangement from the previous models.

  2. 2.

    Model material.

    The similar materials for siltstone and limestone in the model were selected based on the original rock parameters and orthogonal testing8,2526. Given that the real slope and the indoor model are scaled down by a geometric similarity ratio (\(\:{\text{C}}_{\text{L}}\) = 400), achieving the correct similar material ratio is crucial for the success of the physical simulation test. Building on previous research, the main materials used in this study include gypsum, iron powder, barite, and water as a mixing agent. After extensive testing of various combinations through orthogonal tests, the optimal model material parameters were established, as shown in Table 3. The mass ratios of gypsum, iron powder, barite, and water for siltstone and limestone are 1.9:22.2:66.7:9.2 and 1.7:15:75:8.3, respectively.

  3. 3.

    The stacking of the model and the monitoring instrument.

    In constructing the physical simulation model, the methodology employed involves the strategic placement of laying and resistance wire boards, along with a paraffin board, at specific locations. The assembly of the model utilizes the unit plate method, where the unit plates are available in two dimensions: 20 * 10 * 2 (cm) and 20 * 15 * 2 (cm). During the stacking process, the unit plates are arranged side by side by width, creating a base layer width of 25 cm. The subsequent layers were then alternated between widths of 10 cm and 15 cm to ensure structural integrity and variability.

    For the purpose of monitoring the model’s behavior under test conditions, several key instruments are deployed. These instruments include 6 rod displacement meters, a three-dimensional laser scanner, and a digital camera. The rod displacement meter, which is crucial for measuring slope movements, is installed at the slope’s summit and secured using a bracket. The three-dimensional laser scanner, equipped with fixed brackets at both the front and side of the model, facilitates comprehensive scanning during the testing phase. The arrangement and positioning of these monitoring tools are detailed in Fig. 5.

Model mining

The selection of a mining method plays a crucial role in the study of mining slopes, with the ideal approach causing minimal disturbance to the slope, allowing for efficient and complete extraction, and not impacting the subsequent deformation of the slope. Traditional physical extraction methods, such as the use of sandbags or round wooden sticks27, have been noted to inadvertently disturb the slope and complicate complete mining, thereby affecting the slope’s later deformation. In this experiment, an innovative electric heating method, termed the ‘melting wax and pumping stick’ technique, was employed to simulate the mining process6,8. This method involved creating a model goaf with a width of 200 m, which, after applying a similarity ratio, equated to a 50 cm width in the model. The mining area was simulated using four wax plates per layer, each plate measuring 12.5 cm in width and 2 cm in thickness, with a total of eight plates across two layers, as illustrated in Fig. 6. To facilitate the melting process, each stick was wrapped with resistance wire, enabling the paraffin wax to be efficiently melted through electrical heating. Additionally, to ensure complete melting of the paraffin wax, four thin wooden boards wrapped with resistance wires were strategically placed beneath the wax plates.

In the model experiment, the upper layer is mined first, followed by the lower layer, with the mining direction progressing from outside the slope towards the inside. Each mining activity involved the removal of one wax plate measuring 12.5 cm in length, which corresponded to a simulated actual slope mining distance of 50 m. The mining sequence is shown in Fig. 6. The mining time of each wax plate is approximately 8–15 min, and the judgment basis of the next wax plate is that there is no obvious change in the sensor data after the previous mining. Throughout the testing phase, the model was meticulously documented and analysed using three-dimensional laser scanning both before and after each mining activity. Following the final, or eighth, mining operation, the procedure allowed the model to continue undergoing deformation. The test was concluded once the data from the slope top rod displacement meter indicated stability over an extended period, specifically after 24 h. This meticulous approach ensured a detailed observation of the impact of the mining process on the structural integrity and deformation patterns of the model.

Results

Progressive failure of slope

During the experiment, as the wax plates in the goaf were sequentially mined, all three models exhibited significant deformation. In both Model 1 and Model 2, there was a clear displacement observable on the slope’s free surface, with Model 1 showing particularly pronounced deformation. For Model 3, the goaf was positioned internally within the slope, leading to the majority of the deformation being confined inside the slope, thereby minimally affecting the free surface.

Following the second mining operation in Model 1, the overlying rock experienced deformation, extending approximately three times the thickness of the goaf, as indicated at location 1 in Fig. 7a. After the fourth mining, the deformation progressed to the slope table above the goaf, resulting in more pronounced overall deformation towards the front of the slope. This phase marked a significant alteration in the orientation of the rock strata within the deformed overlying layers, with the upper strata of the slope maintaining a gentle incline but with a reduced dip angle, nearing horizontal. The middle and upper portions of the rock strata of the slope assumed a more gradual slope. Dense fractures developed at the slope’s summit (Fig. 7b location 1), affecting the slope shoulder to a depth of approximately 40 cm, with clearly visible tensile fractures due to the forward tilting of the free face. The middle section of the slope exhibited outwards bulging (Fig. 7b location 2), and the slope’s base underwent significant sinking (Fig. 7b location 3), descending approximately 15 mm downwards and 3 mm outwards.

Fig. 7
figure 7

Model 1 The deformation after the 2nd, 4th, 6th and 8th mining and the fracture distribution at the end of the test.

Full size image

After the sixth mining, a longitudinal crack extending more than 16 cm emerged approximately 20 cm from the slope shoulder (Fig. 7c location 1), with the crack opening reaching up to 4 mm. Expansion fractures along the edge of the element plate were observed near the displacement sensor at the slope shoulder (Fig. 7c location 3). The deformation intensified after the eighth mining of Model 1 (Fig. 7d), particularly at the slope top, the boundary of the goaf, and the slope toe. The tensile fracture at the slope’s summit widened to approximately 14 mm (Fig. 7d location 4). The No. 1 rod displacement meter fell into the fracture zone, indicating a significant increase in displacement at the slope top. After the sixth mining, the longitudinal fracture’s opening further widened, reaching 13 mm (Fig. 7d location 1), with the overlying strata in the goaf becoming increasingly fragmented. Behind the slope, away from the goaf boundary, a vast array of microfractures emerged, predominantly aligned longitudinally along the unit plate’s boundary and transversely forming dislocation fractures between layers (Fig. 7d location 2). The front of the slope was characterized by stepped outwards extrusion (Fig. 7d location 3), highlighting the extensive deformation and fracturing resulting from the mining operations.

The analysis of the final fracture distribution in Model 1 reveals that the primary area of deformation is focused above the goaf. However, the area influenced by the goaf is extensive, with the most distant fracture at the slope’s top being approximately 40 cm away from the goaf’s inner boundary. This clearly defines the boundary of the main deformation zone, which is highlighted by a green line in Fig. 7e. The boundary of this main deformation zone slopes inwards towards the slope’s interior, while its outer boundary slopes outwards. This means that the main deformation area at the upper part of the boundary on both sides of the goaf narrows as the depth decreases.

Following the second extraction in Model 2, the deformation primarily affected the top three layers above the goaf, as shown at location 1 in Fig. 8a, characterized by the caving and breaking of the roof. After the fourth mining operation, subsidence was mainly observed in the upper strata of the goaf, with the principal area of deformation exhibiting noticeable separation. Longitudinally, the subsidence stretched to the slope’s summit (Fig. 8b location 1), where the top of the slope above the goaf notably collapsed and bent. The main deformation zone expanded progressively from the goaf toward the slope surface. Following the sixth mining (Fig. 8c), the rock layers above the goaf’s outer boundary were fractured and collapsed, while the changes in the strata above the inner boundary of the goaf were relatively similar to those observed after the fourth mining. After the eighth mining of Model 2 (Fig. 8d location 1), the overlying strata within the goaf exhibited a general downwards bending and separation. No significant fractures were visible on the slope’s top plane, although clear downwards bending was noticeable. Additionally, some rock layers at the slope shoulder moved approximately 4 mm toward the slope (Fig. 8d location 2).

Fig. 8
figure 8

The deformation after the 2nd, 4th, 6th and 8th mining and the fracture distribution at the end of the test are shown in the model 2 test.

Full size image

In Model 2, the distribution of fractures is similarly focused above the goaf area. Initially, the distribution range narrows and then broadens from the goaf, with the fracture range expanding significantly near the boundary between limestone and siltstone, mirroring the pattern observed in Model 1. Figure 8e illustrates the boundary of the main deformation zone in Model 2, where both the inner and outer boundaries of the goaf are slanted toward the slope’s exterior. This indicates that the principal direction of deformation is towards the interior of the slope.

Model 3 exhibits overall deformation patterns that are akin to those observed in Model 2. Following the second mining operation (Fig. 9a), the deformation predominantly affects the three strata above the goaf. After the fourth mining, the strata overlying the goaf visibly bend downwards. The fissures at both the inner and outer boundaries of the goaf extend upwards to the limestone layer, as shown in Fig. 9b at location 1. Along the inner boundary of the goaf within the model, longitudinal fractures stretch from the top of the slope to the midpoint of the goaf (location 2). The sixth mining leads to the breaking and collapsing of the rock strata above the goaf’s outer boundary (Fig. 9c), with noticeable bending and subsidence deformation on the slope surface above the goaf. Following the eighth mining, the strata above the goaf’s inner boundary are fractured and deformed (Fig. 9d at location 1). The area of fracture distribution within the overburden separation layer expands upwards, and the strata overlying the goaf bend downwards as a whole. No significant deformation is observed on the slope surface of the free slope.

Fig. 9
figure 9

Model 3 The deformation after the 2nd, 4th, 6th and 8th mining and the fracture distribution at the end of the test.

Full size image

The fracture distribution in Model 3 mirrors that in Model 2, with an expanded fracture distribution range at the limestone and siltstone boundaries. As depicted in Fig. 9e, the boundary of the main deformation zone in Model 3 tilts towards the slope’s exterior, with the primary deformation direction being towards the slope. The boundary angle of the main deformation zone remains consistent, perpendicular to the dip angle of the rock stratum.

Slope model displacement

Deformation monitoring

Upon examining the displacement and strain characteristics at the conclusion of the experiments on the three models, it was observed that the primary displacement and deformation are localized in the area above the goaf. Based on the final displacement of the overlying strata as shown in parts (b), (e), and (h) of Fig. 10, it can be observed that the displacement of the overlying strata increases as they are closer to the goaf. The displacement observed in the models is predominantly vertical, and it increases with increasing burial depth. A comparative analysis of the three models reveals that as the position of the goaf shifts closer to the slope, the deformation zone similarly shifts towards the slope.

Fig. 10
figure 10

Final deformation monitoring of the three model tests (a, d, and g are the point cloud difference results; b, e, and g are the displacements based on DIC; c, f, and i are DIC-based strain conditions, and the overburden is toppled and rotated outwards to the slope in a positive direction).

Full size image

The analysis of point cloud data for the three models, labelled a, d, and g in Fig. 10, distinctly highlights the main deformation zones on the slope surface. For Model 1, the most significant deformation of the slope surface is found at the two extremities—the slope shoulder and slope toe. Conversely, for Models 2 and 3, the deformation of the slope surface is primarily concentrated near the goaf’s centerline.

Digital image correlation (DIC) is a comprehensive, noninvasive optical technique used to measure displacement in experimental setups by analysing the correlation between digital images captured throughout the testing process28. The application of DIC in evaluating displacement characteristics within model test research has evolved into a more established methodology22,29,30,31. Despite the absence of a specific speckle pattern arrangement in this experiment, the naturally high randomness of the model’s surface roughness provides a suitable basis for employing the collected images in DIC analysis and research.

Figure 10b, e, and h illustrate the internal displacement of the model as determined by the two-dimensional digital image correlation method (DIC). The displacement patterns observed across the three models are notably similar, with the maximum displacement exceeding 40 mm, surpassing the thickness of the goaf. In Model 1, the highest displacement on the slope surface is primarily focused on the free surface, which is positioned above the goaf but leans towards the slope’s exterior, impacting the area in front of the slope toe the most. Conversely, in Models 2 and 3, the displacement is mainly localized in the upper region of the goaf, within the interior of the slope shoulder. Figure 10c, f, and i depict the strain conditions of the model. For Model 1, the strain predominantly extends towards the exterior of the slope, with the slope’s strain chiefly concentrated at the slope’s base. Models 2 and 3 exhibit similar patterns, where the strain can be divided into two segments in the middle of the goaf, running perpendicular to the rock surface. Both segments show deformation towards the central line of the goaf.

Displacement of slope top

Figure 11 presents the monitoring data for the displacement at the top of the slope from the start to the finish of the test. The displacement at the top of Model 1’s slope remained stable at 16 h into the test, while the displacements at the tops of Models 2 and 3 ceased to change at 14 h and 16 h, respectively. The greatest displacement in Model 1 was recorded at Sensor 1, which was situated near the slope shoulder and reached a maximum of 52 mm. For Model 2, the highest displacement was observed at Sensor 3, located approximately 12 cm behind the vertical projection of the slope surface at the center of the goaf, with a maximum displacement of approximately 24.5 mm. In Model 3, the maximum displacement occurred at Sensor 5, positioned approximately 10 cm behind the vertical projection of the central slope surface of the goaf, with a displacement of approximately 24 mm.

Fig. 11
figure 11

The time-varying characteristics of the displacement of the slope top of the three models.

Full size image

The maximum vertical displacement of the slope surfaces in Models 2 and 3 were nearly identical, with the peak subsidence of the slope surface located approximately 10 cm from the vertical line towards the slope in the goaf. Analysing the correlation between the mining time and the vertical displacement at the slope tops of the three models, it was found that the initial four mining operations, which targeted the first layer of the coal seam and had a total mining width of 50 cm, did not result in a vertical displacement at the slope top exceeding 10 mm. However, with the mining of plates 5 to 8, the vertical displacement at the slope top increased rapidly, with a significant increase following the completion of mining the second layer. Specifically, Sensors 1 and 2 in Model 1 exhibited a sharp increase in displacement after the final mining operation, indicating ongoing deformation near the slope shoulder. Sensor 1, in particular, experienced a drastic displacement increase of nearly 25 mm due to falling into the fracture at the slope shoulder.

Discussion

Rule of deformation failure

Using the slope shoulder (S) and the slope toe (T) as reference points on a vertical line, the direction from the interior towards the exterior of the slope is considered positive. The horizontal distance from the outer boundary of the goaf to the slope toe (T) is denoted as “a”, the distance between the goaf and the slope shoulder is denoted as “b”, and the distance from the inner boundary of the goaf to the slope shoulder (S) is denoted as “c”. By examining these three horizontal measurements, one can determine the spatial relationship between the goaf and both the shoulder and toe of the slope, leading to the identification of three distinct scenarios.

  1. 1.

    a > 0, b > 0, c < 0. The goaf is located at the shoulder and foot of the slope at the same time (Fig. 12a).

    Fig. 12
    figure 12

    Slope deformation and failure modes under the influence of three goaf positions.

    Full size image

    From the horizontal perspective, the slope is categorized into three zones: the tension influence zone, the collapse toppling deformation zone, and the pushing deformation zone. The tension influence zone arises primarily due to the tensile forces in the rock mass triggered by the slope’s collapse. Within this area, minor fractures appear both on the surface and inside the rock mass, predominantly following the structural planes. The collapse toppling deformation zone represents the core area of slope deformation, where the collapse near the slope’s base leads to the upper portion of the slope collapsing and tilting outwards. This zone often indicates that the slope has already reached a state of instability and damage. The pushing deformation zone, which propels the collapse toppling deformation zone forward and is situated at the forefront of the slope’s base, typically exhibits minimal deformation. However, the deformation characteristics in this zone are quite distinctive, showcasing upturned rock masses in front of the slope and slippage of the slope itself. The deformation behavior observed in this model can be encapsulated as collapse toppling deformation.

  2. 2.

    a < 0, b > 0, c < 0. The goaf spans only the slope shoulder and does not cross the slope toe (Fig. 12b).

    Horizontally, the slope can be segmented into a tension and compression influence zone, a collapse fragmentation zone, and an extrusion deformation zone. During coal seam mining, the overlying rock in the collapse cataclastic zone sinks, causing deformation on both sides of the divide. The upper portion of the tension-compression influence zone experiences tension, whereas the lower part undergoes compression. Due to spatial constraints for deformation, only the upper area undergoes settlement deformation. The outer overburden of the collapse cataclastic zone moves inwards along the bedding planes near the slope’s surface, but the limited space for inwards movement means that the middle and lower sections can only deform toward the slope’s free direction. This leads to the creation of a lateral extrusion deformation zone, where outwards slip deformation can occur. Hence, the deformation pattern observed here can be characterized as collapse slip deformation.

  3. 3.

    a < 0, b = 0, c < 0. The goaf is completely located inside the slope, away from the shoulder and foot of the slope (Fig. 12c).

    When the goaf’s outer boundary is significantly distant from the slope’s shoulder and toe, the slope undergoes subsidence deformation due to the substantial weight of the overlying rock. This occurs because horizontal displacement is no longer feasible on either side of the goaf’s overlying strata, leading to predominantly vertical deformation. Nevertheless, a pushing effect persists, causing the extent of the goaf outside the slope to be generally smaller than that within the slope, indicating an ongoing push tendency. This deformation pattern can be encapsulated as collapse/subsidence push deformation.

    The displacement results depicted in Fig. 11 illustrate a significant increase in the displacement at the top of the slope following double-layer mining, with values ranging from 5 to 10 times that observed during single-layer mining. This displacement reaches approximately 0.6 times the thickness of the goaf. As the goaf’s position shifts relative to the slope, the maximum displacement point at the top of the slope also moves towards the back of the slope. Moreover, the displacement increases closer to the midline of the goaf, which is perpendicular to the beding plane. In the future, under the influence of rainfall, the deformation of the slopes corresponding to the three models is expected to intensify. Specifically, model 1 is at a high risk of experiencing a landslide disaster. For models 2 and 3, the rock mass near the top of the slopes is likely to loosen, increasing the likelihood of collapse.

    The deformation and failure modes of the goaf situated beneath the shoulder and foot of the slope have been validated through numerical model testing in various studies6,8,11,32. Fathi Salmi and colleagues conducted a numerical simulation focusing on a mining slope with the goaf located beneath the slope shoulder, finding results akin to collapse slip deformation, with the overburden rock primarily moving towards the slope direction16. The position of the goaf within the slope influences the extent of the impact of subsidence deformation on the slope shoulder and the slope’s free surface; the greater the distance from the slope shoulder is, the lesser the impact. As the goaf’s position relative to the slope changes, the tensile deformation area of the overlying strata gradually decreases, while the pushing and subsidence deformation area enlarges. Consequently, the impact on the deformation of the slope’s free surface diminishes, and the deformation and failure zone increasingly aligns perpendicularly to the goaf’s midline.

Overburden rock fracture and damage

Fractures serve as the primary indicators of damage within a rock mass, with their number, length, area, and volume being critical variables for describing such damage33. The presence of fissures compromises the integrity of the overlying strata, influencing the deformation and strength properties of the rock mass and consequently complicating the subsidence behavior of the mined rock mass24. In this study, the observed phenomena of overburden deformation in model tests include not only displacement but also the formation of fractures along the contact surfaces of the unit plates, leading to the breaking of these plates. Thus, this research aims to conduct a statistical analysis of the final fracture distribution across various models, examining the fracture distribution patterns within the overburden rock of mining slopes under different goaf positions. This analysis seeks to elucidate the damage patterns of overburden rock, enhancing our understanding of the structural impacts of mining activities.

Fracture statistics

  1. 1.

    Proportion of the fracture area.

    To streamline the statistical analysis, the test model was segmented horizontally into six sections labelled A, B, C, D, E, and F, as depicted in Fig. 13a. Vertically, within the rock stratum, it was divided into ten distinct depth regions. Specifically, areas B, C, D, and E represent the vertical sections across the goaf, each spanning a width of 25 cm. Areas A and F serve as the statistical regions flanking the goaf, with widths of 25 cm and 12.5 cm, respectively. The goafs in the three models correspond to the spaces between areas B and C, C and D, and D and E. A statistical analysis was conducted on the final fracture distribution within each test model. The total area of each statistical region is denoted as \(\:{\text{S}}_{\text{I}}\), and the area occupied by fractures is represented as SfI. The fraction of the area covered by fractures in each segment, \(\:{\text{P}}_{\text{I}}\), is calculated using the following formula:

    Fig. 13
    figure 13

    Statistics of the fracture area ratio and maximum damage zone offset distance of the model statistical partition.

    Full size image
    $$\:{\text{P}}_{\text{I}}\:=\:\frac{{\text{S}}_{\text{fI}}}{{\text{S}}_{\text{I}}}$$
    (3)

    where \(\:\:{\text{P}}_{\text{I}}\)is the proportion of the fracture area in the statistical area in each subarea;

    \(\:{\text{S}}_{\text{fI}}\) -the fracture area of each partition;

    \(\:{\text{S}}_{\text{I}}\)-the total area of each partition;

    \(\:\text{I}\) - partition number, horizontal An ~ F partition and each depth partition in the direction of the vertical rock stratum;

    The \(\:{\text{P}}_{\text{I}}\) distribution fitting curve of each partition in the horizontal direction of the three models conforms to the Gaussian distribution formula (Fig. 13a):

    $$\:y\:=\:{y}_{0}\:+\:\frac{A}{w\sqrt{\pi\:/2}}{\:e}^{-2\frac{{(x-{x}_{c})}^{2}}{{w}^{2}}}$$
    (4)

    The symbol values in the fitting formula are shown in Table 4.

    Table 4 The symbol values in the fitting formula.
    Full size table

    The proportion of fractures per unit area in the statistical area of the model is defined as P, which can be obtained by the following formula:

    $$\:\text{P}\text{\:}\text{=}\text{\:}\frac{\sum\:{\text{S}}_{\text{fI}}}{\sum\:{\text{S}}_{\text{I}}}$$
    (5)

    Figure 14a shows the proportion of fracture area in different buried depth zones at the end of the three model tests, and the change in the P value in the total statistical area of each model is shown in Fig. 14b.

    Fig. 14
    figure 14

    Statistics of the proportion of fractures in the study area under different burial depths and different mining orders.

    Full size image
  2. 2.

    Fissure aperture.

    The study conducted fracture opening measurements across the main deformation zones of the three models, with the findings presented in Fig. 15. The largest fracture openings were predominantly located above the edges of the goaf on both sides. A noticeable trend is that fracture openings tend to decrease with depth, showing a certain level of convergence. Moreover, as the goaf shifts towards the interior of the slope, the overall fracture openings decrease. In Model 1, the fissures generally exhibited larger openings. Notably, the fissures above the inner boundary of the goaf had significantly larger openings than those above the outer boundary. The openings of fissures above the inner boundary were relatively uniform, without the trend of decreasing opening size at shallower depths. Consequently, when the goaf is situated beneath the slope shoulder and toe, the slope undergoes severe deformation, making it susceptible to instability and failure. The area above the inner boundary of the goaf is identified as the zone of maximum tensile failure in the overburden rock.

    Fig. 15
    figure 15

    Fracture opening statistics of the three models.

    Full size image

Overburden rock damage

In this research, the increase in the unit area of fractures is utilized as a measure of the increase in fracture damage within overburden rock. Consequently, the fracture damage increment within the overburden rock’s statistical area, as illustrated in Fig. 13a, exhibits characteristics of a Gaussian distribution. This means that internal fractures within the overburden rock intensify sharply as one moves from the outer boundary of the goaf towards its centre, with the greatest increase in damage occurring near the vertical line of the goaf. Interestingly, the symmetry axis of the Gaussian curve fitted to represent the maximum damage does not align with the vertical line of the goaf (as shown in Fig. 13a). However, studies on underground mining model tests conducted on horizontal strata in plain areas suggest that fractures and deformations of the overlying strata on both sides of the goaf center are relatively symmetrical19,22,23,32,33,34,35,36. In this study, Model 1 shifts towards the outside of the slope, whereas Models 2 and 3 shift towards the inside, aligning with the displacement direction of the overburden rock in the deformation and failure modes of the three models. This indicates that the direction of horizontal displacement of the overlying strata in the goaf points to the offset direction of the most densely fractured area. Notably, the horizontal displacement of the overlying strata in Model 1 is more significant than that in Models 2 and 3, which also corresponds to a larger offset distance of the area with maximum fracture damage.

Based on the analysis of the deformation and failure models, it is evident that the migration phenomenon is intricately linked not only to the dip angle of the rock stratum but also to the presence of the goaf, slope shoulder, and slope foot. By using the centerline of the slope shoulder and slope toe as the baseline (abscissa zero line) and examining the offset distance of the most concentrated area of deformation in the three models, it is observed that the offset phenomenon is influenced by the position of the vertical line in relation to the slope shoulder within the goaf (as depicted in Fig. 13b). Specifically, when the vertical line in the goaf is located outside the slope shoulder, the overburden rock deforms and shifts toward the outside of the slope. Conversely, when the vertical line of the goaf falls inside the slope shoulder, the displacement and fracture concentration in the overburden rock move towards the slope.

The analysis of fracture proportions relative to burial depth (shown in Fig. 14a) reveals that the greater the depth and the closer to the goaf, the greater the damage to the overburden rock (as indicated by the proportion of fractures). Furthermore, all three models exhibit a trend where the damage increment ratio decreases in shallower parts and increases in the middle to deeper sections. For Model 1, the damage increment initially decreases and then increases with increasing depth, which is intimately connected to the deformation and failure patterns of the overlying strata above the goaf. As illustrated in Fig. 12a, this area experiences collapse toppling deformation, which is smaller in scale than the main deformation zones of the other two models, resulting in a more limited range of deformation and fractures. The outer side of this deformation zone is the slope’s free surface, where horizontal deformation is unrestricted, leading to greater horizontal displacement than that of the other models. Consequently, the primary mode of deformation occurs along the layers.

Analysing the trend of fracture proportions within the total statistical area, as shown in Fig. 14b, it is observed that the fractures in all three models increase as mining progresses, indicating an overall and growing trend in the damage to the overburden rock. Notably, after the fourth mining operation, which involves an actual mining width of 200 m, there is a marked increase in mining damage across all the models, aligning with the slope top displacement monitoring results. However, the fracture proportions in Model 1 and Model 3 peak after the 5th and 6th mining operations, respectively, and then begin to decrease, even as the slope top displacement continues to increase. This suggests that the subsidence of the overlying strata at this stage reduces the openness of fractures near the goaf, while the increase in the openness of fractures in the middle and upper parts is limited, leading to a decrease in the overall fracture area proportion of the overlying strata. This is interpreted as a compaction phenomenon of the overlying strata under the influence of gravity stress.

If the assessment of overburden damage is based solely on the proportion of the fracture area, Model 3 appears to have the largest damage increment, although the openness of its fractures is generally less than that observed in Models 1 and 2. Within Model 1, the fracture area proportion is greater in zone B than in zone C, but the opposite is true for the open zone. It is posited that Models 1 and 2 have more space for horizontal displacement. Thus, the increase in damage is reflected not only in the increase in fracture area but also in the number of fractures, the degree of fracture openness, and the number of dislocations. Macroscopically, this is manifested in rock bending fractures, increased fracture openness, and a reduction in fracture surface roughness due to dislocation deformation. These aspects are identified as the focus of further research.

Conclusions

By utilizing a conceptual engineering geological model derived from investigating and summarizing typical mining slope cases, this study employs physical simulation tests to uncover the deformation and failure patterns of high-steep mining slopes in gently inclined inner siltstone under varying goaf positions. It also examines the fissure distribution and damage patterns of the overlying strata above the goafs.

This study identified distinct behaviors depending on the relative positions of the slope shoulder, slope toe, and goaf. When both the slope shoulder and slope toe are positioned above the goaf, the slope toe sinks, and the slope’s top part undergoes tensile deformation. The overburden rock above the goaf topples towards the slope’s outer direction, with the subsidence displacement of both the overburden rock and slope surface exceeding the goaf’s thickness, resulting in collapse and toppling of the overall slope. If only the slope shoulder is above the goaf, the overburden rock collapses toward the goaf’s center, causing outwards slip in the middle and lower parts of the slope due to a pulling and pushing effect, leading to collapse slip deformation. When the goaf’s outer boundary is within the slope shoulder, the overburden rock collapses similarly to plain underground mining, but proximity to the slope shoulder can drag the slope’s upper part, affecting its stability.

The study further notes that the goaf’s location significantly impacts the deformation, fracture distribution, and damage to the overburden of the gently inclined internal mining slope. By comparing three physical models under different mining sequences, it was found that the relationship between the goaf and the shoulder of the slope plays a crucial role in the deformation and failure of the mining slope. The change in the proportion of fracture area in the overlying strata serves as a primary indicator of the overburden damage increase. The fractures in the overlying strata follow a Gaussian distribution, with the densest area near the goaf’s center, although the maximum damage area’s center does not align with the goaf’s centerline. The study revealed that the position of the goaf’s center in relation to the slope shoulder dictates the fracture concentration area’s migration direction and the horizontal displacement direction of the overlying strata. Additionally, the offset distance increases significantly when the goaf’s center is outside the slope shoulder. The findings also indicate that overburden rock damage escalates with coal seam mining, particularly after reaching a mining width of 200 m.