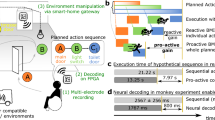
Abstract
In the field of Brain Machine Interface (BMI), the process of translating motor intention into a machine command is denoted as decoding. However, despite recent advancements, decoding remains a formidable challenge within BMI. The utilization of current decoding algorithms in the field of BMI often involves computational complexity and requires the use of computers. This is primarily due to the reliance on mathematical models to address the decoding issue and perform subsequent output calculations. Unfortunately, computers are not feasible for implantable BMI systems due to their size and power consumption. To address this predicament, this study proposes a pioneering approach inspired by hyperdimensional computing. This approach first involves identifying the pattern of each stimulus by considering the normal firing rate distribution of each neuron. Subsequently, the newly observed firing pattern for each input is compared with the patterns detected at each moment for each neuron. The algorithm, which shares similarities with hyperdimensional computing, identifies the most similar pattern as the final output. This approach reduces the dependence on mathematical models. The efficacy of this method is assessed through the utilization of an authentic dataset acquired from the Frontal Eye Field (FEF) of two male rhesus monkeys. The output space encompasses eight possible angles. The results demonstrate an accuracy rate of 51.5% while exhibiting significantly low computational complexity, involving a mere 2050 adder operators. Furthermore, the proposed algorithm is implemented on a field-programmable gate array (FPGA) and as an ASIC designe in a standard CMOS 180 nm technology, underscoring its suitability for real-time implantable BMI applications. The implementation required only 2.3 Kbytes of RAM, occupied an area of 2.2 mm2, and consumed 9.32 µW at a 1.8 V power supply. Consequently, the proposed solution represents an accurate, low computational complexity, hardware-friendly, and real-time approach.
Similar content being viewed by others
Introduction
Roughly 1 in 50 people worldwide suffer from paralysis1,2. A Brain machine interface (BMI) has the ability to interface with the brain cortex to decode the intent and to make simple commands to the external devices1,3,4,5 such as spellers6,7, robotic arm for feeding8 and wheelchairs9,10,11. In this way, this technology has the potential to restore or improve human physical or mental functions12,13,14. Intra-cortical BMIs, which collect neural signals from the surface of the motor cortex and process them through several signal processing steps, are among the most promising forms of BMIs1. These signal processing steps include spike detection15,16, spike sorting17,18,19,20 and decoding21,22, with decoding being the primary step in converting neural activities into actual commands23.
Most decoding methods employ the information encoded into the number of neural spikes existing in a time period, which is called firing rate24,25. This implies that each neuron has its own firing rate at a given moment for each stimulus. To model a mapping function between the firing rate and the output space, several approaches have been proposed. For instance, in wiener filter a linear filter is simply used to decode the output space26,27,28,29. In other researches such as15, an extended version of wiener filter which included the Wiener filter and a non-linear function like polynomial is utilized as Wiener cascade filter. The Kalman filter, another popular method, is an extension of the Wiener filter as well27. The algorithm of Kalman filter has two steps which are prediction and update. The method first predicts the current output based on the previous state, followed by an update using an averaging procedure1. As the actual state is required for accurate output, this method is optimized for closed loop systems. The next wildly used method is Support Vector Machine (SVM)30,31. In SVM methods, firstly the input space is generally mapped to another space by a nonlinear kernel; then, it is mapped to the final output space using a linear function3,32. Another commonly used approach is neural network33. For instance, feedforward neural network employes a sequential hidden layer to map the input space to another space, which is then converted to the desired output with a final layer34,35,36. These algorithms typically consider the firing pattern of a single moment as their input and suggest a mathematical model to decode it to the desired output. However, there is another group of algorithms that employs a different approach. Several papers have attempted to incorporate temporal information of spike trains in decoding procedures, revealing its importance not only in neural signals of the visual and auditory cortex37,38,39, but also in motor cortex decoding40. For example, in41 a recurrent neural network (RNN) is proposed to employ several firing rates of the neurons as the inputs to decode the desired output. Similar analysis can be observed in42 where the accuracies of several RNN algorithms are compared with the algorithms which are not considering firing rate changes. Temporal information can be considered by other procedure in the algorithms as well; for instance, in41 spike train distance is taken as the input for temporal information. Finally, in22 a new input space is proposed to efficiently utilize the temporal information in a zero-one vector as a hardware friendly approach.
Although all of the cited methods are accurate and efficient in their applications, all of them are trying to estimate a mathematical model from the input to the output space. This perspective would generally conduct to a noticeable volume of computational complexity and needs a power hungry and not easily portable computer; therefore, it is an impractical approach for long-term use as a real BMI system23. On-chip implementation of an algorithm can significantly reduce size and power consumption, resulting in a computing device that is suitable as an implantable processor and real-time decoding system with negligible latency43. Additionally, integrating the neural recording part and decoding algorithm can decrease the data transmission rate to the outside world of the brain, another desirable feature in an ideal BMI implant44,45. Thus, computational complexity and the design of a complicated architecture to implement the mathematical model are as important as algorithm accuracy in an implantable BMI. For this reason, several hardware-friendly approaches, such as those presented in1,22,43,46,47, have been proposed. This paper centers around a classification decoding issue, utilizing a real dataset captured from two male rhesus monkeys engaged in a saccade test, where the output space comprises eight potential angles. The primary objective of this study is to reduce reliance on a mathematical model during the decoding procedures. The proposed method recognizes firing patterns over time as temporal information, inspired by hyperdimensional computing principles48. In this type of computing, data is converted to a hyper vector utilizing a memory and specific procedures. The value of vector elements is unimportant as a number, but rather their similarity in pattern is utilized as the decision factor in classification problems49. As this approach significantly decreases the need for numeric computation, computational complexity is greatly reduced while algorithm accuracy remains acceptable in many cases50. Therefore, in this paper a method for extracting the firing rate pattern is firstly proposed and then it is used for decoding with a simple comparison. Results show that not only the necessary memory for hardware implementation would be considerably lower comparing the others, but also the computational complexity is negligible. To summarize, this paper presents several significant achievements. Firstly, it introduces a straightforward approach that enhances the decoding process by incorporating temporal information from neural signals. Furthermore, the paper optimizes hyperdimensional computing techniques to improve the accuracy of decoding in BMI systems. The proposed algorithm demonstrates reasonably accurate results, showcasing promising potential for practical applications. Additionally, the paper proposes a hardware-friendly approach specifically tailored for implantable BMI systems, taking into account the constraints and requirements of the hardware. By considering both accuracy and computational complexity, the method achieves notable performance compared to other employed decoding algorithms. These findings hold significant value for the development of real-time implantable BMI systems.
The remainder of this paper is organized in the following manner. Section 2 provides an overview of the dataset utilized for the algorithm’s evaluation, including a discussion of its pattern. Section 3 presents the proposed decoding algorithm. Section 4 details an efficient hardware implementation of the algorithm. Lastly, from Sects. 5 to 8, the paper reports the evaluation results, discussions, limitation of study, and conclusions, respectively.
Analyzing dataset characteristics
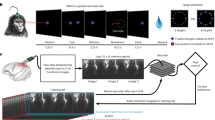
This paper utilizes a dataset from30 for analysis, training, and evaluation purposes. The recorded data pertains to the Frontal Eye Field (FEF) of two male rhesus monkeys. As shown in Fig. 1, the monkey should firstly look at the center dot on the screen for one second. Next, a target in one of the 8 different angles (0, 45, 90, 135, 180, 225, 270, and 315 degrees) would be visible just for one second, but the monkey should still focus on the centered dot. After the center dot is disappeared, if the monkey looks at the correct target angle, he would take a drop of juice as a reward. This routine is monitored by a surgically implanted multisite linear array electrode which makes simultaneously recording from 16 channels possible. Then in30 by a spike sorting algorithm51, the detected spikes are presented in 32 neurons each 1ms for 792 recorded trials to make the dataset available.
Having introduced the recording setup, the recorded data can now be analyzed. As most decoding methods rely on the rate coding hypothesis25, the firing rate over time of two different neurons is illustrated in Fig. 2.
The number of detected spikes is reported in a non-overlapping time window of 35ms in the graph illustrated in Fig. 2. The double-hump response of the neurons is attributed to the nature of the trials, with the first hump corresponding to the initial presentation of the target to the monkey, while the second hump corresponds to the saccade time. The response of a specific neuron is distinct for each angle, as seen in Fig. 2, with each neuron having its own firing rate for each stimulus when compared to the other neuron. Other decoding algorithms utilize this information to decode the output space. Therefore, an algorithm that can model the differences in patterns between each neuron and for each stimulus has the potential to decode the output space.
Furthermore, as illustrated in Fig. 3, when studying the probability density of the fires related to a specific neuron at a particular time, it becomes apparent that a neuron firing rate is not always a fixed number, but rather has an approximately normal distribution. As a result, it is not possible to accurately detect the firing pattern using a simple comparison, and an algorithm is required, which is proposed in the following section.
Proposing the pattern detection method
To model the differences across multiple neurons, stimuli, and time points, two approaches can be adopted: mathematical-based and pattern-based algorithms. Mathematical-based methods, such as SVM utilize mathematical algorithms with multipliers and other operators to distinguish between different outputs. However, this approach typically results in high computational complexity and is not easily conducive to hardware-friendly architectures. In contrast, hyperdimensional computing (HDC) employs a binary vector approach to convert data into a specific pattern. HDC then compares the current vector with unique patterns related to each output in order to specify the output space52. Since mathematical operators are limited in HDC, computational complexity is low, making it suitable for hardware implementation goals. However, HDC requires memory to convert the actual input data to the binary vector, necessitating the use of a RAM in hardware design. The volume of memory is crucial for accuracy in HDC, particularly in decoding problems such as the dataset presented in Sect. 250. It has been discovered that a significant volume of binary memory is essential to achieve an acceptable level of accuracy, making the final hardware inefficient. Consequently, another approach is required.
As can be observed in Fig. 2, each neuron has a specific mean firing rate for each stimulus at a certain moment. Additionally, based on Fig. 3, although the firing rate is not a fixed number, it mostly falls within a known range. Therefore, if several neurons are simultaneously firing in their specific ranges only when a known stimulus is occurring, the output space can be decoded. Consequently, the firing pattern of all neurons should be compared with each known stimulus, and the final output is the one whose pattern is most similar to the current pattern. To accomplish this, the algorithm should solve two problems: the firing range and the comparison method.
Finding the upper and lower bound of firing range
Based on Fig. 3, the distribution of firing rates is normal and can be described using the mean value and standard deviation (STD). As it is known, in a normal distribution, 68.27% of the values fall within one standard deviation of the mean value. Since most of the information is collected in range of STD around the mean value, it would be logical to consider this range as the relevant firing rate range. This implies that if the firing rate of a neuron falls within this range, it is likely important for the specific output or stimulus, whereas firing rates outside this range may be attributed to another stimulus or simply noise due to errors in fire detection or sorting stages prior to the decoding process. By focusing only on firing rates within the relevant range, not only can the important range for each output be determined, but the method is also more robust against errors caused by previous stages.
Comparison method
To compare the current firing rate pattern with a known stimulus, an approach similar to HDC is employed. In this method, a binary vector with a specific size is created, and then the vector is compared with known output vectors that are also binary. The equality of each element in the current vector should be checked against its corresponding elements in the output vectors. If the element is equal, the considered output is given a positive point. At the end of the comparison, the final output is the one that has achieved the highest point. Moreover, according to22, it has been demonstrated that incorporating several firing rates related to the past, in addition to the current moment, leads to an increase in decoding accuracy. This improvement is attributed to the incorporation of temporal information in the algorithm, which is similar to the approach used in RNNs. To this end, a vector similar to the one presented in Fig. 4 is utilized, where the firing rates of all neurons from successive time bins related to the past, in addition to the current moment, are employed. Therefore, the size of the vector is \(\:N\times\:B\), where N is the number of neurons and B is the number of successive time bins.
In the subsequent step, the firing rate pattern is analyzed to determine the extent of its similarity with the patterns of known stimuli. To this end, each neuron’s firing rate is first compared with the firing rate range determined in the previous step. If the neuron’s firing rate falls within the range of the corresponding stimulus at the relevant moment, it is considered a similar pattern and is mapped to one in the new binary vector; otherwise, it is not similar and is mapped to zero. Consequently, since the firing rate range is different for each stimulus (8 angles), neuron, and moment, the initial firing rate vector is converted into 8 binary vectors with a size of \(\:N\times\:B\). Since each threshold is optimized for each output in the mapping to one and zero, the perfect match for each output would be a vector in which all elements are one. This important feature eliminates the need for another vector for the final comparison and determination of the perfect match. Thus, the final output is the one that has the most number of ones.
To provide clarity regarding the proposed decoding algorithm, the training and testing procedures are illustrated in Fig. 5, as follow.
As depicted in Fig. 5, the system does not require a complicated training procedure. The training stage is limited to determining the optimal values for the window size and the number of time bins, as well as the mean and standard deviation values for each neuron, output, and moment. The procedure for calculating the mean and standard deviation has been explained previously, while the procedure for determining the optimum firing rate window size and the number of successive firing rates is not clear. To select an optimal value for these parameters, two procedures can be suggested. In the first procedure, similar to the one presented in22, a primary but logical value is first set for one of the parameters, and then the second parameter is determined by testing several values within a logical range to achieve maximum accuracy. Finally, using the new optimal value and a similar approach, the primary value is changed to the optimal one for the first parameter. Although this routine is effective, the optimal values are biased by the initial value selection due to the dependency of the parameters and the output accuracy. Therefore, it is suggested to evaluate the accuracy of the algorithm by tuning both parameters simultaneously and selecting the optimal values based on analysis. As shown in Fig. 6, the accuracy of the decoder is evaluated by varying the window size and time bins.
The analysis presented in Fig. 6 highlights two important facts. Firstly, increasing the number of successive time bins improves the accuracy of the method, but this improvement becomes almost saturated after 8 bins. This implies that there is enough information in 8 successive firing rates to achieve accurate decoding. Since more time bins lead to more firing range being saved in hardware RAM, which results in an increase in chip size, it is logical to set the number of time bins to its minimum value with the highest accuracy. Consequently, the optimum number of time bins for this dataset is 8. Furthermore, changes in the window size for calculating firing rates indicate that when the window is too narrow, the collected information is insufficient to extract the specific pattern for each stimulus. This fact is due to the nature of the algorithm, where a small window size does not allow for the firing rates to be easily separable, leading to difficulty in distinguishing different patterns from each other, and resulting in low prediction accuracy. On the other hand, increasing the window size makes the difference more recognizable, thus raising accuracy until it reaches a plateau at around 38ms. Since the final goal of this paper is hardware implementation, it is necessary to choose the minimum window size. Increasing the window size results in an increase in firing range, which leads to a need for a hardware RAM with a larger volume to store the bigger numbers. Therefore, since the accuracy of the algorithm reaches an acceptable range at 38ms, and increasing the window size is almost ineffective, 38ms is an optimal choice for this dataset.
After determining the window size and the number of time bins based on Fig. 6, all the necessary parameters are specified. The next step is to propose an optimal architecture for the algorithm.
Hardware implementation
In order to achieve efficiency in a BMI system, it is crucial to take into account factors beyond the accuracy of the algorithm, such as power consumption and hardware utilization. Furthermore, implementing the algorithm as dedicated hardware can enable real-time processing, which is particularly advantageous for BMI systems. Consequently, in this section a hardware architecture is presented as the proposed decoder. To begin, the system architecture will be elucidated, followed by a detailed analysis of its subsections.
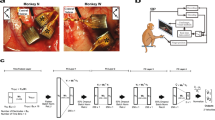
Figure 7 depicts the proposed hardware architecture designed to implement the algorithm. In this system, the detected spikes of the 32 neurons are reported to the hardware by neuron fire inputs, which then would be employed for firing rate calculation by firing rate calculator. The firing rates are reset to zero when the number of clock pulses (CLK) equals the merging value, which is used to determine the temporal window size for counting the number of firing events. This process enables the calculation of firing rates within each window size bin. Subsequently, the firing rates serve as inputs for eight class modules, each responsible for calculating the scores corresponding to one of the eight possible classes. The system selects the class with the highest score as the final output once the required number of firing rates has been processed by the module. The time bin input specifies this required number. During the initialization stage, the system can be loaded with pre-calculated threshold values using the initial values, which can be set through the Initial mode input. The final output is registered by the output reg, while the control and timing module governs the timing of the system’s operations.
In Fig. 7 there are eight modules to calculate the scores related to each class. The details of each module are presented in Fig. 8. A RAM is employed to store the respective thresholds for each neuron and time bin. The RAM’s functionality is regulated by inputs such as initial mode, initial values, enable, and CLK. To streamline the design and minimize input requirements, the control and timing module in Fig. 7 utilizes a shared initial values bus for all eight classes. This enables the independent selection of each module through the enable input during the initiation phase. Once the RAM has been loaded, the comparator and counting unit in Fig. 8 determine the count of neurons falling within the specified range. This count then serves as an input for the accumulator, which tallies the total number of neurons over successive bins, as governed by the time bin input. Upon completion of the determined time bins, the accumulator is reset to zero, ready for subsequent decoding processes.
The simplicity and compactness of the system are evident. The minimal hardware requirements and the reduced RAM usage contribute to an efficient design in terms of power consumption, computational complexity, and occupied area. These advantageous aspects will be further elucidated and discussed in detail in the next section.
Experimental results
In the preceding sections, assertions were made regarding the reduction in computational complexity through the elimination of mathematical models, as well as the feasibility of the decoding process through the analysis of firing rates using the proposed algorithm. This section aims to substantiate these claims by evaluating the performance of the proposed method in comparison to other commonly employed decoding algorithms. Through this evaluation, the efficacy and superiority of the proposed method will be demonstrated.
Evaluation metrics and charecteristics
Given the influence of the database specifications on the evaluations, it is imperative to apply the same simulations not only to the proposed method but also to commonly used decoders. To this end, the simulations were conducted for non-recurrent methods, including the Wiener filter, Wiener cascade, SVM with a linear kernel function, and Feedforward neural network. Furthermore, recurrent approaches such as LSTM43, Elman53 and Gated recurrent unite (GRU) neural networks54 were also included in the simulations. The algorithm evaluations were performed on a personal computer equipped with an Intel Core i7-4710HQ CPU operating at a frequency of 2.50 GHz, accompanied by a memory capacity of 16 GB. The algorithm was implemented using MATLAB software, specifically version R2018b. Additionally, the synthesized architecture reports were generated using Xilinx ISE 14.7. In terms of accuracy reports, the metric used for assessment is prediction accuracy, which is determined by calculating the ratio of correct outputs to the total number of predictions. This value is then presented as a percentage.
Algorithm evaluation
To ensure a fair comparison of all methods at their optimal performance, similar to the proposed algorithm in this paper, the aforementioned decoders were fine-tuned to achieve their highest level of accuracy while maintaining an optimal level of computational complexity. For non-recurrent methods, firing rates were calculated based on a window size of 35ms. In the case of recurrent neural networks, in addition to the current firing rate (with the same length), eight previously calculated firing rates were utilized as inputs. It is important to note that these parameters represent the most optimal settings for the decoders to attain accurate results while maintaining a reasonable level of computational complexity.
In Fig. 9 the results of different approaches are illustrated. As it can be observed in Fig. 9a, it is evident that the common non-recurrent methods exhibit nearly identical levels of accuracy, with the Wiener filter displaying the highest degree of accuracy among these methods. The double-hump pattern observed in the graph is a result of the experimental nature, where the first hump corresponds to the time when the target is initially presented to the monkey, and the second hump represents the saccade time. Furthermore, upon comparing the results presented in Fig. 9b with those of the non-recurrent methods, it becomes apparent that recurrent networks generally achieve higher levels of accuracy. This is attributed to their ability to analyze the output space based on the temporal changes in input, allowing them to model more precise functions for the problem at hand. This capability becomes particularly pronounced as algorithms become more complex, culminating in the maximum prediction accuracy achieved by LSTM. Lastly, the results of the proposed method in this paper are compared with an alternative approach presented in22 as shown in Fig. 9c22. exhibits greater accuracy than the proposed algorithm due to the consideration of weightings for each input using the SVM model, whereas the proposed method treats all inputs as having equal value. Consequently, non-recurrent methods and the proposed algorithm in this paper can be categorized as low-accuracy methods, while recurrent networks and the method presented in22 represent high-accuracy approaches.
The training stage holds significant importance in every machine learning algorithm. One crucial aspect of this stage is the amount of data required to initialize the relative coefficients and factors. For instance, due to its complexity, LSTM is more sensitive to the volume of the available database compared to the Wiener filter. It is not always feasible to have a substantial volume of data for training purposes. Thus, in addition to the proposed method, the impact of database volume on both the Wiener filter and LSTM, representing the most accurate non-recurrent and recurrent methods, respectively, is evaluated. The results obtained from different database volumes during the training stage are collected and presented in Fig. 10.
The observation reveals that LSTM, being the most complex method with a larger number of coefficients, is more susceptible to the reduction in database size. In contrast, the impact on the Wiener filter, which has fewer coefficients and a simpler model, is more manageable. On the other hand, the proposed method in this paper demonstrates the highest level of robustness, as it does not rely on any mathematical models or coefficients. Although a larger database volume generally leads to more accurate mean and standard deviation values, the proposed algorithm is capable of determining sufficiently accurate values for calculations without the need for a mathematical model. Consequently, it is reasonable to conclude that the proposed method can still be trained effectively even with a smaller database volume.
Hardware evaluation
In a BMI system, computational complexity is a crucial consideration alongside accuracy. The ability to implement the algorithm on a hardware platform, such as a Field-Programmable Gate Array (FPGA) or an Application-Specific Integrated Circuit (ASIC) design, offers the potential for a real-time, efficient solution in terms of size and power consumption55,56. This section aims to analyze the factors that are pertinent to hardware implementation. Key factors include the number of adders, multipliers, and non-linear functions, all of which impact the feasibility of hardware implementation. To facilitate comparison between different algorithms, Table 1 presents these factors. Within the non-recurrent segment of Table 1, the Wiener filter, feedforward neural network, and linear SVM are considered as candidates representing the most accurate, moderately accurate, and least accurate methods, respectively. Similarly, the Elman and LSTM networks are chosen to represent the least accurate and most accurate recurrent methods, respectively. Lastly, the decoder presented in22 is compared as a similar approach that utilizes a binary input space (zero and one).
Upon examining Table 1, a significant disparity in resource utilization between recurrent methods and the others becomes apparent, while the higher accuracy achieved by the recurrent methods. For example, in the case of LSTM, nearly 400 times more adder operators are employed compared to the proposed algorithm in this paper, resulting in a mere 10% increase in accuracy. Consequently, recurrent methods are more suitable when maximum accuracy is paramount and computational complexity is not a major concern. Conversely, the method presented in22 is recommended due to its significantly lower computational complexity and high accuracy. Given the similar accuracy range between the proposed method and non-recurrent decoders, a comparison between these methods is warranted. Although the proposed method in this paper utilizes more adder operators, it does not require any multipliers. In hardware implementation, multipliers consume more resources compared to adder operators. For instance, according to57, each multiplier is equivalent to 10 adder operators in terms of computational complexity. Consequently, not only does the proposed method exhibit higher accuracy, but it also demonstrates superior hardware efficiency compared to the Wiener filter.
Discussion
Another perspective for comparing computational complexity can be obtained by referring to Table 2. In numerous studies, the designed architecture is replicated on a FPGA to achieve improved size and power efficiency. Hence, in order to assess computational complexity from a different angle, Table 2 presents the FPGA resources required for various approaches.
Table 2 presents the synthesized architecture using Xilinx ISE 14.7 for Xilinx Virtex5 vsx50 FPGA, with the corresponding reports collected. It should be noted that the CLK frequency for the proposed method based on the input of the dataset is 1 kHz. Upon examination, it is evident that the proposed method requires fewer memory elements compared to the other approaches. This discrepancy arises from the fact that the proposed algorithm does not rely on coefficients or mathematical models. Instead, it utilizes a simple comparator and two integer values associated with the relative firing rates. In contrast, the other methods necessitate storing coefficients of mathematical models in RAMs, followed by the utilization of these coefficients within the mathematical models to calculate the corresponding outputs. This disparity is particularly pronounced in the case of the feedforward network, where the model is complex and requires a significantly larger number of coefficients.
Based on the reported accuracy and resource utilization, it is evident that a trade-off has occurred. The proposed algorithm exhibits a moderate level of accuracy, with a maximum achieved accuracy of approximately 51%, which is lower than a more accurate method referenced as22, which attains a maximum accuracy of 62%. However, referring to Tables 1 and 2, it can be observed that the number of operators and the required RAM volume are nearly halved. This implies that by sacrificing 10% accuracy, the hardware requirements are significantly reduced. This achievement is particularly noteworthy when implementing the design on an ASIC, where size and power consumption are crucial constraints. Table 3 presents post-synthesis reports comparing the proposed method to two other designs shown below.
The table above clearly shows the important achievements of this work. As mentioned previously, the proposed method requires nearly half the RAM storage compared to the approach in22, while both methods utilize relatively simple algorithms. This halving of RAM requirements directly translates to a significant reduction in chip size. This factor is crucial, especially since it also has a substantial impact on power dissipation. The power consumption of a chip is the result of both dynamic and static power. While dynamic power is related to the design’s frequency and algorithm complexity, static power is heavily influenced by RAM size. Therefore, when the RAM requirement is halved and the algorithm consists primarily of basic operations like counters and comparators, the power dissipation decreases noticeably, as illustrated in Table 3. Furthermore, since the proposed method only uses a simple counter to count spikes within a time window, the system can operate at a low input clock frequency of 1 kHz, as mentioned in Sect. 2. This further reduces the dynamic power consumption. Consequently, the designed chip can be smaller in size and consume less power due to the reduced hardware footprint. This makes the proposed architecture more appealing for a BMI system intended for implantation into the brain.
Limitation of study
In the context of a practical Brain Machine Interface (BMI) system, real-time processing, design size, and power consumption pose significant challenges. Ideally, to minimize the communication rate between the brain and external devices, it is preferable to complete the processing within a chip implanted in the brain. However, pursuing this objective may introduce conflicts in the system’s constraints. As previously discussed for the proposed method, reducing power consumption and design size necessitates sacrificing 10% of the system’s accuracy. Similar trade-offs and limitations arise in various aspects and are outlined in this section.
The approach presented in this research paper is specifically tailored for classification problems similar to the dataset used, whereas other studies, such as42, may address output spaces that are not classification-oriented. Consequently, the proposed solution is constrained to these specific types of decoding tasks, which encompass both binary and multi-class problems.
Moreover, Given the varied results obtained from a range of experiments, it is logical to consider utilizing the approach presented in22 when prioritizing a high level of output accuracy. Conversely, in scenarios where factors such as computational complexity and the ability to train with a minimal database volume are equally critical, it is recommended to select the proposed method outlined in this paper as a suitable decoder solution.
Another limiting factor in the application of this approach is the hardware architecture. As acknowledged, when an algorithm is implemented as a hardware design, it is optimized for that particular system. For instance, in this design, the input space consists of 32 neurons; however, in other cases, this number may differ. Although it is conceivable to reconfigure the architecture for an alternative solution, it is not easily realizable.
Although the dataset used in this paper does not originate from the motor cortex, it still provides insights into the advantages and limitations of the presented method. The accuracy of all decoders for this dataset is relatively low, as it only utilizes 32 neurons from the FEF, while other studies such as60 may employ a larger number of input channels, such as 96. If the evaluation were to be repeated using a different dataset, it is expected that the numbers, particularly the accuracy results, would scale accordingly. However, the overall conclusion would remain the same. Since this paper aims to minimize the utilization of mathematical models, the computational complexity is kept to a minimum. The inclusion of certain assumptions, such as treating all neurons equally in terms of weights across different stimuli and moments, would lead to reduced accuracy when compared to alternative approaches.
Conclusion, future work and findings
Decoding plays an important role in BMI systems by translating motor brain intentions into machine-readable commands. The prevailing approach in many methods involves utilizing firing rate as input and employing a mathematical model to establish a mapping between the input space and the desired output. However, this approach often leads to high computational complexity, making it difficult and impractical for hardware implementation, particularly in the context of implantable BMI solutions. As a result, alternative decoding strategies that address these limitations are required.
In contrast to alternative approaches, the algorithm presented in this study introduces a collective comparison of firing rates, eliminating the need for a mathematical model in the decoding process. By incorporating HDC approach and drawing inspiration from conventional methods that leverage firing rates, the proposed decoding algorithm exhibits several advantageous characteristics, including binary value computation and a decoder with moderate accuracy. The analyses conducted indicate that by sacrificing 10% of output accuracy, the algorithm achieves a significant reduction in required RAM and hardware operators, effectively halving their sizes and power consumption, which are beneficial for hardware implementation. The proposed method follows a straightforward routine, enabling training with smaller databases and demonstrating minimal computational complexity. Furthermore, the algorithm is specifically designed to be implemented as a hardware-friendly architecture, ensuring real-time capability and reduced memory requirements. In summary, the key achievements of this work are:
-
Proposing a novel decoding approach inspired by hyperdimensional computing principles.
-
Demonstrating reasonable accuracy in an 8-class classification problem.
-
Developing a hardware implementation for the proposed algorithm.
-
Evaluating the algorithm on both FPGA and ASIC platforms.
-
Significantly reducing hardware resources to decrease power consumption and chip size.
-
Enhancing the robustness of the training procedure for low-volume datasets.
In this study, all firing values for different neurons and time bins were treated as equal. However, it is evident that not all neurons exhibit equal and significant changes in their firing rates in response to different stimulations. Therefore, it is plausible that by tracking these variations and assigning different weights to each firing rate, the accuracy of the methods could be enhanced. This approach bears similarity to the linear SVM presented in22, although it deviates from its training procedure.
Data availability
The data that support the findings of this study are available from Behrad Noudoost. But restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available. Data are however available from Mohammad-Reza A. Dehaqani (Dehaqani@ut.ac.ir) at reasonable request and with permission of Behrad Noudoost.
References
Shaikh, S. et al. Towards intelligent intracortical BMI (i $^ 2$ BMI): Low-power neuromorphic decoders that outperform Kalman filters. IEEE Trans. Biomed. Circuits Syst.13(6), 1615–1624 (2019).
Armour, B. S. et al. Prevalence and causes of paralysis—United States, 2013. Am. J. Public Health. 106(10), 1855–1857 (2016).
Shen, X. et al. Intermediate sensory feedback assisted multi-step neural decoding for reinforcement learning based brain-machine interfaces. IEEE Trans. Neural Syst. Rehabil. Eng.30, 2834–2844 (2022).
García-Murillo, D. G., Álvarez-Meza, A. M. & Castellanos-Dominguez, C. G. Kcs-fcnet: Kernel cross-spectral functional connectivity network for eeg-based motor imagery classification. Diagnostics. 13(6), 1122 (2023).
Choi, H., Park, J. & Yang, Y. M. Whitening technique based on gram–schmidt orthogonalization for motor imagery classification of brain–computer interface applications. Sensors. 22, 6042 (2022).
Birbaumer, N. et al. A spelling device for the paralysed. Nature. 398(6725), 297–298 (1999).
Perdikis, S. et al. Clinical evaluation of BrainTree, a motor imagery hybrid BCI speller. J. Neural Eng.11(3), 036003 (2014).
Collinger, J. L. et al. High-performance neuroprosthetic control by an individual with tetraplegia. Lancet. 381, 557–564 (2013).
Galán, F. et al. A brain-actuated wheelchair: asynchronous and non-invasive brain–computer interfaces for continuous control of robots. Clin. Neurophysiol.119(9), 2159–2169 (2008).
Leeb, R. et al. Towards independence: a BCI telepresence robot for people with severe motor disabilities. Proc. IEEE. 103(6), 969–982 (2015).
Sharma, R., Kim, M. & Gupta, A. Motor imagery classification in brain-machine interface with machine learning algorithms: Classical approach to multi-layer perceptron model. Biomed. Signal Process. Control. 71, 103101 (2022).
Dumitrescu, C., Costea, I. M. & Semenescu, A. Using brain-computer interface to control a virtual drone using non-invasive motor imagery and machine learning. Appl. Sci.11, 11876 (2021).
Syrov, N. et al. Mental strategies in a P300-BCI: Visuomotor transformation is an option. Diagnostics. 12(11), 2607 (2022).
Ko, L. W. et al. Exploration of user’s mental state changes during performing brain–computer interface. Sensors. 20(11), 3169 (2020).
Zhang, Z. & Constandinou, T. G. Firing-rate-modulated spike detection and neural decoding co-design. J. Neural Eng.20(3), 036003 (2023).
Kim, K. H. & Kim, S. J. Neural spike sorting under nearly 0-dB signal-to-noise ratio using nonlinear energy operator and artificial neural-network classifier. IEEE Trans. Biomed. Eng.47, 1406–1411 (2000).
Park, I. Y. et al. Deep learning-based template matching spike classification for extracellular recordings. Appl. Sci.10(1), 301 (2019).
Kalantari, F., Hosseini-Nejad, H. & Sodagar, A. M. Hardware-efficient, on-the-fly, on-implant spike sorter dedicated to brain-implantable microsystems. IEEE Trans. Very Large Scale Integr. VLSI Syst.30(8), 1098–1106 (2022).
Li, Z. et al. An accurate and robust method for spike sorting based on convolutional neural networks. Brain Sci.10, 835 (2020).
Sukiban, J. et al. Evaluation of spike sorting algorithms: Application to human subthalamic nucleus recordings and simulations. Neuroscience. 414, 168–185 (2019).
Dong, Y. et al. Decoder calibration framework for intracortical brain-computer interface system via domain adaptation. Biomed. Signal Process. Control. 81, 104453 (2023).
Katoozian, D. et al. A hardware efficient intra-cortical neural decoding approach based on spike train temporal information. Integr. Computer-Aided Eng.29(4), 431–445 (2022).
Chen, Y., Yao, E. & Basu, A. A 128-channel extreme learning machine-based neural decoder for brain machine interfaces. IEEE Trans. Biomed. Circ. Syst. 10(3), 679–692 (2015).
Dayan, P. & Abbott, L. F. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. (MIT Press, 2005).
Rieke, F. et al. Spikes: Exploring the Neural code. (MIT Press, 1999).
Pan, H. et al. A closed-loop BMI system design based on the improved SJIT model and the network of Izhikevich neurons. Neurocomputing. 401, 271–280 (2020).
Ahmadi, N., Constandinou, T. G. & Bouganis, C. S. Robust and accurate decoding of hand kinematics from entire spiking activity using deep learning. J. Neural Eng.18(2), 026011 (2021).
Wu, H., Feng, J. & Zeng, Y. Neural decoding for macaque’s finger position: Convolutional space model. IEEE Trans. Neural Syst. Rehabil. Eng.27(3), 543–551 (2019).
Pan, H. et al. A closed-loop brain–machine interface framework design for motor rehabilitation. Biomed. Signal Process. Control. 58, 101877 (2020).
Dehaqani, M. R. A. et al. Selective changes in noise correlations contribute to an enhanced representation of saccadic targets in prefrontal neuronal ensembles. Cereb. Cortex. 28, 3046–3063 (2018).
Li, C. et al. Generative decoding of intracortical neuronal signals for online control of robotic arm to intercept moving objects. J. Phys. Conf. Series. 1576(1). (IOP Publishing, 2020).
Li, C. et al. Serial decoding of macaque intracortical activity for feedforward control of coherent sequential reach. in 10th International IEEE/EMBS Conference on Neural Engineering (NER). IEEE, 2021. (2021).
Baggenstoss, P. M. On the duality between belief networks and feed-forward neural networks. IEEE Trans. Neural Netw. Learn. Syst.30(1), 190–200 (2018).
Taeckens, E., Dong, R. & Shah, S. A biologically plausible spiking neural network for decoding kinematics in the hippocampus and premotor cortex. in 11th International IEEE/EMBS Conference on Neural Engineering (NER). IEEE, 2023. (2023).
Zhang, P. et al. Reinforcement learning based fast self-recalibrating decoder for Intracortical brain–machine interface. Sensors. 20, 5528 (2020).
Sarić, R. et al. FPGA-based real-time epileptic seizure classification using Artificial neural network. Biomed. Signal Process. Control. 62, 102106 (2020).
Bair, W. & Koch, C. Temporal precision of spike trains in extrastriate cortex of the behaving macaque monkey. Neural Comput.8(6), 1185–1202 (1996).
Buracas, G. T. et al. Efficient discrimination of temporal patterns by motion-sensitive neurons in primate visual cortex. Neuron. 20(5), 959–969 (1998).
Salinas, E. & Sejnowski, T. J. Correlated neuronal activity and the flow of neural information. Nat. Rev. Neurosci.2, 539–550 (2001).
Chew, G. et al. 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). IEEE, 2015. (2015).
Ran, X. et al. Decoding velocity from spikes using a new architecture of recurrent neural network. in 9th International IEEE/EMBS Conference on Neural Engineering (NER). IEEE, 2019. (2019).
Glaser, J. I. et al. Mach. Learn. Neural Decoding Eneuro7(4) (2020).
Heelan, C., Nurmikko, A. V. & Truccolo, W. FPGA implementation of deep-learning recurrent neural networks with sub-millisecond real-time latency for BCI-decoding of large-scale neural sensors (104 nodes). in 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). IEEE, 2018. (2018).
Stevenson, I. H. & Kording, K. P. How advances in neural recording affect data analysis. Nat. Neurosci.14(2), 139–142 (2011).
Ahmadi-Dastgerdi, N. et al. A vector quantization-based spike compression approach dedicated to multichannel neural recording microsystems. Int. J. Neural Syst.32, 2250001 (2022).
Ghanbarpour, G., Hoque, A., Assaad, M. & Ghanbarpour, M. New Model for Wilson and Morris–Lecar Neuron models: Validation and digital implementation on FPGA. IEEE Access.. 26. (2024).
Chaudhary, M. A., Hazzazi, F. & Ghanbarpour, M. Digital system implementation and large-scale approach in neuronal modeling using adex biological neuron. in IEEE Transactions on Circuits and Systems II: Express Briefs. (2024).
Thomas, A., Dasgupta, S. & Rosing, T. A theoretical perspective on hyperdimensional computing. J. Artif. Intell. Res.72, 215–249 (2021).
Karunaratne, G. et al. In-memory hyperdimensional computing. Nat. Electron.3, 327–337 (2020).
Ge, L. & Parhi, K. K. Classification using hyperdimensional computing: A review. IEEE Circuits Syst. Mag.20(2), 30–47 (2020).
Buccino, A. P., Garcia, S. & Yger, P. Spike sorting: New trends and challenges of the era of high-density probes. Progress Biomed. Eng.4(2), 022005 (2022).
Burrello, A. et al. Laelaps: An energy-efficient seizure detection algorithm from long-term human iEEG recordings without false alarms. in 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE). IEEE, (2019).
Du, Y. et al. Design of blender IMC control system based on simple recurrent networks. in 2009 International Conference on Machine Learning and Cybernetics. Vol. 2. IEEE, (2009).
Heck, J. C. & Salem, F. M. Simplified minimal gated unit variations for recurrent neural networks. in IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS). IEEE, 2017. (2017).
Islam, M. T. et al. FPGA implementation of nerve cell using Izhikevich neuronal model as Spike Generator (SG). in IEEE Access. Dec 14. (2023).
Ghanbarpour, M., Naderi, A., Ghanbari, B., Haghiri, S. & Ahmadi, A. Digital hardware implementation of Morris-Lecar, Izhikevich, and Hodgkin-Huxley neuron models with high accuracy and low resources. in IEEE Transactions on Circuits and Systems I: Regular Papers. Aug 22. (2023).
Zviagintsev, A., Perelman, Y. & Ginosar, R. Low-power architectures for spike sorting. in Conference Proceedings. 2nd International IEEE EMBS Conference on Neural Engineering,. IEEE, 2005. (2005).
Zhou, F. et al. Field-programmable gate array implementation of a probabilistic neural network for motor cortical decoding in rats. J. Neurosci. Methods. 185(2), 299–306 (2010).
Lee, K. H. & Verma, N. A low-power processor with configurable embedded machine-learning accelerators for high-order and adaptive analysis of medical-sensor signals. IEEE J. Solid-State Circuits. 48(7), 1625–1637 (2013).
Ma, X. et al. Using adversarial networks to extend brain computer interface decoding accuracy over time. Elife. 12, e84296 (2023).
Acknowledgements
The authors express their gratitude to Behrad Noudoost for generously providing the experimental data, which played a fundamental role in the evaluation conducted for this study.
Author information
Authors and Affiliations
Contributions
Danial Katoozian wrote the main manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Declaration of Generative AI and AI-assisted technologies in the writing process
During the preparation of this work the authors used https://poe.com/ in order to improve the readability and the language of the paper. After using this tool, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Katoozian, D., Hosseini-Nejad, H. & Dehaqani, MR.A. A new approach for neural decoding by inspiring of hyperdimensional computing for implantable intra-cortical BMIs. Sci Rep 14, 23291 (2024). https://doi.org/10.1038/s41598-024-74681-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-74681-1