Introduction

With the development of 3D point cloud processing technology, 3D point cloud segmentation is playing a significant role in many areas, such as scene reconstruction1,2,3, autonomous driving4, and other fields. It is vital for these industries to learn the semantic information of point clouds accurately.

3D data have rich geometry, shape, and scale information, which can be represented in different ways, including voxels, meshes, and point clouds. Among them, point clouds are the most convenient for deep learning processing. Different from regular 2D images, 3D point clouds are unstructured, which makes the 2D CNN framework not applicable to point cloud semantic segmentation directly.

Early semantic segmentation methods like support vector machines(SVM), random forests, and decision trees5,6,7 showed good performance on small amounts of point cloud data but could not satisfy the big one. It is challenging for semantic segmentation in different complex scenes. To address this issue, deep learning-based methods have been proposed, such as voxel-based methods8,9,10, projection-based methods11,12,13,14,15, and point-based methods16,17,18,19,20,21,22,23,24,25,26,27,28,29,30.

Voxel-based point cloud segmentation methods organized irregular point cloud data by dividing them into multiple regular voxel grids. These methods had good scalability but cost a large amount of memory and had low computational efficiency. Projection-based point cloud segmentation methods projected 3D point cloud into 2D images through various views, such as multi-view, spherical projection, etc., and then processed images by using the 2D frameworks. These methods could utilize the existing advanced 2D image processing algorithms directly but were prone to projection distortion and not suitable for complex scenes.

Point-based methods could operate the points directly, and preserve spatial information better than others. PointNet16, the classic point-wise MLP method, utilized shared multi-layer perceptions to acquire feature information of each point. It solved the problem of point cloud permutation invariance but lacked local feature extraction. PointNet++ 17 overcame the shortcomings of PointNet in local feature extraction, but due to the feature extraction layer by layer, its computational complexity was relatively high and required more computing resources, making it unsuitable for applications that required fast processing of large amounts of point cloud data. PointWeb18 introduced the Adaptive Feature Adjustment (AFA) module for finding interactions between points to extract contextual features from local neighborhoods. It was still not able to handle information about relationships between point clouds and tasks with local features. PointNeXt23 was an extension of the PointNet++. It aimed to improve the performance of point cloud processing by improving the training strategy and the model extension strategy but did not explore deeply on architectural innovations. Point-M2AE24 designed a multi-scale masking strategy to preserve local geometric integrity at different scales. Due to the multi-scale processing, Point-M2AE required high computational resources, and the performance of the model relied to some extent on the choice of masking strategy, and experiments were needed to determine the optimal masking ratio. By using cross-attention transformer, CASSPR25 combined point-based and voxel-based approaches to fully utilize multi-scale spatial context to achieve fine matching of subtle geometric features. Due to the fusion, the computational complexity could be high, especially on large-scale point clouds, and the performance may degrade when the information in a single scan was limited to a small area. SOE-Net26 demonstrated good advantages in point cloud-based location recognition tasks by combining self-attention and direction encoding mechanisms, but also faces challenges such as increased computational complexity and increased difficulty in model training. OPOCA27 proposed an innovative annotation method with significant advantages, such as high annotation efficiency and high segmentation accuracy. However, this method also had some disadvantages, such as dependence on the selection of annotation points, limited performance in handling complex scenes, and its generality and applicability to be verified. SegTrans28 showed significant benefits in the MLS point cloud semantic segmentation through transfer learning techniques and was a promising approach, but also faced challenges such as for some categories, the performance may still be not as good as expected.

Due to the correspondence between the graph structure and the point cloud data, graph-based methods were widely emerged recently to promote the development of point cloud processing. They converted point cloud data into the graph to preserve the geometric features between nodes and edges of the point cloud, and graph convolutional networks could be used for feature extraction. DGCNN29 dynamically constructed point cloud structural information using KNN, and DeepGCNs30 solved the problem that GCNs could not iterate multiple layers, making huge contributions to the subsequent development of GCNs. Graph U-Nets31 was an encoder-decoder model for graph data representation learning that introduced the gPool and gUnpool layers for pooling and unpooling graphs, respectively. These operations make it possible to implement U-Net-like structures on graph data, but they are depth-limited.

This paper proposes a novel segmentation network EIDU-Net. It makes full use of the complementation between geometric details in the original point cloud and high-level features to ensure learning effectiveness while reducing information loss. The edge-preserved graph pooling (EGP) layer, the key module of the EIDU-Net, is designed to retain additional edge feature information from the original point cloud during pooling operations. Accordingly, the edge-preserved graph unpooling (EGU) layer can restore the feature graph more efficiently based on the additionally retained edge features.

Our contributions are as follows:

  • We propose a novel encoder-decoder network (EIDU-Net), which integrates Inception DenseGCN to ensure features can be learned at multiple levels and scales.

  • We propose edge-preserved graph pooling(EGP) operation and edge-preserved graph unpooling(EGU) operation, which improve the traditional graph pooling and unpooling layer to maximize retention of spatial position feature information during the iteration process.

  • We build the Terracotta Warrior dataset to challenge the proposed EIDU-Net on point cloud semantic segmentation task. The final results demonstrate that the proposed EIDU-Net achieves significant improvements in self-built datasets and public datasets.

Experiment and results

In this section, we test the proposed EIDU-Net on both Area 5 and 6-fold of S3DIS32. We compare our network with previous models on point cloud semantic segmentation. The experiments demonstrate that our EIDU-Net achieves good results in point cloud semantic segmentation. Some ablation studies are conducted to examine the contribution of different parameter settings in the model to performance improvement.

Datasets and evaluation metrics

We perform experiments on the SIDIS dataset to evaluate the robustness of the EIDU-Net model. The momentum and initial learning rate are 0.9 and 0.001. Each input point is represented with a 9-dim vector. The models are trained with 100 epochs and batch size 12. The S3DIS dataset contains rich indoor structural information, covering point clouds of over 610 rooms, about 2.73 million points. The point clouds are annotated by semantic categories, including 13 object categories, such as walls, windows, doors, tables, chairs, and a clutter category. Evaluating semantic segmentation performance on this dataset can reflect the algorithm’s generalization ability for complex indoor scenes.

To normatively evaluate the segmentation performance of the EIDU-Net, the OA, mIoU, and mAcc are used in this article. They are defined as follows:

$${\text{OA}}=\frac{{\mathop \sum \nolimits_{{{\text{i}}=0}}^{{\text{k}}} {{\text{c}}_{{\text{ii}}}}}}{{\mathop \sum \nolimits_{{{\text{i}}=0}}^{{\text{k}}} \mathop \sum \nolimits_{{{\text{j}}=0}}^{{\text{k}}} {{\text{c}}_{{\text{ij}}}}}}$$
(1)
$${\text{mACC}}=\frac{1}{{{\text{k}}+1}}\mathop \sum \limits_{{{\text{i}}=0}}^{{\text{k}}} \frac{{{{\text{c}}_{{\text{ii}}}}}}{{\mathop \sum \nolimits_{{{\text{j}}=0}}^{{\text{k}}} {{\text{c}}_{{\text{ij}}}}}}$$
(2)
$${\text{mIoU}}=\frac{1}{{{\text{k}}+1}}\mathop \sum \limits_{{{\text{i}}=0}}^{{\text{k}}} \frac{{{{\text{p}}_{{\text{ii}}}}}}{{\mathop \sum \nolimits_{{{\text{i}}=0}}^{{\text{k}}} {{\text{p}}_{{\text{ij}}}}+\mathop \sum \nolimits_{{{\text{i}}=0}}^{{\text{k}}} {{\text{p}}_{{\text{ji}}}} - {{\text{p}}_{{\text{ii}}}}}}$$
(3)

where k means the dataset has k categories. cij is the number of points from ground truth i and predicted as class j.

Evaluation on the S3DIS dataset

The quantitative results of our network are compared with previous methods, including PointNet16, DGCNN29, SegCloud33, PointCNN19, SPGraph34, HPEIN35, MinkowskiNet36, PAG37, PointWeb18, PCT38, SegGCN39, KPConv40, RandLA-Net41, DPFA-Net42, and JSNet + + 43. The results of these methods are mostly taken from existing literature. Our experimental results are shown in Tables 1 and 2, which demonstrate our method achieves improvements over both baselines. Overall, compared with other methods, our method achieves better accuracy on the S3DIS dataset.

As shown in Fig. 1, EIDU-Net achieves good performance on indoor scene segmentation. EIDU-Net can effectively segment complex indoor structures. We attribute this decent result to the EGP and EGU, as they help the model better aggregate local information in the data, leading to better-detailed segmentation results.

Table 3 demonstrates the experimental results for specific categories in semantic segmentation on the S3DIS dataset. It is worth noting that our method attains better accuracy on the wall and sofa classes. The results indicate that our EIDU-Net is adequate for the large-scale point cloud semantic segmentation task.

Table 1 Results on S3DIS Area-5 dataset for semantic segmentation.
Full size table
Table 2 Results on S3DIS 6-fold dataset for semantic segmentation.
Full size table
Fig. 1
figure 1

Visualization results on S3DIS.

Full size image
Table 3 mIoU results on S3DIS area-5 dataset for semantic segmentation.
Full size table

Different components

To verify the effect of different modules in the model, we conduct ablation experiments on Area 5 of S3DIS. The result is presented in Table 4. When replacing the EGP and EGU modules with the Graph Pooling and the Graph UnPooling of Graph U-Nets31, the OA and the mACC values decreased to 86.9 and 74.4. Similarly, lacking either of these two modules alone also leads to a decrease in OA and mACC. Based on the analysis of the results, it can be seen that aggregating feature details during pooling and unpooling helps reduce feature loss and improve final segmentation performance. Therefore, It is credible that optimizing pooling operations and unpooling operations for 3D data is effective and meaningful.

Table 4 Ablation results on S3DIS area-5 dataset.
Full size table

The influences of different numbers of DenseGCN layers

Although DeepGCNs solved the problem that GCNs could not iterate deeply, considering EIDG is just a basic module in the dual-nested structure, the appropriate number of iteration layers inside the DenseGcn needs to be evaluated through experiments. We conduct experiments with the number of layers set to 2–5.

As shown in Fig. 2, when the number of layers reaches 3, the segmentation effect no longer improves significantly and even shows a downward trend. The results show that 3 layers of DenseGCN are already sufficient. Due to the overfitting, further increasing the number of iteration layers will reduce the efficiency.

Fig. 2
figure 2

Ablation Study on different numbers of DenseGCN layers.

Full size image

The influences of different numbers of EIDU-Net layers

In this section, the reason for conducting the ablation study is also to consider that too many iterations will affect the final segmentation effect. We set the number of layers of EIDU-Net from 1 to 5 for experiments. Figure 3 shows the number of layers of EIDU-Net has a significant impact and 3 seems to be the most suitable number of layers.

Fig. 3
figure 3

Ablation Study on different numbers of EIDU-Net layers.

Full size image

Application on virtual restoration of real-world terracotta warriors

In recent years, point cloud processing for cultural heritage digitization can effectively avoid secondary damage to artifacts, which is of great significance for cultural relic protection and restoration. Among them, point cloud semantic segmentation can help researchers restore cultural relics more efficiently and accurately by semantically segmenting the digitized cultural relic models. As one of the focal points of our laboratory research is the virtual restoration of ceramic cultural relics, the Terracotta Warriors are the most notable ceramic cultural relics in our research, which are considered as one of the world’s eighth wonders. In order to further confirm the effectiveness of the proposed EIDU-Net, we apply it to the challenged real-world datasets, i.e. Terracotta Warrior models.

Generally, 3D laser scanners can only scan partial point clouds of an object. In order to reconstruct the complete object, it is necessary to scan point clouds from different viewpoints and calculate view transformations based on point correspondences between point clouds. Then it is necessary to align point clouds from individual viewpoints to the same coordinate system and merge them into a complete 3D model. By following the steps above, we collect 200 complete Terracotta Warrior models by 3D object scanner, each composed of about 500,000 points, including xyz data, vertical normals, and RGB data. 160 models are utilized for training and 40 aside for testing. As shown in Fig. 4(a), we eliminate the vertical normals and RGB data, remaining xyz coordinates as input.

In traditional studies of point cloud semantic segmentation on the Terracotta Warriors datasets, the Terracotta Warriors 3D models are generally divided into six parts: head, body, left hand, right hand, left leg, and right leg. To better facilitate the cultural relic restoration and test the performance of our EIDU-Net, we separate the hands and arms of the original Terracotta Warriors models, dividing them into eight parts: head, body, left hand, left arm, right hand, right arm, left leg, and right leg.

Fig. 4
figure 4

Visualization results on Terracotta Warriors. (a) Input point clouds. (b) Ours.

Full size image

Our experimental results in Table 5 show that the OA can reach the best effect of 89.7%, the mIoU can reach 70.3% and the mAcc can reach 84.2%. From Fig. 4(b), we can see the eight parts of the Terracotta Warriors are segmented well, but the segmentation boundaries of some contacting parts are not clear enough (as shown in the red circles). The reason for this problem is that the unique manufacturing process of the Terracotta Warriors causes some parts to stick together, which leads to the incompletation of the Terracotta Warriors models. For example, the inner arm parts and body parts of some Terracotta Warriors models are adherent, which affects the final training results. Subsequently, we consider optimising the point cloud segmentation model jointly with the point cloud completion method. For example, ASFM-Net44 achieves high-quality point cloud completion through an asymmetric twin feature matching mechanism and a multi-scale feature extraction module, providing richer geometric and semantic information for the subsequent segmentation task.

Overall, under conditions of segmenting models into more categories and with incomplete parts in some models across the dataset, our method achieves good performance on semantic segmentation, which demonstrates the robustness and efficacy of EIDU-Net.

Table 5 Results on the terracotta warrior dataset.
Full size table

Discussion

The proposed EIDU-Net model is used for supervised learning of point cloud segmentation and achieves good results on the S3DIS and the Terracotta Warriors dataset. As graph structures can better represent irregular data such as point clouds, this paper solves the problem that traditional GCN cannot iterate multiple layers by using DenseGCN, and learns multi-scale features through different dilation scales to obtain more detailed and deeper semantic feature information, so that GCNs can process large-scale and more complex graph data; the EGP and EGU proposed in this paper aggregate the feature information of edge points in the original point cloud to global features, reduce the loss of feature information in pooling and unpooling operations, and solve the problem of being unable to continue GCN; U-shaped structure is designed to fuse low-level and high-level features, and the performance and accuracy of the model are improved in segmentation tasks. Ablation studies prove that although increasing the number of network layers can improve feature learning to some extent, too many layers will lead to a gradual decline in performance due to overfitting. Therefore, while deepening the model architecture, we should also find ways to optimize the effectiveness of each individual feature extraction module.

Methods

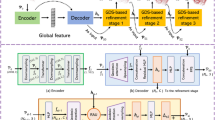
This section introduces the proposed Edge-preserved Inception DenseGCN U-Net (EIDU-Net), which is designed as an encoder-decoder structure. Inception DenseGCN is set as the feature extraction module and some adjustments are made. In particular, two kinds of skip connections that work with the feature extraction module are utilized to ensure the learning of multi-scale and hierarchical features of 3D points. To adapt to the encoder-decoder structure and reduce the loss of feature information, the feature aggregation modules are designed as Edge-preserved Graph Pooling (EGP) and Edge-preserved Graph Unpooling (EGU). EGP is on the basis of the graph pooling layer and adds the operation of aggregating edge features of central nodes and neighbor nodes during the pooling operation. In subsequent operations, it reduces the loss of feature information due to pooling operations with skip connections. Similarly, in the EGU operation process, unpooling is performed better based on the previously saved information. EIDU-Net propagates feature information at different levels to the end through two different skip connections, ensuring the aggregation effect of local geometric details and high-level features.

Edge-preserved graph pooling

Pooling operation was first widely used in convolutional neural networks (mainly including max pooling and average pooling), and was later gradually implemented in graph convolutions. The difference is that the pooling operations of the CNN framework cannot be applied to graph convolution networks, which would destroy the spatial structure of the feature graph. The proposal of Graph U-net31 presented a classic pooling method suitable for graph convolution. The graph pooling layer incorporated a top-k scoring mechanism into the pooling process to ensure important feature nodes not lost.

Unlike CNN pooling operations, graph convolution pooling operations did not lose spatial information. In the Inception DenseGCN module45, the original framework only had one layer of the feature extraction module. It directly adopted the multi-branch structure similar to CNN to integrate the feature information learned. Finally, the max pooling layer and two MLP layers were performed to obtain a fixed-length global feature for the classification and segmentation task.

The reasons for optimizing the pooling layer are: (1) to further deepen the network hierarchy of the encoder-decoder structure. The features after max pooling layer in the original method lose a lot of spatial information and cannot continue the next GCN operation; (2) because classical pooling operations for graph convolutions, such as Graph Pooling operation, also lose some feature information during the normal convolution process. We hope to optimize this step to reduce the loss of feature information.

As shown in Fig. 5, the left figure shows traditional graph pooling based on the top-k algorithm {t1,t2,t3}. The right figure shows our EGP. Compared with the traditional method, after selecting k nodes by top-k, EGP constructs local neighborhood graphs for these k nodes from the original point cloud data, and selects their neighbors by random downsampling {t5,t6,t7,t8,t10,t11}. In this way, our model can better preserve local geometric information.

To solve this problem, we propose an optimized graph pooling method Edge-preserved Graph Pooling (EGP), which can more effectively capture local geometric details. EGP adds a novel process operation on the basis of original graph pooling to aggregate the features of high-scoring central nodes and their edge nodes. We place the EGP module after two DenseGCN layers with different dilation scales. In this layer, we first divide and select nodes in the feature graph through the top-k algorithm of graph pooling, and obtain k top-scoring nodes in descending order of scores, as illustrated in Fig. 6. We set these k nodes as central nodes, and construct their local neighborhood graphs respectively with the original point cloud data. Then the density of edge nodes in local neighborhood graphs is reduced by random downsampling, as shown in Fig. 6(a). Finally, the features of the central nodes and the remaining edge nodes are aggregated. In this way, the feature of top-k key nodes can be better retained, and their local structure information can be better aggregated.

Fig. 5
figure 5

Illustration of the EGP modules.

Full size image
Fig. 6
figure 6

Illustration of the EGP module. (a) The flow of the encoder module. The circular graph indicates that in the EGP process. (b) Illustration of the downsampling module for point cloud segmentation. d is the dilation rate and r is the random downsampling rate of EGP.

Full size image

Through EGP, the central node and its edge nodes are combined into an enhanced node and the local feature information of each central node can be retained better. Our EGP module is designed as:

$$\left\{ {\begin{array}{*{20}{l}} Score={{\text{X}}^\ell}{{\text{P}}^\ell }/\left\| {{{\text{P}}^\ell }} \right\| \\idx=rank\left( {{\text{Score}},{\text{k}}} \right) \\{\text{X}}_{p}^{\prime }={{\text{X}}_p} \oplus h\left({{\text{X}}_{{\text{j}}}^{1}, \ldots,{\text{X}}_{{\text{j}}}^{{\text{i}}}} \right) \\\widetilde {{{\text{Score}}}}=sigmoid\left({{\text{y}}\left( {{\text{idx}}} \right)} \right) \\{{{{\tilde {X}}}}^\ell }={{\text{X}}^\ell }\left({{\text{idx}},:} \right) \\{{\text{X}}^{\ell +1}}={{{{\tilde{X}}}}^\ell } \odot \left( {\widetilde{{{\text{Score}}}}1_{{\text{C}}}^{{\text{T}}}} \right) \end{array}}\right.$$
(4)

where k is the number of nodes that are selected by top-k arithmetic. The idx and \(\:{\text{X}}^{\mathcal{l}}\left(\text{i}\text{d}\text{x},:\right)\) are the indices and feature matrices of the selected points, respectively, which are used to construct the new graph structure. Xp is the feature of the selected node and \(\:{\text{X}}_{\text{j}}^{\text{i}}\) is the feature of its selected neighbors by random downsampling.

Edge-preserved Graph UnPooling

In the encoder-decoder structure, the low-layer 3D point features need to be restored to the corresponding feature density. Corresponding to the improvement of EGP pooling, Edge-preserved Graph Unpooling (EGU) also sets the nodes in the feature graph as central nodes during the graph unpooling operation, and also constructs their local neighborhood graphs with the original point cloud data. After randomly reducing the edge nodes in the neighborhood graphs through random downsampling, the feature information of the central nodes and the remaining edge nodes are aggregated. In the process of gradual upsampling, the central nodes and edge nodes are concatenated to enhance the features through locally detailed features, which improves the expressive ability of the model. Our EGU module is designed as:

$${\text{X}}_{q}^{\prime }={\text{X}}_{{{\rm q}}}^{{{\rm f}}}\oplus \omega \left( {{{\text{X}}_{{\rm q}}}_{{\text{j}}}^{1},\ldots ,{\text{X}}_{{{{\rm qj}}}}^{{{\rm i}}}} \right)$$
(5)

where \(\:{\text{X}}_{\text{q}}^{\text{f}}\) is the feature from corresponding layers of the encoder by skip connection and \(\:{\upomega\:}\left(\:\right)\) is the inverse distance weighted average operation.

Fig. 7
figure 7

Illustration of the EIDU-Net modules.

Full size image

Edge-preserved Inception DenseGcn U-Net

Inspired by the encoder–decoder structure, our model contains downsampling part as encoder and an upsampling part as decoder. As shown in Fig. 7, the encoder-decoder structure combining EGP and EGU is the outer nested structure in EIDU-Net. The encoder part consists of three layers, which gradually extract point features while performing pooling operations through EGP. Correspondingly, the decoder part consists of similar structure. Each layer of the decoder part can better aggregate local feature information through skip connections with the corresponding encoding layer. In addition, the black line shows that the three modules of the encoder separately recover feature density layer-by-layer through the EGU module and aggregate information at the end. The red lines indicate that the original point cloud data provides neighborhood graph information of the selected central points to the EGP module and EGU module.

Conclusion

The EIDU-Net model proposed in this paper plays an important role in promoting the research of point cloud segmentation that I know of, and provides new ideas for point cloud segmentation methods. By using deepGCN to extract the topological feature of points, it not only obtains the information of individual points and the relationship between points, but also expresses the feature information of point clouds more accurately and meticulously; in each pooling(EGP) and unpooling(EGU) operation, the top-k strategy is used to obtain k center points and random neighborhood information aggregation, which not only ensures the learning efficiency of the model, but also reduces the loss of geometric information; the U-shaped structure is utilized to fuse low-level and high-level features to further improve the segmentation accuracy. The experimental results verify the superiority and rationality of the proposed model. In the future, we can try to utilize the U2Net model to further enhance the accuracy of the segmentation results and apply the optimized model to more fields, such as the field of autonomous driving. In addition, we can also explore joint training methods for point cloud completion(ASFM-Net for instance) and segmentation tasks, so that the completion and segmentation processes can promote each other and improve the overall performance for the more common scenes with occlusion. For example, a joint loss function can be designed to optimize both the completion and segmentation tasks, achieving more efficient model training.