Introduction

The impact of the construction industry on resource consumption and pollution emissions has become a global concern. The Global State of Construction Report shows that CO2 emissions from building operations increased by 5% in 2022 compared to 2020, reaching a record high of 10 Gt CO21. To achieve carbon peak and neutrality goals, increasing interest is being directed towards green building and sustainability transition2,3. Concrete waste is a significant factor in construction pollution, and its recycling is crucial to saving energy and reducing pollution4,5,6. The main recycling approach involves pre-treating concrete and reusing it in engineering projects7,8,9. Additionally, the capture and storage of CO2 within concrete is a promising strategy to reducing greenhouse gas emissions and increasing the strength of concrete10,11,12. The main chemical reaction involved in carbonation is the reaction between CO2 and the hydration products of cement, resulting in the formation of CaCO313,14. The spontaneity of the reaction and the relative stability of the carbonate produced results in the great potential of this technology for application12,15,16. However, the carbonation process in natural environments is slow, and more efficient methods are required to enhance CO2 capture and storage17.

In recent years, researchers have explored various carbonation processes, with a particular focus on accelerated carbonation methods. Liang et al.18 and Tam et al.19 have summarized the existing techniques for CO2 curing, including standard carbonation20,21,22, pressurized carbonation23,24, flow-through CO2 curing and water-CO2 cooperative curing25,26. Comparisons between these methods have shown that pressurized carbonation can achieve higher efficiency in a shorter amount of time27,28,29. This method involves injecting CO2 into concrete at a pressure higher than atmospheric pressure (typically ranging from 0.1 to 5 bars), to enhance the overall carbonation process30. Some researchers31,32 have even experimented with ultra-high pressures, ranging from 20 to 100 bars, to further improve carbonation efficiency. However, these approaches consume excessive energy and may impact negatively on concrete strength without providing significant benefits33. Therefore, it is important to investigate a more efficient accelerated carbonation method for CO2 absorption. Additionally, while most studies have focused on simulation models that explain the coupling of multiple physical fields during pressurized carbonation, few have explored empirical models that offer greater convenience and time savings in prediction31,34,35,36,37. Therefore, the development of an empirical model for pressurized carbonation would provide a valuable and convenient prediction tool for carbonation in concrete.

A cyclic carbonation process during a pressurized condition was explored by Zhan et al.38 and He et al.39. In this process, following a period of pressurized carbonation, the CO2 in the reaction chamber is released and the pressure reduced to atmospheric levels. Pressurized carbonation is then conducted again, and these steps are repeated. This multiple cycle approach allows for the renewal of lower CO2 concentrations and a reduction in relative humidity (RH) inside the chamber. As a result, optimal carbonation conditions are restored, leading to an increased reaction rate39. However, it is important to note that this method does not allow for the quick and spontaneous dissipation of free water within the concrete under atmospheric pressure, which can limit the proportion of CO2 captured.

Venhuis et al.40 emphasized the effectiveness of a vacuum environment in removing water from the concrete and creating an open pore network for CO2 penetration. Building upon this advantage, Phung et al.41 and Pu et al.42 introduced negative pressure as an end signal for each pressurization cycle to extract any remaining gas in the reaction chamber when using flue gas for concrete carbonation. Pu et al.42 discovered that six cycles at a pressure of 1 bar within a 24-h period yielded satisfactory carbonation results. However, the short vacuuming time in their method only removed flue gases from the chamber, potentially leaving water trapped in the concrete pores. Additionally, Phung et al.41 employed the RH within the chamber as a threshold for transitioning between the drying and carbonation processes, extending the negative pressure duration. However, as the number of cycles increased and the carbonation rate slowed, it became increasingly challenging for the RH to reach the predetermined threshold, resulting in reduced long-term carbonation efficiency.

In short, the effects of cyclic pressurized carbonation and negative pressure on concrete are still being investigated. However, if the benefits of negative pressure can be maximized and improvements can be made to the cyclic pressurized carbonation process to efficiently remove excess water from concrete while maintaining high carbonation efficiency, there is great potential for reducing the time required for CO2 capture and advancing the development of environmentally friendly building.

In this study, an innovative accelerated carbonation method, inspired by the Deep Breathing Analogy (DBA), is proposed to enhance the efficiency of CO2 capture. The effectiveness of the method is assessed using established carbonation calculation techniques. Through the analysis of experimental data, the correlation between the proportion of captured CO2 and the depth of carbonation is examined. Additionally, an empirical prediction model for pressurized carbonation is proposed to forecast carbonation depth and serve as a reference for predicting the carbonation depth of concrete when employing the DBA method.

Experimental work

Sample preparation

The mix proportions of the concrete are listed in Table 1. The cement used was CEM I 52.5 N (obtained from Hong Kong Green Island Cement Company Limited) and its chemical composition is shown in Table 2. Natural river sand with a size < 5 mm was used as fine aggregate while the coarse aggregate was made up of crushed granite with a maximum size of 10 mm. Cubic samples with dimensions of 100 mm × 100 mm × 100 mm were prepared for carbonation tests while three cubes with dimensions of 150 mm × 150 mm × 150 mm were used for compressive tests to obtain the compressive strength according to the recommendations of Standard GB/T 50,081–201943. After pouring, the samples were cured in water at 20℃ ± 1℃ for 28 days. One week prior to experimentation, the samples were removed from the water to acclimatize under normal environmental conditions, while their moisture content was maintained within a regular range (m = 3.93% ± 0.01%). The calculation formula used to determine the moisture content is provided in Eq. (1).

$$m = {(}M_{{\text{i}}} - M_{{0}} {)/}M_{{0}} \times {\text{100\% }}$$
(1)

where Mi is the mass of the sample in the natural environment and M0 is the mass after being dried to a constant value.

Table 1 Mix proportions and mechanical properties of sample.
Full size table
Table 2 Chemical composition of cement.
Full size table

Experimental design

Experimental setup

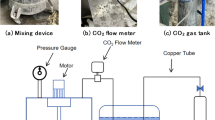
The experimental setup of this novel pressurized carbonation of concrete and a schematic diagram are shown in Fig. 1. A reaction chamber comprised of stainless steel with a capacity of approximately 50 L was customized for accelerated carbonation. A pressure gauge and a CO2 detector were installed to monitor the changes in pressure and CO2 concentration, respectively. Recognizing that concrete carbonation is an exothermic reaction which leads to the evaporation of water, silica gel was placed within the chamber to absorb moisture. To maintain a constant temperature of 30 ℃ ± 2 ℃ and relative humidity of 50% ± 2% throughout the experiments, a temperature and humidity controller was installed to automatically regulate the heating wire and humidifier, while an insulation film was installed around the reaction chamber to enhance thermal stability. Additionally, an electronic balance was employed to non-destructively track the weight changes of each sample throughout the carbonation process.

Fig. 1
figure 1

Experimental setup of carbonation: (a) main experimental setup; and (b) schematic of carbonation chamber.

Full size image

Experimental methods

The suppressed rate of carbonation can be primarily attributed to two factors: the densification of concrete pores by carbonation products and the accumulation of liquid water in micro-pores44,45. This dual effect impedes the further penetration of CO2 and evacuation of water, ultimately limiting the efficiency of the carbonation reaction. In response to this challenge, novel accelerated carbonation processes have been proposed, including the Deep Breathing Analogy (DBA) method. Drawing inspiration from the mechanism of breathing in human lungs, the DBA method incorporates applied positive and negative pressure techniques to enhance the carbonation of concrete. Specifically, this method involves injecting pure CO2 into a reaction chamber (analogous to the lungs) to a predetermined pressure (inspiration), followed by evacuating the gas from the chamber to a certain negative pressure for a period of time after the calcium and magnesium minerals in the sample have reacted with the CO2 (exhalation). One succession of inhalation and exhalation is defined as a cycle. After repeating the cycle several times, excess water is removed from the sample and deeper penetration of CO2 into the sample is promoted.

In order to evaluate the effectiveness of the DBA method and determine an optimal carbonation process, four different DBA processes were designed, as illustrated in Fig. 2 (a-d). The first process (referred to as DBA-A in Fig. 2 (a)) served as the basic DBA method and was implemented to assess its effectiveness. To address the issue of pore blockage caused by excessive water generation during the carbonation reaction, the second process (named DBA-B in Fig. 2 (b)) was designed with further modifications. In DBA-B, the duration of inspiration was shortened and expiration was lengthened by 0.5 h, compared to the previous cycle. Additionally, to explore the optimal duration balance of expiration and inspiration within the same timeframe, the third process (named DBA-C) was proposed, as illustrated in Fig. 2 (c). Furthermore, to overcome the suppression of the carbonation rate caused by the filling of concrete pores with carbonation products in each cycle, the fourth process (referred to as DBA-D) was employed, as shown in Fig. 2 (d). In DBA-D, the pressure for both inspiration and expiration was increased by 0.1 bars in each successive cycle, while keeping the carbonation time and number of cycles unchanged. Additionally, to validate the effectiveness and rationality of these proposed methods, two separate control groups were established, as shown in Fig. 2 (e) and (f). Control Group-1 (CG-1) was maintained at a steady inspiratory pressure of 0.5 bars to evaluate the effect of different expiratory durations at the same pressure on the carbonation of DBA-A, DBA-B and DBA-C. Control Group-2 (CG-2) was maintained at a steady inspiratory pressure of 1 bar to compare the carbonation effect with DBA-D.

Fig. 2
figure 2

Various DBA processes: (a) DBA-A; (b) DBA-B; (c) DBA-C; (d) DBA-D; (e) CG-1; and (f) CG-2.

Full size image

In order to validate that the exhalation of DBA can reduce the RH inside the reaction chamber, taking DBA-A as an example, Fig. 3 illustrates the RH changes inside the chamber monitored by the relative humidity controller during the experiment. Specifically, during exhalation, the humidifier is turned off to facilitate the removal of excess water from the chamber and to lower the RH level below that of the natural environment. During inhalation, the humidifier is activated to restore the RH level in the chamber to the desired set level. It is evident from Fig. 3 that during the exhalation process, negative pressure effectively extracts residual gas and water from the chamber, thereby maintaining the relative humidity at a stable level of 35%-45%. This level is significantly lower than that of the natural environment, thereby promoting rapid water diffusion out of the concrete due to the pressure and humidity gradient.

Fig. 3
figure 3

The changes of relative humidity and pressure of DBA-A.

Full size image

The specific experimental procedures are depicted in Fig. 4. The weights of the samples were measured and recorded prior to the experiment, after which the samples were placed inside the sealed reaction chamber and the base inspiratory pressure was uniformly set at 0.5 bars, as recommended in reference33. Notably, three samples were tested simultaneously in each experiment and, prior to initiating the carbonation process, the chamber pressure was adjusted to -0.5 bars for 0.5 h to remove extra air and moisture. During carbonation, inspiration and expiration duration followed the pattern of the corresponding DBA processes depicted in Fig. 2. To ensure the reliability of the experiment, the weights of samples after the experiment were also recorded to facilitate comparison with those prior to experimentation.

Fig. 4
figure 4

Procedure of experiment.

Full size image

Carbonation calculations

Weight gain of samples

Weight changes in concrete before and after carbonation can reflect the magnitude of carbonation to some extent. In order to circumvent weight differences between the samples and facilitate a clear estimation of weight growth during carbonation, the weight gain of the samples during the carbonation process is calculated using Eq. (2).

$$w = {(}W_{{\text{i}}} - W_{{0}} {)/}W_{{0}} \times {\text{1000 g}}$$
(2)

where w is the weight gain per kilogram of the sample (g); Wi is the weight measured by the electronic balance at moment i; and W0 is the original sample weight prior to the experiment.

Proportion of CO2 captured

Since the DBA method exhales excess water, the weight of this water is difficult to assess. Therefore, to estimate the proportion of CO2 captured, it is assumed that all carbonation products and weight gains are attributed to CaCO3, and the produced water is not considered. This assumption allows for the calculation of the proportion of CO2 captured using molecular mass approximations, as described in Eqs. (3–5)46.

$${\text{CO}}_{{{\text{2captured}}}} {\text{,\% }} = {(}M_{{{\text{CO}}_{{2}} }} /M_{{{\text{max}}{\text{.cap}}}} {)} \times {\text{100\% }}$$
(3)
$$M_{{{\text{CO}}_{{2}} }} = \Delta M_{{{\text{Sample}}}} \times {44}/{100}$$
(4)
$$M_{{{\text{max}}{\text{.cap}}}} = M_{{{\text{cement}}}} \times {65}{\text{.9\% }} \times {44}/{56}$$
(5)

where \(M_{{{\text{CO}}_{{2}} }}\) is the actual amount of CO2 captured (g) and ∆Msample is the weight change of the sample, compared before and after carbonation (g).

Theoretically, the maximum amount of CO2 captured based on the cement content, Mmax.cap, can be calculated using Eq. (5) and the cement weight of each sample, Mcement, can be calculated by referring to the mixing ratio in Table 1. Notably, the values 44, 56 and 100 in Eqs. (4) and (5) represent the molecular mass of CO2, CaO and CaCO3, respectively.

Carbonation depth

Upon completion of the experiment, the samples were cut and the cross-sections were sprayed with a 1% phenolphthalein solution, to measure carbonation depth by observing the resulting change in pH. A typical carbonation cross-section is shown in Fig. 5. It should be noted that the distribution of carbonation within the samples was not uniform due to the irregular accumulation of aggregates in the samples. Therefore, the actual carbonation depth was replaced by an equivalent carbonation depth D, in accordance with the methodology proposed by Zha et al.31. Specifically, after the areas of non-regular un-carbonated regions were calculated using Corel DRAW software, the equivalent carbonation depth D can be estimated by Eq. (6).

$$D = {(}d - \sqrt A {)}/{2}$$
(6)

where D is the equivalent carbonation depth, d is the sample side length and A is the un-carbonated area.

Fig. 5
figure 5

Extraction scheme for un-carbonated area.

Full size image

Results and discussions

Trends of weight gain

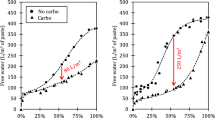
After substituting the recorded weight gain into Eq. (2), the results of the typical DBA method and control groups are presented in Fig. 6. Significantly, the DBA methods expel excess water during the respiratory cycle, which was not quantitatively assessed. As depicted in Fig. 6, the weight gain of CG-1 and CG-2 exceeded that of the DBA methods within the initial 12 h of carbonation. However, due to the DBA method’s water expulsion mechanism, it still achieves greater weight gain than CG-1 and CG-2 in the subsequent 12 h, highlighting the efficiency of the proposed DBA methods.

Fig. 6
figure 6

Results of DBA method and control groups.

Full size image

Additionally, taking DBA-B as an example (middle panel in Fig. 6), a paradoxical surge and subsequent drop in weight gain can be observed during the exhalation stage due to the changes in pressure. However, for the sake of clarity, and facilitating the observation of the trend of weight gain, this phenomenon was not overly displayed in Fig. 6. It is important to note that, although all experiments were conducted under identical environmental conditions, variations in weight gain were noticeable among the different experiments during the first 4 h of carbonation. This is possibly attributable to such factors as sample differences, potential defects in the testing process or other factors, including sample dispersion, ambient RH prior to the experiment and water absorption of the silica gel. These issues should be addressed in future studies, while Fig. 6 was primarily utilized to depict the trends in weight gain throughout the carbonation process and to assess the effectiveness of the DBA method.

It can be seen from the trends of weight gain of CG-1 and CG-2 in Fig. 6 that carbonation primarily occurred within the initial 4 h. This observation aligns with the results of Zhan et al.47, verifying the rationality of setting carbonation at 4 h during the initial stages of the DBA-A, DBA-B and DBA-D methods. Further, with the increase of inspiratory pressure from 0.5 bars to 1 bar, the trend of weight gain of CG-2 is found to be faster than that of CG-1, which is consistent with the phenomenon that carbonation can be enhanced by raising pressure within a certain range33.

The DBA-A, DBA-B and DBA-C methods were devised to investigate the impact of exhalation duration on carbonation efficiency. As shown in Fig. 6, a comparison of the three methods with CG-1 demonstrated that performing a deep breathing cycle at a constant positive pressure does promote a notably improving trend in weight gain. Moreover, it is noteworthy that, following the exhalation process, the weight gain at the start point of latter cycles is lower than that at the end of the last cycle. A possible explanation for this is that the exhalation of DBA method eliminates excess water from the samples, which promotes further carbonation of the minerals, validating the effectiveness of the three DBA method.

It can be seen from the comparison between the DBA-B and DBA-A methods that the difference in the increasing trend between them was inconspicuous. Furthermore, the comparison of the DBA-B and DBA-C methods indicated that the growth of DBA-B was slower than that of DBA-C during the initial 2 h. However, the growth of DBA-B became equivalent to that of the DBA-C method from the fifth cycle. Therefore, to maintain carbonation efficiency, it may be necessary to extend the expiratory time while shortening the inspiratory time for carbonation in the subsequent cycle.

The DBA-D method, as a further improvement of the DBA-A method, aimed to investigate whether a controlled increase in pressure could further enhance deeper carbonation as the cycles advanced. It can be seen from Fig. 6 that, at the fifth cycle (after approximately 18 h), the rate of weight gain of the DBA-D method surpassed that of the DBA-A method. This phenomenon confirmed the feasibility and effectiveness of implementing a proper increase in breathing pressure during each cycle to promote deeper carbonation as the process progresses. The maximum inspiratory pressure of the cycle in the DBA-D method, of 1 bar, was chosen as the inspiratory pressure of the CG-2 to dispel the suspicion that the effective results were solely due to the pressure increase. The results indicated that, although the initial trend of weight gain in the CG-2 was higher than that of the DBA-D method, as the breathing cycle progressed, the DBA-D method was ultimately higher than that of the CG-2.

Overall, the trends of weight gain in all groups of the DBA method exhibited a steeper slope of growth compared to the control groups, reflecting the rationality and reliability of the DBA method.

Proportion of CO2 captured

To further illustrate the efficiency of the DBA method, the proportions of CO2 captured were calculated by Eqs. (3–5) and the results are presented in Fig. 7. The increase in the proportion of CO2 captured is correlated with the cement weight of each sample and the weight change during the carbonation process. Specifically, when the cement weight remained constant, a greater weight difference between samples before and after carbonation resulted in a higher proportion of CO2 captured.

Fig. 7
figure 7

Proportion of CO2 captured and weight change.

Full size image

The results of CG-1 and CG-2 demonstrated that the increase in inspiratory pressure led to only a slight improvement in carbonation efficiency, of 4.63%. This finding is in agreement with the results reported by previous research33. This phenomenon can be attributed to the formation of a dense CaCO3 film within the concrete pores when CO2 enters the pores under pressure gradient, which makes it difficult for CO2 to pass through the film to continue carbonation48.

It can be seen from Fig. 7 that the proportions of CO2 captured during the four DBA method can be ranked in descending order, as DBA-D, DBA-B, DBA-A and DBA-C. Specifically, DBA-A and DBA-B showed significant enhancement in the percentage of CO2 captured, at 43.42% and 93.59%, respectively, higher than that of CG-1 at 0.5 bars. The results of the two DBA method exhibited substantial efficiency gains, providing strong evidence for the effectiveness of the DBA method. Similarly, DBA-A and DBA-B performed 37.07% and 85.03%, respectively, higher than CG-2 at 1 bar pressure. This suggests that simply increasing pressure may not yield the same efficiency as employing the precise DBA method. However, the comparison between CG-1 and DBA-C revealed that the proportion of CO2 captured in DBA-C was lower than that of CG-1 at the same pressure, exhibiting a decrease of 21.35%. This could be attributed to the relatively short carbonation time and extended expiratory time associated with DBA-C, despite it undergoing the equivalent number of breathing cycles. Therefore, there may be a balance between inspiratory and expiratory times, which deserves further exploration in future studies.

Moreover, as the most efficient method, the result of the DBA-D method was higher than CG-1 and CG-2 by 145.91% and 135.03%, respectively. This demonstrates that, with an identical number of cycles and duration, an appropriate increase of breathing pressure within each cycle can effectively alleviate the inhibition effects on carbonation caused by pore closure and blockade. Therefore, the results demonstrate that the DBA-D, DBA-B and DBA-A methods can effectively promote the proportion of CO2 captured.

Carbonation depth

In order to provide additional evidence of the effectiveness of the DBA method, equivalent carbonation depth D was determined using Eq. (6) and the results are presented in Fig. 8.

Fig. 8
figure 8

Mean un-carbonated area and mean carbonation depth of different methods.

Full size image

As shown in Fig. 8, the variation patterns of the carbonation depth of different methods are similar to those of the proportion of CO2 captured in Fig. 7, with the DBA method showing obvious advantages.

Remarkably, the carbonation depth of the DBA-C method slightly exceeded that of CG-1, which could be attributed to potential errors in the extraction of carbonation depth or the assumption used in estimating the proportion of CO2 captured. For instance, the proportion of CO2 captured relied on weight changes and all the weight increases were assumed to result from the production of CaCO3. This assumption deviates from reality and may induce discrepancies in the results. Despite these errors, DBA-D, DBA-B and DBA-A show obvious efficiencies in promoting the carbonation of concrete, regardless of the specific criteria used for evaluation. Above all, it is evident that the novel DBA method is superior to conventional pressurized carbonation in the efficiency of CO2 capture.

Relationship between CO2 capture rate and carbonation depth

The investigation conducted in Section "Carbonation depth" revealed a similar trend in the carbonation depth and proportion of CO2 captured. The relationship between these two variables was explored and is presented in Fig. 9.

Fig. 9
figure 9

Relationship between proportion of CO2 captured and carbonation depth.

Full size image

It can be seen from Fig. 9 that the depth of carbonation and the proportion of CO2 captured were approximately linearly related, which is consistent with the results of Jia et al.49. This verifies the reliability of employing carbonation depth and proportion of CO2 captured as the criteria for assessing carbonation degree; however, using different criteria may have some influence on the final carbonation results.

Evaluation of economic potential

The annual global production of construction and demolition (C&D) waste is estimated to exceed 10 billion tons50,51, with 50–90% of this waste being suitable for use as recycled aggregate in construction52,53. Additionally, Juan et al.54 found that the cement mortar content attached to recycled aggregate ranged from 40–55% using the heat treatment method. To assess the potential amount of CO2 that could be captured by annually produced recycled concrete aggregate (RCA) and its economic value, we assume that 50% of the recyclable concrete aggregate is produced each year, with a mortar content of 40% attached to each unit of recycled aggregate. This results in a cement content of 2 billion tons per year. If the entirety of this cement were to be utilized for carbon capture and sequestration, the theoretical maximum CO2 capture would amount to 1.036 billion tons, by combining Eq. (5).

Carbon credits have been utilized to evaluate the potential economic benefits of captured CO255,56 and, statistically, the carbon offset market is lower than the carbon credit market57. According to World Bank pricing58, if the CO2 captured by recycled aggregates is classified as CO2 removal credits, the average carbon credit price generated by CO2 would be $14/tCO2e. The annual yield of recycled aggregate could theoretically generate $14.504 billion in carbon credits, which has the potential to significantly stimulate the carbon offset market.

Additionally, since the full carbonation of concrete is not always feasible, a 24-h carbonation experiment is commonly used as a representative evaluation. Based on the proportions of CO2 captured, and as presented in Section "Proportion of CO2 captured", the proportions of CO2 captured for CG-1 and CG-2 are 2.81% and 2.94%, respectively, within a 24-h period. If recycled aggregates, as discussed earlier, could be universally and efficiently carbonated, the resulting carbon credits generated within the initial 24 h would amount to $0.408 billion and $0.426 billion, respectively. Furthermore, DBA-D, DBA-B and DBA-A, with carbonation proportions of 6.91%, 5.44% and 4.03%, respectively, would yield $1.002 billion, $0.789 billion and $0.618 billion, respectively. These figures represent a significant increase compared to the conventional pressurized carbonation methods (CG-1 and CG-2).

Analysis of carbonation models

Current carbonation models

Most current carbonation models adopt Fick’s first law as the diffusion principle for concrete carbonation, which is shown in Eq. (7)35.

$$d{(}t{)} = K \cdot \sqrt t$$
(7)

where d(t) is the carbonation depth, K is the influence coefficient of carbonation and t is the time of the carbonation process.

Furthermore, a compilation of typical carbonation models based on this law are displayed in Supplementary Table S1. These models have been proven to be applicable in most engineering and accelerated carbonation tests. Specifically, the MEC model44 is applicable to accelerated carbonation at atmospheric pressure, while the Chinese code model59, fib code model60 and Possan et al. model61 are applicable to natural environments with a CO2 concentration below 0.03%. However, limited information is available for the models relating to pressurized carbonation testing. To propose a more comprehensible and widely accepted predictive model suitable for conventional pressurized carbonation tests, the conditions of CG-1 and CG-2 were substituted into the existing typical models from Eqs. (S1.1) to (S1.4) of Supplementary Table S1 (the specific values of the calculated parameters for each model are shown in Supplementary Table S2). The obtained performance results are presented in Fig. 10.

Fig. 10
figure 10

Performance results for each model.

Full size image

The models presented in this study exhibited significant variation in their results, which can be attributed to two key factors. Firstly, it is evident from Supplementary Table S1 that the definition of the carbonation coefficient K varied between the models and each definition was suitable for a different range, resulting in divergent trends in the growth of the carbonation depth. Secondly, most of these carbonation models were primarily proposed for predicting practical engineering scenarios and, as such, may be ineffective in predicting accelerated carbonation tests, particularly those influenced by pressure.

To investigate a more appropriate model for short-term pressurized carbonation experiments, a total of 19 sets of experimental data from other scholars on pressurized carbonation were collected and are presented in Table 3. CG-1, CG-2 and these experimental conditions were substituted into each model, and the results of the performance are shown in Fig. 11.

Table 3 Experimental data from literature.
Full size table
Fig. 11
figure 11

Comparison between results predicted by present models and test data: (a) performance of MEC model44; (b) performance of Chinese code model59; (c) performance of fib code model60; and (d) performance of Possan et al. model61.

Full size image

As shown in Fig. 11, the predicted results for all the models underestimate the carbonation depth of concrete, which may be attributable to a lack of familiarity with the influence of pressure and other possible factors, which will be discussed later.

Carbonation coefficient analysis

In order to further investigate the carbonation coefficients of pressure, the ratio of the experimental results to the predicted results was defined as Ra, and the relationships between Ra and experimental pressure for each model are shown in Fig. 12.

Fig. 12
figure 12

Relationship between pressure and Ra: (a) MEC model44; (b) Chinese code’s model59; (c)fib’s code model60; and (d) Possan et al.’s model61.

Full size image

The relationship between Ra and pressure can reflect the change trend of pressure coefficient to a certain extent. As depicted in Fig. 12 (a) and (c), both the MEC model and fib’s code model demonstrated an exponential growth tendency with an increase in pressure. This observation is agreement with the finding of Ye et al.’s research on the relationship between pressurized carbonation and carbonation depth36, which found that the carbonation depth increased exponentially with increasing pressure. However, the Chinese code’s model in Fig. 12 (b) and the Possan et al.’s model in Fig. 12 (d) do not exhibit a clear trend in the change of Ra with pressure. To evaluate the reasons causing the discrepancies, main factors regarding the carbonation coefficient K of each model are given in Table 4.

Table 4 The carbonation factors of each model.
Full size table

From Table 4, it can be inferred that the discrepancy of the MEC model in Fig. 12 (a) is due to the ignorance of compressive strength and pressure. Additionally, since the discrepancy was mainly caused by the experimental data from Lu et al.62, the reason need to be further explored and supported by more experimental data, which will not be discussed further here. For the fib’s code model in Fig. 12 (c) which exhibited the most distinct exponential relationship among these models. Its variation pattern is similar to that of the MEC model and its temperature was not considered except for compressive strength and pressure.

Furthermore, the deviation of the Chinese code’s model in Fig. 12 (b) is due to the ignorance of w/c and pressure. For Possan et al.’s model in Fig. 12 (d), the deviation pattern is similar with that of Chinese code’s model, which may be attributed to the ignorance of temperature, w/c and pressure. To clarify this, test data of concrete with large range of w/c is required; however, the w/c of concrete in present experiment and that collected from other tests is too close, which cannot provide sufficient range for further analysis on the influence of the w/c.

Based on the comprehensive error analysis of each model mentioned above, considering the feasibility of the experimental parameters, fib’s code model was chosen to carry out further research and adjustment.

Improved pressurized carbonation model

To facilitate further research, Eq. (S1.3) of fib’s code model60 in Supplementary Table S1 is presented as Eq. (8).

$$d{(}t{)} = \sqrt {{2} \cdot k_{{\text{e}}} \cdot k_{{\text{c}}} \cdot R_{{\text{NAC,0}}}^{{ - 1}} \cdot C_{{\text{S}}} } \cdot \sqrt t \cdot W{(}t{)}$$
(8)

where ke is the environment function, formulated as Eq. (9); kc is the execution transfer parameter for the curing time, formulated as Eq. (10); RNAC,0–1 is the inverse effective carbonation resistance of concrete, described in Eq. (11); Cs is the CO2 concentration (kg/m3), taken as 1.8 kg/m3 for pure CO2; and W(t) is the weather function, as shown in Eq. (12).

$$k_{{\text{e}}} = \left( {\frac{{{1} - \left( {RH_{{{\text{real}}}} /{100}} \right)^{{5}} }}{{{1} - \left( {RH_{{{\text{ref}}}} /{100}} \right)^{{5}} }}} \right)^{{{2}{\text{.5}}}}$$
(9)
$$k_{{\text{c}}} = \left( {t_{{\text{c}}} /{7}} \right)^{{b_{{\text{c}}} }}$$
(10)
$$R_{{\text{NAC,0}}}^{{ - 1}} = k_{{\text{t}}} \cdot R_{{\text{ACC,0}}}^{{ - 1}} + \varepsilon_{{\text{t}}}$$
(11)
$$W{(}t{)} = \left( {t_{{0}} /t} \right)^{{\frac{{\left( {p_{{{\text{SR}}}} \cdot ToW} \right)^{{b_{{\text{w}}} }} }}{{2}}}}$$
(12)

In Eqs. (9–11), RHreal and RHref are the relative testing humidity and reference condition (RHref = 65%), respectively; tc is the period of curing and the exponent of regression bc has a mean value of -0.567; kt is a regression parameter with a mean of 1.25 and εt is an error term with a mean value of 315.5. The inverse effective carbonation resistance RACC,0–1 is taken according to Table 560. It should be noted that the W(t) in Eq. (12) was taken to be 1 as the experiments were all performed in the laboratory.

Table 5 Reference values of RACC,0–160.
Full size table

Based on the above analysis, it can be inferred that the primary reason for the deviation of fib’s code model from the experimental results is its failure to consider the effects of temperature, compressive strength and pressure. Therefore, kT, kfc and kP are defined as the influence coefficients of temperature, compressive strength and pressure, respectively.

The compressive strength coefficient kfc is assumed to grow in power, according to the models in Supplementary Table S1, which is given by Eq. (13).

$$k_{{{\text{fc}}}} {(}f_{{\text{c}}} {)} = a_{{0}} + a_{{1}} \cdot f_{{\text{c}}}^{{{ - }a_{{2}} }}$$
(13)

where a2 is a constant within the range 1–1.7.

Temperature coefficient kT is considered to follow a power function according to the Chinese code model59, and is specifically given by Eq. (14).

$$k_{{\text{T}}} = T^{{{1}/{4}}}$$
(14)

According to Ye et al.36, pressure coefficient kP grows exponentially and its formulae is presented in Eq. (15).

$$k_{{\text{P}}} = {1}{\text{.571}} + {0}{\text{.388}} \cdot {\text{exp}}\left( { - \frac{{{15}{\text{.930}}}}{P}} \right)$$
(15)

Moreover, using the Taylor expansion, the specific forms of kT and kP are:

$$k_{{\text{P}}} {(}P{)} = a_{{3}} + a_{{4}} \cdot k_{{\text{P}}} = a_{{3}} + a_{{4}} \cdot {\text{exp}}\left( {a_{{5}} \cdot P} \right)$$
(16)
$$k_{{\text{T}}} {(}T{)} = a_{{6}} + a_{{7}} \cdot k_{{\text{T}}} = a_{{6}} + a_{{7}} \cdot T^{{a_{{8}} }}$$
(17)

where a0, a1, … , a8 are the constants to be determined from Eqs. (13), (16) and (17).

Furthermore, Eq. (8) can be described as follows:

$$d{(}t{)} = K{(}t{)} \cdot k_{{{\text{fc}}}} {(}f_{{\text{c}}} {)} \cdot k_{{\text{P}}} {(}P{)} \cdot k_{{\text{T}}} {(}T{)}$$
(18)

Here, K(t) is defined as the fib’s code model of Eq. (8).

Due to the excessive number of unknown coefficients, the coefficients were fitted based on the undetermined coefficients method and mathematical induction, with the detailed process illustrated in Fig. 13.

Fig. 13
figure 13

Process of fitting coefficients of model.

Full size image

Specifically, based on the method of coefficients to be determined (blue dashed box), kfc is firstly assumed to be known. Thus Eq. (18) has only two unknown functions: kP and kT. Then, based on the mathematical induction method (yellow dashed box), kP is assumed to be 1, and thereby the unknown parameters a6, a7 and a8 in the function kT can be obtained by data fitting. Subsequently, kT are substituted back into Eq. (18) and the coefficients kP can be updated. In order to obtain more reliable carbonation coefficients, the above determined kT and kP are continuously iterated into Eq. (18) until the unknown constants are stabilized. It should be noted that, if the constants become discrete or if the goodness-of-fit R2 diminishes significantly during the iterations, the assumptions of kfc may be invalid and should be recalibrated. Eventually, following several assumptions and iterations, coefficients kfc, kP and kT are given in Eqs. (19) to (21).

$$k_{{{\text{fc}}}} {(}f_{{\text{c}}} {)} = a_{{0}} + a_{{1}} \cdot f_{{\text{c}}}^{{{ - }a_{{2}} }} = {58} \cdot f_{{\text{c}}}^{{ - 1}}$$
(19)
$$k_{{\text{P}}} {(}P{)} = a_{{3}} + a_{{4}} \cdot {\text{exp}}\left( {a_{{5}} \cdot P} \right) = {0}{\text{.685}} - {0}{\text{.214}} \cdot {\text{exp}}\left( {\frac{P}{{{1}{\text{.609}}}}} \right)$$
(20)
$$k_{{\text{T}}} {(}T{)} = a_{{6}} + a_{{7}} \cdot T^{{a_{{8}} }} = - {32}{\text{.434}} + {15}{\text{.489}} \cdot T^{{{0}{\text{.25}}}}$$
(21)

Ultimately, a prediction model applicable to pressurized carbonation tests over a short period of time is given in Eq. (22).

$$d{(}t{)} = \sqrt {{2} \cdot k_{{\text{e}}} \cdot k_{{\text{c}}} \cdot R_{{\text{NAC,0}}}^{{ - 1}} \cdot C_{{\text{S}}} } \cdot k_{{{\text{fc}}}} {(}f_{{\text{c}}} {)} \cdot k_{{\text{P}}} {(}P{)} \cdot k_{{\text{T}}} {(}T{)} \cdot \sqrt t$$
(22)

where, ke, kc, RNAC,0–1 and CS are the same parameters as those in the fib code model.

Substituting the test data of the CG-1, the CG-2 and the Table 3 into the proposed model, the relationship between the test results and the proposed model is shown in Fig. 14.

Fig. 14
figure 14

Comparison of predicted results and test data.

Full size image

As can be seen from Fig. 14, the predictions of the proposed model are satisfactory. Nonetheless, as a preliminary trial, the proposed model retains certain shortcomings. Specifically, the coefficient RACC,0–1 in the fib’s code model was not given a complete reference value for the type of cement (Table 5), which was taken as 13.4 for this experiment. Compared to existing mechanistic models, the proposed pressurized carbonation model considers more factors, including compressive strength, temperature and pressure. However, it neglects to study the physical and chemical coupling principles among each parameter, leading to relatively lower accuracy. Further exploration in this area is essential to better understand the intricate relationships between these parameters. Nonetheless, the proposed pressurized carbonation model incorporates more variables and offers greater convenience in predicting the carbonation depth of concrete during pressurized carbonation tests.

Conclusions

New accelerated carbonation methods – namely, the Deep Breathing Analogy (DBA) method – are herein proposed and verified by experiments. The following conclusions can be drawn:

  1. (1)

    Novel DBA methods incorporating the mechanics of human lung expiration and inhalation are proposed. These methods have been validated as offering excellent efficiency in terms of the trend of weight gain during the carbonation process, proportion of CO2 captured and carbonation depth. Compared with the conventional pressurized carbonation method, with an inspiratory pressure of 0.5 bars, DBA-D, DBA-B and DBA-A improve the proportion of CO2 captured by 135.03%, 93.59% and 43.42%, respectively.

  2. (2)

    The results of the DBA-A, DBA-B and DBA-D methods show that, during 24 h carbonation, appropriate extension of expiratory time and increased pressure for subsequent cycles significantly affect the proportion of CO2 captured. It has been found that conducting six cycles is adequate to yield substantial results, with a recommended inspiratory time of initial cycle of four hours.

  3. (3)

    When considering the adjustment of pressure, 0.1 bars for each increment is recommended for both expiratory and inspiratory pressures, and the upper limit of the expiratory pressure should not exceed 0.9 bars for safety and practicability. To obtain high efficiency carbonation, the inspiratory time and expiratory time can be reduced and extended in 0.5 h increments, respectively; however, the inspiratory time should not be less than 2.5 h while the expiratory time should not exceed 2 h.

  4. (4)

    An evaluation of the economic benefits of carbonation shows that the full carbonation of annual construction waste could yield a carbon credit gain of $14.504 billion. Additionally, the DBA-D, DBA-B and DBA-A methods could potentially generate carbon credit benefits of $1.002 billion, $0.789 billion and $0.618 billion, respectively, for 24 h carbonation.

  5. (5)

    A new prediction model, suitable for pressurized carbonation testing was proposed. The model incorporated the carbonation coefficient K for each model and considered the effects of temperature, compressive strength and pressure on carbonation. The predictions of the proposed model showed satisfactory agreement with the test data (R2 = 0.859), indicating that the proposed model has good ability in predicting the pressurized carbonation of concrete.

In summary, the proposed DBA method allows RCA to capture more greenhouse gases in a shorter time compared to current techniques. However, as an initial exploration, the DBA method requires a reaction chamber with better gas tightness than current equipment, posing challenges for scaling up and industrial application. Additionally, it is worthwhile to further address that during exhalation, the water in the silica gel inside the reaction chamber can diffuse due to negative pressure, affecting the consistency of the RH level to some extent. Moreover, the analysis of the proposed pressurized carbonation model is based on a small dataset due to the limited availability of relevant databases. Therefore, further research on pressurized carbonation of concrete is necessary, along with a more precise analysis of the model to enhance its goodness of fit.