Introduction

The physics and technology of read heads for hard disk drives (HDD) has been extensively researched and investigated in both theoretical1,2,3, and experimental4,5,6 aspects. Predoninantly the aim is to optimize their performance and suitability for application in HDD with data storage densities exceeding 2 \(\mathrm {Tb/in^2}\). To enhance data storage capacity, it is necessary to decrease the size of data bits. Consequently, a reduction in the physical dimensions of data read and write heads is essential to align them with the smaller data bit dimensions. Scaling down the size of read heads causes an increase in the magnetic fluctuations within the read head structure. As a consequence, the performance of data read heads is negatively affected, resulting in decreased signal-to-noise ratio (SNR) and magnetoresistive (MR) ratio.

The performance of data read heads is determined by several factors, including electrical current density7,8,9the size of the read head10,11and thermal effects12,13,14,15. Among these factors, the thermal effect is becoming increasingly a critical consideration in the design and optimization of read heads. It can directly impact the readback signal, the resistance-area product and MR ratio, which ultimately affect the overall performance of the data reading process. The effect of temperature can arise in several ways, for instance, the annealing temperature during the deposition process16, external temperature and reader heater17. The operating temperature and the heat generated by the reader heater have a direct influence on the spin transport behavior and magnetization alignment within the spin valve stack18,19. Understanding temperature control is essential to maintain high-performance data reading and ensure stability and accuracy under different temperature conditions, enhancing the overall functionality and lifespan of the storage device.

Several experiments have been carried out to study the performance of readers in the presence of thermal fluctuations20,21. However, theoretical study is still required to understand the mechanisms behind the operation of spin transfer torque (STT) based devices, especially for the next-generation readers with promising materials such as Co-based Heusler alloys. The spin transport behavior within the magnetic structure can be described by the spin accumulation model which is based on the drift-diffusion equation22,23,24,25. As is well known, the thermal fluctuations not only influence the spin transport behavior but also affect the magnetization orientation. However, the spin accumulation model, commonly used for studying spin transport in magnetic systems, generally disregards the temperature effect22,26,27,28,29,30.

In the present work, we aim to gain a deeper understanding of the temperature-dependent spin transport in Heusler alloy current-perpendicular-to-plane giant magnetoresistance (CPP-GMR) structures. We will focus on investigating the stability of magnetization within the spin valve structure and analyzing the behavior of MR and MR ratio at different temperatures. The effect of thermal fluctuation on both magnetization and transport behavior are taken into consideration.It has been shown31that there can exist significant differences from the bulk in fluctuations at surfaces and interfaces. We introduce this by modelling diffusive interfaces between the magnetic and non-magnetic layers. This gives rise to the possibility of enhanced magnetization fluctuations due to the reduction in exchange coupling strength due to a loss of neighboring spins in the interface. To reach our goals, the combination of atomistic model and spin accumulation model implemented in the open-source VAMPIRE software package32is employed. The former is used to construct the spin valve structure including the diffusive interfaces and investigate the dynamic of magnetization in the presence of STT and nonzero temperature. The latter focuses on understanding the effect of STT acting on the magnetization. In this simulation-based study, we first examine the temperature dependence of spin-transport parameters using the two-channel model of spin-dependent resistivity, which provides crucial input for the spin accumulation model33,34. Following this, we investigate the dynamics of magnetization including the effect of STT at finite temperatures. Moreover, we evaluate the MR and MR ratio to demonstrate the performance of read sensor for different temperatures and thicknesses.

Results and discussion

Temperature effect on magnetic and transport properties

The role of thermal fluctuations is vital in shaping the temperature variation of the properties of ferromagnetic materials as well as their spin transport characteristics. There are several reports indicating the potential of Heusler alloys for example \(\text {Co}_2\text {Fe}\text {Si}\)(CFS)35,36,37,38,39,40, \(\text {Co}_2\text {FeAl}\)(CFA)35,36,41,42,43,44,45 and \(\text {Co}_2\text {FeAl}_{0.5}\text {Si}_{0.5}\)(CFAS)35,36,46,47,48,49,50 for various spintronic applications. These alloys are considered as promising candidates due to their notable attributes such as high spin polarization, high saturation magnetization, and high Curie temperature. In this work, CFAS, known for its potential, is chosen to serve as the pinned and free layers in the read sensor. By utilizing an atomistic model, we initially examine the effects of temperature on the magnetization of the CFAS layer with dimensions of \(20 \times 20 \times 10 \ \mathrm {nm^3}\). The values of magnetic parameters of CFAS used in this study are shown in table 1. To validate these parameters and the accuracy of the atomistic model, we conduct a direct comparison of the simulated M(T) curve with experimental data from Ref51.. Fig. 1 shows that the simulated results are in good agreement with the experimental study and the simulated Curie temperature of around 1190 K closely approximates the experimental measurement of 1170 K.

Table 1 Magnetic parameters of CFAS material.
Full size table
Fig. 1
figure 1

Comparison of temperature-dependent magnetization of CFAS material between simulation and experiment: The experimental data is extracted from Ref51. and the solid line represents a fitting function: \(M(T)/M(0)=[1-(T/Tc)]^{0.38}\).

Full size image
Fig. 2
figure 2

Temperature dependence of spin transport parameters in CFAS material: (a) spin polarization of conductivity (\(\beta\)), spin polarization of diffusion constant (\(\beta ^\prime\)) and (b) spin diffusion length (\(\lambda _\textrm{sdl}\)): The temperature dependence of \(\beta (T)\) can be explained by the fitting function: \(\beta (T) = \beta (0)- \left( \frac{M(T)}{M(0)}\right) ^{\eta }\) where \(\eta = 2.03\) for CFAS.

Full size image

Next, we investigate the influence of temperature on the magnetization dynamics and spin transport behavior of the trilayer structure CFAS(5nm)/Cu(5nm)/CFAS(5nm) with a diffused interface of 1 nm width in the temperature range from 0 to 400 K. The interface thickness of 1 nm was chosen to make the model more realistic, as the typical interface thickness in the real system is about 1-2 nm56,57,58,59, depending on the materials and the film deposition conditions. Additionally, in this case, we assume that at the interface, different ions diffuse into another material by a few monolayers. This investigation aims to compare the obtained results of resistance-area product (RA) and MR ratio with the previous experimental studies52,54,60,61,62,63, particularly focusing on temperature conditions of 14 K and 400 K. It is worth noting that the definitions and details of the spin transport parameters used in this investigation can be found in the section on the computational model. The low-temperature resistivity for up and down-spin channels are extracted from the temperature-dependent spin polarization parameter of conductivity (\(\beta\)) in experimental data in Ref60., where \(\rho _{0 \uparrow }= 10.7\)\({\mu \Omega \cdot \hbox {m}}\), \(\rho _{0 \downarrow }= 76.2\)\({\mu \Omega \cdot \hbox {m}}\) and the empirical constant \(A= 1.5\times 10^{-11}\)\({\Omega }\hbox {m}/\hbox {K}^{2}\). These parameters are validated by calculating the temperature dependence of parameter \(\beta\) and making a comparison with experimental. It can be seen that the computed results in Fig. 2are very consistent with experimental observation in Ref60.. Following that, the temperature-dependent behavior of the spin-polarization parameter for the diffusion constant can be determined by using Eq. (10), with the density of state of up spin and down spin of \(N_\uparrow (E_F)=0.755\) states/eV and \(N_\downarrow (E_F)=0.399\)states/eV, respectively53. As a result, the spin polarization parameter is \(\beta ^{\prime \prime }=0.33\). As illustrated in Fig. 2 (a), the decrease in spin-dependent conductivities, which is a consequence of the influence of temperature, leads to a reduction in spin-polarization parameters \(\beta\) and \(\beta '\), indicating decreasing efficiency of spin transport within the magnetic structure.

The next point of interest involves investigating the temperature dependence of the spin-diffusion length and diffusion constant in CFAS by using Eqs. (11) and (12). The calculated spin diffusion length as a function of temperature shows a good agreement with the measured data in Ref60. Increasing temperature results in a decrease in the spin diffusion length as depicted in Fig. 2 (b). This confirms the advantage of using Heusler alloys with high saturation magnetization and a high Curie temperature, as they maintain a high \(\beta\) at an operating temperature of 400 K, ensuring efficient spin transport in spintronic devices. The high Curie temperature not only stabilizes the magnetic properties but also allows for a gradual change in \(\beta\) with temperature, reducing thermal fluctuations and enhancing device performance. This behavior, described by spin accumulation and spin current, is discussed in detail in the next section. Additionally, this study demonstrates the important role of temperature on the spin transport properties, emphasizing the need to take into account thermal effects on both magnetization dynamics and spin transport behavior.

Temperature dependence of spin transport behavior

The atomistic model coupled with spin accumulation model is employed to investigate the effect of temperature on the magnetization dynamics of the CFAS(5nm)/Cu(5nm)/CFAS(5nm) system. For simplicity, the magnetization of the pinned layer is assumed to be fixed along the direction of the easy axis by applying an external magnetic field. It is worth noting that, in this work, for simplicity we do not take into consideration the exchange bias effect which usually pins the pinned layer. A charge current with density of 5 MA/cm2 is injected into the system with a diffused interface. Initially, we observe fluctuations in the magnetization of both the pinned and free layers, indicating they could act as a noise source in the read head.

Fig. 3
figure 3

(a) The angle of magnetization in the pinned layer (PL) and free layer (FL) deviated from the easy axis at any finite temperature and (b) the spectrum analysis of the magnetization dynamic of PL and FL at 400 K.

Full size image
Fig. 4
figure 4

The visualization of magnetization (\(M/M_s\)) and spin accumulation (\(m/m_\infty\)) in the pinned layer (PL), spacer layer (SP) and free layer (FL) of CFAS(5nm)/Cu(5nm)/CFAS(5nm) system at 0 K and 400 K.

Full size image

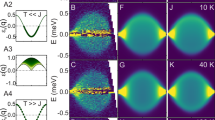
From the calculated results, it is seen that temperature directly influences the fluctuations in the magnetization of the pinned and free layers within the read head. At a non-zero temperature the random thermal field introduces magnetization fluctuations. The fluctuations in the pinned layer are significantly smaller due to the strong pinning field. Nonetheless, as shown in Fig. 3 there is a significant angular dispersion in the pinned layer, which is a contributory factor to the magnetic noise of the reader. To illustrate the deviation of magnetization from the easy axis, the relative angle between the magnetization and easy axis is calculated from the time evolution of magnetization at any finite temperature. The average angle is determined as the system approaches equilibrium, typically within the range of 2-5 ns. As expected the magnetization deviation within the pinned and free layers increases with temperature. The angle within the pinned layer is lower than that within the free layer as shown in Fig. 3 (a). We also determine the power spectrum of the magnetization in the pinned and free layers using the Fast Fourier Transform (FFT) of the x-component of magnetization. The magnetic noise power in the pinned layer is found to be much lower than that in the free layer as demonstrated in Fig. 3 (b). The noise peaks at relatively low frequencies, consistent with an estimated 5GHz Kittel resonance frequency based on the in-plane shape anisotropy of the film.

Fig. 5
figure 5

The spin accumulation and spin current at any position of the CFAS(5nm)/Cu(5nm)/CFAS(5nm) system with parallel state configuration at different temperatures.

Full size image

We now proceed to the investigation of the effect of the magnetization fluctuations on the spin transport by calculating the spin accumulation and spin current. As observed in Figs. 4 and 5, the spin accumulation tends to align in the direction of magnetization due to the s-d exchange interaction. Figs. 4 and 5 demonstrate a complex temperature dependence of the spin accumulation and spin current arising from the combined effects of the temperature-induced magnetization fluctuations and the temperature dependence of the transport properties. Consider first the simplest case of zero temperature, with all spins in the free and pinned layers aligned with the y-axis. Here the charge current induces a spin accumulation along the y-axis which decreases rapidly on entering the Cu layer. The accumulation decreases only slowly because of the very large spin diffusion length of Cu which is 600 nm before increasing in the free layer.

To validate the numerical results presented in Fig. 5, we examine the analytical solution of the y component of spin accumulation and spin current in the pinned layer (x < 5 nm) and then compare these with the numerical results in Fig. 5(b), as depicted in Fig. 6. The zero Kelvin spin current admits of a simple analytical expression since the magnetization and spin accumulation are collinear along the y-axis. The interface condition at the pinned layer is of continuous spin current, thus the spin current immediately at the interface is zero, and applying this condition to Eq. (7), we obtain at the interface

$$\begin{aligned} \frac{d\textbf{m}_{y}(0)}{dz} = \frac{\beta j_e}{2D_0(1-\beta \beta ')}. \end{aligned}$$
(1)

Equating Eq. (1) with the derivative calculated from Eq. (6) then leads to

$$\begin{aligned} \textbf{m}_{y}(z) = \textbf{m}(\infty ) - \frac{\beta j_e \lambda _{sdl}}{2D_0(1-\beta \beta ')} e^{-z/\lambda _{sdl}}. \end{aligned}$$
(2)
Fig. 6
figure 6

(a) y-polarization of the spin accumulation and (b) spin current in the pinned layer at zero K compared with the analytical expressions in Eqs. (2) and (3) .

Full size image

Back substitution into Eq. (7) gives the following expression for the spin current:

$$\begin{aligned} j_{my} =\beta j_e (1-e^{-z/\lambda _{sdl}}). \end{aligned}$$
(3)

A comparison of the analytical results with the compute simulations is shown in Fig. 6. The agreement is very good, in itself a verification of the numerical calculations. We also note the effect of the interface mixing as shown in Fig. 6. It can be seen that there is a continuous variation of the spin accumulation across the interface. As shown in Ref22. this arises from the continuous variation of magnetic and transport properties across the interface and thereby has a bearing on the interface resistance and the RA product to be investigated shortly.

First, however, we consider the effects of temperature, which arise from the combined effects of thermally induced spin fluctuations and the variation of spin transport parameters illustrated in Fig. 2. The effect of the decreasing spin diffusion length at elevated temperature can be seen in the increased change in \(m_y\) across the interface between the pinned CFAS layer and the Cu spacer. The reduced spin polarization of conductivity results in a reduction in spin current with increasing temperature as seen most clearly in \(j_{my}\) (Fig. 5(e)). The accumulation and spin current are also strongly affected by spin fluctuations as seen prominently in the pinned and free magnetic layers, with the former less effected than the latter due to the pinning field applied to this layer. Magnetization fluctuations lead to increasing x- and z- components of accumulation and spin current which have a large effect in the form of a reduction in spin current in the free layer. We note that magnetization fluctuations in the pinned layer drive fluctuations in the free layer, which contribute to the magnetic noise. In the following we show that these factors contribute to fluctuations in the effective RA product of the read sensor.

The calculated spin accumulation and spin current are used to determine the spatial resistance-area (\(\mathrm {RA_i}\)) product at each given time. The total RA is calculated by summing the spatial RA as follows,

$$\begin{aligned} \textrm{RA}_\textrm{total}=\sum _{i=1}^{n}\textrm{RA}_i=\frac{\mathrm {V_{cell}k_BT}}{e^2}\sum _{i=1}^{n}\frac{|\Delta m|}{|jm|} \ \end{aligned}$$
(4)

where \(\Delta m\) is the gradient of spin accumulation, n is the number of microcells, \(\mathrm {V_{cell}}\) is the microcell volume, e is the electron charge. The temperature dependence of RA product and magnetoresistance (MR) ratio of the spin valve stack of CFAS(5nm)/Cu(5nm)/CFAS(5nm) is next investigated. Two configurations are considered: the parallel and anti-parallel states. A charge current with a density of 5 MA/cm2 is introduced into the system. The spatial variation of spin current and spin accumulation are calculated directly from the gradient of spin accumulation (\(\Delta m\)) and spin current as above. At 0 K, the results in Fig. 5 reveal that the gradient of spin accumulation within material far from the interface is close to zero because of the uniform magnetization and spin transport properties, whereas the gradient reaches its peak at the interface between layers because of the different transport properties. At a nonzero temperature, the thermal effect leads to the variation in magnetization and changes in the spin accumulation within the bulk. Clearly an increase in temperature within the ferromagnetic layer leads to more fluctuation in \(\Delta m\) affecting the value of resistance-area product (RA). These fluctuations are larger in the free layer due to the field applied to the pinned layer. However, it should be noted that fluctuations in the pinned layer are transmitted to the free layer, increasing the fluctuations of \(\textbf{m}\). Subsequently, the RA of parallel and anti-parallel states at any given time are calculated. This allows us to determine the average RA and MR ratio at any finite temperature as demonstrated in Fig. 7

Fig. 7
figure 7

(a) The resistance-area product (RA) and (b) MR ratio of CFAS(5nm)/Cu(5nm)/CFAS(5nm) system at any given temperature.

Full size image

From the results, the RA value is higher in the anti-parallel configuration (AP state) compared to the parallel configuration (P state). The value of RA of both states strongly depend on temperature. With increasing temperature, there are fluctuations in the magnetization within the ferromagnetic layer, accompanied by a decrease in the spin transport parameters. This leads to a reduction in the capability to orient the direction of the spin-polarized current. Therefore, the MR ratio of the read head structure decreases with increasing temperature. This observation is consistent with recent studies in Refs64. and65, where it is explained that the significant decrease in MR ratio with increasing temperature is attributed to spin-flip scattering induced by the s-d exchange interaction. Our simulated results exhibit a trend similar to previous experimental studies on the temperature dependence of the MR ratio in similar structures such as \(\mathrm {Co_2MnSi/Cu/Co_2MnSi}\)66,67, CoCrFeAl/Cu/CoFe68, NiMnSb/Cu/NiMnSb69, NiMnSb/Ag/NiMnSb70,71, CFAS/Ag/CFAS52,54,61,63,66, and CoFeGeGa/Ag/CoFeGeGa72. This study indicates a significant role of temperature in influencing the functionality of read head in hard disk drive. Therefore, choosing appropriate ferromagnetic materials with high thermal stability and spin transport parameters becomes another option for enhancing the efficiency of read head operations.

Effect of temperature and thickness on the MR ratio

At present, there is a requirement to increase the areal density in hard disk drives which can be achieved by decreasing the size of data bits in magnetic recording media. This leads towards minimizing the size of the read sensor to align with the data bit size. In the data reading process, the thickness of sensing layer or free layer is a critical factor that influences the performance of the data read head. To accurately read signals without any interference from neighboring bits, the thickness of the free layer should be close to the size of the data bits.

In this section, we finally investigate the effects of temperature and thickness of the free layer on the values of RA and the MR ratio of the CFAS(5nm)/Cu(5nm)/CFAS(\(\textrm{t}_\textrm{FL}\)) structure where the thickness of second CFAS is varied from 2 nm to 10 nm. To make a comparison with previous experiment in Ref4., the thickness dependence of \(\Delta RA\) and MR ratio at low (14 K) and high temperature (400 K) are investigated. Fig. 8 shows the time dependence of the RA product at 14K and 400K for various free layer thicknesses as indicated. The RA value is seen to increase both with temperature and thickness of the free layer. Spin scattering in the magnetic layer can be enhanced by increasing thickness, particularly at high temperatures where the spin scattering is enhanced. It can be seen that RA is subject to fluctuations which reflect the magnetic noise of the sensor.

Fig. 8
figure 8

Time variation of RA in CFAS(5nm)/Cu(5nm)/CFAS(\(\textrm{t}_\textrm{FL}\)) system with various thicknesses at 14 K and 400 K for the parallel state.

Full size image
Fig. 9
figure 9

Thickness dependence of \(\Delta RA\) and MR ratio of CFAS(5nm)/Cu(5nm)/CFAS(\(\textrm{t}_\textrm{FL}\)) system with various thicknesses at 14 K and 400 K.

Full size image

We next calculate \(\Delta RA\) at and MR ratio at both temperatures as demonstrated in Fig. 9. Both decrease with increasing temperature for a combination of two principal reasons. Firstly as the spin transport parameters: \(\beta\), \(\beta '\), \(\lambda _\textrm{sdl}\), decrease with increasing temperature, this results in the reduction of spin transport ability, particularly through the parameter \(\beta\) as the spin-up and down-conductivities converge. Secondly, thermal fluctuation causes the deviation of magnetization from the easy axis direction. This means that the magnetization cannot be completely aligned in the P and AP state which eventually gives rise to lower \(\Delta RA\) and MR ratio at high temperature. Interestingly, as demonstrated in Fig. 9, the value of \(\Delta RA\) and MR ratio are thickness dependent. They increase with increasing film thickness and become fairly unchanged at the thickness greater than the spin diffusion length of CFAS (\(\mathrm {t_{FL}>\lambda _{sdl}}\)) which is about 3 nm and 2 nm at 14 K and 400 K respectively. This result suggests that once the film thickness exceeds the spin diffusion length, further increases in thickness do not significantly affect the \(\Delta RA\)and MR ratio, indicating that the spin diffusion length effectively determines the optimal thickness of sensing layer for maximizing the MR effect. Our findings align closely with prior experimental studies4,73,74, confirming the consistency and reliability of our approach which can be used for the future spintronic designs. We note that the spatial variation of the spin accumulation and the magnetization fluctuations are on too small a lengthscale to be resolved by micromationc models and require the application of atomistic models. From our study, it is suggested that choosing promising ferromagnetic material with advantageous magnetic and spin transport properties, especially a low spin diffusion length, has the potential not only to reduce the thickness of read sensor but also to enhance its performance.

Conclusion

We have investigated the effect of temperature on the performance of read sensor by using an atomistic model coupled with a spin transport model. The magnetization and spin accumulation are calculated self-consistently. The magnetization dynamics of magnetic layer are described by using the LLG equation including the spin torque via the s-d exchange interaction and the spin accumulation. The model is used to interpret the physical mechanism behind MR phenomena. To investigate the thermal influence on the performance of CPP-GMR Heusler alloy, the temperature dependence of spin transport and magnetic properties are needed. Therefore, we introduce the magnetic properties of CFAS as a function of temperature into the atomistic model using temperature dependent spin transport parameters obtained by comparison with experiment. Firstly we investigate the temperature dependence of the spatial variation of spin accumulation and spin current through the reader stack. We find that the detailed atomistic model reveals a complex behavior resulting from the combinations of temperature dependent transport properties and the magnetization fluctuations. The diffusive interfaces introduced into the model also affect the spin transport and lead to continuous spin accumulation through the interface: this also affects the magnetoresistance and MR ratio. The calculations show important details inaccessible to micromagnetic calculations with nanometer discretization.

Subsequently, the model containing the temperature dependent magnetic and spin transport properties is used to calculate the MR ratio of CFAS(5nm)/Cu(5nm)/CFAS(5nm) as a function of temperature. Our findings demonstrate that the value of \(\Delta R\) and MR ratio are temperature dependent and they are inversely proportional to the thickness of the ferromagnetic film. Notably, these values increase asymptotically to a constant value when the film thickness is greater than the spin diffusion length of the material. Consequently, our study suggests that selecting ferromagnetic materials with high thermal stability and high efficient spin transport can enhance the operational efficiency of the read sensor. In addition, the spin diffusion length should be considered as an important factor for the reader design. The suitable ferromagnetic materials with a low spin diffusion length have the potential to decrease the thickness of the film utilized as sensing layer for detecting the magnetization direction within the data bit, yielding high \(\Delta R\) and MR ratio. This study provides valuable insights for the future design of high performance readers, fostering advancements in the field of spintronics, and suggest that detailed atomistic models have an important role in providing basic understanding of the basic physics of reader materials and device design.

Computational model

The data reading process in a hard disk drive involves injecting an electrical current through a spin valve structure to detect the direction of magnetization within data bits by measuring changes in electrical resistance. This injection of spin current through the magnetic structure gives rise to an s-d exchange interaction between the conduction electrons and the local magnetization which can be explained by using the self-consistent solutions of the magnetization and spin accumulation75. The atomistic model combined with the spin accumulation model is used here to describe the magnetization dynamics and spin transport behavior in the magnetic structure. Additionally, to account for the effect of temperature, the spin transport parameters needed for the spin accumulation model can be calculated using the two-channel model of resistivity, with further details provided below.

Spin accumulation and atomistic models

The spin transport behavior in the magnetic system can be described by physical quantities, specifically through spin accumulation and spin current. Here we use a definition of the spin accumulation as the local difference between the spin up- and down densities: \(\textbf{ m} = n^\uparrow - n^\downarrow\). This means that in the bulk of that materials the accumulation has the value \(\textbf{ m}(\infty )\), which can be determined from density functional theory (DFT) calculations as introduced into the spin accumulation formalism as follows. Following the notation given by Chureemart et. al22.,

$$\begin{aligned} m_\infty = \frac{[DOS_\uparrow (E_F) - DOS_\downarrow (E_F)]k_BTe}{V} . \end{aligned}$$
(5)

In a system with an arbitrary direction of magnetization, the general solution for spin accumulation can be represented in the basis coordinate system \({\hat{\textbf{b}}_1},{\hat{\textbf{b}}_2}\) and \({\hat{\textbf{b}}_3}\), which are parallel and perpendicular to the local magnetization. The longitudinal component of spin accumulation aligns with the direction of \({\hat{\textbf{b}}_1}\) , while the two transverse components are along the directions of \({\hat{\textbf{b}}_2}\) and \({\hat{\textbf{b}}_3}\)respectively, and are formulated as follows23,24,25,76:

$$\begin{aligned} {\textbf{m}}_{\Vert }(z)= & [{\textbf{m}}_{\Vert }(\infty )+[{\textbf{m}}_{\Vert }(0)-{\textbf{m}}_{\Vert }(\infty )]e^{-z/\lambda _{sdl}}]{\hat{\textbf{b}}_1}, \nonumber \\ {\textbf{m}}_{\perp ,2}(z)= & 2e^{-k_1z}[{u\cos (k_2z)-v\sin (k_2z)}]{\hat{\textbf{b}}_2}, \nonumber \\ {\textbf{m}}_{\perp ,3}(z)= & 2e^{-k_1z}[{u\sin (k_2z)+v\cos (k_2z)}]{\hat{\textbf{b}}_3}, \end{aligned}$$
(6)

with \({{k_1} \pm i{k_2}} = \sqrt{\lambda _{sf}^{-2} \pm i\lambda _{J}^{-2}}\) and \(\lambda _{sdl} = \sqrt{1-\beta \beta '}\lambda _{sf}\) is the spin diffusion length. The coefficients \({\textbf{m}}_{\Vert }(0)\), u and v can be calculated from the boundary condition by imposing continuity of the spin current at the interface. The spin current \((\textbf{j}_m)\) can be written in terms of the charge current density \((j_e)\) and the spin accumulation as follows,

$$\begin{aligned} {\textbf{j}_m} = \beta {j_e}{\textbf{S}} - 2{D_0}\left[ {\frac{{\partial \textbf{m}}}{{\partial z}} - \beta \beta '{{\textbf{S}}}\left( {{{\textbf{S}}} \cdot \frac{{\partial \textbf{m}}}{{\partial z}}} \right) } \right] , \end{aligned}$$
(7)

where \(\beta\) is the spin polarization for the conductivity, \(\beta '\) is the spin polarization for the diffusion constant, \(D_0\) is the diffusion constant.

The spin accumulation and spin current shown in the above equations are correlated with the direction of magnetization. Hence, it is essential to investigate the dynamics of magnetization which can be achieved by employing the atomistic model through the Landau-Lifshitz-Gilbert (LLG) equation. This provides insights into the time evolution of magnetization under the influence of STT given by32,

$$\begin{aligned} \frac{\partial \textbf{S}}{\partial t}= & -\frac{\gamma }{(1+\alpha ^2)} \left( \textbf{S}\times \textbf{B}_\textrm{eff}\right) -\frac{\gamma \alpha }{(1+\alpha ^2)} [\textbf{S}\times (\textbf{S}\times \textbf{B}_\textrm{eff})] \nonumber \\ \end{aligned}$$
(8)

where \(\textbf{S}\) is the unit vector of atomic spin, \(\gamma\) is the absolute value of gyromagnetic ratio and \(\alpha\) is the damping constant. The effective field acting on each atomic spin, \(\textbf{B}_\textrm{eff}\), can be determined from the Heisenberg spin Hamiltonian \(\mathcal {H}\) describing the energy in the system:

$$\begin{aligned} \mathcal {H}=- \sum \limits _{i < j}{{J_{ij}}{{\mathbf{{S}}}_i}\cdot {{\mathbf{{S}}}_j}}-{k_{\textrm{u}}} \sum \limits _{i}({{\mathbf{{S}}_i}}\cdot {\mathbf{{e}}})^2- \sum \limits _{i}{\mu _{\textrm{s}}^i\textbf{S}}_i \cdot {\mathbf{{B}}_{\textrm{app}}}-J_{\textrm{sd}} \textbf{m} \cdot \textbf{S}_i \, . \end{aligned}$$
(9)

where \(\textbf{S}_{i,j}\) is the unit vector of spin on site (i, j), \(J_{ij}\) is the nearest neighbor exchange integral between spin sites i and j, \(k_{\textrm{u}}\) is the uniaxial anisotropy constant, \(\textbf{e}\) is the easy axis unit vector and \(\mu _{\textrm{s}}^i\) is the magnitude of the spin moment on site i.

The spin Hamiltonian consists of four terms describing different energy contributions in a magnetic system. The first and second terms correspond to the exchange energy and the anisotropy energy respectively. The third term accounts for the Zeeman energy arising from an external magnetic field and the fourth term describes the STT effect via the \(s-d\) exchange interaction. In addition, the demagnetizing field is included into the effective field using a macro-cell approach discretizing the system into many cubic cells and assuming the uniform magnetization within each cell. The dipolar field for a macro-cell k is given by:

$$\begin{aligned} {\textbf{B}_{\textrm{dip,}k}} = \frac{{{\mu _0}}}{{4\pi }}\sum \limits _{l \ne k} {\left[ {\frac{{3({{{\varvec{\mu }}}_l} \cdot \hat{\textbf{r}}_{kl})\hat{\textbf{r}}_{kl} - {{{\varvec{\mu }}}_l}}}{{|r_{kl}{|^3}}}} \right] } \, , \end{aligned}$$
(10)

where \({{\varvec{\mu }}_l} = \sum \limits _{i =1}^{{n_{\textrm{atom}}}} \mu _\textrm{s}^i\textbf{S}_i \,.\) is the magnetic moment of the macro-cell l containing \(n_\textrm{atom}\) spins. \(\mu _0\) is the permeability of free space, \(r_{kl}\) and \(\hat{\textbf{r}}_{kl}\) are the distance between macro-cell k and l and the corresponding unit vector, respectively. With this approach, it is important to note that all spins within a macro-cell experience an identical dipole field.

The temperature effect is taken into account in a effective field by introducing the random field term, denoted as \({\mathbf{{B}}^i_\textrm{th}}\). The statistical properties of the random field are determined by employing the fluctuation-dissipation theorem (FDT) and Fokker-Planck equation, and can be expressed as follows:

$$\begin{aligned} \left\langle {\mathbf{{B}}^i_\textrm{th}(t)} \right\rangle= & 0 \nonumber \\ \left\langle {\mathbf{{B}}^{i}_\textrm{th}(t) \mathbf{{B}}^{j}_\textrm{th}(t')} \right\rangle= & \frac{2\alpha {k_B}T}{{\mu _s}|\gamma |} {\delta _{ij}}\delta (t - t') \,. \end{aligned}$$
(11)

where i, j are the Cartesian components of \(\textbf{B}_\textrm{th}\), \(t,t'\) are the time at which the fluctuations are evaluated, \(\alpha\) is the Gilbert damping constant, T is the temperature, \(k_B\) is the Boltzmann constant and \({\delta _{ij}}\) is the Kronecker delta, and \(\delta (t - t')\) is the Dirac delta function. This leads to a thermal random field acting on each spin, given by,

$$\begin{aligned} \mathbf{{B}}_\textrm{th,i} = \Gamma (t)\sqrt{\frac{2\alpha k_BT}{\gamma \mu _s\Delta t}}, \end{aligned}$$
(12)

where \(\Gamma (t)\) is obtained from a normal distribution. Consequently, the net local field acting on spin site i which includes the demagnetizing field and thermal field can be evaluated as follows,

$$\begin{aligned} {{\textbf{B}}_{\textrm{eff,}i}}= - \frac{1}{{\mu _s}^i}\frac{{\partial {\mathcal {H}}}}{{\partial {{{\textbf{S}}}_i}}} + {{\textbf{B}}_{\textrm{dip},i}}+ {\mathbf{{B}}_\textrm{th,i}}. \end{aligned}$$
(13)

We then apply the spin temperature rescaling method77 to account for the quantum thermodynamic effects, and recover a temperature dependent magnetization curve from our semi-classical simulation in very close agreement experimental measurements as shown later in Fig. 1. The dynamics of magnetization in the presence of STT can be determined by calculating the spin accumulation using Eq. (1) and then substituting it into the spin Hamiltonian \(\mathcal {H}\) from Eq. (4). Subsequently, the LLG equation in Eq. (8) can be integrated to study the behavior of the magnetization. The dynamical behavior of the magnetization and spin accumulation are determined using the atomistic VAMPIRE package32.

Temperature dependence of spin transport parameters

As detailed in spin accumulation model, the spin transport behavior within a magnetic structure is intrinsically associated with transport parameters. The spin-polarization parameters of conductivity and diffusion, spin accumulation at equilibrium and spin diffusion length determine the spin transport behavior25. At elevated temperature, is necessary to determine the temperature variation of transport parameters. This leads to the description of the thermal effects on spin transport behavior and subsequent performance of STT-based devices.

The temperature dependence of spin transport properties can be calculated by using the two-channel model through the spin-dependent conductivity33,34,78,79. The spin polarization parameters of conductivity (\({\beta }\)) and diffusion constant \((\beta ')\) at any finite temperature are expressed as follows:

$$\begin{aligned} {\beta } = \frac{\sigma _\uparrow -\sigma _\downarrow }{\sigma _\uparrow +\sigma _\downarrow } \end{aligned}$$
(14)

and

$$\begin{aligned} {\beta }^{\prime } = \frac{D_\uparrow -D_\downarrow }{D_\uparrow +D_\downarrow } =\frac{\beta -{\beta }^{\prime \prime }}{1-\beta {\beta }^{\prime \prime }}. \end{aligned}$$
(15)

where \(\sigma _{\uparrow (\downarrow )}\) and \(D_{\uparrow (\downarrow )}\) represent the conductivity and diffusion constant for the up(down) spin channel, respectively. \({\beta }^{\prime \prime }=\frac{{N_\uparrow }(E_F)-N_\downarrow (E_F)}{{N_\uparrow } (E_F)+N_\downarrow (E_F)}\) with \(N_{\uparrow }(E_F)\) and \(N_{\downarrow }(E_F)\) are density of states for up and down spins at Fermi energy level.

The spin-diffusion length which is an important length scale where electron spins diffuse between spin-flip scattering events can be considered in terms of the spin-dependent conductivity as follows,

$$\begin{aligned} \lambda _\textrm{sdl}= C(\sigma _\uparrow +\sigma _\downarrow ) \end{aligned}$$
(16)

where The empirical constant C can be derived by fitting the linear correlation between the spin diffusion length and conductivity through experimental data, expressed as, \({\lambda _{sdl}}=C\sigma\). Finally, based on the Elliot-Yafet (EY) mechanism, the variation of the diffusion constant with temperature can be determined using the following:

$$\begin{aligned} D_0=\frac{\lambda _{sdl}^2}{2\kappa (1-\beta \beta ^{\prime })\sigma }, \end{aligned}$$
(17)

with \(\kappa = m_e/ne^2 \epsilon\) , where \(\epsilon\) is the spin-flip probability occurring at momentum scattering events, and n is the conduction electron density.

The key spin-transport parameters explained earlier are directly evaluated using the spin-dependent conductivity, which can be represented in terms of the spin-dependent resistivity \((\rho _{\uparrow })\), \(\rho _{\downarrow })\) and spin mixing resistivity \((\rho _{\uparrow \downarrow })\), given by,

$$\begin{aligned} \sigma _{\uparrow (\downarrow )} = \frac{\rho _{\downarrow (\uparrow )}+2\rho _{\uparrow \downarrow }}{\rho _{\uparrow } \rho _{\downarrow }+\rho _{\uparrow \downarrow }(\rho _{\uparrow }+\rho _{\downarrow })}. \end{aligned}$$
(18)

when

$$\begin{aligned} \rho _j=\rho _{0j}+AT^2 \end{aligned}$$
(19)

where \(j=\uparrow ,\downarrow\) and \(\uparrow \downarrow\), \(\rho _{0j}\) is the low-temperature resistivity and A is the empirical coefficient obtained from the experiments.

Interface model

To achieve a realistic system, it is important to model the interface region resulting from the interdiffusion between atoms in the sputtering process since the interface characteristic plays an vital role in determining spatially dependent spin transport parameters. The spatial variation of the spin transport parameters across the interface can be determined from the concentration of the magnetic ions at any given position, obtained by applying Fick’s law22,23,24. At the interface where two different ion species (denoted as A and B) as shown in Fig. 10, the concentration of a specific ion (A) at any position x can be expressed as,

$$\begin{aligned} C_{A}(x) = \frac{N_{A}(x)}{[N_{A}(x)+N_{B}(x)] }, \end{aligned}$$
(20)

where \(N_{A,B}(x)\) is the number of local ions A or B at any position x.

Fig. 10
figure 10

The interface region containing two different ion species A and B.

Full size image

The diffusive interface is modeled by using Fick’s law. The system including diffusive interface is divided into thin layer with the thickness of \(t_F\). The diffusion of magnetic ion concentration for each layer i at position x and time t can be calculated by the below equation.

$$\begin{aligned} C_i(x,t;T) = \frac{t_F C_0}{\sqrt{\pi } x_0} \cdot exp \left[ - (x/x_0)^2 \right] \end{aligned}$$
(21)

where \(C_0\) is the initial concentration of ions, \(x_0=2\sqrt{D_{ion}t}\), with \(D_{ion}\) being the ion diffusion constant, which depends on the system temperature. These parameters characterize the width of the interface. The ion concentration profile can be obtained by using the superposition of the local concentrations:

$$\begin{aligned} C(x,t)=\sum _i C_i(x,t). \end{aligned}$$
(22)

Subsequently, the position of each atom at the interface is determined randomly based on the ion concentration. The diffusive interface is introduced to relax the usual simplifying assumption of atomically sharp interface, which has a significant effect on the solution of the spin accumulation22. Given the likelihood that diffuse interfaces give rise to large magnetization fluctuations the nature and width of the interface may play an important role.

The concentration of ion is calculated and then used to consider the spatial variation of the diffusive transport parameters, P(x), by using the linear combination of the bulk parameters weighted by the local concentrations as the following equation,

$$\begin{aligned} P(x) = P_A C_{A}(x) +P_{B}[1-C_{A}(x)], \end{aligned}$$
(23)

where \(P_{A, B}\) is the diffusive transport parameter of species A or B. The concentration of ion A at any position x from the interface (\(x=0\)) is represented by \(C_{A}(x)\). It is worth nothing that the width of the interface is defined by the parameter \(x_{1/2}\) representing the full width at half height where \(x_{1/2}=2x_0\) and \(C(x_0)/C(0)=0.5\).